TAO-DFT Study on the Electronic Properties of Diamond-Shaped Graphene Nanoflakes
Abstract
1. Introduction
2. Computational Details
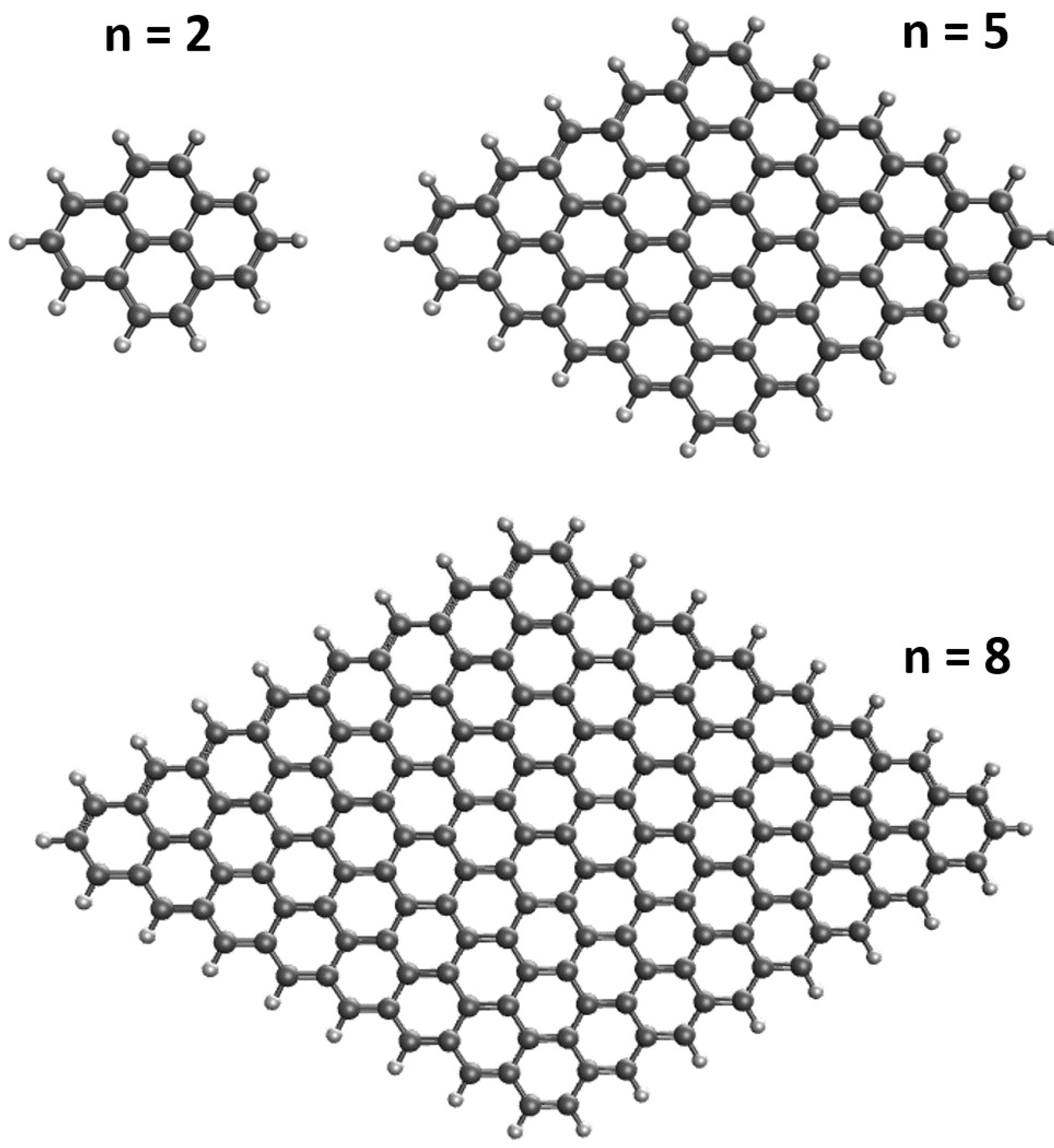
3. Results and Discussion
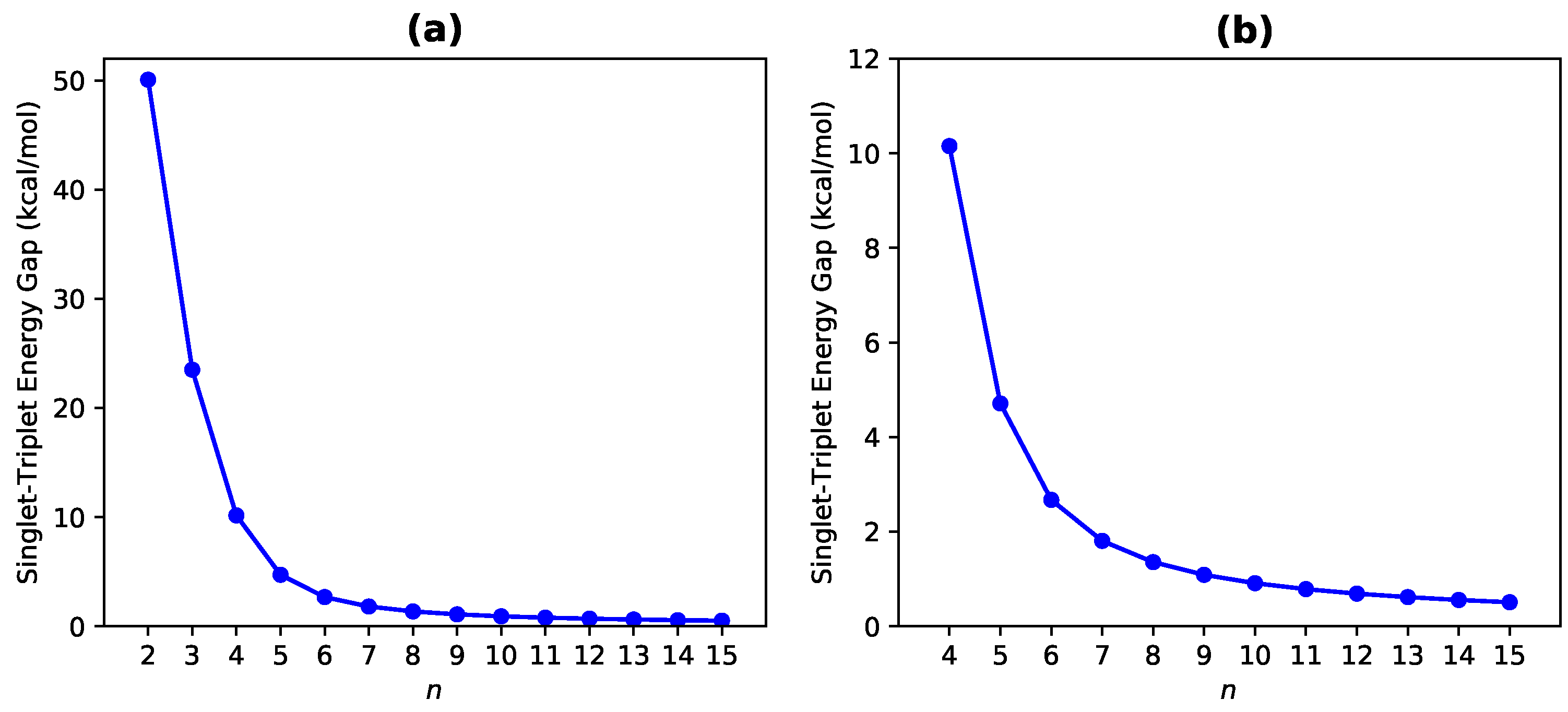
3.1. Singlet-Triplet Energy Gap
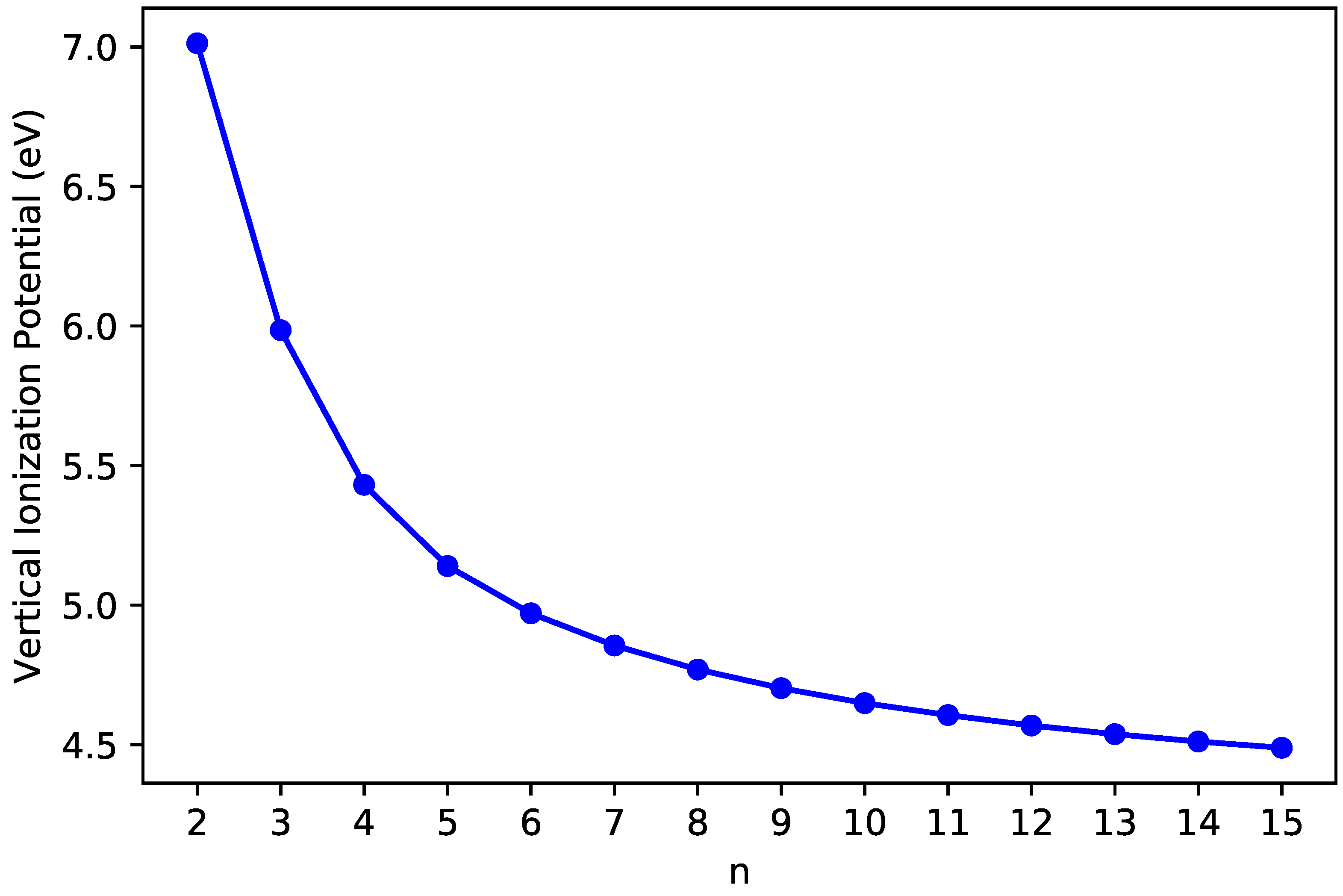
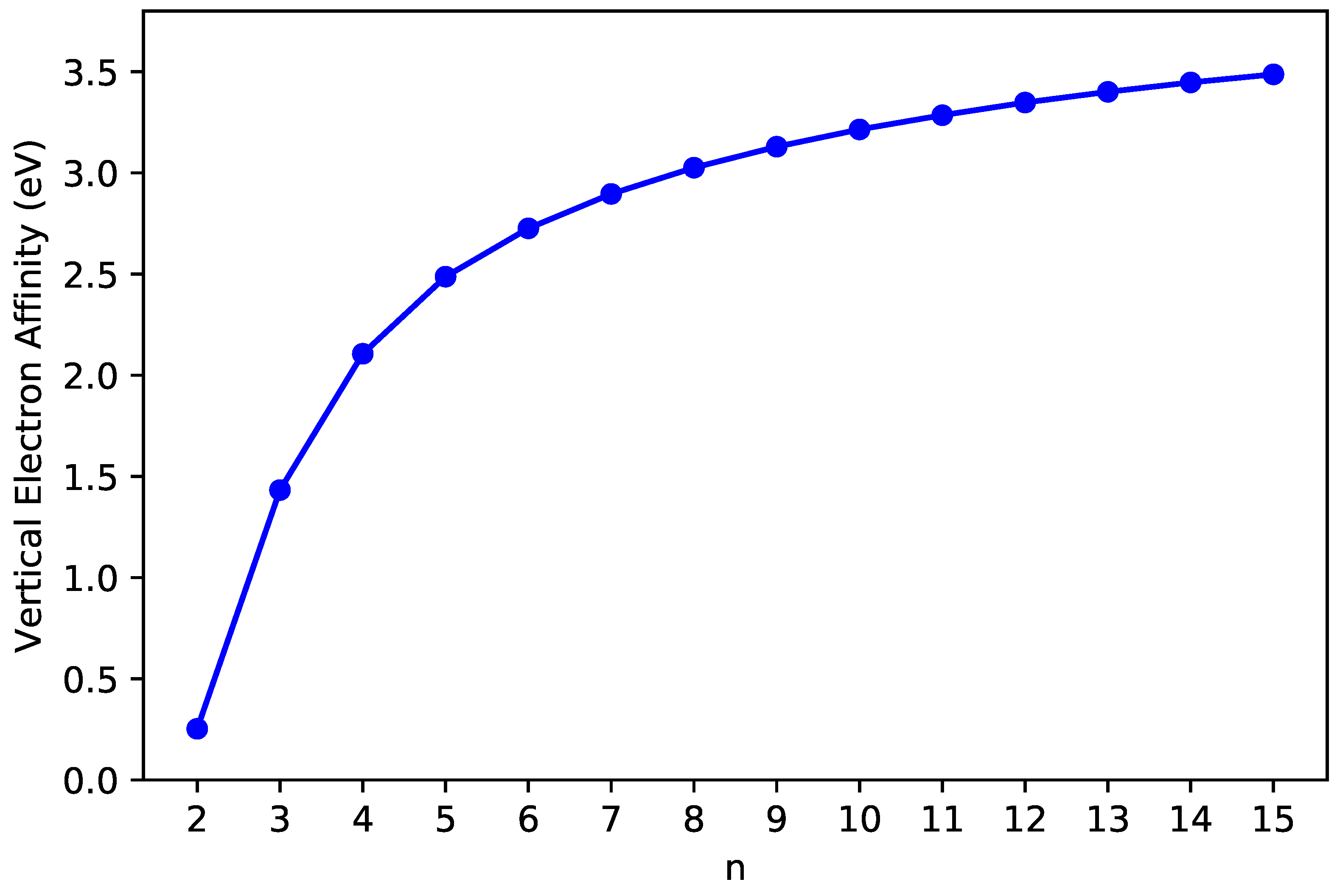
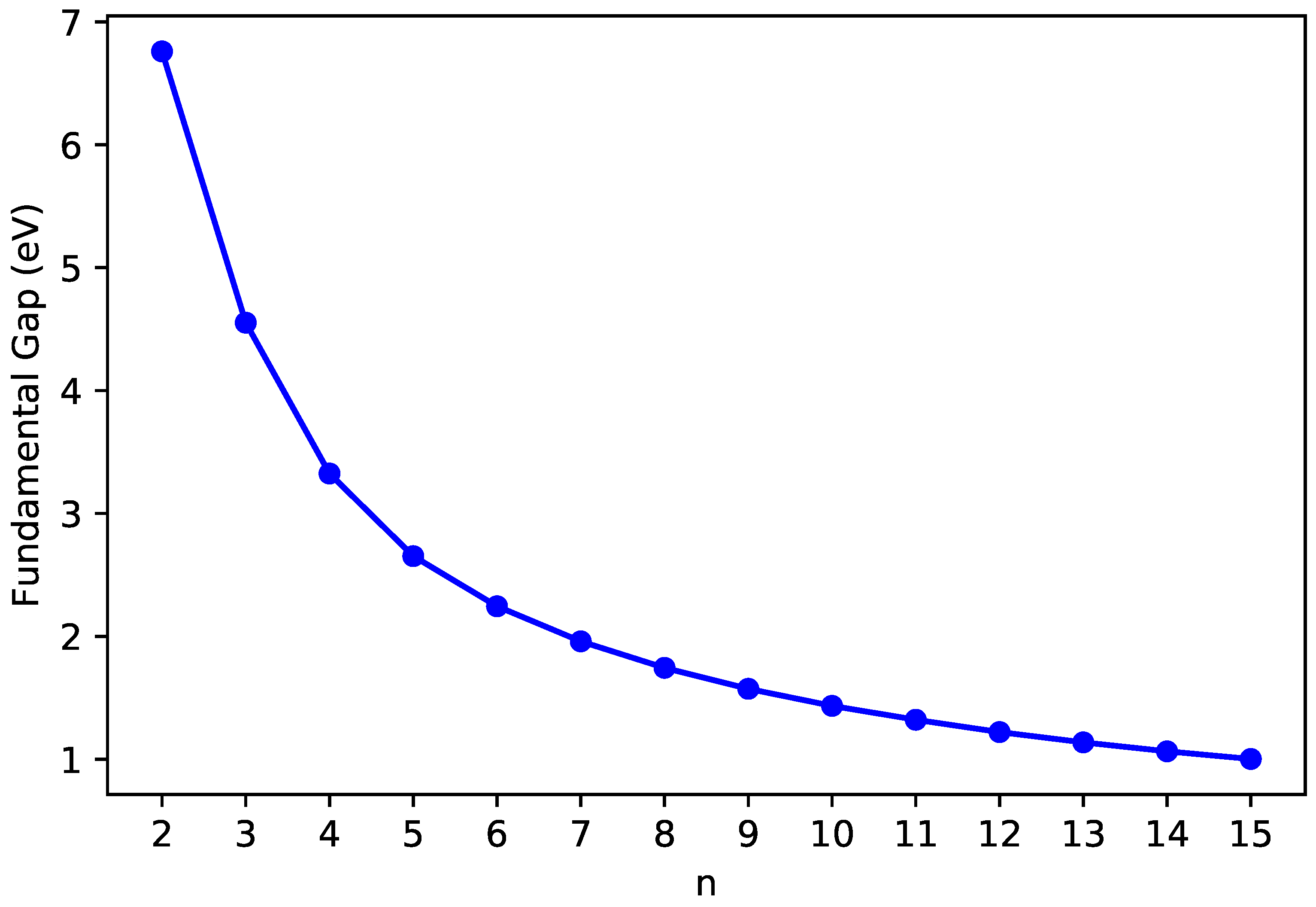
3.2. Vertical Ionization Potential/Electron Affinity as Well as Fundamental Gap
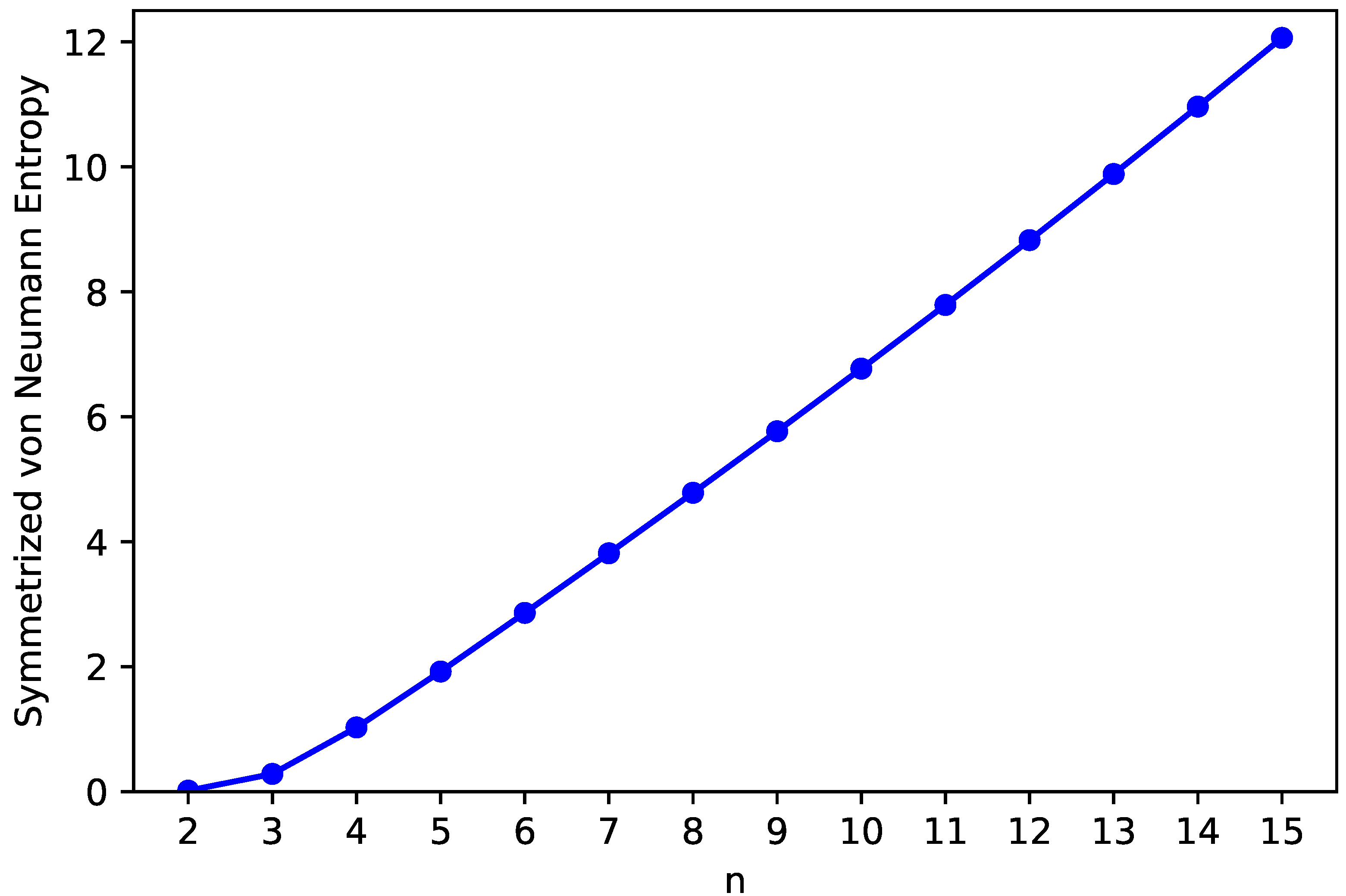
3.3. Symmetrized von Neumann Entropy
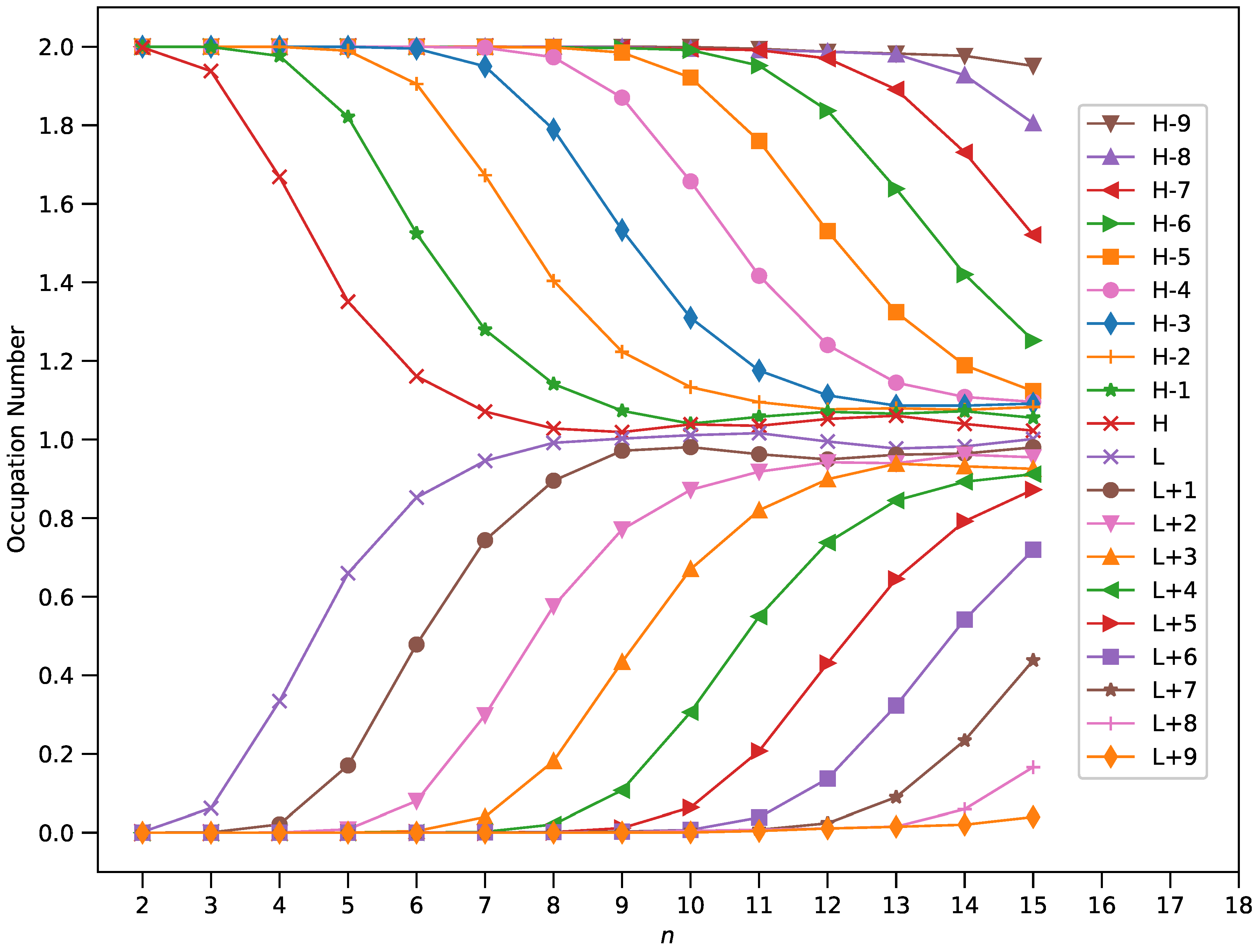
3.4. Active Orbital Occupation Numbers
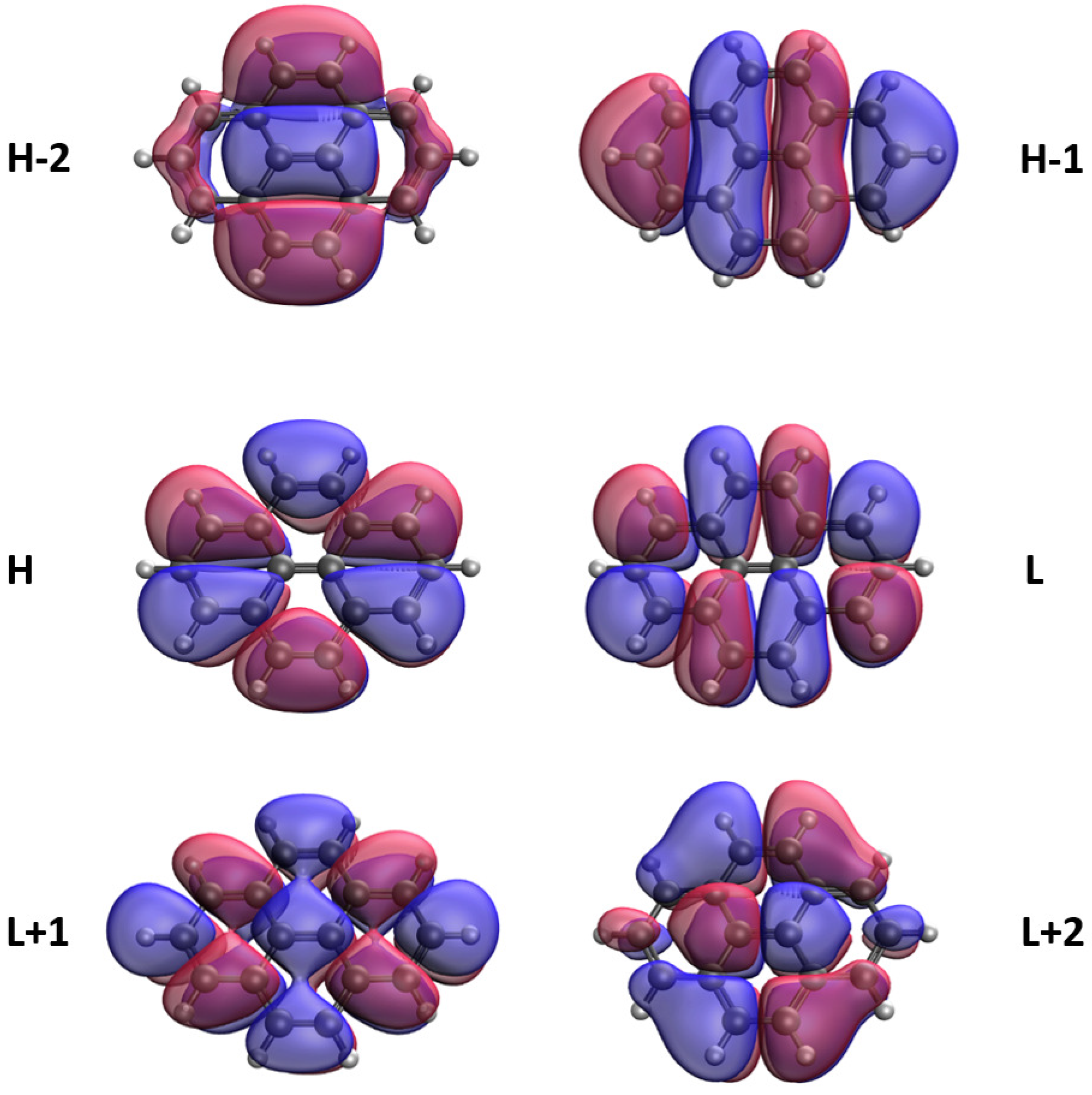
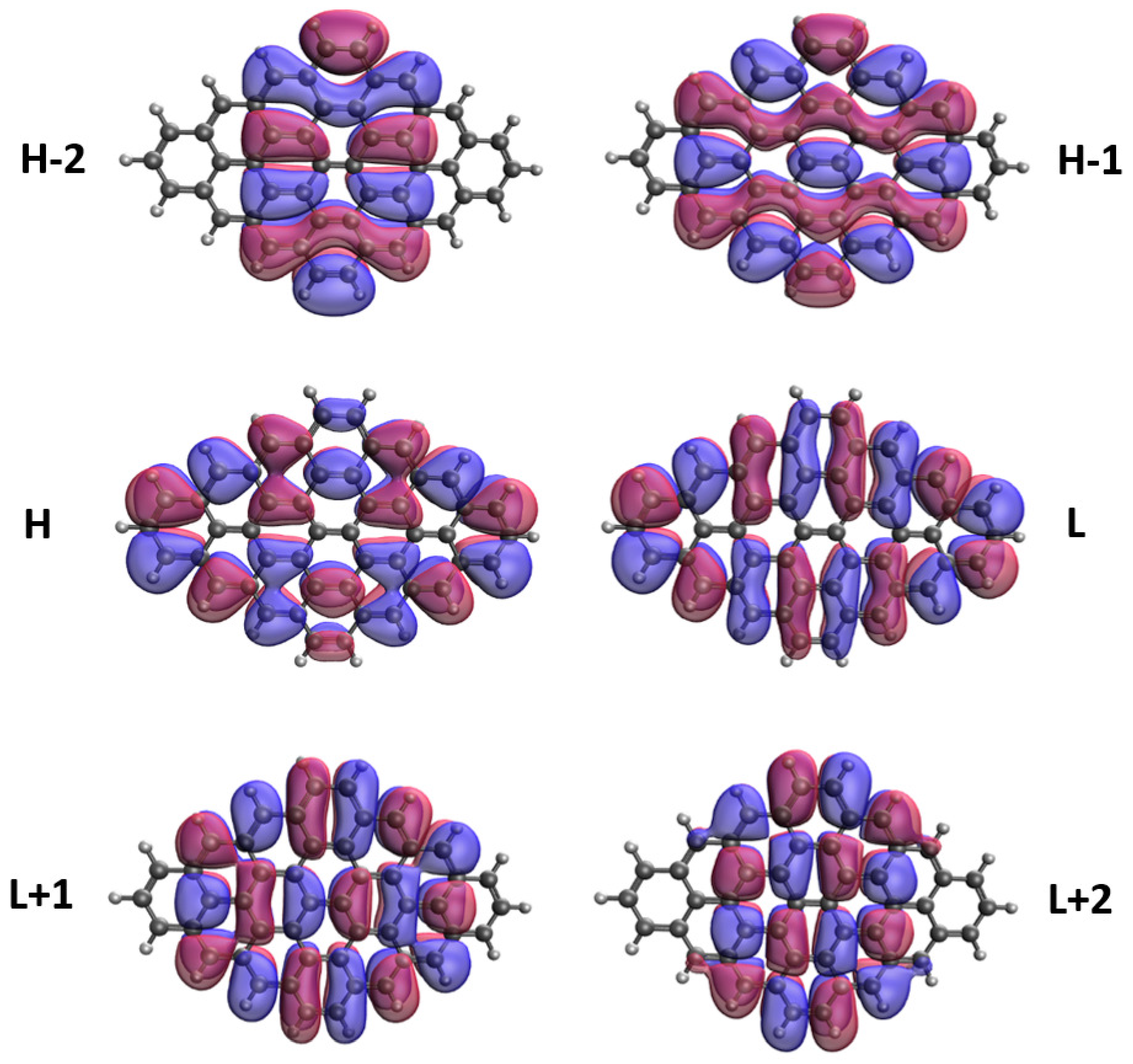
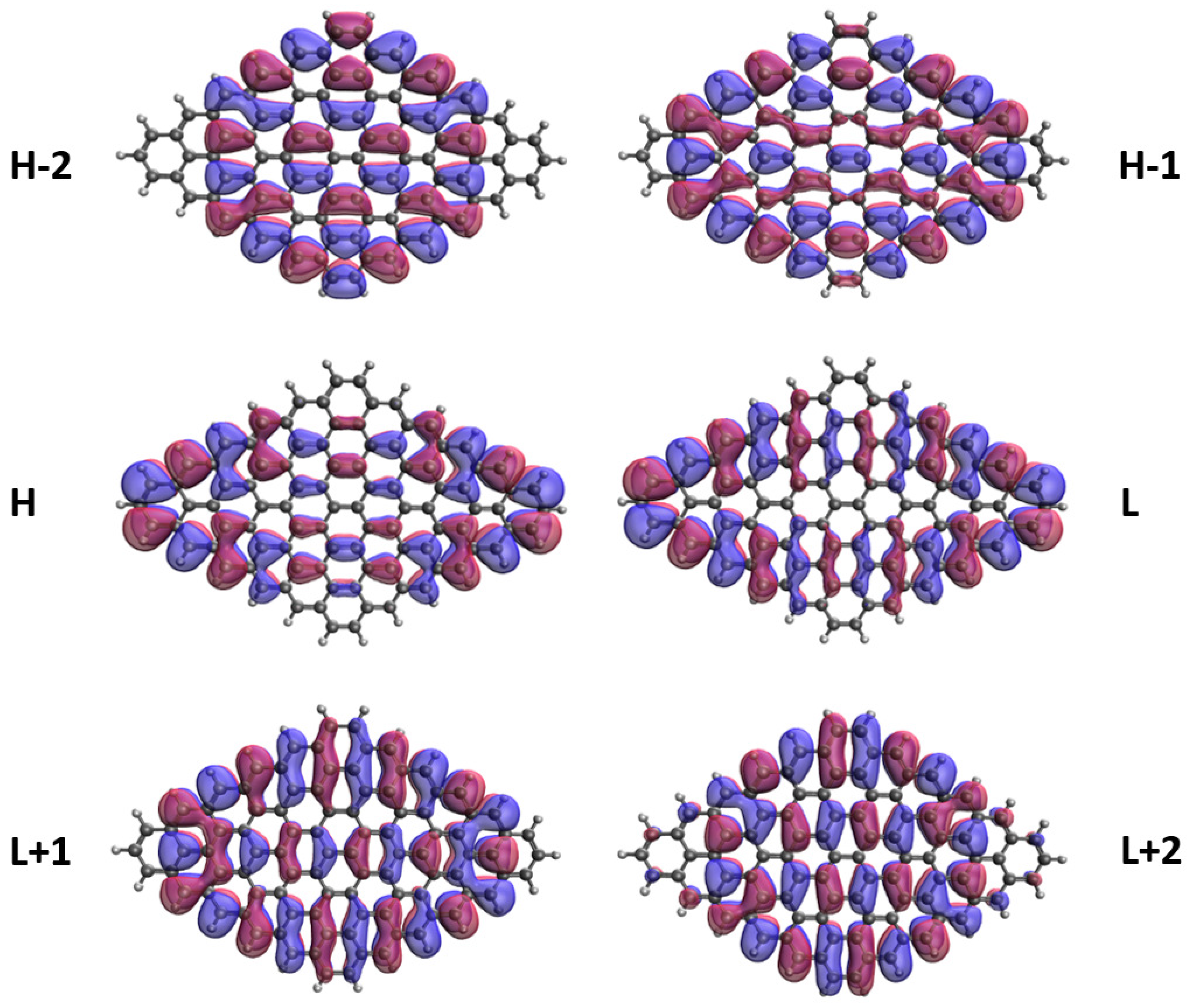
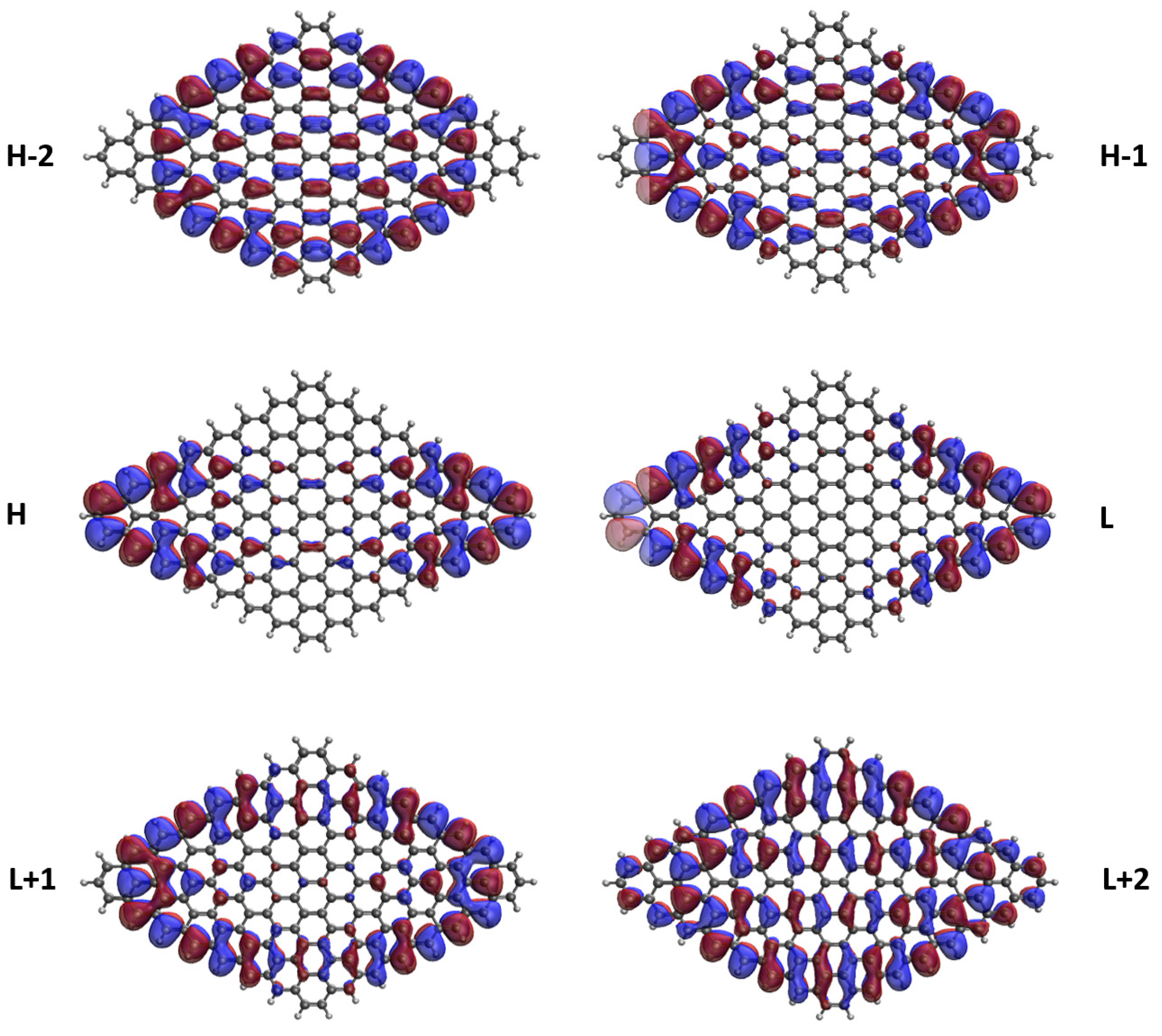
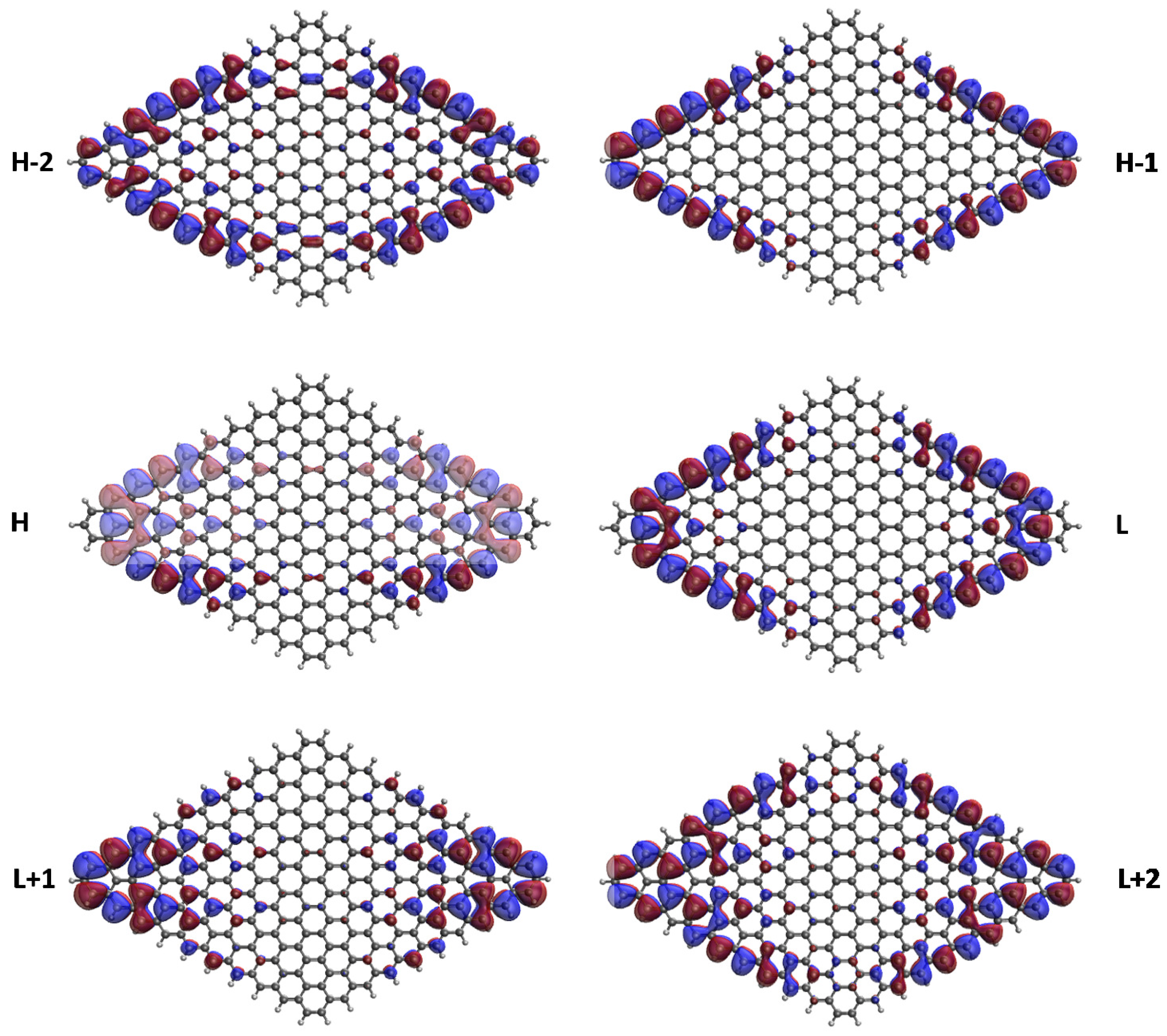
3.5. Real-Space Representation of Active Orbitals
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Owens, F.J. Electronic and magnetic properties of armchair and zigzag graphene nanoribbons. J. Chem. Phys. 2008, 128, 194701. [Google Scholar] [CrossRef]
- Lee, H.; Ihm, J.; Cohen, M.L.; Louie, S.G. Calcium-decorated graphene-based nanostructures for hydrogen storage. Nano Lett. 2010, 10, 793–798. [Google Scholar] [CrossRef]
- Wu, C.-S.; Chai, J.-D. Electronic properties of zigzag graphene nanoribbons studied by TAO-DFT. J. Chem. Theory Comput. 2015, 11, 2003–2011. [Google Scholar] [CrossRef]
- Yeh, C.-N.; Lee, P.-Y.; Chai, J.-D. Electronic and optical properties of the narrowest armchair graphene nanoribbons studied by density functional methods. Aust. J. Chem. 2016, 69, 960–968. [Google Scholar] [CrossRef]
- Mokkath, J.H. Optical response tuning in graphene nanoflakes: A computational study. Chem. Phys. Lett. 2018, 692, 102–105. [Google Scholar] [CrossRef]
- Georgakilas, V.; Vrettos, K.; Katomeri, K.; Kouloumpis, A.; Dimos, K.; Gournis, D.; Zboril, R. Highly dispersible disk-like graphene nanoflakes. Nanoscale 2015, 7, 15059–15064. [Google Scholar] [CrossRef]
- Nagai, H.; Nakano, M.; Yoneda, K.; Fukui, H.; Minami, T.; Bonness, S.; Kishi, R.; Takahashi, H.; Kubo, T.; Kamada, K.; et al. Theoretical study on third-order nonlinear optical properties in hexagonal graphene nanoflakes: Edge shape effect. Chem. Phys. Lett. 2009, 477, 355–359. [Google Scholar] [CrossRef]
- Hu, W.; Lin, L.; Yang, C.; Yang, J. Electronic structure and aromaticity of large-scale hexagonal graphene nanoflakes. J. Chem. Phys. 2014, 141, 214704. [Google Scholar] [CrossRef]
- Mansilla Wettstein, C.; Bonafé, F.P.; Oviedo, M.B.; Sánchez, C.G. Optical properties of graphene nanoflakes: Shape matters. J. Chem. Phys. 2016, 144, 224305. [Google Scholar] [CrossRef]
- Yeh, C.-N.; Wu, C.; Su, H.; Chai, J.-D. Electronic properties of the coronene series from thermally-assisted-occupation density functional theory. RSC Adv. 2018, 8, 34350–34358. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Qin, X.; Lin, L.; Kan, E.; Li, X.; Yang, C.; Yang, J. Room-temperature magnetism and tunable energy gaps in edge-passivated zigzag graphene quantum dots. npj 2D Mater. Appl. 2019, 3, 17. [Google Scholar] [CrossRef]
- Shi, H.; Barnard, A.S.; Snook, I.K. Modelling the role of size, edge structure and terminations on the electronic properties of trigonal graphene nanoflakes. Nanotechnology 2012, 23, 065707. [Google Scholar] [CrossRef]
- Deng, Q.; Chai, J.-D. Electronic properties of triangle-shaped graphene nanoflakes from TAO-DFT. ACS Omega 2019, 4, 14202–14210. [Google Scholar] [CrossRef]
- Ge, Y.; Ji, J.; Shen, Z.; Zhang, Q.; Jian, A.; Duan, Q.; Wang, C.; Jiang, J.; Zhang, W.; Sang, S. First principles study of magnetism induced by topological frustration of bowtie-shaped graphene nanoflake. Carbon 2018, 127, 432–436. [Google Scholar] [CrossRef]
- Wang, W.L.; Meng, S.; Kaxiras, E. Graphene nanoflakes with large spin. Nano Lett. 2008, 8, 241–245. [Google Scholar] [CrossRef]
- Kuc, A.; Heine, T.; Seifert, G. Structural and electronic properties of graphene nanoflakes. Phys. Rev. B 2010, 81, 085430. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Q.; Sun, Q.; Jena, P. Intrinsic ferromagnetism in two-dimensional carbon structures: Triangular graphene nanoflakes linked by carbon chains. Phys. Rev. B 2011, 84, 081402(R). [Google Scholar] [CrossRef]
- Singh, S.K.; Neek-Amal, M.; Peeters, F.M. Electronic properties of graphene nano-flakes: Energy gap, permanent dipole, termination effect, and Raman spectroscopy. J. Chem. Phys. 2014, 140, 074304. [Google Scholar] [CrossRef]
- Wohner, N.; Lam, P.; Sattler, K. Energetic stability of graphene nanoflakes and nanocones. Carbon 2014, 67, 721–735. [Google Scholar] [CrossRef]
- Fernandez, M.; Shi, H.; Barnard, A.S. Geometrical features can predict electronic properties of graphene nanoflakes. Carbon 2016, 103, 142–150. [Google Scholar] [CrossRef]
- Wang, W.L.; Yazyev, O.V.; Meng, S.; Kaxiras, E. Topological frustration in graphene nanoflakes: Magnetic order and spin logic devices. Phys. Rev. Lett. 2009, 102, 157201. [Google Scholar] [CrossRef] [PubMed]
- Trauzettel, B.; Bulaev, D.V.; Loss, D.; Burkard, G. Spin qubits in graphene quantum dots. Nat. Phys. 2007, 3, 192–196. [Google Scholar] [CrossRef]
- Droth, M.; Burkard, G. Spintronics with graphene quantum dots. Phys. Status Solidi RRL 2016, 10, 75–90. [Google Scholar] [CrossRef]
- Pavliček, N.; Mistry, A.; Majzik, Z.; Moll, N.; Meyer, G.; Fox, D.J.; Gross, L. Synthesis and characterization of triangulene. Nat. Nanotechnol. 2017, 12, 308–311. [Google Scholar] [CrossRef]
- Zhao, L.; Kaiser, R.I.; Xu, B.; Ablikim, U.; Ahmed, M.; Joshi, D.; Veber, G.; Fischer, F.R.; Mebel, A.M. Pyrene synthesis in circumstellar envelopes and its role in the formation of 2D nanostructures. Nat. Astron. 2018, 2, 413–419. [Google Scholar] [CrossRef]
- Förster, T.; Kasper, K. Ein Konzentrationsumschlag der Fluoreszenz. Z. Physik. Chem. (Frankfurt) 1954, 1, 275–277. [Google Scholar] [CrossRef]
- Brus, L. Size, dimensionality, and strong electron correlation in nanoscience. Acc. Chem. Res. 2014, 47, 2951–2959. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for density functional theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef] [PubMed]
- Andersson, K.; Malmqvist, P.-Å.; Roos, B.O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218. [Google Scholar] [CrossRef]
- Hachmann, J.; Dorando, J.J.; Aviles, M.; Chan, G.K.L. The radical character of the acenes: A density matrix renormalization group study. J. Chem. Phys. 2007, 127, 134309. [Google Scholar] [CrossRef] [PubMed]
- Gidofalvi, G.; Mazziotti, D.A. Active-space two-electron reduced-density-matrix method: Complete active-space calculations without diagonalization of the N-electron hamiltonian. J. Chem. Phys. 2008, 129, 134108. [Google Scholar] [CrossRef]
- Gryn’ova, G.; Coote, M.L.; Corminboeuf, C. Theory and practice of uncommon molecular electronic configurations. WIREs Comput. Mol. Sci. 2015, 5, 440–459. [Google Scholar] [CrossRef]
- Fosso-Tande, J.; Nguyen, T.-S.; Gidofalvi, G.; DePrince, A.E., III. Large-scale variational two-electron reduced-density-matrix-driven complete active space self-consistent field methods. J. Chem. Theory Comput. 2016, 12, 2260–2271. [Google Scholar] [CrossRef]
- Battaglia, S.; Faginas-Lago, N.; Andrae, D.; Evangelisti, S.; Leininger, T. Increasing radical character of large [n]cyclacenes unveiled by wave function theory. J. Phys. Chem. A 2017, 121, 3746–3756. [Google Scholar] [CrossRef]
- Mullinax, J.W.; Maradzike, E.; Koulias, L.N.; Mostafanejad, M.; Epifanovsky, E.; Gidofalvi, G.; DePrince, A.E., III. Heterogeneous CPU + GPU algorithm for variational two-electron reduced-density matrix-driven complete active-space self-consistent field theory. J. Chem. Theory Comput. 2019, 15, 6164–6178. [Google Scholar] [CrossRef]
- Chai, J.-D. Density functional theory with fractional orbital occupations. J. Chem. Phys. 2012, 136, 154104. [Google Scholar] [CrossRef]
- Chai, J.-D. Thermally-assisted-occupation density functional theory with generalized-gradient approximations. J. Chem. Phys. 2014, 140, 18A521. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D. Role of exact exchange in thermally-assisted-occupation density functional theory: A proposal of new hybrid schemes. J. Chem. Phys. 2017, 146, 044102. [Google Scholar] [CrossRef] [PubMed]
- Xuan, F.; Chai, J.-D.; Su, H. Local density approximation for the short-range exchange free energy functional. ACS Omega 2019, 4, 7675–7683. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-Y.; Hui, K.; Chung, J.-H.; Chai, J.-D. Self-consistent determination of the fictitious temperature in thermally-assisted-occupation density functional theory. RSC Adv. 2017, 7, 50496–50507. [Google Scholar] [CrossRef]
- Yeh, C.-N.; Chai, J.-D. Role of Kekulé and non-Kekulé structures in the radical character of alternant polycyclic aromatic hydrocarbons: A TAO-DFT study. Sci. Rep. 2016, 6, 30562. [Google Scholar] [CrossRef]
- Seenithurai, S.; Chai, J.-D. Effect of Li adsorption on the electronic and hydrogen storage properties of acenes: A dispersion-corrected TAO-DFT study. Sci. Rep. 2016, 6, 33081. [Google Scholar] [CrossRef]
- Wu, C.-S.; Lee, P.-Y.; Chai, J.-D. Electronic properties of cyclacenes from TAO-DFT. Sci. Rep. 2016, 6, 37249. [Google Scholar] [CrossRef]
- Seenithurai, S.; Chai, J.-D. Effect of Li termination on the electronic and hydrogen storage properties of linear carbon chains: A TAO-DFT study. Sci. Rep. 2017, 7, 4966. [Google Scholar] [CrossRef]
- Seenithurai, S.; Chai, J.-D. Electronic and hydrogen storage properties of Li-terminated linear boron chains studied by TAO-DFT. Sci. Rep. 2018, 8, 13538. [Google Scholar] [CrossRef]
- Chung, J.-H.; Chai, J.-D. Electronic properties of Möbius cyclacenes studied by thermally-assisted-occupation density functional theory. Sci. Rep. 2019, 9, 2907. [Google Scholar] [CrossRef]
- Seenithurai, S.; Chai, J.-D. Electronic properties of linear and cyclic boron nanoribbons from thermally-assisted-occupation density functional theory. Sci. Rep. 2019, 9, 12139. [Google Scholar] [CrossRef] [PubMed]
- Hanson-Heine, M.W.D.; Rogers, D.M.; Woodward, S.; Hirst, J.D. Dewar benzenoids discovered in carbon nanobelts. J. Phys. Chem. Lett. 2020, 11, 3769–3772. [Google Scholar] [CrossRef] [PubMed]
- Manassir, M.; Pakiari, A.H. Total non-Lewis structures: An application to predict the stability and reactivity of linear and angular polyacenes. J. Mol. Graph. Model. 2020. [Google Scholar] [CrossRef]
- Hanson-Heine, M.W.D. Static correlation in vibrational frequencies studied using thermally-assisted-occupation density functional theory. Chem. Phys. Lett. 2020, 739, 137012. [Google Scholar] [CrossRef]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
- Su, Y.; Wang, X.; Wang, L.; Zhang, Z.; Wang, X.; Song, Y.; Power, P.P. Thermally controlling the singlet-triplet energy gap of a diradical in the solid state. Chem. Sci. 2016, 7, 6514–6518. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Wu, Z.; Xie, G.; Zhong, C.; Zhu, Z.; Cong, H.; Ma, D.; Yang, C. Achieving a balance between small singlet-triplet energy splitting and high fluorescence radiative rate in a quinoxaline-based orange-red thermally activated delayed fluorescence emitter. Chem. Commun. 2016, 52, 11012–11015. [Google Scholar] [CrossRef] [PubMed]
- Rajamalli, P.; Senthilkumar, N.; Gandeepan, P.; Ren-Wu, C.-C.; Lin, H.W.; Cheng, C.H. A method for reducing the singlet-triplet energy gaps of TADF materials for improving the blue OLED efficiency. ACS Appl. Mater. Interfaces 2016, 8, 27026–27034. [Google Scholar] [CrossRef]
- Rajamalli, P.; Senthilkumar, N.; Gandeepan, P.; Huang, P.-Y.; Huang, M.-J.; Ren-Wu, C.-Z.; Yang, C.-Y.; Chiu, M.-J.; Chu, L.-K.; Lin, H.-W.; et al. A new molecular design based on thermally activated delayed fluorescence for highly efficient organic light emitting diodes. J. Am. Chem. Soc. 2016, 138, 628–634. [Google Scholar] [CrossRef]
- Rivero, P.; Jiménez-Hoyos, C.A.; Scuseria, G.E. Entanglement and polyradical character of polycyclic aromatic hydrocarbons predicted by projected Hartree-Fock theory. J. Phys. Chem. B 2013, 117, 12750–12758. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.-J.; Seenithurai, S.; Chai, J.-D. TAO-DFT Study on the Electronic Properties of Diamond-Shaped Graphene Nanoflakes. Nanomaterials 2020, 10, 1236. https://doi.org/10.3390/nano10061236
Huang H-J, Seenithurai S, Chai J-D. TAO-DFT Study on the Electronic Properties of Diamond-Shaped Graphene Nanoflakes. Nanomaterials. 2020; 10(6):1236. https://doi.org/10.3390/nano10061236
Chicago/Turabian StyleHuang, Hong-Jui, Sonai Seenithurai, and Jeng-Da Chai. 2020. "TAO-DFT Study on the Electronic Properties of Diamond-Shaped Graphene Nanoflakes" Nanomaterials 10, no. 6: 1236. https://doi.org/10.3390/nano10061236
APA StyleHuang, H.-J., Seenithurai, S., & Chai, J.-D. (2020). TAO-DFT Study on the Electronic Properties of Diamond-Shaped Graphene Nanoflakes. Nanomaterials, 10(6), 1236. https://doi.org/10.3390/nano10061236






