Filtering Characteristics of Phonon Polaritons Waves Based on Dielectric-h-BN-Dielectric Structure in Mid-Infrared Band
Abstract
1. Introduction
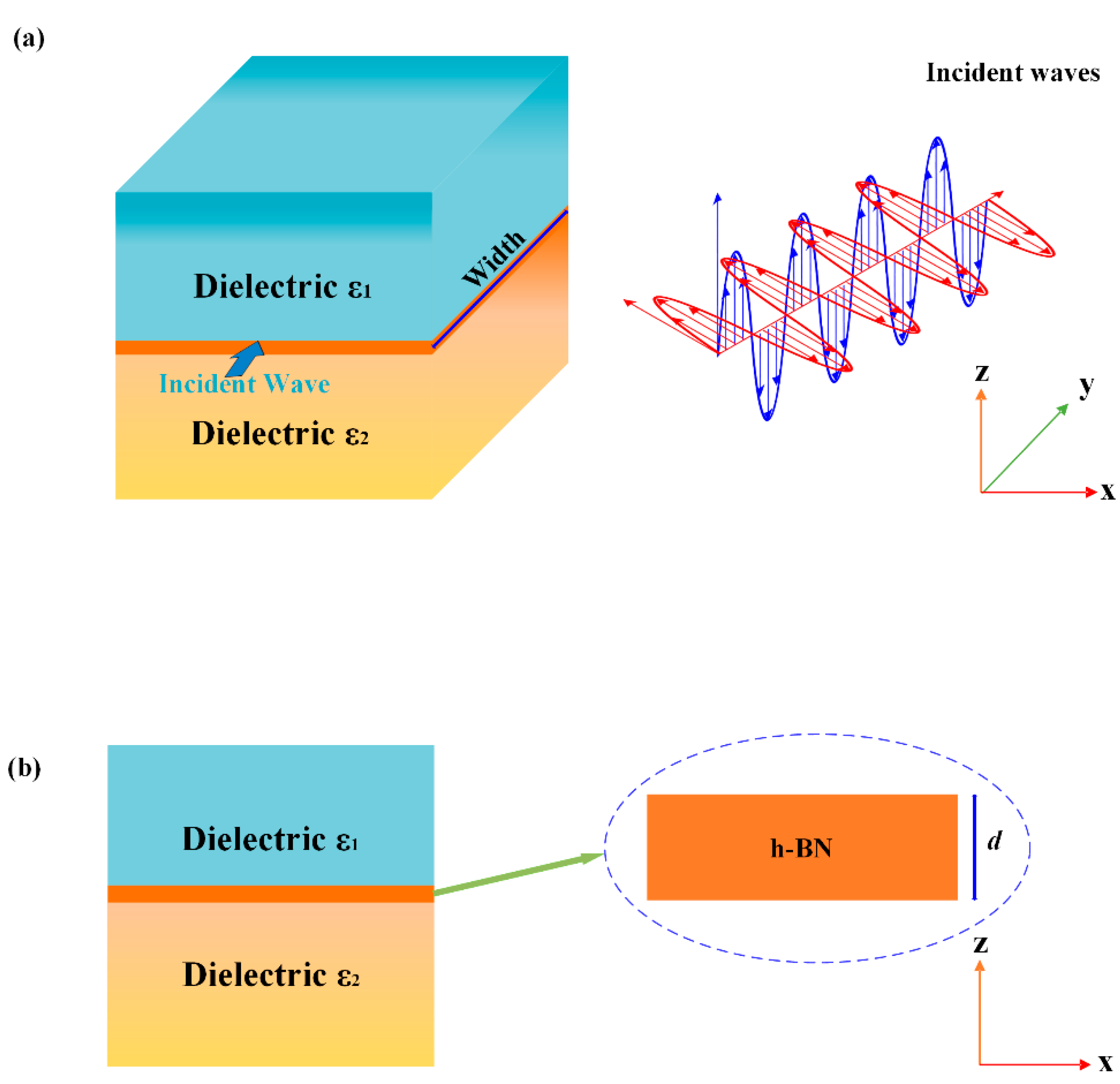
2. Structural Design and Methodology
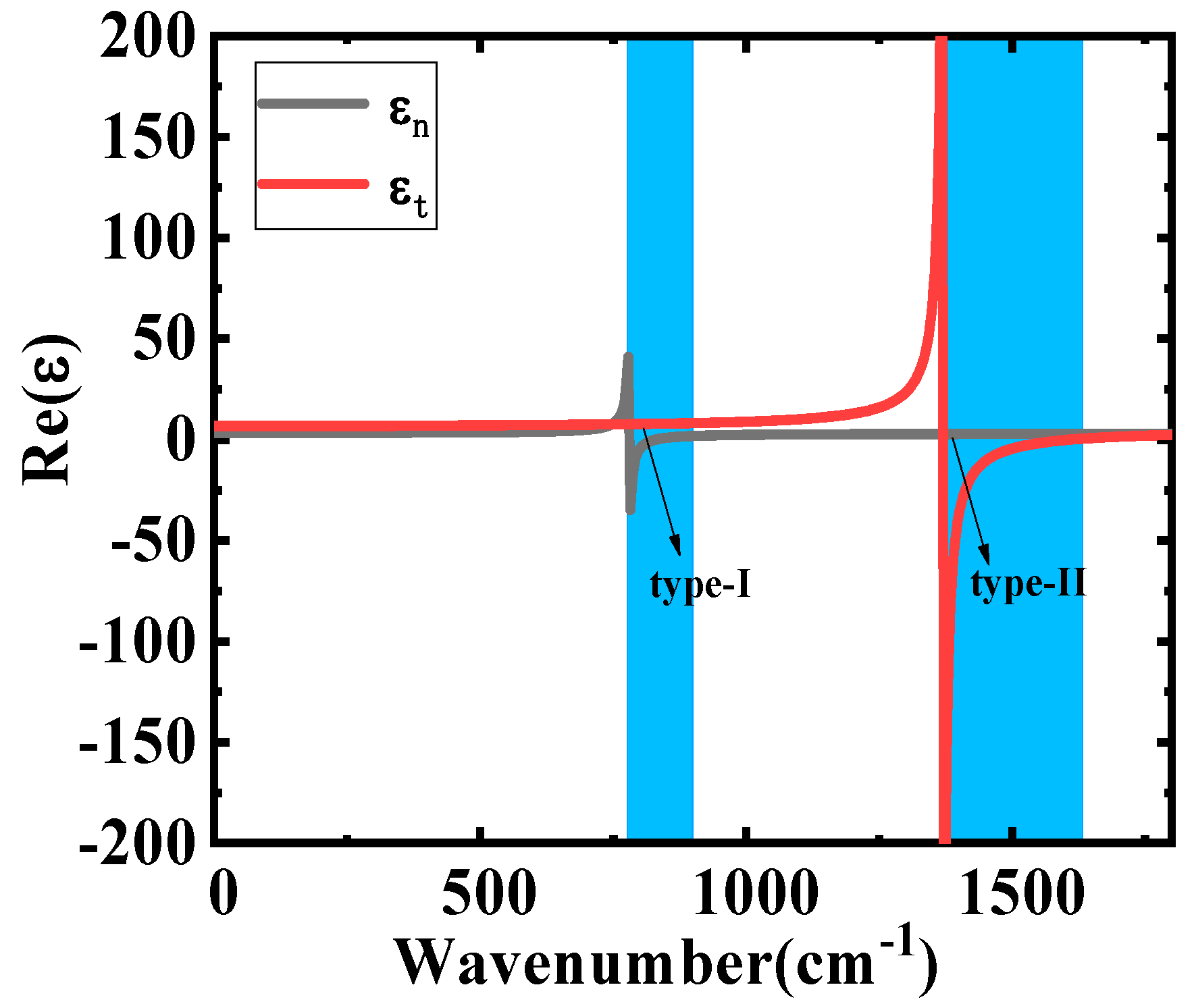
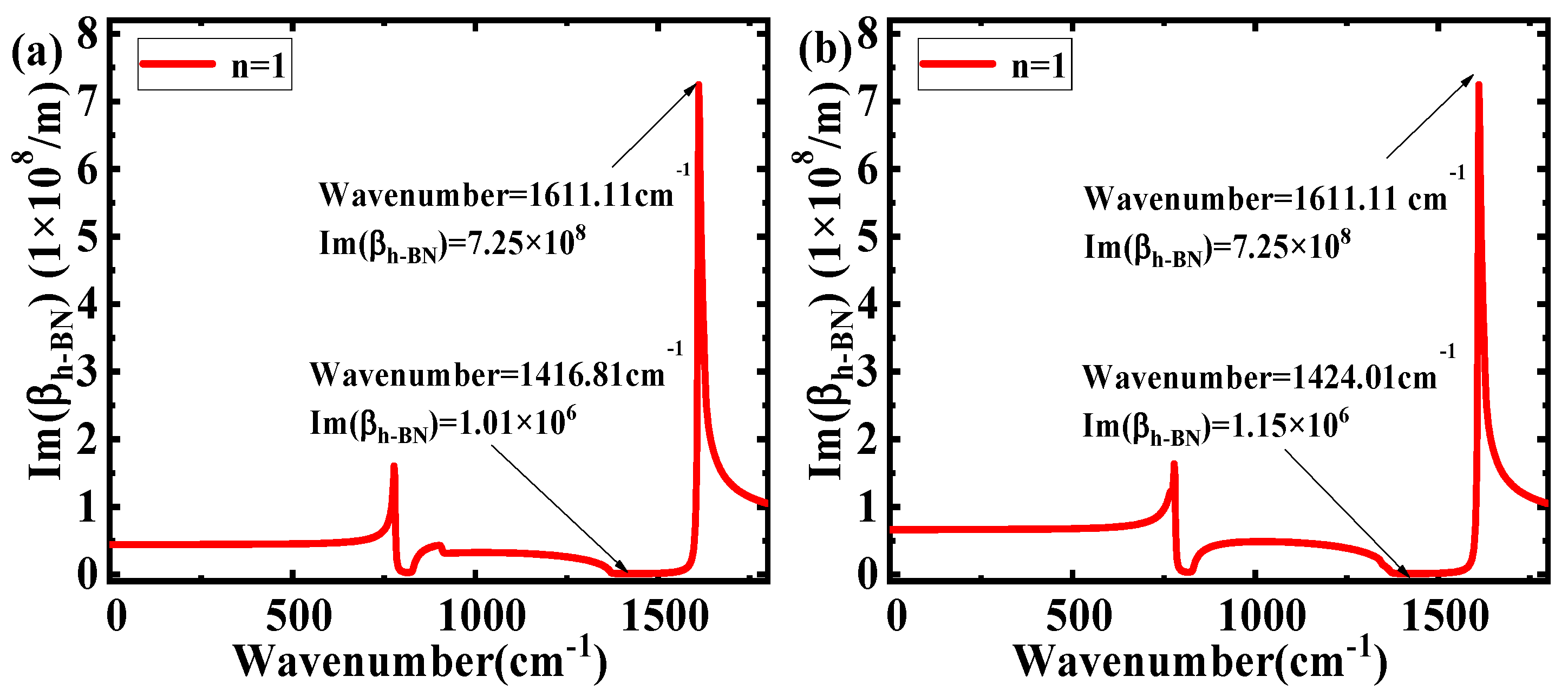
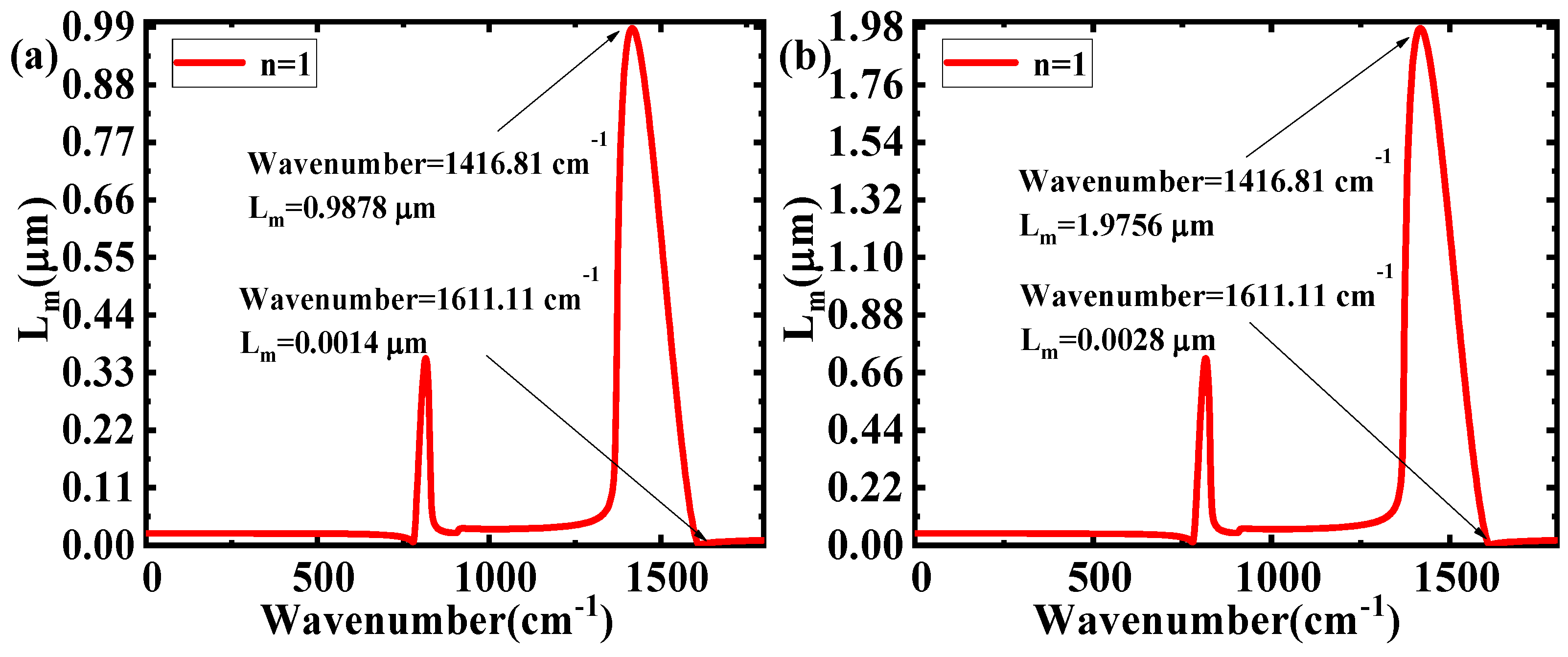
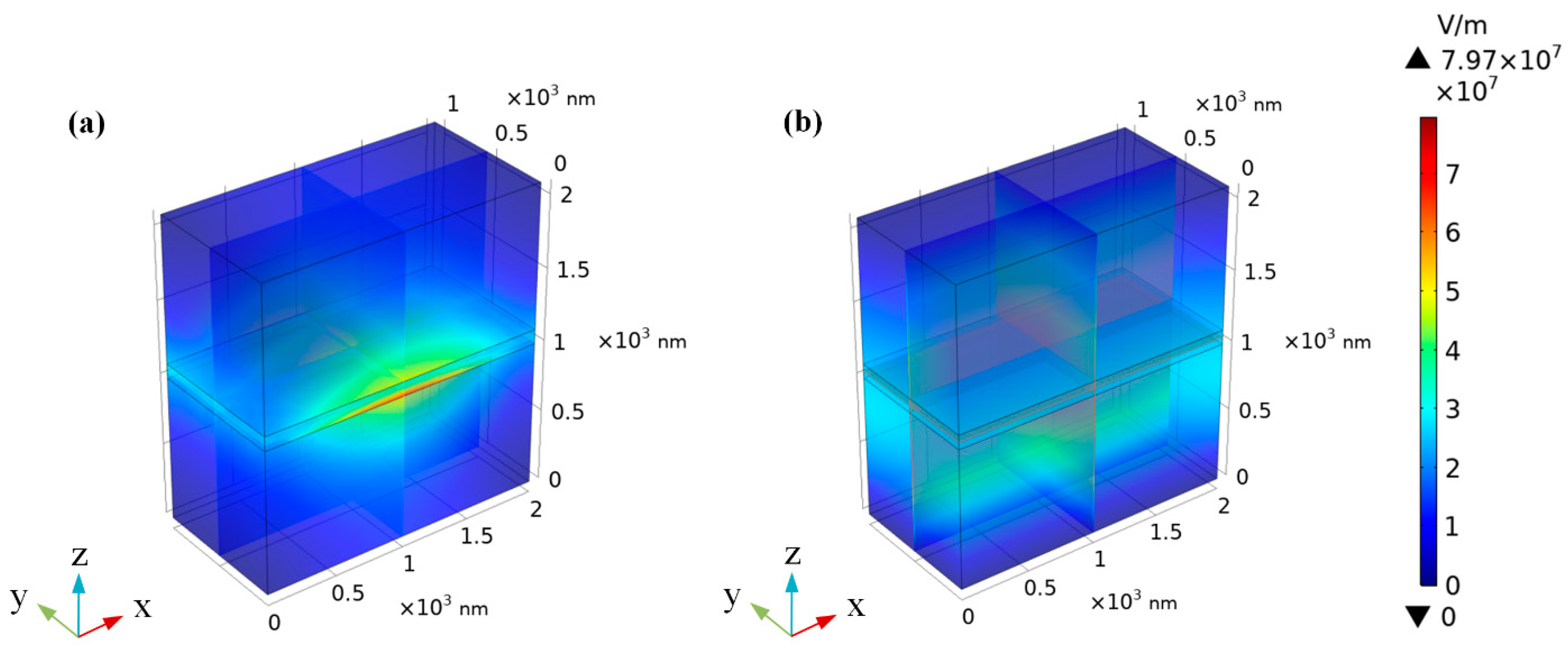
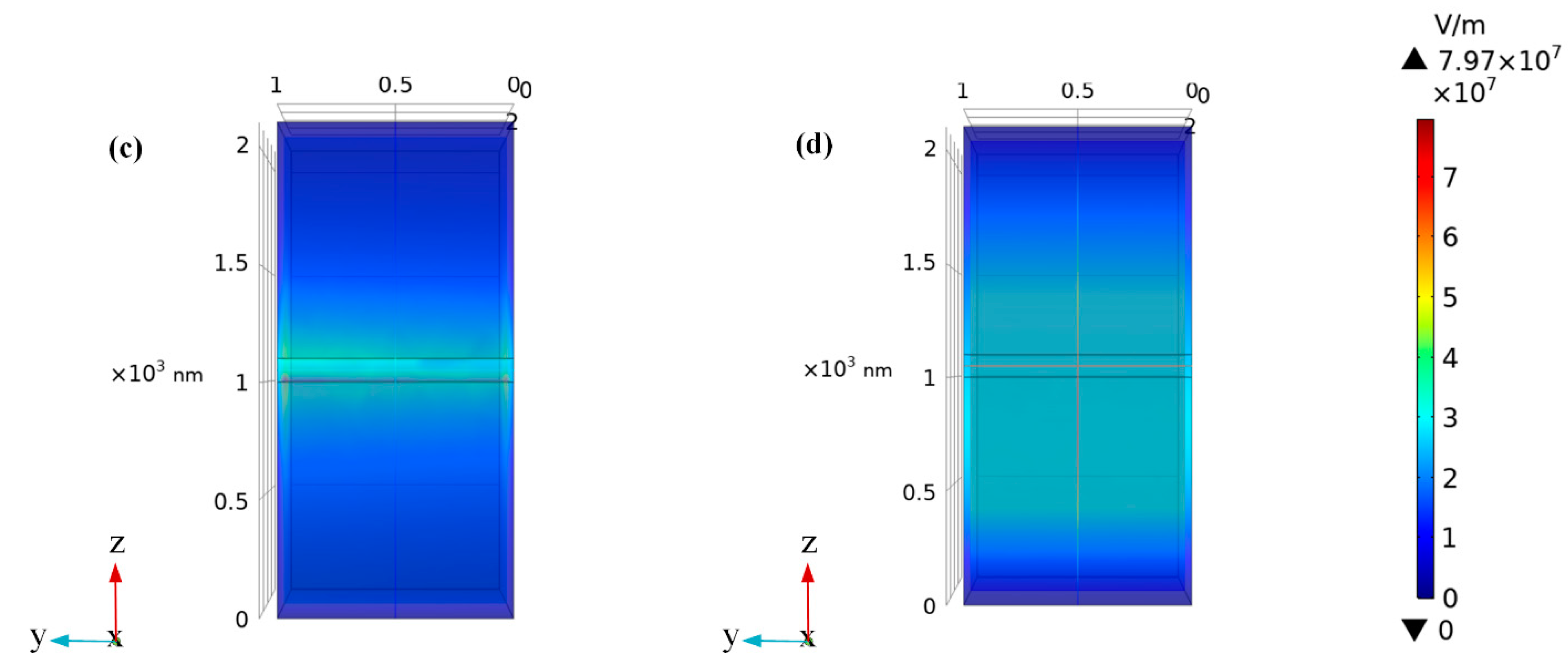
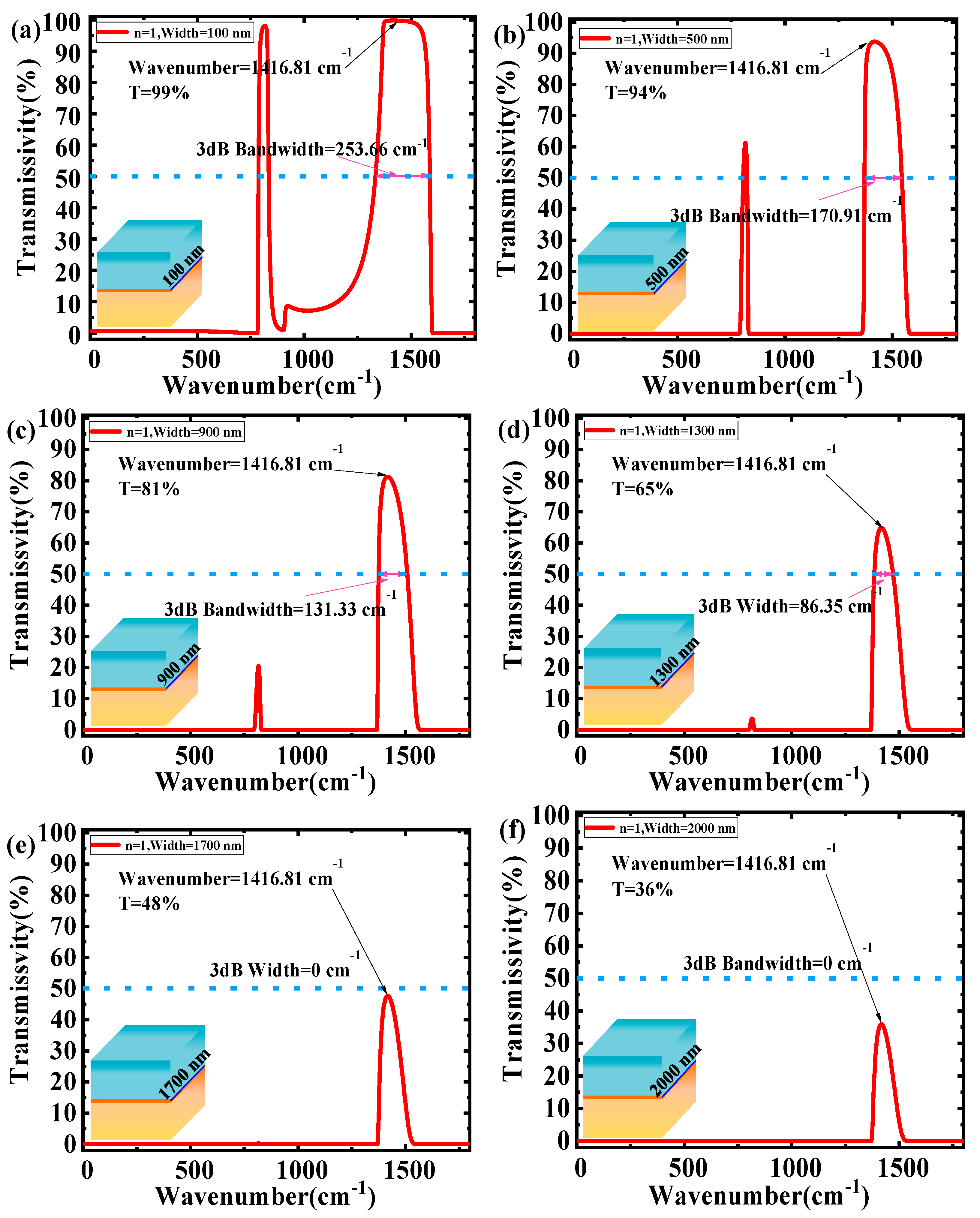
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gonçalves, P.A.D.; Bertelsen, L.P.; Xiao, S.; Mortensen, N.A. Plasmon-exciton polaritons in two-dimensional semiconductor/metal interfaces. Phys. Rev. B 2018, 97, 041402. [Google Scholar] [CrossRef]
- Berini, P. Long-range surface plasmon polaritons. Adv. Opt. Photon 2009, 1, 484–588. [Google Scholar] [CrossRef]
- Basov, D.N.; Fogler, M.M.; De Abajo, F.J.G. Polaritons in van der Waals materials. Science 2016, 354, aag1992. [Google Scholar] [CrossRef] [PubMed]
- Foteinopoulou, S.; Devarapu, G.C.R.; Subramania, G.S.; Krishna, S.; Wasserman, D. Phonon-polaritonics: Enabling powerful capabilities for infrared photonics. Nanophotonics 2019, 8, 2129–2175. [Google Scholar] [CrossRef]
- Ambrosio, A.; Tamagnone, M.; Chaudhary, K.; Jauregui, L.A.; Kim, P.; Wilson, W.L.; Capasso, F. Selective excitation and imaging of ultraslow phonon polaritons in thin hexagonal boron nitride crystals. Light. Sci. Appl. 2018, 7, 27. [Google Scholar] [CrossRef] [PubMed]
- Low, T.; Chaves, A.; Caldwell, J.D.; Kumar, A.; Fang, N.X.; Avouris, P.; Heinz, T.F.; Guinea, F.; Martin-Moreno, L.; Koppens, F. Polaritons in layered two-dimensional materials. Nat. Mater. 2016, 16, 182–194. [Google Scholar] [CrossRef]
- Li, J.; Gan, R.; Guo, Q.; Liu, H.; Xu, J.; Yi, F. Tailoring optical responses of infrared plasmonic metamaterial absorbers by optical phonons. Opt. Express 2018, 26, 16769–16781. [Google Scholar] [CrossRef]
- Liu, P.Q.; Reno, J.L.; Brener, I. Quenching of Infrared-Active Optical Phonons in Nanolayers of Crystalline Materials by Graphene Surface Plasmons. ACS Photon 2018, 5, 2706–2711. [Google Scholar] [CrossRef]
- Dai, S.; Tymchenko, M.; Yang, Y.; Ma, Q.; Pita-Vidal, M.; Watanabe, K.; Taniguchi, T.; Jarillo-Herrero, P.; Fogler, M.M.; Alu, A.; et al. Manipulation and Steering of Hyperbolic Surface Polaritons in Hexagonal Boron Nitride. Adv. Mater. 2018, 30, e1706358. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, P.; Lin, X.; Li, E.; Wang, Z.; Zhang, B.; Chen, H. Type-I hyperbolic metasurfaces for highly-squeezed designer polaritons with negative group velocity. Nat. Commun. 2019, 10, 2002. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, M.; Zhang, S.R.; Xiong, J.; Wang, J.M.; Zhang, D.H.; He, F.M.; Li, Z.P. Permittivity and its temperature dependence in hexagonal structure BN dominated by the local electric field. Chin. Phys. B 2012, 21, 77701. [Google Scholar] [CrossRef]
- Nemilentsau, A.; Stauber, T.; Gómez-Santos, G.; Luskin, M.; Low, T. Switchable and unidirectional plasmonic beacons in hyperbolic 2D materials. arXiv 2018, arXiv:1808.01012. [Google Scholar]
- Li, P.; Dolado, I.; Alfaro-Mozaz, F.J.; Casanova, F.; Hueso, L.E.; Liu, S.; Edgar, J.H.; Nikitin, A.Y.; Vélez, S.; Hillenbrand, R. Infrared hyperbolic metasurface based on nanostructured van der Waals materials. Science 2018, 359, 892–896. [Google Scholar] [CrossRef] [PubMed]
- Brown, L.V.; Davanço, M.; Sun, Z.; Kretinin, A.V.; Chen, Y.; Matson, J.R.; Vurgaftman, I.; Sharac, N.; Giles, A.J.; Fogler, M.M.; et al. Nanoscale Mapping and Spectroscopy of Nonradiative Hyperbolic Modes in Hexagonal Boron Nitride Nanostructures. Nano Lett. 2018, 18, 1628–1636. [Google Scholar] [CrossRef]
- Qu, S.; Liu, H.; Dong, L.; Wu, L.; Ma, C.; Wang, S. Graphene-Hexagonal Boron Nitride Heterostructure as a Tunable Phonon–Plasmon Coupling System. Crystals 2017, 7, 49. [Google Scholar] [CrossRef]
- Dai, S.; Ma, Q.; Liu, M.K.; Andersen, T.; Fei, Z.; Goldflam, M.D.; Wagner, M.; Watanabe, K.; Taniguchi, T.; Thiemens, M.; et al. Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial. Nat. Nanotechnol. 2015, 10, 682–686. [Google Scholar] [CrossRef]
- Jia, Y.; Zhao, H.; Guo, Q.; Wang, X.; Wang, H.; Xia, F. Tunable Plasmon–Phonon Polaritons in Layered Graphene–Hexagonal Boron Nitride Heterostructures. ACS Photon 2015, 2, 907–912. [Google Scholar] [CrossRef]
- Woessner, A.; Lundeberg, M.B.; Gao, Y.; Principi, A.; Alonso-González, P.; Carrega, M.; Watanabe, K.; Taniguchi, T.; Vignale, G.; Polini, M.; et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat. Mater. 2014, 14, 421–425. [Google Scholar] [CrossRef]
- Hajian, H.; Ghobadi, A.; Serebryannikov, A.E.; Butun, B.; VandenBosch, G.A.E.; Ozbay, E. VO2-hBN-graphene-based bi-functional metamaterial for mid-infrared bi-tunable asymmetric transmission and nearly perfect resonant absorption. J. Opt. Soc. Am. B 2019, 36, 1607–1615. [Google Scholar] [CrossRef]
- Guo, X.; Hu, H.; Hu, D.; Liao, B.; Chen, K.; Liu, L.; Zhu, X.; Yang, X.; Dai, Q. High-efficiency modulation of coupling between different polaritons in an in-plane graphene/hexagonal boron nitride heterostructure. Nanoscale 2019, 11, 2703–2709. [Google Scholar] [CrossRef]
- Maier, M.; Nemilentsau, A.; Low, T.; Luskin, M. Ultracompact Amplitude Modulator by Coupling Hyperbolic Polaritons over a Graphene-Covered Gap. ACS Photon 2017, 5, 544–551. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Tian, C.; Xu, Q.; Zhang, X.; Li, Y.; Zhang, X.; Han, J.; Zhang, W. Terahertz spoof surface-plasmon-polariton subwavelength waveguide. Photon Res. 2017, 6, 18–23. [Google Scholar] [CrossRef]
- Li, P.; Lewin, M.; Kretinin, A.V.; Caldwell, J.D.; Novoselov, K.S.; Taniguchi, T.; Watanabe, K.; Gaussmann, F.; Taubner, T. Hyperbolic phonon-polaritons in boron nitride for near-field optical imaging and focusing. Nat. Commun. 2015, 6, 7507. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Fei, Z.; Ma, Q.; Rodin, A.; Wagner, M.; McLeod, A.S.; Liu, M.K.; Gannett, W.; Regan, W.; Watanabe, K.; et al. Tunable Phonon Polaritons in Atomically Thin van der Waals Crystals of Boron Nitride. Science 2014, 343, 1125–1129. [Google Scholar] [CrossRef]
- Zhu, B.; Wu, B.; Gao, Y.; Li, H.; Ren, G.; Jian, S. Nanofocusing of hybrid plasmons-phonons-polaritons in a graphene-hexagonal boron nitride heterostructure. Opt. Lett. 2016, 41, 4578. [Google Scholar] [CrossRef]
- Caldwell, J.D.; Kretinin, A.V.; Chen, Y.; Giannini, V.; Fogler, M.M.; Francescato, Y.; Ellis, C.T.; Tischler, J.G.; Woods, C.R.; Giles, A.J.; et al. Sub-diffractional volume-confined polaritons in the natural hyperbolic material hexagonal boron nitride. Nat. Commun. 2014, 5, 5221. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, M.; Wang, S.; Liu, Z.; Wang, Y.; Han, T.; Liu, H. Filtering Characteristics of Phonon Polaritons Waves Based on Dielectric-h-BN-Dielectric Structure in Mid-Infrared Band. Nanomaterials 2020, 10, 878. https://doi.org/10.3390/nano10050878
Cai M, Wang S, Liu Z, Wang Y, Han T, Liu H. Filtering Characteristics of Phonon Polaritons Waves Based on Dielectric-h-BN-Dielectric Structure in Mid-Infrared Band. Nanomaterials. 2020; 10(5):878. https://doi.org/10.3390/nano10050878
Chicago/Turabian StyleCai, Ming, Shulong Wang, Zhihong Liu, Yindi Wang, Tao Han, and Hongxia Liu. 2020. "Filtering Characteristics of Phonon Polaritons Waves Based on Dielectric-h-BN-Dielectric Structure in Mid-Infrared Band" Nanomaterials 10, no. 5: 878. https://doi.org/10.3390/nano10050878
APA StyleCai, M., Wang, S., Liu, Z., Wang, Y., Han, T., & Liu, H. (2020). Filtering Characteristics of Phonon Polaritons Waves Based on Dielectric-h-BN-Dielectric Structure in Mid-Infrared Band. Nanomaterials, 10(5), 878. https://doi.org/10.3390/nano10050878






