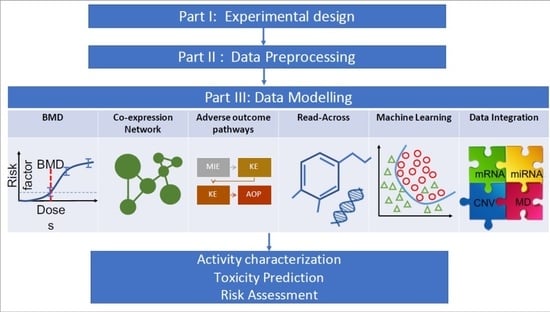
Transcriptomics in Toxicogenomics, Part III: Data Modelling for Risk Assessment
Abstract
1. Introduction
2. Benchmark Dose Modelling
3. Gene Co-Expression Network Analysis
Algorithms to Infer Gene Co-Expression Networks
4. Read-Across
5. Adverse Outcome Pathways
6. Machine Learning in Toxicogenomics
6.1. Dimensionality Reduction and Feature Selection
Stability and Applicability Domain
6.2. Clustering
6.3. Classification
6.4. Regression
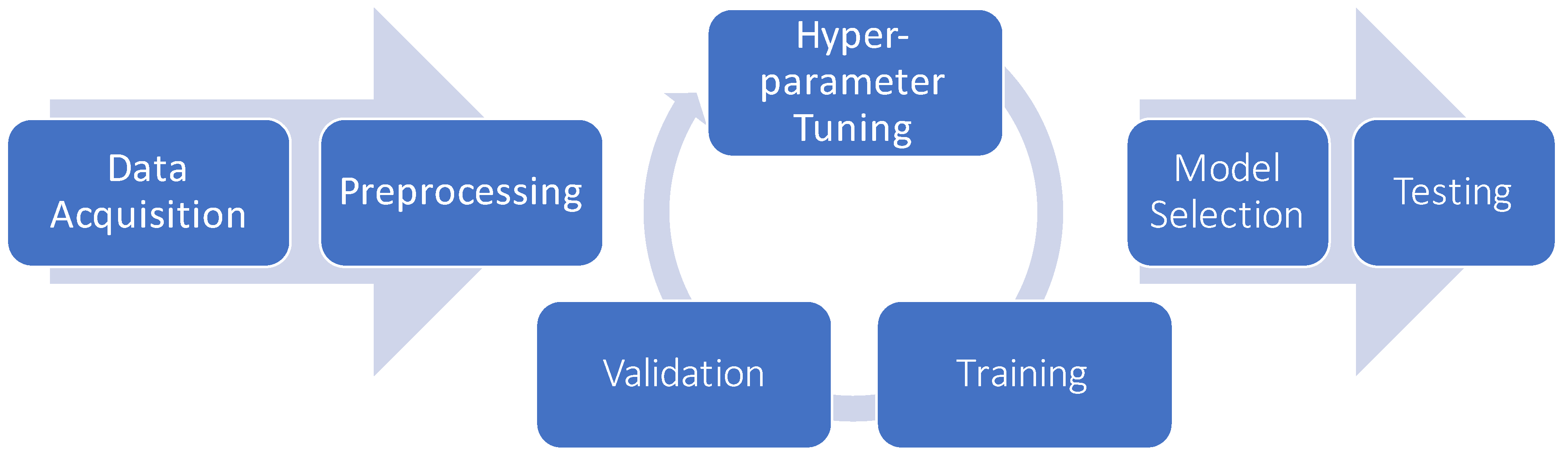
6.5. Model Selection and Hyper-Parameter Optimization
6.5.1. Deep Learning
6.6. Data Integration for Multi-Omics Analyses
Integrate Transcriptomic Datasets with Molecular Descriptors for Hybrid Qsar Models
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | applicability domain |
| AI | artificial intelligence |
| AIC | Akaike criterion |
| ANNs | artificial neural networks |
| AOP | adverse outcome pathways |
| ATHENA | Analysis Tool for Heritable and Environmental Network Associations |
| BMD | benchmark dose |
| BMDL | benchmark dose lower bound |
| BMDU | benchmark dose upper bound |
| BMR | benchmark regulation |
| CART | classification and regression trees |
| CFS | correlation feature selection |
| CNN | convolutional neural network |
| CNV | copy number variation |
| CMAP | Connectivity Map |
| DAGs | directed acyclic graphs |
| dGCs | donkey granulosa cells |
| DL | deep learning |
| DT | decision trees |
| EFSA | European Food Safety Authority |
| FN | false negative |
| FNN | feedforward neural network |
| FP | false positive |
| GCN | graph convolutional network |
| GENN | grammatical evolution neural network |
| GFA | group factor analysis |
| GO | gene ontology |
| GTEx | Genotype-Tissue Expression |
| KE | key events |
| K-NN | k-nearest neighbors |
| IC50 | half maximal inhibitory concentration |
| L1000 | Library of Integrated Network-Based Cellular Signatures 1000 |
| LDA | linear discriminant analysis |
| LDrA | Latent Dirichlet Allocation |
| LR | logistic regression |
| MDS | multidimensional scaling |
| MF | matrix factorization |
| MI | mutual information |
| ML | machine learning |
| MOA | mechanism of action |
| MOE | molecular initiating event |
| MVDA | multi-view data analysis |
| miRNA | microRNA |
| MTF | bayesian multi-tensor factorization |
| NAM | novell assessment methods |
| NB | naive bayes |
| OECD | Organisation for Economic Co-operation and Development |
| Open TG-GATEs | Open Toxicogenomics Project-Genomics Assisted Toxicity Evaluation System |
| PCA | principal component analysis |
| PLSDA | partial least squares discriminant analysis |
| POD | point of departure |
| PPI | protein-protein interactions |
| PTGS | Predictive Toxicogenomics Space |
| QSAR | quantitative structure activity relationship |
| ReLU | Rectified Linear Unit |
| RF | random forest |
| RIVM | Rijksinstituut voor Volksgezondheid en Milieu institute |
| RNA-Seq | RNA sequencing |
| SNF | similarity network fusion |
| SNP | single nucleotide polymorphism |
| SVM | support vector machines |
| tSNE | t-distributed stochastic neighbour embedding |
| TGx | Toxicogenomics |
| TN | true negative |
| TP | true positive |
| UMAP | Uniform Manifold Approximation and Projection |
References
- Grimm, D. The dose can make the poison: Lessons learned from adverse in vivo toxicities caused by RNAi overexpression. Silence 2011, 2, 8. [Google Scholar] [CrossRef] [PubMed]
- Kinaret, P.; Marwah, V.; Fortino, V.; Ilves, M.; Wolff, H.; Ruokolainen, L.; Auvinen, P.; Savolainen, K.; Alenius, H.; Greco, D. Network analysis reveals similar transcriptomic responses to intrinsic properties of carbon nanomaterials in vitro and in vivo. ACS Nano 2017, 11, 3786–3796. [Google Scholar] [CrossRef] [PubMed]
- Scala, G.; Kinaret, P.; Marwah, V.; Sund, J.; Fortino, V.; Greco, D. Multi-omics analysis of ten carbon nanomaterials effects highlights cell type specific patterns of molecular regulation and adaptation. NanoImpact 2018, 11, 99–108. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.F.; Pennings, J.L.; Piersma, A.H. A review of toxicogenomic approaches in developmental toxicology. In Developmental Toxicology; Springer: Berlin, Germany, 2012; pp. 347–371. [Google Scholar]
- Alexander-Dann, B.; Pruteanu, L.L.; Oerton, E.; Sharma, N.; Berindan-Neagoe, I.; Módos, D.; Bender, A. Developments in toxicogenomics: Understanding and predicting compound-induced toxicity from gene expression data. Mol. Omics 2018, 14, 218–236. [Google Scholar] [CrossRef]
- Eichner, J.; Wrzodek, C.; Römer, M.; Ellinger-Ziegelbauer, H.; Zell, A. Evaluation of toxicogenomics approaches for assessing the risk of nongenotoxic carcinogenicity in rat liver. PLoS ONE 2014, 9. [Google Scholar] [CrossRef]
- Waters, M.D.; Fostel, J.M. Toxicogenomics and systems toxicology: Aims and prospects. Nat. Rev. Genet. 2004, 5, 936–948. [Google Scholar] [CrossRef]
- Iorio, F.; Bosotti, R.; Scacheri, E.; Belcastro, V.; Mithbaokar, P.; Ferriero, R.; Murino, L.; Tagliaferri, R.; Brunetti-Pierri, N.; Isacchi, A.; et al. Discovery of drug mode of action and drug repositioning from transcriptional responses. Proc. Natl. Acad. Sci. USA 2010, 107, 14621–14626. [Google Scholar] [CrossRef]
- Napolitano, F.; Zhao, Y.; Moreira, V.M.; Tagliaferri, R.; Kere, J.; D’Amato, M.; Greco, D. Drug repositioning: A machine-learning approach through data integration. J. Cheminformatics 2013, 5, 30. [Google Scholar] [CrossRef]
- Waring, J.F.; Jolly, R.A.; Ciurlionis, R.; Lum, P.Y.; Praestgaard, J.T.; Morfitt, D.C.; Buratto, B.; Roberts, C.; Schadt, E.; Ulrich, R.G. Clustering of hepatotoxins based on mechanism of toxicity using gene expression profiles. Toxicol. Appl. Pharmacol. 2001, 175, 28–42. [Google Scholar] [CrossRef]
- Hamadeh, H.K.; Bushel, P.R.; Jayadev, S.; DiSorbo, O.; Bennett, L.; Li, L.; Tennant, R.; Stoll, R.; Barrett, J.C.; Paules, R.S.; et al. Prediction of compound signature using high density gene expression profiling. Toxicol. Sci. 2002, 67, 232–240. [Google Scholar] [CrossRef]
- Kohonen, P.; Parkkinen, J.A.; Willighagen, E.L.; Ceder, R.; Wennerberg, K.; Kaski, S.; Grafström, R.C. A transcriptomics data-driven gene space accurately predicts liver cytopathology and drug-induced liver injury. Nat. Commun. 2017, 8, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Nagata, K.; Washio, T.; Kawahara, Y.; Unami, A. Toxicity prediction from toxicogenomic data based on class association rule mining. Toxicol. Rep. 2014, 1, 1133–1142. [Google Scholar] [CrossRef] [PubMed]
- Nymark, P.; Bakker, M.; Dekkers, S.; Franken, R.; Fransman, W.; García-Bilbao, A.; Greco, D.; Gulumian, M.; Hadrup, N.; Halappanavar, S.; et al. Toward Rigorous Materials Production: New Approach Methodologies Have Extensive Potential to Improve Current Safety Assessment Practices. Small 2020, 1904749. [Google Scholar] [CrossRef] [PubMed]
- ECHA. New Approach Methodologies in Regulatory Science. In Proceedings of the a Scientific Workshop, Helsinki, Finland, 19–20 April 2016. [Google Scholar]
- Farmahin, R.; Williams, A.; Kuo, B.; Chepelev, N.L.; Thomas, R.S.; Barton-Maclaren, T.S.; Curran, I.H.; Nong, A.; Wade, M.G.; Yauk, C.L. Recommended approaches in the application of toxicogenomics to derive points of departure for chemical risk assessment. Arch. Toxicol. 2017, 91, 2045–2065. [Google Scholar] [CrossRef]
- Moffat, I.; Chepelev, N.L.; Labib, S.; Bourdon-Lacombe, J.; Kuo, B.; Buick, J.K.; Lemieux, F.; Williams, A.; Halappanavar, S.; Malik, A.I.; et al. Comparison of toxicogenomics and traditional approaches to inform mode of action and points of departure in human health risk assessment of benzo [a] pyrene in drinking water. Crit. Rev. Toxicol. 2015, 45, 1–43. [Google Scholar] [CrossRef]
- Halappanavar, S.; Rahman, L.; Nikota, J.; Poulsen, S.S.; Ding, Y.; Jackson, P.; Wallin, H.; Schmid, O.; Vogel, U.; Williams, A. Ranking of nanomaterial potency to induce pathway perturbations associated with lung responses. NanoImpact 2019, 14, 100158. [Google Scholar] [CrossRef]
- Dean, J.L.; Zhao, Q.J.; Lambert, J.C.; Hawkins, B.S.; Thomas, R.S.; Wesselkamper, S.C. Editor’s highlight: Application of gene set enrichment analysis for identification of chemically induced, biologically relevant transcriptomic networks and potential utilization in human health risk assessment. Toxicol. Sci. 2017, 157, 85–99. [Google Scholar]
- Serra, A.; Letunic, I.; Fortino, V.; Handy, R.D.; Fadeel, B.; Tagliaferri, R.; Greco, D. INSIdE NANO: A systems biology framework to contextualize the mechanism-of-action of engineered nanomaterials. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef]
- Varsou, D.D.; Tsiliki, G.; Nymark, P.; Kohonen, P.; Grafström, R.; Sarimveis, H. toxFlow: A web-based application for read-across toxicity prediction using omics and physicochemical data. J. Chem. Inf. Model. 2018, 58, 543–549. [Google Scholar] [CrossRef]
- Barel, G.; Herwig, R. Network and pathway analysis of toxicogenomics data. Front. Genet. 2018, 9, 484. [Google Scholar] [CrossRef]
- Jabeen, A.; Ahmad, N.; Raza, K. Machine learning-based state-of-the-art methods for the classification of rna-seq data. In Classification in BioApps; Springer: Berlin, Germany, 2018; pp. 133–172. [Google Scholar]
- Serra, A.; Galdi, P.; Tagliaferri, R. Machine learning for bioinformatics and neuroimaging. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1248. [Google Scholar] [CrossRef]
- Serra, A.; Fratello, M.; Fortino, V.; Raiconi, G.; Tagliaferri, R.; Greco, D. MVDA: A multi-view genomic data integration methodology. BMC Bioinform. 2015, 16, 261. [Google Scholar] [CrossRef]
- Fortino, V.; Kinaret, P.; Fyhrquist, N.; Alenius, H.; Greco, D. A robust and accurate method for feature selection and prioritization from multi-class OMICs data. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Huang, R.; Roberts, R.; Tong, W. Toxicogenomics: A 2020 Vision. Trends Pharmacol. Sci. 2019, 40, 92–103. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wang, G. Machine learning based toxicity prediction: From chemical structural description to transcriptome analysis. Int. J. Mol. Sci. 2018, 19, 2358. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; Gift, J.S.; Zhao, Q.J. Introduction to benchmark dose methods and US EPA’s benchmark dose software (BMDS) version 2.1. 1. Toxicol. Appl. Pharmacol. 2011, 254, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Haber, L.T.; Dourson, M.L.; Allen, B.C.; Hertzberg, R.C.; Parker, A.; Vincent, M.J.; Maier, A.; Boobis, A.R. Benchmark dose (BMD) modeling: Current practice, issues, and challenges. Crit. Rev. Toxicol. 2018, 48, 387–415. [Google Scholar] [CrossRef] [PubMed]
- Serra, A.; Saarimäki, L.A.; Fratello, M.; Marwah, V.S.; Greco, D. BMDx: A graphical Shiny application to perform Benchmark Dose analysis for transcriptomics data. Bioinformatics 2020. [Google Scholar] [CrossRef]
- Hu, J.; Kapoor, M.; Zhang, W.; Hamilton, S.R.; Coombes, K.R. Analysis of dose–response effects on gene expression data with comparison of two microarray platforms. Bioinformatics 2005, 21, 3524–3529. [Google Scholar] [CrossRef][Green Version]
- Thomas, R.S.; Allen, B.C.; Nong, A.; Yang, L.; Bermudez, E.; Clewell III, H.J.; Andersen, M.E. A method to integrate benchmark dose estimates with genomic data to assess the functional effects of chemical exposure. Toxicol. Sci. 2007, 98, 240–248. [Google Scholar] [CrossRef]
- Abraham, K.; Mielke, H.; Lampen, A. Hazard characterization of 3-MCPD using benchmark dose modeling: Factors influencing the outcome. Eur. J. Lipid Sci. Technol. 2012, 114, 1225–1226. [Google Scholar] [CrossRef]
- Committee, E.S.; Hardy, A.; Benford, D.; Halldorsson, T.; Jeger, M.J.; Knutsen, H.K.; More, S.; Naegeli, H.; Noteborn, H.; Ockleford, C.; et al. Guidance on the use of the weight of evidence approach in scientific assessments. EFSA J. 2017, 15, e04971. [Google Scholar]
- Committee, E.S.; Hardy, A.; Benford, D.; Halldorsson, T.; Jeger, M.J.; Knutsen, K.H.; More, S.; Mortensen, A.; Naegeli, H.; Noteborn, H.; et al. Update: Use of the benchmark dose approach in risk assessment. EFSA J. 2017, 15, e04658. [Google Scholar]
- Slob, W. Joint project on benchmark dose modelling with RIVM. EFSA Support. Publ. 2018, 15, 1497E. [Google Scholar] [CrossRef]
- Varewyck, M.; Verbeke, T. Software for benchmark dose modelling. EFSA Support. Publ. 2017, 14, 1170E. [Google Scholar] [CrossRef]
- Yang, L.; Allen, B.C.; Thomas, R.S. BMDExpress: A software tool for the benchmark dose analyses of genomic data. BMC Genom. 2007, 8, 387. [Google Scholar] [CrossRef]
- Kuo, B.; Francina Webster, A.; Thomas, R.S.; Yauk, C.L. BMDExpress Data Viewer-a visualization tool to analyze BMDExpress datasets. J. Appl. Toxicol. 2016, 36, 1048–1059. [Google Scholar] [CrossRef]
- Phillips, J.R.; Svoboda, D.L.; Tandon, A.; Patel, S.; Sedykh, A.; Mav, D.; Kuo, B.; Yauk, C.L.; Yang, L.; Thomas, R.S.; et al. BMDExpress 2: Enhanced transcriptomic dose-response analysis workflow. Bioinformatics 2019, 35, 1780–1782. [Google Scholar] [CrossRef]
- Pramana, S.; Lin, D.; Haldermans, P.; Shkedy, Z.; Verbeke, T.; Göhlmann, H.; De Bondt, A.; Talloen, W.; Bijnens, L. IsoGene: An R package for analyzing dose-response studies in microarray experiments. R J. 2010, 2, 5–12. [Google Scholar] [CrossRef]
- Otava, M.; Sengupta, R.; Shkedy, Z.; Lin, D.; Pramana, S.; Verbeke, T.; Haldermans, P.; Hothorn, L.A.; Gerhard, D.; Kuiper, R.M.; et al. IsoGeneGUI: Multiple approaches for dose-response analysis of microarray data using R. R J. 2017, 9, 14–26. [Google Scholar] [CrossRef]
- Lin, D.; Shkedy, Z.; Yekutieli, D.; Burzykowski, T.; Göhlmann, H.W.; De Bondt, A.; Perera, T.; Geerts, T.; Bijnens, L. Testing for trends in dose-response microarray experiments: A comparison of several testing procedures, multiplicity and resampling-based inference. Stat. Appl. Genet. Mol. Biol. 2007, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Sutherland, J.; Webster, Y.; Willy, J.; Searfoss, G.; Goldstein, K.; Irizarry, A.; Hall, D.; Stevens, J. Toxicogenomic module associations with pathogenesis: A network-based approach to understanding drug toxicity. Pharmacogenomics J. 2018, 18, 377–390. [Google Scholar] [CrossRef] [PubMed]
- Stuart, J.M.; Segal, E.; Koller, D.; Kim, S.K. A gene-coexpression network for global discovery of conserved genetic modules. Science 2003, 302, 249–255. [Google Scholar] [CrossRef] [PubMed]
- Emamjomeh, A.; Robat, E.S.; Zahiri, J.; Solouki, M.; Khosravi, P. Gene co-expression network reconstruction: A review on computational methods for inferring functional information from plant-based expression data. Plant Biotechnol. Rep. 2017, 11, 71–86. [Google Scholar] [CrossRef]
- Chen, J.; Aronow, B.J.; Jegga, A.G. Disease candidate gene identification and prioritization using protein interaction networks. BMC Bioinform. 2009, 10, 73. [Google Scholar]
- van Dam, S.; Vosa, U.; van der Graaf, A.; Franke, L.; de Magalhaes, J.P. Gene co-expression analysis for functional classification and gene–disease predictions. Briefings Bioinform. 2018, 19, 575–592. [Google Scholar] [CrossRef]
- Marwah, V.S.; Kinaret, P.A.S.; Serra, A.; Scala, G.; Lauerma, A.; Fortino, V.; Greco, D. Inform: Inference of network response modules. Bioinformatics 2018, 34, 2136–2138. [Google Scholar] [CrossRef]
- Serra, A.; Tagliaferri, R. Unsupervised Learning: Clustering. In Encyclopedia of Bioinformatics and Computational Biology; Elsevier: Amsterdam, The Netherlands, 2019; pp. 350–357. [Google Scholar]
- Wang, Y.R.; Huang, H. Review on statistical methods for gene network reconstruction using expression data. J. Theor. Biol. 2014, 362, 53–61. [Google Scholar] [CrossRef]
- Grzegorczyk, M.; Aderhold, A.; Husmeier, D. Overview and evaluation of recent methods for statistical inference of gene regulatory networks from time series data. In Gene Regulatory Networks; Springer: Berlin, Germany, 2019; pp. 49–94. [Google Scholar]
- Erola, P.; Bonnet, E.; Michoel, T. Learning differential module networks across multiple experimental conditions. In Gene Regulatory Networks; Springer: Berlin, Germany, 2019; pp. 303–321. [Google Scholar]
- Bansal, M.; Belcastro, V.; Ambesi-Impiombato, A.; Di Bernardo, D. How to infer gene networks from expression profiles. Mol. Syst. Biol. 2007, 3, 78. [Google Scholar] [CrossRef]
- Butte, A.J.; Kohane, I.S. Mutual information relevance networks: Functional genomic clustering using pairwise entropy measurements. In Biocomputing 2000; World Scientific: Singapore, 1999; pp. 418–429. [Google Scholar]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Dalla Favera, R.; Califano, A. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinform. 2006, 7, S7. [Google Scholar] [CrossRef]
- Faith, J.J.; Hayete, B.; Thaden, J.T.; Mogno, I.; Wierzbowski, J.; Cottarel, G.; Kasif, S.; Collins, J.J.; Gardner, T.S. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007, 5. [Google Scholar] [CrossRef] [PubMed]
- Glass, K.; Huttenhower, C.; Quackenbush, J.; Yuan, G.C. Passing messages between biological networks to refine predicted interactions. PLoS ONE 2013, 8, e64832. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Horvath, S. A general framework for weighted gene co-expression network analysis. Stat. Appl. Genet. Mol. Biol. 2005, 4, 17. [Google Scholar] [CrossRef] [PubMed]
- Meyer, P.E.; Kontos, K.; Lafitte, F.; Bontempi, G. Information-Theoretic Inference of Large Transcriptional Regulatory Networks. EURASIP J. Bioinform. Syst. Biol. 2007. [Google Scholar] [CrossRef]
- Opgen-Rhein, R.; Strimmer, K. From correlation to causation networks: A simple approximate learning algorithm and its application to high-dimensional plant gene expression data. BMC Syst. Biol. 2007, 1, 37. [Google Scholar] [CrossRef]
- Serra, A.; Coretto, P.; Fratello, M.; Tagliaferri, R. Robust and sparse correlation matrix estimation for the analysis of high-dimensional genomics data. Bioinformatics 2018, 34, 625–634. [Google Scholar] [CrossRef]
- Freytag, S.; Gagnon-Bartsch, J.; Speed, T.P.; Bahlo, M. Systematic noise degrades gene co-expression signals but can be corrected. BMC Bioinform. 2015, 16, 309. [Google Scholar] [CrossRef]
- Parsana, P.; Ruberman, C.; Jaffe, A.E.; Schatz, M.C.; Battle, A.; Leek, J.T. Addressing confounding artifacts in reconstruction of gene co-expression networks. Genome Biol. 2019, 20, 1–6. [Google Scholar] [CrossRef]
- Tsamardinos, I.; Aliferis, C.F.; Statnikov, A.R.; Statnikov, E. Algorithms for large scale Markov blanket discovery. In Proceedings of the FLAIRS Conference, St. Augustine, FL, USA, 12–14 May 2003; Volume 2, pp. 376–380. [Google Scholar]
- Liu, F.; Zhang, S.W.; Guo, W.F.; Wei, Z.G.; Chen, L. Inference of gene regulatory network based on local bayesian networks. PLoS Comput. Biol. 2016, 12, e1005024. [Google Scholar] [CrossRef]
- Zhu, H.; Bouhifd, M.; Kleinstreuer, N.; Kroese, E.D.; Liu, Z.; Luechtefeld, T.; Pamies, D.; Shen, J.; Strauss, V.; Wu, S.; et al. t4 report: Supporting read-across using biological data. Altex 2016, 33, 167. [Google Scholar] [CrossRef]
- Floris, M.; Manganaro, A.; Nicolotti, O.; Medda, R.; Mangiatordi, G.F.; Benfenati, E. A generalizable definition of chemical similarity for read-across. J. Cheminformatics 2014, 6, 39. [Google Scholar] [CrossRef] [PubMed]
- Patlewicz, G.; Helman, G.; Pradeep, P.; Shah, I. Navigating through the minefield of read-across tools: A review of in silico tools for grouping. Comput. Toxicol. 2017, 3, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Low, Y.; Sedykh, A.; Fourches, D.; Golbraikh, A.; Whelan, M.; Rusyn, I.; Tropsha, A. Integrative chemical–biological read-across approach for chemical hazard classification. Chem. Res. Toxicol. 2013, 26, 1199–1208. [Google Scholar] [CrossRef] [PubMed]
- Ganter, B.; Snyder, R.D.; Halbert, D.N.; Lee, M.D. Toxicogenomics in drug discovery and development: Mechanistic analysis of compound/class-dependent effects using the DrugMatrix®database. Pharmacogenomics 2006, 7, 1025–1044. [Google Scholar] [CrossRef]
- Lamb, J. The Connectivity Map: A new tool for biomedical research. Nat. Rev. Cancer 2007, 7, 54–60. [Google Scholar] [CrossRef]
- Subramanian, A.; Narayan, R.; Corsello, S.M.; Peck, D.D.; Natoli, T.E.; Lu, X.; Gould, J.; Davis, J.F.; Tubelli, A.A.; Asiedu, J.K.; et al. A next generation connectivity map: L1000 platform and the first 1,000,000 profiles. Cell 2017, 171, 1437–1452. [Google Scholar] [CrossRef]
- Varsou, D.D.; Afantitis, A.; Melagraki, G.; Sarimveis, H. Read-across predictions of nanoparticle hazard endpoints: A mathematical optimization approach. Nanoscale Adv. 2019, 1, 3485–3498. [Google Scholar] [CrossRef]
- Nymark, P.; Kohonen, P.; Hongisto, V.; Grafström, R.C. Toxic and genomic influences of inhaled nanomaterials as a basis for predicting adverse outcome. Ann. Am. Thorac. Soc. 2018, 15, S91–S97. [Google Scholar] [CrossRef]
- Nymark, P.; Rieswijk, L.; Ehrhart, F.; Jeliazkova, N.; Tsiliki, G.; Sarimveis, H.; Evelo, C.T.; Hongisto, V.; Kohonen, P.; Willighagen, E.; et al. A data fusion pipeline for generating and enriching adverse outcome pathway descriptions. Toxicol. Sci. 2018, 162, 264–275. [Google Scholar] [CrossRef]
- Vinken, M. Omics-based input and output in the development and use of adverse outcome pathways. Curr. Opin. Toxicol. 2019. [Google Scholar] [CrossRef]
- Martens, M.; Verbruggen, T.; Nymark, P.; Grafström, R.; Burgoon, L.D.; Aladjov, H.; Torres Andón, F.; Evelo, C.T.; Willighagen, E.L. Introducing WikiPathways as a data-source to support adverse outcome pathways for regulatory risk assessment of chemicals and nanomaterials. Front. Genet. 2018, 9, 661. [Google Scholar] [CrossRef]
- Varsou, D.D.; Melagraki, G.; Sarimveis, H.; Afantitis, A. MouseTox: An online toxicity assessment tool for small molecules through enalos cloud platform. Food Chem. Toxicol. 2017, 110, 83–93. [Google Scholar] [CrossRef]
- Afantitis, A.; Melagraki, G.; Tsoumanis, A.; Valsami-Jones, E.; Lynch, I. A nanoinformatics decision support tool for the virtual screening of gold nanoparticle cellular association using protein corona fingerprints. Nanotoxicology 2018, 12, 1148–1165. [Google Scholar] [CrossRef]
- Vo, A.H.; Van Vleet, T.R.; Gupta, R.R.; Liguori, M.J.; Rao, M.S. An Overview of Machine Learning and Big Data for Drug Toxicity Evaluation. Chem. Res. Toxicol. 2019. [Google Scholar] [CrossRef]
- Ulrich, R.; Friend, S.H. Toxicogenomics and drug discovery: Will new technologies help us produce better drugs? Nat. Rev. Drug Discov. 2002, 1, 84–88. [Google Scholar] [CrossRef]
- Khan, S.R.; Baghdasarian, A.; Fahlman, R.P.; Michail, K.; Siraki, A.G. Current status and future prospects of toxicogenomics in drug discovery. Drug Discov. Today 2014, 19, 562–578. [Google Scholar] [CrossRef]
- Rueda-Zarate, H.A.; Imaz-Rosshandler, I.; Cardenas-Ovando, R.A.; Castillo-Fernandez, J.E.; Noguez-Monroy, J.; Rangel-Escareno, C. A computational toxicogenomics approach identifies a list of highly hepatotoxic compounds from a large microarray database. PLoS ONE 2017, 12, e0176284. [Google Scholar] [CrossRef]
- Su, R.; Wu, H.; Liu, X.; Wei, L. Predicting drug-induced hepatotoxicity based on biological feature maps and diverse classification strategies. Briefings Bioinformat. 2019. [Google Scholar] [CrossRef]
- Clarke, R.; Ressom, H.W.; Wang, A.; Xuan, J.; Liu, M.C.; Gehan, E.A.; Wang, Y. The properties of high-dimensional data spaces: Implications for exploring gene and protein expression data. Nat. Rev. Cancer 2008, 8, 37–49. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Mach, N.; Berri, M.; Esquerre, D.; Chevaleyre, C.; Lemonnier, G.; Billon, Y.; Lepage, P.; Oswald, I.P.; Dore, J.; Rogel-Gaillard, C.; et al. Extensive expression differences along porcine small intestine evidenced by transcriptome sequencing. PLoS ONE 2014, 9. [Google Scholar] [CrossRef]
- Maaten, L.v.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.A.; Kwok, I.W.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2019, 37, 38. [Google Scholar] [CrossRef]
- Khan, S.A.; Aittokallio, T.; Scherer, A.; Grafström, R.; Kohonen, P. Matrix and Tensor Factorization Methods for Toxicogenomic Modeling and Prediction. In Advances in Computational Toxicology; Springer: Berlin, Germany, 2019; pp. 57–74. [Google Scholar]
- Wang, L.; Xi, Y.; Sung, S.; Qiao, H. RNA-seq assistant: Machine learning based methods to identify more transcriptional regulated genes. BMC Genom. 2018, 19, 546. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Fratello, M.; Tagliaferri, R. Decision trees and random forests. In Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics; Elsevier: Amsterdam, The Netherlands, 2018; p. 374. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; De Andres, S.A. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef]
- Trevino, V.; Falciani, F. GALGO: An R package for multivariate variable selection using genetic algorithms. Bioinformatics 2006, 22, 1154–1156. [Google Scholar] [CrossRef]
- Singh, A.; Shannon, C.P.; Gautier, B.; Rohart, F.; Vacher, M.; Tebbutt, S.J.; Lê Cao, K.A. DIABLO: An integrative approach for identifying key molecular drivers from multi-omics assays. Bioinformatics 2019, 35, 3055–3062. [Google Scholar] [CrossRef]
- Fortino, V.; Scala, G.G.D. Feature Set Optimization in Biomarker Discovery from Genome Scale Data. Bioinformatics 2020, 2, 8. [Google Scholar] [CrossRef]
- Furxhi, I.; Murphy, F.; Sheehan, B.; Mullins, M.; Mantecca, P. Predicting Nanomaterials toxicity pathways based on genome-wide transcriptomics studies using Bayesian networks. In Proceedings of the 2018 IEEE 18th International Conference on Nanotechnology (IEEE-NANO), Cork, Ireland, 23–26 July 2018; pp. 1–4. [Google Scholar]
- Furxhi, I.; Murphy, F.; Mullins, M.; Poland, C.A. Machine learning prediction of nanoparticle in vitro toxicity: A comparative study of classifiers and ensemble-classifiers using the Copeland Index. Toxicol. Lett. 2019, 312, 157–166. [Google Scholar] [CrossRef]
- Eichner, J.; Kossler, N.; Wrzodek, C.; Kalkuhl, A.; Toft, D.B.; Ostenfeldt, N.; Richard, V.; Zell, A. A toxicogenomic approach for the prediction of murine hepatocarcinogenesis using ensemble feature selection. PLoS ONE 2013, 8, e73938. [Google Scholar] [CrossRef]
- Su, R.; Wu, H.; Xu, B.; Liu, X.; Wei, L. Developing a multi-dose computational model for drug-induced hepatotoxicity prediction based on toxicogenomics data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 16, 1231–1239. [Google Scholar] [CrossRef]
- Lustgarten, J.L.; Gopalakrishnan, V.; Visweswaran, S. Measuring stability of feature selection in biomedical datasets. AMIA Annu. Symp. Proc. 2009, 2009, 406. [Google Scholar]
- Kalousis, A.; Prados, J.; Hilario, M. Stability of feature selection algorithms: A study on high-dimensional spaces. Knowl. Inf. Syst. 2007, 12, 95–116. [Google Scholar] [CrossRef]
- Nogueira, S.; Sechidis, K.; Brown, G. On the stability of feature selection algorithms. J. Mach. Learn. Res. 2017, 18, 6345–6398. [Google Scholar]
- OECD, O. Guidance Document on the Validation of (Quantitative) Structure-Activity Relationship [(Q) SAR] Models; Organisation for Economic Co-operation and Development: Paris, France, 2007. [Google Scholar]
- Fourches, D.; Pu, D.; Tassa, C.; Weissleder, R.; Shaw, S.Y.; Mumper, R.J.; Tropsha, A. Quantitative nanostructure- activity relationship modeling. ACS Nano 2010, 4, 5703–5712. [Google Scholar] [CrossRef]
- Gramatica, P. Principles of QSAR models validation: Internal and external. QSAR Comb. Sci. 2007, 26, 694–701. [Google Scholar] [CrossRef]
- Roy, K.; Kar, S.; Ambure, P. On a simple approach for determining applicability domain of QSAR models. Chemom. Intell. Lab. Syst. 2015, 145, 22–29. [Google Scholar] [CrossRef]
- Sheridan, R.P.; Feuston, B.P.; Maiorov, V.N.; Kearsley, S.K. Similarity to molecules in the training set is a good discriminator for prediction accuracy in QSAR. J. Chem. Inf. Comput. Sci. 2004, 44, 1912–1928. [Google Scholar] [CrossRef]
- Singh, K.P.; Gupta, S. Nano-QSAR modeling for predicting biological activity of diverse nanomaterials. RSC Adv. 2014, 4, 13215–13230. [Google Scholar] [CrossRef]
- Serra, A.; Önlü, S.; Festa, P.; Fortino, V.; Greco, D. MaNGA: A novel multi-objective multi-niche genetic algorithm for QSAR modelling. Bioinformatics 2019, 36, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C.T. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef]
- Nyström-Persson, J.; Natsume-Kitatani, Y.; Igarashi, Y.; Satoh, D.; Mizuguchi, K. Interactive Toxicogenomics: Gene set discovery, clustering and analysis in Toxygates. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Ben-Dor, A.; Shamir, R.; Yakhini, Z. Clustering gene expression patterns. J. Comput. Biol. 1999, 6, 281–297. [Google Scholar] [CrossRef]
- Andreopoulos, B.; An, A.; Wang, X.; Schroeder, M. A roadmap of clustering algorithms: Finding a match for a biomedical application. Briefings Bioinform. 2009, 10, 297–314. [Google Scholar] [CrossRef]
- Arbelaitz, O.; Gurrutxaga, I.; Muguerza, J.; PéRez, J.M.; Perona, I. An extensive comparative study of cluster validity indices. Pattern Recognit. 2013, 46, 243–256. [Google Scholar] [CrossRef]
- Pfitzner, D.; Leibbrandt, R.; Powers, D. Characterization and evaluation of similarity measures for pairs of clusterings. Knowl. Inf. Syst. 2009, 19, 361. [Google Scholar] [CrossRef]
- Gao, C.; Weisman, D.; Gou, N.; Ilyin, V.; Gu, A.Z. Analyzing high dimensional toxicogenomic data using consensus clustering. Environ. Sci. Technol. 2012, 46, 8413–8421. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier analysis. Data Mining; Springer: Berlin, Germany, 2015; pp. 237–263. [Google Scholar]
- Campos, G.O.; Zimek, A.; Sander, J.; Campello, R.J.; Micenková, B.; Schubert, E.; Assent, I.; Houle, M.E. On the evaluation of unsupervised outlier detection: Measures, datasets, and an empirical study. Data Min. Knowl. Discov. 2016, 30, 891–927. [Google Scholar] [CrossRef]
- Brannon, A.R.; Reddy, A.; Seiler, M.; Arreola, A.; Moore, D.T.; Pruthi, R.S.; Wallen, E.M.; Nielsen, M.E.; Liu, H.; Nathanson, K.L.; et al. Molecular stratification of clear cell renal cell carcinoma by consensus clustering reveals distinct subtypes and survival patterns. Genes Cancer 2010, 1, 152–163. [Google Scholar] [CrossRef]
- McNicholas, P.D.; Murphy, T.B. Model-based clustering of microarray expression data via latent Gaussian mixture models. Bioinformatics 2010, 26, 2705–2712. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.N.; Malek, M.B.; Begum, A.A.; Rahman, M.; Mollah, M.; Haque, N. Assessment of Drugs Toxicity and Associated Biomarker Genes Using Hierarchical Clustering. Medicina 2019, 55, 451. [Google Scholar] [CrossRef] [PubMed]
- Low, Y.; Uehara, T.; Minowa, Y.; Yamada, H.; Ohno, Y.; Urushidani, T.; Sedykh, A.; Muratov, E.; Kuz’min, V.; Fourches, D.; et al. Predicting drug-induced hepatotoxicity using QSAR and toxicogenomics approaches. Chem. Res. Toxicol. 2011, 24, 1251–1262. [Google Scholar] [CrossRef] [PubMed]
- Auerbach, S.S.; Shah, R.R.; Mav, D.; Smith, C.S.; Walker, N.J.; Vallant, M.K.; Boorman, G.A.; Irwin, R.D. Predicting the hepatocarcinogenic potential of alkenylbenzene flavoring agents using toxicogenomics and machine learning. Toxicol. Appl. Pharmacol. 2010, 243, 300–314. [Google Scholar] [CrossRef] [PubMed]
- Minowa, Y.; Kondo, C.; Uehara, T.; Morikawa, Y.; Okuno, Y.; Nakatsu, N.; Ono, A.; Maruyama, T.; Kato, I.; Yamate, J.; et al. Toxicogenomic multigene biomarker for predicting the future onset of proximal tubular injury in rats. Toxicology 2012, 297, 47–56. [Google Scholar] [CrossRef]
- Galdi, P.; Tagliaferri, R. Data mining: Accuracy and error measures for classification and prediction. Encyclopedia Bioinformat. Comput. Biol. 2018, 431–436. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Liu, J.; Jolly, R.A.; Smith, A.T.; Searfoss, G.H.; Goldstein, K.M.; Uversky, V.N.; Dunker, K.; Li, S.; Thomas, C.E.; Wei, T. Predictive Power Estimation Algorithm (PPEA)-a new algorithm to reduce overfitting for genomic biomarker discovery. PLoS ONE 2011, 6. [Google Scholar] [CrossRef]
- Lunardon, N.; Menardi, G.; Torelli, N. ROSE: A Package for Binary Imbalanced Learning. R J. 2014, 6. [Google Scholar] [CrossRef]
- Menardi, G.; Torelli, N. Training and assessing classification rules with imbalanced data. Data Min. Knowl. Discov. 2014, 28, 92–122. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Kovács, G. An empirical comparison and evaluation of minority oversampling techniques on a large number of imbalanced datasets. Appl. Soft Comput. 2019, 83, 105662. [Google Scholar] [CrossRef]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Et Biophys. Acta (BBA)-Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Chicco, D. Ten quick tips for machine learning in computational biology. BioData Min. 2017, 10, 35. [Google Scholar] [CrossRef]
- Schüttler, A.; Altenburger, R.; Ammar, M.; Bader-Blukott, M.; Jakobs, G.; Knapp, J.; Krüger, J.; Reiche, K.; Wu, G.M.; Busch, W. Map and model—moving from observation to prediction in toxicogenomics. GigaScience 2019, 8, giz057. [Google Scholar] [CrossRef]
- Prieto, A.; Prieto, B.; Ortigosa, E.M.; Ros, E.; Pelayo, F.; Ortega, J.; Rojas, I. Neural networks: An overview of early research, current frameworks and new challenges. Neurocomputing 2016, 214, 242–268. [Google Scholar] [CrossRef]
- Liu, R.; Madore, M.; Glover, K.P.; Feasel, M.G.; Wallqvist, A. Assessing deep and shallow learning methods for quantitative prediction of acute chemical toxicity. Toxicol. Sci. 2018, 164, 512–526. [Google Scholar] [CrossRef]
- Soufan, O.; Ewald, J.; Viau, C.; Crump, D.; Hecker, M.; Basu, N.; Xia, J. T1000: A reduced gene set prioritized for toxicogenomic studies. PeerJ 2019, 7, e7975. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality reduction: A comparative. J. Mach. Learn. Res. 2009, 10, 13. [Google Scholar]
- Cunningham, J.P.; Ghahramani, Z. Linear dimensionality reduction: Survey, insights, and generalizations. J. Mach. Learn. Res. 2015, 16, 2859–2900. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Berrendero, J.R.; Cuevas, A.; Torrecilla, J.L. The mRMR variable selection method: A comparative study for functional data. J. Stat. Comput. Simul. 2016, 86, 891–907. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef]
- Aliper, A.; Plis, S.; Artemov, A.; Ulloa, A.; Mamoshina, P.; Zhavoronkov, A. Deep learning applications for predicting pharmacological properties of drugs and drug repurposing using transcriptomic data. Mol. Pharm. 2016, 13, 2524–2530. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; Springer: Berlin, Germany, 2012; pp. 1097–1105. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Lyu, B.; Haque, A. Deep learning based tumor type classification using gene expression data. In Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics, Washington, DC, USA, 29 August–1 September 2018; pp. 89–96. [Google Scholar]
- Urda, D.; Montes-Torres, J.; Moreno, F.; Franco, L.; Jerez, J.M. Deep learning to analyze RNA-seq gene expression data. In International Work-Conference on Artificial Neural Networks; Springer: Berlin, Germany, 2017; pp. 50–59. [Google Scholar]
- Ma, S.; Zhang, Z. OmicsMapNet: Transforming omics data to take advantage of Deep Convolutional Neural Network for discovery. arXiv 2018, arXiv:1804.05283. [Google Scholar]
- Yuan, Y.; Bar-Joseph, Z. GCNG: Graph convolutional networks for inferring cell-cell interactions. bioRxiv 2019. [Google Scholar] [CrossRef]
- Wang, H.; Liu, R.; Schyman, P.; Wallqvist, A. Deep Neural Network Models for Predicting Chemically Induced Liver Toxicity Endpoints From Transcriptomic Responses. Front. Pharmacol. 2019, 10, 42. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Narayan, R.; Subramanian, A.; Xie, X. Gene expression inference with deep learning. Bioinformatics 2016, 32, 1832–1839. [Google Scholar] [CrossRef] [PubMed]
- Popova, M.; Isayev, O.; Tropsha, A. Deep reinforcement learning for de novo drug design. Sci. Adv. 2018, 4, eaap7885. [Google Scholar] [CrossRef]
- Serra, A.; Fratello, M.; Greco, D.; Tagliaferri, R. Data integration in genomics and systems biology. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 1272–1279. [Google Scholar]
- Fratello, M.; Serra, A.; Fortino, V.; Raiconi, G.; Tagliaferri, R.; Greco, D. A multi-view genomic data simulator. BMC Bioinform. 2015, 16, 151. [Google Scholar] [CrossRef]
- Jiang, H.; Deng, Y.; Chen, H.S.; Tao, L.; Sha, Q.; Chen, J.; Tsai, C.J.; Zhang, S. Joint analysis of two microarray gene-expression datasets to select lung adenocarcinoma marker genes. BMC Bioinform. 2004, 5, 81. [Google Scholar] [CrossRef]
- Wang, J.; Do, K.A.; Wen, S.; Tsavachidis, S.; McDonnell, T.J.; Logothetis, C.J.; Coombes, K.R. Merging microarray data, robust feature selection, and predicting prognosis in prostate cancer. Cancer Inform. 2006, 2, 117693510600200009. [Google Scholar] [CrossRef]
- Irizarry, R.A.; Bolstad, B.M.; Collin, F.; Cope, L.M.; Hobbs, B.; Speed, T.P. Summaries of Affymetrix GeneChip probe level data. Nucleic Acids Res. 2003, 31, e15. [Google Scholar] [CrossRef]
- Shabalin, A.A.; Tjelmeland, H.; Fan, C.; Perou, C.M.; Nobel, A.B. Merging two gene-expression studies via cross-platform normalization. Bioinformatics 2008, 24, 1154–1160. [Google Scholar] [CrossRef]
- Qiao, X.; Zhang, H.H.; Liu, Y.; Todd, M.J.; Marron, J.S. Weighted distance weighted discrimination and its asymptotic properties. J. Am. Stat. Assoc. 2010, 105, 401–414. [Google Scholar] [CrossRef]
- Hong, F.; Breitling, R.; McEntee, C.W.; Wittner, B.S.; Nemhauser, J.L.; Chory, J. RankProd: A bioconductor package for detecting differentially expressed genes in meta-analysis. Bioinformatics 2006, 22, 2825–2827. [Google Scholar] [CrossRef] [PubMed]
- DeConde, R.P.; Hawley, S.; Falcon, S.; Clegg, N.; Knudsen, B.; Etzioni, R. Combining results of microarray experiments: A rank aggregation approach. Stat. Appl. Genet. Mol. Biol. 2006, 5, 15. [Google Scholar] [CrossRef]
- Bushel, P.R.; Tong, W. Integrative Toxicogenomics: Analytical Strategies to Amalgamate Exposure Effects With Genomic Sciences. Front. Genet. 2018, 9, 563. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.L.; Song, J.L.; Ji, C.L.; Feng, Y.L.; Yu, J.; Nyachoti, C.M.; Yang, G.S. Zearalenone exposure enhanced the expression of tumorigenesis genes in donkey granulosa cells via the PTEN/PI3K/AKT signaling pathway. Front. Genet. 2018, 9, 293. [Google Scholar] [CrossRef] [PubMed]
- Scala, G.; Marwah, V.; Kinaret, P.; Sund, J.; Fortino, V.; Greco, D. Integration of genome-wide mRNA and miRNA expression, and DNA methylation data of three cell lines exposed to ten carbon nanomaterials. Data Brief 2018, 19, 1046–1057. [Google Scholar] [CrossRef] [PubMed]
- Pavlidis, P.; Weston, J.; Cai, J.; Grundy, W.N. Gene functional classification from heterogeneous data. In Proceedings of the Fifth Annual International Conference on Computational Biology, Montreal, QC, Canadal, 22–25 April 2001; pp. 249–255. [Google Scholar]
- Kim, D.; Li, R.; Dudek, S.M.; Ritchie, M.D. ATHENA: Identifying interactions between different levels of genomic data associated with cancer clinical outcomes using grammatical evolution neural network. BioData Min. 2013, 6, 23. [Google Scholar] [CrossRef]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kains, B.; Goldenberg, A. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333. [Google Scholar] [CrossRef]
- Yang, Z.; Michailidis, G. A non-negative matrix factorization method for detecting modules in heterogeneous omics multi-modal data. Bioinformatics 2016, 32, 1–8. [Google Scholar] [CrossRef]
- Perualila-Tan, N.; Kasim, A.; Talloen, W.; Verbist, B.; Göhlmann, H.W.; Shkedy, Z.; QSTAR Consortium. A joint modeling approach for uncovering associations between gene expression, bioactivity and chemical structure in early drug discovery to guide lead selection and genomic biomarker development. Stat. Appl. Genet. Mol. Biol. 2016, 15, 291–304. [Google Scholar] [CrossRef]
- Serra, A.; Önlü, S.; Coretto, P.; Greco, D. An integrated quantitative structure and mechanism of action-activity relationship model of human serum albumin binding. J. Cheminformatics 2019, 11, 38. [Google Scholar] [CrossRef]
- Wilkinson, M.D.; Dumontier, M.; Aalbersberg, I.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.W.; da Silva Santos, L.B.; Bourne, P.E.; et al. The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data 2016, 3, 160018. [Google Scholar] [CrossRef] [PubMed]
| BMDS | PROAST | BMDExpress 2 | ISOgene | BMDx | |
|---|---|---|---|---|---|
| EPA Models * | X | X | |||
| Probe id | - | - | X | ||
| Gene id | - | - | X | ||
| BMD/BMDL | X | X | X | X | |
| BMDU | X | X | X | ||
| IC50 | X | ||||
| EC50 | X | ||||
| Enrichment Analysis | - | - | X | X | |
| Interactive enriched maps | - | - | X | ||
| Comparisons at different time points | - | - | X | ||
| GUI | X | X | X | X | X |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serra, A.; Fratello, M.; Cattelani, L.; Liampa, I.; Melagraki, G.; Kohonen, P.; Nymark, P.; Federico, A.; Kinaret, P.A.S.; Jagiello, K.; et al. Transcriptomics in Toxicogenomics, Part III: Data Modelling for Risk Assessment. Nanomaterials 2020, 10, 708. https://doi.org/10.3390/nano10040708
Serra A, Fratello M, Cattelani L, Liampa I, Melagraki G, Kohonen P, Nymark P, Federico A, Kinaret PAS, Jagiello K, et al. Transcriptomics in Toxicogenomics, Part III: Data Modelling for Risk Assessment. Nanomaterials. 2020; 10(4):708. https://doi.org/10.3390/nano10040708
Chicago/Turabian StyleSerra, Angela, Michele Fratello, Luca Cattelani, Irene Liampa, Georgia Melagraki, Pekka Kohonen, Penny Nymark, Antonio Federico, Pia Anneli Sofia Kinaret, Karolina Jagiello, and et al. 2020. "Transcriptomics in Toxicogenomics, Part III: Data Modelling for Risk Assessment" Nanomaterials 10, no. 4: 708. https://doi.org/10.3390/nano10040708
APA StyleSerra, A., Fratello, M., Cattelani, L., Liampa, I., Melagraki, G., Kohonen, P., Nymark, P., Federico, A., Kinaret, P. A. S., Jagiello, K., Ha, M. K., Choi, J.-S., Sanabria, N., Gulumian, M., Puzyn, T., Yoon, T.-H., Sarimveis, H., Grafström, R., Afantitis, A., & Greco, D. (2020). Transcriptomics in Toxicogenomics, Part III: Data Modelling for Risk Assessment. Nanomaterials, 10(4), 708. https://doi.org/10.3390/nano10040708