Prediction of Thermo-Physical Properties of TiO2-Al2O3/Water Nanoparticles by Using Artificial Neural Network
Abstract
1. Introduction
2. Test section
Synthesis of TiO2-Al2O3 Nanoparticles and Characterization
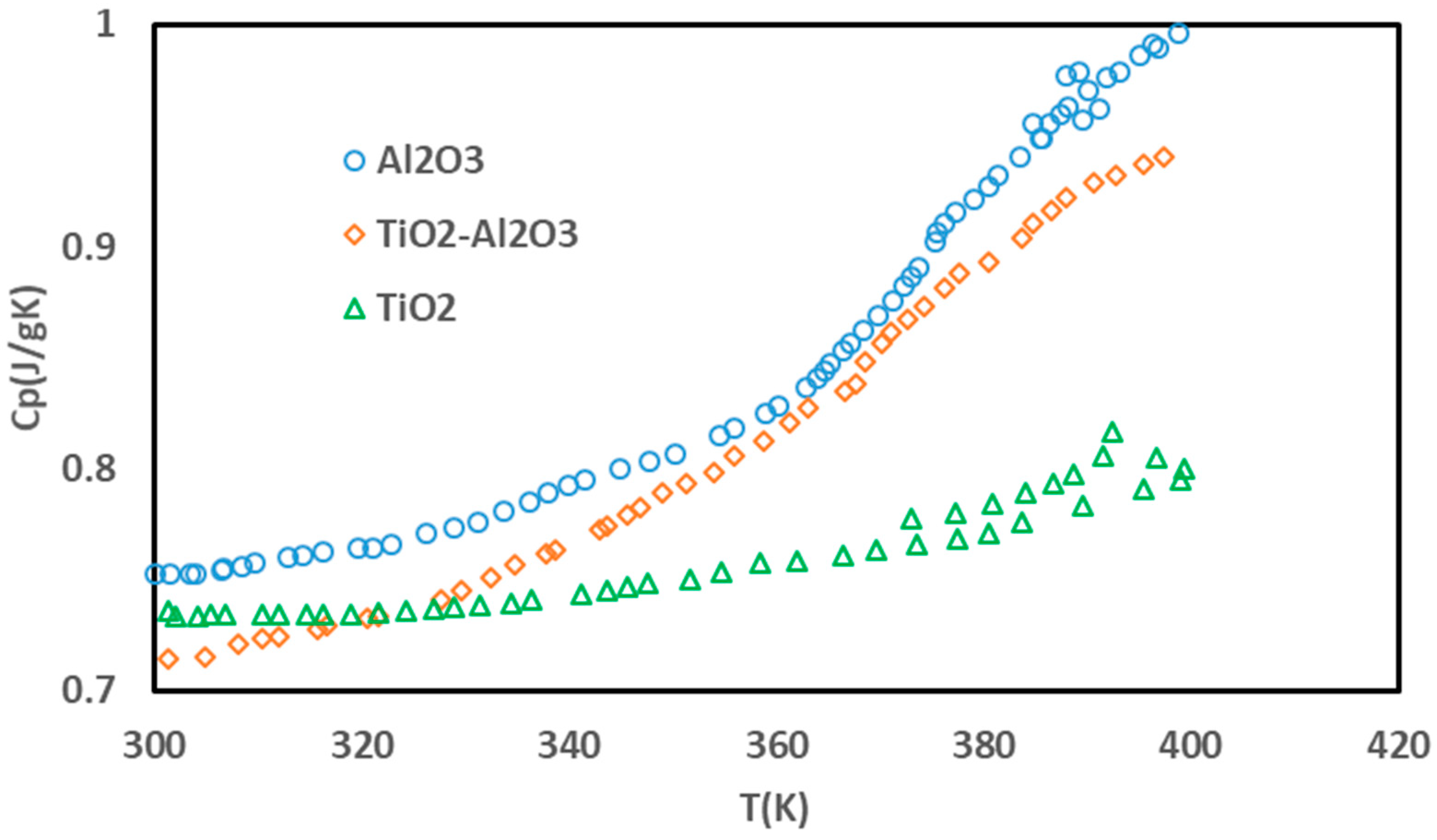
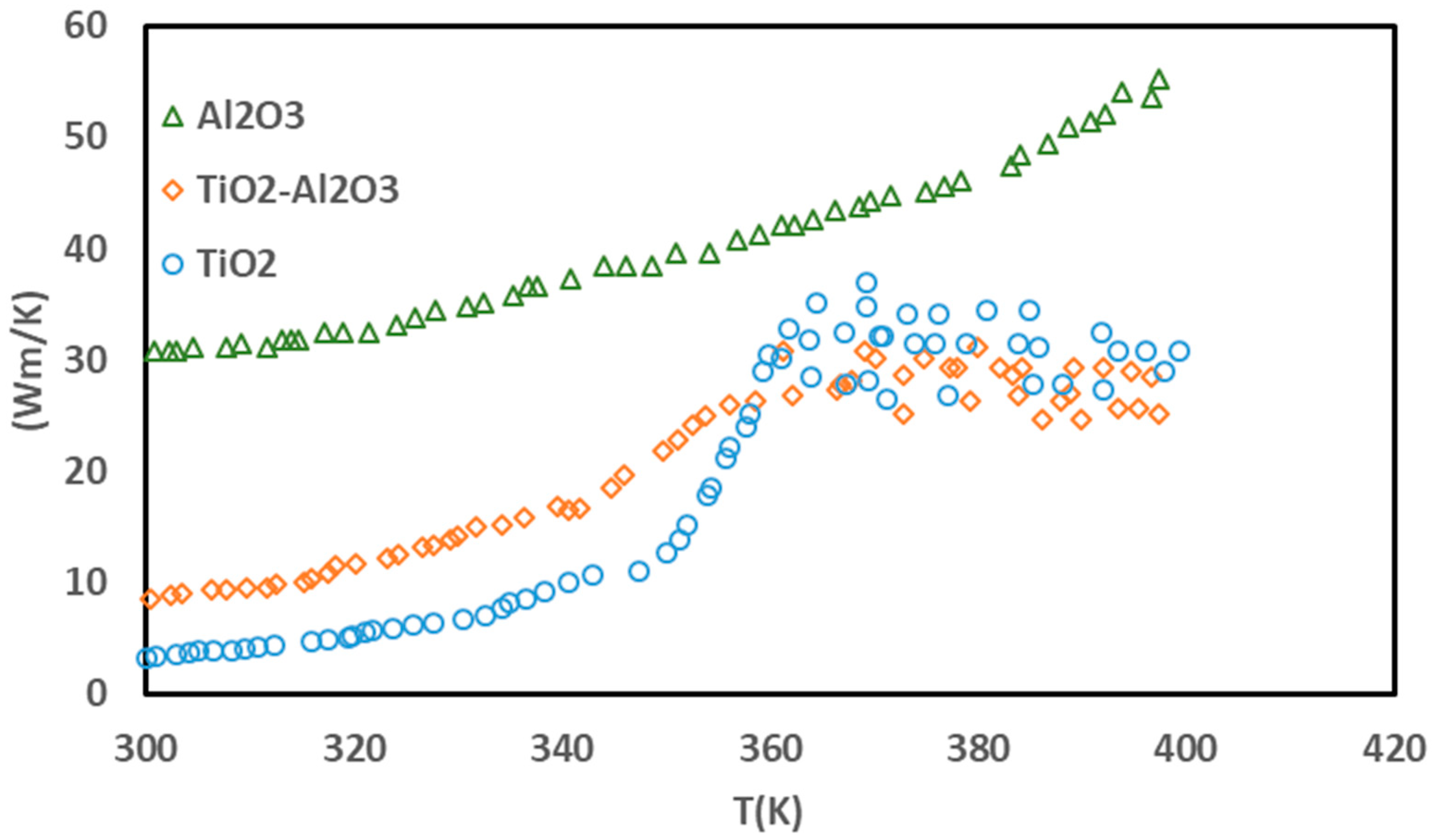
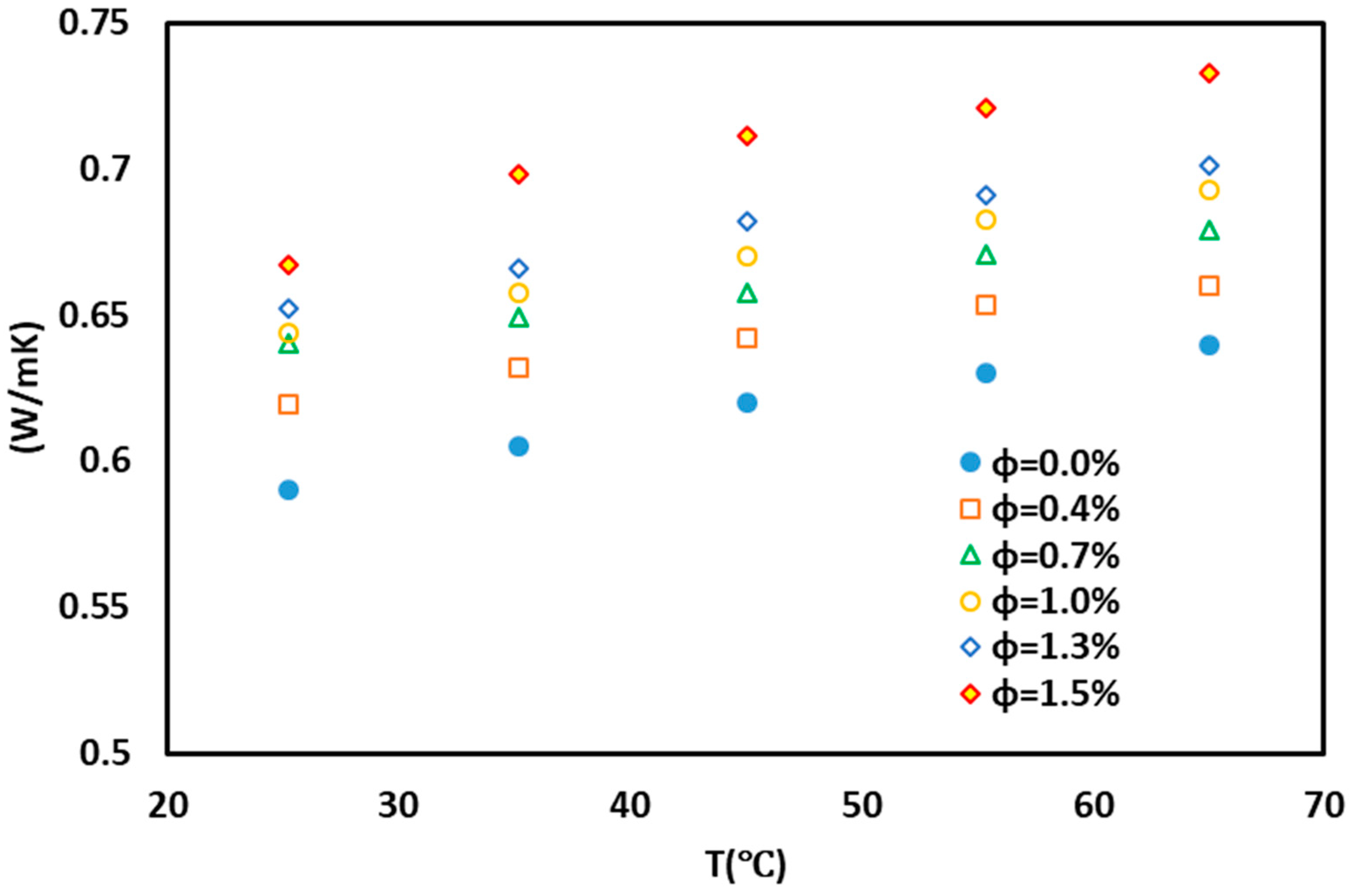
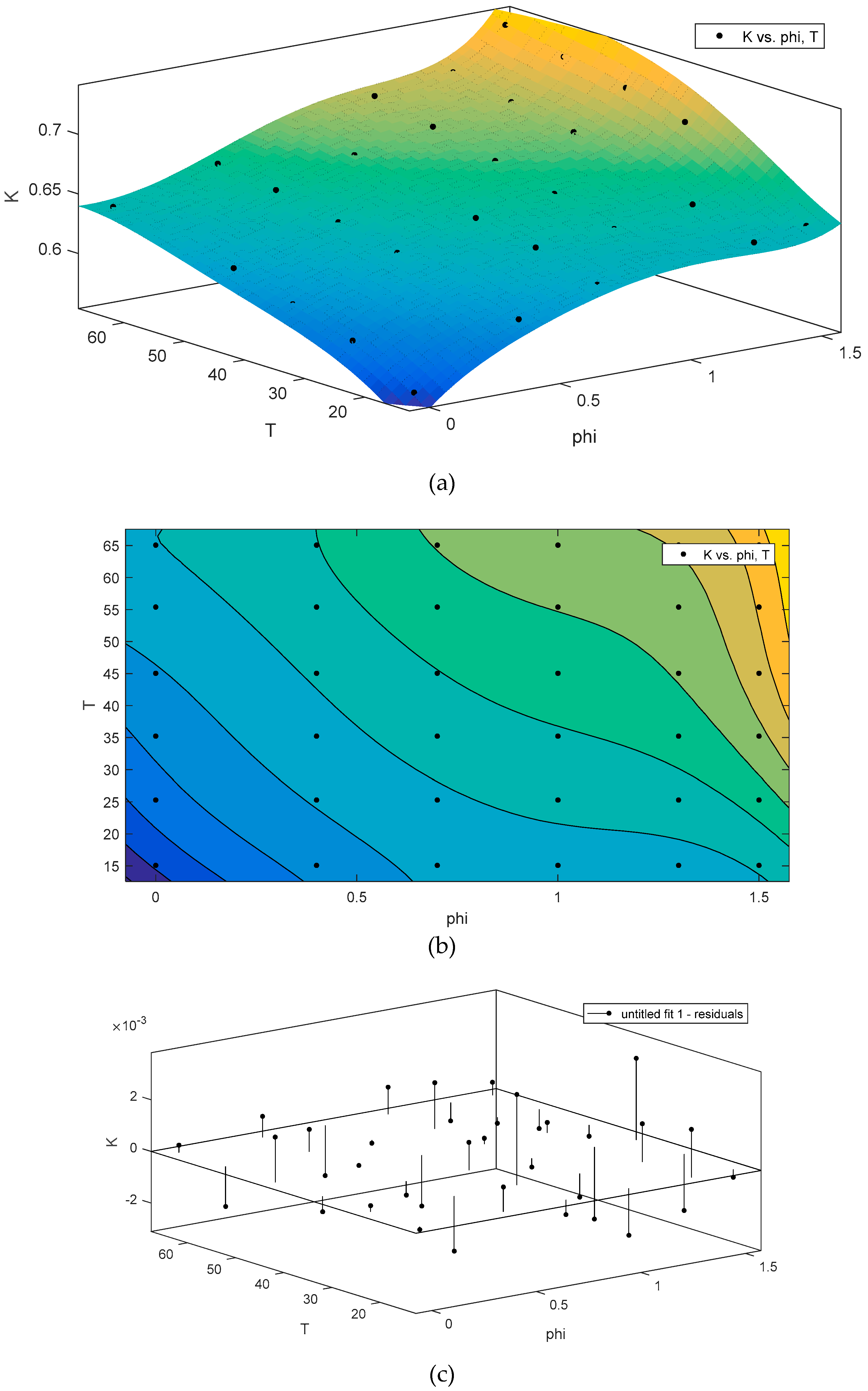
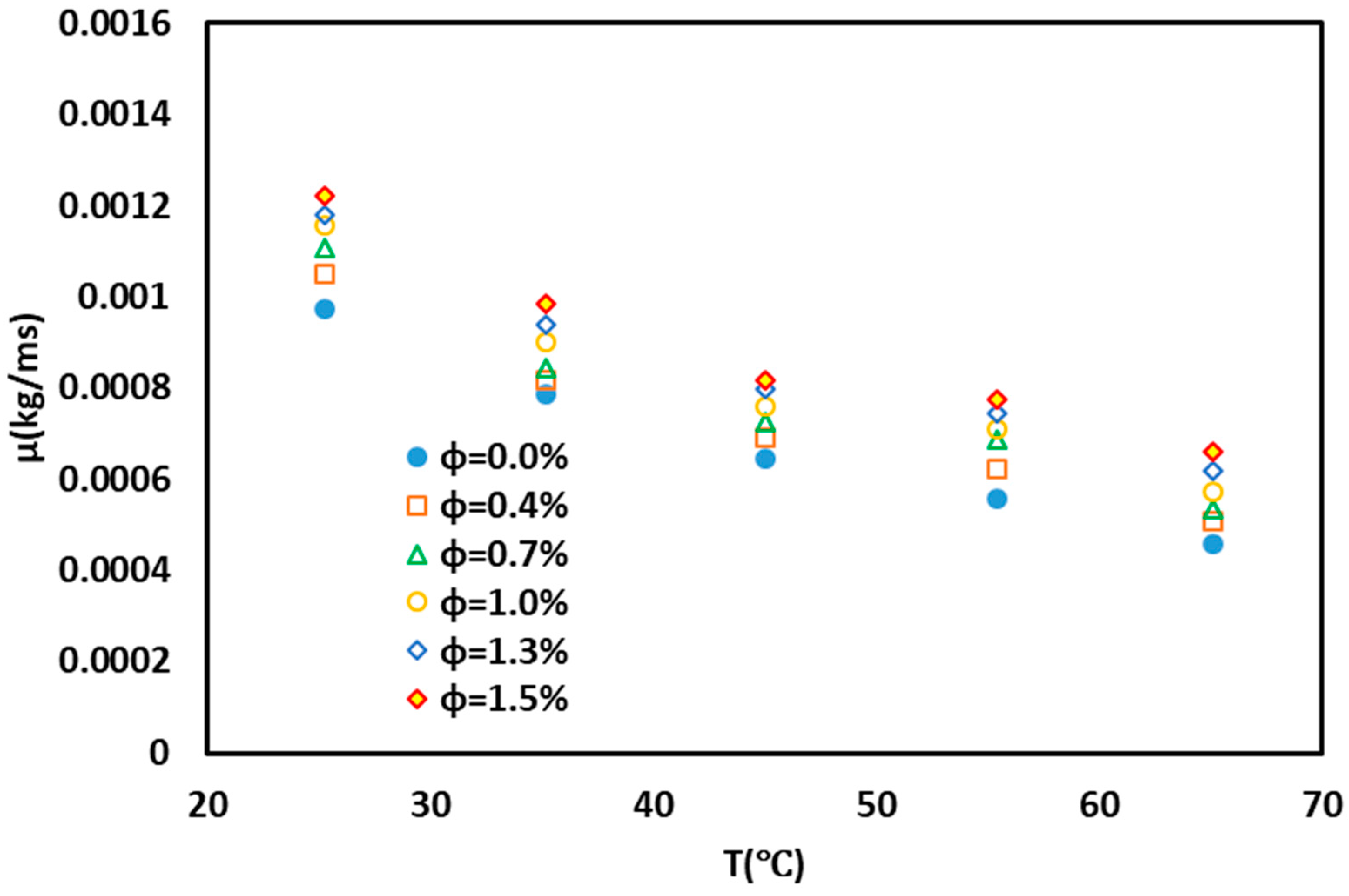
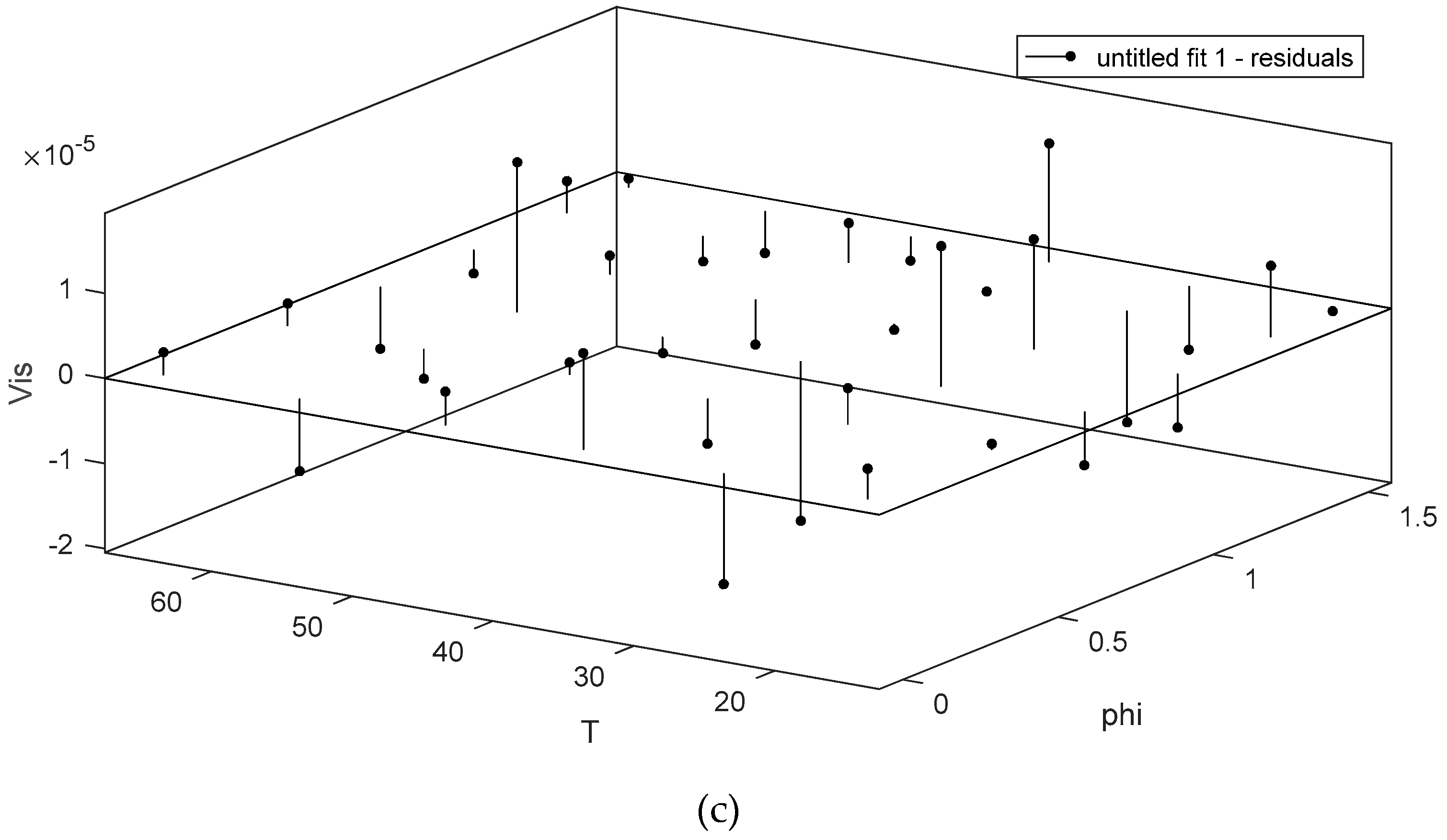
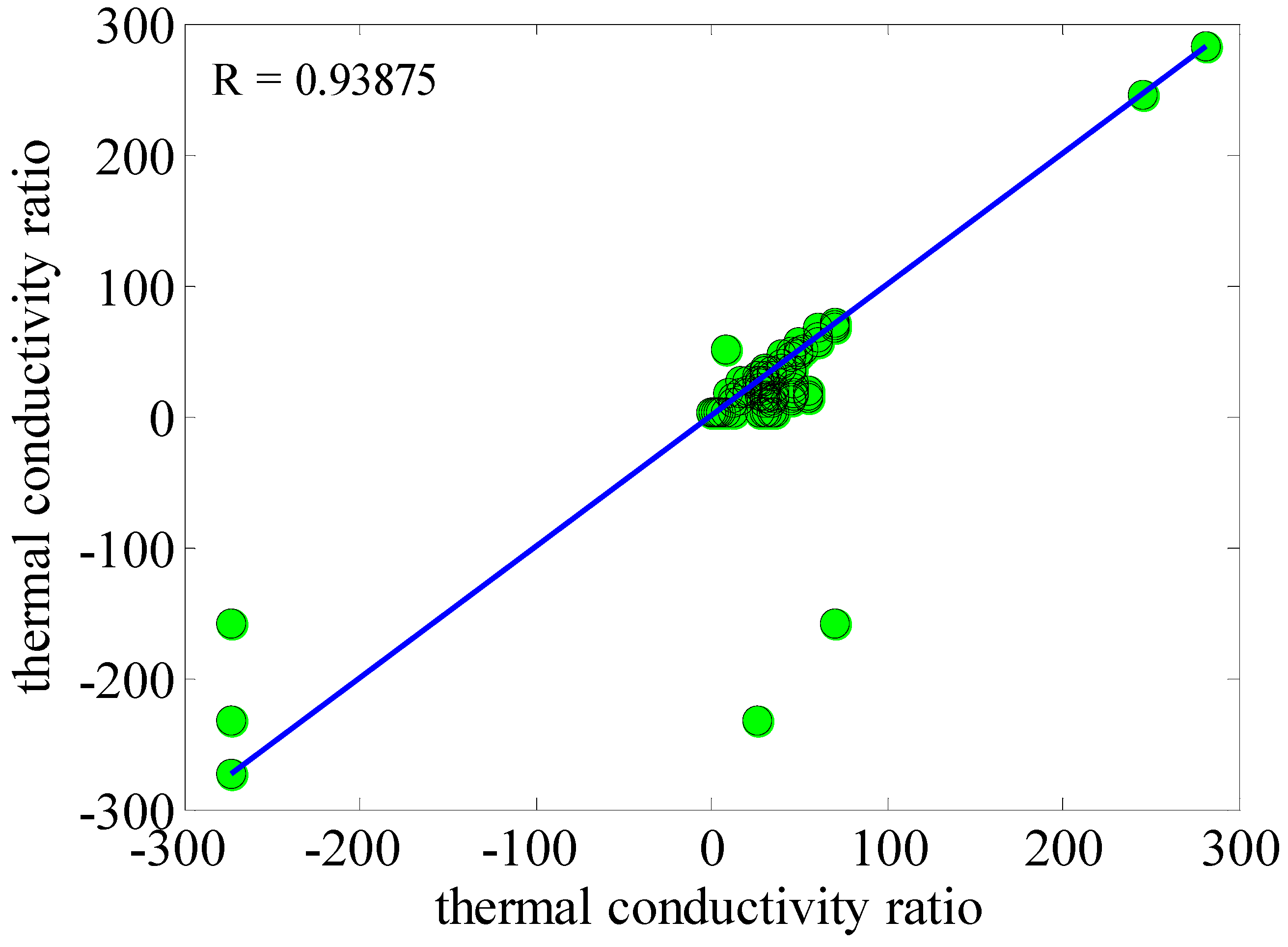
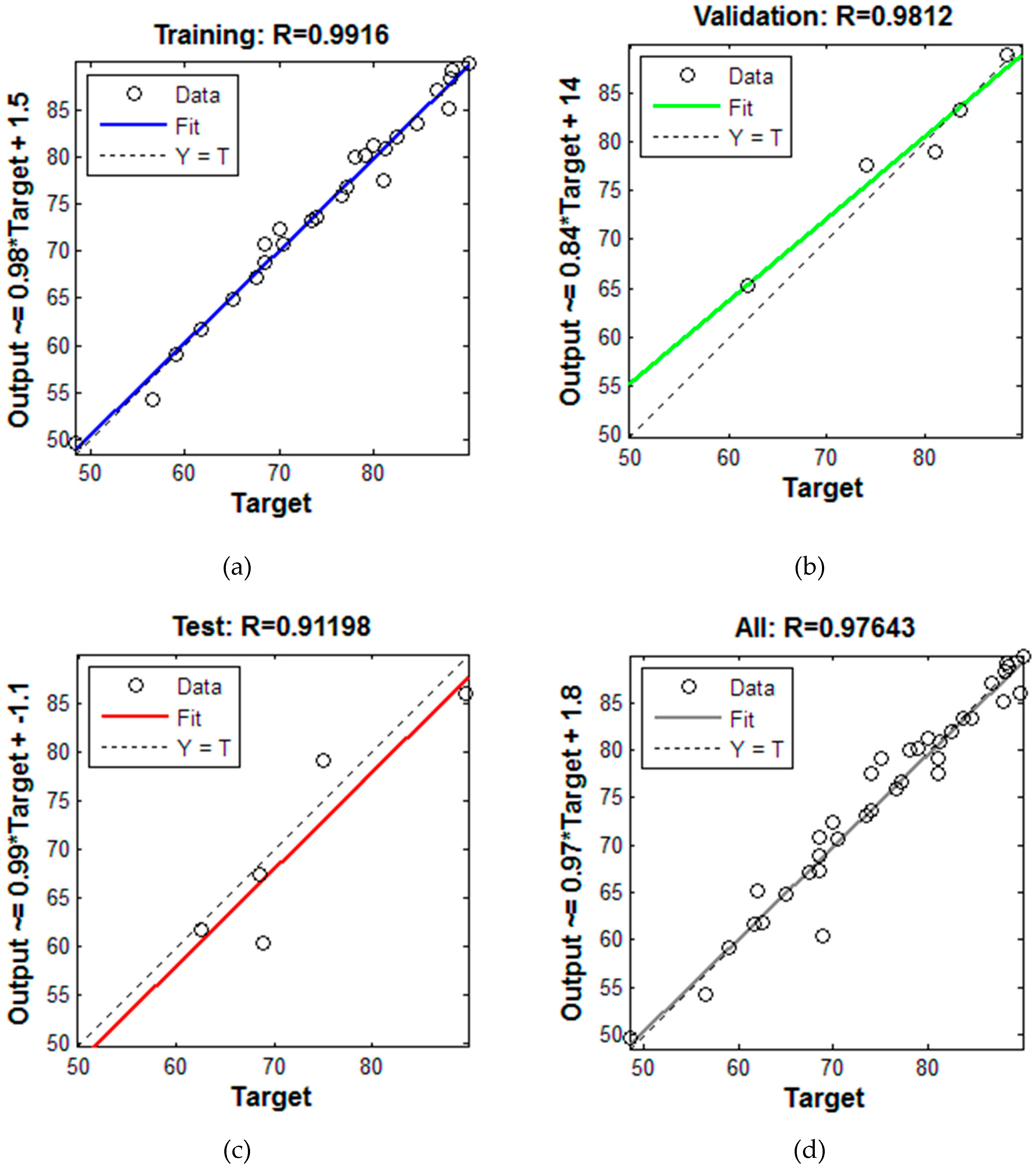
3. Results and Discussion
| p10 = 3.494 × 10−1 (1.966 × 10−1, 5.022 × 10−1) |
| p01 = 7.815 × 10−3 (−1.715 × 10−2, 3.279 × 10−2) |
| p20 = −3.843 × 10−1 (−8.201 × 10−1, 5.145 × 10−2) |
| p11 = −1.749 × 10−2 (−2.926 × 10−2, −5.721 × 10−3) |
| p02 = −1.736 × 10−4 (−1.623 × 10−3, 1.276 × 10−3) |
| p30 = 4.467 × 10−1 (−2.094 × 10−1, 1.103) |
| p21 = 8.337 × 10−3 (−1.159 × 10−3, 1.783 × 10−2) |
| p12 = 4.972 × 10−4 (7.729 × 10−5, 9.171 × 10−4) |
| p03 = 1.163 × 10−6 (−3.839 × 10−5, 4.071 × 10−5) |
| p40 = −3.24 × 10−1 (−7.665 × 10−1, 1.186 × 10−1) |
| p31 = −4.751 × 10−3 (−1.065 × 10−2, 1.146 × 10−3) |
| p22 = −4.931 × 10−5 (−2.011 × 10−4, 1.025 × 10−4) |
| p13 = −7.265 × 10−6 (−1.401 × 10−5, −5.195 × 10−7) |
| p04 = 1.758 × 10−8 (−4.95 × 10−7, 5.302 × 10−7) |
| p50 = 8.486 × 10−2 (−2.493 × 10−2, 1.946 × 10−1) |
| p41 = 2.198 × 10−3 (5.41 × 10−4, 3.855 × 10−3) |
| p32 = −2.4 × 10−5 (−6.092 × 10−5, 1.293 × 10−5) |
| p23 = 5.426 × 10−7 (−5.136 × 10−7, 1.599 × 10−6) |
| p14 = 3.898 × 10−8 (−1.76 × 10−9, 7.971 × 10−8) |
| p05 = −2.131 × 10−10 (−2.756 × 10−9, 2.33 × 10−9) |
| p00 = 4.794 × 10−1 (3.199 × 10−1, 6.388 × 10−1) |
| p00 = 1.043 × 10−3 (1.442 × 10−4, 1.941 × 10−3) |
| p10 = −1.066 × 10−4 (−9.675 × 10−4, 7.544 × 10−4) |
| p01 = 4.699 × 10−5 (−9.37 × 10−5, 1.877 × 10−4) |
| p20 = −5.178 × 10−4 (−2.973 × 10−3, 1.937 × 10−3) |
| p11 = 4.561 × 10−5 (−2.071 × 10−5, 1.119 × 10−4) |
| p02 = −3.333 × 10−6 (−1.15 × 10−5, 4.832 × 10−6) |
| p30 = 4.982 × 10−4 (−3.198 × 10−3, 4.195 × 10−3) |
| p21 = 2.274 × 10−5 (−3.076 × 10−5, 7.625 × 10−5) |
| p12 = −2.283 × 10−6 (−4.649 × 10−6, 8.235 × 10−8) |
| p03 = 6.58 × 10−8 (−1.57 × 10−7, 2.886 × 10−7) |
| p40 = −2.457 × 10−4 (−2.739 × 10−3, 2.248 × 10−3) |
| p31 = −1.03 × 10−5 (−4.352 × 10−5, 2.292 × 10−5) |
| p22 = −3.773 × 10−7 (−1.233 × 10−6, 4.781 × 10−7) |
| p13 = 4.347 × 10−8 (5.466 × 10−9, 8.147 × 10−8) |
| p04 = −4.355 × 10−10 (−3.324 × 10−9, 2.453 × 10−9) |
| p50 = 4.998 × 10−5 (−5.686 × 10−4, 6.685 × 10−4) |
| p41 = 1.876 × 10−6 (−7.46 × 10−6, 1.121 × 10−5) |
| p32 = 6.451 × 10−8 (−1.435 × 10−7, 2.725 × 10−7) |
| p23 = 2.166 × 10−9 (−3.785 × 10−9, 8.116 × 10−9) |
| p14 = −2.81 × 10−10 (−5.105 × 10−10, −5.151 × 10−11) |
| p05 = 1.276 × 10−13 (−1.42 × 10−11, 1.445 × 10−11) |
| Goodness of fit: |
| SSE: 2.306 × 10−9 |
| R-square: 0.9991 |
| Adjusted R-square: 0.9979 |
| RMSE: 1.24 × 10−5 |
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahmadi, M.H.; Ghazvini, M.; Alhuyi Nazari, M.; Ahmadi, M.A.; Pourfayaz, F.; Lorenzini, G.; Ming, T. Renewable energy harvesting with the application of nanotechnology: A review. Int. J. Energy Res. 2018, 43, 1387–1410. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ghazvini, M.; Baghban, A.; Hadipoor, M.; Seifaddini, P. Computing Approaches for Thermal C onductivity Estimation of CNT/Water Nanofluid. Rev. des Compos. des Matériaux Avancés Soft 2019, 29, 71–82. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Baghban, A.; Sadeghzadeh, M.; Zamen, M.; Mosavi, A.; Shamshirband, S.; Kumar, R.; Mohammadi-Khanaposhtani, M. Evaluation of electrical efficiency of photovoltaic thermal solar collector. Eng. Appl. Comput. Fluid Mech. 2020, 14, 545–565. [Google Scholar] [CrossRef]
- Sadeghzadeh, M.; Ahmadi, M.H.; Kahani, M.; Sakhaeinia, H.; Chaji, H.; Chen, L. Smart modeling by using artificial intelligent techniques on thermal performance of flat-plate solar collector using nanofluid. Energy Sci. Eng. 2019, 7, 1649–1658. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ghazvini, M.; Sadeghzadeh, M.; Alhuyi Nazari, M.; Kumar, R.; Naeimi, A.; Ming, T. Solar power technology for electricity generation: A critical review. Energy Sci. Eng. 2018, 6, 340–361. [Google Scholar] [CrossRef]
- Shulepova, E.V.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Mixed convection of Al2O3–H2O nanoliquid in a square chamber with complicated fin. Int. J. Mech. Sci. 2020, 165, 105192. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ghazvini, M.; Sadeghzadeh, M.; Alhuyi Nazari, M.; Ghalandari, M. Utilization of hybrid nanofluids in solar energy applications: A review. Nano Struct. Nano Objects 2019, 20, 100386. [Google Scholar] [CrossRef]
- Nazari, M.A.; Ahmadi, M.H.; Sadeghzadeh, M.; Shafii, M.B.; Goodarzi, M. A review on application of nanofluid in various types of heat pipes. J. Cent. South Univ. 2019, 26, 1021–1041. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Tatar, A.; Seifaddini, P.; Ghazvini, M.; Ghasempour, R.; Sheremet, M.A. Thermal conductivity and dynamic viscosity modeling of Fe2O3/water nanofluid by applying various connectionist approaches. Numer. Heat Transf. Part A Appl. 2018, 74, 1301–1322. [Google Scholar] [CrossRef]
- Baghban, A.; Kahani, M.; Nazari, M.A.; Ahmadi, M.H.; Yan, W.-M. Sensitivity analysis and application of machine learning methods to predict the heat transfer performance of CNT/water nanofluid flows through coils. Int. J. Heat Mass Transf. 2019, 128, 825–835. [Google Scholar] [CrossRef]
- Paluru, S.; Sudarsana Reddy, P.; Sheremet, M.A. A comparative study of Al2O3 and TiO2 nanofluid flow over a wedge with non-linear thermal radiation. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 1291–1317. [Google Scholar]
- Baghban, A.; Jalali, A.; Shafiee, M.; Ahmadi, M.H.; Chau, K.; Baghban, A.; Jalali, A.; Shafiee, M.; Ahmadi, M.H.; Chau, K.-W. Developing an ANFIS-based swarm concept model for estimating the relative viscosity of nanofluids. Eng. Appl. Comput. Fluid Mech. 2019, 13, 26–39. [Google Scholar] [CrossRef]
- Maddah, H.; Aghayari, R.; Ahmadi, M.H.; Rahimzadeh, M.; Ghasemi, N. Prediction and modeling of MWCNT/Carbon (60/40)/SAE 10 W 40/SAE 85 W 90(50/50) nanofluid viscosity using artificial neural network (ANN) and self-organizing map (SOM). J. Therm. Anal. Calorim. 2018, 134, 2275–2286. [Google Scholar] [CrossRef]
- Maddah, H.; Aghayari, R.; Mirzaee, M.; Ahmadi, M.H.; Sadeghzadeh, M.; Chamkha, A.J. Factorial experimental design for the thermal performance of a double pipe heat exchanger using Al2O3-TiO2hybrid nanofluid. Int. Commun. Heat Mass Transf. 2018, 97, 92–102. [Google Scholar] [CrossRef]
- Ahmadi, M.-A.; Ahmadi, M.H.; Fahim Alavi, M.; Nazemzadegan, M.R.; Ghasempour, R.; Shamshirband, S. Determination of thermal conductivity ratio of CuO/ethylene glycol nanofluid by connectionist approach. J. Taiwan Inst. Chem. Eng. 2018, 91, 383–395. [Google Scholar] [CrossRef]
- Kahani, M.; Ahmadi, M.H.; Tatar, A.; Sadeghzadeh, M. Development of multilayer perceptron artificial neural network (MLP-ANN) and least square support vector machine (LSSVM) models to predict Nusselt number and pressure drop of TiO2/water nanofluid flows through non-straight pathways. Numer. Heat Transf. Part A Appl. 2018, 74, 1190–1206. [Google Scholar] [CrossRef]
- Baghban, A.; Pourfayaz, F.; Ahmadi, M.H.; Kasaeian, A.; Pourkiaei, S.M.; Lorenzini, G. Connectionist intelligent model estimates of convective heat transfer coefficient of nanofluids in circular cross-sectional channels. J. Therm. Anal. Calorim. 2018, 132, 1213–1239. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Alhuyi Nazari, M.; Ghasempour, R.; Madah, H.; Shafii, M.B.; Ahmadi, M.A. Thermal conductivity ratio prediction of Al2O3/water nanofluid by applying connectionist methods. Colloids Surfaces A Physicochem. Eng. Asp. 2018, 541, 154–164. [Google Scholar] [CrossRef]
- Nazari, M.A.; Ghasempour, R.; Ahmadi, M.H.; Heydarian, G.; Shafii, M.B. Experimental investigation of graphene oxide nanofluid on heat transfer enhancement of pulsating heat pipe. Int. Commun. Heat Mass Transf. 2018, 91, 90–94. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Ahmadi, M.H.; Nazari, M.A.; Sadeghzadeh, M.; Chen, L. A review on the utilized machine learning approaches for modeling the dynamic viscosity of nanofluids. Renew. Sustain. Energy Rev. 2019, 114, 109345. [Google Scholar] [CrossRef]
- Rezaei, M.H.; Sadeghzadeh, M.; Alhuyi Nazari, M.; Ahmadi, M.H.; Astaraei, F.R. Applying GMDH artificial neural network in modeling CO2 emissions in four nordic countries. Int. J. Low Carbon Technol. 2018, 13, 266–271. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Sadeghzadeh, M.; Raffiee, A.H.; Chau, K. Applying GMDH neural network to estimate the thermal resistance and thermal conductivity of pulsating heat pipes. Eng. Appl. Comput. Fluid Mech. 2019, 13, 327–336. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Baghban, A.; Sadeghzadeh, M.; Hadipoor, M.; Ghazvini, M. Evolving connectionist approaches to compute thermal conductivity of TiO2/water nanofluid. Phys. A Stat. Mech. Its Appl. 2019, 540, 122489. [Google Scholar] [CrossRef]
- Nasirzadehroshenin, F.; Sadeghzadeh, M.; Khadang, A.; Maddah, H.; Ahmadi, M.H.; Sakhaeinia, H.; Chen, L. Modeling of heat transfer performance of carbon nanotube nanofluid in a tube with fixed wall temperature by using ANN-GA. Eur. Phys. J. Plus 2020, 135, 217. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Sadeghzadeh, M.; Maddah, H.; Solouk, A.; Kumar, R.; Chau, K. Precise smart model for estimating dynamic viscosity of SiO2/ethylene glycol–water nanofluid. Eng. Appl. Comput. Fluid Mech. 2019, 13, 1095–1105. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Rostamian, H.; Esfandeh, S.; Afrand, M. Modeling and prediction of rheological behavior of Al2O3-MWCNT/5W50 hybrid nano-lubricant by artificial neural network using experimental data. Phys. A Stat. Mech. Its Appl. 2018, 510, 625–634. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Tatar, A.; Ahangar, M.R.H.; Rostamian, H. A comparison of performance of several artificial intelligence methods for predicting the dynamic viscosity of TiO2/SAE 50 nano-lubricant. Phys. E Low-dimensional Syst. Nanostructures 2018, 96, 85–93. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Rostamian, H.; Reza Sarlak, M.; Rejvani, M.; Alirezaie, A. Rheological behavior characteristics of TiO2-MWCNT/10w40 hybrid nano-oil affected by temperature, concentration and shear rate: An experimental study and a neural network simulating. Phys. E Low Dimens. Syst. Nanostructures 2017, 94, 231–240. [Google Scholar] [CrossRef]
- Bahrami, M.; Akbari, M.; Bagherzadeh, S.A.; Karimipour, A.; Afrand, M.; Goodarzi, M. Develop 24 dissimilar ANNs by suitable architectures & training algorithms via sensitivity analysis to better statistical presentation: Measure MSEs between targets & ANN for Fe–CuO/Eg–Water nanofluid. Phys. A Stat. Mech. Its Appl. 2019, 519, 159–168. [Google Scholar]
- Nafchi, P.M.; Karimipour, A.; Afrand, M. The evaluation on a new non-Newtonian hybrid mixture composed of TiO2/ZnO/EG to present a statistical approach of power law for its rheological and thermal properties. Phys. A Stat. Mech. Its Appl. 2019, 516, 1–18. [Google Scholar] [CrossRef]
- Mikhailenko, S.A.; Sheremet, M.; Öztop, H.; Abu-Hamdeh, N. Thermal convection in Al2O3-water nanoliquid rotating chamber with a local isothermal heater. Int. J. Mech. Sci. 2019, 156, 137–145. [Google Scholar] [CrossRef]
- Vafaei, M.; Afrand, M.; Sina, N.; Kalbasi, R.; Sourani, F.; Teimouri, H. Evaluation of thermal conductivity of MgO-MWCNTs/EG hybrid nanofluids based on experimental data by selecting optimal artificial neural networks. Phys. E Low Dimens. Syst. Nanostructures 2017, 85, 90–96. [Google Scholar] [CrossRef]
- Afrand, M.; Hemmat Esfe, M.; Abedini, E.; Teimouri, H. Predicting the effects of magnesium oxide nanoparticles and temperature on the thermal conductivity of water using artificial neural network and experimental data. Phys. E Low Dimens. Syst. Nanostructures 2017, 87, 242–247. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Nadooshan, A.A.; Arshi, A.; Alirezaie, A. Convective heat transfer and pressure drop of aqua based TiO2 nanofluids at different diameters of nanoparticles: Data analysis and modeling with artificial neural network. Phys. E Low Dimens. Syst. Nanostructures 2018, 97, 155–161. [Google Scholar] [CrossRef]
- Azizi, S.; Awad, M.M.; Ahmadloo, E. Prediction of water holdup in vertical and inclined oil–water two-phase flow using artificial neural network. Int. J. Multiph. Flow 2016, 80, 181–187. [Google Scholar] [CrossRef]
- Azizi, S.; Ahmadloo, E.; Awad, M.M. Prediction of void fraction for gas–liquid flow in horizontal, upward and downward inclined pipes using artificial neural network. Int. J. Multiph. Flow 2016, 87, 35–44. [Google Scholar] [CrossRef]
- Li, Y.; White, T.; Lim, S. Low-temperature synthesis and microstructural control of titania nano-particles. J. Solid State Chem. 2004, 177, 1372–1381. [Google Scholar] [CrossRef]
- Li, B.; Wang, X.; Yan, M.; Li, L. Preparation and characterization of nano-TiO2 powder. Mater. Chem. Phys. 2003, 78, 184–188. [Google Scholar] [CrossRef]
- Zhang, R.; Gao, L. Preparation of nanosized titania by hydrolysis of alkoxide titanium in micelles. Mater. Res. Bull. 2002, 37, 1659–1666. [Google Scholar] [CrossRef]
- Pavasupree, S.; Suzuki, Y.; Pivsa-Art, S.; Yoshikawa, S. Synthesis and characterization of nanoporous, nanorods, nanowires metal oxides. Sci. Technol. Adv. Mater. 2005, 6, 224–229. [Google Scholar] [CrossRef]
- Colón, G.; Hidalgo, M.; Navío, J. A novel preparation of high surface area TiO2 nanoparticles from alkoxide precursor and using active carbon as additive. Catal. Today 2002, 76, 91–101. [Google Scholar] [CrossRef]
- Oliveira, M.; Machado, A.V. Preparation of Polymer-Based Nanocomposites by Different Routes; Portuguese Foundation of Science and Technology: Lisbon, Portugal, 2013. [Google Scholar]
- Ghasemi, N.; Mirzaee, M.; Aghayari, R.; Maddah, H. Investigating Created Properties of Nanoparticles Based Drilling Mud. Heat Mass Transf. 2018, 54, 1381–1393. [Google Scholar] [CrossRef]
- Ganguly, S.; Sikdar, S.; Basu, S. Experimental investigation of the effective electrical conductivity of aluminum oxide nanofluids. Powder Technol. 2009, 196, 326–330. [Google Scholar] [CrossRef]
- Ahammed, N.; Asirvatham, L.G.; Wongwises, S. Effect of volume concentration and temperature on viscosity and surface tension of graphene–water nanofluid for heat transfer applications. J. Therm. Anal. Calorim. 2016, 123, 1399–1409. [Google Scholar] [CrossRef]
- Toghraie, D.; Chaharsoghi, V.A.; Afrand, M. Measurement of thermal conductivity of ZnO–TiO2/EG hybrid nanofluid. J. Therm. Anal. Calorim. 2016, 125, 527–535. [Google Scholar] [CrossRef]


| Parameter | Range |
|---|---|
| Temperature (°C) | 10–70 |
| Volumetric Concentration (%) | 0.25–6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghzadeh, M.; Maddah, H.; Ahmadi, M.H.; Khadang, A.; Ghazvini, M.; Mosavi, A.; Nabipour, N. Prediction of Thermo-Physical Properties of TiO2-Al2O3/Water Nanoparticles by Using Artificial Neural Network. Nanomaterials 2020, 10, 697. https://doi.org/10.3390/nano10040697
Sadeghzadeh M, Maddah H, Ahmadi MH, Khadang A, Ghazvini M, Mosavi A, Nabipour N. Prediction of Thermo-Physical Properties of TiO2-Al2O3/Water Nanoparticles by Using Artificial Neural Network. Nanomaterials. 2020; 10(4):697. https://doi.org/10.3390/nano10040697
Chicago/Turabian StyleSadeghzadeh, Milad, Heydar Maddah, Mohammad Hossein Ahmadi, Amirhosein Khadang, Mahyar Ghazvini, Amirhosein Mosavi, and Narjes Nabipour. 2020. "Prediction of Thermo-Physical Properties of TiO2-Al2O3/Water Nanoparticles by Using Artificial Neural Network" Nanomaterials 10, no. 4: 697. https://doi.org/10.3390/nano10040697
APA StyleSadeghzadeh, M., Maddah, H., Ahmadi, M. H., Khadang, A., Ghazvini, M., Mosavi, A., & Nabipour, N. (2020). Prediction of Thermo-Physical Properties of TiO2-Al2O3/Water Nanoparticles by Using Artificial Neural Network. Nanomaterials, 10(4), 697. https://doi.org/10.3390/nano10040697







