Damage Monitoring of Structural Resins Loaded with Carbon Fillers: Experimental and Theoretical Study
Abstract
:1. Introduction
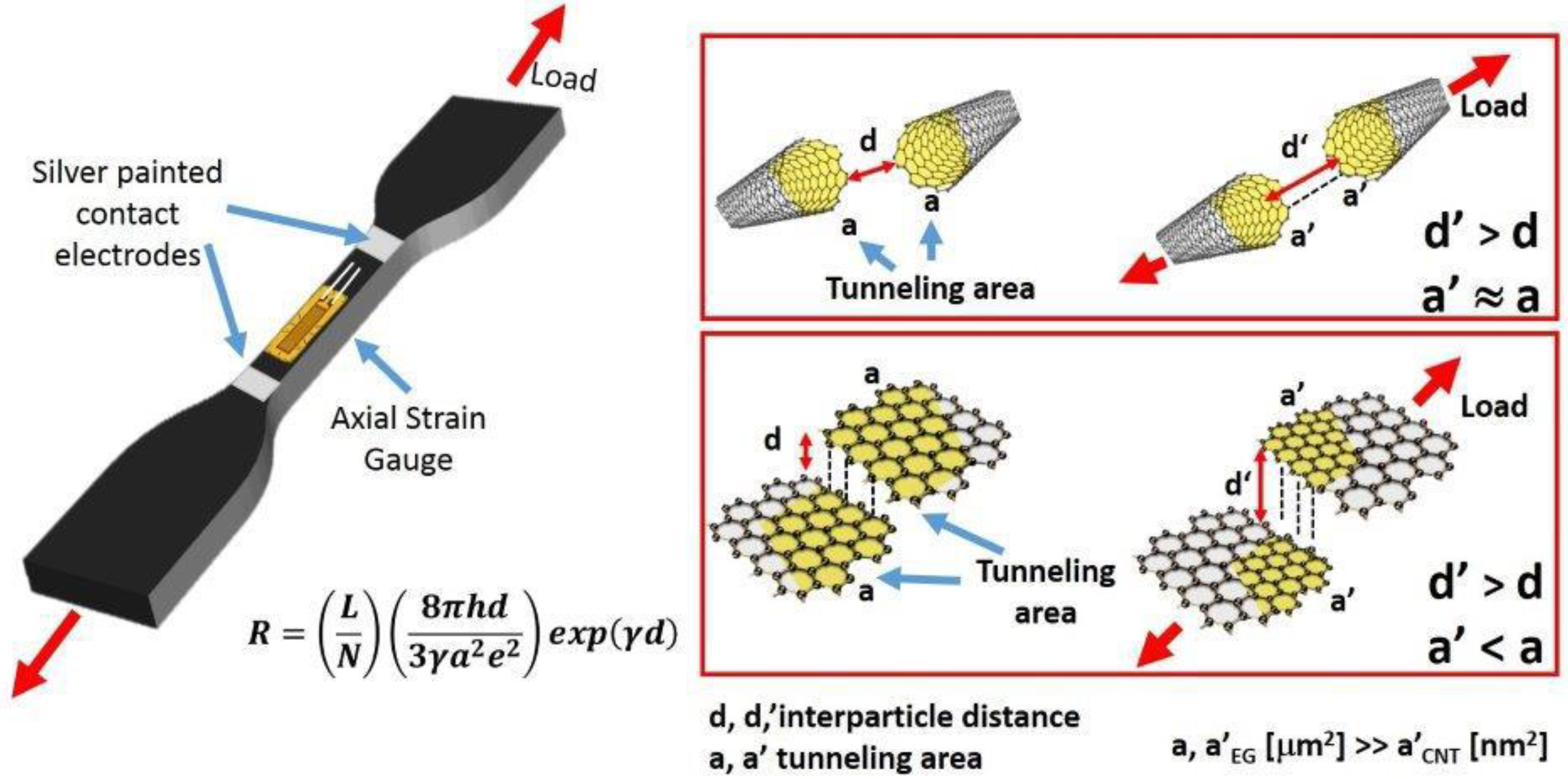
2. Materials and Methods
3. Results and Discussion
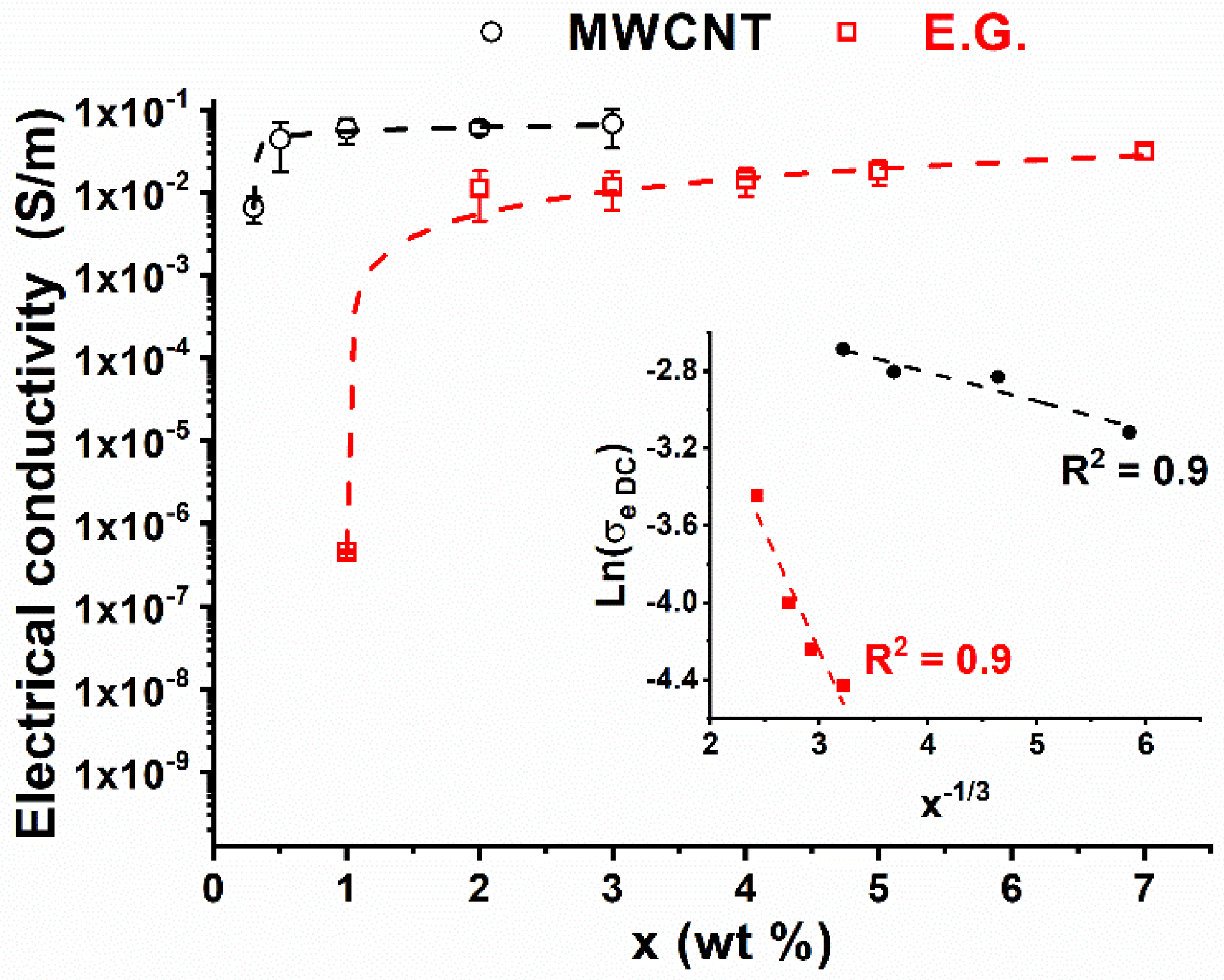
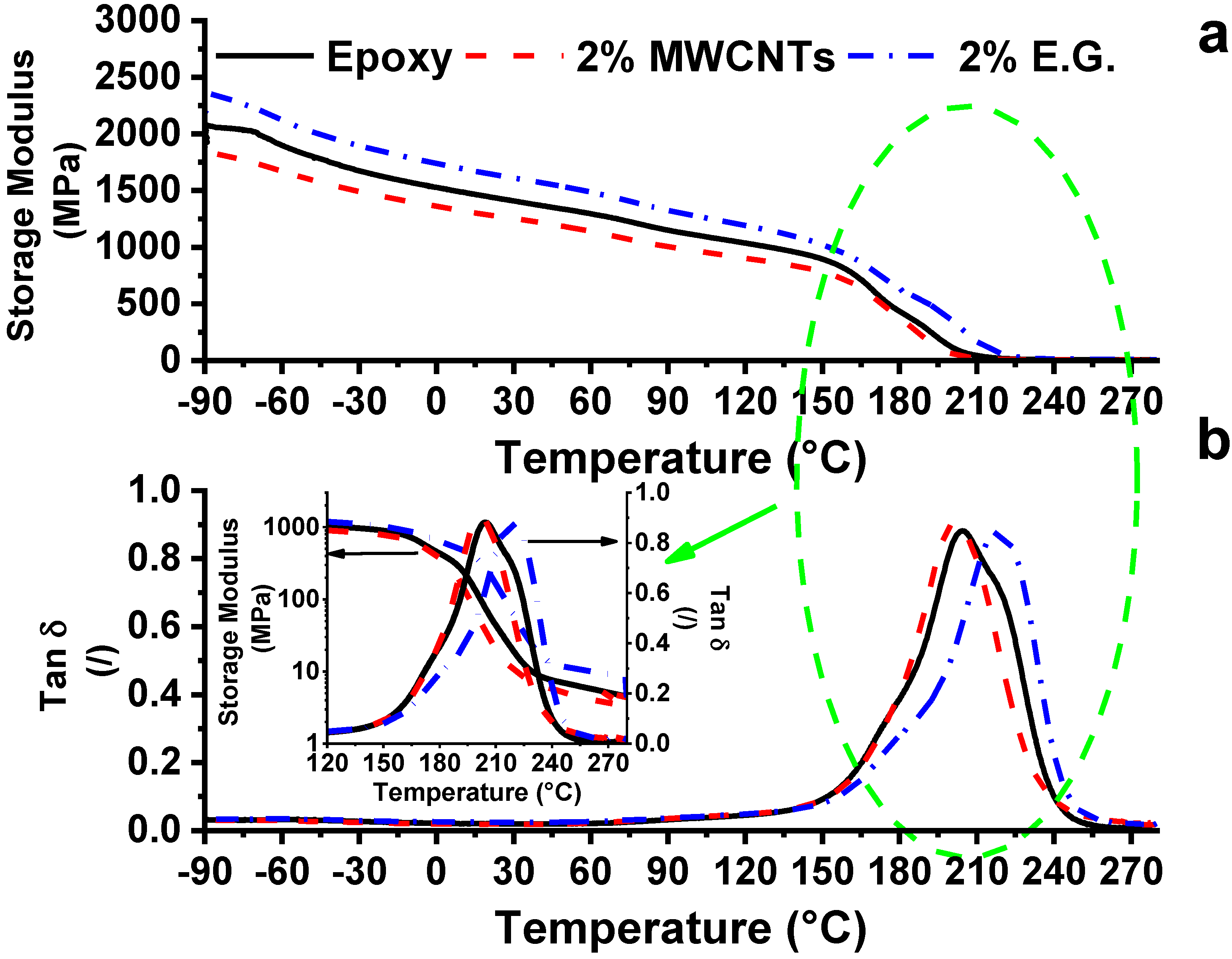
3.1. Electrical and Mechanical Properties
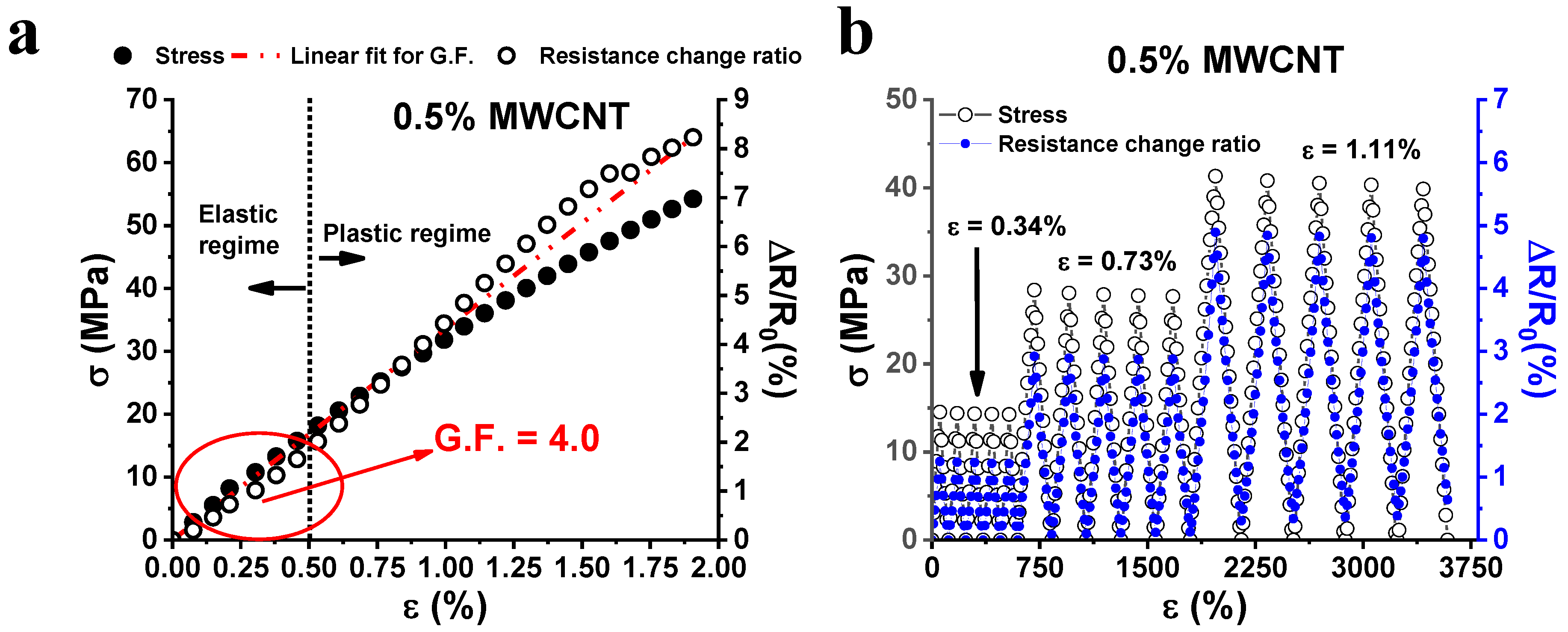
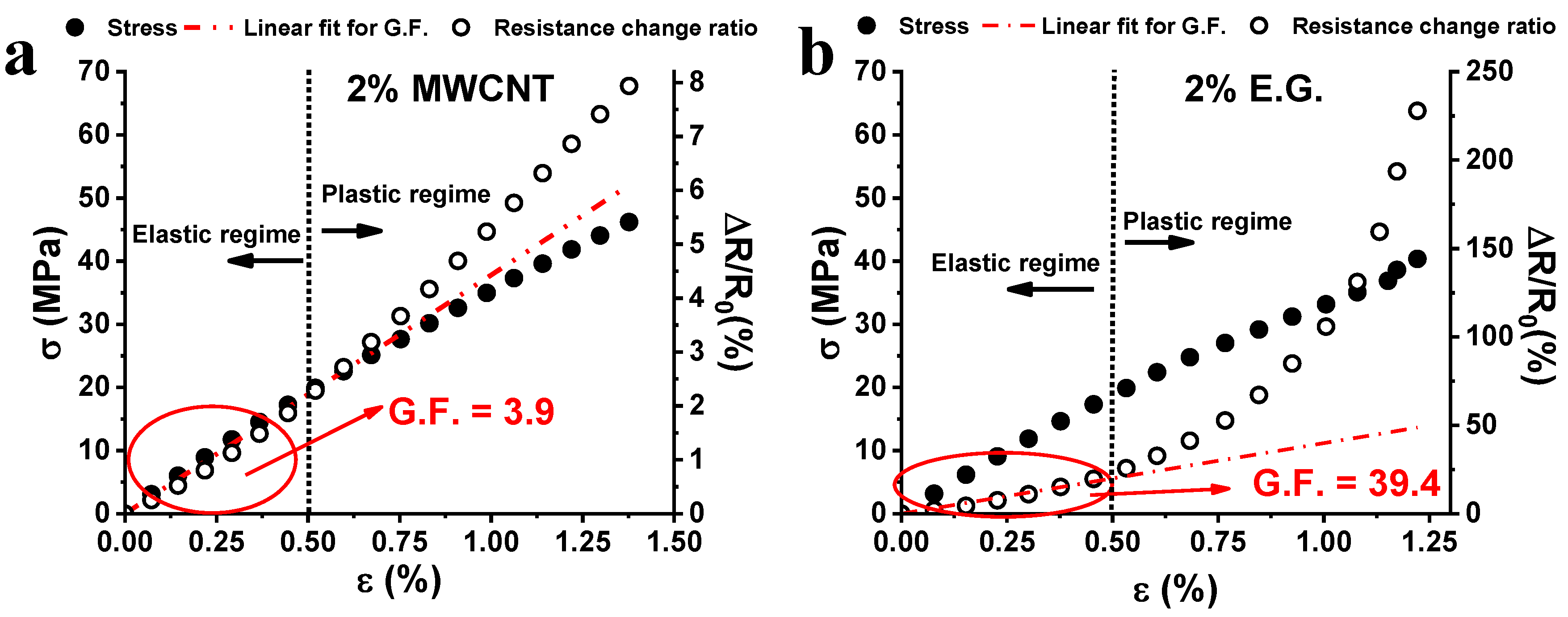
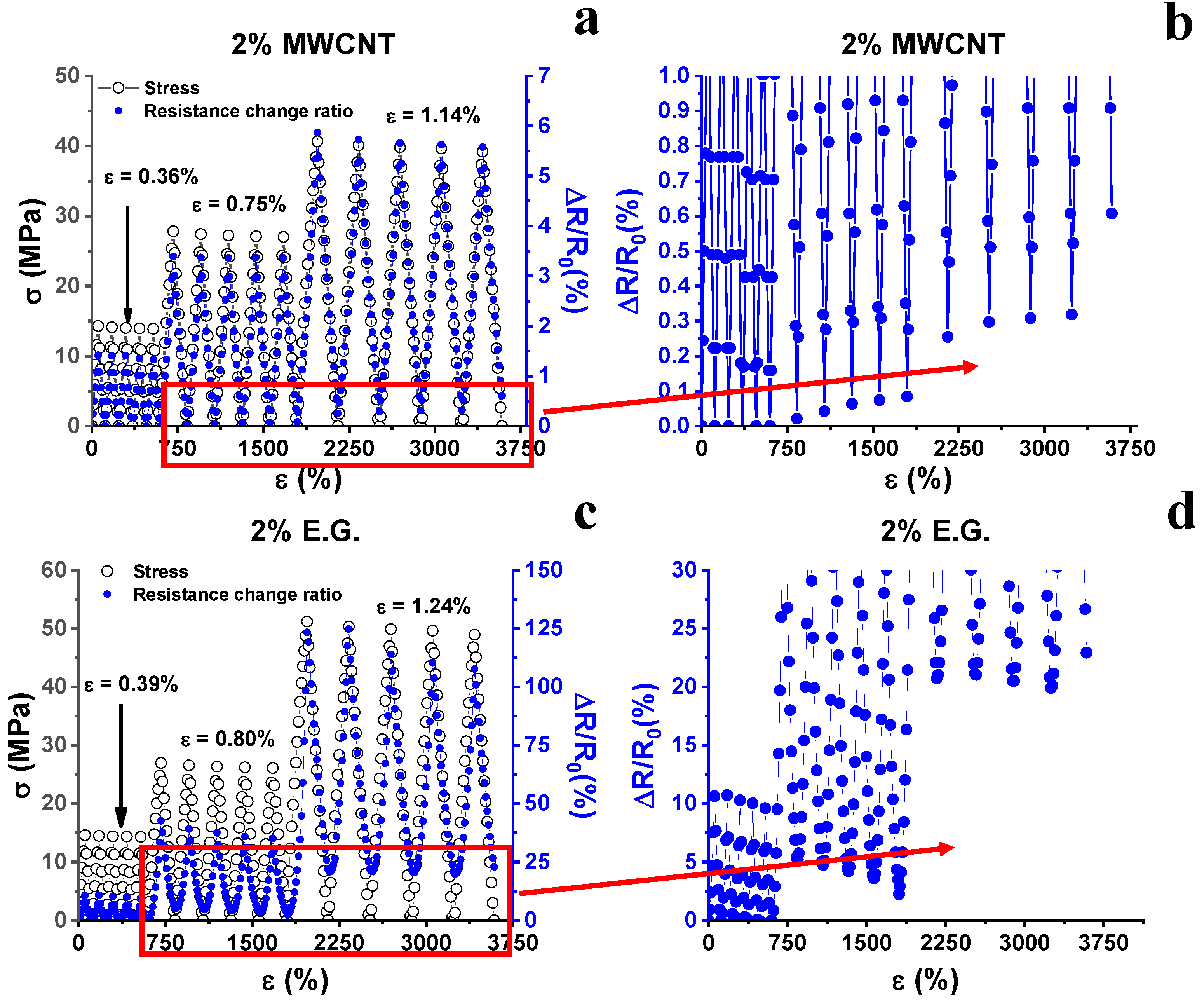
3.2. Piezoresistive Characterization
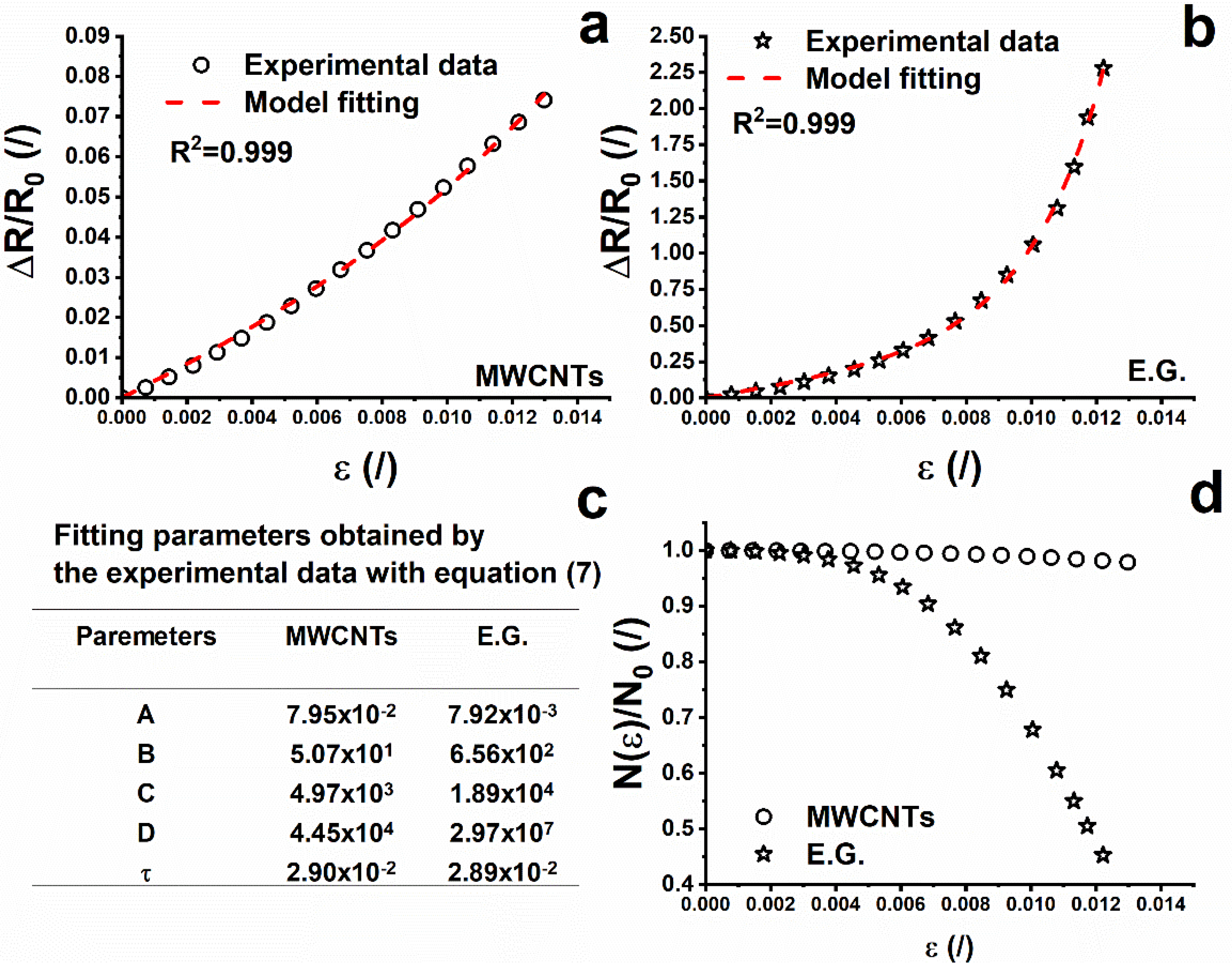
3.3. Modeling of the Electro-Mechanical Mechanism
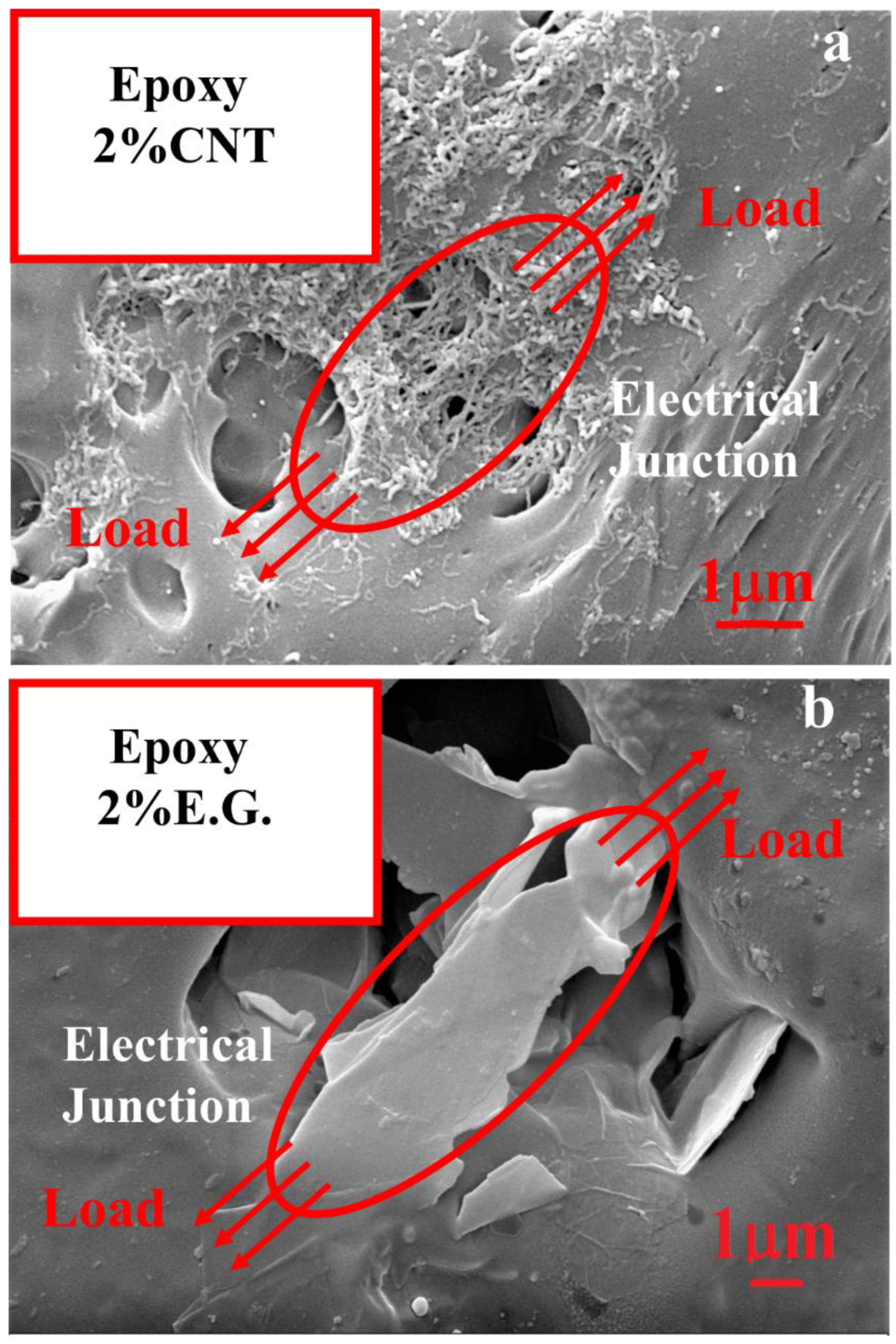
3.4. Morphological Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Staszewski, W.; Boller, C.; Tomlinson, G.R. Health Monitoring of Aerospace Structures: Smart Sensor Technologies and Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Spinelli, G.; Lamberti, P.; Tucci, V.; Vertuccio, L.; Guadagno, L. Experimental and theoretical study on piezoresistive properties of a structural resin reinforced with carbon nanotubes for strain sensing and damage monitoring. Compos. B Eng. 2018, 145, 90–99. [Google Scholar] [CrossRef]
- Vertuccio, L.; De Santis, F.; Pantani, R.; Lafdi, K.; Guadagno, L. Effective de-icing skin using graphene-based flexible heater. Compos. B Eng. 2019, 162, 600–610. [Google Scholar] [CrossRef]
- Vertuccio, L.; Guadagno, L.; Spinelli, G.; Lamberti, P.; Tucci, V.; Russo, S. Piezoresistive properties of resin reinforced with carbon nanotubes for health-monitoring of aircraft primary structures. Compos. B: Eng. 2016, 107, 192–202. [Google Scholar] [CrossRef]
- Vertuccio, L.; Guadagno, L.; Spinelli, G.; Lamberti, P.; Zarrelli, M.; Russo, S.; Iannuzzo, G. Smart coatings of epoxy based CNTs designed to meet practical expectations in aeronautics. Compos. B Eng. 2018, 147, 42–46. [Google Scholar] [CrossRef]
- Chiacchiarelli, L.M.; Rallini, M.; Monti, M.; Puglia, D.; Kenny, J.M.; Torre, L. The role of irreversible and reversible phenomena in the piezoresistive behavior of graphene epoxy nanocomposites applied to structural health monitoring. Compos. Sci. Technol. 2013, 80, 73–79. [Google Scholar] [CrossRef]
- Moriche, R.; Sánchez, M.; Jiménez-Suárez, A.; Prolongo, S.; Urena, A. Strain monitoring mechanisms of sensors based on the addition of graphene nanoplatelets into an epoxy matrix. Compos. Sci. Technol. 2016, 123, 65–70. [Google Scholar] [CrossRef]
- Zha, J.-W.; Zhang, B.; Li, R.K.; Dang, Z.-M. High-performance strain sensors based on functionalized graphene nanoplates for damage monitoring. Compos. Sci. Technol. 2016, 123, 32–38. [Google Scholar] [CrossRef]
- Vertuccio, L.; Vittoria, V.; Guadagno, L.; De Santis, F. Strain and damage monitoring in carbon-nanotube-based composite under cyclic strain. Compos. Part A Appl. Sci. Manuf. 2015, 71, 9–16. [Google Scholar] [CrossRef]
- Guadagno, L.; Naddeo, C.; Raimondo, M.; Barra, G.; Vertuccio, L.; Russo, S.; Lafdi, K.; Tucci, V.; Spinelli, G.; Lamberti, P. Influence of carbon nanoparticles/epoxy matrix interaction on mechanical, electrical and transport properties of structural advanced materials. Nanotechnology 2017, 28, 094001. [Google Scholar] [CrossRef]
- Rawal, S.; Ravine, J.; Czerw, R. Graphene nanoplatelet membranes for aerospace applications. Nanotechnology 2011, 1, 411–414. [Google Scholar]
- Bao, Q.; Zhang, H.; Yang, J.x.; Wang, S.; Tang, D.Y.; Jose, R.; Ramakrishna, S.; Lim, C.T.; Loh, K.P. Graphene–polymer nanofiber membrane for ultrafast photonics. Adv. Funct. Mater. 2010, 20, 782–791. [Google Scholar] [CrossRef]
- Batrakov, K.; Kuzhir, P.; Maksimenko, S.; Paddubskaya, A.; Voronovich, S.; Lambin, P.; Kaplas, T.; Svirko, Y. Flexible transparent graphene/polymer multilayers for efficient electromagnetic field absorption. Sci. Rep. 2014, 4, 7191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watanabe, A.O.; Jeong, S.; Kim, S.; Kim, Y.; Min, J.; Wong, D.; Pulugurtha, M.R.; Mullapudi, R.; Kim, J.; Tummala, R.R. Highly-effective integrated EMI shields with graphene and nanomagnetic multilayered composites. In Proceedings of the 2016 IEEE 66th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 31 May–3 June 2016; pp. 206–210. [Google Scholar]
- Hill, E.W.; Vijayaragahvan, A.; Novoselov, K. Graphene sensors. IEEE Sens. J. 2011, 11, 3161–3170. [Google Scholar] [CrossRef]
- Li, W.; Dichiara, A.; Bai, J. Carbon nanotube–graphene nanoplatelet hybrids as high-performance multifunctional reinforcements in epoxy composites. Compos. Sci. Technol. 2013, 74, 221–227. [Google Scholar] [CrossRef]
- Galpaya, D.; Wang, M.; Liu, M.; Motta, N.; Waclawik, E.R.; Yan, C. Recent advances in fabrication and characterization of graphene-polymer nanocomposites. Graphene 2012, 1, 30–49. [Google Scholar] [CrossRef] [Green Version]
- Guadagno, L.; Raimondo, M.; Vertuccio, L.; Mauro, M.; Guerra, G.; Lafdi, K.; De Vivo, B.; Lamberti, P.; Spinelli, G.; Tucci, V. Optimization of graphene-based materials outperforming host epoxy matrices. RSC Adv. 2015, 5, 36969–36978. [Google Scholar] [CrossRef] [Green Version]
- Kuilla, T.; Bhadra, S.; Yao, D.; Kim, N.H.; Bose, S.; Lee, J.H. Recent advances in graphene based polymer composites. Prog. Polym. Sci. 2010, 35, 1350–1375. [Google Scholar] [CrossRef]
- Vertuccio, L.; Russo, S.; Raimondo, M.; Lafdi, K.; Guadagno, L. Influence of carbon nanofillers on the curing kinetics of epoxy-amine resin. RSC Adv. 2015, 5, 90437–90450. [Google Scholar] [CrossRef]
- Standard, A. D638: Standard Test Method for Tensile Properties of Plastics; ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Ku-Herrera, J.; Aviles, F. Cyclic tension and compression piezoresistivity of carbon nanotube/vinyl ester composites in the elastic and plastic regimes. Carbon 2012, 50, 2592–2598. [Google Scholar] [CrossRef]
- Oliva-Avilés, A.; Avilés, F.; Sosa, V. Electrical and piezoresistive properties of multi-walled carbon nanotube/polymer composite films aligned by an electric field. Carbon 2011, 49, 2989–2997. [Google Scholar] [CrossRef]
- Huang, J.C. Carbon black filled conducting polymers and polymer blends. Adv. Polym. Tech. 2002, 21, 299–313. [Google Scholar] [CrossRef]
- Nan, C.-W.; Shen, Y.; Ma, J. Physical properties of composites near percolation. Annu. Rev. Mater. Res. 2010, 40, 131–151. [Google Scholar] [CrossRef]
- Connor, M.T.; Roy, S.; Ezquerra, T.A.; Calleja, F.J.B. Broadband ac conductivity of conductor-polymer composites. Phys. Rev. B 1998, 57, 2286. [Google Scholar] [CrossRef] [Green Version]
- Kilbride, B.e.; Coleman, J.; Fraysse, J.; Fournet, P.; Cadek, M.; Drury, A.; Hutzler, S.; Roth, S.; Blau, W. Experimental observation of scaling laws for alternating current and direct current conductivity in polymer-carbon nanotube composite thin films. J. Appl. Phys. 2002, 92, 4024–4030. [Google Scholar] [CrossRef]
- Mdarhri, A.; Carmona, F.; Brosseau, C.; Delhaes, P. Direct current electrical and microwave properties of polymer-multiwalled carbon nanotubes composites. J. Appl. Phys. 2008, 103, 054303. [Google Scholar] [CrossRef]
- De Vivo, B.; Lamberti, P.; Spinelli, G.; Tucci, V. Numerical investigation on the influence factors of the electrical properties of carbon nanotubes-filled composites. J. Appl. Phys. 2013, 113, 244301. [Google Scholar] [CrossRef]
- Jing, Z.; Guang-Yu, Z.; Dong-Xia, S. Review of graphene-based strain sensors. Chin. Phys. B 2013, 22, 057701. [Google Scholar]
- Kang, I.; Heung, Y.Y.; Kim, J.H.; Lee, J.W.; Gollapudi, R.; Subramaniam, S.; Narasimhadevara, S.; Hurd, D.; Kirikera, G.R.; Shanov, V. Introduction to carbon nanotube and nanofiber smart materials. Compos. B Eng. 2006, 37, 382–394. [Google Scholar] [CrossRef]
- Wang, B.; Lee, B.-K.; Kwak, M.-J.; Lee, D.-W. Graphene/polydimethylsiloxane nanocomposite strain sensor. Rev. Sci. Instrum. 2013, 84, 105005. [Google Scholar] [CrossRef]
- Kotsilkova, R.; Fragiadakis, D.; Pissis, P. Reinforcement effect of carbon nanofillers in an epoxy resin system: Rheology, molecular dynamics, and mechanical studies. J. Polym. Sci. Pol. Phys. 2005, 43, 522–533. [Google Scholar] [CrossRef]
- Li, B.; Zhong, W.-H. Review on polymer/graphite nanoplatelet nanocomposites. J. Mater. Sci. 2011, 46, 5595–5614. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Z.; Moon, K.S.; Wong, C. Glass transition and relaxation behavior of epoxy nanocomposites. J. Polym. Sci. Pol. Phys. 2004, 42, 3849–3858. [Google Scholar] [CrossRef]
- Li, C.; Thostenson, E.T.; Chou, T.-W. Dominant role of tunneling resistance in the electrical conductivity of carbon nanotube–based composites. Appl. Phys. Lett. 2007, 91, 223114. [Google Scholar] [CrossRef]
- Hu, N.; Karube, Y.; Arai, M.; Watanabe, T.; Yan, C.; Li, Y.; Liu, Y.; Fukunaga, H. Investigation on sensitivity of a polymer/carbon nanotube composite strain sensor. Carbon 2010, 48, 680–687. [Google Scholar] [CrossRef]
- Kang, I.; Schulz, M.J.; Kim, J.H.; Shanov, V.; Shi, D. A carbon nanotube strain sensor for structural health monitoring. Smart Mater. Struct. 2006, 15, 737. [Google Scholar] [CrossRef]
- Njuguna, M.; Yan, C.; Hu, N.; Bell, J.; Yarlagadda, P. Sandwiched carbon nanotube film as strain sensor. Compos. B Eng. 2012, 43, 2711–2717. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Pascal, T.A.; Kim, H.; Goddard III, W.A.; Greer, J.R. Electronic−mechanical coupling in graphene from in situ nanoindentation experiments and multiscale atomistic simulations. Nano Lett. 2011, 11, 1241–1246. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.; Bae, S.; Jang, H.; Jang, S.; Zhu, S.-E.; Sim, S.H.; Song, Y.I.; Hong, B.H.; Ahn, J.-H. Wafer-scale synthesis and transfer of graphene films. Nano Lett. 2010, 10, 490–493. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Li, Y.; Dai, K.; Zheng, G.; Liu, C.; Shen, C.; Yan, X.; Guo, J.; Guo, Z. Electrically conductive thermoplastic elastomer nanocomposites at ultralow graphene loading levels for strain sensor applications. J. Mater. Chem. C 2016, 4, 157–166. [Google Scholar] [CrossRef]
- Yan, C.; Wang, J.; Kang, W.; Cui, M.; Wang, X.; Foo, C.Y.; Chee, K.J.; Lee, P.S. Highly stretchable piezoresistive graphene–nanocellulose nanopaper for strain sensors. Adv. Mater. 2014, 26, 2022–2027. [Google Scholar] [CrossRef]
- Lee, C.; Jug, L.; Meng, E. High strain biocompatible polydimethylsiloxane-based conductive graphene and multiwalled carbon nanotube nanocomposite strain sensors. Appl. Phys. Lett. 2013, 102, 183511. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; He, C.; Yang, R.; Shi, Z.; Cheng, M.; Yang, W.; Xie, G.; Wang, D.; Shi, D.; Zhang, G. Ultra-sensitive strain sensors based on piezoresistive nanographene films. Appl. Phys. Lett. 2012, 101, 063112. [Google Scholar] [CrossRef]
- Zhang, X.W.; Pan, Y.; Zheng, Q.; Yi, X.S. Time dependence of piezoresistance for the conductor-filled polymer composites. J. Polym. Sci. Pol. Phys. 2000, 38, 2739–2749. [Google Scholar] [CrossRef]
- Simmons, J.G. Generalized formula for the electric tunnel effect between similar electrodes separated by a thin insulating film. J. Appl. Phys. 1963, 34, 1793–1803. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Meng, S.; Tebyetekerwa, M.; Li, Y.; Pionteck, J.; Sun, B.; Qin, Z.; Zhu, M. Highly sensitive and stretchable piezoresistive strain sensor based on conductive poly (styrene-butadiene-styrene)/few layer graphene composite fiber. Compos. Part A Appl. Sci. Manuf. 2018, 105, 291–299. [Google Scholar] [CrossRef]
- Sheng, P.; Sichel, E.; Gittleman, J. Fluctuation-induced tunneling conduction in carbon-polyvinylchloride composites. Phys. Rev. Lett. 1978, 40, 1197. [Google Scholar] [CrossRef]
- Knite, M.; Teteris, V.; Kiploka, A.; Kaupuzs, J. Polyisoprene-carbon black nanocomposites as tensile strain and pressure sensor materials. Sens. Actuators A Phys. 2004, 110, 142–149. [Google Scholar] [CrossRef]
- Hao, B.; Ma, Q.; Yang, S.; Mäder, E.; Ma, P.-C. Comparative study on monitoring structural damage in fiber-reinforced polymers using glass fibers with carbon nanotubes and graphene coating. Compos. Sci. Tech. 2016, 129, 38–45. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Cha, J.Y.; Ham, H.; Huh, H.; So, D.-S.; Kang, I. Preparation of piezoresistive nano smart hybrid material based on graphene. Curr. Appl. Phys. 2011, 11, S350–S352. [Google Scholar] [CrossRef]
- Spinelli, G.; Giustiniani, A.; Lamberti, P.; Tucci, V.; Zamboni, W. Numerical study of electrical behaviour in carbon nanotube composites. Int. J. Appl. Electrom. 2012, 39, 21–27. [Google Scholar] [CrossRef]
| Operating Conditions | Specific |
|---|---|
| Sample dimension | 1 × 10 × 25 mm3 (thickness, width, and length, respectively) |
| Configuration | 3-points bending mode |
| Displacement amplitude | 0.02 mm |
| Frequency operating condition | 1 Hz |
| Temperature operating condition | from −90 °C to 280 °C |
| Scanning rate | 3 °C/min−1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spinelli, G.; Lamberti, P.; Tucci, V.; Guadagno, L.; Vertuccio, L. Damage Monitoring of Structural Resins Loaded with Carbon Fillers: Experimental and Theoretical Study. Nanomaterials 2020, 10, 434. https://doi.org/10.3390/nano10030434
Spinelli G, Lamberti P, Tucci V, Guadagno L, Vertuccio L. Damage Monitoring of Structural Resins Loaded with Carbon Fillers: Experimental and Theoretical Study. Nanomaterials. 2020; 10(3):434. https://doi.org/10.3390/nano10030434
Chicago/Turabian StyleSpinelli, Giovanni, Patrizia Lamberti, Vincenzo Tucci, Liberata Guadagno, and Luigi Vertuccio. 2020. "Damage Monitoring of Structural Resins Loaded with Carbon Fillers: Experimental and Theoretical Study" Nanomaterials 10, no. 3: 434. https://doi.org/10.3390/nano10030434
APA StyleSpinelli, G., Lamberti, P., Tucci, V., Guadagno, L., & Vertuccio, L. (2020). Damage Monitoring of Structural Resins Loaded with Carbon Fillers: Experimental and Theoretical Study. Nanomaterials, 10(3), 434. https://doi.org/10.3390/nano10030434









