Magnetoelectric Composites: Applications, Coupling Mechanisms, and Future Directions
Abstract
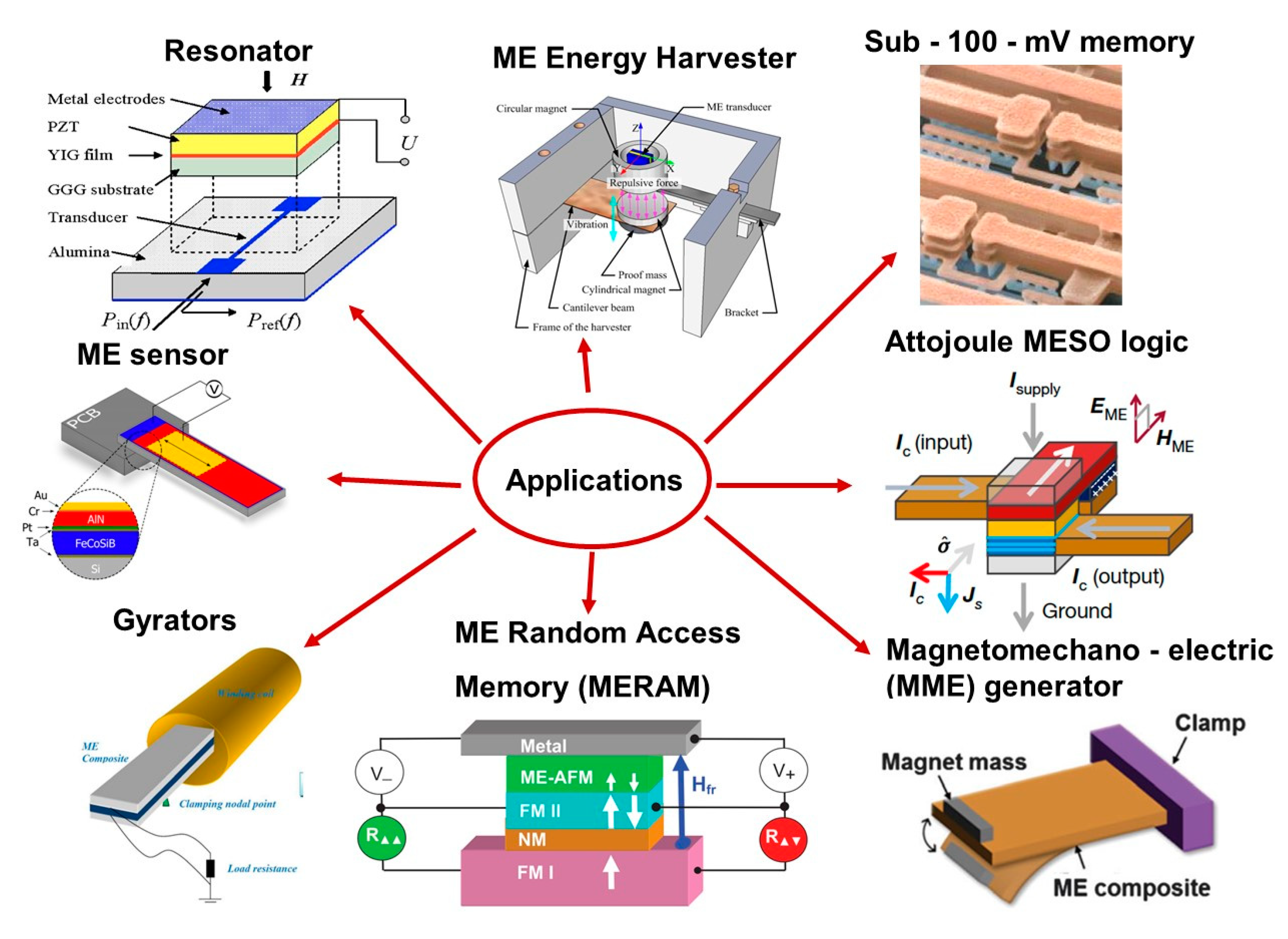
:1. Introduction
2. ME Effect
2.1. Direct ME Coupling
2.2. Converse ME Coupling
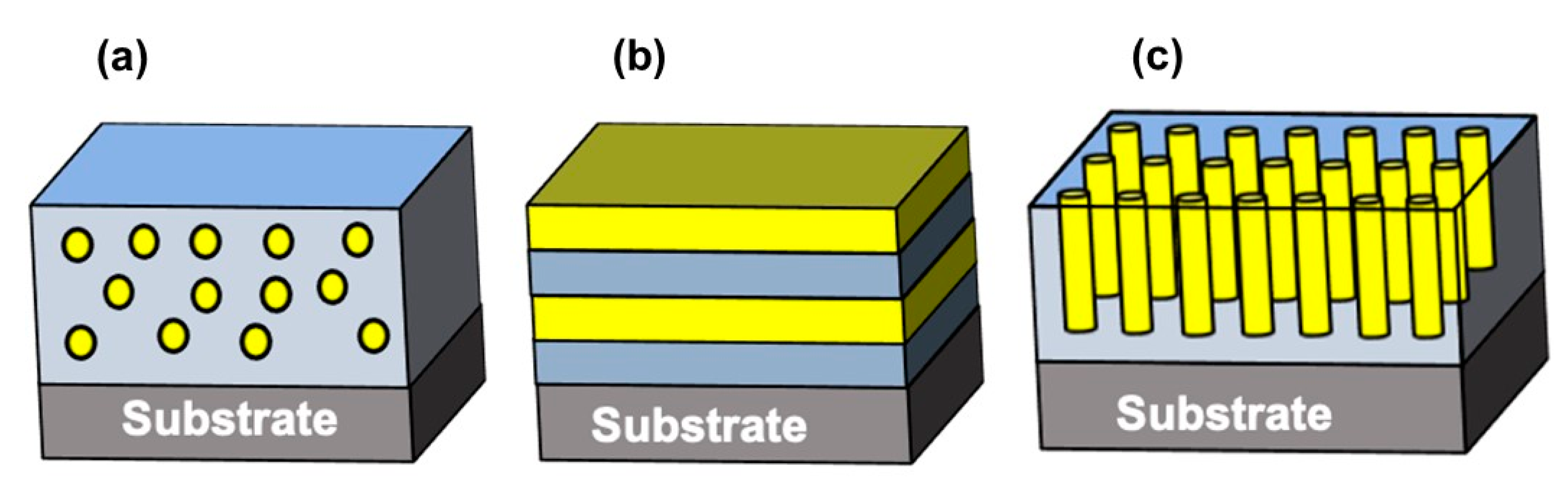
3. Mechanisms of ME Coupling
3.1. Strain Mediated ME Coupling
3.2. Charge Mediated ME Coupling
3.3. ME Coupling Due to Spin Exchange
4. ME Coupling Coefficient
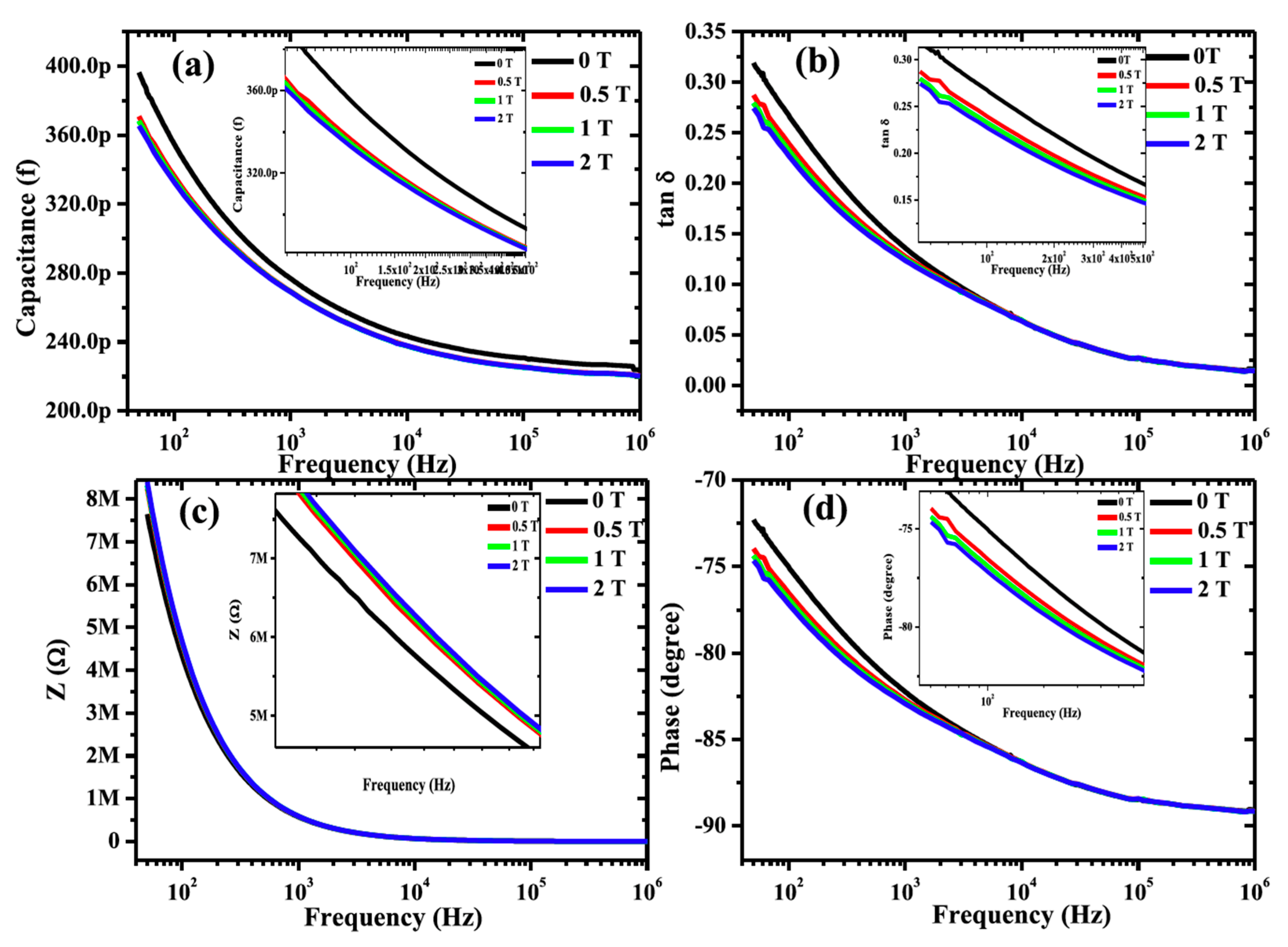
5. Magnetodielectric Coupling
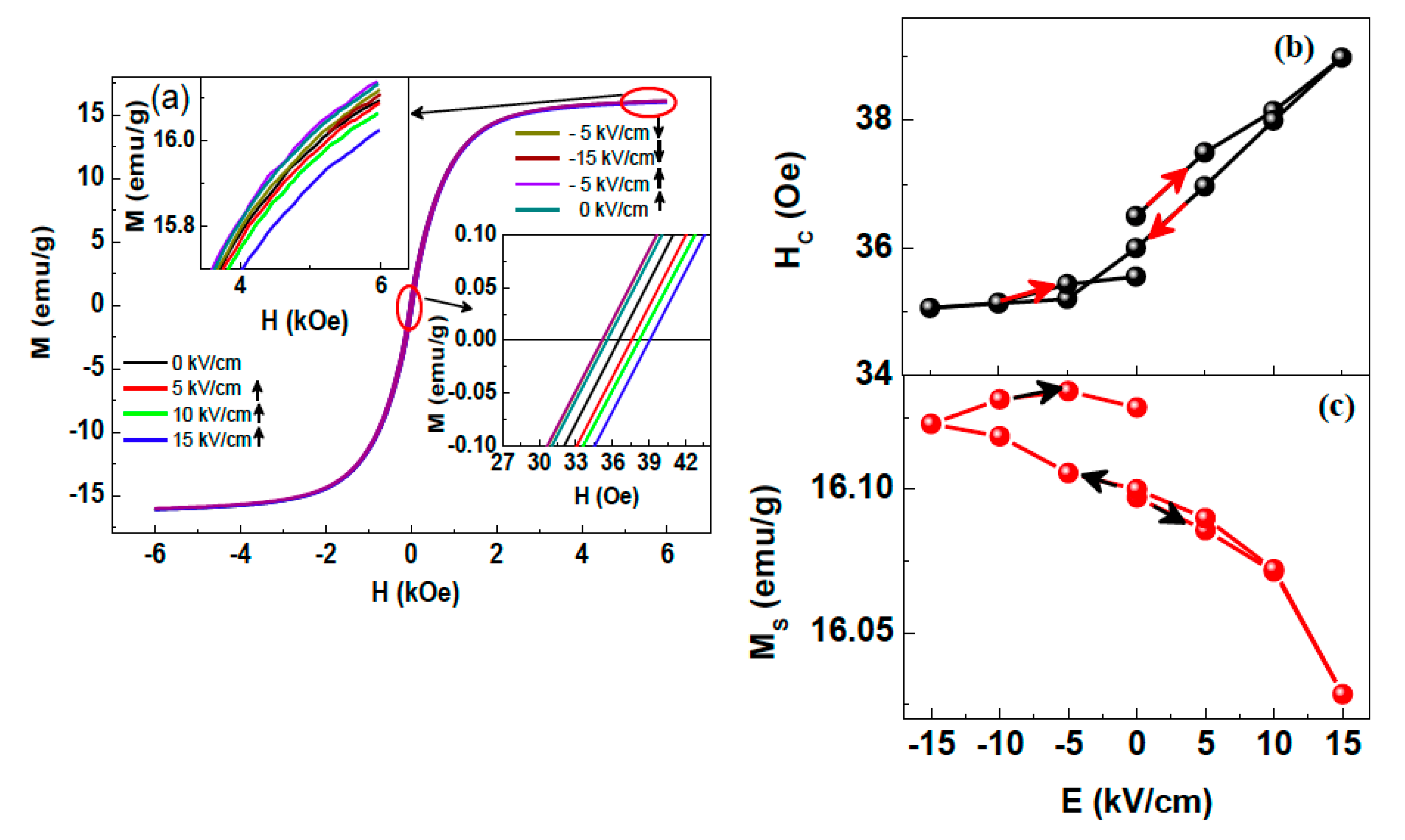
6. Nature of ME Coupling
7. Summary and Future Directions
- Discovery of new lead-free room temperature ME materials guided by theory having strong cross coupling between magnetization and polarization, low leakage current, and high remanent magnetization should be given the top priority.
- Elucidate the effect of microstructure on ME coupling.
- Explore new FE and magnetic domain structures, such as magnetic skyrmions and polar vortices, as this might lead to different types of ME coupling.
- Examine the behavior of ferroic order parameters under the application ultrafast stimuli (optical, acoustic, and electrical).
- Investigate the role of MF orderings on the emergence of different quantum phenomena as this could open completely new directions.
- Maintain the thermal stability at RT of strongly coupled magnetic and FE orderings at 10-nm length scale is one of the most important requirements for emerging technologies.
- Advanced characterization tools are required in order to study multiferroic and ME properties at the nanometer and atomic lengthscale.
- The FE and/or ME switching voltage should be ≤100 mV for realization of ultra-low power devices.
- Successful integration on-chip, compatibility with different process technologies, and optimizing the ME device performance are all required for ME materials to penetrate practical device applications.
Author Contributions
Funding
Conflicts of Interest
References
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123. [Google Scholar] [CrossRef]
- Eerenstein, W.; Mathur, N.; Scott, J.F. Multiferroic and magnetoelectric materials. Nature 2006, 442, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Scott, J.F. Room-temperature multiferroic magnetoelectrics. NPG Asia Mater. 2013, 5, e72. [Google Scholar] [CrossRef] [Green Version]
- Manipatruni, S.; Nikonov, D.; Lin, C.-C.; Gosavi, T.A.; Liu, H.; Prasad, B.; Huang, Y.-L.; Bonturim, E.; Ramesh, R.; Young, I.A. Scalable energy-efficient magnetoelectric spin–orbit logic. Nature 2019, 565, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Scott, J.F. Multiferroic memories. Nat. Mater. 2007, 6, 256–257. [Google Scholar] [CrossRef]
- Kumari, S.; Pradhan, D.K.; Ortega, N.; Pradhan, K.; DeVreugd, C.; Srinivasan, G.; Kumar, A.; Paudel, T.R.; Tsymbal, E.Y.; Bumstead, A.M.; et al. Palladium-based ferroelectrics and multiferroics: Theory and experiment. Phys. Rev. B 2017, 95, 214109. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, D.K.; Mishra, A.K.; Kumari, S.; Basu, A.; Somayazulu, M.; Gradauskaite, E.; Smith, R.M.; Gardner, J.; Turner, P.W.; N’Diaye, A.T.; et al. Studies of Multiferroic Palladium Perovskites. Sci. Rep. 2019, 9, 1685. [Google Scholar] [CrossRef] [Green Version]
- Van Aken, B.B.; Rivera, J.-P.; Schmid, H.; Fiebig, M. Observation of ferrotoroidic domains. Nature 2007, 449, 702–705. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019, 18, 203–212. [Google Scholar] [CrossRef]
- Cheong, S.-W.; Mostovoy, M. Multiferroics: A magnetic twist for ferroelectricity. Nat. Mater. 2007, 6, 13–20. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, D.K.; Puli, V.S.; Narayan Tripathy, S.; Pradhan, D.K.; Scott, J.; Katiyar, R.S. Room temperature multiferroic properties of Pb (Fe0. 5Nb0. 5) O3-Co0. 65Zn0. 35Fe2O4 composites. J. Appl. Phys. 2013, 114, 234106. [Google Scholar] [CrossRef]
- Ma, J.; Hu, J.; Li, Z.; Nan, C.-W. Recent progress in multiferroic magnetoelectric composites: From bulk to thin films. Adv. Mater. 2011, 23, 1062–1087. [Google Scholar] [CrossRef] [PubMed]
- Bibes, M.; Barthélémy, A. Towards a magnetoelectric memory. Nat. Mater. 2008, 7, 425–426. [Google Scholar] [CrossRef] [PubMed]
- Andrew, J.S.; Starr, J.D.; Budi, M.A. Prospects for nanostructured multiferroic composite materials. Scr. Mater. 2014, 74, 38–43. [Google Scholar] [CrossRef]
- Ortega, N.; Kumar, A.; Scott, J.F.; Katiyar, R.S. Multifunctional magnetoelectric materials for device applications. J. Phys. Condens. Matter 2015, 27, 504002. [Google Scholar] [CrossRef]
- Kumari, S.; Pradhan, D.K.; Katiyar, R.S.; Kumar, A. Ferroelectric, ferromagnetic, and multiferroic heterostructures for possible applications as tunnel junctions. In Magnetic, Ferroelectric, and Multiferroic Metal Oxides; Elsevier: Amsterdam, The Netherlands, 2018; pp. 571–591. ISBN 9780128111802. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Kumari, S.; Vasudevan, R.K.; Dugu, S.; Das, P.T.; Puli, V.S.; Pradhan, D.K.; Kalinin, S.V.; Katiyar, R.S.; Rack, P.D. Room temperature multiferroicity and magnetodielectric coupling in 0–3 composite thin films. J. Appl. Phys. 2020, 127, 194104. [Google Scholar] [CrossRef]
- Jeong, D.S.; Thomas, R.; Katiyar, R.; Scott, J.F.; Kohlstedt, H.; Petraru, A.; Hwang, C.S. Emerging memories: Resistive switching mechanisms and current status. Rep. Prog. Phys. 2012, 75, 076502. [Google Scholar] [CrossRef]
- Thomas, R.; Scott, J.F.; Bose, D.N.; Katiyar, R.S. Multiferroic thin-film integration onto semiconductor devices. J. Phys. Condens. Matter 2010, 22, 423201. [Google Scholar] [CrossRef]
- Scott, J.F. Ferroelectric memories. Lock Thermogr. 2000, 246, 1400–1405. [Google Scholar] [CrossRef]
- Hill, N.A. Why are there so few magnetic ferroelectrics? J. Phys. Chem. B 2000, 104, 6694–6709. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Puli, V.S.; Kumari, S.; Sahoo, S.; Das, P.T.; Pradhan, K.; Pradhan, D.K.; Scott, J.F.; Katiyar, R.S. Studies of phase transitions and magnetoelectric coupling in PFN-CZFO multiferroic composites. J. Phys. Chem. C 2016, 120, 1936–1944. [Google Scholar] [CrossRef]
- Evans, D.M.; Alexe, M.; Schilling, A.; Kumar, A.; Sanchez, D.; Ortega, N.; Katiyar, R.S.; Scott, J.F.; Gregg, J.M. The nature of magnetoelectric coupling in Pb (Zr,Ti) O3-Pb (Fe,Ta) O3. Adv. Mater. 2015, 27, 6068–6073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tripathy, S.N.; Pradhan, D.K.; Mishra, K.K.; Sen, S.; Palai, R.; Paulch, M.; Scott, J.F.; Katiyar, R.S.; Pradhan, D.K. Phase transition and enhanced magneto-dielectric response in BiFeO3-DyMnO3 multiferroics. J. Appl. Phys. 2015, 117, 144103. [Google Scholar] [CrossRef] [Green Version]
- Tripathy, S.N.; Mishra, K.K.; Sen, S.; Mishra, B.G.; Pradhan, D.K.; Palai, R.; Pradhan, D.K. Phase transition and magneto-electric coupling of BiFeO3-YMnO3 multiferroic nanoceramics. J. Appl. Phys. 2013, 114, 144104. [Google Scholar] [CrossRef]
- Puli, V.S.; Pradhan, D.K.; Gollapudi, S.; Coondoo, I.; Panwar, N.; Adireddy, S.; Chrisey, D.B.; Katiyar, R.S. Magnetoelectric coupling effect in transition metal modified polycrystalline BiFeO3 thin films. J. Magn. Magn. Mater. 2014, 369, 9–13. [Google Scholar] [CrossRef]
- Puli, V.S.; Pradhan, D.K.; Martinez, R.; Coondoo, I.; Panwar, N.; Katiyar, R. Temperature dependent magnetic, dielectric studies of Sm-substituted Bulk BiFeO3. J. Supercond. Nov. Magn. 2011, 25, 1109–1114. [Google Scholar] [CrossRef]
- Yang, C.-H.; Seidel, J.; Kim, S.Y.; Rossen, P.B.; Yu, P.; Gajek, M.; Chu, Y.H.; Martin, L.W.; Holcomb, M.B.; He, Q.; et al. Electric modulation of conduction in multiferroic Ca-doped BiFeO3 films. Nat. Mater. 2009, 8, 485–493. [Google Scholar] [CrossRef]
- Martin, L.; Chu, Y.-H.; Ramesh, R. Advances in the growth and characterization of magnetic, ferroelectric, and multiferroic oxide thin films. Mater. Sci. Eng. R Rep. 2010, 68, 89–133. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, K.; Das, K.; Sarkar, B.; Ghosh, S.; De, S.K.; Sinha, G.; Lahtinen, J. Enhanced magnetic and dielectric properties of Eu and Co co-doped BiFeO3 nanoparticles. Appl. Phys. Lett. 2012, 101, 42401. [Google Scholar] [CrossRef]
- Sahoo, S.; Pradhan, D.K.; Choudhary, R.; Mathur, B. Dielectric relaxation and conductivity studies of (K0. 5Bi0. 5) (Fe0. 5Nb0. 5) O3 ceramics. Adv. Mater. Lett. 2012, 3, 97–101. [Google Scholar] [CrossRef]
- Nan, C.-W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Vaz, C.A.F.; Hoffman, J.; Ahn, C.H.; Ramesh, R. Magnetoelectric coupling effects in multiferroic complex oxide composite structures. Adv. Mater. 2010, 22, 2900–2918. [Google Scholar] [CrossRef] [PubMed]
- Vaz, C.A.F.; Staub, U. Artificial multiferroic heterostructures. J. Mater. Chem. C 2013, 1, 6731–6742. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, G. Magnetoelectric composites. Annu. Rev. Mater. Res. 2010, 40, 153–178. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Chowdhury, R.N.P.; Nath, T.K. Magnetoelectric properties of PbZr0.53Ti0.47O3-Ni0.65Zn0.35Fe2O4 multiferroic nanocomposites. Appl. Nanosci. 2012, 2, 261–273. [Google Scholar] [CrossRef] [Green Version]
- Leung, C.M.; Li, J.; Viehland, D.; Zhuang, X. A review on applications of magnetoelectric composites: From heterostructural uncooled magnetic sensors, energy harvesters to highly efficient power converters. J. Phys. D Appl. Phys. 2018, 51, 263002. [Google Scholar] [CrossRef]
- Palneedi, H.; Annapureddy, V.; Priya, S.; Ryu, J. Status and perspectives of multiferroic magnetoelectric composite materials and applications. Actuators 2016, 5, 9. [Google Scholar] [CrossRef] [Green Version]
- Fetisov, Y.K.; Srinivasan, G. Electric field tuning characteristics of a ferrite-piezoelectric microwave resonator. Appl. Phys. Lett. 2006, 88, 143503. [Google Scholar] [CrossRef]
- Barman, R.; Kaur, D. Multiferroic tunnel junction of Ni50.3Mn36.9Sb12.8/BiFeO3/Ni50.3Mn36.9Sb12.8 for magneto-electric random access memory devices. Appl. Phys. Lett. 2016, 108, 092404. [Google Scholar] [CrossRef]
- Ryu, J.; Kang, J.-E.; Zhou, Y.; Choi, S.-Y.; Yoon, W.-H.; Park, D.-S.; Choi, J.-J.; Hahn, B.-D.; Ahn, C.-W.; Kim, J.-W.; et al. Ubiquitous magneto-mechano-electric generator. Energy Environ. Sci. 2015, 8, 2402–2408. [Google Scholar] [CrossRef]
- Kleemann, W. Magnetoelectric spintronics. J. Appl. Phys. 2013, 114, 27013. [Google Scholar] [CrossRef]
- Zhuang, X.; Leung, C.M.; Sreenivasulu, G.; Gao, M.; Zhang, J.; Srinivasan, G.; Li, J.; Viehland, D. Upper limit for power conversion in magnetoelectric gyrators. Appl. Phys. Lett. 2017, 111, 163902. [Google Scholar] [CrossRef]
- Yarar, E.; Salzer, S.; Hrkac, V.; Piorra, A.; Höft, M.; Knöchel, R.; Smazna, D.; Quandt, E. Inverse bilayer magnetoelectric thin film sensor. Appl. Phys. Lett. 2016, 109, 022901. [Google Scholar] [CrossRef]
- Naifar, S.; Bradai, S.; Viehweger, C.; Kanoun, O. Survey of electromagnetic and magnetoelectric vibration energy harvesters for low frequency excitation. Measurement 2017, 106, 251–263. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Lin, Y.; Nan, C.-W. Multiferroic magnetoelectric composite nanostructures. NPG Asia Mater. 2010, 2, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, D.K.; Kumari, S.; Strelcov, E.; Pradhan, D.K.; Katiyar, R.S.; Kalinin, S.V.; Laanait, N.; Vasudevan, R.K. Reconstructing phase diagrams from local measurements via Gaussian processes: Mapping the temperature-composition space to confidence. NPJ Comput. Mater. 2018, 4, 23. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Wang, B.; Zheng, Y.; Ryba, E. Critical phase transition temperatures of 1–3 type multiferroic composite thin films. J. Phys. D Appl. Phys. 2007, 40, 1614. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Yao, J.; Yang, T.; Wang, Z.; Hu, J.-M.; Chen, C.; Sun, R.; Tian, Z.; Li, J.; et al. Magnetoelectric quasi-(0–3) nanocomposite heterostructures. Nat. Commun. 2015, 6, 6680. [Google Scholar] [CrossRef]
- Hu, J.-M.; Duan, C.-G.; Nan, C.-W.; Chen, L.-Q. Understanding and designing magnetoelectric heterostructures guided by computation: Progresses, remaining questions, and perspectives. NPJ Comput. Mater. 2017, 3, 18. [Google Scholar] [CrossRef]
- Kumari, S.; Mottaghi, N.; Huang, C.-Y.; Trappen, R.; Bhandari, G.; Yousefi, S.; Cabrera, G.; Seehra, M.S.; Holcomb, M.B. Effects of Oxygen Modification on the Structural and Magnetic Properties of Highly Epitaxial La0.7Sr0.3MnO3 (LSMO) thin films. Sci. Rep. 2020, 10, 3659. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, D.K.; Barik, S.K.; Sahoo, S.; Puli, V.S.; Katiyar, R. Investigations on electrical and magnetic properties of multiferroic [(1 − x)Pb(Fe0.5Nb0.5) O3−xNi0.65Zn0.35Fe2O4] composites. J. Appl. Phys. 2013, 113, 144104. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Kumari, S.; Puli, V.S.; Das, P.T.; Pradhan, D.K.; Kumar, A.; Scott, J.F.; Katiyar, R.S. Correlation of dielectric, electrical and magnetic properties near the magnetic phase transition temperature of cobalt zinc ferrite. Phys. Chem. Chem. Phys. 2017, 19, 210–218. [Google Scholar] [CrossRef] [Green Version]
- Molegraaf, H.J.A.; Hoffman, J.; Vaz, C.A.F.; Gariglio, S.; Van Der Marel, D.; Ahn, C.H.; Triscone, J.-M. Magnetoelectric effects in complex oxides with competing ground states. Adv. Mater. 2009, 21, 3470–3474. [Google Scholar] [CrossRef]
- Vafaee, M.; Finizio, S.; Deniz, H.; Hesse, D.; Zabel, H.; Jakob, G.; Kläui, M. The effect of interface roughness on exchange bias in La0.7Sr0.3MnO3-BiFeO3 heterostructures. Appl. Phys. Lett. 2016, 108, 072401. [Google Scholar] [CrossRef] [Green Version]
- Yi, D.; Yu, P.; Chen, Y.C.; Lee, H.H.; He, Q.; Chu, Y.H.; Ramesh, R. Tailoring magnetoelectric coupling in BiFeO3/La0.7Sr0.3MnO3 heterostructure through the interface engineering. Adv. Mater. 2019, 31, 1806335. [Google Scholar] [CrossRef]
- Ortega, N.; Bhattacharya, P.; Katiyar, R.; Dutta, P.; Manivannan, A.; Seehra, M.; Takeuchi, I.; Majumder, S. Multiferroic properties of Pb(Zr,Ti)O3/CoFe2O4 composite thin films. Am. Inst. Phys. 2006, 126105. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, D.K.; Kumari, S.; Li, L.; Vasudevan, R.K.; Das, P.T.; Puli, V.S.; Pradhan, D.K.; Kumar, A.; Misra, P.; Pradhan, A.K.; et al. Studies on dielectric, optical, magnetic, magnetic domain structure, and resistance switching characteristics of highly c-axis oriented NZFO thin films. J. Appl. Phys. 2017, 122, 033902. [Google Scholar] [CrossRef]
- Kumar, M.; Shankar, S.; Dwivedi, G.; Anshul, A.; Thakur, O.P.; Ghosh, A.K. Magneto-dielectric coupling and transport properties of the ferromagnetic-BaTiO3 composites. Appl. Phys. Lett. 2015, 106, 072903. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Barik, S.K.; Puli, V.S.; Sahoo, S.; Katiyar, R.S. Dielectric and magnetic properties of Pb (Fe0.5Nb0.5)O3-Ni0.65Zn0.35Fe2O4 composites. ECS Trans. 2013, 50, 59. [Google Scholar] [CrossRef]
- Choi, E.-M.; Weal, E.; Bi, Z.; Wang, H.; Kursumovic, A.; Fix, T.; Blamire, M.G.; MacManus-Driscoll, J.L. Strong room temperature exchange bias in self-assembled BiFeO3-Fe3O4 nanocomposite heteroepitaxial films. Appl. Phys. Lett. 2013, 102, 012905. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Misra, P.; Puli, V.S.; Sahoo, S.; Pradhan, D.K.; Katiyar, R.S. Studies on structural, dielectric, and transport properties of Ni0.65Zn0.35Fe2O4. J. Appl. Phys. 2014, 115, 243904. [Google Scholar] [CrossRef]
- Curie, P. Sur la symétrie dans les phénomènes physiques, symétrie d’un champ électrique et d’un champ magnétique. J. Phys. Théor. Appl. 1894, 3, 393–415. [Google Scholar] [CrossRef]
- Van Suchtelen, J. Product properties: A new application of composite materials. Philips Res. Rep. 1972, 27, 28–37. [Google Scholar]
- Pradhan, D.K.; Kumari, S.; Vasudevan, R.K.; Strelcov, E.; Puli, V.S.; Pradhan, D.K.; Kumar, A.; Gregg, J.M.; Pradhan, A.K.; Kalinin, S.V.; et al. Exploring the magnetoelectric coupling at the composite interfaces of FE/FM/FE heterostructures. Sci. Rep. 2018, 8, 17381. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Sahoo, S.; Barik, S.K.; Puli, V.S.; Misra, P.; Katiyar, R.S. Studies on magnetoelectric coupling in PFN-NZFO composite at room temperature. J. Appl. Phys. 2014, 115, 194105. [Google Scholar] [CrossRef]
- Sanchez, D.A.; Ortega, N.; Kumar, A.; Roque-Malherbe, R.; Polanco, R.; Scott, J.F.; Katiyar, R.S. Symmetries and multiferroic properties of novel room-temperature magnetoelectrics: Lead iron tantalate-lead zirconate titanate (PFT/PZT). AIP Adv. 2011, 1, 042169. [Google Scholar] [CrossRef]
- Schlom, D.G.; Chen, L.-Q.; Fennie, C.J.; Gopalan, V.; Muller, D.A.; Pan, X.; Ramesh, R.; Uecker, R. Elastic strain engineering of ferroic oxides. MRS Bull. 2014, 39, 118–130. [Google Scholar] [CrossRef] [Green Version]
- Ma, F.D.; Jin, Y.M.; Wang, Y.U.; Kampe, S.; Dong, S. Phase field modeling and simulation of particulate magnetoelectric composites: Effects of connectivity, conductivity, poling and bias field. Acta Mater. 2014, 70, 45–55. [Google Scholar] [CrossRef]
- Duan, C.-G.; Jaswal, S.S.; Tsymbal, E.Y. Predicted magnetoelectric effect in Fe/BaTiO3 multilayers: Ferroelectric control of magnetism. Phys. Rev. Lett. 2006, 97, 047201. [Google Scholar] [CrossRef] [Green Version]
- Fechner, M.; Maznichenko, I.V.; Ostanin, S.; Ernst, A.; Henk, J.; Bruno, P.; Mertig, I. Magnetic phase transition in two-phase multiferroics predicted from first principles. Phys. Rev. B 2008, 78, 212406. [Google Scholar] [CrossRef]
- Meyerheim, H.L.; Klimenta, F.; Ernst, A.; Mohseni, K.; Ostanin, S.; Fechner, M.; Parihar, S.; Maznichenko, I.V.; Mertig, I.; Kirschner, J. Structural secrets of multiferroic interfaces. Phys. Rev. Lett. 2011, 106, 087203. [Google Scholar] [CrossRef] [PubMed]
- Nogués, J.; Schuller, I.K. Exchange bias. J. Magn. Magn. Mater. 1999, 192, 203–232. [Google Scholar] [CrossRef]
- Huijben, M.; Yu, P.; Martin, L.W.; Molegraaf, H.J.A.; Chu, Y.-H.; Holcomb, M.B.; Balke, N.; Rijnders, G.; Ramesh, R. Ultrathin limit of exchange bias coupling at oxide multiferroic/ferromagnetic interfaces. Adv. Mater. 2013, 25, 4739–4745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zandalazini, C.; Esquinazi, P.; Bridoux, G.; Barzola-Quiquia, J.; Ohldag, H.; Arenholz, E. Uncompensated magnetization and exchange-bias field in La0.7Sr0.3MnO3/YMnO3 bilayers: The influence of the ferromagnetic layer. J. Magn. Magn. Mater. 2011, 323, 2892–2898. [Google Scholar] [CrossRef] [Green Version]
- White, J.S.; Bator, M.; Hu, Y.; Luetkens, H.; Stahn, J.; Capelli, S.; Das, S.; Döbeli, M.; Lippert, T.; Malik, V.K.; et al. Strain-induced ferromagnetism in antiferromagnetic LuMnO3 thin films. Phys. Rev. Lett. 2013, 111, 037201. [Google Scholar] [CrossRef] [Green Version]
- Laukhin, V.; Skumryev, V.; Martí, X.; Hrabovsky, D.; Sánchez, F.; García-Cuenca, M.V.; Ferrater, C.; Varela, M.; Lüders, U.; Bobo, J.F.; et al. Electric-field control of exchange bias in multiferroic epitaxial heterostructures. Phys. Rev. Lett. 2006, 97, 227201. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.M.; Cybart, S.A.; Yu, P.; Rossell, M.D.; Zhang, J.X.; Ramesh, R.; Dynes, R.C. Reversible electric control of exchange bias in a multiferroic field-effect device. Nat. Mater. 2010, 9, 756–761. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Weak ferromagnetism and magnetoelectric coupling in bismuth ferrite. Phys. Rev. B 2005, 71, 060401. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-J.; Hsieh, Y.-H.; Liao, S.-C.; Hu, Z.; Huang, M.; Kuo, W.-C.; Chin, Y.-Y.; Uen, T.-M.; Juang, J.-Y.; Lai, C.-H.; et al. Strong magnetic enhancement in self-assembled multiferroic-ferrimagnetic nanostructures. Nanoscale 2013, 5, 4449. [Google Scholar] [CrossRef]
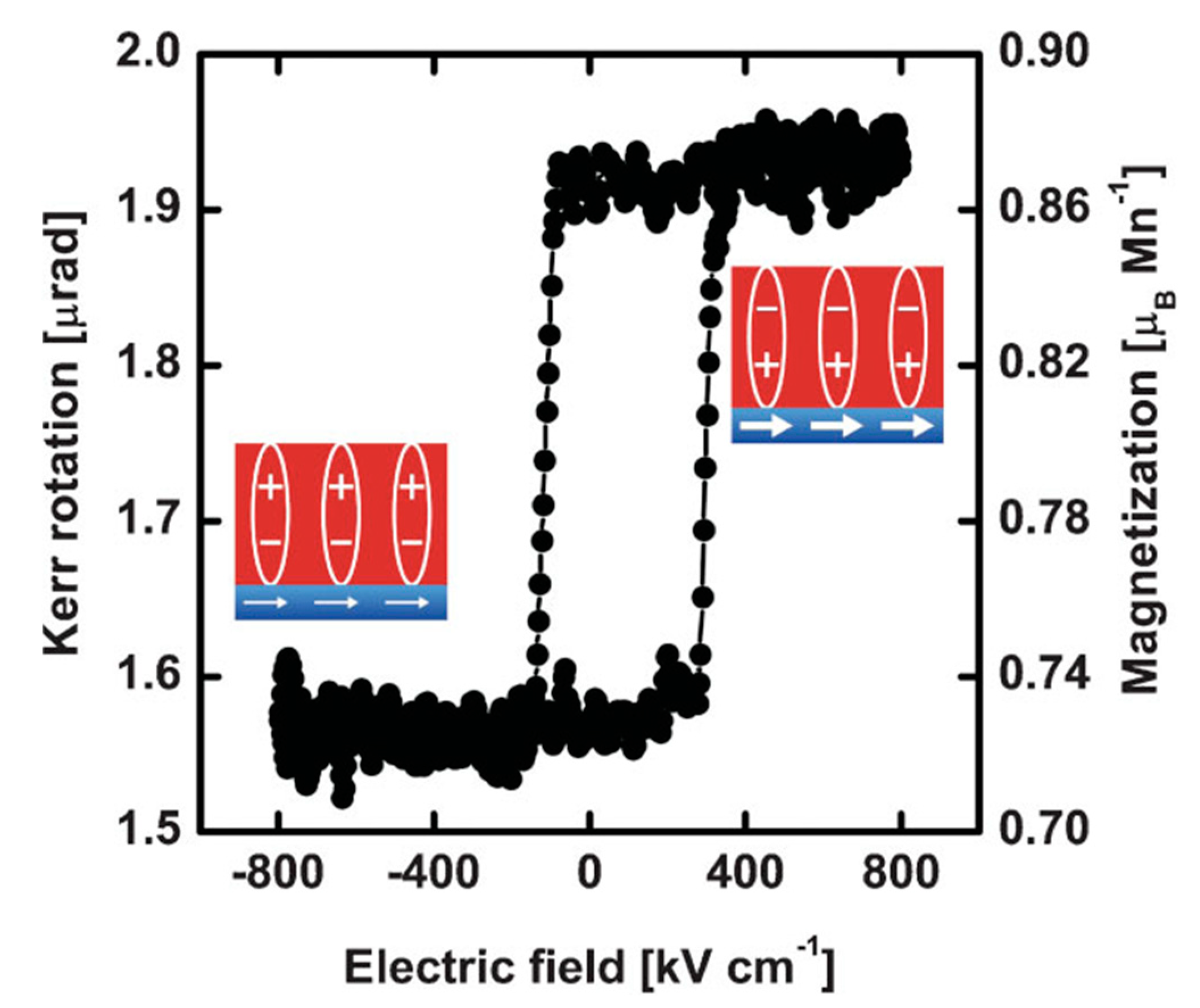
- Heron, J.T.; Bosse, J.L.; He, Q.; Gao, Y.; Trassin, M.; Ye, L.; Clarkson, J.D.; Wang, C.; Liu, J.; Salahuddin, S.; et al. Deterministic switching of ferromagnetism at room temperature using an electric field. Nat. Cell Biol. 2014, 516, 370–373. [Google Scholar] [CrossRef]
- Vopson, M.M.; Fetisov, Y.K.; Caruntu, G.; Srinivasan, G. Measurement techniques of the magneto-electric coupling in multiferroics. Materials 2017, 10, 963. [Google Scholar] [CrossRef] [PubMed]
- Vopson, M.M. Fundamentals of multiferroic materials and their possible applications. Crit. Rev. Solid State Mater. Sci. 2015, 40, 223–250. [Google Scholar] [CrossRef] [Green Version]
- Islam, R.A.; Priya, S. Synthesis of high magnetoelectric coefficient composites using annealing and aging route. Int. J. Appl. Ceram. Technol. 2006, 3, 353–363. [Google Scholar] [CrossRef]
- Ryu, J.; Carazo, A.V.; Uchino, K.; Kim, H.-E. Piezoelectric and magnetoelectric properties of lead zirconate titanate/Ni-ferrite particulate composites. J. Electroceramics 2001, 7, 17–24. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, J.; So, L.; Sun, C.; Lo, C.; Or, S.; Chan, H.L. The effect of magnetic nanoparticles on the morphology, ferroelectric, and magnetoelectric behaviors of CFO/P (VDF-TrFE) 0–3 nanocomposites. J. Appl. Phys. 2009, 105, 054102. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, G.; DeVreugd, C.P.; Flattery, C.S.; Laletsin, V.M.; Paddubnaya, N. Magnetoelectric interactions in hot-pressed nickel zinc ferrite and lead zirconante titanate composites. Appl. Phys. Lett. 2004, 85, 2550–2552. [Google Scholar] [CrossRef]
- Zhai, J.; Cai, N.; Shi, Z.; Lin, Y.; Nan, C.-W. Magnetic-dielectric properties of NiFe2O4/PZT particulate composites. J. Phys. D Appl. Phys. 2004, 37, 823. [Google Scholar] [CrossRef]
- Boomgaard, J.V.D.; Van Run, A.M.J.G.; Van Suchtelen, J. Magnetoelectricity in piezoelectric-magnetostrictive composites. Ferroelectrics 1976, 10, 295–298. [Google Scholar] [CrossRef]
- Sheikh, A.D.; Mathe, V. Effect of the piezomagnetic NiFe2O4 phase on the piezoelectric Pb(Mg1/3Nb2/3)0.67Ti0.33O3 phase in magnetoelectric composites. Smart Mater. Struct. 2009, 18, 065014. [Google Scholar] [CrossRef]
- Boomgaard, J.V.D.; Born, R.A.J. A sintered magnetoelectric composite material BaTiO3-Ni(Co,Mn)Fe2O4. J. Mater. Sci. 1978, 13, 1538–1548. [Google Scholar] [CrossRef]
- Fang, Z.; Lu, S.G.; Li, F.; Datta, S.; Zhang, Q.; El Tahchi, M. Enhancing the magnetoelectric response of Metglas/polyvinylidene fluoride laminates by exploiting the flux concentration effect. Appl. Phys. Lett. 2009, 95, 112903. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gray, D.; Berry, D.; Gao, J.; Li, M.; Li, J.; Viehland, D. An extremely low equivalent magnetic noise magnetoelectric sensor. Adv. Mater. 2011, 23, 4111–4114. [Google Scholar] [CrossRef] [PubMed]
- Chu, Z.; Shi, H.; Shi, W.; Liu, G.; Wu, J.; Yang, J.; Dong, S. Enhanced resonance magnetoelectric coupling in (1–1) connectivity composites. Adv. Mater. 2017, 29, 1606022. [Google Scholar]
- Zhai, J.; Dong, S.; Xing, J.; Li, J.; Viehland, D. Giant magnetoelectric effect in Metglas/polyvinylidene-fluoride laminates. Appl. Phys. Lett. 2006, 89, 83507. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Yang, S.C.; Apo, D.J.; Maurya, D.; Priya, S. Tunable self-biased magnetoelectric response in homogenous laminates. Appl. Phys. Lett. 2012, 101, 232905. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Wang, Z.; Wang, Y.; Li, J.; Viehland, D. Giant magnetoelectric effect in self-biased laminates under zero magnetic field. Appl. Phys. Lett. 2013, 102, 082404. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Zhai, J.; Xing, Z.; Li, J.; Viehland, D. Giant magnetoelectric effect (under a dc magnetic bias of 2 Oe) in laminate composites of FeBSiC alloy ribbons and Pb(Zn[sub 1∕3],Nb[sub 2∕3])O[sub 3]-7% PbTiO[sub 3] fibers. Appl. Phys. Lett. 2007, 91, 22915. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Zhai, J.; Li, J.; Viehland, D. Near-ideal magnetoelectricity in high-permeability magnetostrictive/piezofiber laminates with a (2–1) connectivity. Appl. Phys. Lett. 2006, 89, 252904. [Google Scholar] [CrossRef] [Green Version]
- Laletin, U.; Sreenivasulu, G.; Petrov, V.M.; Garg, T.; Kulkarni, A.R.; Venkataramani, N.; Srinivasan, G. Hysteresis and remanence in magnetoelectric effects in functionally graded magnetostrictive-piezoelectric layered composites. Phys. Rev. B 2012, 85, 104404. [Google Scholar] [CrossRef]
- Ryu, J.; Priya, S.; Uchino, K.; Kim, H.-E. Magnetoelectric effect in composites of magnetostrictive and piezoelectric materials. J. Electroceramics 2002, 8, 107–119. [Google Scholar] [CrossRef]
- Lu, M.-C.; Mei, L.; Jeong, D.-Y.; Xiang, J.; Xie, H.; Zhang, Q.M. Enhancing the magnetoelectric response of Terfenol-D/polyvinylidene fluoride/Terfenol-D laminates by exploiting the shear mode effect. Appl. Phys. Lett. 2015, 106, 112905. [Google Scholar] [CrossRef]
- Yan, Y.; Zhou, Y.; Priya, S. Giant self-biased magnetoelectric coupling in co-fired textured layered composites. Appl. Phys. Lett. 2013, 102, 052907. [Google Scholar] [CrossRef] [Green Version]
- Israel, C.; Mathur, N.D.; Scott, J.F. A one-cent room-temperature magnetoelectric sensor. Nat. Mater. 2008, 7, 93–94. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, Y.; Ma, J.; Lin, Y.; Nan, C.-W. Magnetoelectric behavior of BaTiO3 films directly grown on CoFe2O4 ceramics. J. Appl. Phys. 2008, 104, 014101. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Shen, Y.; Lin, Y.; Nan, C.W. Enhanced magnetoelectric coupling in Pb(Zr0.52Ti0.48)O3 film-on-CoFe2O4 bulk ceramic composite with LaNiO3 bottom electrode. J. Mater. Sci. 2012, 48, 1021–1026. [Google Scholar] [CrossRef]
- Palneedi, H.; Maurya, D.; Kim, G.-Y.; Annapureddy, V.; Noh, M.-S.; Kang, C.; Kim, J.-W.; Choi, J.-J.; Choi, S.-Y.; Chung, S.-Y.; et al. Unleashing the full potential of magnetoelectric coupling in film heterostructures. Adv. Mater. 2017, 29, 1605688. [Google Scholar] [CrossRef]
- Feng, M.; Wang, J.-J.; Hu, J.-M.; Wang, J.; Ma, J.; Li, H.-B.; Shen, Y.; Lin, Y.-H.; Chen, L.-Q.; Nan, C.-W. Optimizing direct magnetoelectric coupling in Pb(Zr,Ti)O3/Ni multiferroic film heterostructures. Appl. Phys. Lett. 2015, 106, 072901. [Google Scholar] [CrossRef] [Green Version]
- Liang, W.; Li, Z.; Bi, Z.; Nan, T.; Du, H.; Nan, C.; Chen, C.; Jia, Q.; Lin, Y. Role of the interface on the magnetoelectric properties of BaTiO3thin films deposited on polycrystalline Ni foils. J. Mater. Chem. C 2014, 2, 708–714. [Google Scholar] [CrossRef]
- Park, C.-S.; Ryu, J.; Choi, J.-J.; Park, D.-S.; Ahn, C.-W.; Priya, S. Giant magnetoelectric coefficient in 3–2 nanocomposite thick films. Jpn. J. Appl. Phys. 2009, 48, 080204. [Google Scholar] [CrossRef]
- Ryu, H.; Murugavel, P.; Lee, J.H.; Chae, S.; Noh, T.W.; Oh, Y.S.; Kim, H.J.; Kim, K.H.; Jang, J.H.; Kim, M.; et al. Magnetoelectric effects of nanoparticulate Pb(Zr0.52Ti0.48)O3-NiFe2O4 composite films. Appl. Phys. Lett. 2006, 89, 102907. [Google Scholar] [CrossRef] [Green Version]
- Wan, J.G.; Wang, X.-W.; Wu, Y.J.; Zeng, M.; Wang, Y.; Jiang, H.; Zhou, W.; Wang, G.; Liu, J.-M. Magnetoelectric CoFe2O4–Pb(Zr,Ti)O3 composite thin films derived by a sol-gel process. Appl. Phys. Lett. 2005, 86, 122501. [Google Scholar] [CrossRef]
- Lorenz, M.; Lazenka, V.; Schwinkendorf, P.; Van Bael, M.J.; Vantomme, A.; Temst, K.; Grundmann, M.; Höche, T. Epitaxial coherence at interfaces as origin of high magnetoelectric coupling in multiferroic BaTiO3-BiFeO3 superlattices. Adv. Mater. Interfaces 2016, 3, 1500822. [Google Scholar] [CrossRef]
- Lage, E.; Urs, N.O.; Röbisch, V.; Teliban, I.; Knöchel, R.; Meyners, D.; Mccord, J.; Quandt, E. Magnetic domain control and voltage response of exchange biased magnetoelectric composites. Appl. Phys. Lett. 2014, 104, 132405. [Google Scholar] [CrossRef]
- Ma, Y.; Cheng, W.; Ning, M.; Ong, C. Magnetoelectric effect in epitaxial Pb(Zr0.52Ti0.48)O3/La0.7Sr0.3MnO3 composite thin film. Appl. Phys. Lett. 2007, 90, 152911. [Google Scholar] [CrossRef]
- Deng, C.; Zhang, Y.; Ma, J.; Lin, Y.; Nan, C.-W. Magnetic-electric properties of epitaxial multiferroic NiFe2O4-BaTiO3 heterostructure. J. Appl. Phys. 2007, 102, 074114. [Google Scholar] [CrossRef]
- He, H.; Ma, J.; Lin, Y.; Nan, C. Enhanced magnetoelectric properties in Pb(Zr,Ti)O3-CoFe2O4 layered thin films with LaNiO3 as a buffer layer. J. Phys. D Appl. Phys. 2009, 42, 095008. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, C.; Ma, J.; Lin, Y.; Nan, C.-W. Enhancement in magnetoelectric response in CoFe2O4–BaTiO3 heterostructure. Appl. Phys. Lett. 2008, 92, 062911. [Google Scholar] [CrossRef]
- Greve, H.; Woltermann, E.; Quenzer, H.-J.; Wagner, B.; Quandt, E. Giant magnetoelectric coefficients in (Fe90Co10)78Si12B10-AlN thin film composites. Appl. Phys. Lett. 2010, 96, 182501. [Google Scholar] [CrossRef]
- Ryu, S.; Park, J.H.; Jang, H.M. Magnetoelectric coupling of [00 l]-oriented Pb(Zr0.4Ti0.6)O3-Ni0.8Zn0.2Fe2O4 multilayered thin films. Appl. Phys. Lett. 2007, 91, 142910. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.H.; Ma, F.; Liu, Y.; Li, J. Multiferroic CoFe2O4-Pb(Zr0.52Ti0.48)O3 core-shell nanofibers and their magnetoelectric coupling. Nanoscale 2011, 3, 3152–3158. [Google Scholar] [CrossRef]
- Ma, J.; Shi, Z.; Nan, C.W. Magnetoelectric properties of composites of single Pb(Zr,Ti)O3 rods and Terfenol-D/epoxy with a single-period of 1–3-type structure. Adv. Mater. 2007, 19, 2571–2573. [Google Scholar] [CrossRef]
- Rasmussen, E. Structural and magnetoelectric properties of MFe2O4-PZT (M = Ni, Co) and Lax (Ca, Sr)-PZT multilayer composites. Appl. Phys. A 2004, 78, 721–728. [Google Scholar]
- Srinivasan, G.; Rasmussen, E.T.; Gallegos, J.; Srinivasan, R.; Bokhan, Y.I.; Laletin, V.M. Magnetoelectric bilayer and multilayer structures of magnetostrictive and piezoelectric oxides. Phys. Rev. B 2001, 64, 214408. [Google Scholar] [CrossRef]
- Schmidt, R.; Ventura, J.; Langenberg, E.; Nemes, N.M.; Munuera, C.; Varela, M.; García-Hernández, M.; León, C.; Santamaria, J. Magnetoimpedance spectroscopy of epitaxial multiferroic thin films. Phys. Rev. B 2012, 86, 035113. [Google Scholar] [CrossRef] [Green Version]
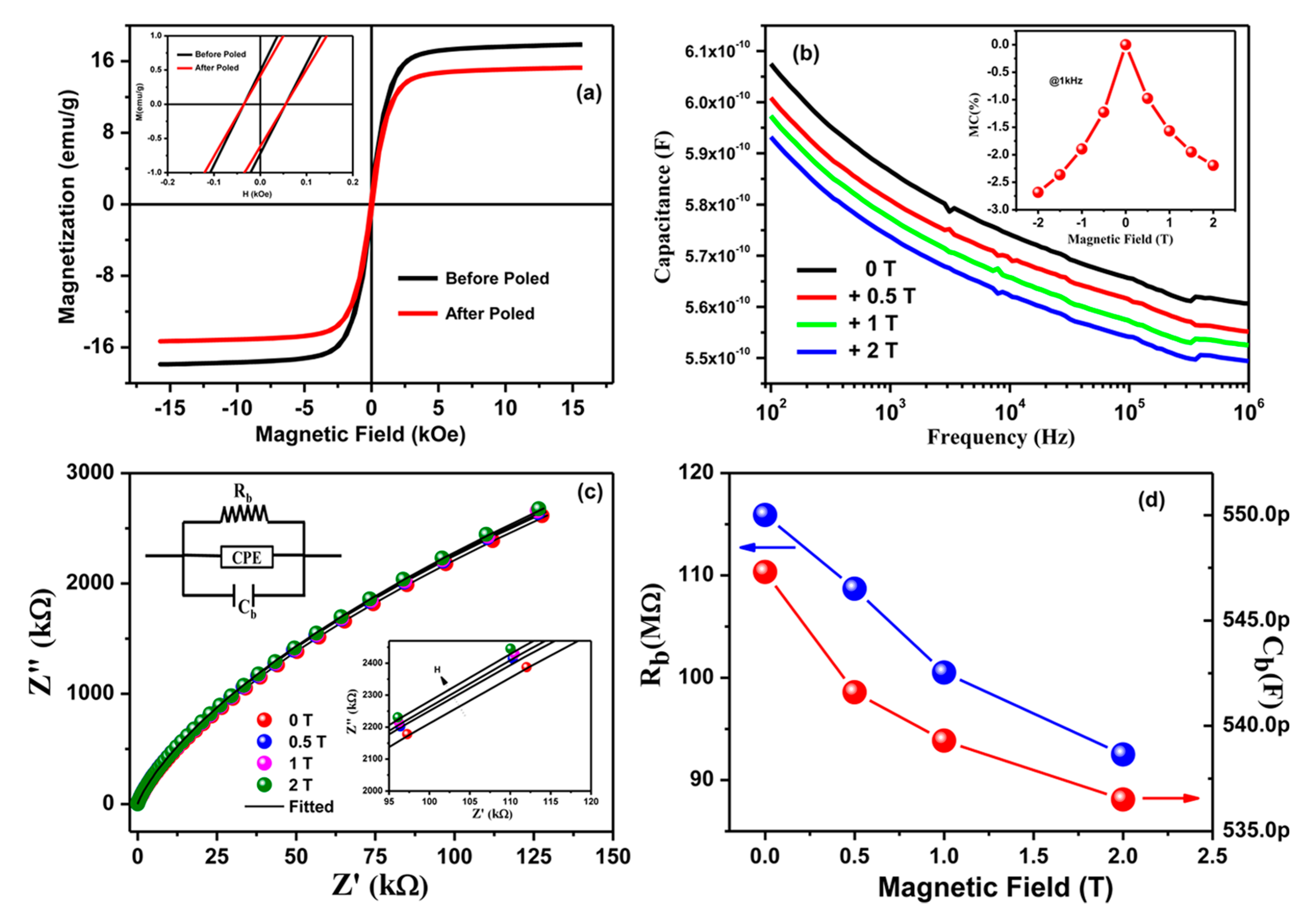
- Catalan, G. Magnetocapacitance without magnetoelectric coupling. Appl. Phys. Lett. 2006, 88, 102902. [Google Scholar] [CrossRef]
- Kumari, S.; Pradhan, D.K.; Das, P.T.; Ortega, N.; Pradhan, K.; Kumar, A.; Scott, J.F.; Katiyar, R.S. Evidence of strong magneto-dielectric coupling and enhanced electrical insulation at room temperature in Nd and Mn co-doped bismuth ferrite. J. Appl. Phys. 2017, 122, 144102. [Google Scholar] [CrossRef]
- Catalan, G.; O’neill, D.; Bowman, R.M.; Gregg, J.M. Relaxor features in ferroelectric superlattices: A Maxwell–Wagner approach. Appl. Phys. Lett. 2000, 77, 3078–3080. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Kumari, S.; Puli, V.S.; Pradhan, D.K.; Kumar, A.; Kalinin, S.V.; Vasudevan, R.K.; Katiyar, R.S.; Rack, P.D. Exploring phase transitions and magnetoelectric coupling of epitaxial asymmetric multilayer heterostructures. J. Mater. Chem. C 2020, 8, 12113–12122. [Google Scholar] [CrossRef]

| Bulk | HDC (Oe) | fAC (Hz) | Note | Reference | |
|---|---|---|---|---|---|
| 0.9Pb(Zr0.52Ti0.48)O3-0.1NiFe1.9Mn0.1O4 | 100 | 1000 | 140 | 0-3 composite, Longitudinal | [84] |
| PZT-20 wt%NiCo0.02Cu0.02Mn0.1Fe1.8O4 | 1250 | 100 | 115 | 0-3 composite, Longitudinal | [85] |
| P(VDF-TrFE)-CoFe2O4 | 2000 | 5000 | 40 | 0-3 composite, Longitudinal | [86] |
| Ni0.8Zn0.2Fe2O4-0.41 vol% PZT | 250 | 100 | 45 | 0-3 composite, Transverse | [87] |
| 0.68Pb(Zr0.57Ti0.43)O3-0.32NiFe2O4 | 1000 | 1000 | 80 | 0-3 composite, Longitudinal | [88] |
| 0.62BTO-0.38CoFe2O4 (1.5 wt% excess TiO2 | 560 | 1000 | 130 | 3-3 composite, Longitudinal | [89] |
| PMN-PT-NiFe2O4 | 2400 | 0 | 10.43 | 0-3 composite, Transverse | [90] |
| 0.6BTO-0.4Ni(Co,Mn)Fe2O4 | 500 | 1000 | 81.7 | 3-3 composite, Longitudinal | [91] |
| Metglas/PVDF | 2 | 20 | 21,460 | 2-2 composite, Transverse | [92] |
| Metglas/PMN-PT (fiber)/Metglas | 8 | 1000 | 52000 | 2-1 composite, Longitudinal | [93] |
| Metglas (fiber)/PMN-PT (fiber)/Metglas (fiber) | 2 | 1000 (23000) | 29310 (7,000,000) | 1-1 composite, Transverse | [94] |
| Metglas/PVDF/Metglas | 8 | 1000 | 7200 | 2-2 composite, Transverse | [95] |
| Metglas/PMT | - | 1000 | 63.3 | 2-2 composite, Transverse | [96] |
| Metglas/PZT (fiber)/Metglas | - | 1000 (33,700) | 12,000 (380,000) | 2-1 composite, Longitudinal | [97] |
| FeBSiC/PZN-PT (fiber)/FeBSiC | 2 | 1000 (20,000) | 10500 (400,000) | 2-1 composite, Transverse | [98] |
| FeBSiC/PZT (fiber)/FeBSiC | 4 | 1 (22,000) | 22,000 (500,000) | 2-1 composite, Longitudinal | [99] |
| PZT/Ni0.7Zn0.3Fe2O4/Ni | - | 20 | 280 | 2-2 composite, Transverse | [100] |
| Terfenol-D/PMN-PT/Terfenol-D | 4000 | 1000 | 10,300 | 2-2 composite, Longitudinal | [101] |
| Terfenol-D/PVDF/Terfenol-D | 2300 | 1000 | 7930 | 2-2 composite, Longitudinal, Shear mode | [102] |
| NCZF/textured 0.675PMN-0.325PT/NCZF | - | 1000 | 1200 | 2-2 composite, Transverse. | [103] |
| Ni/Doped-BaTiO3 | 7000 | - | 7.1 | 2-2 composite, Longitudinal | [104] |
| BaTiO3/CoFe2O4 (bulk ceramic) | 730 | 1000 | 38 | Transverse, PLD | [105] |
| Pb(Zr0.52Ti0.48)O3/CoFe2O4 (bulk ceramic) | 600 | 1000 | 155 | Transverse, sol–gel | [106] |
| Pb(Zr,Ti)O3/Metglas (bulk foil) | 22 | 1000 | 7000 | Transverse, GSV deposition with laser annealing | [107] |
| Pb(Zr0.52Ti0.48)O3/Ni (bulk foil) | 86 | 1000 | 772 | Transverse, sol–gel | [108] |
| BaTiO3/Ni (bulk foil) | 87 | 1000 | 90 | Transverse, CSD | [109] |
| Nanostructures | HDC (Oe) | fAC (Hz) | Note | Reference | |
|---|---|---|---|---|---|
| NCZF/0.8PZT-0.2PZN | 2600 | 1000 | 150 | 0-3 composite, Transverse | [110] |
| 0.65Pb(Zr0.52Ti0.48)O3–0.35NiFe2O4 | 2500 | 194 | 16 | 0-3 composite, PLD, Longitudinal, | [111] |
| BiFeO3–CoFe2O4 | 2900 | - | 338 | 0-3 composite, PLD, Transverse | [49] |
| Pb(Zr0.52Ti0.48)O3–CoFe2O4 | - | 1000 | 220 | 0-3 composite, sol–gel | [112] |
| [BaTiO3–BiFeO3] × 15 | - | 1000 | 49,000 | 2-2 composite, Longitudinal, PLD | [113] |
| Ir0.3Mn0.7/FeCoSiB/AlN | - | 700 | 430,000 | Transverse, Sputtering | [114] |
| La0.7Sr0.3MnO3/Pb(Zr0.52Ti0.48)O3 | 4000 | 1000 | 4 | Longitudinal, PLD | [115] |
| NiFe2O4/BaTiO3 | 100 | 1000 | 12 | Longitudinal, PLD | [116] |
| CoFe2O4/PZT | 6000 | 1000 | 70 | Longitudinal, sol–gel | [117] |
| CoFe2O4/BaTiO3 | 100 | 1000 | 104 | Longitudinal, PLD | [118] |
| FeCoSiB/AlN | 6 | 100(753) | 3100 (737,000) | Transverse, Sputtering | [119] |
| Ni0.8Zn0.2Fe2O4/Pb(Zr0.6Ti0.4)O3 | - | 1000 | 15 | Longitudinal, PLD | [120] |
| CoFe2O4(core)-PZT(shell) nanofiber | 2000 | - | 29,500 | Transverse, nanofiber | [121] |
| PZT-TDE | 1500 | 100 | 500 | 1-3 Composite, Longitudinal | [122] |
| Pb(Fe0.5Nb0.5)O3/Ni0.65Zn0.35Fe2O4/Pb(Fe0.5Nb0.5)O3 | 3000 | 1000 | 383 | 2-2 composite, PLD, Transverse | [65] |
| PZT-CFO | 6000 | 10–1000 | 55–5 | 0-3 composite, PLD, Transverse and Longitudinal | [123] |
| PZT/NiFe2O4 (multilayer) | 2000 | 1000 | 400 | 2-2 composite, PLD | [124] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradhan, D.K.; Kumari, S.; Rack, P.D. Magnetoelectric Composites: Applications, Coupling Mechanisms, and Future Directions. Nanomaterials 2020, 10, 2072. https://doi.org/10.3390/nano10102072
Pradhan DK, Kumari S, Rack PD. Magnetoelectric Composites: Applications, Coupling Mechanisms, and Future Directions. Nanomaterials. 2020; 10(10):2072. https://doi.org/10.3390/nano10102072
Chicago/Turabian StylePradhan, Dhiren K., Shalini Kumari, and Philip D. Rack. 2020. "Magnetoelectric Composites: Applications, Coupling Mechanisms, and Future Directions" Nanomaterials 10, no. 10: 2072. https://doi.org/10.3390/nano10102072
APA StylePradhan, D. K., Kumari, S., & Rack, P. D. (2020). Magnetoelectric Composites: Applications, Coupling Mechanisms, and Future Directions. Nanomaterials, 10(10), 2072. https://doi.org/10.3390/nano10102072







