Tunable Electronic Properties of Type-II SiS2/WSe2 Hetero-Bilayers
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
3.1. Structural Features of the Monolayer SiS2, WSe2 and SiS2/WSe2 Hetero-Bilayer
3.2. Electronic Properties of the SiS2/WSe2 Hetero-Bilayer
3.3. Effect of Biaxial Strain on Electronic Properties of SiS2/WSe2 Hetero-Bilayer
3.4. Effect of Electric Field on Electronic Properties of SiS2/WSe2 Hetero-Bilayer
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhimanapati, G.R.; Lin, Z.; Meunier, V.; Jung, Y.; Cha, J.; Schulman, D.S.; Xiao, D.; Son, Y.; Strano, M.S.; Cooper, V.R.; et al. Recent Advances in Two-Dimensional Materials beyond Graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tran, V.; Soklaski, R.; Liang, Y.; Yang, L. Layer-controlled band gap and anisotropic excitons in few-layer black phosphorus. Phys. Rev. B 2014, 89, 235319. [Google Scholar] [CrossRef] [Green Version]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [Green Version]
- Ruppert, C.; Aslan, O.B.; Heinz, T.F. Optical Properties and Band Gap of Single- and Few-Layer MoTe2 Crystals. Nano Lett. 2014, 14, 6231–6236. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Huang, L.; Huo, N.; Li, Y.; Chen, H.; Yang, J.; Wei, Z.; Li, J.; Li, S.-S. Electric-Field Tunable Band Offsets in Black Phosphorus and MoS2 van der Waals p-n Heterostructure. J. Phys. Chem. Lett. 2015, 6, 2483–2488. [Google Scholar] [CrossRef]
- Zhou, B.; Gong, S.-J.; Jiang, K.; Xu, L.; Shang, L.; Zhang, J.; Hu, Z.; Chu, J. A type-II GaSe/GeS heterobilayer with strain enhanced photovoltaic properties and external electric field effects. J. Mater. Chem. C 2020, 8, 89–97. [Google Scholar] [CrossRef]
- Kumar, R.; Das, D.; Singh, A.K. C2N/WS2 van der Waals type-II heterostructure as a promising water splitting photocatalyst. J. Catal. 2018, 359, 143–150. [Google Scholar] [CrossRef]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Lui, C.H.; Mak, K.F.; Shan, J.; Heinz, T.F. Ultrafast Photoluminescence from Graphene. Phys. Rev. Lett. 2010, 105, 127404. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Q.; Meng, R.; Jiang, J.; Liang, Q.; Tan, C.; Sun, X. The electronic and optical properties of novel germanene and antimonene heterostructures. J. Mater. Chem. C 2016, 4, 5434–5441. [Google Scholar] [CrossRef]
- Barhoumi, M.; Lazaar, K.; Said, M. DFT study of the electronic and vibrational properties of silicene/stanene heterobilayer. Phys. E Low Dimens. Syst. Nanostruct. 2019, 111, 127–129. [Google Scholar] [CrossRef]
- Chiu, M.H.; Zhang, C.; Shiu, H.W.; Chuu, C.P.; Chen, C.H.; Chang, C.Y.; Chen, C.H.; Chou, M.Y.; Shih, C.K.; Li, L.J. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 2015, 6, 7666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, W.; Xia, C.; Zhao, X.; Wang, T.; Jia, Y. Effects of strain and electric field on electronic structures and Schottky barrier in graphene and SnS hybrid heterostructures. Carbon 2016, 109, 737–746. [Google Scholar] [CrossRef]
- Ghorbani-Asl, M.; Bristowe, P.D.; Koziol, K.; Heine, T.; Kuc, A. Effect of compression on the electronic, optical and transport properties of MoS2/graphene-based junctions. 2D Mater. 2016, 3, 025018. [Google Scholar] [CrossRef]
- Wan, W.; Li, X.; Li, X.; Xu, B.; Zhan, L.; Zhao, Z.; Zhang, P.; Wu, S.Q.; Zhu, Z.-z.; Huang, H.; et al. Interlayer coupling of a direct van der Waals epitaxial MoS2/graphene heterostructure. RSC Adv. 2016, 6, 323–330. [Google Scholar] [CrossRef]
- Vu, T.V.; Hieu, N.V.; Phuc, H.V.; Bui, H.; Idrees, M.; Amin, B.; Hieu, N.N. Graphene/WSeTe van der Waals heterostructure: Controllable electronic properties and Schottky barrier via interlayer coupling and electric field. Appl. Surf. Sci. 2020, 507, 145036. [Google Scholar] [CrossRef]
- Tongay, S.; Zhou, J.; Ataca, C.; Liu, J.; Kang, J.S.; Matthews, T.S.; You, L.; Li, J.; Grossman, J.C.; Wu, J. Broad-Range Modulation of Light Emission in Two-Dimensional Semiconductors by Molecular Physisorption Gating. Nano Lett. 2013, 13, 2831–2836. [Google Scholar] [CrossRef] [PubMed]
- Rivera, P.; Schaibley, J.R.; Jones, A.M.; Ross, J.S.; Wu, S.; Aivazian, G.; Klement, P.; Seyler, K.; Clark, G.; Ghimire, N.J.; et al. Observation of long-lived interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nat. Commun. 2015, 6, 6242. [Google Scholar] [CrossRef] [Green Version]
- Jin, C.; Regan, E.C.; Yan, A.; Iqbal Bakti Utama, M.; Wang, D.; Zhao, S.; Qin, Y.; Yang, S.; Zheng, Z.; Shi, S.; et al. Observation of moire excitons in WSe2/WS2 heterostructure superlattices. Nature 2019, 567, 76–80. [Google Scholar] [CrossRef]
- Unuchek, D.; Ciarrocchi, A.; Avsar, A.; Watanabe, K.; Taniguchi, T.; Kis, A. Room-temperature electrical control of exciton flux in a van der Waals heterostructure. Nat. Cell Biol. 2018, 560, 340–344. [Google Scholar] [CrossRef]
- Sun, M.; Chou, J.-P.; Yu, J.; Tang, W. Effects of structural imperfection on the electronic properties of graphene/WSe2 heterostructures. J. Mater. Chem. C 2017, 5, 10383–10390. [Google Scholar] [CrossRef]
- Kang, J.; Tongay, S.; Zhou, J.; Li, J.; Wu, J. Band offsets and heterostructures of two-dimensional semiconductors. Appl. Phys. Lett. 2013, 102, 012111. [Google Scholar] [CrossRef] [Green Version]
- Ren, K.; Sun, M.; Luo, Y.; Wang, S.; Yu, J.; Tang, W. First-principle study of electronic and optical properties of two-dimensional materials-based heterostructures based on transition metal dichalcogenides and boron phosphide. Appl. Surf. Sci. 2019, 476, 70–75. [Google Scholar] [CrossRef]
- Torun, E.; Miranda, H.P.C.; Molina-Sánchez, A.; Wirtz, L. Interlayer and intralayer excitons in MoS2/WS2 and MoSe2/WSe2 heterobilayers. Phys. Rev. B 2018, 97, 245427. [Google Scholar] [CrossRef] [Green Version]
- Si, K.; Ma, J.; Lu, C.; Zhou, Y.; He, C.; Yang, D.; Wang, X.; Xu, X. A two-dimensional MoS2/WSe2 van der Waals heterostructure for enhanced photoelectric performance. Appl. Surf. Sci. 2020, 507. [Google Scholar] [CrossRef]
- Aretouli, K.E.; Tsoutsou, D.; Tsipas, P.; Marquez-Velasco, J.; Aminalragia Giamini, S.; Kelaidis, N.; Psycharis, V.; Dimoulas, A. Epitaxial 2D SnSe2/ 2D WSe2 van der Waals Heterostructures. ACS Appl. Mater. Interfaces 2016, 8, 23222–23229. [Google Scholar] [CrossRef]
- Nguyen, H.T.T.; Obeid, M.M.; Bafekry, A.; Idrees, M.; Vu, T.V.; Phuc, H.V.; Hieu, N.N.; Hoa, L.T.; Amin, B.; Nguyen, C.V. Interfacial characteristics, Schottky contact, and optical performance of a graphene/Ga2SSe van der Waals heterostructure: Strain engineering and electric field tunability. Phys. Rev. B 2020, 102, 075414. [Google Scholar] [CrossRef]
- Zeng, H.; Zhao, J.; Cheng, A.-Q.; Zhang, L.; He, Z.; Chen, R.-S. Tuning electronic and optical properties of arsenene/C3N van der Waals heterostructure by vertical strain and external electric field. Nanotechnology 2018, 29, 075201. [Google Scholar] [CrossRef] [PubMed]
- Li, X.D.; Wu, S.-Q.; Zhu, Z.-Z. Band gap control and transformation of monolayer-MoS2 -based hetero-bilayers. J. Mater. Chem. C 2015, 3, 9403–9411. [Google Scholar] [CrossRef]
- Naseri, M.; Abutalib, M.; Alkhambashi, M.; Gu, J.; Jalilian, J.; Farouk, A.; Batle, J. Prediction of novel SiX2 (X = S, Se) monolayer semiconductors by density functional theory. Phys. E Phys. E Low Dimens. Syst. Nanostruct. 2019, 114, 113581. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Ambrosetti, A.; Ferri, N.; DiStasio, R.A., Jr.; Tkatchenko, A. Wavelike charge density fluctuations and van der Waals interactions at the nanoscale. Science 2016, 351, 1171–1176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chadi, D.J. Special points for Brillouin-zone integrations. Phys. Rev. B 1977, 16, 1746–1747. [Google Scholar] [CrossRef]
- Rasmussen, F.A.; Thygesen, K.S. Computational 2D Materials Database: Electronic Structure of Transition-Metal Dichalcogenides and Oxides. J. Phys. Chem. C 2015, 119, 13169–13183. [Google Scholar] [CrossRef]
- Yun, W.S.; Han, S.W.; Hong, S.C.; Kim, I.G.; Lee, J.D. Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-MX2 semiconductors (M=Mo, W;X=S, Se, Te). Phys. Rev. B 2012, 85, 033305. [Google Scholar] [CrossRef]
- Lu, N.; Guo, H.; Zhuo, Z.; Wang, L.; Wu, X.; Zeng, X.C. Twisted MX2/MoS2 heterobilayers: Effect of van der Waals interaction on the electronic structure. Nanoscale 2017, 9, 19131–19138. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Wang, Y.; Ni, J.; Shi, L.; Shi, S.; Tang, W. First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M=Mo, Nb, W, Ta; X=S, Se, Te) monolayers. Phys. B Condens. Matter 2011, 406, 2254–2260. [Google Scholar] [CrossRef]
- Tsao, H.-W.; Kaun, C.-C.; Su, Y.-H. Decorating a WSe2 monolayer with Au nanoparticles: A study combined first-principles calculation with material genome approach. Surf. Coatings Technol. 2020, 388, 125563. [Google Scholar] [CrossRef]
- Yang, F.; Han, J.; Zhang, L.; Tang, X.; Zhuo, Z.; Tao, Y.; Cao, X.; Dai, Y. Adjustable electronic and optical properties of BlueP/MoS2 van der Waals heterostructure by external strain: A First-principles study. Nanotechnology 2020, 31, 375706. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, M.; Zhou, Y.; Ren, C.; Zhong, X.; Wang, J. First-principles predication of facet-dependent electronic and optical properties in InSe/GaAs heterostructure with potential in solar energy utilization. J. Alloys Compd. 2020, 842, 155901. [Google Scholar] [CrossRef]
- Hu, L.; Yi, W.; Rao, T.; Tang, J.; Hu, C.; Yin, H.; Hao, H.; Zhang, L.; Li, C.; Li, T. Two-dimensional type-II g-C3N4/SiP-GaS heterojunctions as water splitting photocatalysts: First-principles predictions. Phys. Chem. Chem. Phys. 2020, 22, 15649–15657. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, F.; Deng, M.; Wang, Y. Enhanced visible-light photocatalytic activity of a g-C3N4/BiVO4 nanocomposite: A first-principles study. Phys. Chem. Chem. Phys. 2015, 17, 10218–10226. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Wei, X.; Guo, T.; Fan, J.; Ni, L.; Weng, Y.; Zha, Z.; Liu, J.; Tian, Y.; et al. Type-II tunable SiC/InSe heterostructures under an electric field and biaxial strain. Phys. Chem. Chem. Phys. 2020, 22, 9647–9655. [Google Scholar] [CrossRef]
- Li, X.; Dai, Y.; Ma, Y.; Liu, Q.; Huang, B. Intriguing electronic properties of two-dimensional MoS2/TM2CO2 (TM = Ti, Zr, or Hf) hetero-bilayers: Type-II semiconductors with tunable band gaps. Nanotechnology 2015, 26, 135703. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, S.; Wang, Y.; Duan, H.M.; Long, M. First-Principles Study of Strain Modulation in S3P2/Black Phosphorene vdW Heterostructured Nanosheets for Flexible Electronics. ACS Appl. Nano Mater. 2020, 3, 4407–4417. [Google Scholar] [CrossRef]
- Qu, L.-H.; Deng, Z.-Y.; Yu, J.; Lu, X.-K.; Zhong, C.-G.; Zhou, P.-X.; Lu, T.-S.; Zhang, J.-M.; Fu, X.-L. Mechanical and electronic properties of graphitic carbon nitride (g-C3N4) under biaxial strain. Vacuum 2020, 176, 109358. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, B.; Qian, Q.; Gao, Z.; Tang, X.; Li, B. Strain-tunable III-nitride/ZnO heterostructures for photocatalytic water-splitting: A hybrid functional calculation. APL Mater. 2020, 8, 041114. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Yang, Y.; Xiao, Y.; Zhao, Y.; Luo, D.; Zheng, Z.; Huang, L. Tunable electronic structure of graphdiyne/MoS2 van der Waals heterostructure. Mater. Lett. 2018, 228, 289–292. [Google Scholar] [CrossRef]
- Caglayan, R.; Mogulkoc, Y.; Alkan, B. First principles study on optoelectronic properties of energetically stable Si/InS van der Waals heterobilayers. J. Mater. Sci. 2020, 55, 15199–15212. [Google Scholar] [CrossRef]

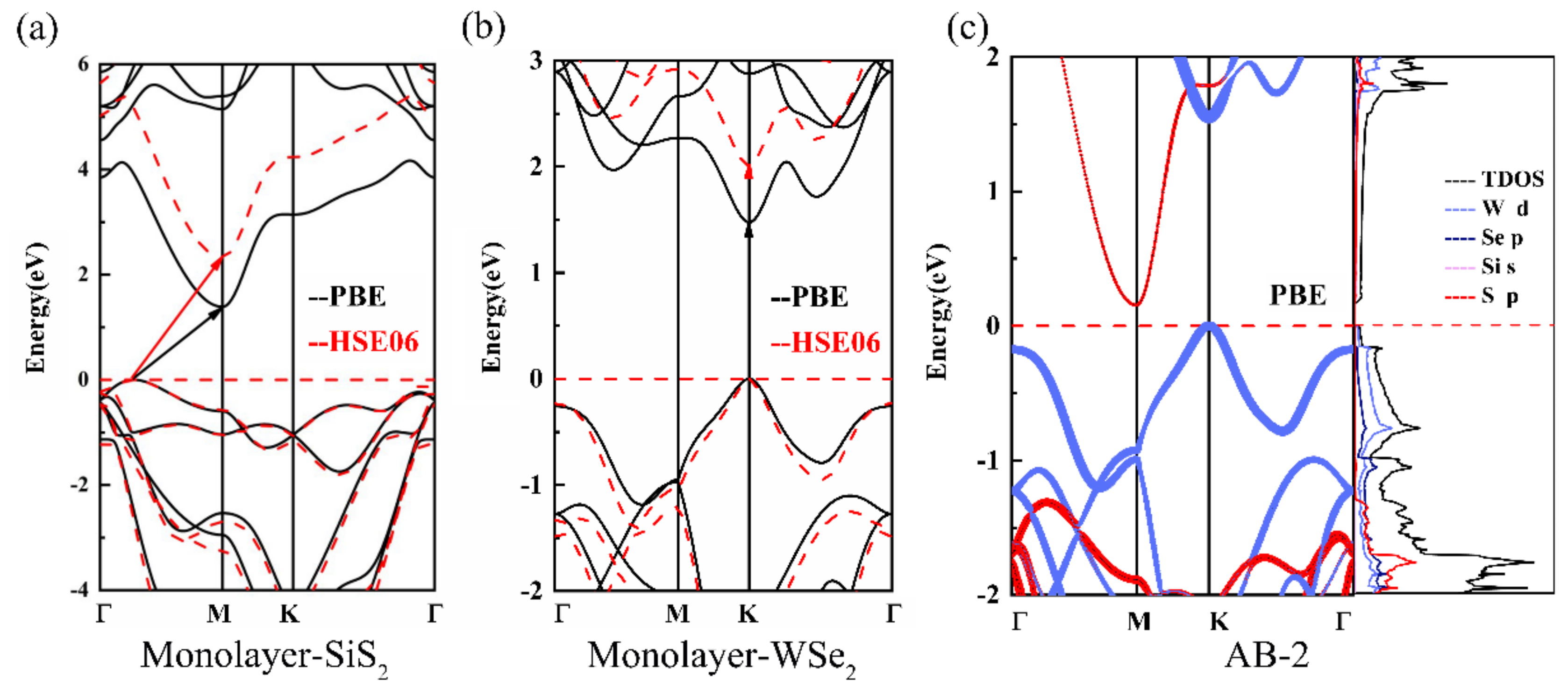


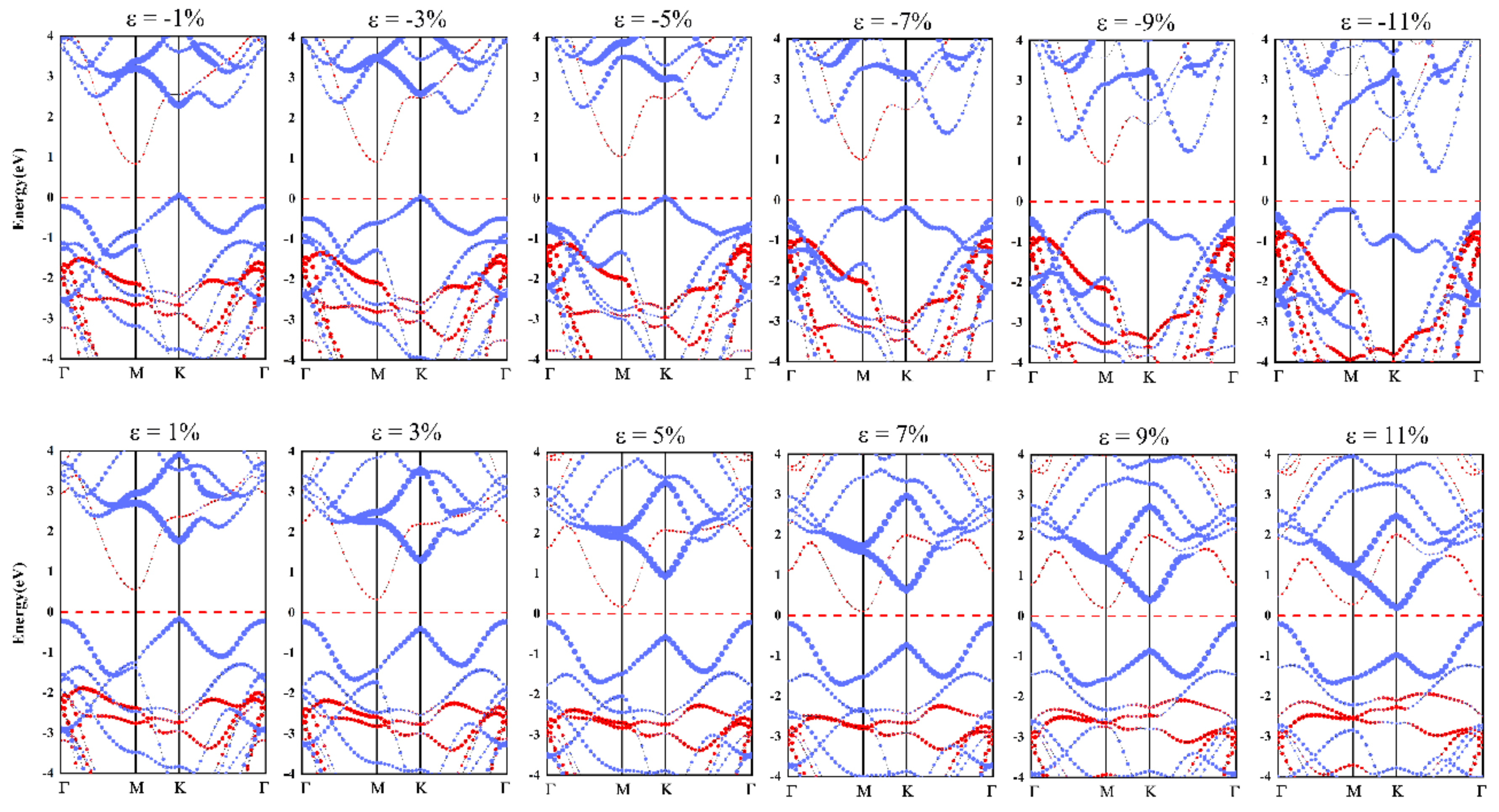

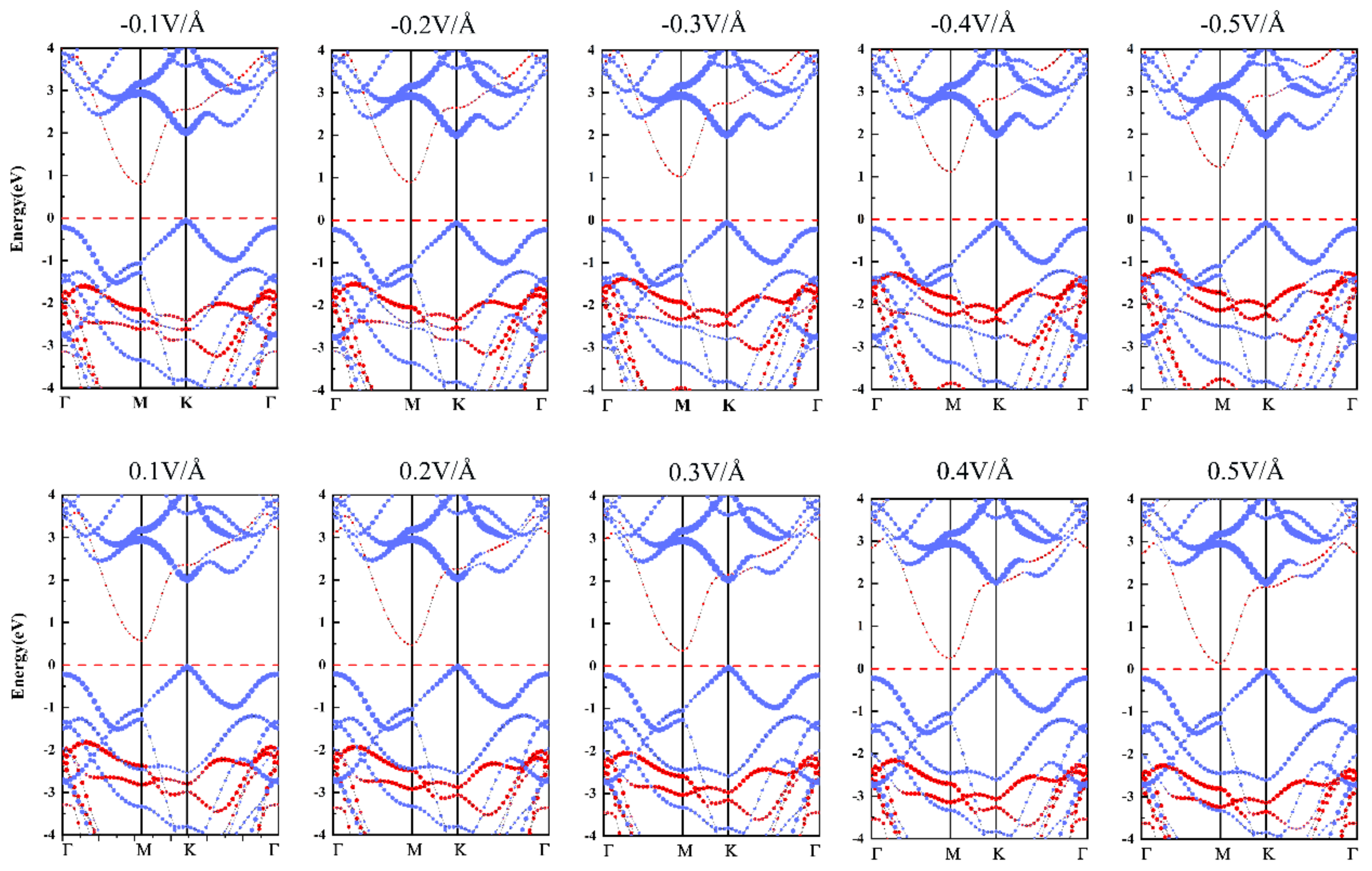
| Stacking Mode | a (Å) | s (Å) | |||||
|---|---|---|---|---|---|---|---|
| AA-1 | −182.5 | 3.315 | 2.325 | 2.541 | 3.192 | metal | / |
| AA-2 | −125.1 | 3.315 | 2.326 | 2.542 | 3.784 | metal | / |
| AB-1 | −194.2 | 3.315 | 2.325 | 2.540 | 3.144 | metal | / |
| AB-2 | −197.0 | 3.315 | 2.324 | 2.541 | 3.125 | 0.154 | 0.738 |
| AC-1 | −125.0 | 3.314 | 2.325 | 2.541 | 3.788 | metal | / |
| AC-2 | −175.0 | 3.317 | 2.325 | 2.542 | 3.234 | metal | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Li, X.; Niu, R.; Zhang, N.; Hu, T.; Zhang, L. Tunable Electronic Properties of Type-II SiS2/WSe2 Hetero-Bilayers. Nanomaterials 2020, 10, 2037. https://doi.org/10.3390/nano10102037
Guan Y, Li X, Niu R, Zhang N, Hu T, Zhang L. Tunable Electronic Properties of Type-II SiS2/WSe2 Hetero-Bilayers. Nanomaterials. 2020; 10(10):2037. https://doi.org/10.3390/nano10102037
Chicago/Turabian StyleGuan, Yue, Xiaodan Li, Ruixia Niu, Ningxia Zhang, Taotao Hu, and Liyao Zhang. 2020. "Tunable Electronic Properties of Type-II SiS2/WSe2 Hetero-Bilayers" Nanomaterials 10, no. 10: 2037. https://doi.org/10.3390/nano10102037
APA StyleGuan, Y., Li, X., Niu, R., Zhang, N., Hu, T., & Zhang, L. (2020). Tunable Electronic Properties of Type-II SiS2/WSe2 Hetero-Bilayers. Nanomaterials, 10(10), 2037. https://doi.org/10.3390/nano10102037




