Analysis of Biomechanical Characteristics of Bone Tissues Using a Bayesian Neural Network: A Narrative Review
Abstract
1. Background
2. Materials and Methods
2.1. Literature Search
2.2. Inclusion and Exclusion Criteria:
- Works containing data (experimental/modelling) on the elastic properties of cortical and/or cancellous bone tissue.
- Articles that discuss the effect of age, anatomical region or structure on elastic properties.
- Publications that explicitly mention bone marrow as a factor in mechanical response.
- Articles limited to fracture strength characteristics (no elastic behaviour) or considering only the micro- or nano-scale (example: studies of hydroxyapatite crystals).
- Works that do not have full text (conference abstracts only) or are in closed access without the possibility of evaluating methods.
- Studies focusing solely on pathologies (bone tumours) that do not describe basic elastic characteristics.
2.3. Analysing the Data Collected
- Bone type: cortical (compact) vs. cancellous (trabecular).
- Anatomical section: long tubular bones (femur, shoulder, etc.), skull bones, vertebrae, pelvic bones, ribs, sternum, etc.
- Age groups: young (20–35 years), middle-aged (35–60 years), elderly (>60 years), and experimental models in young/old animals.
- Methods for determining elastic properties: in vitro mechanical tests (static or dynamic), ultrasonic technique, FE models (finite element), poroelastic models, shear, torsion, compression, tension tests.
- Bone marrow accounting/unaccounting: whether sample purification was performed or whether marrow fluid was simulated in the models.
3. Results
3.1. Overview of the Selected Studies
3.2. Summary of the 45 Main Publications
3.3. Characterisation of Bone Type Features in the Anatomical Zones of the Skeleton
3.4. Influence of Age and Gender
3.5. The Role of Bone Marrow
3.6. General Conclusions of the Analysis
- Bone types (femur, shoulder, skull, vertebra, pelvic bone), where the cortical layer can reach up to 30 GPa in the young and drop to 10 GPa in the elderly, and the cancellous component ranges from 0.2 to 5 GPa;
- Age-related changes, which most noticeably affect the spongy structures, sometimes resulting in a 30–50% loss of stiffness, although the cortical tissue also loses an average of 10–30%;
- Tissue type (cortical vs. cancellous), with cancellous bone being significantly more variable and anisotropic;
- Localisation in the bone (periphery vs. centre), as the periphery is often represented by a denser cortical shell and the centre by a porous trabecular network;
- The effects of bone marrow, which may play little or no role at low loading rates, but under conditions of rapid impact and confinement increase stiffness, forming a hydraulic stiffening effect.
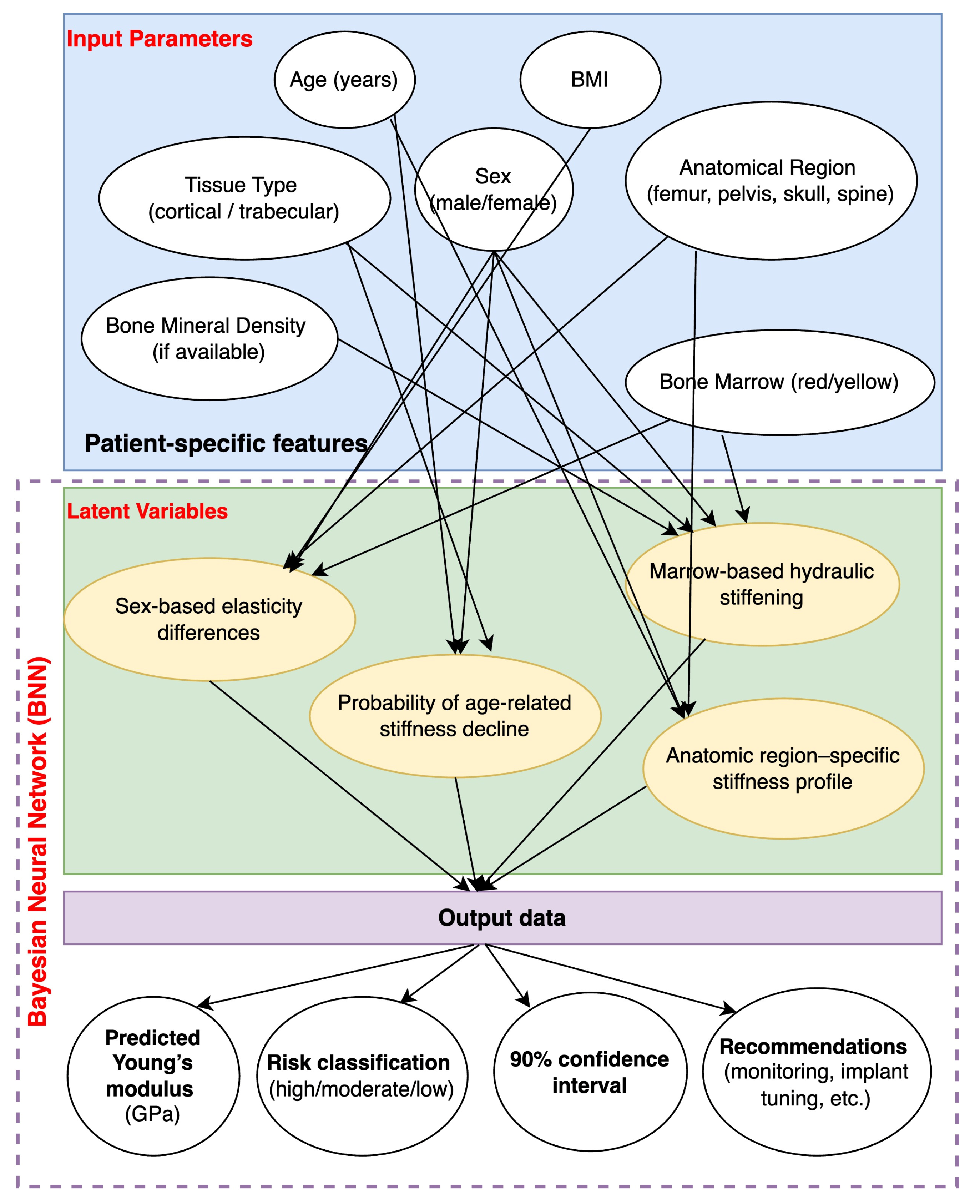
4. Future Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BMI | Body Mass Index |
| BNN | Bayesian Neural Network |
| CT | Computed Tomography |
| E | Modulus of Elasticity |
| FEA | Finite Element Analysis |
| GPa | Gigapascal |
| PINNs | Physics-Informed Neural Networks |
| SDE | Stochastic Differential Equations |
Appendix A
| Author (Year) | Abstract | Introduction | Methodology | Results | Discussion | Others | Score |
|---|---|---|---|---|---|---|---|
| 1. Rosa et al. (2022) [1] | ★ | ★ | ★ | ★ | ★ | 0 | 5/6 |
| 2. Niu et al. (2023) [2] | ★ | ★ | ★ | ★ | 0 | ★ | 5/6 |
| 3. Hart et al. (n.d.) [3] | ★ | ★ | 0 | ★ | 0 | ★ | 4/6 |
| 4. Sansalone et al. (2012) [15] | ★ | ★ | ★ | ★ | ★ | 0 | 5/6 |
| 5. Pritchard et al. (2013) [16] | ★ | 0 | ★ | ★ | ★ | 0 | 4/6 |
| 6. Pope et al. (1974) [61] | ★ | ★ | 0 | ★ | 0 | ★ | 4/6 |
| 7. Cole & Van Der Meulen (2020) [5] | ★ | ★ | ★ | 0 | ★ | ★ | 5/6 |
| 8. Martin (1991) [17] | ★ | 0 | 0 | ★ | ★ | ★ | 4/6 |
| 9. Goldstein (1987) [18] | ★ | ★ | ★ | ★ | ★ | 0 | 5/6 |
| 10. Augat et al. (1998) [19] | ★ | ★ | 0 | ★ | 0 | ★ | 4/6 |
| 11. Bouxsein (2001) [20] | ★ | ★ | ★ | ★ | ★ | ★ | 6/6 |
| 12. Gomez & Nahum (2002) [6] | ★ | 0 | ★ | ★ | ★ | ★ | 5/6 |
| 13. Morgan et al. (2018) [7] | ★ | ★ | 0 | ★ | ★ | 0 | 4/6 |
| 14. Ingole et al. (2021) [21] | ★ | ★ | ★ | ★ | 0 | ★ | 5/6 |
| 15. Battafarano et al. (2021) [22] | 0 | ★ | ★ | ★ | ★ | ★ | 5/6 |
| 16. Garcia-Giner et al. (2021) [23] | ★ | ★ | 0 | ★ | 0 | 0 | 3/6 |
| 17. Álvarez-Lloret et al. (2021) [24] | ★ | ★ | ★ | ★ | ★ | 0 | 5/6 |
| 18. Nefjodovs et al. (2023) [25] | 0 | ★ | 0 | ★ | ★ | ★ | 4/6 |
| 19. Gasik et al. (2021) [26] | ★ | ★ | ★ | ★ | 0 | 0 | 4/6 |
| 20. Grill et al. (2025) [27] | ★ | ★ | 0 | ★ | ★ | 0 | 4/6 |
| 21. Bhattarai et al. (2018) [28] | 0 | ★ | ★ | ★ | 0 | ★ | 4/6 |
| 22. Ferraz (2024) [29] | ★ | ★ | 0 | ★ | ★ | ★ | 5/6 |
| 23. Castro-Franco et al. (2020) [30] | ★ | 0 | ★ | ★ | ★ | ★ | 5/6 |
| 24. Łuczak et al. (2024) [31] | ★ | 0 | 0 | ★ | ★ | ★ | 4/6 |
| 25. Costăchescu et al. (2023) [32] | ★ | ★ | ★ | ★ | ★ | 0 | 5/6 |
| 26. Zhao et al. (2023) [4] | 0 | ★ | 0 | ★ | 0 | ★ | 3/6 |
| 27. Zhao et al. (2018) [8] | ★ | ★ | ★ | ★ | 0 | ★ | 5/6 |
| 28. Turner et al. (1999) [9] | ★ | 0 | 0 | ★ | ★ | 0 | 3/6 |
| 29. Ashman et al. (1987) [33] | ★ | ★ | ★ | 0 | 0 | ★ | 4/6 |
| 30. Sansalone et al. (2010) [15] | ★ | ★ | 0 | ★ | ★ | ★ | 5/6 |
| 31. Hamandi et al. (2021) [35] | ★ | ★ | ★ | ★ | 0 | ★ | 5/6 |
| 32. Nikolov & Raabe (2008) [36] | ★ | 0 | 0 | ★ | ★ | 0 | 3/6 |
| 33. Salguero et al. (2014) [37] | ★ | ★ | ★ | 0 | ★ | 0 | 4/6 |
| 34. Blázquez-Carmona et al. (2024) [10] | ★ | 0 | ★ | ★ | 0 | ★ | 4/6 |
| 35. Katz et al. (1984) [38] | ★ | ★ | 0 | ★ | ★ | ★ | 5/6 |
| 36. Turek et al. (2025) [39] | ★ | ★ | ★ | ★ | 0 | 0 | 4/6 |
| 37. Stojković et al. (2023) [11] | ★ | 0 | 0 | ★ | ★ | ★ | 4/6 |
| 38. Ibrahim et al. (2020) [40] | ★ | ★ | ★ | 0 | ★ | 0 | 4/6 |
| 39. Ibrahim et al. (2024) [12] | 0 | ★ | ★ | ★ | ★ | 0 | 4/6 |
| 40. Sanz et al. (2023) [13] | ★ | 0 | 0 | ★ | ★ | ★ | 4/6 |
| 41. Bazyar et al. (2023) [41] | ★ | ★ | ★ | 0 | ★ | ★ | 5/6 |
| 42. Baleani et al. (2024) [42] | ★ | ★ | 0 | ★ | 0 | ★ | 4/6 |
| 43. Lin & Kang (2021) [43] | ★ | ★ | ★ | ★ | ★ | ★ | 6/6 |
| 44. Hamandi & Goswami (2021) [35] | ★ | 0 | ★ | 0 | ★ | ★ | 4/6 |
| 45. Hamandi & Goswami (2022) [46] | ★ | ★ | 0 | ★ | ★ | 0 | 4/6 |
| Experimental Methods | Authors, Year of Publication | Journal of Publication | Types of Specimens | Numbers of Specimens | Gender | Age | Anatomic Sites | Main Findings or Summaries |
|---|---|---|---|---|---|---|---|---|
| Mechanical tests (3-point bending, compression) | 1. Rosa et al. (2022) [1] | Applied Sciences | Cylindrical/rectangular sections from long bones (in vitro) | 30 | Both | 30–65 | Femoral diaphysis, tibial cortex. | Demonstrates that bone is an outstanding natural “composite”, highlighting the synergy between collagen matrix and mineral phase; mechanical performance correlates with porosity and fibre orientation. |
| Ultrasound + CT correlation | 2. Niu et al. (2023) [2] | Journal of Functional Biomaterials | Intact cadaveric bones (ex vivo) | 25 | Mixed | 40–80 | Vertebral bodies | Emphasises the role of microstructural features in modulating bone’s elastic modulus; proposes new analysis approaches combining imaging and acoustic velocity measures. |
| Scanning electron microscopy (SEM) + hardness testing | 3. Hart et al. (n.d.) [3] | - (Online article/PMC) | Human cortical bone slices | 12 | Not specified | 20–45 | Femoral midshaft | Biological basis of bone strength (anatomy and physiology) analysing microcracks on SEM images; highlights measuring different mechanical parameters (microhardness, porosity). |
| Nanoindentation + morphological assessment | 4. Sansalone et al. (2012) [15] | Bone | Femoral neck trabecular bone (human) | 18 | Both | 40–75 | Human femoral neck | Demonstrates that distribution of mineralisation significantly affects local mechanical properties in the femoral neck; higher heterogeneity→ different local stiffness values. |
| DXA-based + ex vivo destructive testing | 5. Pritchard et al. (2013) [16] | Bone | Bones from diabetic vs. non-diabetic patients | 20 | Not specified | 50–70 | Knee osteoarthritis and T2D bone surfaces | Observed elevated and more homogeneous mineralisation in type 2 diabetes with osteoarthritis, indicating potential differences in stiffness compared to osteoarthritis alone. |
| Literature review + mechanical perspective | 6. Pope et al. (1974) [61] | CRC Press eBooks | - | - | - | - | General overview | Summarises fundamental mechanical properties of bone, focusing on how composition and hierarchical structure govern the elastic/plastic behaviour. |
| Finite Element Analysis (FEA) + micro-CT | 7. Cole & Van Der Meulen (2020) [5] | Contemporary Endocrinology | Micro-CT scanned mouse tibiae, in silico simulation | 16 | Both | Various (adult mice) | Tibial cortical/trabecular | Demonstrates how FEA can link changes in bone geometry to predicted strain distribution, relevant for endocrine disorders affecting bone. |
| Statistical analysis of mechanical tests | 8. Martin (1991) [17] | Journal of Biomechanics | Various literature data reanalysis | - | - | - | Multiple (long bones) | Identifies determinants of mechanical properties (mineral density, collagen cross-links) through reanalysis of prior datasets; highlights role of microdamage in older bones. |
| In vitro tension/compression | 9. Goldstein (1987) [18] | Journal of Biomechanics | Bovine/human trabecular bone samples | 28 | - | - | Distal femur, vertebrae | The mechanical properties of trabecular bone heavily depend on anatomic location and function; cortical-trabecular transitions also matter. |
| Ultrasonic measurement of anisotropy | 10. Augat et al. (1998) [19] | Medical Engineering & Physics | Human/mammalian trabecular bone blocks | 20 | Both | 30–75 | Distal radius, proximal tibia. | Demonstrates anisotropy in the elastic modulus of trabecular bone from different regions, correlating with load direction. |
| Review: age-related fractures | 11. Bouxsein (2001) [20] | Elsevier eBooks | - | - | - | - | General (osteoporotic fractures) | Discusses the link between mechanical properties and fracture risk in older adults, emphasizing that material properties + architecture synergy is key to understanding fragility. |
| Comparative approach: bone vs. trauma | 12. Gomez & Nahum (2002) [6] | Springer eBooks | - | - | - | - | Various (long bones, spongy bone) | Biomechanics of bone in accidental injury context; highlights energy absorption capacity in relation to microstructure and orientation. |
| Multiscale mechanical analysis | 13. Morgan et al. (2018) [7] | Annual Review of Biomedical Engineering | Human trabecular + cortical data compilation | Large meta-study | Both | 20–80 (various) | Multiple (femur, tibia, spine) | Summarises healthy/diseased states; indicates that while architecture drastically changes with osteoporosis, lamellar-level properties remain comparatively stable. |
| Sintered hydroxyapatite mechanical test | 14. Ingole et al. (2021) [21] | Minerals | Hydroxyapatite-based materials (compression, HPC) | - | - | - | Synthetic bone regeneration setups | Found that nanostructured hydroxyapatite can match certain mechanical benchmarks of bone, focusing on bone tissue engineering applications. |
| Bone graft/tissue engineering review | 15. Battafarano et al. (2021) [22] | International Journal of Molecular Sciences | - | - | - | - | Highly loaded skeletal sites | Summarises strategies for bone regeneration with biomaterials; mechanical stability is essential in sites subject to high loads. |
| Nanoscale imaging | 16. Garcia-Giner et al. (2021) [23] | Applied Sciences | Human bone pathologies (micro-CT + SEM) | 10 | Both | 50–70 | Various (skull, femur) | Reviews imaging and analysis methods for bone pathologies at the nanoscale, discussing correlation with reduced mechanical competence. |
| Metal contamination and mineral properties | 17. Álvarez-Lloret et al. (2021) [24] | Minerals | Alveolar bone under lead exposure | 8 | Both | 30–45 (animal model) | Alveolar bone | Shows that chronic lead exposure alters mineral properties and mechanical stability, which may serve as a model for human alveolar bone changes. |
| Wood as bone surrogate | 18. Nefjodovs et al. (2023) [25] | Journal of Functional Biomaterials | Wood-based surrogates in mechanical tests | - | - | - | - | Reviews feasibility of using wood as a renewable material to mimic certain structural aspects of bone (porosity, anisotropy); discusses limitations for direct mechanical comparison. |
| Implant design approaches | 19. Gasik et al. (2021) [26] | Materials | Dental implants (in vivo + in silico) | - | - | - | Mandibular bone | Analyses how bone-implant interface mechanics vary by bone density and location; suggests consideration of both cortical and trabecular compartments for robust design. |
| Bone regeneration (mini-review) | 20. Grill et al. (2025) [27] | Bioengineering | - | - | - | - | Various (general approach) | Short overview on bone regeneration techniques; mechanical perspectives on scaffolds and host bone integration. |
| Electrospun fibrous materials | 21. Bhattarai et al. (2018) [28] | Membranes | Fibrous polymer scaffolds (experimental) | - | - | - | Tissue engineering applications | Discusses mechanical properties of natural vs. synthetic electrospun scaffolds for bone repair. |
| Bone substitute materials | 22. Ferraz (2024) [29] | International Journal of Molecular Sciences | Biomaterials in bone TE (ex vivo/in vivo) | - | - | - | Various load-bearing sites | Emphasises composite scaffolds that replicate bone’s mechanical environment, focusing on mechanical + biological synergy. |
| Proximal humerus characterisation | 23. Castro-Franco et al. (2020) [30] | Applied Sciences | Humerus mechanical property evaluation | 12 | Both | 45–70 | Proximal humerus | Reviews the proximal humerus in biomechanical studies, highlights incomplete data on anisotropy and a need for standardised protocols. |
| Emerging technologies in bone repair | 24. Łuczak et al. (2024) [31] | International Journal of Molecular Sciences | - | - | - | - | Future bone regeneration devices | Summary of upcoming biomaterials, 3D printing, and mechanical testing strategies for advanced bone scaffolds. |
| Screw osteointegration | 25. Costăchescu et al. (2023) [32] | Materials | Screw pull-out mechanical tests | 40 | Both | 40–65 | Femoral condyles + tibial plateau | Concludes that enhancing biomechanical resistance to pull-out effect depends on correct match of screw geometry and local bone density. |
| Bone organoids (review) | 26. Zhao et al. (2023) [4] | Advanced Healthcare Materials | In vitro bone organoid models | - | - | - | - | Highlights recent advances and future challenges in the development of bone organoids; discusses mechanical environment’s importance in organoid maturity. |
| Compression test standardisation | 27. Zhao et al. (2018) [8] | Bone and Joint Research | Human cortical bone blocks | 40 | Both | 55–80 years | Femoral diaphysis (cortical regions) | The article emphasises the significant variability in bone stiffness results due to differences in testing protocols (specimen geometry, end-face quality, specimen orientation). The authors propose a standardised approach to compression testing to reduce variability and increase comparability between different studies. |
| Elastic properties (microscopic) | 28. Turner et al. (1999) [9] | Journal of Biomechanics | Human cortical + trabecular (micro-tests) | - | Both | 20–70 | Various (femur, tibia) | Finds that, at the microscopic level, cortical and trabecular tissues can show surprisingly similar elastic properties, if tested under consistent protocols. |
| Ultrasonic technique | 29. Ashman et al. (1987) [33] | Journal of Biomechanics | Cancellous bone, ultrasonic velocity | 20 | - | - | Distal femur, proximal tibia. | Concludes that acoustic-based methods can measure elastic properties of cancellous bone, showing site-specific differences. |
| Heterogeneous anisotropic elastic properties | 30. Sansalone et al. (2010) [15] | Journal of Biomechanics | Human femoral bone cubes (10 mm) | 14 | Both | 50–80 | Femoral diaphysis/neck | Found significant anisotropy at multiple scales; link to remodelling pattern and local mineralisation. |
| Retrospective evaluation (anisotropic) | 31. Hamandi et al. (2021) [35] | Bioengineering | Literature data and finite element comparisons | - | - | - | Various (long bones) | Proposed a framework for matching anisotropic material behaviour vs. elastic, elastic-plastic, and hyper-elastic properties in bone. |
| Hierarchical modelling | 32. Nikolov & Raabe (2008) [36] | Biophysical Journal | Multiscale model (submicron) | - | - | - | Collagen-mineral arrangement | Shows that extrafibrillar mineralisation drastically affects submicron elasticity; hierarchical modelling bridging nano to macro scale. |
| Micromechanical modelling | 33. Salguero et al. (2014) [37] | Journal of Biomechanics | Cortical bone (modelling) | - | - | - | Mid-diaphyseal cortical (human) | Accounted for anisotropy of dense tissue in micromechanical modelling, concluding that orientation of vascular channels is a key factor. |
| Woven bone mechanical properties | 34. Blázquez-Carmona et al. (2024) [10] | Frontiers in Bioengineering and Biotechnology | Healing woven bone specimens (animal) | 20 | Both | ~2–3 months post-surgery | Femoral defect model | Observes how structural and chemical properties of woven bone under healing correlate with local variations in elastic modulus. |
| Remodelling effect | 35. Katz et al. (1984) [38] | Calcified Tissue International | Various bone sites (thin sections) | 15 | Mixed | ~40–65 | Femur, tibia. | Argues that remodelling significantly alters elastic properties; local histological changes lead to different stiffness regions. |
| Aspect-Related mechanical testing | 36. Turek et al. (2025) [39] | Applied Sciences | Metacarpal bone of mares (equine) | 28 | Female (mares) | Adult equines | 3rd metacarpal bone | Shows that cortical bone mechanical properties in horses vary by aspect and that consistent anatomic referencing is crucial. |
| Electron Beam Melting (EBM) lattice | 37. Stojković et al. (2023) [11] | Metals | 3D-printed Ti6Al4V scaffolds | 16 | - | - | Anatomically shaped lattice bone scaffold | Noted adjustable elasticity by controlling lattice geometry; relevant for load-bearing implants. |
| Hardness and collagen | 38. Ibrahim et al. (2020) [40] | Journal of Functional Biomaterials | Bone microhardness test (Vickers), ex vivo | 10 | Not specified | ~30–60 | Femoral cortical/trabecular | Identifies hardness as an important indicator of bone quality; collagen plays a major role in local hardness variations. |
| Viscoelastic deformation | 39. Ibrahim et al. (2024) [12] | Journal of Functional Biomaterials | Vickers hardness + time-dependent analysis | 8 | Both | 40–65 | Femoral diaphysis | Discovers a novel mechanism of time-dependent (viscoelastic) deformation under indentation, reinforcing the significance of collagen matrix. |
| Juvenile bone properties | 40. Sanz et al. (2023) [13] | Materials | Juvenile long bones (mechanical tests) | 25 | Both (juvenile) | 5–15 years | Tibia, femur | Variation in mechanical behaviour found as a function of age in juvenile bones; potential collision/trauma analysis. |
| Finite Element modelling (femur) | 41. Bazyar et al. (2023) [41] | Biomechanics | Human femur FE modelling + material property assignment | - | Both | 55–70 (cadaveric) | Proximal femur | Overview of property definition in FE models of the femur; emphasises how small changes in anisotropy input can alter simulation outcomes. |
| Tensile Yield Strain | 42. Baleani et al. (2024) [42] | Bioengineering | Femoral diaphysis (human) testing | 14 | Mixed | 35–70 | Human femoral diaphysis | Suggests that tensile yield strain remains constant among healthy adults, providing a reference baseline for future mechanical evaluations. |
| Uniaxial tensile test review | 43. Lin & Kang (2021) [43] | Materials | Literature review + some new tests | ~40 | Mixed | 20–60 | Long bones, cortical shell | Provides practical guidelines on measuring stress–strain curves of compact bone under uniaxial tension; notes pitfalls and recommended protocols. |
| Anisotropic vs. Hyperelastic | 44. Hamandi & Goswami (2021) [35] | Bioengineering | Literature-based + new computational approach | - | - | - | Various (long bones) | Developed a framework to compare anisotropic, elastic-plastic, and hyperelastic models for bone, concluding anisotropy is essential for accuracy. |
| Hierarchical structure (nano-level) | 45. Hamandi & Goswami (2022) [46] | Bioengineering | Bone hierarchical data (nanoindentation, micro-CT) | 10 | Mixed | 30–70 | Femoral cortical, tibial cortical. | Emphasises that hierarchical structure and nano-level features significantly influence macro-level mechanical response. |
References
- Rosa, N.; Moura, M.F.S.F.; Olhero, S.; Simoes, R.; Magalhães, F.D.; Marques, A.T.; Ferreira, J.P.S.; Reis, A.R.; Carvalho, M.; Parente, M. Bone: An outstanding composite material. Appl. Sci. 2022, 12, 3381. [Google Scholar] [CrossRef]
- Niu, Y.; Du, T.; Liu, Y. Biomechanical characteristics and analysis approaches of bone and bone substitute materials. J. Funct. Biomater. 2023, 14, 212. [Google Scholar] [CrossRef] [PubMed]
- Hart, N.H.; Newton, R.U.; Tan, J.; Rantalainen, T.; Chivers, P.; Siafarikas, A.; Nimphius, S. Biological basis of bone strength: Anatomy, physiology and measurement. J. Musculoskelet. Neuronal Interact. 2020, 20, 347. [Google Scholar] [PubMed]
- Zhao, D.; Saiding, Q.; Li, Y.; Tang, Y.; Cui, W. Bone organoids: Recent advances and future challenges. Adv. Healthc. Mater. 2023, 13, 2302088. [Google Scholar] [CrossRef]
- Cole, J.H.; Van Der Meulen, M.C.H. Biomechanics of bone. In Contemporary Endocrinology; Springer International Publishing: Cham, Switzerland, 2020; pp. 185–209. [Google Scholar] [CrossRef]
- Gomez, M.A.; Nahum, A.M. Biomechanics of bone. In Accidental Injury: Biomechanics and Prevention; Springer: Berlin/Heidelberg, Germany, 2002; pp. 206–227. [Google Scholar] [CrossRef]
- Morgan, E.F.; Unnikrisnan, G.U.; Hussein, A.I. Bone mechanical properties in healthy and diseased states. Annu. Rev. Biomed. Eng. 2018, 20, 119–143. [Google Scholar] [CrossRef]
- Zhao, S.; Arnold, M.; Ma, S.; Abel, R.L.; Cobb, J.P.; Hansen, U.; Boughton, O. Standardizing compression testing for measuring the stiffness of human bone. Bone Jt. Res. 2018, 7, 524–538. [Google Scholar] [CrossRef]
- Turner, C.H.; Rho, J.; Takano, Y.; Tsui, T.Y.; Pharr, G.M. The elastic properties of trabecular and cortical bone tissues are similar: Results from two microscopic measurement techniques. J. Biomech. 1999, 32, 437–441. [Google Scholar] [CrossRef]
- Blázquez-Carmona, P.; Mora-Macías, J.; Pajares, A.; Mármol, Á.; Reina-Romo, E. On the influence of structural and chemical properties on the elastic modulus of woven bone under healing. Front. Bioeng. Biotechnol. 2024, 12, 1476473. [Google Scholar] [CrossRef]
- Stojković, J.R.; Stojković, M.; Turudija, R.; Aranđelović, J.; Marinkovic, D. Adjustable elasticity of anatomically shaped lattice bone scaffold built by electron beam melting TI6AL4V powder. Metals 2023, 13, 1522. [Google Scholar] [CrossRef]
- Ibrahim, A.; Jiang, Z.; Shirvani, K.; Dalili, A.; Hamid, Z.A. A Novel Viscoelastic Deformation Mechanism Uncovered during Vickers Hardness Study of Bone. J. Funct. Biomater. 2024, 15, 87. [Google Scholar] [CrossRef]
- Sanz, C.V.; Rodríguez, I.V.; Forriol, F.; Tejado, E.; Lopez-Valdes, F.J. Variation in juvenile long bone properties as a function of age: Mechanical and compositional characterisation. Materials 2023, 16, 1637. [Google Scholar] [CrossRef]
- García-Vilana, S.; Sánchez-Molina, D.; Abdi, H. Acoustic Emission in Bone Biomechanics: A Comprehensive review of mechanical properties and predictive damage modelling. Sensors 2025, 25, 598. [Google Scholar] [CrossRef]
- Sansalone, V.; Bousson, V.; Naili, S.; Bergot, C.; Peyrin, F.; Laredo, J.D.; Haïat, G. Anatomical distribution of the degree of mineralisation of bone tissue in human femoral neck: Impact on biomechanical properties. Bone 2012, 50, 876–884. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, J.M.; Papaioannou, A.; Tomowich, C.; Giangregorio, L.M.; Atkinson, S.A.; Beattie, K.A.; Adachi, J.D.; DeBeer, J.; Winemaker, M.; Avram, V.; et al. Bone mineralisation is elevated and less heterogeneous in adults with type 2 diabetes and osteoarthritis compared to controls with osteoarthritis alone. Bone 2013, 54, 76–82. [Google Scholar] [CrossRef]
- Martin, R.B. Determinants of the mechanical properties of bones. J. Biomech. 1991, 24, 79–88. [Google Scholar] [CrossRef]
- Goldstein, S.A. The mechanical properties of trabecular bone: Dependence on anatomic location and function. J. Biomech. 1987, 20, 1055–1061. [Google Scholar] [CrossRef] [PubMed]
- Augat, P.; Link, T.; Lang, T.F.; Lin, J.C.; Majumdar, S.; Genant, H.K. Anisotropy of the elastic modulus of trabecular bone specimens from different anatomical locations. Med. Eng. Phys. 1998, 20, 124–131. [Google Scholar] [CrossRef]
- Bouxsein, M.L. Biomechanics of Age-Related Fractures. In Osteoporosis; Elsevier: Amsterdam, The Netherlands, 2001; pp. 509–531. [Google Scholar] [CrossRef]
- Ingole, V.H.; Ghule, S.S.; Vuherer, T.; Kokol, V.; Ghule, A.V. Mechanical properties of differently nanostructured and High-Pressure compressed Hydroxyapatite-Based materials for bone tissue regeneration. Minerals 2021, 11, 1390. [Google Scholar] [CrossRef]
- Battafarano, G.; Rossi, M.; De Martino, V.; Marampon, F.; Borro, L.; Secinaro, A.; Del Fattore, A. Strategies for bone regeneration: From graft to tissue engineering. Int. J. Mol. Sci. 2021, 22, 1128. [Google Scholar] [CrossRef]
- Garcia-Giner, V.; Han, Z.; Giuliani, F.; Porter, A.E. Nanoscale imaging and analysis of bone pathologies. Appl. Sci. 2021, 11, 12033. [Google Scholar] [CrossRef]
- Álvarez-Lloret, P.; Benavides-Reyes, C.; Lee, C.M.; Martínez, M.P.; Conti, M.I.; Rodríguez-Navarro, A.B.; González-López, S.; Perez-Huerta, A.; Terrizzi, A.R. Chronic lead exposure alters mineral properties in alveolar bone. Minerals 2021, 11, 642. [Google Scholar] [CrossRef]
- Nefjodovs, V.; Andze, L.; Andzs, M.; Filipova, I.; Tupciauskas, R.; Vecbiskena, L.; Kapickis, M. Wood as a possible renewable material for bone implants—Literature review. J. Funct. Biomater. 2023, 14, 266. [Google Scholar] [CrossRef] [PubMed]
- Gasik, M.; Lambert, F.; Bacevic, M. Biomechanical properties of bone and mucosa for design and application of dental implants. Materials 2021, 14, 2845. [Google Scholar] [CrossRef] [PubMed]
- Grill, S.L.; Brouillet, F.; Drouet, C. Bone Regeneration: Mini-Review and Appealing Perspectives. Bioengineering 2025, 12, 38. [Google Scholar] [CrossRef]
- Bhattarai, D.P.; Aguilar, L.E.; Park, C.H.; Kim, C.S. A review on properties of natural and synthetic based electrospun fibrous materials for bone tissue engineering. Membranes 2018, 8, 62. [Google Scholar] [CrossRef]
- Ferraz, M.P. An overview on the big players in bone tissue engineering: Biomaterials, scaffolds and cells. Int. J. Mol. Sci. 2024, 25, 3836. [Google Scholar] [CrossRef]
- Castro-Franco, A.D.; Mendoza-Muñoz, I.; González-Ángeles, Á.; Cruz-Sotelo, S.E.; Castañeda, A.M.; Siqueiros-Hernández, M. Trends in the characterisation of the proximal humerus in Biomechanical Studies: A review. Appl. Sci. 2020, 10, 6514. [Google Scholar] [CrossRef]
- Łuczak, J.W.; Palusińska, M.; Matak, D.; Pietrzak, D.; Nakielski, P.; Lewicki, S.; Grodzik, M.; Szymański, Ł. The Future of Bone Repair: Emerging technologies and biomaterials in bone regeneration. Int. J. Mol. Sci. 2024, 25, 12766. [Google Scholar] [CrossRef]
- Costăchescu, B.; Niculescu, A.-G.; Grumezescu, A.M.; Teleanu, D.M. Screw Osteointegration—Increasing biomechanical resistance to Pull-Out effect. Materials 2023, 16, 5582. [Google Scholar] [CrossRef]
- Ashman, R.B.; Corin, J.D.; Turner, C.H. Elastic properties of cancellous bone: Measurement by an ultrasonic technique. J. Biomech. 1987, 20, 979–986. [Google Scholar] [CrossRef]
- Sansalone, V.; Naili, S.; Bousson, V.; Bergot, C.; Peyrin, F.; Zarka, J.; Laredo, J.D.; Haïat, G. Determination of the heterogeneous anisotropic elastic properties of human femoral bone: From nanoscopic to organ scale. J. Biomech. 2010, 43, 1857–1863. [Google Scholar] [CrossRef]
- Hamandi, F.; Tsatalis, J.T.; Goswami, T. Retrospective Evaluation and Framework Development of Bone Anisotropic Material Behaviour Compared with Elastic, Elastic-Plastic, and Hyper-Elastic Properties. Bioengineering 2021, 9, 9. [Google Scholar] [CrossRef]
- Nikolov, S.; Raabe, D. Hierarchical modelling of the elastic properties of bone at submicron scales: The role of extrafibrillar mineralization. Biophys. J. 2008, 94, 4220–4232. [Google Scholar] [CrossRef]
- Salguero, L.; Saadat, F.; Sevostianov, I. Micromechanical modelling of elastic properties of cortical bone accounting for anisotropy of dense tissue. J. Biomech. 2014, 47, 3279–3287. [Google Scholar] [CrossRef]
- Katz, J.L.; Yoon, H.S.; Lipson, S.; Maharidge, R.; Meunier, A.; Christel, P. The effects of remodelling on the elastic properties of bone. Calcif. Tissue Int. 1984, 36 (Suppl. S1), S31–S36. [Google Scholar] [CrossRef]
- Turek, B.; Mikułowski, G.; Szara, T.; Dołasiński, M.; Jasiński, T.; Domino, M. Aspect-Related mechanical properties of the cortical bone in the third metacarpal bone of mares. Appl. Sci. 2025, 15, 1593. [Google Scholar] [CrossRef]
- Ibrahim, A.; Magliulo, N.; Groben, J.; Padilla, A.; Akbik, F.; Hamid, Z.A. Hardness, an important indicator of bone quality, and the role of collagen in bone hardness. J. Funct. Biomater. 2020, 11, 85. [Google Scholar] [CrossRef]
- Bazyar, P.; Baumgart, A.; Altenbach, H.; Usbeck, A. An overview of selected material properties in finite element modelling of the human femur. Biomechanics 2023, 3, 124–135. [Google Scholar] [CrossRef]
- Baleani, M.; Erani, P.; Acciaioli, A.; Schileo, E. Tensile Yield Strain of Human Cortical Bone from the Femoral Diaphysis Is Constant among Healthy Adults and across the Anatomical Quadrants. Bioengineering 2024, 11, 395. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Kang, J.-H. Mechanical properties of compact bone defined by the Stress-Strain curve measured using uniaxial tensile Test: A concise review and Practical guide. Materials 2021, 14, 4224. [Google Scholar] [CrossRef]
- Solarino, G.; Vicenti, G.; Picca, G.; Rifino, F.; Carrozzo, M.; Moretti, B. A review of gender differences in hip fracture anatomy, morbidity, mortality and function. Ital. J. Gend.-Specif. Med 2016, 2, 55–59. [Google Scholar] [CrossRef]
- Oefner, C.; Riemer, E.; Funke, K.; Werner, M.; Heyde, C.-E.; Schoenfelder, S. Determination of Anisotropic Elastic Parameters from Morphological Parameters of Cancellous Bone for Osteoporotic Lumbar Spine. Med. Biol. Eng. Comput. 2021, 60, 263–278. [Google Scholar] [CrossRef]
- Hamandi, F.; Goswami, T. Hierarchical structure and properties of the bone at nano level. Bioengineering 2022, 9, 677. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Stylianou, A.; Chliveros, G.; Malamou, A. Determining spatial variability of elastic properties for biological samples using AFM. Micromachines 2023, 14, 182. [Google Scholar] [CrossRef]
- Sun, C.; Dong, E.; Chen, J.; Zheng, J.; Kang, J.; Jin, Z.; Liu, C.; Wang, L.; Li, D. The promotion of mechanical properties by bone ingrowth in Additive-Manufactured Titanium Scaffolds. J. Funct. Biomater. 2022, 13, 127. [Google Scholar] [CrossRef]
- Zeng, Y.; Meng, Q.; Chen, Y.; Zou, D.; Tao, L. Age-Related study and collision response of material properties of long bones in Chinese pedestrian lower limbs. Appl. Sci. 2022, 12, 6911. [Google Scholar] [CrossRef]
- Singh, N.; Trajkovski, A.; Trajkovski, J.; Kunc, R.; Matas, J.F.R. A pilot study on the Age-Dependent, biomechanical properties of longitudinal ligaments in the human cervical spine. Bioengineering 2025, 12, 61. [Google Scholar] [CrossRef]
- Aurégan, J.-C.; Bosser, C.; Bachy-Razzouk, M.; Bensidhoum, M.; Hoc, T. In vivo assessment of skin surface pattern: Exploring its potential as an indicator of bone biomechanical properties. Bioengineering 2023, 10, 1338. [Google Scholar] [CrossRef]
- Kulić, M.; Bagavac, P.; Bekić, M.; Krstulović-Opara, L. Ex vivo biomechanical bone testing of pig femur as an experimental model. Bioengineering 2024, 11, 572. [Google Scholar] [CrossRef]
- Leng, H.; Reyes, M.J.; Dong, X.N.; Wang, X. Effect of age on mechanical properties of the collagen phase in different orientations of human cortical bone. Bone 2013, 55, 288–291. [Google Scholar] [CrossRef]
- De Lacerda Schickert, S.; Van Den Beucken, J.J.J.P.; Leeuwenburgh, S.C.G.; Jansen, J.A. Pre-Clinical evaluation of biological bone substitute materials for application in highly loaded skeletal sites. G.; Jansen, J.A. Pre-Clinical evaluation of biological bone substitute materials for application in highly loaded skeletal sites. Biomolecules 2020, 10, 883. [Google Scholar] [CrossRef]
- Belluzzi, E.; Todros, S.; Pozzuoli, A.; Ruggieri, P.; Carniel, E.L.; Berardo, A. Human Cartilage Biomechanics: Experimental and Theoretical Approaches towards the Identification of Mechanical Properties in Healthy and Osteoarthritic Conditions. Processes 2023, 11, 1014. [Google Scholar] [CrossRef]
- Pallua, J.D.; Putzer, D.; Jäger, E.; Degenhart, G.; Arora, R.; Schmölz, W. Characterizing the mechanical behaviour of bone and bone surrogates in compression using PQCT. Materials 2022, 15, 5065. [Google Scholar] [CrossRef]
- Nguyen, H.-Q.; Nguyen, T.-N.-T.; Pham, T.-Q.-D.; Nguyen, V.-D.; Van Tran, X.; Dao, T.-T. Crack Propagation in the Tibia Bone within Total Knee Replacement Using the eXtended Finite Element Method. Appl. Sci. 2021, 11, 4435. [Google Scholar] [CrossRef]
- Glatt, V.; Canalis, E.; Stadmeyer, L.; Bouxsein, M.L. Age-Related Changes in Trabecular Architecture Differ in Female and Male C57BL/6J Mice. J. Bone Miner. Res. 2007, 22, 1197–1207. [Google Scholar] [CrossRef] [PubMed]
- Ngartera, L.; Issaka, M.A.; Nadarajah, S. Application of Bayesian Neural Networks in Healthcare: Three Case Studies. Mach. Learn. Knowl. Extr. 2024, 6, 2639–2658. [Google Scholar] [CrossRef]
- Mukhtar, A.M.; Könke, C. Fracture mechanics and micro crack detection in bone: A short communication. In Conference Medical Device Materials V. Novelty; ASM International: Almere, The Netherlands, 2011. [Google Scholar]
- Pope, M.H.; Outwater, J.O. Mechanical Properties of Bone as a Function of Position and Orientation. J. Biomech. 1974, 7, 61–66. [Google Scholar] [CrossRef]
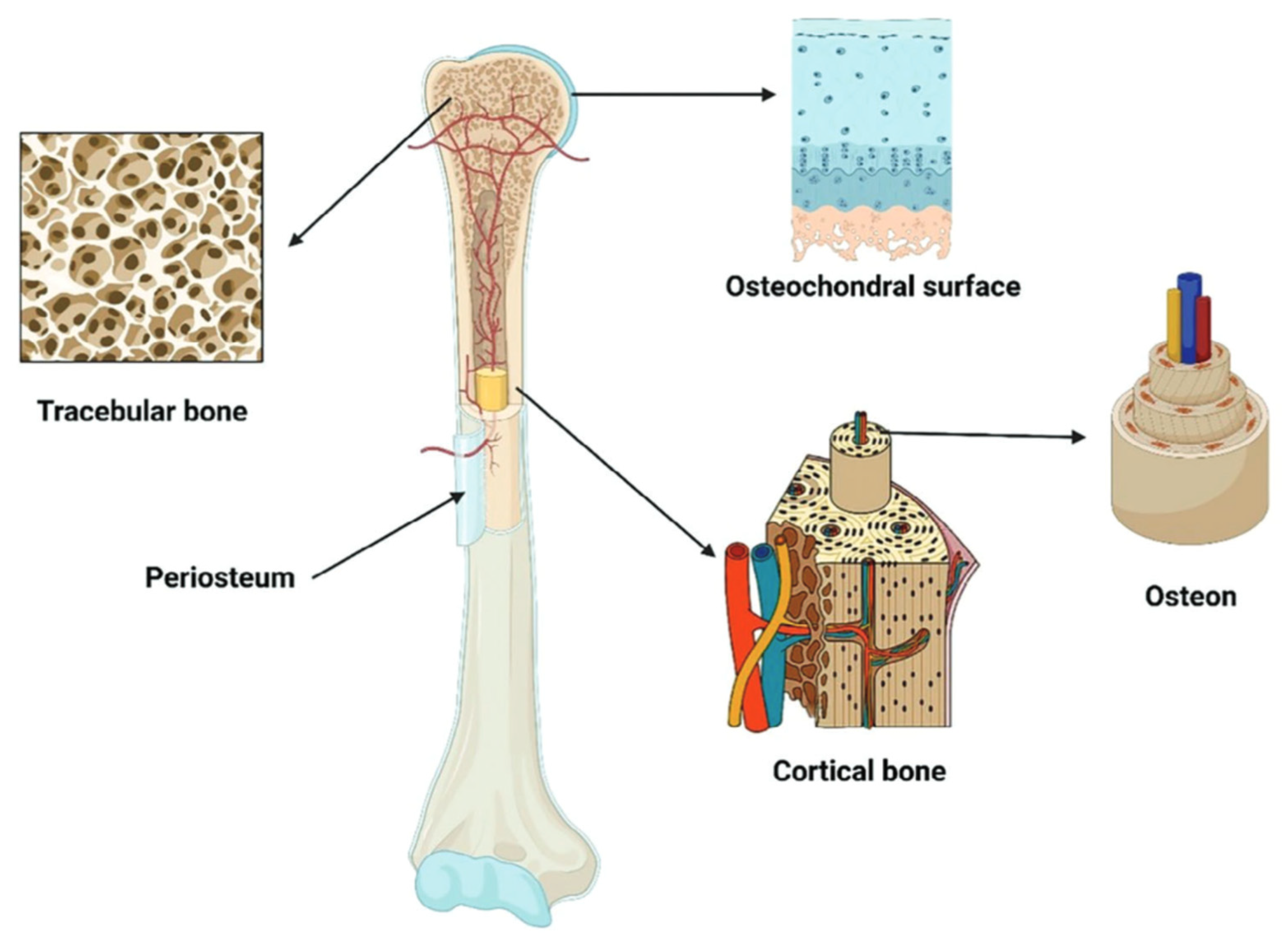

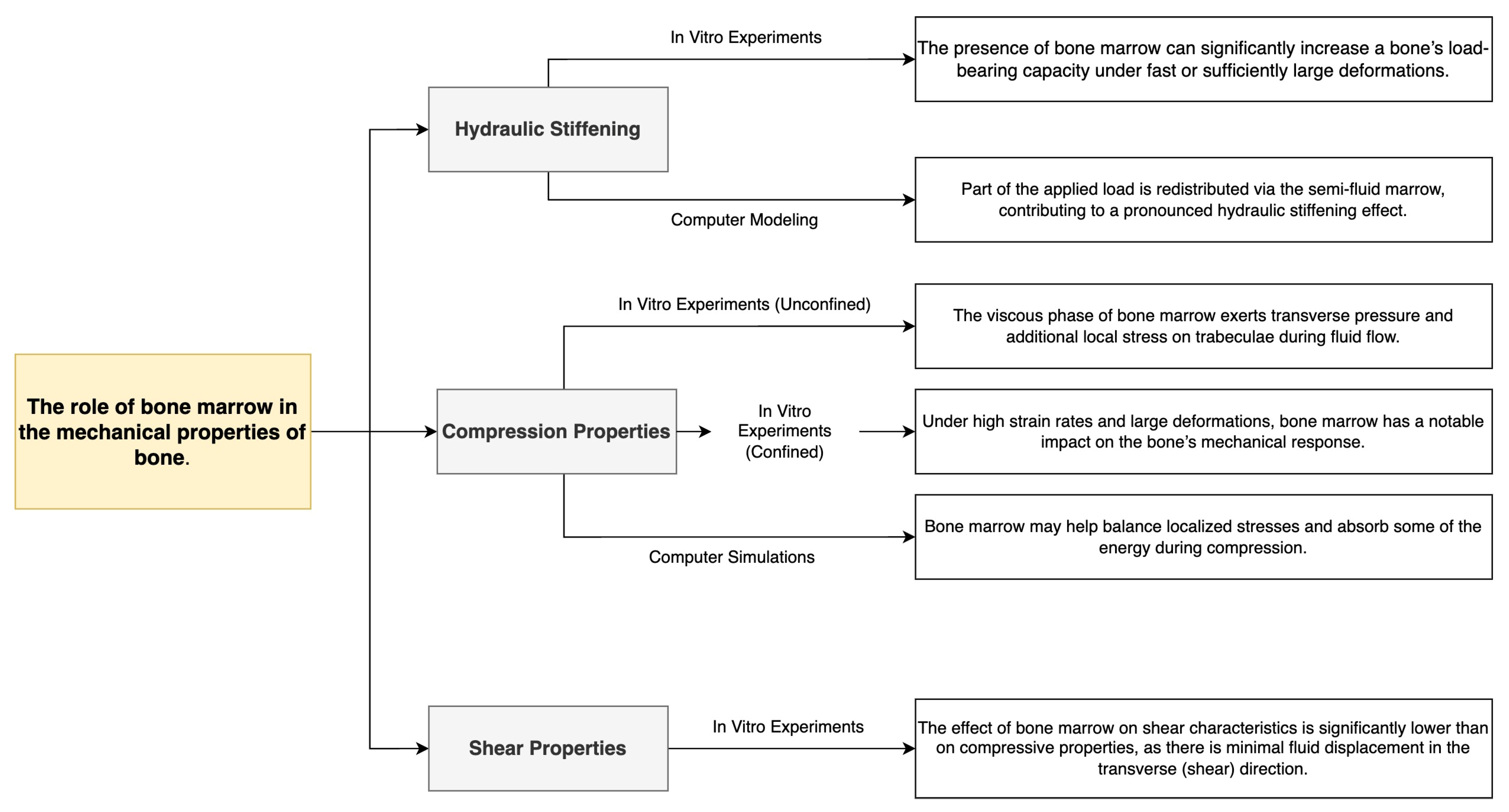
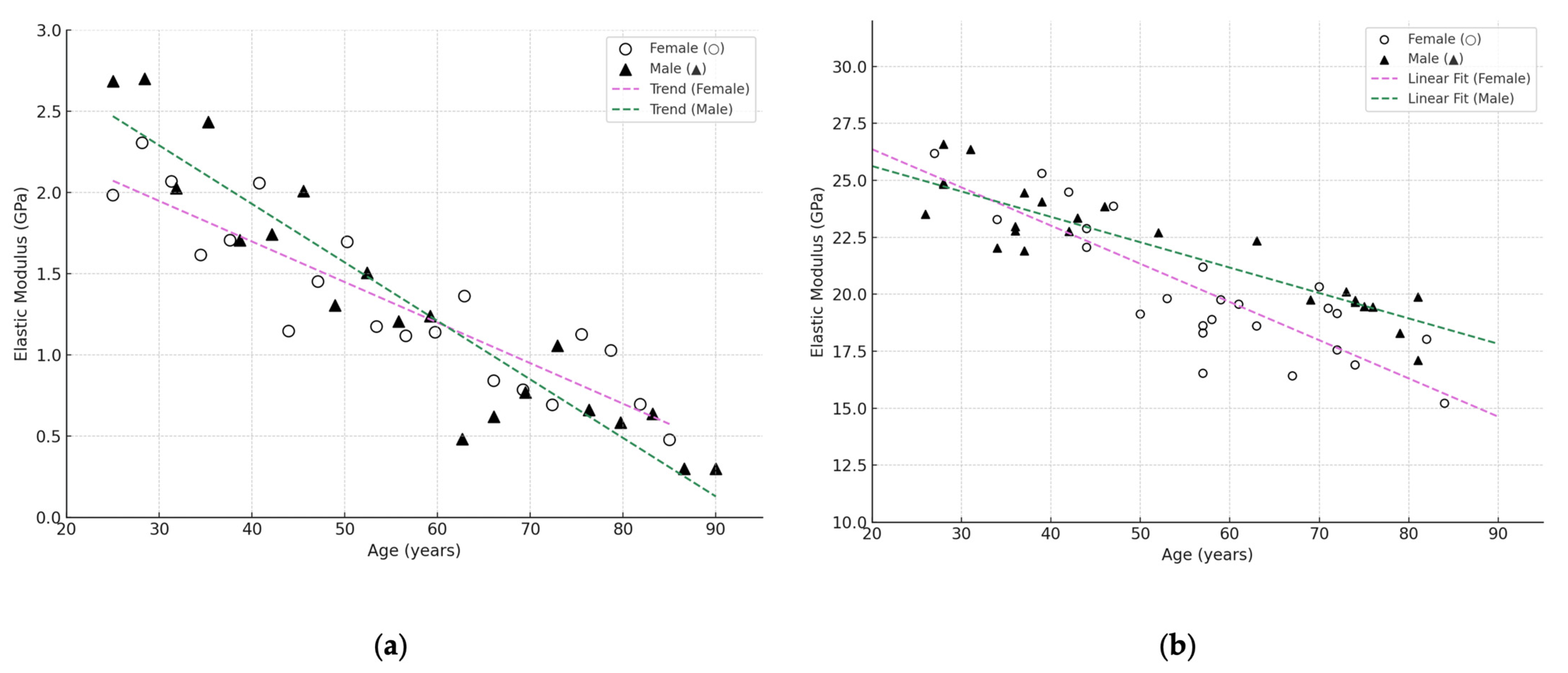
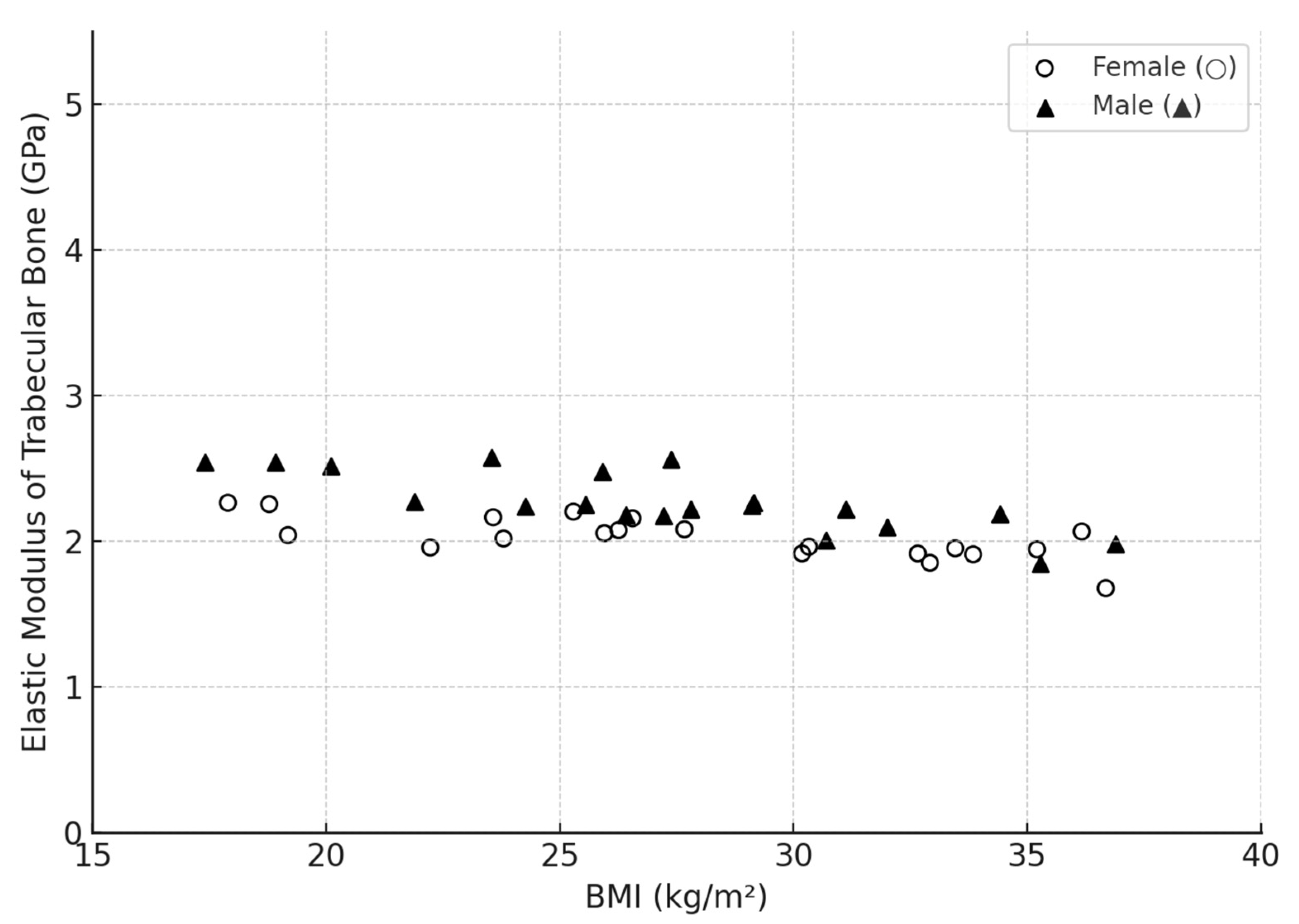
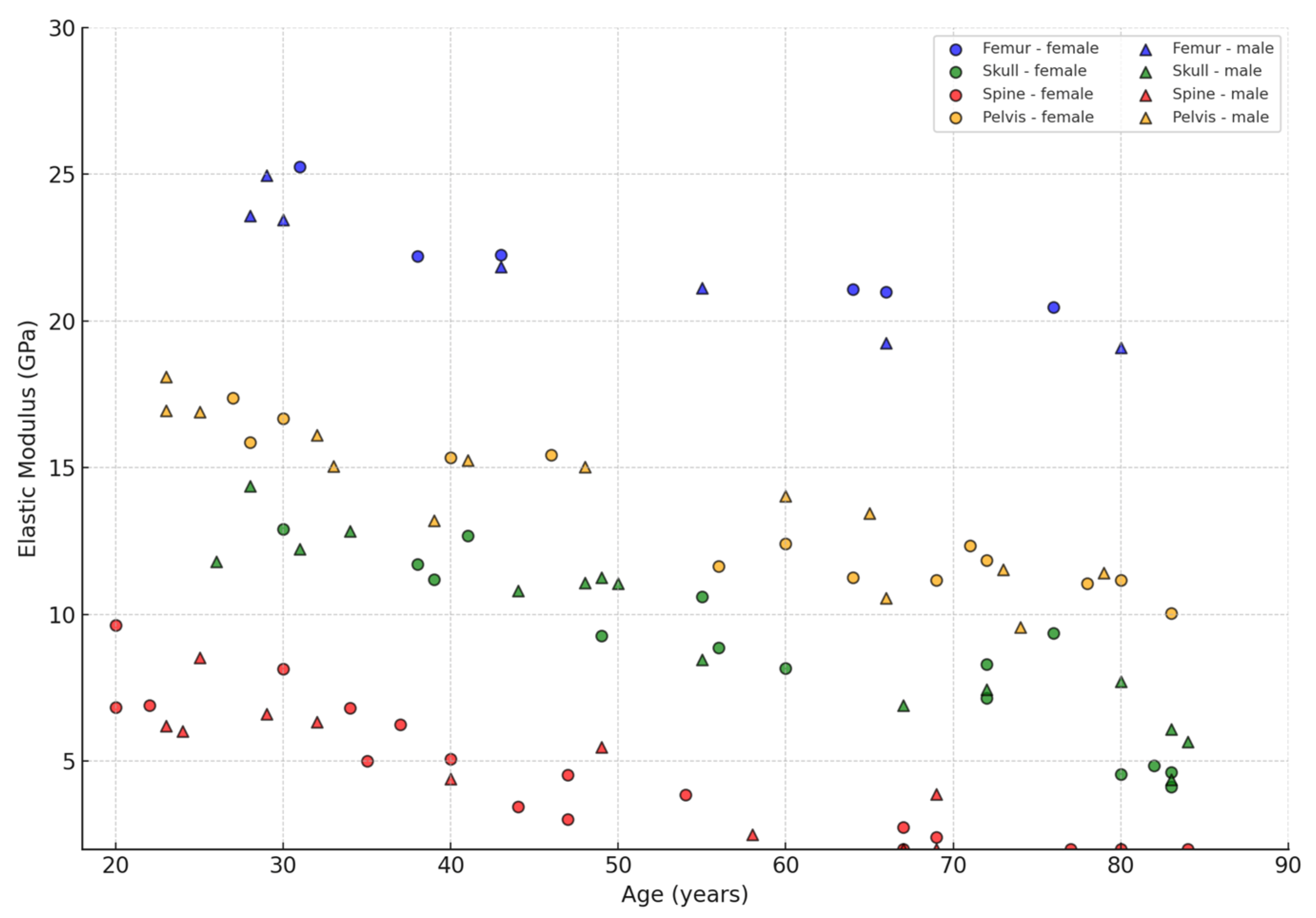
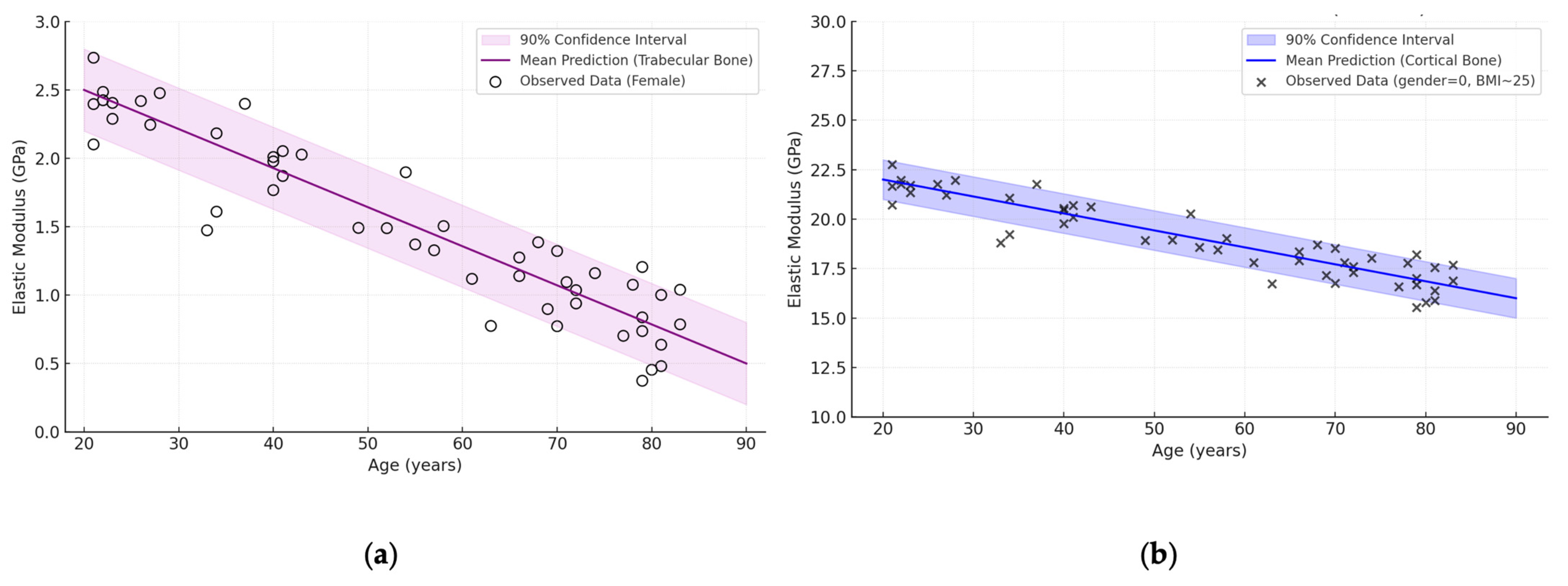
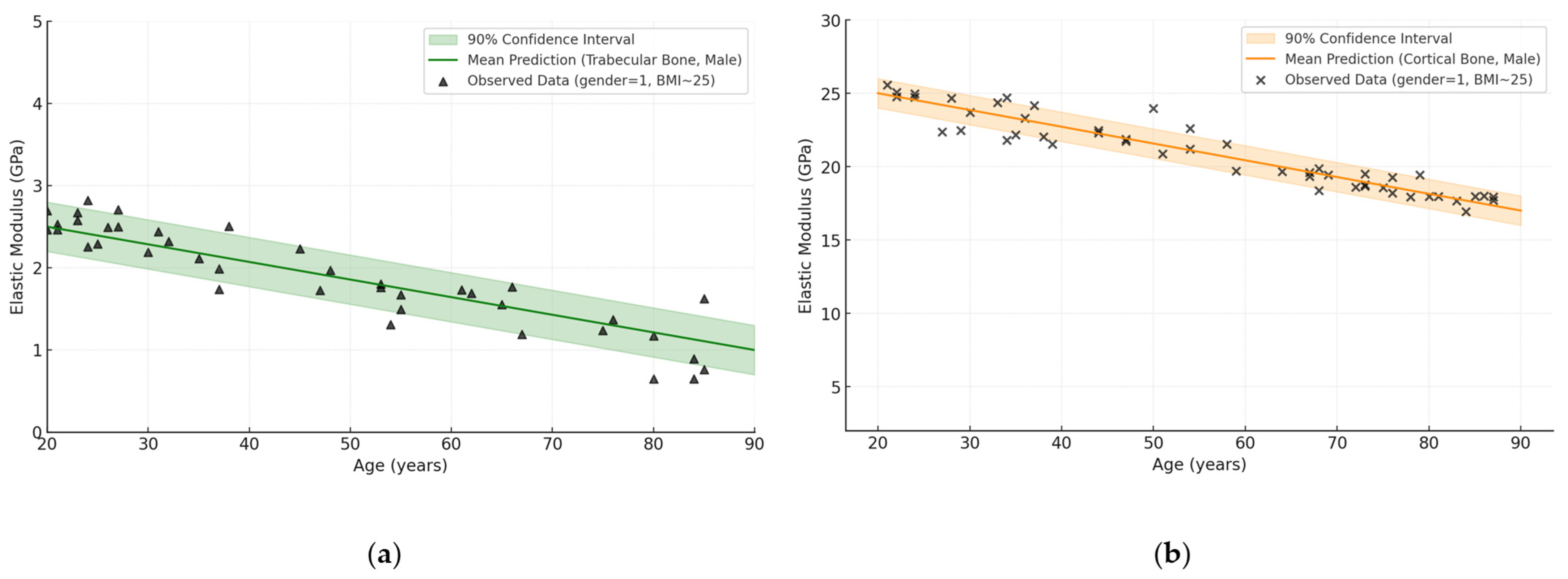
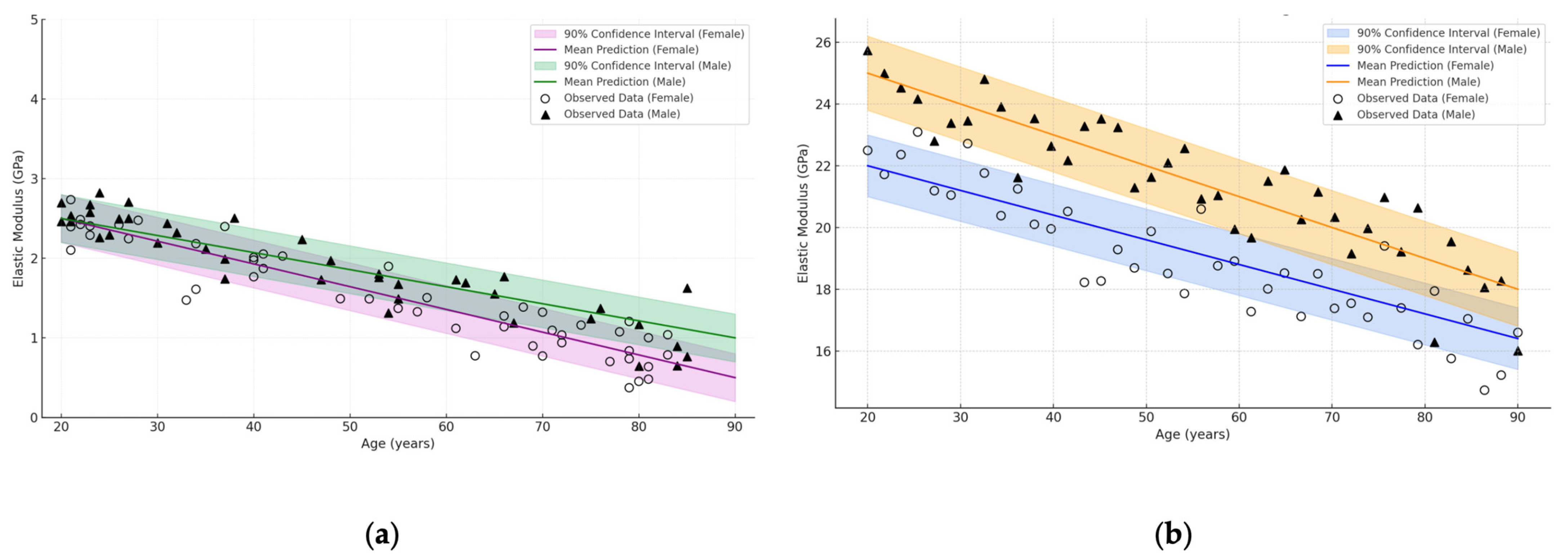
| Bone Region | Tissue Type | Age Group | Young’s Modulus (Eyoung’s), GPa | Notes |
|---|---|---|---|---|
| Femur (shaft/diaphysis) | Cortical | The young ones (20–40 years old) | 18–30 | The most rigid layer; resistance to bending and stretching [6,7,17]. |
| Femur (shaft/diaphysis) | Cortical | The elderly (65–70+ years). | 10–25 | Decrease in min. density, appearance of micropores; often associated with osteoporosis [14,15,16,17,18,19,20,21,22,23]. |
| Femur (epiphysis/head/neck) | Trabecular. | The young ones (20–35 years old) | 1–2 | High porosity; actively involved in load cushioning [24,34,45,53]. |
| Femur (epiphysis/head/neck) | Trabecular | The elderly (60–70+ years). | 0.5–1.2 | Osteoporotic changes, reduction in the number and thickness of trabeculae are possible. |
| Pelvis (wing of the ilium) | Cortical | The young ones (20–40 years old) | 15–20 | Somewhat lower density than femoral, but still quite stiff [42,43,44,45,46]. |
| Pelvis (wing of the ilium) | Cortical | The elderly (60–70+ years). | 10–15 | Decrease in min. density in the cortical layer, age-related porosity [21,22,23,24,25,26,27,28] |
| Pelvis (wing of the ilium) | Trabecular | The young ones (20–40 years old) | 1.5–2 | Fairly high elasticity; important for pelvic energy capacity [38,39,40,41,42,43,44,45] |
| Pelvis (wing of the ilium) | Trabecular | The elderly (60–70+ years). | 0.8–1.2 | Diminished performance, osteopenia/osteoporosis reduce load-bearing properties [23]. |
| Vertebrae (vertebral bodies) | Trabecular | Young/middle-aged | 1–2 | Axial load support; reduced ~2-fold in osteopenia [19,20,21,22,23,24,25,26,27,28,29,30,31,32]. |
| Vertebrae (vertebral bodies) | Trabecular | The elderly (70+ years). | 0.3–0.5 | A serious loss of strength (−30–50%) is possible by old age [20,21,22,23,24,25,26,27,28,29]. |
| Cranium (skull, cortical layer). | Cortical (outer/inner plates) | Adults (30–60 years old). | 7–15 | Thin layer, different pattern of collagen fibres, values may be lower [9,10,11,12,13,14,15]. |
| Cranium. | Trabecular (spongy layer) | Different age categories | 0.2–1.5 | Large variations in density are observed with age-related changes [21,22]. |
| №. | Types of Bone Tissue | Modulus of Elasticity (GPa) |
|---|---|---|
| 1 | Cortical (hips, shoulders, tibia) | E = 29.571 − 0.1857x |
| 2 | Cortical (skull) | E = 13.829 − 0.0943x |
| 3 | Cortical (pelvis) | E = 29.5 − 0.4x |
| 4 | Trabecular (hips, vertebrae) | E = 1.979 − 0.0243x |
| 5 | Trabecular (pelvis) | E = 2.95 − 0.04x |
| 6 | Trabecular (total range) | E = 8.0143 − 0.1171x |
| Note: x-age from 20 to 75 years old. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beisekenov, N.; Sadenova, M.; Azamatov, B.; Syrnev, B. Analysis of Biomechanical Characteristics of Bone Tissues Using a Bayesian Neural Network: A Narrative Review. J. Funct. Biomater. 2025, 16, 168. https://doi.org/10.3390/jfb16050168
Beisekenov N, Sadenova M, Azamatov B, Syrnev B. Analysis of Biomechanical Characteristics of Bone Tissues Using a Bayesian Neural Network: A Narrative Review. Journal of Functional Biomaterials. 2025; 16(5):168. https://doi.org/10.3390/jfb16050168
Chicago/Turabian StyleBeisekenov, Nail, Marzhan Sadenova, Bagdat Azamatov, and Boris Syrnev. 2025. "Analysis of Biomechanical Characteristics of Bone Tissues Using a Bayesian Neural Network: A Narrative Review" Journal of Functional Biomaterials 16, no. 5: 168. https://doi.org/10.3390/jfb16050168
APA StyleBeisekenov, N., Sadenova, M., Azamatov, B., & Syrnev, B. (2025). Analysis of Biomechanical Characteristics of Bone Tissues Using a Bayesian Neural Network: A Narrative Review. Journal of Functional Biomaterials, 16(5), 168. https://doi.org/10.3390/jfb16050168







