Online Assessment and Game-Based Development of Inductive Reasoning
Abstract
:1. Introduction
1.1. Definition and Assessment of Inductive Reasoning
- A: {a1: similarity; a2: difference; a3: similarity and difference}
- of
- B: {b1: attributes; b2: relations}
- with
- C: {c1: verbal; c2: pictorial; c3: geometrical; c4: numerical; c5: other}
- material (Klauer and Phye 2008, p. 87).
1.2. Fostering Inductive Reasoning in Educational Settings
1.3. Possibilities of Technology-Based Assessment and Game-Based Learning in Fostering Inductive Reasoning
1.4. The Present Research
- RQ 1: What are the psychometric features of the online figurative test?
- RQ 2: Is Klauer’s model empirically supported by our data?
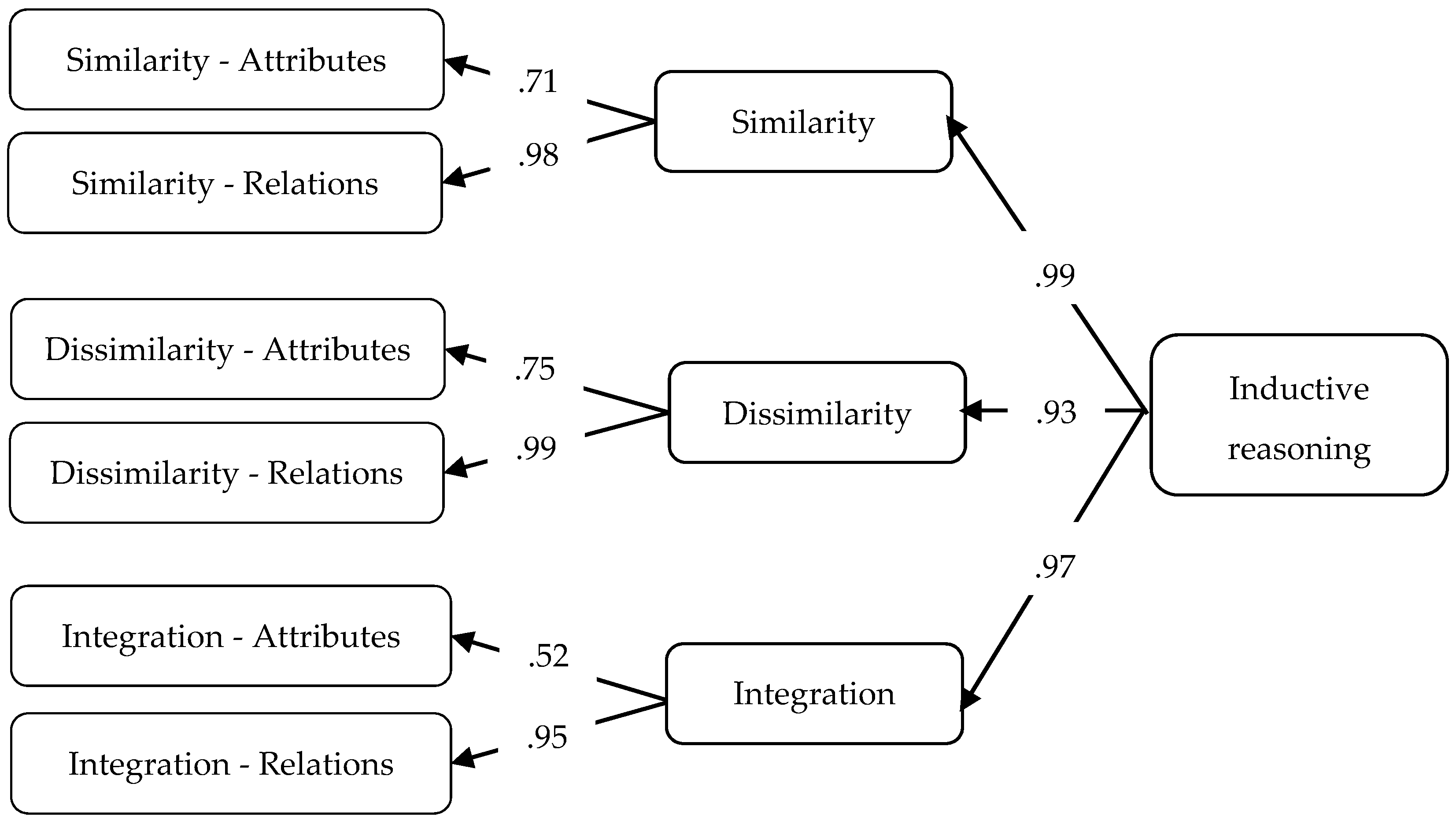
- RQ 3: Is the hierarchical model suggested by Christou and Papageorgiou empirically supported by our data?
- RQ 4: Does the training program effectively develop inductive reasoning in grade 5?
- RQ 5: How does our intervention program affect the development of the different inductive reasoning processes?
2. Materials and Methods
2.1. Participants
2.2. Instruments
2.2.1. The Online Assessment Tool
2.2.2. The Online Training Program: Save the Tree of Life
2.3. Procedures
3. Results
3.1. Assessment of Inductive Reasoning
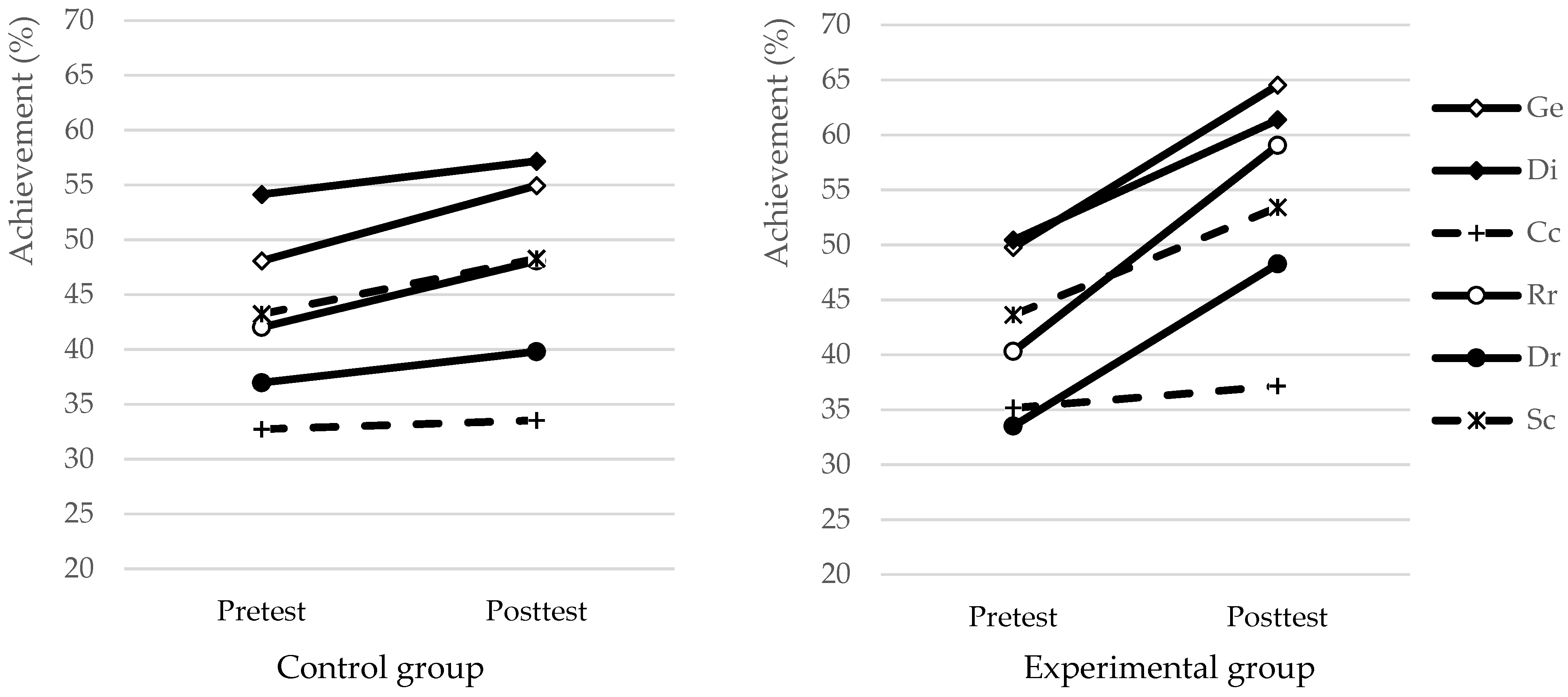
3.2. Fostering Inductive Reasoning
4. Discussion
4.1. Assessment of Inductive Reasoning Strategies
4.2. Fostering Inductive Reasoning Strategies
4.3. Limitations and Further Research
4.4. Pedagogical Implications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adey, Philip, Benő Csapó, Andreas Demetriou, Jarkko Hautamäki, and Michael Shayer. 2007. Can We Be Intelligent about Intelligence? Educational Research Review 2: 75–97. [Google Scholar] [CrossRef]
- Barkl, Sophie, Amy Porter, and Paul Ginns. 2012. Cognitive Training for Children: Effects on Inductive Reasoning, Deductive Reasoning, and Mathematics Achievement in an Australian School Setting: Cognitive Training for Children. Psychology in the Schools 49: 828–42. [Google Scholar] [CrossRef]
- Cai, Zhihui, Peipei Mao, Dandan Wang, Jinbo He, Xinjie Chen, and Xitao Fan. 2022. Effects of Scaffolding in Digital Game-Based Learning on Student’s Achievement: A Three-Level Meta-Analysis. Educational Psychology Review 34: 537–74. [Google Scholar] [CrossRef]
- Carroll, John Bissen. 1993. Human Cognitive Abilities: A Survey of Factor Analytic Studies. New York: Cambridge University Press. [Google Scholar]
- Chen, Xieling, Di Zou, Gary Cheng, and Haoran Xie. 2020. Detecting Latent Topics and Trends in Educational Technologies over Four Decades Using Structural Topic Modeling: A Retrospective of All Volumes of Computers & Education. Computers & Education 151: 103855. [Google Scholar]
- Christou, Constantinos, and Eleni Papageorgiou. 2007. A framework of mathematics inductive reasoning. Learning and Instruction 17: 55–66. [Google Scholar] [CrossRef]
- Csapó, Benő. 1997. The Development of Inductive Reasoning: Cross-Sectional Assessments in an Educational Context. International Journal of Behavioral Development 20: 609–26. [Google Scholar] [CrossRef]
- Csapó, Benő. 1999. Improving thinking through the content of teaching. In Teaching and Learning Thinking Skills. Edited by Johan H. M. Hamers, Johannes E. H. van Luit and Benő Csapó. Lisse: Swets and Zeitlinger, pp. 37–62. [Google Scholar]
- Csapó, Benő, and Gyöngyvér Molnár. 2019. Online Diagnostic Assessment in Support of Personalized Teaching and Learning: The eDia System. Frontiers in Psychology 10: 1522. [Google Scholar] [CrossRef]
- Csapó, Benő, András Lőrincz, and Gyöngyvér Molnár. 2012a. Innovative Assessment Technologies in Educational Games Designed for Young Students. In Assessment in Game-Based Learning. Edited by Dirk Ifenthaler, Deniz Eseryel and Xun Ge. New York: Springer, pp. 235–54. [Google Scholar]
- Csapó, Benő, John Ainley, Randy Bennett, Thibaud Latour, and Nancy Law. 2012b. Technological issues of computer-based assessment of 21st century skills. In Assessment & Teaching of 21st Century Skills. Edited by Patrick Griffin, Barry McGaw and Esther Care. New York: Springer, pp. 143–230. [Google Scholar]
- de Koning, Els, and Johan H. M. Hamers. 1999. Teaching Inductive Reasoning: Theoretical background and educational implications. In Teaching and Learning Thinking Skills. Edited by Johan H. M. Hamers, Johannes E. H. van Luit and Benő Csapó. Lisse: Swets and Zeitlinger, pp. 157–88. [Google Scholar]
- de Koning, Els, Jo H. M. Hamers, Klaas Sijtsma, and Adri Vermeer. 2002. Teaching Inductive Reasoning in Primary Education. Developmental Review 22: 211–41. [Google Scholar] [CrossRef]
- de Koning, Els, Klaas Sijtsma, and Johan H. M. Hamers. 2003. Construction and validation of test for inductive reasoning. European Journal of Psychological Assessment 191: 24–39. [Google Scholar] [CrossRef]
- Demetriou, Andreas, Nikolaos Makris, George Spanoudis, Smaragda Kazi, Michael Shayer, and Elena Kazali. 2018. Mapping the Dimensions of General Intelligence: An Integrated Differential-Developmental Theory. Human Development 61: 4–42. [Google Scholar] [CrossRef]
- Dunbar, Kevin, and Jonathan Fugelsang. 2005. Scientific thinking and reasoning. In The Cambridge Handbook of Thinking and Reasoning. Edited by Keith James Holyoak and Robert G. Morrison. New York: Cambridge University Press, pp. 705–25. [Google Scholar]
- Goel, Vinod, and Raymond J. Dolan. 2004. Differential Involvement of Left Prefrontal Cortex in Inductive and Deductive Reasoning. Cognition 93: B109–21. [Google Scholar] [CrossRef] [PubMed]
- Guerin, Julia M., Shari L. Wade, and Quintino R. Mano. 2021. Does reasoning training improve fluid reasoning and academic achievement for children and adolescents? A systematic review. Trends in Neuroscience and Education 23: 100153. [Google Scholar] [CrossRef] [PubMed]
- Hamers, Johan H. M., Els de Koning, and Klaas Sijtsma. 1998. Inductive Reasoning in Third Grade: Intervention Promises and Constraints. Contemporary Educational Psychology 23: 132–48. [Google Scholar] [CrossRef] [PubMed]
- Hayes, Brett K., Rachel G. Stephens, Jeremy Ngo, and John C. Dunn. 2018. The Dimensionality of Reasoning: Inductive and Deductive Inference Can Be Explained by a Single Process. Journal of Experimental Psychology: Learning, Memory, and Cognition 44: 1333–51. [Google Scholar] [CrossRef]
- Heit, Even. 2007. What is induction and why study it? In Inductive Reasoning: Experimental, Developmental, and Computational Approaches. Edited by Aidan Feeney and Even Heit. New York: Cambridge University Press, pp. 1–24. [Google Scholar]
- Jung, Carl Gustav. 1968. The Archetypes and the Collective Unconscious. Princeton: Princeton University. [Google Scholar]
- Klauer, Karl Josef. 1989. Denktraining für Kinder I [Cognitive Training for Children 1]. Göttingen: Hogrefe. [Google Scholar]
- Klauer, Karl Josef. 1990. Paradigmatic teaching of inductive thinking. In Learning and Instruction. European Research in an International Context. Analysis of Complex Skills and Complex Knowledge Domains. Edited by Heinz Mandl, Eric De Corte, Neville Bennett and Helmut Friedrich. Oxford: Pergamon Press, pp. 23–45. [Google Scholar]
- Klauer, Karl Josef. 1991. Denktraining für Kinder II [Cognitive Training for Children 1]. Göttingen: Hogrefe. [Google Scholar]
- Klauer, Karl Josef. 1993. Denktraining für Jugendliche [Cognitive Training for Youth]. Göttingen: Hogrefe. [Google Scholar]
- Klauer, Karl Josef. 1996. Teaching Inductive Reasoning: Some Theory and Three Experimental Studies. Learning and Instruction 6: 37–57. [Google Scholar] [CrossRef]
- Klauer, Karl Josef. 1999. Fostering higher order reasoning skills: The case of inductive reasoning. In Teaching and Learning Thinking Skills. Edited by Johan H. M. Hamers, Johannes E. H. van Luit and Benő Csapó. Lisse: Swets and Zeitlinger, pp. 131–56. [Google Scholar]
- Klauer, Karl Josef, and Gary D. Phye. 2008. Inductive Reasoning: A Training Approach. Review of Educational Research 78: 85–123. [Google Scholar] [CrossRef]
- Klauer, Karl Josef, Klaus Willmes, and Gary D. Phye. 2002. Inducing Inductive Reasoning: Does It Transfer to Fluid Intelligence? Contemporary Educational Psychology 27: 1–25. [Google Scholar] [CrossRef]
- Kovacs, Kristof, and Andrew R. A. Conway. 2016. Process Overlap Theory: A Unified Account of the General Factor of Intelligence. Psychological Inquiry 273: 151–77. [Google Scholar]
- Kucher, Tetyana. 2021. Principles and Best Practices of Designing Digital Game-Based Learning Environments. International Journal of Technology in Education and Science 5: 213–23. [Google Scholar] [CrossRef]
- Molnár, Gyöngyvér. 2011. Playful Fostering of 6- to 8-Year-Old Students’ Inductive Reasoning. Thinking Skills and Creativity 6: 91–99. [Google Scholar] [CrossRef]
- Molnár, Gyöngyvér, and András Lőrinczrincz. 2012. Innovative assessment technologies: Comparing ‘face-to-face’ and game-based development of thinking skills in classroom settings. In International Proceedings of Economics Development and Research. Management and Education Innovation. Singapore: IACSIT Press, pp. 150–54. [Google Scholar]
- Molnár, Gyöngyvér, and Benő Csapó. 2019. Making the Psychological Dimension of Learning Visible: Using Technology-Based Assessment to Monitor Students’ Cognitive Development. Frontiers in Psychology 10: 1368. [Google Scholar] [CrossRef]
- Molnár, Gyöngyvér, Attila Pásztor, and Benő Csapó. 2019. The eLea online training platform. Paper presented at the 17th Conference on Educational Assessment, Szeged, Hungary, April 11–13. [Google Scholar]
- Molnár, Gyöngyvér, Brigitta Mikszai-Réthey, Attila Pásztor, and Tímea Magyar. 2012. Innovative Assessment Technologies in Educational Games Designed for Integrating Assessment into Teaching. Paper presented at the EARLI SIG1 Conference, Brussels, Belgium, August 29–31. [Google Scholar]
- Molnár, Gyöngyvér, Samuel Greiff, and Benő Csapó. 2013. Inductive Reasoning, Domain Specific and Complex Problem Solving: Relations and Development. Thinking Skills and Creativity 9: 35–45. [Google Scholar] [CrossRef]
- Mousa, Mojahed, and Gyöngyvér Molnár. 2020. Computer-Based Training in Math Improves Inductive Reasoning of 9- to 11-Year-Old Children. Thinking Skills and Creativity 37: 100687. [Google Scholar] [CrossRef]
- Nisbet, John. 1993. The Thinking Curriculum. Educational Psychology 13: 281–90. [Google Scholar] [CrossRef]
- Pásztor, Attila. 2014a. Lehetőségek és kihívások a digitális játék alapú tanulásban: Egy induktív gondolkodást fejlesztő tréning hatásvizsgálata. [Possibilities and challenges in digital game-based learning: Effectiveness of a training program for fostering inductive reasoning]. Magyar Pedagógia 114: 281–301. [Google Scholar]
- Pásztor, Attila. 2014b. Playful Fostering of Inductive Reasoning through Mathematical Content in Computer-Based Environment. Paper presented at the 12th Conference on Educational Assessment, Szeged, Hungary, May 1–3. [Google Scholar]
- Pásztor, Attila. 2016. Az Induktív Gondolkodás Technológia alapú mérése és Fejlesztése [Technology-Based Assessment and Development of Inductive Reasoning]. Ph.D. thesis, University of Szeged, Szeged, Hungary. [Google Scholar]
- Pellegrino, James. W., and Robert Glaser. 1982. Analyzing aptitudes for learning: Inductive reasoning. In Advances in Instructional Psychology. Edited by Robert Glaser. Hillsdale: Lawrence Erlbaum Associates, Publishers Hillsdale, vol. 2, pp. 269–345. [Google Scholar]
- Perret, Patrick. 2015. Children’s Inductive Reasoning: Developmental and Educational Perspectives. Journal of Cognitive Education and Psychology 14: 389–408. [Google Scholar] [CrossRef]
- Resnick, Lauren. B., and Leopold E. Klopfer, eds. 1989. Toward the Thinking Curriculum: Current Cognitive Research. 1989 ASCD Yearbook. Alexandria: Association for Supervision and Curriculum Development. [Google Scholar]
- Sloman, Steven A., and David Lagnado. 2005. The problem of induction. In The Cambridge Handbook of Thinking and Reasoning. Edited by Keith James Holyoak and Robert G. Morrison. New York: Cambridge University Press, pp. 95–116. [Google Scholar]
- Spearman, Charles. 1923. The Nature of Intelligence and the Principles of Cognition. London: Macmillan. [Google Scholar]
- Stephens, Rachel G., John C. Dunn, and Brett K. Hayes. 2018. Are there two processes in reasoning? The dimensionality of inductive and deductive inferences. Psychological Review 125: 218–44. [Google Scholar] [CrossRef]
- Sternberg, Robert J. 2018. The triarchic theory of successful intelligence. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 3rd ed. Edited by Dawn P. Flanagan and Patti L. Harrison. New York: Guilford Press, pp. 174–94. [Google Scholar]
- Sternberg, Robert J., and Michael K. Gardner. 1983. Unities in Inductive Reasoning. Journal of Experimental Psychology: General 112: 80–116. [Google Scholar] [CrossRef]
- Tomic, Welko. 1995. Training in Inductive Reasoning and Problem Solving. Contemporary Educational Psychology 20: 483–90. [Google Scholar] [CrossRef]
- Tomic, Welco, and Johannes Kingma. 1998. Accelerating intelligence development through inductive reasoning training. In Conceptual Issues in Research on Intelligence. Edited by Welco Tomic and Johannes Kingma. Stanford: JAI Press, pp. 291–305. [Google Scholar]
- Tomic, Welko, and Karl Josef Klauer. 1996. On the Effects of Training Inductive Reasoning: How Far Does It Transfer and How Long Do the Effects Persist? European Journal of Psychology of Education 11: 283–99. [Google Scholar] [CrossRef]
- Wouters, Pieter, and Herre van Oostendorp. 2013. A Meta-Analytic Review of the Role of Instructional Support in Game-Based Learning. Computers & Education 60: 412–25. [Google Scholar]
- Wouters, Pieter, Christof van Nimwegen, Herre van Oostendorp, and Erik D. van der Spek. 2013. A Meta-Analysis of the Cognitive and Motivational Effects of Serious Games. Journal of Educational Psychology 105: 249–65. [Google Scholar] [CrossRef]
- Young, Michael F., Stephen Slota, Andrew B. Cutter, Gerard Jalette, Greg Mullin, Benedict Lai, Zeus Simeoni, Matthew Tran, and Mariya Yukhymenko. 2012. Our princess is in another castle: A review of trends in serious gaming for education. Review of Educational Research 82: 61–89. [Google Scholar] [CrossRef]




| Process | Facet Identification | Cognitive Operation Required | Item Formats |
|---|---|---|---|
| Generalization | a1b1 | Similarity of attributes | Class formation |
| Class expansion | |||
| Finding common attributes | |||
| Discrimination | a2b2 | Discrimination of attributes | Identifying disturbing items |
| Cross classification | a3b1 | Similarity and difference in attributes | 4-fold scheme |
| 6-fold scheme | |||
| 9-fold scheme | |||
| Recognizing relationships | a1b2 | Similarity of relationships | Series completion |
| Ordered series | |||
| Analogy | |||
| Differentiating relationships | a2b2 | Differences in relationships | Disturbed series |
| System construction | a3b2 | Similarity and difference in relationships | Matrices |
| Subtests | Number of Items | Cronbach’s Alpha |
|---|---|---|
| Generalization | 9 | .77 |
| Discrimination | 9 | .61 |
| Cross classification | 9 | .71 |
| Recognizing relationships | 9 | .76 |
| Differentiating relationships | 9 | .63 |
| System construction | 9 | .72 |
| Inductive reasoning strategies | 54 | .91 |
| Model | χ2 | df | p | CFI | TLI | RMSEA (95% CI) |
|---|---|---|---|---|---|---|
| 1 dimension | 1752.97 | 1377 | .01 | .911 | .908 | .032 (.027–.036) |
| 6 dimensions | 1454.23 | 1362 | .04 | .978 | .977 | .016 (.004–.023) |
| Subtests | IND | Ge | Di | Cc | Rr | Dr |
|---|---|---|---|---|---|---|
| Generalization (Ge) | .73 | |||||
| Discrimination (Di) | .72 | .50 | ||||
| Cross classification (Cc) | .59 | .31 | .29 | |||
| Recognizing relationships (Rr) | .84 | .52 | .51 | .37 | ||
| Differentiating relationships (Dr) | .79 | .48 | .49 | .38 | .62 | |
| System construction (Sc) | .80 | .43 | .48 | .34 | .70 | .63 |
| Subtests | Number of Items | Mean (SD) % |
|---|---|---|
| Generalization | 9 | 54.02 (26.85) |
| Discrimination | 9 | 57.01 (22.76) |
| Cross classification | 9 | 37.04 (24.29) |
| Recognizing relationships | 9 | 53.02 (28.33) |
| Differentiating relationships | 9 | 39.58 (21.37) |
| System construction | 9 | 47.40 (26.10) |
| Similarity | 18 | 53.52 (24.02) |
| Dissimilarity | 18 | 48.29 (19.05) |
| Integration | 18 | 42.22 (20.62) |
| Inductive reasoning strategies | 54 | 48.01 (18.67) |
| Group | Pretest (%) | Posttest (%) | Change (%) | Pre- and Posttest | Effect Size (Cohen’s d) | ||
|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | t-Test ** | |||
| Control (N = 55) | 42.86 | 15.78 | 46.97 | 16.69 | 4.1 | t = −3.336 p <.01 | .25 |
| Experimental (N = 67) | 42.12 | 19.05 | 53.95 | 18.42 | 11.8 | t = −9.057 p <.01 | .63 |
| t-test * | t = −.230 p = .82 n.s. | t = 2.173 p = .03 | – | – | |||
| Inductive Reasoning Process | Control Group (%) | Change (%) | Exp. Group (%) | Change (%) | Corr. e.s. (Cohen’s d) | ||
|---|---|---|---|---|---|---|---|
| Pre M. (SD) | Post M. (SD) | Pre M. (SD) | Post M. (SD) | ||||
| Generalization | 48.1 (27.1) | 54.9 (27.8) | 6.9 * | 49.8 (28.2) | 64.5 (23.9) | 14.8 ** | .31 |
| Discrimination | 54.1 (22.5) | 57.2 (23.8) | 3.0 | 50.4 (24.0) | 61.4 (24.2) | 10.9 ** | .32 |
| Cross classification | 32.7 (17.6) | 33.5 (20.6) | 0.8 | 35.2 (25.8) | 37.1 (26.3) | 2.0 | .03 |
| Recognizing relationships | 42.0 (26.2) | 48.1 (25.8) | 6.1 | 40.3 (30.1) | 59.0 (27.3) | 18.7 ** | .42 |
| Differentiating relationships | 37.0 (18.9) | 39.8 (19.2) | 2.8 | 33.5 (19.4) | 48.3 (23.7) | 14.8 ** | .53 |
| System construction | 43.2 (24.4) | 48.3 (25.3) | 5.1 | 43.6 (23.9) | 53.4 (24.4) | 9.8 ** | .20 |
| Similarity | 45.1 (22.1) | 51.5 (22.9) | 6.5 ** | 45.0 (25.3) | 61.8 (22.5) | 16.7 ** | .41 |
| Dissimilarity | 45.6 (15.9) | 48.5 (17.7) | 2.9 | 42.0 (18.4) | 54.8 (21.4) | 12.9 ** | .47 |
| Integration | 38.0 (19.9) | 40.9 (18.5) | 2.9 | 39.4 (20.2) | 45.3 (20.1) | 5.9 ** | .13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pásztor, A.; Magyar, A.; Pásztor-Kovács, A.; Rausch, A. Online Assessment and Game-Based Development of Inductive Reasoning. J. Intell. 2022, 10, 59. https://doi.org/10.3390/jintelligence10030059
Pásztor A, Magyar A, Pásztor-Kovács A, Rausch A. Online Assessment and Game-Based Development of Inductive Reasoning. Journal of Intelligence. 2022; 10(3):59. https://doi.org/10.3390/jintelligence10030059
Chicago/Turabian StylePásztor, Attila, Andrea Magyar, Anita Pásztor-Kovács, and Attila Rausch. 2022. "Online Assessment and Game-Based Development of Inductive Reasoning" Journal of Intelligence 10, no. 3: 59. https://doi.org/10.3390/jintelligence10030059
APA StylePásztor, A., Magyar, A., Pásztor-Kovács, A., & Rausch, A. (2022). Online Assessment and Game-Based Development of Inductive Reasoning. Journal of Intelligence, 10(3), 59. https://doi.org/10.3390/jintelligence10030059





