Algebraic Analysis of a Simplified Encryption Algorithm GOST R 34.12-2015
Abstract
1. Introduction
- SAT solvers: MiniSat, CryptoMiniSat, Glucose, Riss, Slime, Lingeling, Plingeling, CaDiCaL, etc.
- Methods based on a Gröbner basis: Buchberger’s algorithm, F4, F5, Matrix-F5, Tropical F5, Method of Four Russians, etc.
- Methods based on the linearization principle: relinearization, extended linearization (XL), extended sparse linearization (XSL), MutantXL, FXL, ElimLin, etc.
2. GOST R 34.12-2015
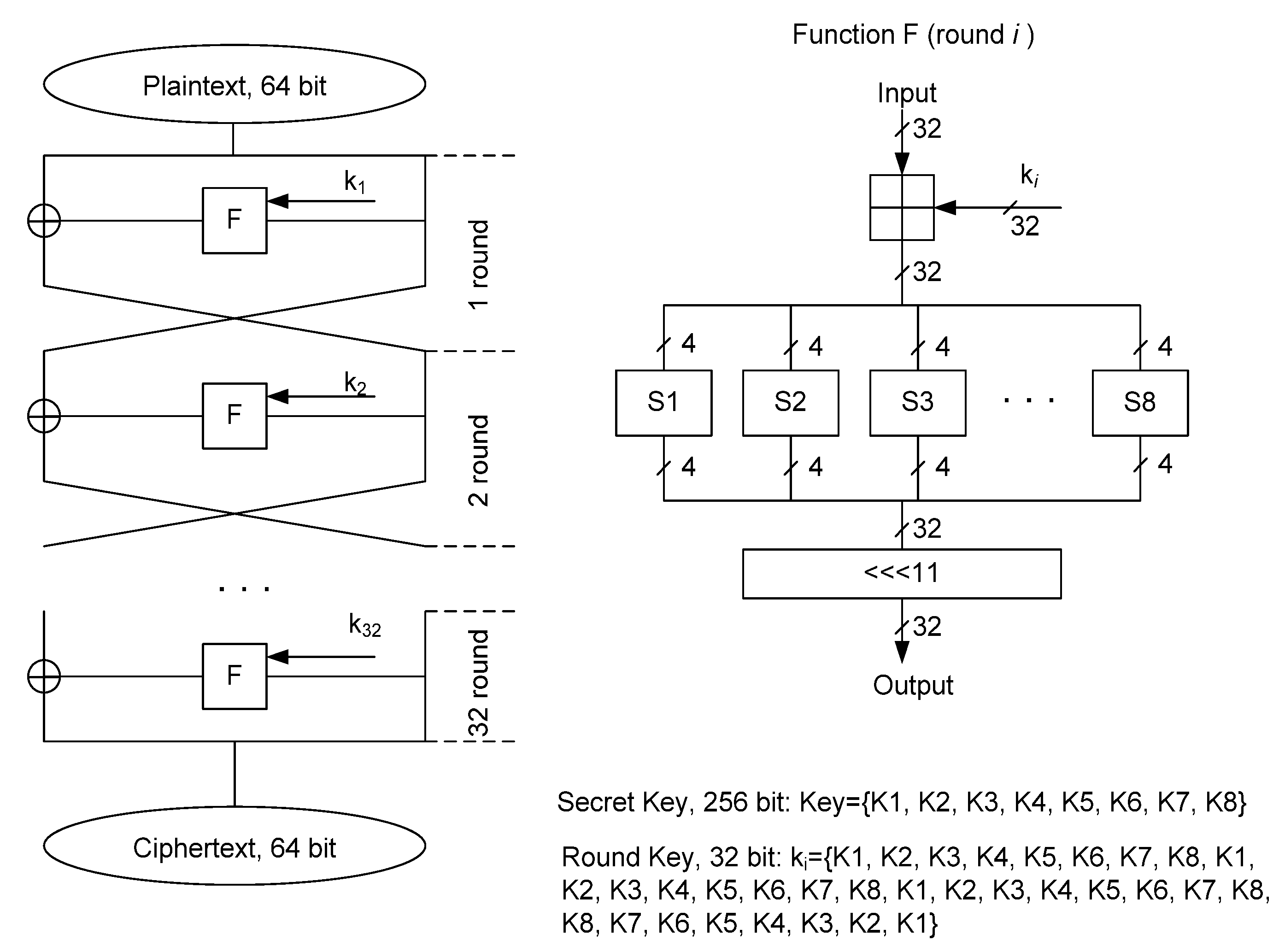
2.1. Magma Cipher (GOST R 34.12-2015 n = 64) and Magma ⊕
- Mixing data with secret key bits using module 232 addition;
- S-box bit substitution;
- 11 position cyclic shift to the left.
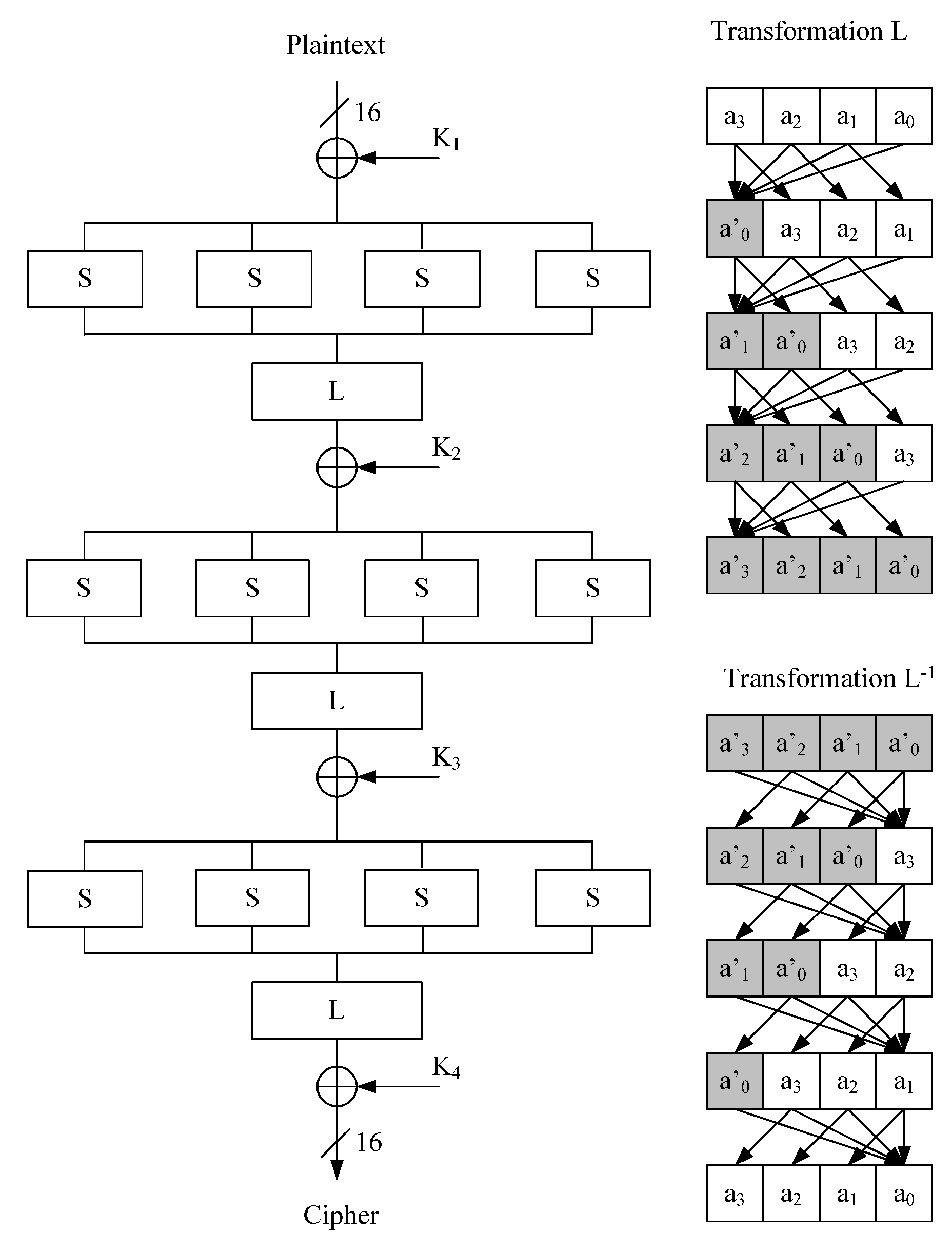
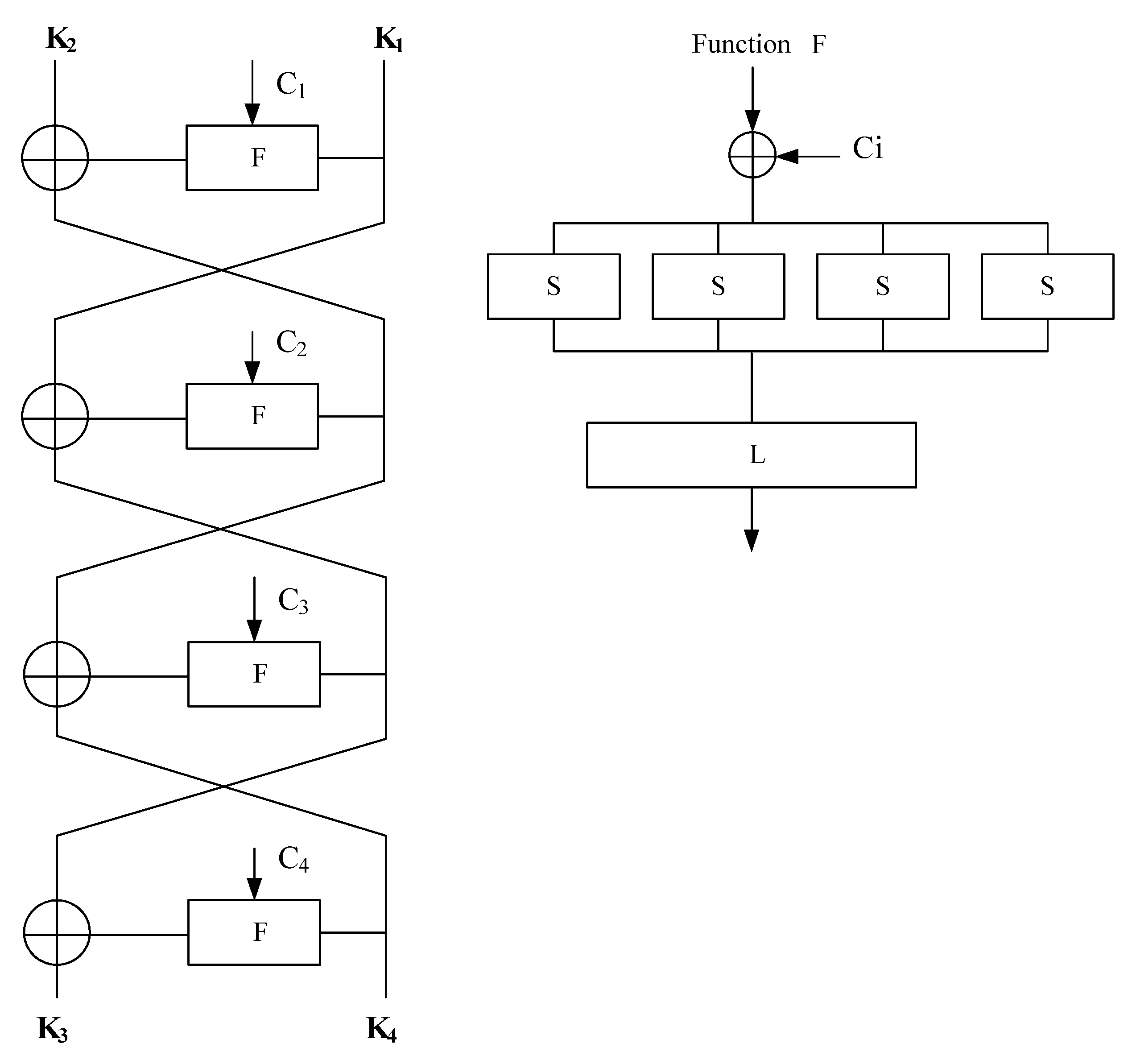
2.2. Kuznyechik Cipher (GOST R 34.12-2015 n = 128) and S-KN2 Cipher
- Byte exchange with S-block;
- linear mixing bits L;
- mixing data with secret key bits using module 2 addition.
- Byte exchange with S-block. The data block is divided into 16 bytes. Each byte is replaced by a new value according to the table defined in the standard;
- linear mixing bits L. The operation is performed by using the multiplication of polynomials in the given field. Multiplication is performed 16 times until all bytes are changed;
- mixing data with secret key bits using module 2 addition.
3. Methods of Algebraic Analysis
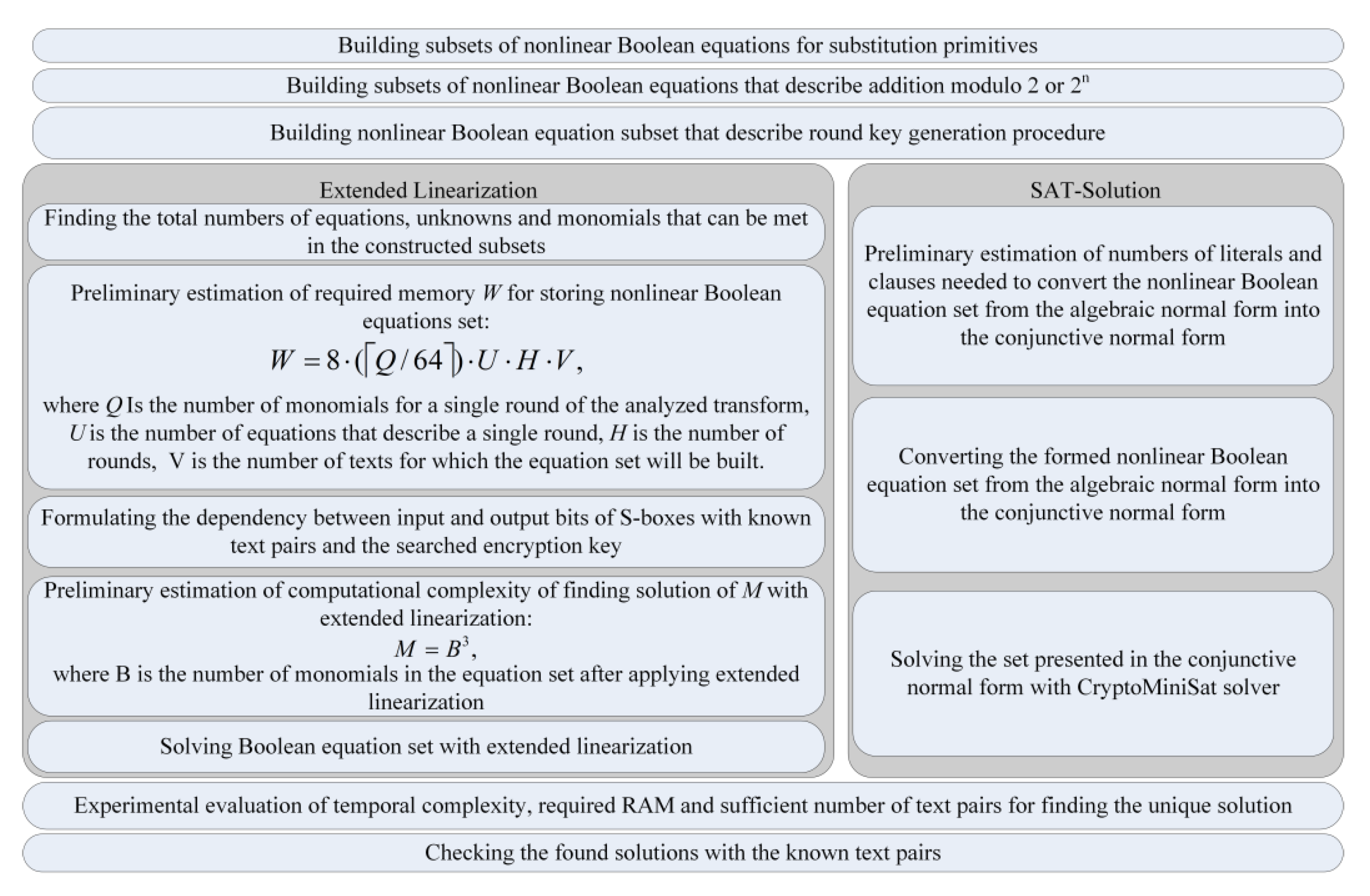
3.1. Extended Linearization Method
- Formation of the set of all possible multiplications of variables of degree , where
- Composition of all multiplications of the form , where ,
- Consideration of each monomial of degree greater than as a new variable and applying the Gauss elimination method to the equations obtained in (b).
- Repeat step (c) until the result is at least one equation with a single unknown .
- Simplification of equations and repetition of the process to find the values of other unknowns.
3.2. SAT Solvers for Solving a System of Boolean Algebraic Equations
- Variable propagation. If there is only one variable left in the sentence, assign it such a value that the sentence becomes true (put the variable in the subset A if there is no negation in the sentence, or put it in the set B if there is negation).
- The elimination of “pure variables”. If a variable is found in the formula with only negation or only without negation, then it is called “pure” and it can be assigned such a value that it is always “true” (in this way we reduce the number of free variables).
- Clauses of addition modulo two are distinguished at the beginning of the search for solutions. They have their own separate search list, a separate extension mechanism, and a categorization algorithm. The use of such opportunities leads to a speed increase in searching for solutions of Boolean equations systems.
- Clauses of addition modulo two (binary) are processed by special methods. First, the search is usually performed using special heuristics. Secondly, a tree structure is constructed of them, reflecting which of the variables is equivalent or anti-valent. The upper level of the constructed trees is usually replaced by lower values in the tree, thereby reducing the number of classes and variables in the analyzed task. This usually leads to the necessity of reassigning variables.
- Technical and cryptographic SAT problems are very different, so CryptoMiniSat allows you to change the restart settings and change the type of learning heuristics using the Glucose or MiniSat training methods.
- Clauses are removed from CNF as soon as at least one of the literals included in this clause takes a value equal to true. Unlike the MiniSat, the literals equal to false are also deleted in the clauses, thereby allowing the clause to be reduced.
- The removal of dependent variables is carried out among the associated clauses of addition modulo two. Dependent variables are variables that are found only in one clause of addition modulo two. This simplification allows you to remove the variable from the task. It should be remembered that such a variable cannot be removed by using the exclusion of “pure” literals.
- Variables take values “false” and “true” at fixed intervals. If one of the search branches leads to an error (returning an impracticable formula), then the second branch is checked. Moreover, the results of checking both branches of the search are saved for subsequent comparison.
- Representation of cryptographic transformation as a system of Boolean equations in the algebraic normal form (ANF).
- Convert the equation system from ANF to CNF.
- Solve a SAT problem to find a set of solutions by SAT solvers.
- Replacing constant 1 by a new unknown, since CNF should not contain constants.
- Replacing all products of unknowns by new variables (apply the linearization method to the original nonlinear system).
- The splitting of long chains formed as the addition modulo two unknowns into substrings of shorter length (for example, only four unknowns).
- Representation of the transformed system in CNF.
4. Generation of a System of Boolean Equations Describing an Encryption Algorithm
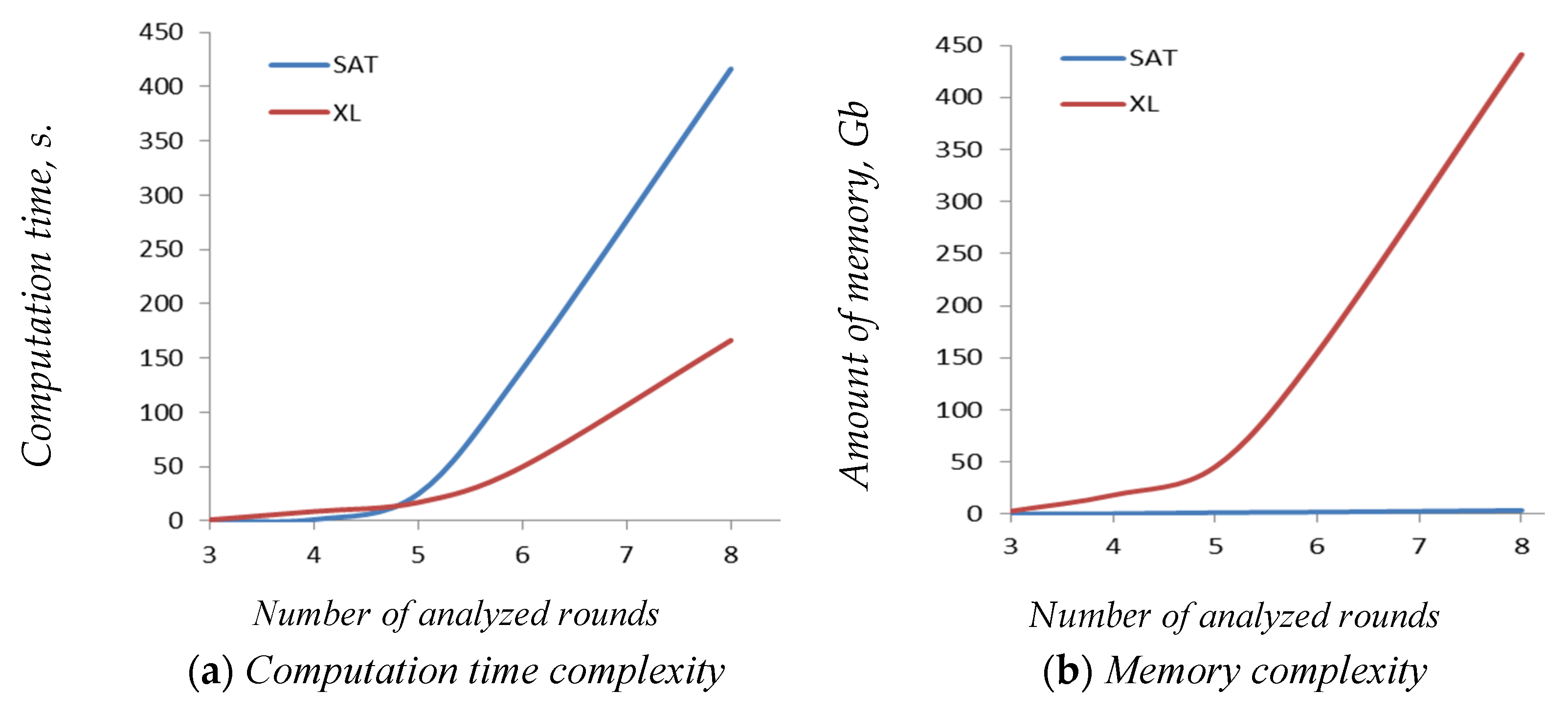
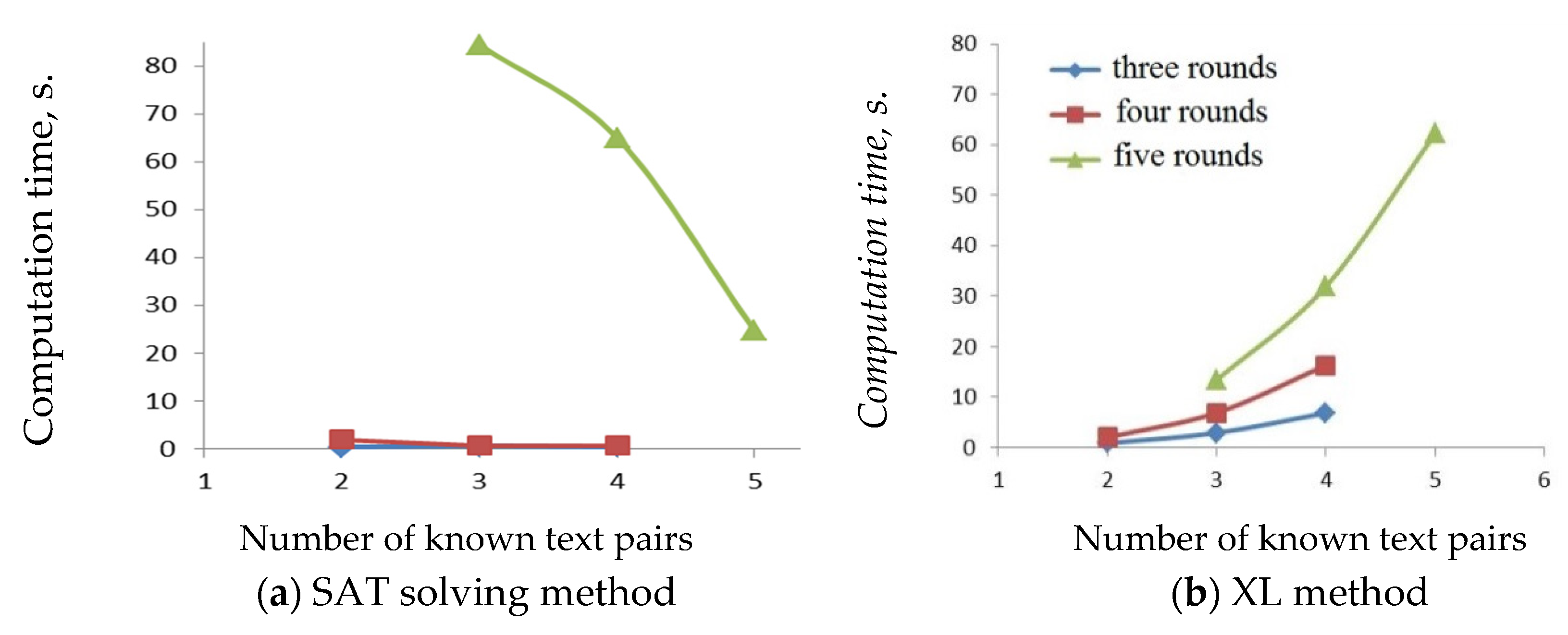
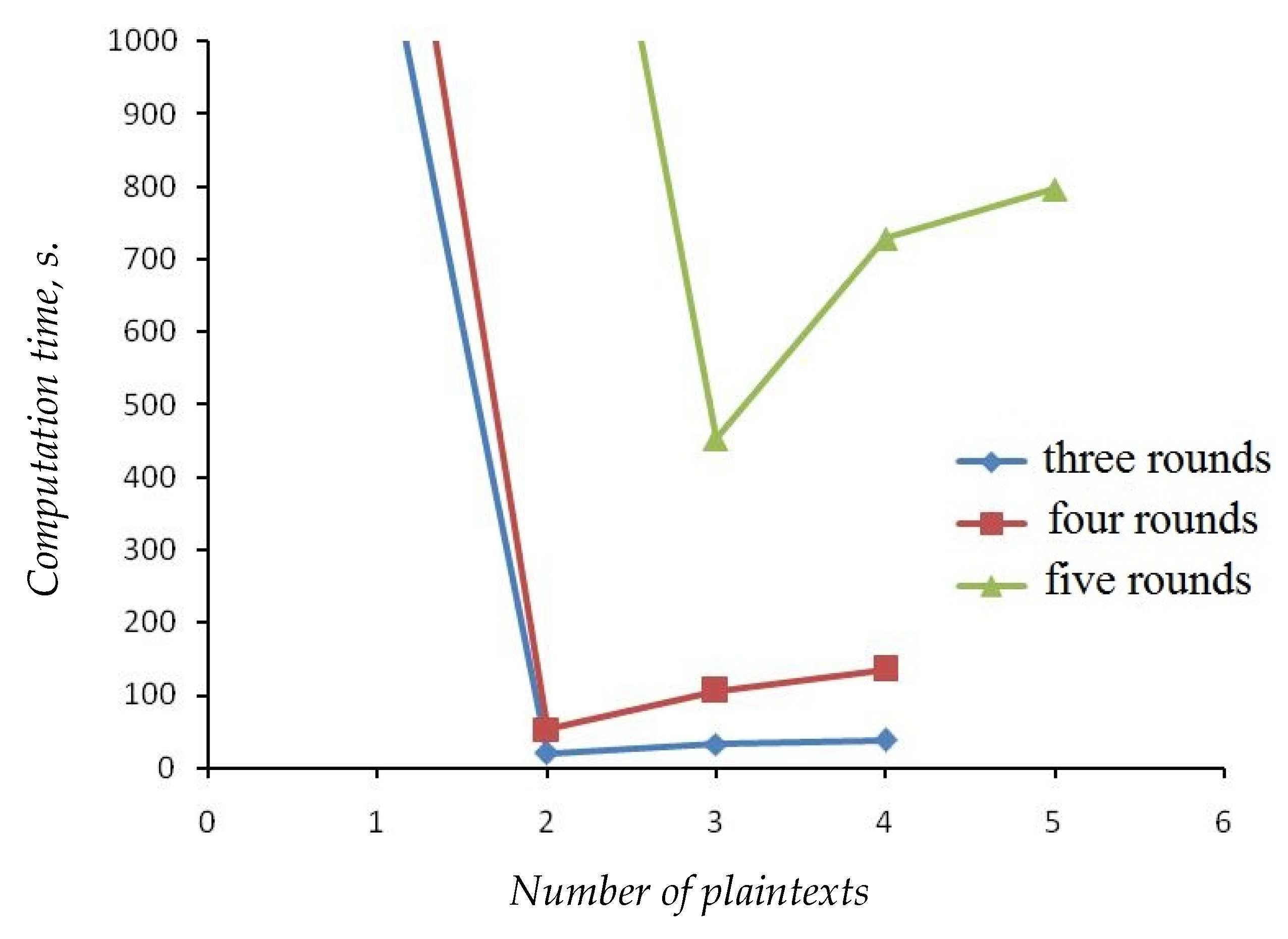
5. Assessment Approaches by Algebraic Analysis Methods
- The mathematical structure of the encryption algorithm;
- the structure of the substitution operations (as they are defined in the algorithm);
- available known data (the number of plaintext-ciphertext pairs).
- the encryption key value (or some sets of possible values);
- parameters of the nonlinear Boolean equation system: the numbers of equations, unknowns, and monomials;
- the computational complexity of solving the Boolean equation system;
- the time complexity of solving the Boolean equation system;
- the minimal number of known data (text pairs) that are needed to find the key in a reasonable time;
- the required RAM for analysis.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Courtois, N. Algebraic Complexity Reduction and Cryptanalysis of GOST. Available online: http://www.nicolascourtois.com/papers/gostac11.pdf (accessed on 27 May 2020).
- Shannon, C.E. Communication Theory of Secrecy Systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Pasalic, E. On Cryptographically Significant Mappings over GF(2). Available online: Arithmetic of Finite Fields. In Proceedings of the Second International Workshop, WAIFI, Siena, Italy, 6–9 July 2008; pp. 189–204. [Google Scholar]
- Arabnezhad-Khanoki, H.; Sadeghiyan, B.; Pieprzyk, J. Algebraic Attack Efficiency Versus S-Box Representation. Available online: https://eprint.iacr.org/2017/007.pdf (accessed on 27 May 2020).
- Dehnavi, S.M.; Rishakani, A.M.; Mirzaeeshamsabad, M.R.; Maimani, H.; Pasha, E. Cryptographic Properties of Addition Modulo 2n. Available online: https://eprint.iacr.org/2016/181.pdf (accessed on 27 May 2020).
- Greve, B.; Ytrehus, Ø.; Raddum, H. Variable Elimination-a Tool for Algebraic Cryptanalysis. Available online: https://eprint.iacr.org/2019/112.pdf (accessed on 27 May 2020).
- Bernstein, D.J.; Yang, B.-Y. Asymptotically Faster Quantum Algorithmsto Solve Multivariate Quadratic Equations. Available online: https://eprint.iacr.org/2017/1206.pdf (accessed on 27 May 2020).
- Cheng, C.-M.; Chou, T.; Niederhagen, R.; Yang, B.-Y. Solving Quadratic Equations with XLon Parallel Architectures. Extended Version. Available online: https://eprint.iacr.org/2016/412.pdf (accessed on 27 May 2020).
- Liu, F.; Isobe, T.; Meier, W.; Yang, Z. Algebraic Attacks on Round-ReducedKeccak/Xoodoo. Available online: https://eprint.iacr.org/2020/346.pdf (accessed on 27 May 2020).
- Arabnezhad-Khanoki, H.; Sadeghiyan, B. Toward a More Efficient Gröbner-Based Algebraic Cryptanalysis. Available online: https://eprint.iacr.org/2019/1415.pdf (accessed on 27 May 2020).
- Albrecht, M.R.; Cid, C.; Grassi, L.; Khovratovich, D.; Lüftenegger, R.; Rechberger, C.; Schofnegger, M. Algebraic Cryptanalysis of STARK-Friendly Designs: Application toMARVELlous and MiMC. Available online: https://eprint.iacr.org/2019/419.pdf (accessed on 27 May 2020).
- Matheis, K.; Steinwandt, R.; Suárez Corona, A. Algebraic Properties of the Block Cipher DESL. Symmetry 2019, 11, 1411. [Google Scholar] [CrossRef]
- Soeken, M. Determining the Multiplicative Complexity of Boolean Functions Using SAT. Available online: https://eprint.iacr.org/2020/530.pdf (accessed on 27 May 2020).
- Schaffhauser, A. SAT Solvers and their Limits with NFSR-based Stream Ciphers: An Example with Grain v1. In Proceedings of the Third Central European Cybersecurity Conference (CECC 2019), Munich, Germany, 15–16 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Pavlenko, A.; Semenov, A.; Ulyantsev, V. Evolutionary Computation Techniques for Constructing SAT-Based Attacks in Algebraic Cryptanalysis. In Applications of Evolutionary Computation; EvoApplications 2019; Lecture Notes in Computer Science; Kaufmann, P., Castillo, P., Eds.; Springer: Cham, Switzerland, 2019; Volume 11454. [Google Scholar]
- Horáček, J. Algebraic and Logic Solving Methods for Cryptanalysis. Ph.D. Thesis, University of Passau, Passau, Germany, 2020. Available online: https://opus4.kobv.de/opus4-uni-passau/files/773/horacek_dissertation.pdf (accessed on 27 May 2020).
- Ishchukova, E.; Babenko, L.; Anikeev, M. Two Simplified Versions of Kuznyechik Cipher (GOST R 34.12-2015). In Proceedings of the 10th International Conference on Security of Information and Networks, Jaipur, India, 13–15 October 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 287–290. [Google Scholar] [CrossRef]
- Information Technology Cryptographic Data Security Block Ciphers English Version. Available online: https://tc26.ru/upload/iblock/fc9/GOST_R_34_12_2015_ENG.pdf (accessed on 27 May 2020).
- Stallings, W. Cryptography and Network Security: Principles and Practice; Prentice Hall Pub: Upper Saddle River, NJ, USA, 1998; p. 562. [Google Scholar]
- Mini Advanced Encryption Standard (Mini-AES): A Testbed for Cryptanalysis Students, by Raphael Chung-Wei Phan. Cryptologia 2002, 26, 283–306. [CrossRef]
- Musa, M.A.; Schaefer, E.F.; Wedig, S. A simplified AES algorithm and its linear and differential cryptanalyses. Cryptologia 2003, 27, 148–177. [Google Scholar] [CrossRef]
- Gilbert, H. A Simplified Representation of AES. In Advances in Cryptology–ASIACRYPT 2014; Lecture Notes in Computer Science; Sarkar, P., Iwata, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8873. [Google Scholar]
- Sunjiv Soyjaudah, K.M.; Sumithra Devi, K.A. Overview of Linear Cryptanalysis on S-DES and Block Ciphers using Hill Cipher Method. Int. J. Comput. Appl. 2013, 63. [Google Scholar]
- Ooi, K.S.; Vito, B.C. Cryptanalysis of S-DES. IACR Cryptol. ePrint Arch. 2002, 2002, 45. Available online: https://eprint.iacr.org/2002/045.pdf (accessed on 27 May 2020).
- Nalini, N.; Rao, G.R. Cryptanalysis of Simplified Data Encryption Standard via Optimisation Heuristics. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2006, 6, 240–246. [Google Scholar]
- Vimalathithan, R.; Valarmathi, M.L. Cryptanalysis of S-DES using Genetic Algorithm. Int. J. Recent Trends Eng. 2009, 2, 76–79. [Google Scholar]
- Dworak, K.; Boryczka, U. Cryptanalysis of SDES Using Modified Version of Binary Particle Swarm Optimization. In Computational Collective Intelligence; Lecture Notes in Computer Science; Núñez, M., Nguyen, N., Camacho, D., Trawiński, B., Eds.; Springer: Cham, Switzerland, 2015; Volume 9330. [Google Scholar]
- Phan, R.C.-W. Impossible Differential Cryptanalysis of Mini-AES. Cryptologia 2003, 27, 361–374. [Google Scholar] [CrossRef]
- Hitapuru, B.; Indarjani, S. Square attack on Mini-AES and Simplified AES using all variants of active nibble position. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; Volume 1729. [Google Scholar]
- Mansoori, S.D.; Bizaki, H.K. On the vulnerability of Simplified AES Algorithm Against Linear Cryptanalysis. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2007, 7, 257–263. [Google Scholar]
- Campbell, S.; Grinchenko, M.; Smith, W. Linear Cryptanalysis of Simplified AES Under Change of S-Box. Cryptologia 2013, 37, 120–138. [Google Scholar] [CrossRef]
- Simmons, S. Algebraic Cryptanalysis of Simplified AES. Cryptologia 2009, 33, 305–314. Available online: http://www.nku.edu/~christensen/Alg%20cryptanalysis%20SAES.pdf (accessed on 27 May 2020). [CrossRef]
- Courtois, N.; Klimov, A.; Patarin, J.; Shamir, A. Efficient algorithms for solving over defined systems of multivariate polynomial equations. In EUROCRYPT 2000; Lecture Notes in Computer Science; Springer: Berlin, Heidelberg, Germany, 2000; Volume 1807, pp. 392–407. [Google Scholar] [CrossRef]
- Ripatti, A.V. Algorithms of Splitting and van der Waerden Numbers. Available online: https://habrahabr.ru/post/224069/ (accessed on 27 May 2020). (In Russian).
- Bard, G.; Courtois, N.; Jefferson, C. Efficient Methods for Conversion and Solution of Sparse Systems of Low-Degree Multivariate Polynomials over GF (2) via SAT-Solvers. Cryptology ePrint Archive. 2007, Volume 24. Available online: https://eprint.iacr.org/2007/024.pdf (accessed on 27 May 2020).
- Albrecht, M. Tools for Algebraic Cryptanalysis. In Proceedings of the ECRYPT Workshop on Tools for Cryptanalysis, Egham, UK, 22–23 June 2010; pp. 13–14. [Google Scholar]
- Soos, M. ANF2CNF Script Released. Available online: http://www.msoos.org/2010/09/anf2cnf-script-released/ (accessed on 27 May 2020).
- Soos, M. ANF to CNF Conversion. Available online: http://www.msoos.org/2010/07/anf-to-cnf-conversion/ (accessed on 27 May 2020).
- Courtois, N.; Bard, G. Algebraic Cryptanalysis of the Data Encryption Standard. In Proceedings of the 11-th IMA Conference, Cirencester, UK, 18–20 December 2007; pp. 152–169. [Google Scholar]
- Courtois, N.; Debraize, B. Specific S-Box Criteria in Algebraic Attacks on Block Ciphers with Several Known Plaintexts. In Proceedings of the WEWoRC 2007, Bochum, Germany, 4–6 July 2007; Volume 4945, pp. 100–113. [Google Scholar]
- Maro, E.A. Modeling of algebraic analysis of PRESENT cipher by SAT solvers. In Proceedings of the VIII International Workshop on Mathematical Models and their Applications (IWMMA-2019), Krasnoyarsk, Russia, 18–21 November 2019; IOP Conference Series: Materials Science and Engineering. Volume 734. [Google Scholar]
- The Sage Developers. SageMath, the Sage Mathematics Software System; Version 9.1; The Sage Developers: Newcastle upon Tyne, UK, 2020; Available online: http://www.sagemath.org (accessed on 27 May 2020).
- Sage Reference Manual: Sat Release 7.5. Available online: http://doc.sagemath.org/pdf/en/reference/sat/sat.pdf (accessed on 27 May 2020).
- Sage Reference Manual: Cryptography Release 7.5. Available online: http://doc.sagemath.org/pdf/en/reference/cryptography/cryptography.pdf (accessed on 27 May 2020).
| S1 | 12 | 4 | 6 | 2 | 10 | 5 | 11 | 9 | 14 | 8 | 13 | 7 | 0 | 3 | 15 | 1 |
| S2 | 6 | 8 | 2 | 3 | 9 | 10 | 5 | 12 | 1 | 14 | 4 | 7 | 11 | 13 | 0 | 15 |
| S3 | 11 | 3 | 5 | 8 | 2 | 15 | 10 | 13 | 14 | 1 | 7 | 4 | 12 | 9 | 6 | 0 |
| S4 | 12 | 8 | 2 | 1 | 13 | 4 | 15 | 6 | 7 | 0 | 10 | 5 | 3 | 14 | 9 | 11 |
| S5 | 7 | 15 | 5 | 10 | 8 | 1 | 6 | 13 | 0 | 9 | 3 | 14 | 11 | 4 | 2 | 12 |
| S6 | 5 | 13 | 15 | 6 | 9 | 2 | 12 | 10 | 11 | 7 | 8 | 1 | 4 | 3 | 14 | 0 |
| S7 | 8 | 14 | 2 | 5 | 6 | 9 | 1 | 12 | 15 | 4 | 11 | 0 | 13 | 10 | 3 | 7 |
| S8 | 1 | 7 | 14 | 13 | 0 | 5 | 8 | 3 | 4 | 15 | 10 | 6 | 9 | 12 | 11 | 2 |
| Input | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Output | 3 | 6 | a | 7 | f | 0 | 5 | b | 2 | c | 1 | e | 4 | 9 | d | 8 |
| Input | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Output | 5 | a | 8 | 0 | c | 6 | 1 | 3 | f | d | 2 | 7 | 9 | e | b | 4 |
| S-Block Input | S-Block Output | All Compositions of S-Block Inputs and Outputs | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All possible S-block inputs (from 0 to 2s) | xs | … | x1 | ys | … | y1 | xsxs−1 | … | x2 × 1 | ysys−1 | … | y2y1 | xsys | … | x1y1 |
| 0 | … | 0 | 1 | … | 1 | ||||||||||
| … | |||||||||||||||
| 1 | … | 1 | 0 | … | 1 | ||||||||||
| SAT Method | XL Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of Known Text Pairs | Number of Equations | Number of Unknowns | Number of Literals | Number of Clauses | Number of Solutions | Total Time, s | Search Time, s | RAM, GByte | Complexity by Number of Additions | Search Time, s |
| Three rounds of Magma | ||||||||||
| 2 | 1008 | 160 | 2997 | 52,438 | 32 | 20 | 0.26 | 0.11 | 236,33 | 0.86 |
| 3 | 1512 | 192 | 4306 | 78,516 | 2 | 32.7 | 0.52 | 0.14 | 238,08 | 2.91 |
| 4 | 2016 | 224 | 5512 | 104,654 | 1 | 38.51 | 0.48 | 0.16 | 239,32 | 6.86 |
| Three rounds of Magma (with weakened S-boxes) | ||||||||||
| 2 | 1200 | 352 | 1470 | 9400 | 8 | 28.51 | 0.35 | 0.13 | 236,67 | 1.09 |
| 3 | 1800 | 480 | 1965 | 14,084 | 1 | 39.91 | 0.47 | 0.14 | 238,43 | 3.71 |
| Three rounds of Magma (with S-box S(X) = X) | ||||||||||
| 2 | 1200 | 352 | 1292 | 7393 | 2048 | 21.11 | 2.10 | 0.28 | 236.67 | 1.09 |
| 3 | 1800 | 480 | 1889 | 11,014 | 1 | 37.19 | 1.07 | 0.16 | 238.43 | 3.71 |
| Three rounds of Magma | ||||||||||
| 2 | 1200 | 352 | 2819 | 38,811 | 1 | 36.55 | 0.35 | 0.13 | 236,67 | 1.09 |
| Four rounds of Magma | ||||||||||
| 2 | 1344 | 256 | 6492 | 114,472 | 256 | 52.59 | 1.93 | 0.32 | 237,57 | 2.04 |
| 3 | 2016 | 320 | 9435 | 171,324 | 2 | 106.33 | 0.71 | 0.39 | 239,33 | 6.91 |
| 4 | 2688 | 384 | 12,384 | 228,358 | 1 | 135.42 | 0.69 | 0.48 | 240,57 | 16.32 |
| Four rounds of Magma (with weakened S-boxes) | ||||||||||
| 2 | 1600 | 512 | 2940 | 16,642 | 128 | 96.10 | 0.77 | 0.31 | 237,92 | 2.6 |
| 3 | 2400 | 704 | 3869 | 24,982 | 2 | 142.36 | 0.88 | 0.35 | 239,67 | 8.75 |
| 4 | 3200 | 896 | 4798 | 33,316 | 2 | 195.61 | 1.23 | 0.36 | 240,92 | 20.79 |
| 5 | 4000 | 1088 | 5725 | 41,646 | 2 | 294.72 | 1.51 | 0.38 | 241,88 | 40.46 |
| 6 | 4800 | 1280 | 6839 | 49,922 | 2 | 612.03 | 4.11 | 0.39 | 242,67 | 69.98 |
| 7 | 5600 | 1472 | 7951 | 58,174 | 1 | 700.96 | 2.63 | 0.41 | 243,34 | 111.43 |
| Four rounds of Magma (with S-box S(X) = X) | ||||||||||
| 3 | 2400 | 704 | 3726 | 19,280 | 4 | 106.76 | 1.33 | 0.28 | 239,67 | 8.75 |
| 4 | 3200 | 896 | 4606 | 25,830 | 2 | 144.66 | 1.10 | 0.30 | 240,92 | 20.79 |
| 5 | 4000 | 1088 | 5484 | 32,294 | 1 | 242.21 | 1.24 | 0.35 | 241,88 | 40.46 |
| Four rounds of Magma | ||||||||||
| 2 | 1600 | 512 | 4839 | 67,886 | 4 | 93.44 | 10.27 | 0.37 | 237,91 | 2.58 |
| 3 | 2400 | 704 | 7202 | 101,968 | 1 | 202.56 | 1.32 | 0.48 | 239,67 | 8.75 |
| Five rounds of Magma | ||||||||||
| 3 | 2520 | 448 | 14,696 | 266,200 | 4 | 452.74 | 84.41 | 1.38 | 240,29 | 13.44 |
| 4 | 3360 | 554 | 19,448 | 354,354 | 2 | 729.15 | 124.47 | 1.44 | 241,54 | 31.97 |
| 5 | 4200 | 640 | 24,259 | 443,932 | 1 | 797.21 | 24.66 | 1.52 | 242,50 | 62.20 |
| Five rounds of Magma (with weakened S-boxes) | ||||||||||
| 3 | 3000 | 928 | 5932 | 39,549 | 4 | 320.17 | 4.15 | 1.62 | 240,64 | 17.14 |
| 4 | 4000 | 1184 | 7436 | 52,872 | 2 | 488.65 | 4.47 | 1.76 | 241,88 | 40.46 |
| 5 | 5000 | 1440 | 9194 | 66,113 | 2 | 478.31 | 2.51 | 1.87 | 242,85 | 79.25 |
| 6 | 6000 | 1696 | 10,705 | 79,506 | 2 | 875.24 | 6.91 | 2.13 | 243,64 | 137.09 |
| 7 | 7000 | 1952 | 12,459 | 92,707 | 1 | 1135.61 | 3.36 | 2.26 | 244,30 | 216.27 |
| Five rounds of Magma (with S-box S(X) = X) | ||||||||||
| 3 | 3000 | 928 | 5338 | 32,873 | 40 | 678.80 | 520.89 | 1.73 | 240,64 | 17.14 |
| 4 | 4000 | 1184 | 7068 | 43,926 | 2 | 415.31 | 28.65 | 1.82 | 241,88 | 40.46 |
| 5 | 5000 | 1440 | 8787 | 54,647 | 1 | 501.18 | 4.92 | 1.85 | 242,85 | 79.25 |
| Five rounds of Magma | ||||||||||
| 3 | 3000 | 928 | 10,596 | 152,045 | 1 | 394.68 | 24.96 | 1.42 | 240,64 | 17.14 |
| Eight rounds of Magma (with weakened S-boxes) | ||||||||||
| 4 | 5376 | 2048 | 15,395 | 110,844 | 4096 | 5972.41 | 1843.67 | 4.59 | 243,92 | 166.3 |
| Eight rounds of Magma (with S-box S(X) = X) | ||||||||||
| 4 | 5376 | 2048 | 13,764 | 92,370 | 1024 | 4842.31 | 1374.12 | 3.86 | 243,92 | 166.3 |
| Eight rounds of Magma | ||||||||||
| 4 | 5376 | 2048 | 30,062 | 431,267 | 1 | 3029.56 | 416.31 | 3.6 | 243,92 | 166.3 |
| Number of Known Text Pairs | Number of Equations | Number of Unknowns | Complexity by Number of Additions | RAM, GByte |
|---|---|---|---|---|
| One-round S-KN2 cipher | ||||
| 1 | 88 | 32 | 225,57 | 0.001 |
| 2 | 176 | 48 | 228,32 | 0.008 |
| 3 | 264 | 64 | 230,12 | 0.028 |
| Two-round S-KN2 cipher | ||||
| 1 | 176 | 64 | 228,57 | 0.008 |
| 2 | 352 | 96 | 231,57 | 0.066 |
| 3 | 528 | 128 | 233,33 | 0.224 |
| Three-round S-KN2 cipher | ||||
| 1 | 264 | 80 | 230,33 | 0.028 |
| 2 | 528 | 112 | 233,16 | 0.187 |
| 3 | 792 | 144 | 235,08 | 0.756 |
| Four-round S-KN2 cipher | ||||
| 1 | 352 | 112 | 231,57 | 0.066 |
| 2 | 704 | 160 | 234,57 | 0.531 |
| 3 | 1056 | 208 | 236,33 | 1.191 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishchukova, E.; Maro, E.; Pristalov, P. Algebraic Analysis of a Simplified Encryption Algorithm GOST R 34.12-2015. Computation 2020, 8, 51. https://doi.org/10.3390/computation8020051
Ishchukova E, Maro E, Pristalov P. Algebraic Analysis of a Simplified Encryption Algorithm GOST R 34.12-2015. Computation. 2020; 8(2):51. https://doi.org/10.3390/computation8020051
Chicago/Turabian StyleIshchukova, Evgenia, Ekaterina Maro, and Pavel Pristalov. 2020. "Algebraic Analysis of a Simplified Encryption Algorithm GOST R 34.12-2015" Computation 8, no. 2: 51. https://doi.org/10.3390/computation8020051
APA StyleIshchukova, E., Maro, E., & Pristalov, P. (2020). Algebraic Analysis of a Simplified Encryption Algorithm GOST R 34.12-2015. Computation, 8(2), 51. https://doi.org/10.3390/computation8020051





