1. Introduction
The importance of identifying the sequence and the 3-D structure of proteins is crucial to understand their function and behavior within living organisms; for instance, mis-folding of proteins is believed to be related to neurodegenerative diseases such as Parkinson’s and Alzheimer. Current methods require long sequencing times that represent a serious bottleneck for the needs of the rising importance of proteomics. Then, fast and efficient techniques (especially for large protein chains) are required and solid-state nanopores and nanogaps are emerging as promising tools for single molecule analysis [
1,
2,
3]. In this framework, a new sequencer consisting of arrays of nano-gaps between graphene nano-ribbons has recently been proposed [
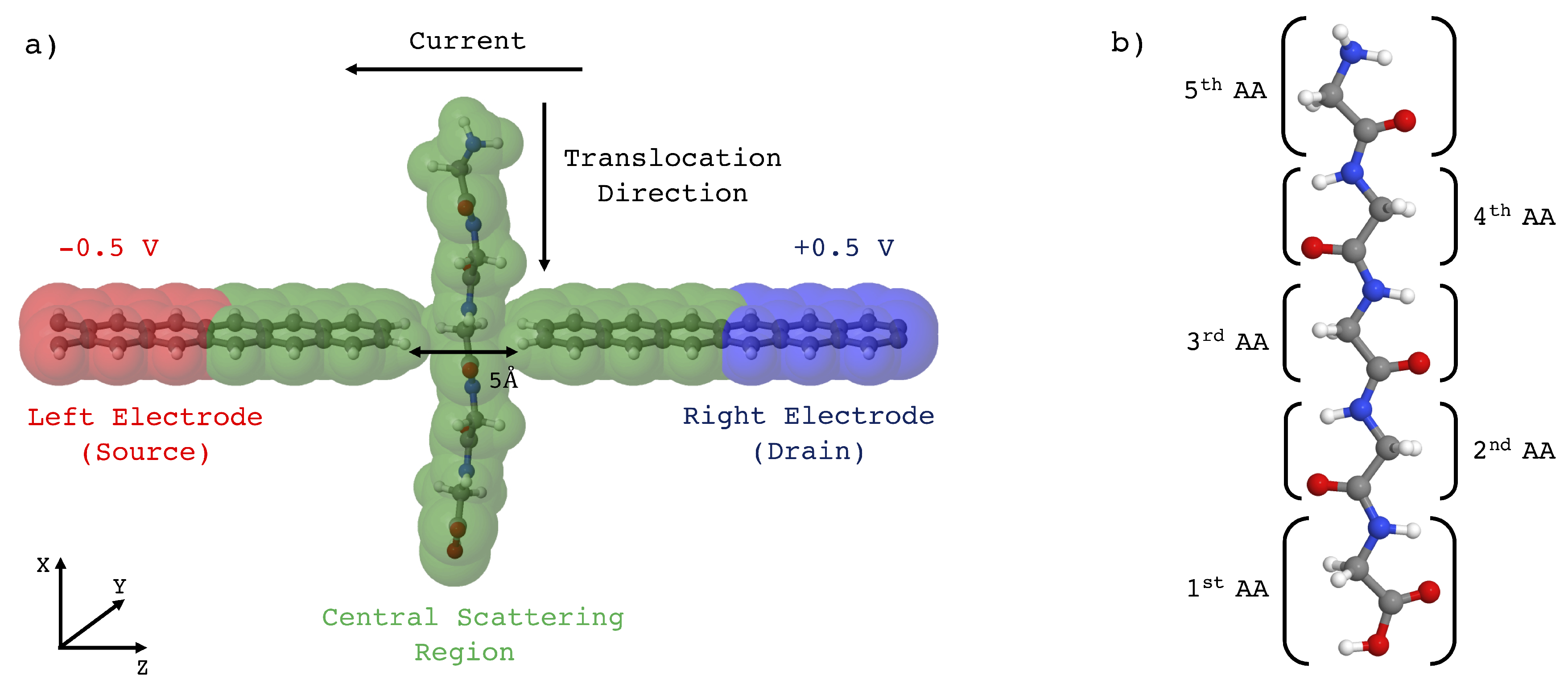
4], as schematically represented in
Figure 1a, exploiting the ideal 2D structure of the leads that allows an atomistic resolution sensing. While the molecule (in this case an amino acids chain) is led to translocate through the gap between the two leads, a tunneling current is induced to flow across the leads where a voltage bias is applied, thus allowing in principle the atomistic recognition of the specific portion of the molecule right in the middle of the gap. The collected signal could be processed and employed to obtain the primary structure of a peptide or a protein. A Density Functional Theory (DFT) based ab initio study, in conjunction with the Non Equilibrium Green Function (NEGF) method [
5,
6] and the Landauer-Büttiker approach [
7], has evidenced clear peptide bond fingerprints made of two well defined current peaks of the order of magnitude of nA in the case of glycine poly-peptides translocating across a 5 Å wide nano-gap [
4]. The same ideal nano-gap device has been considered to study also an-elastic phenomena that are ignored in the DFT-NEGF model: inelastic electcron tunneling spectra have revealed that that phonon assisted tunneling events and non linear I-V characteristics are important issues and that the non-linear features related to these phenomena allow the identification of peptide bond and amino-acids side chains as well [
8]. The most advanced current nano-technological processes have allowed the manufacturing of stable graphene 1 nm wide nanogaps [
9] and even sub-nanometer gaps with other materials [
10]. However the realization of stable 5 Å nano-gaps, as the ones employed in the previous proof of principles studies on the amino-acid recognition by tunneling current, is still to come. Hence, in order to get closer to nanogap configurations practically achievable on the basis of the present technological capabilities, it is important to try to enlarge the gap size and to investigate further the effect of the gap size on the tunneling current signal. The present work is therefore devoted to study, employing the above mentioned DFT-NEGF approach, the change of the transport properties of the system composed by the peptide and the graphene nanoribbon as the nano-gap size is increased. Therefore, while we have re-calculated with a denser resolution the current signal for a 5 Å nano-gap, we have extended the study of the tunneling current signal for new nano-gaps of 6 Å and 7 Å widths with the same augmented resolution. We have focussed our study on the paradigmatic case of a Gly homo-peptide.
2. Theoretical Method
The ideal device is schematically drawn in
Figure 1. Two semi-infinite narrow zig-zag graphene nanorobbons [
11] 2-ZGNR are employed as electrodes. It is important to evidence that the electronic ground state of such ribbons is a semi-conducting ferromagnetic state [
12,
13]; however, the metallic unpolarized configurations is reported to be stable when a bias is applied and in presence of ballistic conduction [
14,
15]. Moreover it is known that the spin polarized ground state undergoes a transition to semi-metallic conduction properties when the ZGNR is doped with N atoms [
16] or when a transverse electric field is applied [
17]. Then we have chosen the unpolarized metallic phase of the hydrogenated ZGNR as a paradigmatic case of metallic or half-metallic ideal 2D graphene based electrodes. The metallic behavior of the electrodes employed in the present case is evidenced in
Figure 2.
Because the aim of the present article is to study the tunneling current signal by increasing the gap size, we have used three sub-nanometers gaps of respectively 5, 6 and 7 Å.
The gap devices have been fully relaxed in the context of DFT using the Quantum ESPRESSO package [
18]: electronic structures are calculated in the framework of a plane-wave basis set expansion, using a plane-wave energy cutoff of 70 Ry and an artificial smearing of 0.005 Ry. PBE (Perdew-Burke-Ernzerhof) [
19] functional is used for the electron exchange and correlation potential
and norm-conserving pseudopotetials built with the Troullier-Martins scheme [
20] are employed to reduce the number of electrons that are treated explicitly. Self-consistent calculation are performed until the convergence threshold of 0.001 a.u. for the total force was achieved.
The initial stage was aimed to collect the homopeptide configurations during the translocation across the gap. This stage has been performed through non-equilibrium steered classical molecular dynamics (SMD) simulations [
21] in water with a total number of atoms
. The SMD simulations have been performed at
K constant temperature using the Berendsen thermostat and a constant velocity steering protocol (
Å/fs). The Gly homopeptide has been translocated across the gap five times in sequence employing the periodic boundary conditions perpendicularly to the GNR plane. It is important to evidence that we are only dealing with completely linearized zig-zag configuration of the peptide: a larger peptide or protein should be eventually led to translocate across the nano-gap after complete de-naturation and only its primary structure is analyzed.
Then we have selected those configurations having meaningful groups located in the gap and in the GNR plane, namely the carboxyl (
) and the amino (
) groups (that are bonded together in the peptide bond), the side chain (
) and the middle-bond configurations between these three groups; water molecules have been removed [
4,
22] and structures have been further relaxed at
K, in the context of the density functional theory (DFT), using the SIESTA package [
5]. The necessity of this relaxing stage in the context of DFT arises for two main reasons: the first is that the interaction between the ZGNR leads and the peptide during the classical steered MD is basically incorrect due to absence of the electronic (or band structure) part of the interaction between the atoms that might be important especially for distributed wave functions such as the ones of the pseudo-
ZGNR orbitals; secondly the peptide is a little bit strained at the end of the steered MD step due to the large value of the velocity that, for computational reasons, has been employed: this strain needs to be relaxed. In this stage the threshold for the maximum module of the force acting on the atoms was set to 0.1 eV/Å in order to approach a local energy minimum and keep part of the thermal ionic disorder of the initial configuration; the RMSD measured between the quantum relaxed and the SMD configurations is of the order of RMSD ≈ 3.38 Å (RMSD/atom
Å). In
Figure 3 it can be appreciated the change of the atomic positions after this relaxation stage.
Split-double-
basis set augmented with polarization orbitals (DZP) are employed for H, O, C and N atoms, using a mesh cutoff of 250 Ry, PBE (Perdew-Burke-Ernzerhof) [
19] functional for the electron exchange-correlation potential and norm-conserving Troullier-Martins pseudopotentials [
20]. As mentioned, quantum transport calculations have been performed in the context of DFT-NEGF using the TRANSIESTA code [
5,
23]; the basis set, the electron exchange and correlation potential functional and pseudopotentials are the same used in the previous structural relaxation step.
According to the DFT-NEGF method, the calculation of the transport properties is obtained starting from a block decomposed Hamiltonian:
where
and
are, respectively, the decoupled Hamiltonians of the left (right) electrode and the scattering region,
represents the interaction of left (right) electrode with the scattering region and
is the self-energy of the left (right) lead that describes a complex re-normalization of the electrons energy due to the coupling of the left (right) lead with the semi-infinite electrodes.
For an external bias voltage
V applied along the
z direction, the current
is given by Landauer-Büttiker formula [
6]
where
is the Fermi-Dirac distribution function and
is the electrochemical potential of the left(right) electrode.
is the transmission coefficient that is calculated from the Hamiltonian of Equation (
1), with the external bias voltage
V included in the interaction terms, and is defined as:
where
is the Green’s function of the system and
is the left(right) coupling function [
24]. All DFT and quantum transport calculations have been carried out in dry ambient, since the presence of water does not affect the transport properties of the ZGNR nanogap because of the hyrdophobic character of graphene [
22]. Moreover, the sizes of the gap considered prevent the passage at the same time of the peptide chain and of water molecules. Although DFT is a ground state theory and not a steady-state one, the DFT-NEGF scheme is the most popular approach for steady-state transport in nanostructures and has been successfully applied in many cases often giving current values close to the ones obtained with other formally correct methods [
25,
26].
3. Results and Discussion
As already mentioned, we have calculated the tunneling current and the transport properties of the system for different gap sizes of 5, 6 and 7 Å. The translocating molecule is a peptide composed by five amino acids but only the central three are taken into account for the present results: indeed the first and the fifth amino acids of the peptide chain are adjacent to the C and the N-terminal groups whose lone pairs could affect the measured current (see
Figure 1). The chosen bias between the electrodes is 1 V, that is a common value found in literature in systems concerning tunneling currents or molecular junction [
27,
28,
29]. We have not observed any distortion or problem due to the employed bias, neither for the atomistic structure nor for the electron density and wave-functions. However we are aware that the employed bias could represent a problem in real measurements with ZGNR electrodes due to the large electric field in the gap: enlarging the gap, as we are reporting here, is certainly beneficial for this aspect but further studies are needed, and will be planned, to reduce the bias without affecting too much the level of the current signal. In
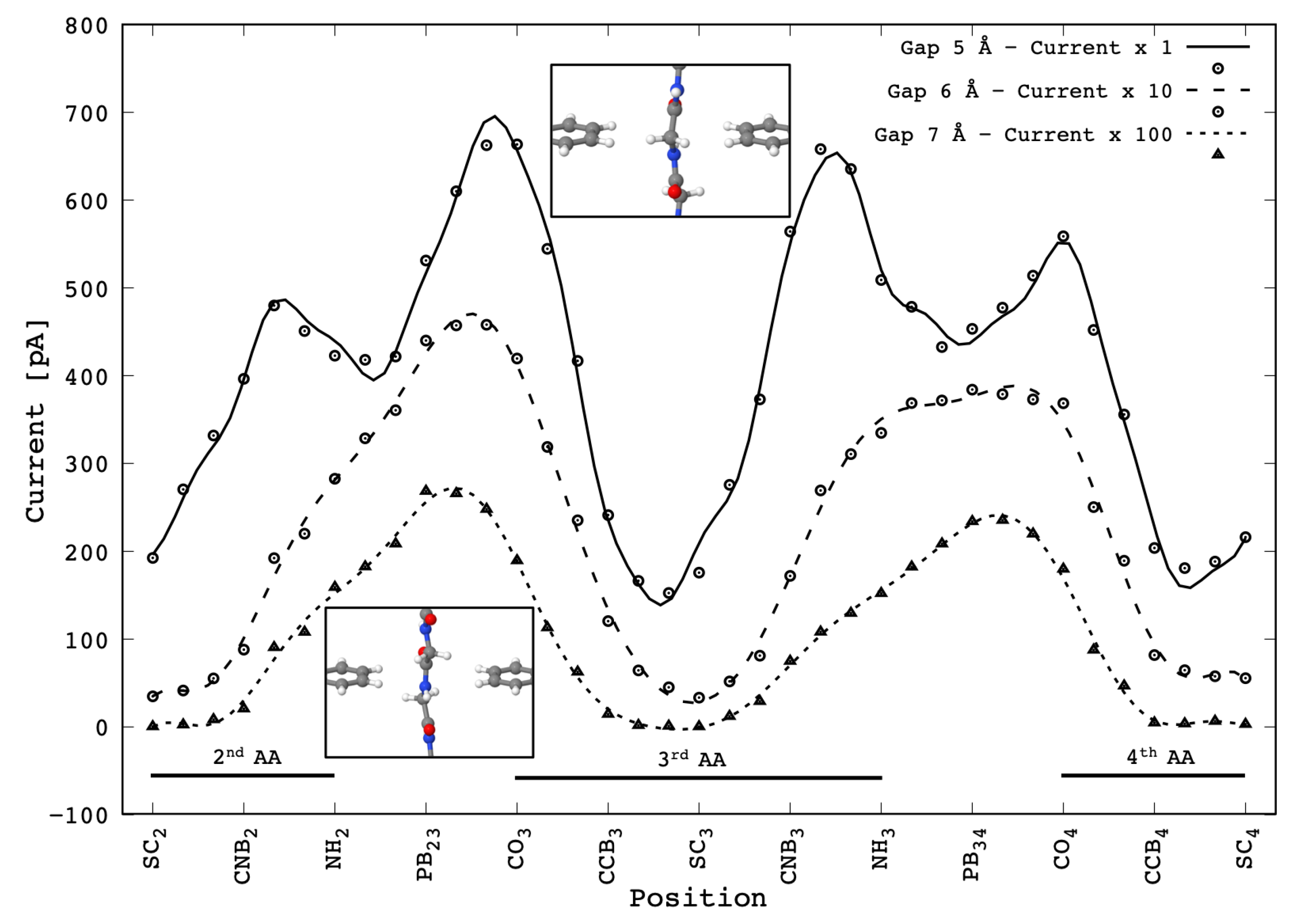
Figure 4 are reported the current signals calculated for the translocating Gly peptide across the gap with different widths. Each value of the calculated signal have been obtained in quasi-static conditions, that is an idealized quasi-stationary translocation dynamics where the atoms have been relaxed at
K at each translocation stage as described in
Section 2. In the present case we have improved the method employed to obtain the current signal point by point with respect to the recent data published elsewhere [
4]: the current values calculated for the positions between two adjacent relaxed configurations were averaged from the ones obtained by a rigid translation of the peptide from the adjacent relaxed configurations.
The reported curves show that the current signal decreases, as expected, by about one order of magnitude with the gap-size increase by 1 Å. Then the maximum current measured decreases from the order of magnitude of ≈1 nA to ≈10 pA. It should be stressed that in any case the current levels predicted are well within the range of measurable currents. The signal measured for the 5 Å gap is in good agreement with that reported elsewhere [
4], which was obtained with a coarser sampling grid—the two peaks signal corresponding to each PB during the translocation is basically the same except for the peak height ratio of the second PB which is probably due to the thermal fluctuation during the SMD. We remind that the minima occurring when the Gly side chains (or better the
group that includes the
-carbon and the hydrogen side chain) are in the middle of the gap (
,
and
configurations) are fingerprints of the PB being contributed by just the
groups involved in two adjacent PBs [
4].
What is interesting is the change of the signal shape as the gap size is increased—in these cases the two peaks features are lost and just one broad structured peak per PB is evidenced. We remind that the double peak feature found in the 5 Å gap case is due to the coupling of the upper and lower side chains in correspondence with the and groups in the middle of the gap.
It is important to show that the calculated signal is obtained from a completely de-naturated peptide being characterized by its zig-zag primary structure only and no secondary structure. Therefore the current signal in
Figure 4 does not apply in the case of peptides or proteins organized in a secondary structure such as
-helix or
-sheet—in these cases, the situation would be completely different and the atomistic resolution and amino-acid sequencing is unlikely with the present device setup.
For a better comprehension of the current signals observed, the transmission functions of the system for the
and
configurations have been analyzed in the case of the 5 Å and 7 Å wide gaps and are shown in
Figure 5. Here both the configurations show the same overall behavior—the contributions to the current are mainly due to the states in the energy range
. This rise corresponds to the energy shift of the pseudo-
HOMO band of the left lead up to the same energy of the right lead pseudo-
LUMO band [
4]. Furthermore, the channel decomposition of the transmission matrix evidences the presence of just one transmission channel for all the configurations here considered with no exception. The disappearance of the characteristic double peak is related to the drop of the
transmission function peak in the 7 Å wide gap case causing an inversion of the peak hierarchy with respect to the same configuration in the 5 Å wide gap case. The same, but at a lesser extent, occurs also for the 6 Å wide gap (not reported).
Bond current formulation [
30,
31,
32] gives the access to the knowledge on the atomic sites that play important roles in the transport phenomena. To study the current flows, each section of the peptide chain, and each amino-acid as well, has been ideally decomposed into chemically meaningful atomic groups, namely the
and the
groups involved in the PBs, the side chain and the
chemical group that includes the C-
carbon [
4]. In the Gly case, the side chain and
group are grouped together into the
group. Then we calculated the current due to the electrons injected from the left lead (that is at a negative bias) into the chemical groups of interest depending on the configuration chosen. The calculated injected local currents, grouped in chemical groups, are reported in
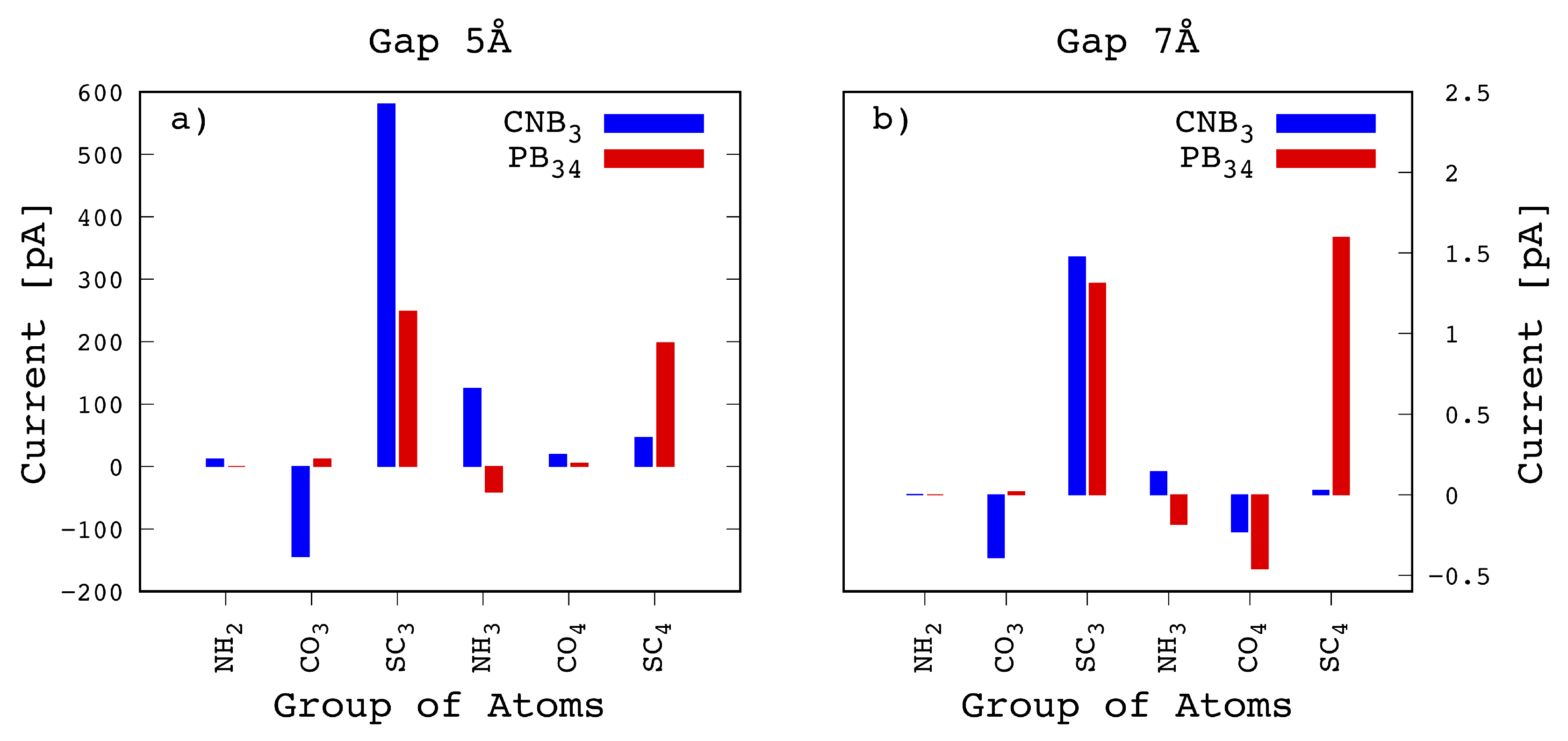
Figure 6. Here we have considered the two different configurations already considered in
Figure 5, namely
and
, being the ones corresponding to the double peak signal in the 5 Å wide gap device. From
Figure 6a it emerges that the main contribution to the first peak comes from from
with a very intense peak of 580 pA, which is larger than the sum of the two main contributions from the
and
(respectively of 248 and 198 pA) calculated for the
configuration. This is the reason why for the 5 Å gap the tunneling current is characterized by the double peak feature. In
Figure 6b the same configurations is reported for the case of the 7 Å wide gap. In this case we see that the
contribution to the current drops down to similar values as the
and
ones for the
configuration. Moreover we also see that the
atomic contribution to the transmission, that is minoritary but not negligible in the
case for the 5 Å wide gap, is largely reduced for the 7 Å wide gap. As a consequence the double peak feature disappears as already evidenced in
Figure 4.
The reasons behind this behavior can be understood by looking at the projected non-equiilibrium density of states. In
Figure 7 are reported the non equilibrium density of states projected onto the states belonging to the nearby side chains of the
and
configurations for the 5 Å (
Figure 7a) and 7 Å (
Figure 7b) gap cases. The right hand piece of the PDOS curves is related to the left spectral density matrix that accounts for the electron injection from the left lead into the central region; as we can see, the PDOS on the
and
groups keep the same shape in both the cases whatever the gap size. However concerning the intensity, while for
we just observe an almost equal intensity reduction for
and
with the gap size, in the
case the PDOS hierarchy reverses and the
contribution drops well below the
one indicating a poor injection from the left lead across
that was the major contribution for the
case in the 5 Å gap. This indicates a poor superposition of the orbitals of
with the pseudo-
and pseudo-
GNR orbitals that degrades as soon as the gap size increases.