Gas Transport in Mixed Matrix Membranes: Two Methods for Time Lag Determination
Abstract
1. Introduction
2. Materials and Methods
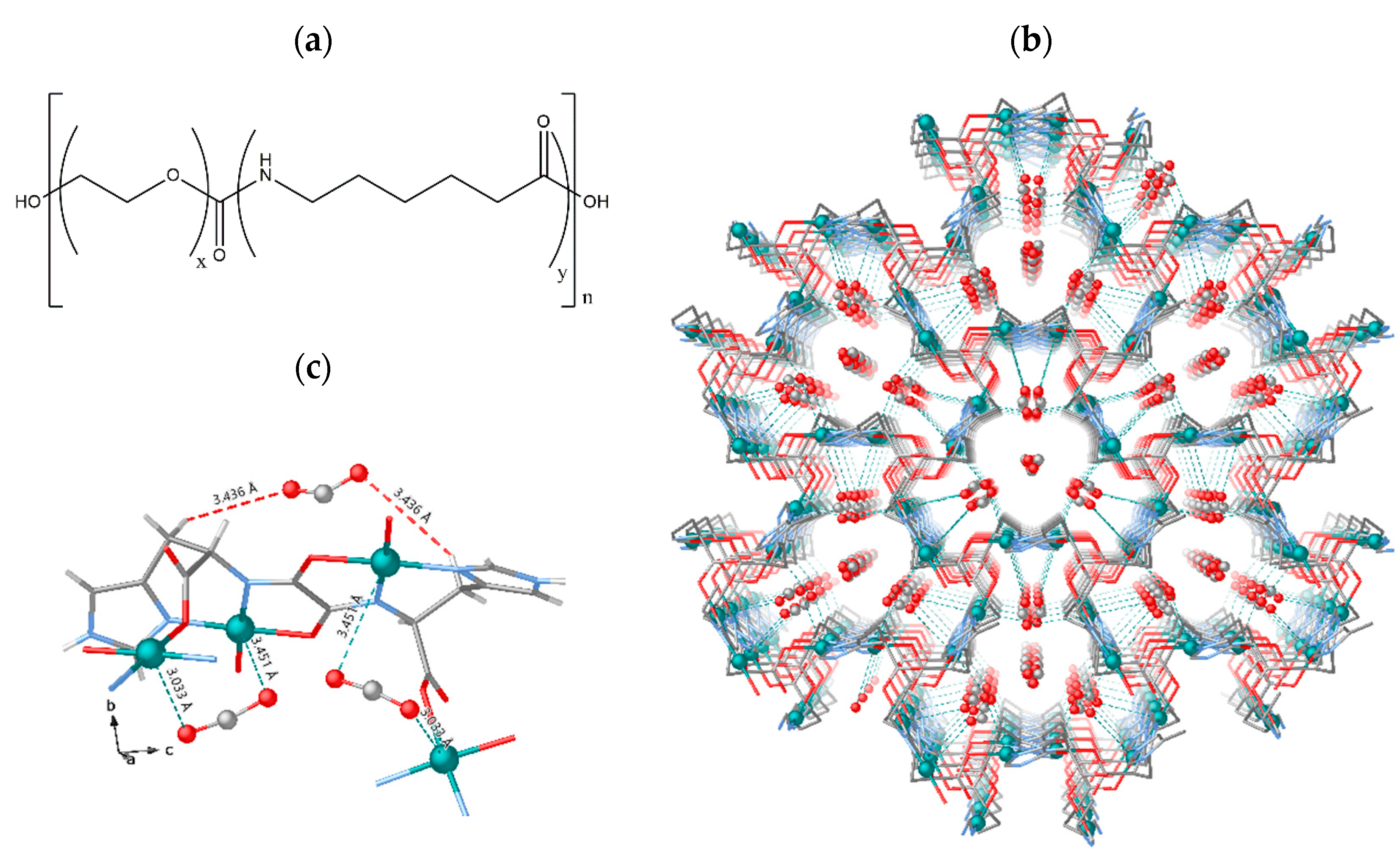
2.1. Materials and Membrane Preparation
2.2. Gas permeation Tests
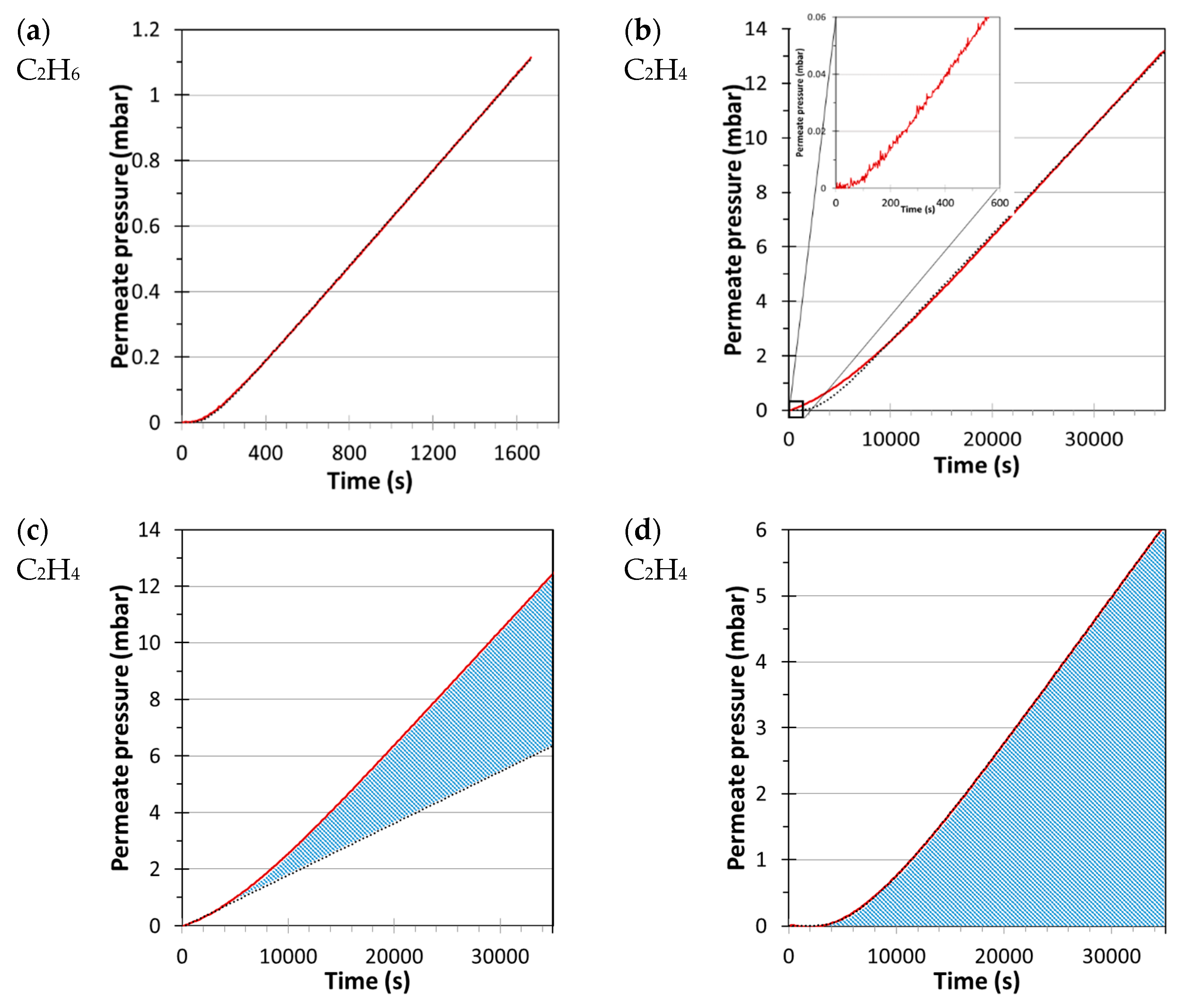
2.2.1. Data Analysis by the Tangent Method for Both Instruments
2.2.2. Fitting Method for a Constant Volume/Pressure Increase Instrument
2.2.3. Fitting Method for a Variable Volume/Constant Pressure Instrument
3. Results and Discussion
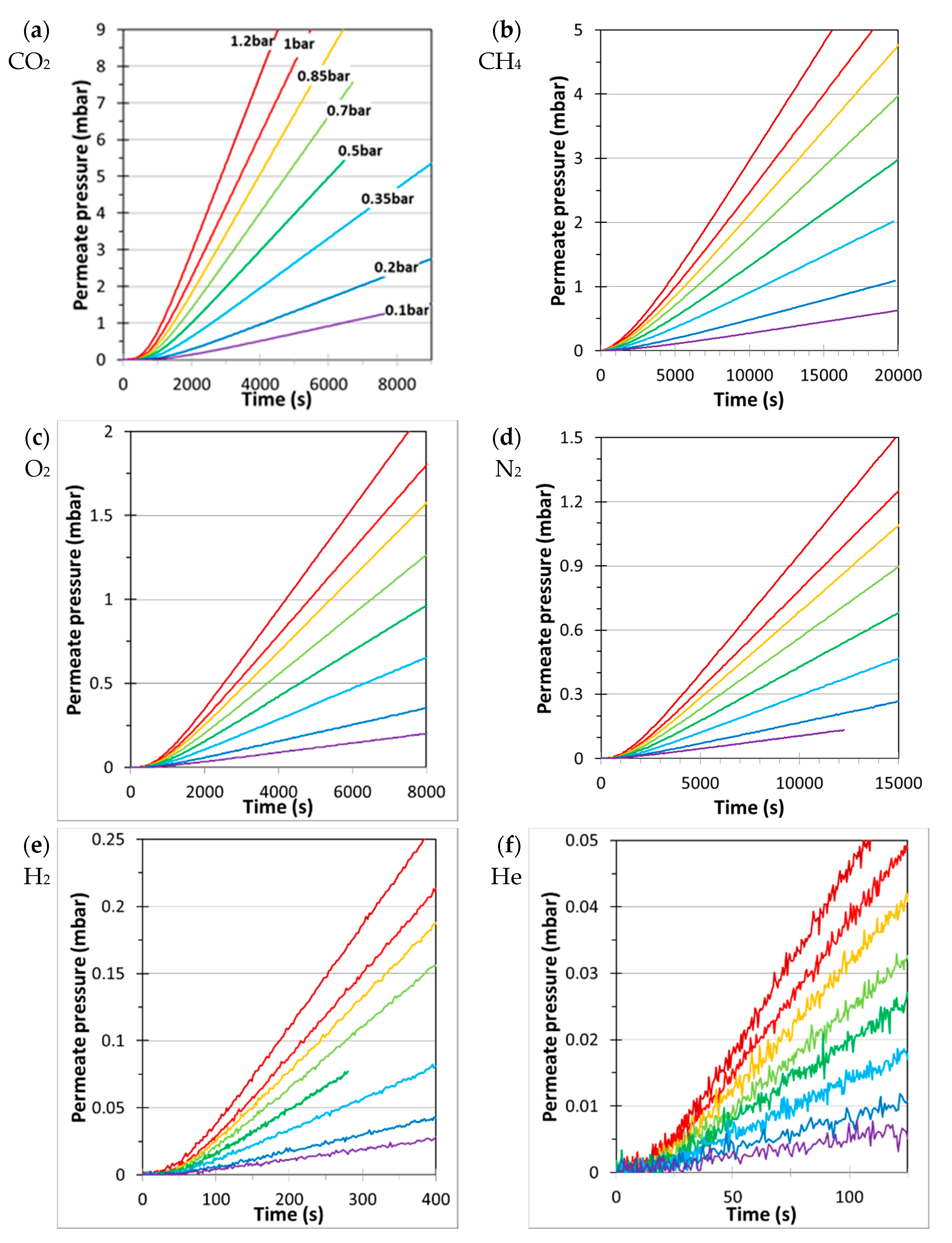
3.1. Single Gas Transport
3.2. Mixed Gas Transport
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Tangent Method | Fitting Method | Difference % (Fitting-Tangent) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gas | pFeed | P | Θ | D | S | P | Θ | D | S | P | Θ | D | S |
| O2 | 1200 | 3.10 | 888 | 4.22 | 0.551 | 3.09 | 861 | 4.36 | 0.53 | −0.48 | −3.10 | 3.20 | −3.57 |
| 1000 | 3.11 | 893 | 4.20 | 0.554 | 3.10 | 878 | 4.27 | 0.54 | −0.31 | −1.62 | 1.65 | −1.93 | |
| 850 | 3.11 | 892 | 4.20 | 0.555 | 3.10 | 878 | 4.27 | 0.54 | −0.28 | −1.62 | 1.65 | −1.90 | |
| 680 | 3.12 | 893 | 4.20 | 0.557 | 3.11 | 875 | 4.29 | 0.54 | −0.35 | −2.01 | 2.06 | −2.35 | |
| 520 | 3.14 | 900 | 4.17 | 0.565 | 3.12 | 871 | 4.31 | 0.54 | −0.40 | −3.20 | 3.31 | −3.59 | |
| 350 | 3.17 | 881 | 4.25 | 0.558 | 3.15 | 855 | 4.39 | 0.54 | −0.40 | −3.00 | 3.09 | −3.39 | |
| 180 | 3.24 | 851 | 4.41 | 0.552 | 3.23 | 822 | 4.56 | 0.53 | −0.34 | −3.42 | 3.55 | −3.75 | |
| 100 | 3.36 | 838 | 4.47 | 0.563 | 3.52 | 788 | 4.76 | 0.55 | 4.61 | −5.96 | 6.34 | −1.63 | |
| N2 | 1200 | 1.16 | 1514 | 2.48 | 0.351 | 1.15 | 1449 | 2.59 | 0.33 | −0.51 | −4.27 | 4.46 | −4.75 |
| 1000 | 1.15 | 1533 | 2.45 | 0.353 | 1.15 | 1496 | 2.51 | 0.34 | −0.34 | −2.46 | 2.52 | −2.79 | |
| 850 | 1.16 | 1542 | 2.43 | 0.356 | 1.15 | 1494 | 2.51 | 0.34 | −0.39 | −3.10 | 3.20 | −3.48 | |
| 680 | 1.16 | 1549 | 2.42 | 0.359 | 1.15 | 1487 | 2.52 | 0.34 | −0.43 | −4.06 | 4.23 | −4.47 | |
| 520 | 1.17 | 1556 | 2.41 | 0.365 | 1.17 | 1483 | 2.53 | 0.35 | −0.53 | −4.67 | 4.90 | −5.18 | |
| 350 | 1.20 | 1554 | 2.41 | 0.372 | 1.19 | 1454 | 2.58 | 0.35 | −0.67 | −6.45 | 6.90 | −7.08 | |
| 180 | 1.29 | 1554 | 2.41 | 0.400 | 1.27 | 1364 | 2.75 | 0.35 | −1.05 | −12.3 | 14.0 | −13.2 | |
| 100 | 1.48 | 1258 | 2.98 | 0.373 | 1.45 | 1072 | 3.50 | 0.31 | −2.34 | −14.8 | 17.3 | −16.8 | |
| CH4 | 1200 | 3.79 | 1924 | 1.95 | 1.46 | 3.71 | 1654 | 2.27 | 1.23 | −2.11 | −14.0 | 16.3 | −15.8 |
| 1000 | 3.80 | 1972 | 1.90 | 1.50 | 3.72 | 1698 | 2.21 | 1.26 | −2.18 | −13.9 | 16.1 | −15.8 | |
| 850 | 3.80 | 1998 | 1.88 | 1.52 | 3.75 | 1796 | 2.09 | 1.35 | −1.36 | −10.1 | 11.3 | −11.3 | |
| 680 | 3.81 | 2054 | 1.83 | 1.57 | 3.72 | 1737 | 2.16 | 1.29 | −2.58 | −15.5 | 18.3 | −17.6 | |
| 520 | 3.83 | 2088 | 1.80 | 1.60 | 3.77 | 1857 | 2.02 | 1.40 | −1.5 | −11.1 | 12.5 | −12.4 | |
| 350 | 3.88 | 2219 | 1.69 | 1.72 | 3.75 | 1793 | 2.09 | 1.35 | −3.36 | −19.2 | 23.8 | −21.9 | |
| 180 | 4.04 | 2352 | 1.59 | 1.90 | 3.88 | 1869 | 2.01 | 1.45 | −3.84 | −20.5 | 25.8 | −23.6 | |
| 100 | 4.20 | 2366 | 1.59 | 1.99 | 4.12 | 2064 | 1.82 | 1.70 | −1.94 | −12.8 | 14.6 | −14.5 | |
| H2 | 1200 | 7.73 | 56.8 | 66.0 | 0.088 | 7.71 | 53.9 | 69.6 | 0.083 | −0.24 | −5.06 | 5.33 | −5.28 |
| 1000 | 7.73 | 58.6 | 63.9 | 0.091 | 7.72 | 58.1 | 64.5 | 0.09 | −0.09 | −0.91 | 0.92 | −1.00 | |
| 850 | 7.75 | 59.7 | 62.8 | 0.093 | 7.74 | 58.8 | 63.8 | 0.091 | −0.18 | −1.52 | 1.55 | −1.70 | |
| 680 | 7.76 | 61.1 | 61.3 | 0.095 | 7.75 | 59.4 | 63.1 | 0.092 | −0.18 | −2.82 | 2.9 | −2.99 | |
| 520 | 7.77 | 60.7 | 61.8 | 0.094 | 7.72 | 58.1 | 64.5 | 0.09 | −0.60 | −4.25 | 4.44 | −4.83 | |
| 350 | 7.80 | 60.5 | 61.9 | 0.094 | 7.75 | 57.1 | 65.7 | 0.089 | −0.63 | −5.67 | 6.01 | −6.26 | |
| 180 | 7.87 | 61.8 | 60.7 | 0.097 | 7.83 | 57.5 | 65.2 | 0.09 | −0.50 | −6.91 | 7.42 | −7.38 | |
| 100 | 8.30 | 57.3 | 65.5 | 0.095 | 8.27 | 51.5 | 72.9 | 0.085 | −0.40 | −10.2 | 11.3 | −10.5 | |
| He | 1200 | 5.27 | 18.7 | 200 | 0.020 | 5.21 | 18.6 | 201 | 0.019 | −1.19 | −0.46 | 0.46 | −1.64 |
| 1000 | 5.29 | 18.9 | 198 | 0.020 | 5.22 | 18.8 | 200 | 0.02 | −1.42 | −0.83 | 0.83 | −2.24 | |
| 850 | 5.27 | 18.6 | 202 | 0.020 | 5.26 | 19.3 | 195 | 0.02 | −0.14 | 3.64 | −3.52 | 3.50 | |
| 680 | 5.11 | 19.7 | 190 | 0.020 | 5.14 | 20.3 | 185 | 0.021 | 0.56 | 2.81 | −2.73 | 3.39 | |
| 520 | 5.18 | 17.5 | 214 | 0.018 | 5.34 | 19.8 | 190 | 0.021 | 2.98 | 12. 7 | −11.2 | 16.0 | |
| 350 | 5.57 | 19.7 | 190 | 0.022 | 5.46 | 18.3 | 205 | 0.02 | −2.05 | −7.03 | 7.56 | −8.94 | |
| 180 | 5.49 | 19.7 | 191 | 0.022 | 5.63 | 18.7 | 200 | 0.021 | 2.61 | −4.87 | 5.11 | −2.38 | |
| 100 | 6.33 | 19.0 | 197 | 0.024 | 6.17 | 20.0 | 188 | 0.025 | −2.56 | 4.94 | −4.71 | 2.26 | |
| CO2 | 1200 | 65.8 | 784 | 4.78 | 10.3 | 66.0 | 801 | 4.68 | 10.6 | 0.38 | 2.22 | −2.18 | 2.61 |
| 1000 | 65.3 | 838 | 4.48 | 10.9 | 65.5 | 870 | 4.31 | 11.4 | 0.27 | 3.88 | −3.74 | 4.16 | |
| 850 | 65.3 | 891 | 4.21 | 11.6 | 65.4 | 917 | 4.09 | 12.0 | 0.13 | 2.93 | −2.85 | 3.07 | |
| 680 | 65.1 | 944 | 3.97 | 12.3 | 65.2 | 973 | 3.85 | 12.7 | 0.22 | 3.16 | −3.06 | 3.39 | |
| 520 | 65.1 | 1023 | 3.66 | 13.3 | 65.2 | 1048 | 3.58 | 13.7 | 0.13 | 2.45 | −2.39 | 2.58 | |
| 350 | 65.1 | 1123 | 3.34 | 14.6 | 64.7 | 1142 | 3.28 | 14.8 | −0.49 | 1.65 | −1.63 | 1.15 | |
| 180 | 64.8 | 1308 | 2.87 | 16.9 | 64.5 | 1325 | 2.83 | 17.1 | −0.41 | 1.32 | −1.31 | 0.91 | |
| 100 | 64.6 | 1513 | 2.48 | 19.5 | 64.0 | 1515 | 2.48 | 19.4 | −0.83 | 0.10 | −0.10 | −0.73 | |
| C2H6 | 1000 | 9.15 | 154 | 24.4 | 0.28 | 9.07 | 142 | 26.3 | 0.26 | −0.87 | −7.79 | 7.79 | −7.14 |
Appendix B
 ), N2 (
), N2 ( ), O2 (
), O2 ( ), CH4 (
), CH4 ( ), H2 (
), H2 ( ), He (
), He ( ).
).
 ), N2 (
), N2 ( ), O2 (
), O2 ( ), CH4 (
), CH4 ( ), H2 (
), H2 ( ), He (
), He ( ).
).
References
- Park, H.B.; Kamcev, J.; Robeson, L.M.; Elimelech, M.; Freeman, B.D. Maximizing the right stuff: The trade-off between membrane permeability and selectivity. Science (80-) 2017, 356, eaab0530. [Google Scholar] [CrossRef] [PubMed]
- Sholl, D.S.; Lively, R.P. Seven chemical separations to change the world. Nature 2016, 532, 435–437. [Google Scholar] [CrossRef]
- Galizia, M.; Chi, W.S.; Smith, Z.P.; Merkel, T.C.; Baker, R.W.; Freeman, B.D. 50th Anniversary Perspective: Polymers and Mixed Matrix Membranes for Gas and Vapor Separation: A Review and Prospective Opportunities. Macromolecules 2017, 50, 7809–7843. [Google Scholar] [CrossRef]
- Esposito, E.; Dellamuzia, L.; Moretti, U.; Fuoco, A.; Giorno, L.; Jansen, J.C. Simultaneous production of biomethane and food grade CO2 from biogas: An industrial case study. Energy Environ. Sci. 2019, 12, 281–289. [Google Scholar] [CrossRef]
- Comesaña-Gándara, B.; Chen, J.; Bezzu, C.G.; Carta, M.; Rose, I.; Ferrari, M.C.; Esposito, E.; Fuoco, A.; Jansen, J.C.; McKeown, N.B. Redefining the Robeson upper bounds for CO2 /CH4 and CO2 /N2 separations using a series of ultrapermeable benzotriptycene-based polymers of intrinsic microporosity. Energy Environ. Sci. 2019, 12, 2733–2740. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Memb. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of separation factor versus permeability for polymeric membranes. J. Memb. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Chuah, C.Y.; Goh, K.; Yang, Y.; Gong, H.; Li, W.; Enis Karahan, H.D.; Guiver, M.; Wang, R.; Bae, T.H. Harnessing Filler Materials for Enhancing Biogas Separation Membranes. Chem. Rev. 2018, 118, 8655–8769. [Google Scholar] [CrossRef]
- Sabetghadam, A.; Seoane, B.; Keskin, D.; Duim, N.; Rodenas, T.; Shahid, S.; Sorribas, S.; Le Guillouzer, C.; Clet, G.; Tellez, C.; et al. Metal Organic Framework Crystals in Mixed-Matrix Membranes: Impact of the Filler Morphology on the Gas Separation Performance. Adv. Funct. Mater. 2016, 26, 3154–3163. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Bavykina, A.V.; Chu, L.; Shan, M.; Sabetghadam, A.; Miro, H.; Kapteijn, F.; Gascon, J. Molecular-Scale Hybrid Membranes Derived from Metal-Organic Polyhedra for Gas Separation. ACS Appl. Mater. Interfaces 2018, 10, 21381–21389. [Google Scholar] [CrossRef]
- Ghalei, B.; Sakurai, K.; Kinoshita, Y.; Wakimoto, K.; Isfahani, A.P.; Song, Q.; Doitomi, K.; Furukawa, S.; Hirao, H.; Kusuda, H.; et al. Enhanced selectivity in mixed matrix membranes for CO2 capture through efficient dispersion of amine-functionalized MOF nanoparticles. Nat. Energy 2017, 2, 17086. [Google Scholar] [CrossRef]
- Nagaraju, D.; Bhagat, D.G.; Banerjee, R.; Kharul, U.K. In Situ growth of metal-organic frameworks on a porous ultrafiltration membrane for gas separation. J. Mater. Chem. A 2013, 1, 8828–8835. [Google Scholar] [CrossRef]
- Fuoco, A.; Khdhayyer, R.M.; Attfield, P.M.; Esposito, E.; Jansen, C.J.; Budd, M.P. Synthesis and Transport Properties of Novel MOF/PIM-1/MOF Sandwich Membranes for Gas Separation. Membranes 2017, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, R.; Koros, W.J. Mixed matrix membrane materials with glassy polymers. Part 1. Polym. Eng. Sci. 2002, 42, 1420–1431. [Google Scholar] [CrossRef]
- Petropoulos, J.H. A comparative study of approaches applied to the permeability of binary composite polymeric materials. J. Polym. Sci. Polym. Phys. Ed. 1985, 23, 1309–1324. [Google Scholar] [CrossRef]
- Zimmerman, C.M.; Singh, A.; Koros, W.J. Tailoring mixed matrix composite membranes for gas separations. J. Memb. Sci. 1997, 137, 145–154. [Google Scholar] [CrossRef]
- Shimekit, B.; Mukhtar, H.; Murugesan, T. Prediction of the relative permeability of gases in mixed matrix membranes. J. Memb. Sci. 2011, 373, 152–159. [Google Scholar] [CrossRef]
- Vinh-Thang, H.; Kaliaguine, S. Predictive models for mixed-matrix membrane performance: A review. Chem. Rev. 2013, 113, 4980–5028. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780511709333. [Google Scholar]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Memb. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The Solution-Diffusion Model: A Unified Approach to Membrane Permeation. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; John Wiley& Sons, Ltd.: Chichester, UK, 2006; pp. 159–189. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975; ISBN 0198533446. [Google Scholar]
- Daynes, H.A. The Process of Diffusion through a Rubber Membrane. Proc. R. Soc. A Math. Phys. Eng. Sci. 1920, 97, 286–307. [Google Scholar] [CrossRef]
- Amarantos, S.G.; Tsimillis, K.; Savvakis, C.; Petropoulos, J.H. Kinetic analysis of transient permeation curves. J. Memb. Sci. 1983, 13, 259–272. [Google Scholar] [CrossRef]
- Tsimillis, K.; Petropoulos, J.H. Experimental study of a simple anomalous diffusion system by time-lag and transient-state kinetic analysis. J. Phys. Chem. 1977, 81, 2185–2191. [Google Scholar] [CrossRef]
- Strzelewicz, A.; Grzywna, Z.J. On the permeation time lag for different transport equations by Frisch method. J. Memb. Sci. 2008, 322, 460–465. [Google Scholar] [CrossRef]
- Frisch, H.L. Anomalous Polymer-Penetrant Permeation. J. Chem. Phys. 1962, 37, 2408–2413. [Google Scholar] [CrossRef]
- Follain, N.; Valleton, J.M.; Lebrun, L.; Alexandre, B.; Schaetzel, P.; Metayer, M.; Marais, S. Simulation of kinetic curves in mass transfer phenomena for a concentration-dependent diffusion coefficient in polymer membranes. J. Memb. Sci. 2010, 349, 195–207. [Google Scholar] [CrossRef]
- Favre, E.; Morliere, N.; Roizard, D. Experimental evidence and implications of an imperfect upstream pressure step for the time-lag technique. J. Memb. Sci. 2002, 207, 59–72. [Google Scholar] [CrossRef]
- Beckman, I.N.; Shalygin, M.G.; Teplyakov, V.V. Particularities of Membrane Gas Separation Under Unsteady State Conditions. In Mass Transfer in Chemical Engineering Processes; Markoš, J., Ed.; InTech: Rijeka, Croatia, 2011; pp. 205–232. ISBN 978-953-307-619-5. [Google Scholar]
- Beckman, I.N.; Syrtsova, D.A.; Shalygin, M.G.; Kandasamy, P.; Teplyakov, V.V. Transmembrane gas transfer: Mathematics of diffusion and experimental practice. J. Memb. Sci. 2020, 601, 117737. [Google Scholar] [CrossRef]
- Shalygin, M.G.; Kozlova, A.A.; Syrtsova, D.A.; Markova, S.Y.; Ryabova, O.R.; Teplyakov, V.V. Diffusion Transport of Water and Methanol Vapors in Polyvinyltrimethylsilane. Membr. Membr. Technol. 2019, 1, 183–189. [Google Scholar] [CrossRef]
- Yasuda, H.; Rosengren, K. Isobaric measurement of gas permeability of polymers. J. Appl. Polym. Sci. 1970, 14, 2839–2877. [Google Scholar] [CrossRef]
- Fraga, S.C.; Monteleone, M.; Lanč, M.; Esposito, E.; Fuoco, A.; Giorno, L.; Pilnáček, K.; Friess, K.; Carta, M.; McKeown, N.B.; et al. A novel time lag method for the analysis of mixed gas diffusion in polymeric membranes by on-line mass spectrometry: Method development and validation. J. Memb. Sci. 2018, 561, 39–58. [Google Scholar] [CrossRef]
- Mon, M.; Ferrando-Soria, J.; Verdaguer, M.; Train, C.; Paillard, C.; Dkhil, B.; Versace, C.; Bruno, R.; Armentano, D.; Pardo, E. Postsynthetic Approach for the Rational Design of Chiral Ferroelectric Metal–Organic Frameworks. J. Am. Chem. Soc. 2017, 139, 8098–8101. [Google Scholar] [CrossRef] [PubMed]
- Mon, M.; Bruno, R.; Tiburcio, E.; Grau-Atienza, A.; Sepúlveda-Escribano, A.; Ramos-Fernandez, E.V.; Fuoco, A.; Esposito, E.; Monteleone, M.; Jansen, J.C.; et al. Efficient Gas Separation and Transport Mechanism in Rare Hemilabile Metal–Organic Framework. Chem. Mater. 2019, 31, 5856–5866. [Google Scholar] [CrossRef]
- Monteleone, M.; Esposito, E.; Fuoco, A.; Lanč, M.; Pilnáček, K.; Friess, K.; Bezzu, C.; Carta, M.; McKeown, N.; Jansen, J.C. A Novel Time Lag Method for the Analysis of Mixed Gas Diffusion in Polymeric Membranes by On-Line Mass Spectrometry: Pressure Dependence of Transport Parameters. Membranes (Basel) 2018, 8, 73. [Google Scholar] [CrossRef] [PubMed]
- Jansen, J.C.; Friess, K.; Drioli, E. Organic vapour transport in glassy perfluoropolymer membranes: A simple semi-quantitative approach to analyze clustering phenomena by time lag measurements. J. Memb. Sci. 2011, 367, 141–151. [Google Scholar] [CrossRef]
- Teplyakov, V.; Meares, P. Correlation aspects of the selective gas permeabilities of polymeric materials and membranes. Gas. Sep. Purif. 1990, 4, 66–74. [Google Scholar] [CrossRef]
- Esposito, E.; Bruno, R.; Monteleone, M.; Fuoco, A.; Ferrando Soria, J.; Pardo, E.; Armentano, D.; Jansen, J.C. Glassy PEEK-WC vs. Rubbery Pebax®1657 Polymers: Effect on the Gas Transport in CuNi-MOF Based Mixed Matrix Membranes. Appl. Sci. 2020, 10, 1310. [Google Scholar] [CrossRef]
- Longo, M.; De Santo, M.P.; Esposito, E.; Fuoco, A.; Monteleone, M.; Giorno, L.; Jansen, J.C. Force spectroscopy determination of Young’s modulus in mixed matrix membranes. Polymer (Guildf) 2018, 156, 22–29. [Google Scholar] [CrossRef]
- Paul, D.R. Effect of immobilizing adsorption on the diffusion time lag. J. Polym. Sci. Part A-2 Polym. Phys. 1969, 7, 1811–1818. [Google Scholar] [CrossRef]
- Grzywna, Z.; Podkowka, J. Effect of immobilizing adsorption on mass transport through polymer films. J. Memb. Sci. 1981, 8, 23–31. [Google Scholar] [CrossRef]
- Fuoco, A.; Rizzuto, C.; Tocci, E.; Monteleone, M.; Esposito, E.; Budd, P.M.; Carta, M.; Comesaña-Gándara, B.; McKeown, N.B.; Jansen, J.C. The origin of size-selective gas transport through polymers of intrinsic microporosity. J. Mater. Chem. A 2019, 7, 20121–20126. [Google Scholar] [CrossRef]



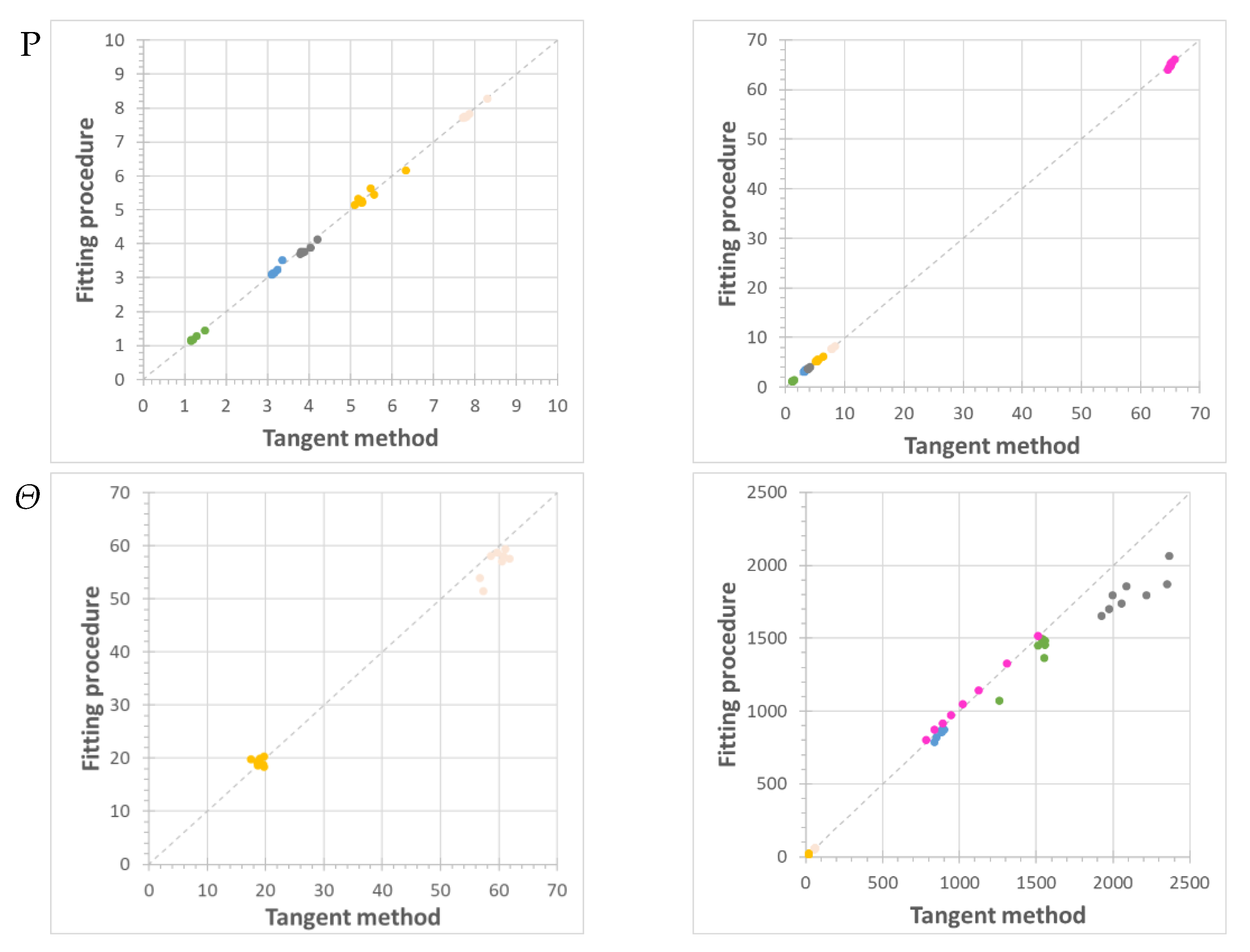
 ) and the Pebax®1657/CuII2(S,S)-hismox MMMs calculated via the tangent method (blue triangle,
) and the Pebax®1657/CuII2(S,S)-hismox MMMs calculated via the tangent method (blue triangle,  ) and the fitting procedure (filled circle,
) and the fitting procedure (filled circle,  ). Filled square symbols (
). Filled square symbols ( ) indicate the slow term, and open square symbols (
) indicate the slow term, and open square symbols ( ) indicate the fast term of the fit with two different effective diffusion coefficients.
) indicate the fast term of the fit with two different effective diffusion coefficients.
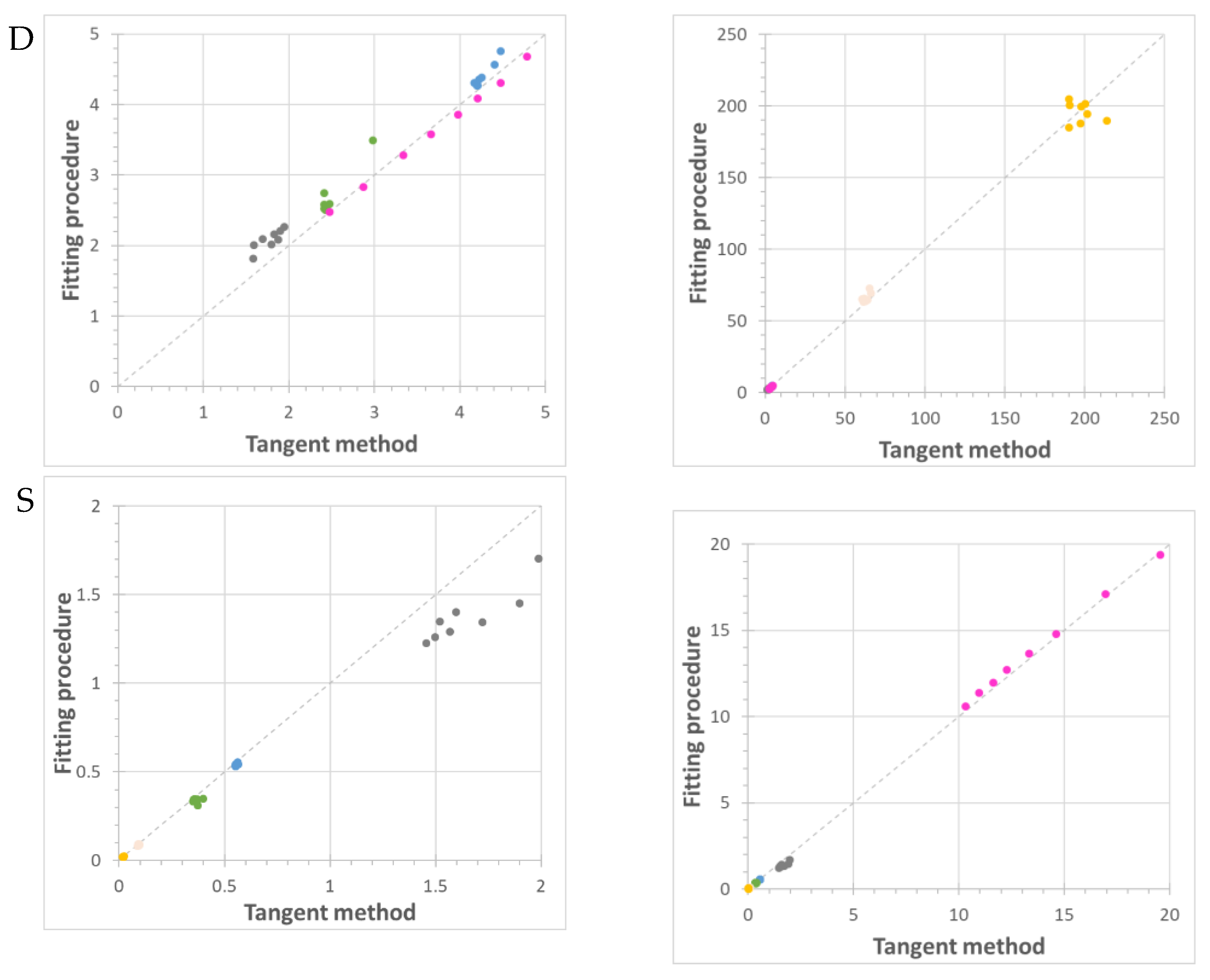
 ) and the Pebax®1657/CuII2(S,S)-hismox MMMs calculated via the tangent method (blue triangle,
) and the Pebax®1657/CuII2(S,S)-hismox MMMs calculated via the tangent method (blue triangle,  ) and the fitting procedure (filled circle,
) and the fitting procedure (filled circle,  ). Filled square symbols (
). Filled square symbols ( ) indicate the slow term, and open square symbols (
) indicate the slow term, and open square symbols ( ) indicate the fast term of the fit with two different effective diffusion coefficients.
) indicate the fast term of the fit with two different effective diffusion coefficients.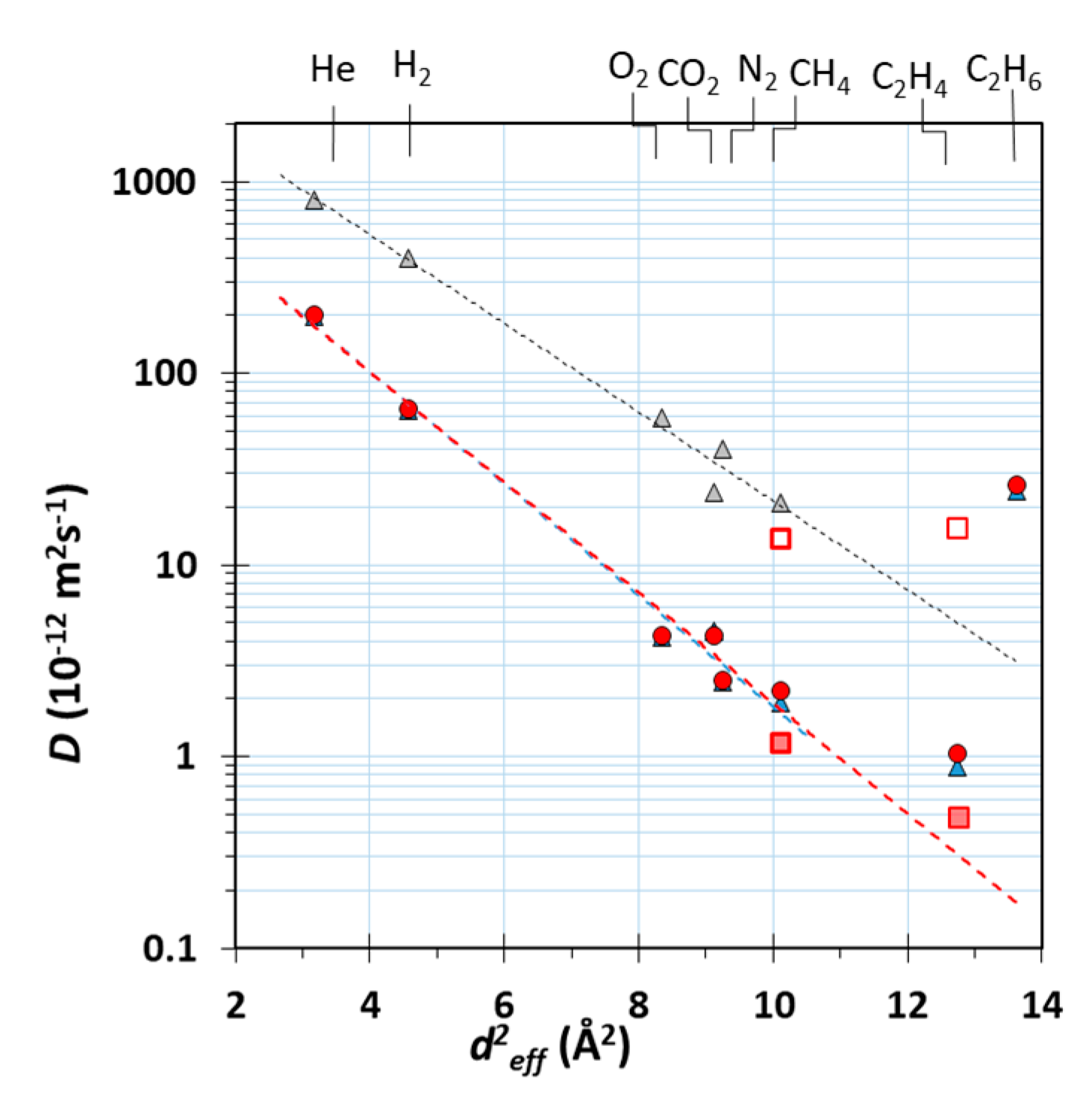
| Tangent Method | Fitting Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Gas | P | D | S | P1 | P2 | D1 | D2 | S1 | S2 |
| CH4 | 3.79 | 1.95 | 1.46 | 1.66 | 2.11 | 13.5 | 1.19 | 0.09 | 1.32 |
| C2H4 | 14.4 | 0.87 | 12.4 | 6.49 | 7.93 | 15.6 | 0.48 | 0.31 | 12.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuoco, A.; Monteleone, M.; Esposito, E.; Bruno, R.; Ferrando-Soria, J.; Pardo, E.; Armentano, D.; Jansen, J.C. Gas Transport in Mixed Matrix Membranes: Two Methods for Time Lag Determination. Computation 2020, 8, 28. https://doi.org/10.3390/computation8020028
Fuoco A, Monteleone M, Esposito E, Bruno R, Ferrando-Soria J, Pardo E, Armentano D, Jansen JC. Gas Transport in Mixed Matrix Membranes: Two Methods for Time Lag Determination. Computation. 2020; 8(2):28. https://doi.org/10.3390/computation8020028
Chicago/Turabian StyleFuoco, Alessio, Marcello Monteleone, Elisa Esposito, Rosaria Bruno, Jesús Ferrando-Soria, Emilio Pardo, Donatella Armentano, and Johannes Carolus Jansen. 2020. "Gas Transport in Mixed Matrix Membranes: Two Methods for Time Lag Determination" Computation 8, no. 2: 28. https://doi.org/10.3390/computation8020028
APA StyleFuoco, A., Monteleone, M., Esposito, E., Bruno, R., Ferrando-Soria, J., Pardo, E., Armentano, D., & Jansen, J. C. (2020). Gas Transport in Mixed Matrix Membranes: Two Methods for Time Lag Determination. Computation, 8(2), 28. https://doi.org/10.3390/computation8020028











