Underwater Optical Wireless Communications with Chromatic Dispersion and Time Jitter
Abstract
1. Introduction
2. Group Velocity Dispersion Estimation
3. Link Performance Estimation
4. Time Jitter and Attenuation
5. The Probability of Fade
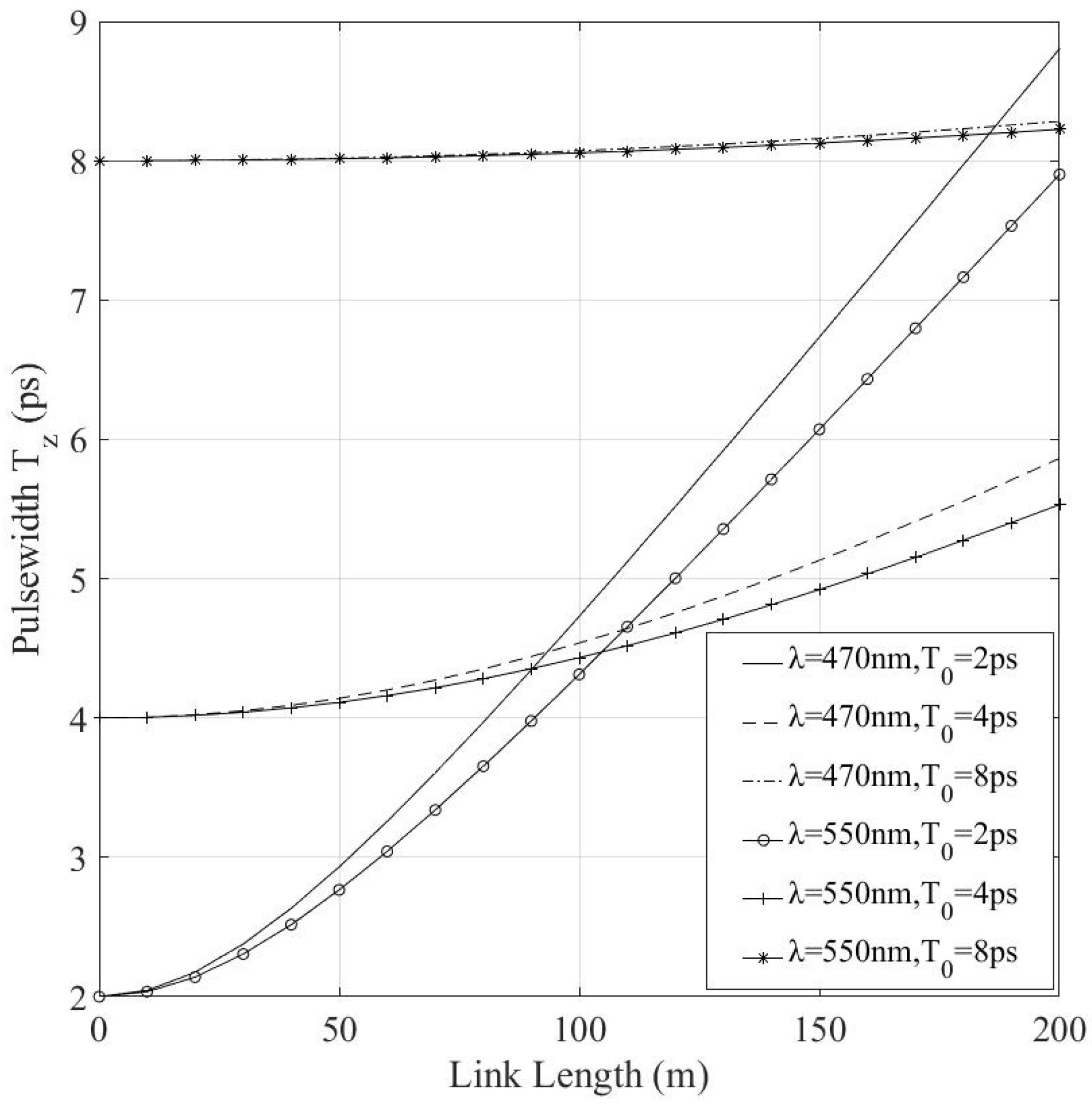
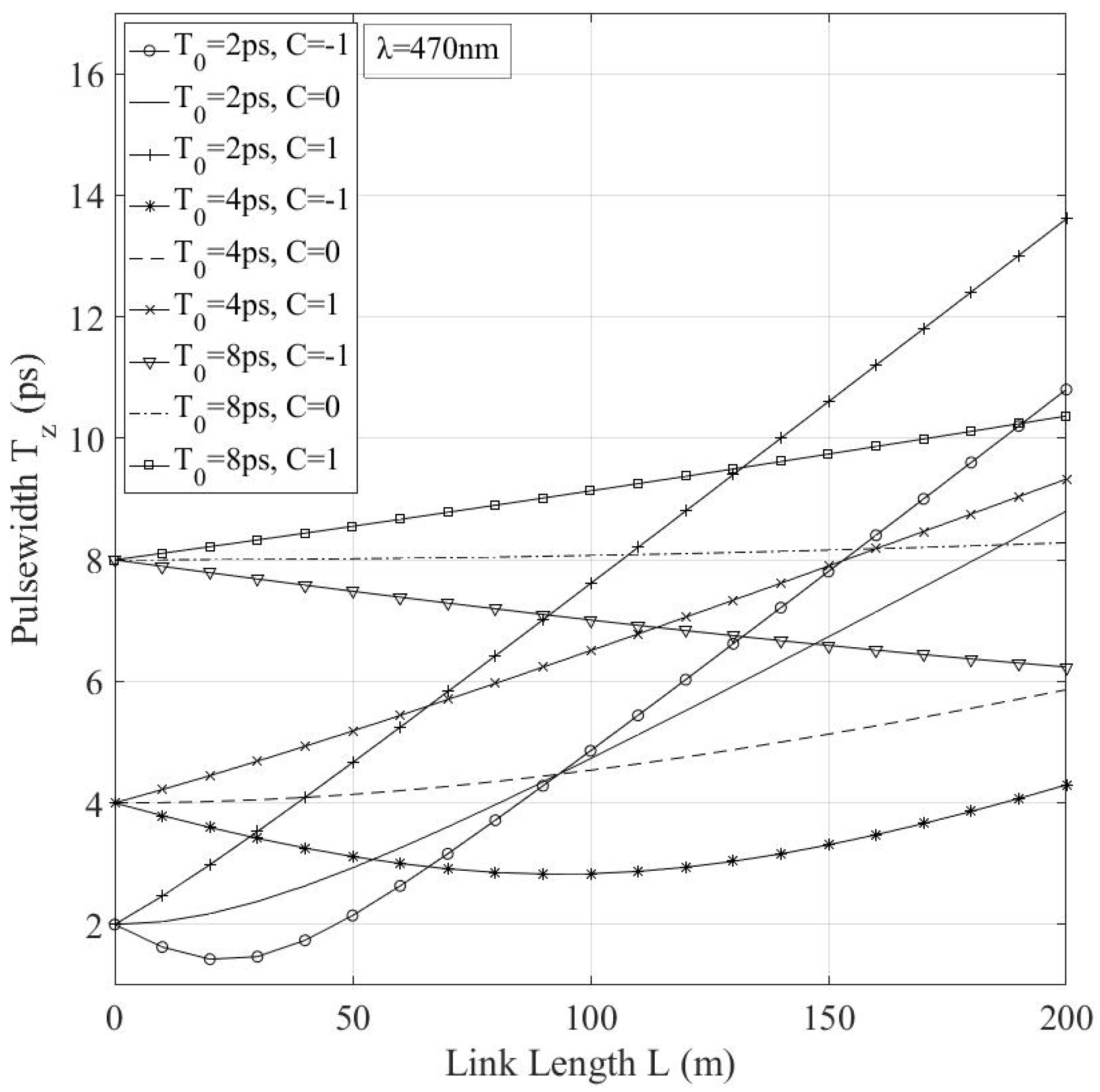
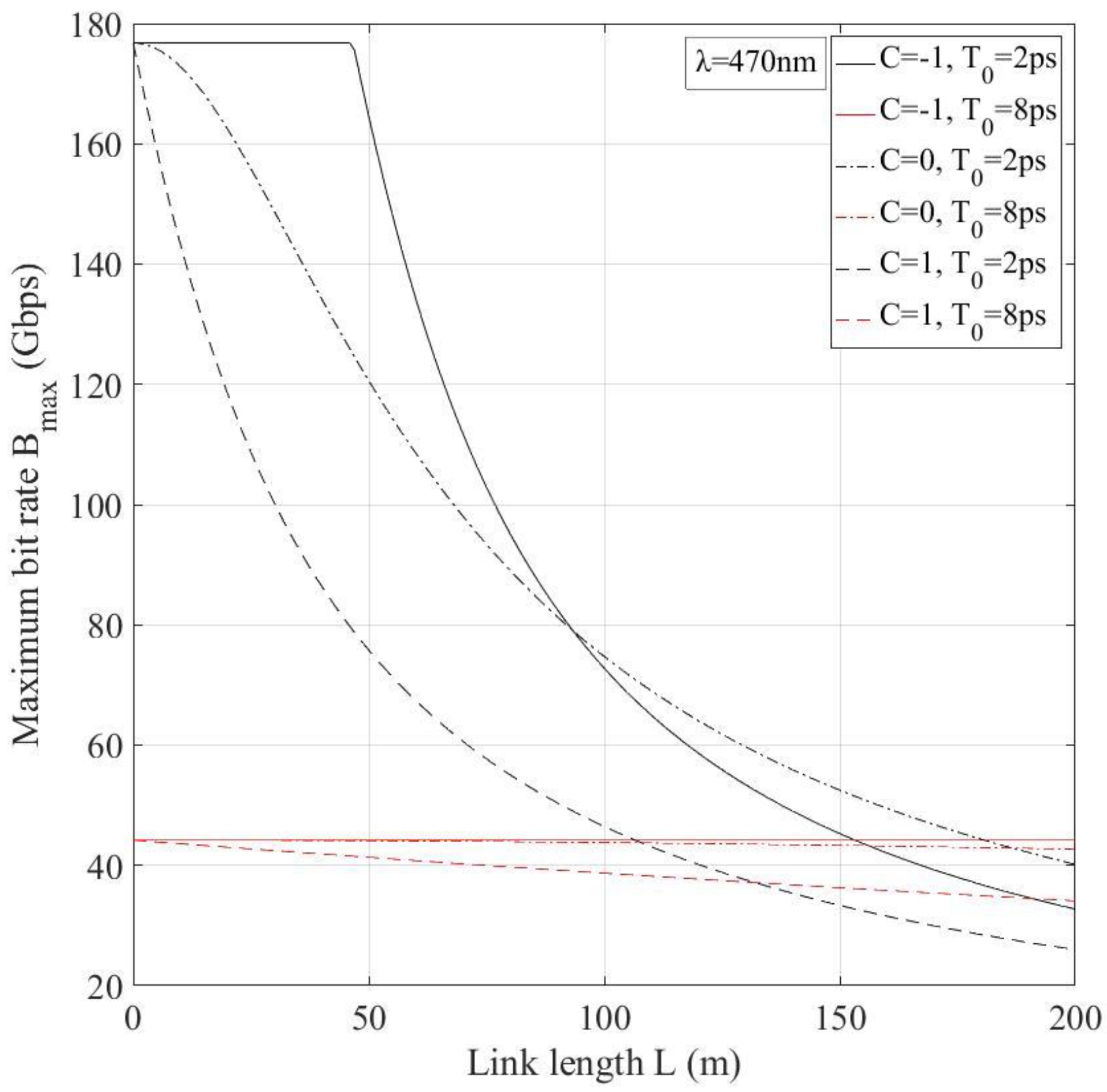
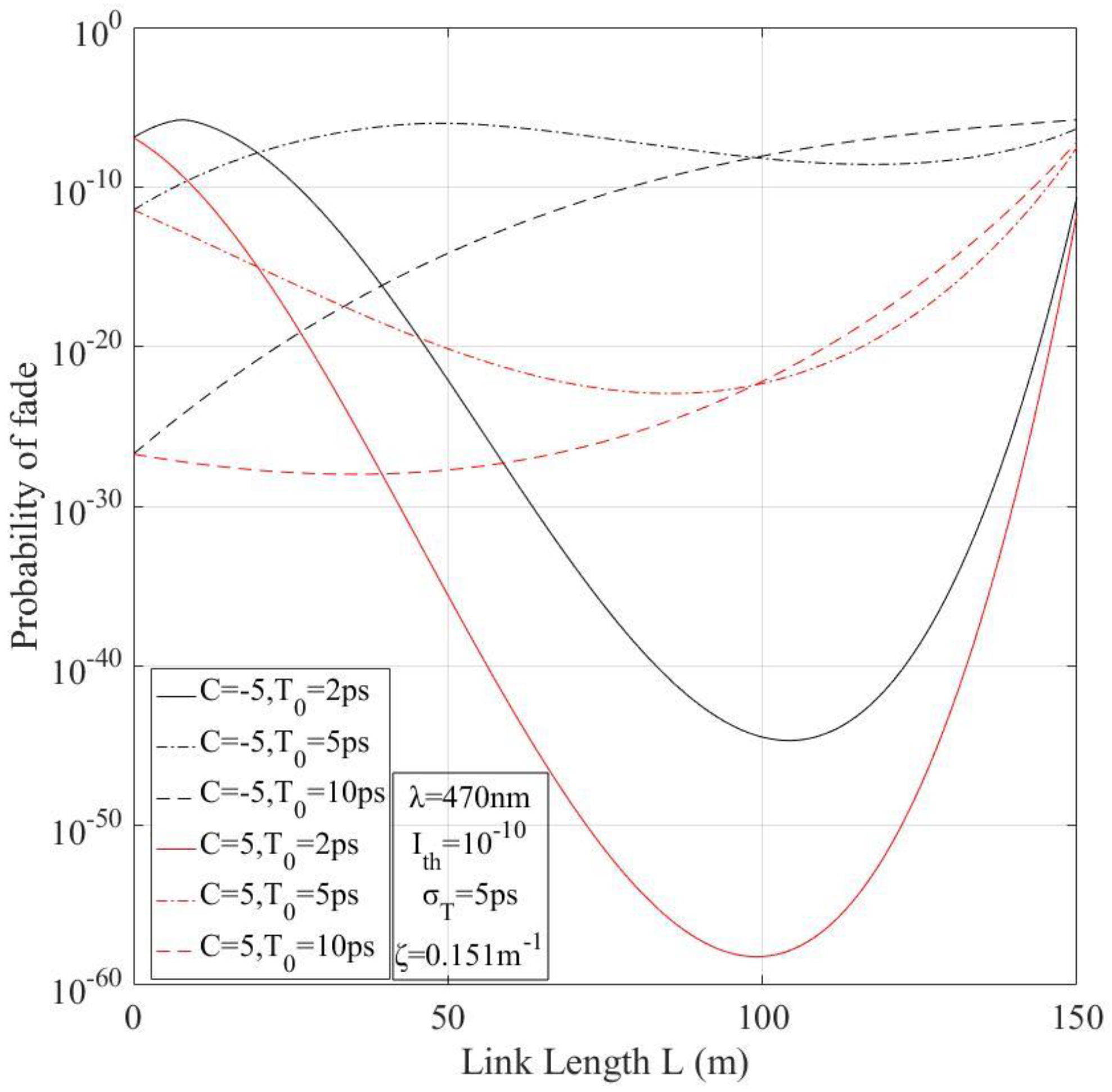
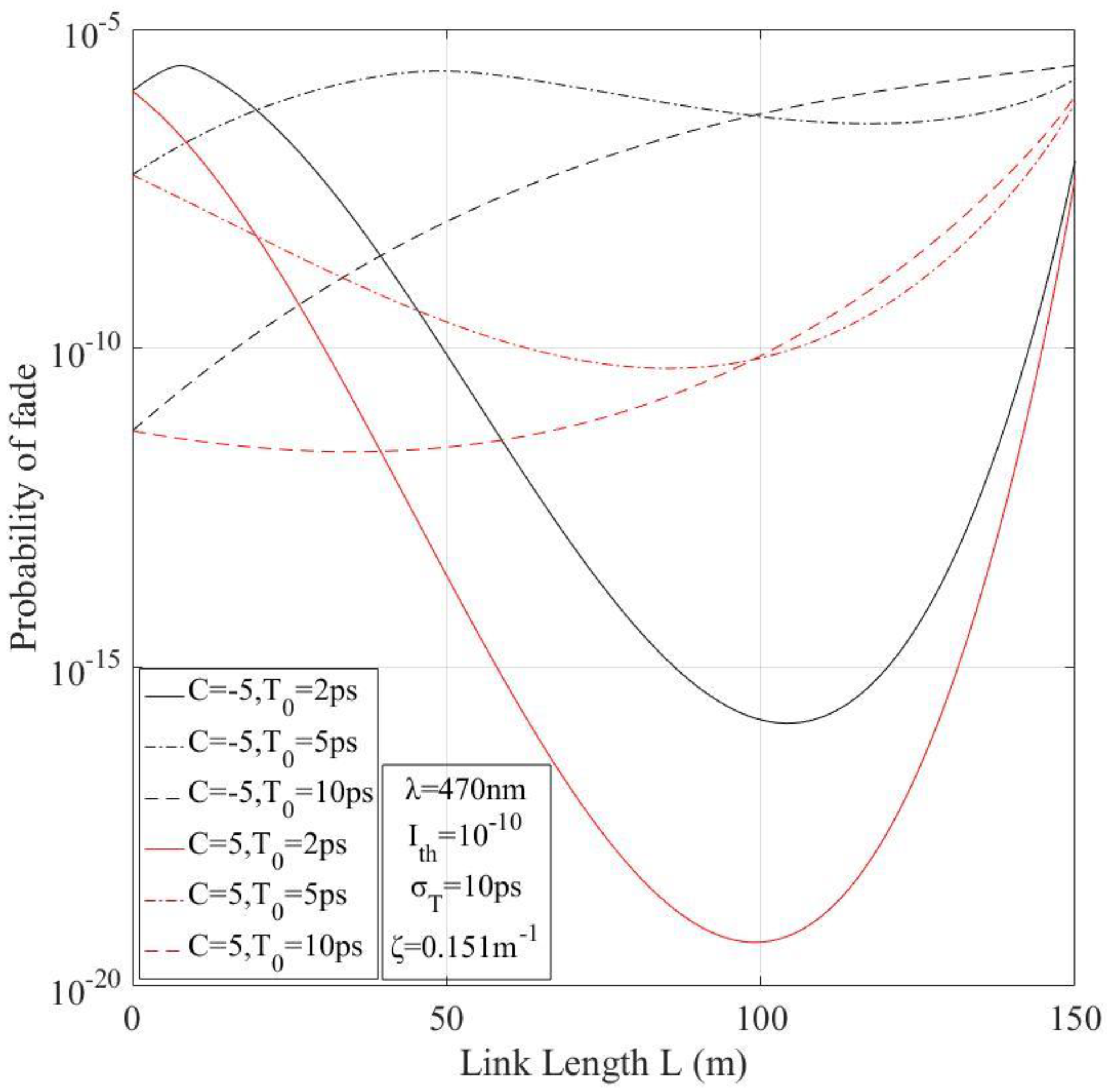
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Melodia, T.; Kulhandjian, H.; Kuo, L.-C.; Demirors, E. Advances in Underwater Acoustic Networking. In Mobile Ad Hoc Networking; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 804–852. [Google Scholar]
- Stojanovic, M.; Preisig, J. Underwater Acoustic Communication Channels: Propagation Models and Statistical Characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Challenges for efficient communication in underwater acoustic sensor networks. ACM SIGBED Rev. 2007, 1, 3–8. [Google Scholar] [CrossRef]
- Anguita, D.; Brizzolara, D.; Parodi, G. Prospects and Problems of Optical Diffuse Wireless Communication for Underwater Wireless Sensor Networks. In Wireless Sensor Networks: Application-Centric Design; IntechOpen: London, UK, 2010. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Underwater Optical Wireless Communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, S.; Cui, J. Prospects and Problems of Wireless Communication for Underwater Sensor Networks. Wirel. Commun. Mob. Comput. 2008, 8, 977–994. [Google Scholar]
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A Survey of Underwater Optical Wireless Communications. IEEE Commun. Surv. Tutor. 2017, 19, 204–238. [Google Scholar] [CrossRef]
- Saeed, N.; Celik, A.; Al-Naffouri, T.Y.; Alouini, M.-S. Underwater Optical Wireless Communications, Networking, and Localization: A Survey. Ad Hoc Netw. 2019, 94, 101935. [Google Scholar] [CrossRef]
- Haltrin, V.I. Chlorophyll-based model of seawater optical properties. Appl. Opt. 1999, 38, 6826–6832. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Cheng, J.; Wang, Z. On Integrated Stochastic Channel Model for Underwater Optical Wireless Communications. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Young, E.Y.S.; Bullock, A.M. Underwater-airborne laser communication system: Characterization of the channel. High-Power Lasers Appl. 2003, 4975, 146–157. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics, 3rd ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Crisp, J. Introduction to Fiber Optics, 2nd ed.; Newnes: Oxford, UK, 2005. [Google Scholar]
- Ramaswami, R.; Sivarajan, K.N.; Sasaki, G.H. Optical Networks, 3rd ed.; Elsevier: Burlington, NJ, USA, 2010. [Google Scholar]
- Stassinakis, A.N.; Nistazakis, H.E.; Peppas, K.P.; Tombras, G.S. Improving the availability of terrestrial FSO links over log normal atmospheric turbulence channels using dispersive chirped Gaussian pulses. Opt. Laser Technol. 2013, 54, 329–334. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, W.; Xie, X. Analysis of temporal broadening of optical pulses by atmospheric dispersion in laser communication system. Opt. Commun. 2012, 285, 3169–3173. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Frantzeskakis, D.J.; Atai, J.; Malomed, B.A.; Efremidis, N.; Hizanidis, K. Multichannel pulse dynamics in a stabilized Ginzburg-Landau system. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2002, 65, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hizanidis, K.; Malomed, B.A.; Nistazakis, H.E.; Frantzeskakis, D.J. Stabilizing soliton transmission by third-order dispersion in dispersion-compensated fibre links. Pure Appl. Opt. 1998, 7, 57–62. [Google Scholar] [CrossRef]
- Jaruwatanadilok, S. Channel Modeling and Performance Evaluation using Vector Radiative Transfer Theory. IEEE J. Sel. Areas Commun. 2008, 26, 1620–1627. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Underhill, M.J. Time jitter and phase noise—Now and in the future? In Proceedings of the 2012 IEEE International Frequency Control Symposium Proceedings, Baltimore, MD, USA, 21–24 May 2012; pp. 1–8. [Google Scholar]
- Ghassemlooy, Z.; Arnon, S.; Uysal, M.; Xu, Z.; Cheng, J. Emerging Optical Wireless Communications-Advances and Challenges. IEEE J. Sel. Areas Commun. 2015, 33, 1738–1749. [Google Scholar] [CrossRef]
- Grigoryan, V.S.; Menyuk, C.R.; Mu, R.M. Calculation of timing and amplitude jitter in dispersion-managed optical fiber communications using linearization. J. Light. Technol. 1999, 17, 1347–1356. [Google Scholar] [CrossRef]
- Gnauck, A.H.; Mecozzi, A.; Clausen, C.B.; Park, S.G.; Shtaif, M. Cancellation of timing and amplitude jitter in symmetric links using highly dispersed pulses. IEEE Photonics Technol. Lett. 2002, 13, 445–447. [Google Scholar]
- Santhanam, J.; Agrawal, G.P. Raman-induced timing jitter in dispersion-managed optical communication systems. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 632–639. [Google Scholar] [CrossRef]
- Johnson, L.J. The Underwater Optical Channel. 2012, pp. 1–18. Available online: https://www.researchgate.net/publication/280050464_The_Underwater_Optical_Channel/citation/download (accessed on 11 July 2019).
- Wei, W.; Zhang, X.; Rao, J.; Wang, W. Time domain dispersion of underwater optical wireless communication. Chin. Opt. Lett. 2011, 9, 030101–030104. [Google Scholar] [CrossRef]
- Austin, R.W.; Halikas, G. The index of refraction of seawater. In UC San Diego: Scripps Institution of Oceanography; 1976; Available online: https://escholarship.org/uc/item/8px2019m (accessed on 11 July 2019).
- McNeil, G.T. Metrical Fundamentals of Underwater Lens System. Opt. Eng. 1977, 16, 162128. [Google Scholar] [CrossRef]
- Marcuse, D. Pulse distortion in single-mode fibers. 3: Chirped pulses. Appl. Opt. 1981, 20, 3573–3779. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Kevrekidis, P.G.; Malomed, B.A.; Frantzeskakis, D.J.; Bishop, A.R. Targeted transfer of solitons in continua and lattices. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2002, 66, 015601. [Google Scholar] [CrossRef] [PubMed]
- Nistazakis, H.E.; Rapti, Z.; Frantzeskakis, D.J.; Kevrekidis, P.G.; Sodano, P.; Trombettoni, A. Rabi switch of condensate wave functions in a multicomponent Bose gas. Phys. Rev. A At. Mol. Opt. Phys. 2008, 78, 023635. [Google Scholar] [CrossRef]
- Driben, R.; Malomed, B.A.; Chu, P.L. Transmission of pulses in a dispersion-managed fiber link with extra nonlinear segments. Opt. Commun. 2005, 245, 227–236. [Google Scholar] [CrossRef]
- Marcuse, D. Pulse distortion in single-mode fibers. Appl. Opt. 1980, 19, 1653. [Google Scholar] [CrossRef] [PubMed]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes, 3rd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Arnon, S. Underwater optical wireless communication network. Opt. Eng. 2010, 49, 015001. [Google Scholar] [CrossRef]
- Cochenour, B.; Mullen, L.; Laux, A. Spatial and temporal dispersion in high bandwidth underwater laser communication links. In Proceedings of the MILCOM 2008–2008 IEEE Military Communications Conference, San Diego, CA, USA, 16–19 November 2008. [Google Scholar]
- Sandalidis, H.; Tsiftsis, T.; Karagiannidis, G. Optical wireless communications with heterodyne detection over turbulence channels with pointing errors. J. Lightwave Technol. 2009, 27, 4440–4445. [Google Scholar] [CrossRef]
- Gappmair, W.; Hranilovic, S.; Leitgeb, E. Performance of PPM on terrestrial FSO links with turbulence and pointing errors. IEEE Commun. Lett. 2010, 14, 468–470. [Google Scholar] [CrossRef]
- Johnson, L.J.; Jasman, F.; Green, R.J.; Leeson, M.S. Recent advances in underwater optical wireless communications. Underw. Technol. 2014, 32, 167–175. [Google Scholar] [CrossRef]
- Barrios, R.; Dios, F. Probability of fade and BER performance of FSO links over the exponentiated Weibull fading channel under aperture averaging. In Proc. SPIE 8540, Unmanned/Unattended Sensors and Sensor Networks IX; SPIE Security + Defence: Edinburgh, UK, 2012; Volume 8540, p. 85400D. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Volos, C.K.; Tombras, G.S. FSO links with diversity pointing errors and temporal broadening of the pulses over weak to strong atmospheric turbulence channels. Optik 2016, 127, 3402–3409. [Google Scholar] [CrossRef]
- Vetelino, F.S.; Young, C.; Andrews, L. Fade statistics and aperture averaging for Gaussian beam waves in moderate-to-strong turbulence. Appl. Opt. 2007, 46, 3780. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yu, H.-Y.; Zhu, Y.-J. A Long Distance Underwater Visible Light Communication System with Single Photon Avalanche Diode. IEEE Photonics J. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Chancey, M.A. Short Range Underwater Optical Communication Links. Master’s Thesis, North Carolina State University, Raleigh, NC, USA, 2005. [Google Scholar]
- Partan, J.; Kurose, J.; Levine, B.N. A survey of practical issues in underwater networks. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2007, 11, 23. [Google Scholar] [CrossRef]
- Farr, N.; Chave, A.; Freitag, L.; Preisig, J.; White, S.; Yoerger, D.; Sonnichsen, F. Optical Modem Technology for Seafloor Observatories. In Proceedings of the OCEANS 2006, Boston, MA, USA, 18–21 September 2006; pp. 1–6. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roumelas, G.D.; Nistazakis, H.E.; Stassinakis, A.N.; Volos, C.K.; Tsigopoulos, A.D. Underwater Optical Wireless Communications with Chromatic Dispersion and Time Jitter. Computation 2019, 7, 35. https://doi.org/10.3390/computation7030035
Roumelas GD, Nistazakis HE, Stassinakis AN, Volos CK, Tsigopoulos AD. Underwater Optical Wireless Communications with Chromatic Dispersion and Time Jitter. Computation. 2019; 7(3):35. https://doi.org/10.3390/computation7030035
Chicago/Turabian StyleRoumelas, George D., Hector E. Nistazakis, Argyris N. Stassinakis, Christos K. Volos, and Andreas D. Tsigopoulos. 2019. "Underwater Optical Wireless Communications with Chromatic Dispersion and Time Jitter" Computation 7, no. 3: 35. https://doi.org/10.3390/computation7030035
APA StyleRoumelas, G. D., Nistazakis, H. E., Stassinakis, A. N., Volos, C. K., & Tsigopoulos, A. D. (2019). Underwater Optical Wireless Communications with Chromatic Dispersion and Time Jitter. Computation, 7(3), 35. https://doi.org/10.3390/computation7030035






