Molecular Dynamics of Water Embedded Carbon Nanocones: Surface Waves Observation
Abstract
1. Introduction
2. Materials and Methods
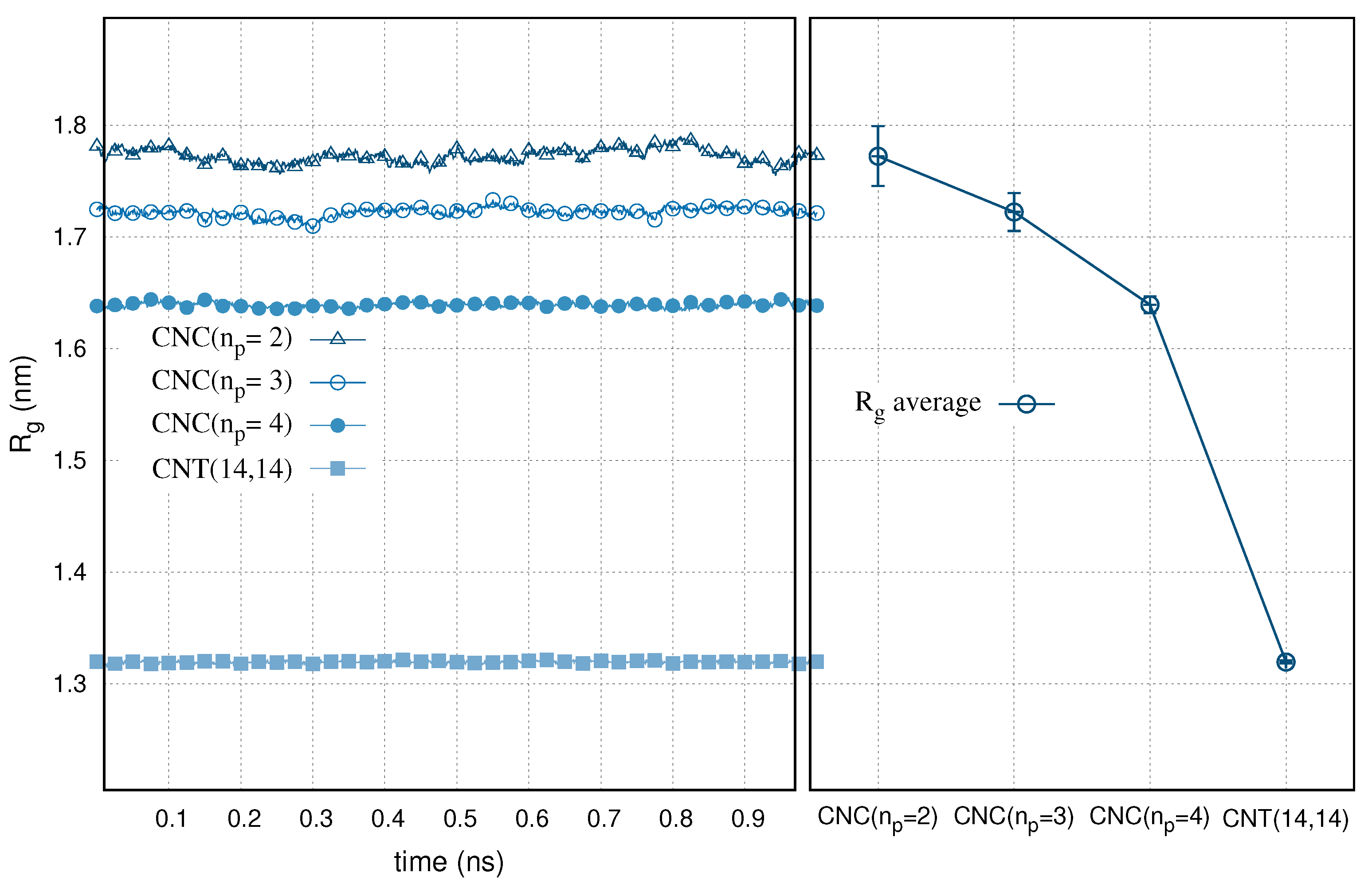
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bonomi, M.; Branduardi, D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raiteri, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.; et al. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180, 1961–1972. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Aktulga, H.M.; Fogarty, J.C.; Pandit, S.A.; Grama, A.Y. Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques. Parallel Comput. 2012, 38, 245–259. [Google Scholar] [CrossRef]
- Niels, H.; van Gunsteren, W. Practical Aspects of Free-Energy Calculations: A Review. J. Chem. Theor. Comput. 2014, 10, 2632–2647. [Google Scholar]
- Bennett, G.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Martins, S.A.; Sousa, S.F.; Ramos, M.J.; Fernandes, P.A. Prediction of Solvation Free Energies with Thermodynamic Integration Using the General Amber Force Field. J. Chem. Theor. Comput. 2014, 10, 3570–3577. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R.; Pitera, J.W.; Swope, W.C.; Pande, V.S. Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J. Chem. Phys. 2003, 119, 5740–5761. [Google Scholar] [CrossRef]
- Cournia, Z.; Allen, B.; Sherman, W. Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model. 2017, 57, 2911–2937. [Google Scholar] [CrossRef]
- Redmill, P.S.; Capps, S.L.; Cummings, P.T.; McCabe, C. A molecular dynamics study of the Gibbs free energy of solvation of fullerene particles in octanol and water. Carbon 2009, 47, 2865–2874. [Google Scholar] [CrossRef]
- Chaban, V.V.; Fileti, E.E. Free energy of solvation of carbon nanotubes in pyridinium-based ionic liquids. Phys. Chem. Chem. Phys. 2009, 418, 20357–20362. [Google Scholar] [CrossRef]
- Ohba, T.; Yamamoto, S.; Kodaira, T.; Hata, K. hanging Water Affinity from Hydrophobic to Hydrophilic in Hydrophobic Channels. Langmuir 2015, 31, 1058–1063. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Dumont, R.S.; Dickson, J.M. Nonequilibrium molecular dynamics simulation of pressure-driven water transport through modified CNT membranes. J. Chem. Phys. 2013, 138, 124701. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yang, C.; Zhao, K.; Li, J.; Wu, H. Ultrashort single-walled carbon nanotubes in a lipid bilayer as a new nanopore sensor. Nat. Commun. 2013, 4, 2989. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Xu, J.; Su, H.; Liu, X.; Zhao, H.; Feng, H.; Das, R. Two-dimensional (2D) nanoporous membranes with sub-nanopores in reverse osmosis desalination: Latest developments and future directions. Desalination 2019, 451, 18–34. [Google Scholar] [CrossRef]
- Gelpí, J.; Hospital, A.; Goñi, R.; Orozco, M. Molecular dynamics simulations: Advances and applications. Adv. Appl. Bioinform. Chem. 2015, 10, 37. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Kong, Z.; Zhang, L.; Liang, L. Controlled interval of aligned carbon nanotubes arrays for water desalination: A molecular dynamics simulation study. Desalination 2016, 395, 28–32. [Google Scholar] [CrossRef]
- Yu, P.; Wurster, D.E. Thermodynamic Evaluation of the Interaction Driven by Hydrophobic Bonding in the Aqueous Phase. J. Pharm. Sci. 2019, 108, 173–177. [Google Scholar] [CrossRef] [PubMed]
- Bahamon, D.; Carro, L.; Guri, S.; Vega, L. Computational study of ibuprofen removal from water by adsorption in realistic activated carbons. J. Colloid Interf. Sci. 2017, 498, 323–334. [Google Scholar] [CrossRef] [PubMed]
- Konatham, D.; Yu, J.; Ho, T.A.; Striolo, A. Simulation Insights for Graphene-Based Water Desalination Membranes. Langmuir 2013, 29, 11884–11897. [Google Scholar] [CrossRef]
- Shahbabaei, M.; Tang, D.; Kim, D. Simulation insight into water transport mechanisms through multilayer graphene-based membrane. Comput. Mater. Sci. 2017, 128, 87–97. [Google Scholar] [CrossRef]
- Calabrò, F. Modeling the effects of material chemistry on water flow enhancement in nanotube membranes. MRS Bull. 2017, 42, 289–293. [Google Scholar] [CrossRef]
- Sam, A.; Kannam, S.K.; Hartkamp, R.; Sathian, S.P. Water flow in carbon nanotubes: The effect of tube flexibility and thermostat. J. Chem. Phys. 2017, 146, 234701. [Google Scholar] [CrossRef]
- Tinti, A.; Giacomello, A.; Grosu, Y.; Casciola, C.M. Intrusion and extrusion of water in hydrophobic nanopores. Proc. Nat. Acad. Sci. USA 2017, 114, E10266–E10273. [Google Scholar] [CrossRef]
- Pascal, T.A.; Goddard, W.A.; Jung, Y. Entropy and the driving force for the filling of carbon nanotubes with water. Proc. Nat. Acad. Sci. USA 2011, 108, 11794–11798. [Google Scholar] [CrossRef]
- Corry, B. Designing Carbon Nanotube Membranes for Efficient Water Desalination. J. Phys. Chem. B 2008, 112, 1427–1434. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, H.; Liu, X.; Hu, X. Water transport confined in graphene oxide channels through the rarefied effect. Phys. Chem. Chem. Phys. 2018, 20, 9780–9786. [Google Scholar] [CrossRef]
- Cao, W.; Wang, J.; Ma, M. Carbon nanostructure based mechano-nanofluidics. J. Micromechan. Microeng. 2018, 28, 033001. [Google Scholar] [CrossRef]
- Shaat, M. Viscosity of Water Interfaces with Hydrophobic Nanopores: Application to Water Flow in Carbon Nanotubes. Langmuir 2017, 33, 12814–12819. [Google Scholar] [CrossRef]
- Chakraborty, S.; Kumar, H.; Dasgupta, C.; Maiti, P.K. Confined Water: Structure, Dynamics, and Thermodynamics. Acc. Chem. Res. 2017, 50, 2139–2146. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Y.; Zhou, J.; Lu, X. Diameter and helicity effects on static properties of water molecules confined in carbon nanotubes. Phys. Chem. Chem. Phys. 2004, 6, 829–835. [Google Scholar] [CrossRef]
- Kumar, H.; Dasgupta, C.; Maiti, P.K. Driving force of water entry into hydrophobic channels of carbon nanotubes: entropy or energy? Mol. Simul. 2015, 41, 504–511. [Google Scholar] [CrossRef]
- Waghe, A.; Rasaiah, J.C.; Hummer, G. Entropy of single-file water in (6,6) carbon nanotubes. J. Chem. Phys. 2012, 137, 044709. [Google Scholar] [CrossRef]
- Young, M.K.; Hannah, E.; Joon, H.K. Molecular dynamics simulation of seawater reverse osmosis desalination using carbon nanotube membranes. Desalin. Water Treat. 2016, 57, 20169–20176. [Google Scholar]
- Mateus, H.K.; José, R.B.; Carolina, F.; Marcia, C.B. Water in nanotubes: The surface effect. Chem. Eng. Sci. 2019, 203, 54–67. [Google Scholar]
- Paul, S.; Taraphder, S. Functionalized single walled carbon nanotubes as template for water storage device. Chem. Phys. 2016, 479, 42–52. [Google Scholar] [CrossRef]
- Lopez, C.F.; Nielsen, S.O.; Moore, P.B.; Klein, M.L. Understanding nature’s design for a nanosyringe. Proc. Natl. Acad. Sci. USA 2004, 101, 4431–4434. [Google Scholar] [CrossRef]
- Panahi, A.; Hossein, M. Sabour Electrokinetics desalination of water using fluorinated carbon nanotubes embedded in silicon membrane: Insights from molecular dynamics simulation. Chem. Eng. Sci. 2017, 173, 60–73. [Google Scholar]
- Rizzuto, C.; Pugliese, G.; Bahattab, M.A.; Aljlil, S.A.; Drioli, E.; Tocci, E. Multiwalled carbon nanotube membranes for water purification. Sep. Purif. Tech. 2018, 193, 378–385. [Google Scholar] [CrossRef]
- Geng, J.; Kim, K.; Zhang, J.; Escalada, A.; Tunuguntla, R.; Comolli, L.; Allen, F.; Shnyrova, A.; Rae, C.K.; Munoz, D.; et al. Stochastic transport through carbon nanotubes in lipid bilayers and live cell membranes. Nature 2014, 514, 612–615. [Google Scholar] [CrossRef]
- Choi, M.; Kim, H.; Ho Lee, B.; Kim, T.; Rho, J.; Kim, K.M.; Kim, K. Understanding carbon nanotube channel formation in the lipid membrane. Nanotechnology 2018, 29, 115702. [Google Scholar] [CrossRef]
- Ruiz, L.; Wu, Y.; Keten, S. Tailoring the water structure and transport in nanotubes with tunable interiors. Nanoscale 2015, 7, 121–132. [Google Scholar] [CrossRef]
- Nikhil, M.; Ponmalai, K. Structure, stability and water permeation of ([D-Leu-L-Lys-(D-Gln-L-Ala)3]) cyclic peptide nanotube: A molecular dynamics study. Mol. Simul. 2018, 44, 225–235. [Google Scholar]
- Vögele, M.; Köfinger, J.; Hummer, G. Molecular dynamics simulations of carbon nanotube porins in lipid bilayers. Faraday Discuss 2018, 209, 341–358. [Google Scholar] [CrossRef]
- Tunuguntla, R.H.; Zhang, Y.; Henley, R.Y.; Yao, Y.; Pham, T.A.; Wanunu, M.; Noy, A. Response to Comment on “Enhanced water permeability and tunable ion selectivity in subnanometer carbon nanotube porins”. Science 2018, 359, 792–796. [Google Scholar] [CrossRef]
- Marbach, S.; Dean, S.D.; Bocquet, L. Transport and dispersion across wiggling nanopores. Nat. Phys. 2018, 14, 1108–1113. [Google Scholar] [CrossRef]
- Zeng, S.; Chen, J.; Wang, X.; Zhou, G.; Chen, L.; Dai, C. Selective Transport through the Ultrashort Carbon Nanotubes Embedded in Lipid Bilayers. J. Phys. Chem. C 2018, 122, 27681–27688. [Google Scholar] [CrossRef]
- Gotzias, A.; Heiberg-Andersen, H.; Kainourgiakis, M.; Steriotis, T. Grand canonical Monte Carlo simulations of hydrogen adsorption in carbon cones. Appl. Surf. Sci. 2010, 256, 5226–5231. [Google Scholar] [CrossRef]
- Gotzias, A.; Heiberg-Andersen, H.; Kainourgiakis, M.; Steriotis, T. A grand canonical Monte Carlo study of hydrogen adsorption in carbon nanohorns and nanocones at 77K. Carbon 2011, 49, 2715–2724. [Google Scholar] [CrossRef]
- Konstantakou, M.; Gotzias, A.; Kainourgiakis, M.; Stubos, A.; Steriotis, T. GCMC Simulations of Gas Adsorption in Carbon Pore Structures. In Applications of Monte Carlo Method in Science and Engineering; Mordechai, S., Ed.; IntechOpen: London, UK, 2011. [Google Scholar]
- Liu, Y.-P.; Li, J.-T.; Song, Q.; Zhuang, J.; Ning, X.-J. A Scheme for the Growth of Graphene Sheets Embedded with Nanocones. Crystals 2017, 7, 35. [Google Scholar] [CrossRef]
- Nazeer, W.; Farooq, A.; Younas, M.; Munir, M.; Kang, S.M. On Molecular Descriptors of Carbon Nanocones. Biomolecules 2018, 8, 92. [Google Scholar] [CrossRef]
- Arepalli, S. Modified carbon nanostructures for display and energy storage. In Nanoelectronic Device Applications Handbook; Morris, J.E., Ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 93–108. [Google Scholar]
- Narjabadifam, A.; Vakili-Tahami, F.; Zehsaz, M. Modal analysis of multi-walled carbon nanocones using molecular dynamics simulation. Comput. Mater. Sci. 2017, 137, 55–66. [Google Scholar] [CrossRef]
- Narjabadifam, A.; Vakili-Tahami, F.; Zehsaz, M.; Seyyed, F.; Mir, M. Three-dimensional modal analysis of carbon nanocones using molecular dynamics simulation. J. Vacuum Sci. Tech. B 2015, 33, 051805. [Google Scholar] [CrossRef]
- Ge, M.; Sattler, K. Observation of fullerene cones. Chem. Phys. Lett. 1994, 220, 192–196. [Google Scholar] [CrossRef]
- Heiberg-Andersen, H.; Helgesen, G.; Knudsen, K.; Patrick Pinheiro, J.; Svåsand, E.; Skjeltorp, A. Nanocones–A different form of carbon with unique properties. MRS Proc. 2005, 901. [Google Scholar] [CrossRef]
- Heiberg-Andersen, H.; Skjeltorp, A. Stability of Conjugated Carbon Nanocones. J. Math. Chem. 2005, 38, 589–604. [Google Scholar] [CrossRef]
- Cox, B.J.; Hill, J.M. Carbon Nanocones with Curvature Effects Close to the Vertex. Nanomaterials (Basel) 2018, 8, 624. [Google Scholar] [CrossRef] [PubMed]
- Ansari, R.; Sadeghi, F.; Darvizeh, M. Continuum study on the oscillatory characteristics of carbon nanocones inside single-walled carbon nanotubes. Phys. B: Condens. Matt. 2016, 482, 28–37. [Google Scholar] [CrossRef]
- Krishnan, A.; Dujardin, E.; Treacy, M.; Hugdahl, J.; Ebbesen, L.S. Graphitic cones and the nucleation of curved carbon surfaces. Nature 1997, 388, 451–454. [Google Scholar] [CrossRef]
- Bultheel, A.; Ori, O. Topological modeling of 1-Pentagon carbon nanocones—Topological efficiency and magic sizes. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 291–302. [Google Scholar] [CrossRef]
- Naess, S.N.; Elgsaeter, A.; Helgesen, G.; Knudsen, K.D. Carbon nanocones: wall structure and morphology. Sci. Tech. Adv. Mater. 2009, 10, 065002. [Google Scholar] [CrossRef]
- Wohner, N.; Lam, P.; Sattler, K. Energetic stability of graphene nanoflakes and nanocones. Carbon 2014, 67, 721–735. [Google Scholar] [CrossRef]
- Ansari, R.; Sadeghi, F. On the mechanics of C60 fullerene inside open carbon nanocones: A continuum study. Phys. E: Low-dimens. Syst. Nanostruct. 2015, 69, 1–12. [Google Scholar] [CrossRef]
- Ulloa, P.; Pacheco, M.; Latge, A. Optical properties of graphene nanocones under electric and magnetic fields. J. Phys. Condens. Matt. 2017, 29, 455304. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Hafner, J.H.; Rinzler, A.G.; Colbert, D.T.; Smalley, R.E. Nanotubes as nanoprobes in scanning probe microscopy. Nature 1996, 384, 147–150. [Google Scholar] [CrossRef]
- Chen, I.-C.; Chen, L.-H.; Ye, X.-R.; Daraio, C.; Jin, S.; Orme, C.A.; Quist, A.; Lal, R. Extremely sharp carbon nanocone probes for atomic force microscopy imaging. Appl. Phys. Lett. 2006, 88, 153102. [Google Scholar] [CrossRef]
- Furmaniak, S.; Gauden, P.; Patrykiejew, A.; Miśkiewicz, R.; Kowalczyk, P. Carbon Nanohorns as Reaction Nanochambers—A Systematic Monte Carlo Study. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.; Zhang, Y.; Yan, Y.; Král, P.; Zhang, J. Highly efficient water desalination in carbon nanocones. Carbon 2018, 108, 374–379. [Google Scholar] [CrossRef]
- Imbrogno, J.; Belfort, G. Membrane Desalination: Where Are We, and What Can We Learn from Fundamentals? Ann. Rev. Chem. Biomol. Eng. 2016, 7, 29–64. [Google Scholar] [CrossRef]
- Ang, E.Y.M.; Ng, T.Y.; Yeo, J.; Lin, R.; Geethalakshmi, K.R. Nanoscale Fluid Mechanics Working Principles of Transverse Flow Carbon Nanotube Membrane for Enhanced Desalination. Int. J. Appl. Mechan. 2017, 9, 1750034. [Google Scholar] [CrossRef]
- Gupta, K.M.; Zhang, K.; Jiang, J. Water Desalination through Zeolitic Imidazolate Framework Membranes: Significant Role of Functional Groups. Langmuir 2015, 31, 13230–13237. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Minoia, A. Available online: http://chembytes.wikidot.com/buildcstruct (accessed on 9 September 2019).
- Minoia, A.; Guo, D.; Xu, H.; George, S.J.; Schenning, A.P.H.J.; de Feyter, S.; Lazzaroni, R. Assessing the role of chirality in the formation of rosette-like supramolecular assemblies on surfaces. Chem. Commun. 2011, 47, 10924–10926. [Google Scholar] [CrossRef] [PubMed]
- Gotzias, A. Available online: https://github.com/Gotzias/xyz2gro (accessed on 9 September 2019).



| Atom | Mass (g) | (nm) | (kJmol) | OPLS Reference | |
|---|---|---|---|---|---|
| Aromatic ring | C | 12.011 | 0.355 | 0.293 | opls−147 (naphthalene) |
| H | 1.008 | 0.242 | 0.125 | opls−146 | |
| SPC water | O | 15.999 | 0.317 | 0.650 | opls−116 |
| H | 1.008 | 0 | 0 | opls−117 |
| CNC() | CNC() | CNC() | CNT(14,14) | |
|---|---|---|---|---|
| Angle (°) | 84 | 60 | 39 | 0 |
| Diameter (nm) | varying | 1.9 | ||
| C (atoms) | 1021 | 1076 | 1039 | 784 |
| Cube edge (nm) | 6.58 | 5.77 | 5.56 | 5.83 |
| Water (molecules) | 8885 | 5617 | 5247 | 6262 |
| (g/cm) | 0.93 | 0.87 | 0.91 | 0.94 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karataraki, G.; Sapalidis, A.; Tocci, E.; Gotzias, A. Molecular Dynamics of Water Embedded Carbon Nanocones: Surface Waves Observation. Computation 2019, 7, 50. https://doi.org/10.3390/computation7030050
Karataraki G, Sapalidis A, Tocci E, Gotzias A. Molecular Dynamics of Water Embedded Carbon Nanocones: Surface Waves Observation. Computation. 2019; 7(3):50. https://doi.org/10.3390/computation7030050
Chicago/Turabian StyleKarataraki, Georgia, Andreas Sapalidis, Elena Tocci, and Anastasios Gotzias. 2019. "Molecular Dynamics of Water Embedded Carbon Nanocones: Surface Waves Observation" Computation 7, no. 3: 50. https://doi.org/10.3390/computation7030050
APA StyleKarataraki, G., Sapalidis, A., Tocci, E., & Gotzias, A. (2019). Molecular Dynamics of Water Embedded Carbon Nanocones: Surface Waves Observation. Computation, 7(3), 50. https://doi.org/10.3390/computation7030050







