Abstract
The information and communications technology (ICT) industry workforce is now required to deal with ’Big Data’, and there is a need to fill the computational skill shortage in data analytics. The integrated skills of combining computer and mathematics capabilities is much sought after by every industry embarking on digital transformation. Studies conducted internationally and by the Australian Industry Group show the requirements for improving computational skills in the workplace. This research takes a positive step to address this issue by introducing visualization and experiential learning in the ICT curriculum in order to uplift mathematics skills required for data analytics. We present the use of such innovative methods adopted in a higher education setting. The results and positive impact achieved through this study are presented.
1. Introduction
In this globally advanced digital era, Information and Communication Technology (ICT) skills need to be revisited among the workforce [1,2]. With the unprecedented explosion of huge data in both structured and unstructured forms, the resulting ‘Big Data’ in industry requires a trained workforce to effectively derive value from it, using computational skills for performing data analytics [3,4]. ICT capabilities combined with mathematical skills are inherent in managing Big Data, and in performing various computation intensive data analytics that aid in decision making. Apart from the ICT industry, there is a huge demand for such skills across a wide range of industries, including banking, manufacturing, media and entertainment. However, data analytics requires computational skills that integrate mathematical abilities with ICT, which form a rare skill set [1,5,6]. Industries are encouraging their employees to reskill and upskill through further education [7]. Higher education providers are now required to reengineer the curriculum to address this skill shortage in order to prepare the workforce for Industry 4.0 [8,9].
Higher education systems are transforming to introduce lifelong employability skills to enhance discipline-specific skills such as ICT skills. Among the employability skills identified within the Employability Skills Framework in Australia, the most important ones suiting the present digital age are Technology skills and lifelong learning skills [10,11]. The National Research Council in the United States classified the employability skills under three broad domains: Cognitive domain, Intrapersonal domain, and Interpersonal domain [12]. The program for Basic Competencies in Working Life launched in Norway has identified Literacy, Numeracy and ICT skills as basic skills for adults [13]. Many countries worldwide have studied the workforce skill shortage, and have reported the requirement to uplift the numeracy skills for better employability [14,15]. In Australia, numeracy or mathematical skills development is required to meet the computational skills shortage in the rising Big Data analytics in industry [16]. Students cannot be assumed to have the necessary mathematical skills inherently required for data analytics.
However, there are challenges in acquiring mathematics skills through didactic means. In order to have a lifelong learning skill development with the changing ICT landscape, innovative approaches in teaching and student learning are warranted. With a view to address this gap in practice, this research explores the impact of introducing experiential learning and assessment approaches to engage students in developing mathematics skills within a Bachelor degree program in Australia.
Over the past few decades, there has been great emphasis laid on innovative assessment methods in enhancing student learning in various academic levels [17,18]. This has resulted in an evolution of a wide range of assessment practices and strategies. This evolution is more evident in higher education, due to the maturity of students and the degree of flexibility available in such an educational setting. Different courses in higher education adopt different combinations of such assessment methods. While assessment is only one side of the coin of education, learning is considered as the other side of the coin. The meaning attached to learning has also undergone various forms over a period of time, and hence this work addresses the issue of matching the right set of assessment practices in the context of which form of learning is under consideration. Only such a perfect match can lead towards a positive and successful academic impact. A spectrum of research work is continuously undertaken to study the impact of various learning and assessment methods [19,20,21]. In this paper, we explore experiential learning approach in the teaching and assessment for math skill development required for employability in data analytics in the IT industry. Our research aims to study the impact of employing experiential learning pedagogies and assessment practices in a math subject taught within the Bachelor of Information Technology (BIT) curriculum in a higher education institute in Australia.
The rest of the paper is organized as follows. Section 2 provides the research background describing the need for this study, the research aim and its methodology. In Section 3, we present the experiential learning framework with innovative practices adopted for learning and mathematical skills development in the BIT program. The student skill assessments and the research outcomes are discussed in Section 4, and finally Section 5 summarizes with concluding remarks and future work.
2. Research Background
2.1. Need for the Study
In Australia, several industry surveys indicate that Science, Technology, Engineering and Mathematics (STEM) skills are considered fundamental to various jobs [7,9]. For today’s digital era, these skills are more related to integrating the digital skills, such as data analytics, required to solve complex real world problems [22]. The Organisation for Economic Co-operation and Development (OECD)’s Program for International Student Assessment (PISA) survey found a statistically significant relationship between direct exposure to the contemporary working world and higher student scores in the PISA mathematics assessments [23]. The PISA survey indicates that Australia’s performance in mathematics has declined over the past decade, and needs improvement [5,8].
Figure 1 indicates that more than a third of Australian Year 8 students do not have the skills to apply basic mathematical knowledge in straightforward situations, according the Trends in International Mathematics and Science Study (TIMSS). Hence, the TIMSS 2019 Assessment Frameworks emphasize assessing a range of problem-solving situations within mathematics, with about two-thirds of the items requiring students to use applying and reasoning skills [21]. Table 1 shows the target percentages of the TIMSS 2019 Mathematics assessment devoted to content and cognitive domains, with increased emphasis on reason as the students develop their mathematics skills from fourth grade to eighth grade. Reasoning abilities go beyond the competency of arriving at a solution of routine problems, so as to be able to analyze unfamiliar situations, complex contexts and multistep problems. Hence, it is important to continue with this TIMSS framework to achieve improved analytical reasoning skill targets as students graduate and enter into the workforce.
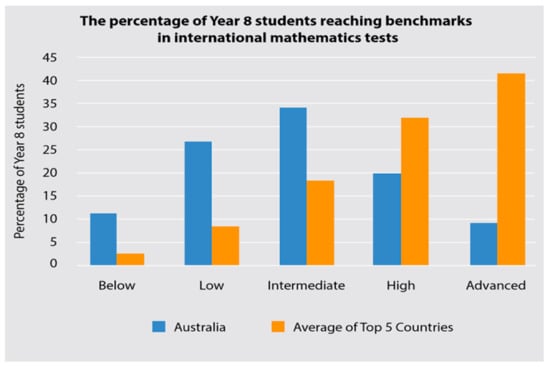
Figure 1.
Comparison of Mathematics Skills in Australia–Trends in International Mathematics and Science Study (TIMSS).

Table 1.
Mathematics Assessment Framework Targets–TIMSS.
Figure 2 shows the recent survey results by the World Economic Forum, indicating data as the first among the top ten workforce skill sets having an impact on the future of jobs in a wide range of industries [4]. Overall, there is a need for the present-day workforce to upskill in Big Data Analytics in order to meet the demand in industry. The Australian workforce is required to develop their math skills via formal education and training programs [8,9,10,11]. Hence, research studies are investigating an innovative pedagogy in higher education to uplift math skills [21,24].

Figure 2.
Top Ten Future Jobs—World Economic Forum [4].
This forms the motivation for this research to focus on developing mathematics skills in a higher education institution.
2.2. Aim of the Study
It has been a common practice for students to adopt rote learning, which would help only for the recall of knowledge temporarily, and does not aid in long-term benefits. Such learning practices do not help in applying knowledge for real world situations. In reality, surface-level learning habits, if continued to be cultivated in adults, lead to their low performance levels at the workplace. In order to cater to the Big Data analytics skills shortage in the Australian workplace, a common core subject to develop math skills, as one of the generic skills, was introduced in the first-year curriculum of the Bachelor of Information Technology (BIT) in a higher education institute. The subject called ‘Mathematics For IT’ was designed to develop the students’ numeracy skills that are relevant to the IT discipline skills requirement, in particular the skills required for data analytics. Previous research has studied and reported on the lack of motivation and student engagement in learning the math skills required for the workplace [25,26]. In this research study, we explore the use of an experiential learning approach to address this problem. This ongoing research project is based on a recent collaboration with industry, to use their software tools for evaluating the impact of visual aids in incorporating the necessary experiential learning activities, to motivate math skill development among the BIT students. Based on these background details, we have developed the research aim and methodology to conduct this study.
2.3. Methods
We adopted a mixed method approach, using survey-based as well as student performance-based outcomes to study the impact of introducing experiential learning theories to the design and delivery of the subject, Mathematics For IT, in a higher education setting. We also conducted a self-assessment of the students’ confidence levels in computational skill, using standard methods from literature [27]. This was completed before the students underwent the experiential learning activities. Overall, we found that a majority of the students coming from diverse backgrounds had difficulties in understanding mathematical concepts and their applications in the real world. Many do not enjoy learning it. Despite the differences in student demographics and any prior teaching methods adopted, in this new design of the subject delivery, we gave importance to the learning experience of the students in order to achieve life-long learning computational skills. Popular software tools that are used in industry were adopted to analyze and present the data, to interpret the analysis and to apply our findings in real-life situations for Big Data Analytics. With this view, we introduced experiential learning activities in the Mathematics For IT subject, with an appropriate software tool for the visualization of the data.
Our impact of experiential learning adopted in computational skill development was determined using the students’ performance in assessments through comparisons between the last cohort and this cohort of students.
3. Proposed Method for Experiential Learning and Visualization
3.1. Role of Assessment in Experiential Learning
Assessment is an essential tool to measure the degree of learning achieved. Though assessment of student learning is always a major concern for the learners, it is also a complex procedure for the tutors to use it as a vehicle for enhancing student learning. There is always a concern from the learners’ side regarding the purpose behind assessment, and whether what they have learnt would be assessed, and also whether the experience gained can be applied to the real world. Additional aspects are about the nature of assessment, fairness of the assessment and whether it is interesting or not. On the other hand, the lecturers try to set the objectives of student assessment mainly to measure the knowledge gained by the student and to gauge the capability of the students, and thereby to enforce quality education. These perspectives of assessments were considered while designing the assessments through experiential learning activities in the subject, Mathematics For IT. Since learning and assessment go hand in hand, it is essential to first define learning as a basis for any assessment to be carried out in an educational setting. With this basis in mind, a definition of learning in the context of higher education is given below [28]:
Learning is a complex process of understanding and creating a knowledge base of the subject under study and integrating the concepts and experiences achieved, so as to relate and apply them in a range of contexts and situations in any social setting.
This definition of learning is quite apt for higher education, since the students need to adopt in-depth approaches to learning that would prepare them for a future of dynamic change. It is during higher education that students are in a good frame of mind to get themselves equipped with lifelong learning characteristics which will help them to become a self-directed as well as an active learner.
From the literature, it is evident that each person’s learning style differs, displaying different approaches to learning in a higher education setting [29]. There are mainly four different learning modes: Concrete experience (CE), reflective observation (RO), abstract conceptualization (AC) and active experimentation (AE). Based on these four learning models, we propose an experiential learning framework to incorporate innovative learning activities using visual aids available in the software tools.
3.2. Proposed Experiential Learning Framework
We adopt Kolb’s experiential learning model with an emphasis of “learning through reflection on doing” [29]. It consists of four stages in a cycle as given below:
- Concrete Experience
- Reflective Observation
- Abstract Conceptualization
- Active Experimentation
In experiential learning, it is important that the learner takes an initiative for active learning. In our proposed experiential learning framework, we motivate the students to engage in learning through an active participation in various classroom activities that are linked to their continuous practical assessments. Assessment, when used creatively and appropriately, could simulate real-life scenarios in the workplace that facilitates students to take initiatives to learn.
We also consider Payne’s theory of associating learning with the cognitive, affective and psychomotor phenomena that take place within each learner [30]. The cognitive domain of a learner can be categorised as: Knowledge, comprehension, application, analysis, synthesis and evaluation. Payne strongly feels that assessment represents a wonderful opportunity to integrate the cognitive, affective and psychomotor aspects of instruction conveyed to a learner.
Our experiential learning framework introduces appropriate active learning activities within the Kolb’s model by assessing the effectiveness of experiential learning in each of the three phases: (a) A reflective learning phase, (b) a phase of learning resulting from the actions inherent to experiential learning, and (c) a further phase of learning from feedback [31,32]. Overall, the success factor associated with our experiential learning framework is that each learner is directly involved in the experience by doing tasks, and then each learner is required to reflect upon the experience gained using analytic skills to promote higher-order thinking strategies, and finally to take corrective action based on any feedback provided.
3.3. Implementation with Visualization
The proposed experiential learning framework was implemented to the design and delivery of the new ’Mathematics For IT’ subject using visualization techniques. The primary aim was to develop computational skills in the specific context of IT discipline, in particular relating to data analytics. Several practical software-based exercises and additional learning skills support scaffolding were introduced to provide a conducive learning environment.
In higher education, there is a wide spectrum of assessment situations ranging from very informal to very formal ones. There are many modes in which different assessment tasks are accomplished. Lecturers put in a lot of effort in moulding these assessment tasks from time to time in order to make them more effective. However, whatever be the method of assessment adopted, the underlying question is: What are the learning skills we wish to inculcate through this assessment task?
An assessment task is used to evaluate one or more of the cognitive domains of learning in each student. But the basic underlying educational purpose is to impart some generic transferable learning skills to the students. There is a whole gamut of generic learning skills that students are desired to achieve in a higher education setting. Some of the common ones are problem-solving skills, communication skills (oral and written communication), reflective, analysing & thinking skills, life-long learning and researching skills, collaborative & team skills, time management skills, task management skills, creativity and innovation skills, etc. Among these, our main focus for the math subject were problem-solving skills, reflective, analysing & thinking skills, and researching skills.
The subject lecturer designed the learning activities hand-in-hand with appropriate assessment tasks to achieve these life-long learning skills. Innovative software tools and techniques were used to design the classroom activities. For example, the definition of Golden Ratio, which has wide applications in IT, is usually expressed as a mathematical Fibonacci sequence given below:
where the Fibonacci sequence is an infinite series of integers, with each term expressed as the sum of the two previous terms. It is defined by the following mathematical function:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 |
The Golden ratio can be expressed in simple approximate form as follows:
Figure 3 provides a visual representation of the above two equations that define the Golden Ratio as the ratio of the hypotenuse of an isosceles triangle to its base. The Golden Ratio has many interesting properties as shown in Figure 3. Such a visual representation facilitates in active learning and retention, since students can understand its implications visually when the size of data grows. For instance, as the value of increases, the rate at which increases can be projected as a graph for the visual interpretation of the Fibonacci function. The teaching team employed suitable software tools for providing such visual representations of numerical concepts and data. These techniques helped the students to apply mathematics to data analytics with data visualization.
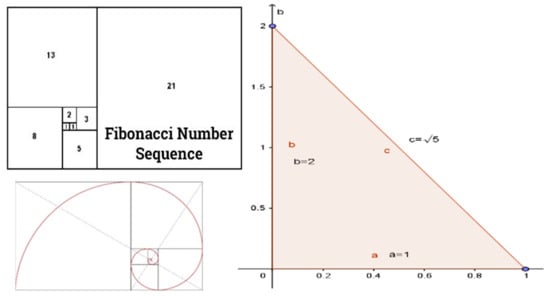
Figure 3.
Visual representations of Golden Ratio.
The impact of experiential learning much depends upon the choice of the assessment method used, the assessment process adopted and the reliability and validity of the assessment scheme. Certain learning skills are achieved through certain assessment methods, and it is not possible to address all of the learning skills through a single assessment method. Hence, for the assessment of learning arising from the classroom activities in the subject, we chose a combination of assessment methods that can collectively encompass the Mathematics For IT learning objectives. In addition, a sound and reliable assessment rubric based on clearly set criteria were devised. Since reflection is a crucial part of the experiential learning process, we incorporated this as one of the assessment components.
The implementation of our proposed experiential learning model involved designing classroom activities with visual representations as exemplified in Figure 3 for the weekly learning and assessment tasks of the subject, Mathematics for IT. The implementation model using Kolb’s experiential learning cycle is given in Figure 4. A recent study has applied revisions of Kolb’s Experiential Learning theoretical model, and concludes that simulations can be effective for introducing young students to simple physical science concepts [33]. Experiential learning has also been used by some studies fostering undergraduate student teachers to create innovative pedagogies, and secondary school students to experience innovative activities [34]. Another study conducted in a Bachelor’s degree program reports that fostering experiential learning strategies favors the students’ understanding of theoretical concepts in Business studies [35]. However, an empirical study exploring the similarities and differences in the learning of metacognitive skills between computer games and mathematics education has shown that there is no direct and explicit connection between the two learning contexts [36]. In the context of our study that requires life-long learning and analytical skills for the IT workforce, it is important to engage industry in education [37]. Hence, we adopted the continuous learning iterative cycle of Plan-Do-Reflect-Think to promote active learning. Further, by engaging students towards using industry collaborated software tools such as Statistical Analytics Systems (SAS) and Excel graphs, we employed the visualization of data.

Figure 4.
Experiential Learning Implementation of a Learning Activity.
Students have gained complex computational skills in areas such as cryptography, and this has led to further research explorations in computational innovation [38]. Our experiential learning strategies are aimed to help students gain an in-depth understanding of the mathematical concepts and methods by applying them to industry problem case studies.
4. Student Performance and Results
Student performance in the renewed subject, Mathematics For IT, was compared from two cohorts in order to evaluate students’ computational skills achievement as a result of the introduction of experiential learning. Cohort 1 consisted of students studying in the first semester (S1) of the old version of the course (without the implementation of Experiential Learning in the Mathematics For IT subject)). Cohort 2 consisted of students in the renewed course (with Experiential Learning implemented in this Mathematics For IT subject) offered in the second semester (S2).
Student performance in the subject was monitored, and performance results at the end of each semester for Cohort 1 and Cohort 2 were compared. Overall, there was an improvement in the grade results obtained by the Cohort 2 students (S2) as compared to the Cohort 1 students (S1), as shown in Figure 5. We compared the performance of students who are low achievers (who scored below average, less than 60 marks). Figure 6 shows that the low achievers of S2 performed better than those from S1.
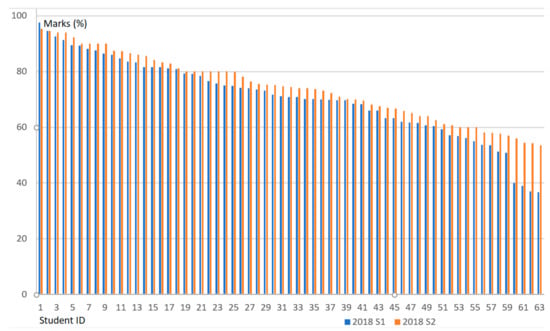
Figure 5.
Comparison of student performance (S1 and S2).
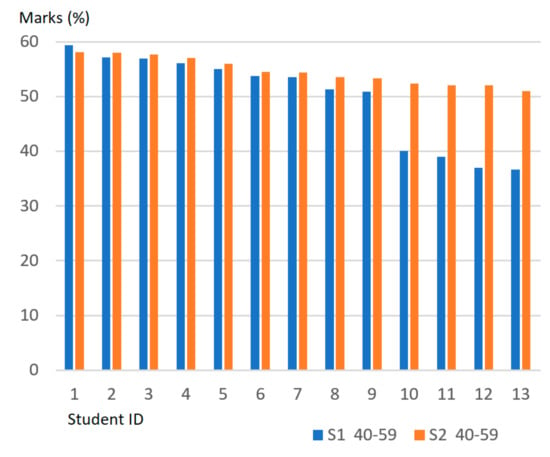
Figure 6.
Comparison of low achievers (S1 and S2).
A summary of various improvements in S2 as compared to S1 are given below:
- (1)
- The previous cohort of students (S1) could not score the ‘Distinction’ grade (70% and above) as shown in Figure 5, while many students in the current cohort (S2) scored this ‘Distinction’ grade
- (2)
- Overall class average score was much higher for S2 as compared to S1
- (3)
- There was a significant lower percentage of students in S2 scoring a ‘Fail’ grade
- (4)
- The student dropouts in S2 were much lower than S1 as shown in Figure 7.
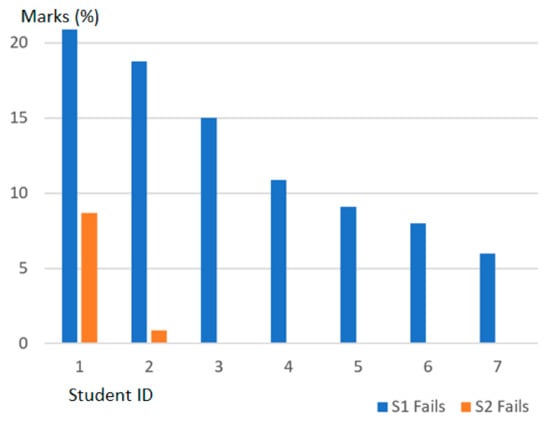 Figure 7. Comparison of student dropouts (S1 and S2).
Figure 7. Comparison of student dropouts (S1 and S2).
The qualitative feedback and comments obtained from the two cohorts of students are summarized below:
- (1)
- About 85% of the students (S2) submitted their assignments in time, which was a major improvement from S1
- (2)
- Students from S1 either liked or did not like mathematics with 50% ratio, while most of S2 students enjoyed it, including those who started with some fear initially
- (3)
- Experiential learning visual exercises with SAS and ‘Mathematician Stories’ were engaging
- (4)
- Additional tutorial support from the Learning and Teaching/Academic Support team was helpful to the students
- (5)
- Students’ (S2) class participation was dynamic and entertaining. E.g. After completing activities for the Proof of triangles using the Pythagoras-Plato formula, employing visual approaches, the students’ response was: “That’s amazing”.
The main areas of improvement in computational skills required for IT were in critical thinking and reasoning for solving complex problems and data analysis. The introduction of industry collaborated software tools to aid in the visualization of data helped the students to understand the application of computational skills in data analytics. In addition, cross-discipline collaboration among the facilitators aided in active learning and an engagement of students in the experiential learning activities within the classroom environment.
Some of the key challenges associated with the classroom delivery of the subject are: (i) Multiple tutorial groups, (ii) large class sizes, and (iii) late enrolments. If the same set of lecturers and support staff in the classrooms are not able to teach in multiple tutorial groups, then it might be difficult to incorporate consistency in facilitating the experiential learning activities. In addition, if the class size in each tutorial group increases beyond a threshold level, individual attention to students may not be feasible. In addition, students who get enrolled late or who miss classes in the first two weeks are not able to catch up with the others in their learning, and this could affect their overall performance in the subject. ‘With large class size, sufficient training among the teaching staff is essential for a planned and consistent delivery of the subject.
5. Conclusions
The ICT workforce has a skill shortage in data analytics, and this paper has taken a modest step to explore this through a research study. Innovative teaching and learning methods such as visualization and experiential learning strategies were adopted in a degree program, and the effect of such an innovative teaching strategy to uplift the computational skills required for complex data analysis was evaluated. The performance of students as they progressed in their mathematics skill development was continuously monitored. Industry collaborated software tools were employed to incorporate visualization of data to equip the students with the skills required for data analytics. The performance of students in the subject, based on the average score achieved, had improved by about 10%, despite the increase in student numbers. In addition, there was a substantial enhancement in the student engagement and motivation observed, which is supported by a huge reduction of about 50% in the number of student dropouts and failures in the subject, as compared to the previous cohort of students. The pedagogical outcome was successful and satisfying for the lecturers.
The positive impact achieved on student learning and mathematics skill development with data analytics capabilities will benefit the graduates when they join the ICT workforce. Future work envisions exploring strategies of extending the study to capstone projects and the students’ work placement impact, so as to complete the feedback loop of their experiential learning cycle.
Author Contributions
Conceptualization, S.V. and F.W.; Methodology, S.V. and F.W.; Software, A.O.; Validation, S.V., A.O. and F.W.; Formal Analysis, S.V. and A.O.; Investigation, A.O.; Resources, A.O. and S.V.; Writing—Original Draft Preparation, S.V.; Writing—Review and Editing, F.W.; Visualization, A.O.; Supervision, S.V.; Project Administration, F.W.; Funding Acquisition, S.V.
Funding
This research was funded by the Melbourne Polytechnic Research and Scholarship Seeding Grant, grant number 1-15-90101-6003-000.
Acknowledgments
The authors wish to acknowledge the support given by Melbourne Polytechnic’s Learning and Teaching department during the administration of the experiential learning activities in the classroom environment.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Davis, N. The Future Relationship Between Technology and Inequality. In CEDA: How Unequal? Insights on Inequality; Committee for Economic Development of Australia: Melbourne, Australia, 2018. [Google Scholar]
- David, A. Soft Skills for Business Success; Deloitte Access Economics: Sydney, Australia, 2017. [Google Scholar]
- David, A. Preparing Young People for The New Work Reality; Foundation for Young Australians: Melbourne, Australia, 2018. [Google Scholar]
- WEF Report. The Future of Jobs Report 2018; World Economic Forum: Geneva, Swiss, 2018. [Google Scholar]
- ACS Report. Australia’s Digital Pulse; Australian Computer Society, Deloitte Access Economics: Sydney, Australia, 2015. [Google Scholar]
- OECD. OECD Report. OECD Science, Technology and Industry Scoreboard 2017. In The Digital Transformation, Organisation for Economic Co-operation and Development; OECD Publishing: Paris, France, 2017. [Google Scholar]
- AIG Report. Tackling Foundation Skills in the Workforce; The Australian Industry Group: Sydney, Australian, 2016; pp. 1–20. [Google Scholar]
- Torii, K. Connecting the Worlds of Learning and Work; Mitchell Institute Report: Melbourne, Australia, 2018. [Google Scholar]
- Optimising STEM Industry-School Partnerships. In Inspiring Australia’s Next Generation; Education Services Australia Final Report: Carlton South, VIC, USA, 2018.
- DIICCSRTE and DEEWR Report; Core Skills for Work Developmental Framework. In The Framework; Department of Industry, Innovation, Science, Research and Tertiary Education: Canberra, Australia, 2013.
- General Capabilities in the Australian Curriculum; ACARA: Canberra, Australia, 2013.
- National Research Council. Education for Life and Work: Developing Transferable Knowledge and Skills in the 21st Century; The National Academies Press: Washington, WA, USA, 2012.
- OECD Report. OECD Skills Strategy Diagnostic Report: Norway; Organisation for Economic Co-operation and Development, OECD Publishing: Paris, France, 2014. [Google Scholar]
- Brisson, B.M.; Dicke, A.L.; Gaspard, H.; Häfner, I.; Flunger, B.; Nagengast, B.; Trautwein, U. Short Intervention, Sustained Effects: Promoting Students’ Math Competence Beliefs, Effort, and Achievement. Am. Educ. Res. J. 2017, 54, 1048–1078. [Google Scholar] [CrossRef]
- How Schools Can Improve Literacy and Numeracy Performance and Why it (Still) Matters; Centre for Education Statistics and Evaluation NSW Department of Education: Sydney, Australia, 2016; pp. 1–13.
- International Comparative Study: The Australian Curriculum and the Singapore Curriculum; Australian Curriculum, Assessment and Reporting Authority: Sydney, Australia, 2018.
- Knowles, M.S. Self-Directed Learning—A Guide for Learners and Teachers; Cambridge Adult Education, Association Press: New York, NY, USA, 1975. [Google Scholar]
- Kolb, D.A.; Osland, J.S.; Rubin, I.M. Individual and Organisational Learning, Chapter 3; Organisational Behavior: An Experiential Approach, 6th ed.; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Venkatraman, S. Student-Centred Assessments and their Impact on Learning–An IS Case Study. In Proceedings of the 11th Pacific Asia Conference on Information System, Brisbane, Queensland, Australia, 4–6 July 2007; pp. 254–368. [Google Scholar]
- Suleman, F. Employability Skills of Higher Education Graduates: Little Consensus on a Much-Discussed Subject. Soci. Behav. Sci. 2016, 228, 169–174. [Google Scholar] [CrossRef]
- Mullis, I.V.S.; Martin, M.O. TIMSSs 2019 Assessment Frameworks; TIMSS & PIRLS International Study Center, Lynch School of Education, Boston College and International Association for the Evaluation of Educational Achievement (IEA): Boston, MA, USA, 2019. [Google Scholar]
- Siekmann, G. What Is STEM? The Need for Unpacking Its Definitions and Applications; National Centre for Vocational Education Research (NCVER): Adelaide, Australia, 2016.
- Kashefpakdel, E.T.; Schleicher, M. The Impact of Career Development Activities on PISA Mathematics Tests; Organisation for Economic Cooperation and Development (OECD): London, UK, 2017. [Google Scholar]
- Venkatraman, S.; Wahr, F.; Souza-Daw, A.; Kaspi, S. Integrating Generic Skills into Disciplinary Curricula. Int. J. Edu. Peda. Sci. 2017, 11, 102–106. [Google Scholar]
- Clark, J.; White, G. Experiential Learning: A Definitive Edge in the Job Market. Am. J. Bus. Educ. 2010, 3, 115–118. [Google Scholar] [CrossRef]
- Stavenga, J.A.; Jong, R.F.; Wierstra, A.; Hermanussen, J. An Exploration of the Relationship Between Academic and Experiential Learning Approaches in Vocational Education. Br. J. Educ. Psychol. 2006, 76, 155–169. [Google Scholar] [CrossRef] [PubMed]
- Fogarty, G.J.; Cretchley, P.; Harman, C.; Ellerton, N.; Konki, N. Validation of a Questionnaire to Measure Mathematics Confidence, Computer Confidence, and Attitudes to the Use of Technology for Learning Mathematics. Math. Edu. Res. J. 2001, 3, 154–160. [Google Scholar] [CrossRef]
- Atkins, M. ‘What Should We be Assessing?’. In Assessment for Learning in Higher Education, Staff and Educational Development Series; Knight, P., Ed.; Kogan Page Ltd.: London, UK, 1995; pp. 25–33. [Google Scholar]
- Kolb, D. Experiential Learning: Experience as the Source of Learning and Development; Prentice Hall: Englewood, NJ, USA, 1984. [Google Scholar]
- Payne, D.A. Applied Educational Assessment; Wadsworth Publishing Company: Belmont, CA, USA, 1997. [Google Scholar]
- Race, P. What has Assessment Done for Us and to Us? In Assessment for Learning in Higher Education, Staff and Educational Development Series; Knight, P., Ed.; Kogan Page Ltd.: London, UK, 1995; pp. 61–74. [Google Scholar]
- Moon, J. A Handbook of Reflective and Experiential Learning: Theory and Practice; Routledge Falmer: London, UK, 2004. [Google Scholar]
- Falloon, G. Using simulations to teach young students science concepts: An Experiential Learning theoretical analysis. Comput. Educ. 2019, 135, 138–159. [Google Scholar] [CrossRef]
- Ng, Y.F.; Chan, K.K.; Lei, H.; Mok, P.; Leung, S.Y. Pedagogy and Innovation in Science Education: A Case Study of an Experiential Learning Science Undergraduate Course. Eur. J. Soci. Behav. Sci. 2019, 5, 2910–2926. [Google Scholar] [CrossRef]
- Rodríguez, A.L.L.; Morant, G. Promoting innovative experiential learning practices to improve academic performance: Empirical evidence from a Spanish Business School. J. Innov. Knowl. 2019, 4, 97–103. [Google Scholar] [CrossRef]
- Yong, S.T.; Gates, P.; Chan, A.T.Y. Similarities and Differences in Learning of Metacognitive Skills: Computer Games Versus Mathematics Education. Int. J. Game-Based Learn. 2019, 199, 1–14. [Google Scholar] [CrossRef]
- Mann, A.; Rehill, J.; Kashefpakdel, E.T. Employer Engagement in Education: Insights from International Evidence for Effective Practice and Future Research; Education Endowment Foundation: London, UK, 2018. [Google Scholar]
- Overmars, A.; Venkatraman, S. An Efficient Golden Ratio Method for Secure Cryptographic Applications. Math Comput. Appl. 2018, 23, 58. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).