Abstract
The dysregulation of inflammation, normally a self-limited response that initiates healing, is a critical component of many diseases. Treatment of inflammatory disease is hampered by an incomplete understanding of the complexities underlying the inflammatory response, motivating the application of systems and computational biology techniques in an effort to decipher this complexity and ultimately improve therapy. Many mathematical models of inflammation are based on systems of deterministic equations that do not account for the biological noise inherent at multiple scales, and consequently the effect of such noise in regulating inflammatory responses has not been studied widely. In this work, noise was added to a deterministic system of the inflammatory response in order to account for biological stochasticity. Our results demonstrate that the inflammatory response is highly dependent on the balance between the concentration of the pathogen and the level of biological noise introduced to the inflammatory network. In cases where the pro- and anti-inflammatory arms of the response do not mount the appropriate defense to the inflammatory stimulus, inflammation transitions to a different state compared to cases in which pro- and anti-inflammatory agents are elaborated adequately and in a timely manner. In this regard, our results show that noise can be both beneficial and detrimental for the inflammatory endpoint. By evaluating the parametric sensitivity of noise characteristics, we suggest that efficiency of inflammatory responses can be controlled. Interestingly, the time period on which parametric intervention can be introduced efficiently in the inflammatory system can be also adjusted by controlling noise. These findings represent a novel understanding of inflammatory systems dynamics and the potential role of stochasticity thereon.
1. Introduction
Inflammation is the dynamic response of the body to adverse stimuli, such as infection and injury, that helps drive wound healing and pathogen clearance to restore homeostasis via a coordinated cascade of interlinked responses [1]. A sufficiently large stimulus will provoke the systemic activation of immune cells and other components involved in inflammation. The systemic inflammatory response involves transcriptional activation of inflammatory genes in multiple cell types, afferent and efferent neural signaling, central secretion of hormones such as cortisol and epinephrine, and the production of hormone-like inflammatory mediators (cytokines/chemokines) as well as “danger” signals secreted from stressed or damaged tissues [1,2,3]. These inter-communicating systems are designed to produce a self-limited inflammatory response that can become activated to the correct degree under appropriate circumstances, perform its function, and then resolve. Under certain conditions such as those of critically ill patients in intensive care, these regulatory processes are insufficient to bring about the resolution of inflammation, often culminating in self-maintaining inflammation that leads to multiple organ dysfunction syndrome (MODS), which has a high mortality rate [4,5,6].
As the progression of inflammation depends largely on the behavior of complex, nonlinear, redundant pathways, mathematical modeling provides a framework for attaining a more fundamental understanding of the inflammatory response [7,8]. Accordingly, numerous mathematical models of various complexity have been developed, deciphering different aspects of inflammation with different levels of detail. In general, these approaches can be divided to equation-based (EBM) and agent-based (ABM) models [8,9]. The primary EBMs used in the inflammation modeling are ODE-based [10,11,12,13,14], and their level of detail can vary from models incorporating descriptions of all well-accepted constituents of the inflammatory response (e.g., innate/adaptive immune elements, effector elements etc.) [15] to more reduced models of whole-organism inflammation [16,17,18]. Agent-based approaches, on the other hand, consist of viewing the inflammatory system as an aggregation of inflammatory agents which can be classified into populations or agent classes based on similar agent-rules [19,20,21].
Inflammation, like all biological responses, naturally includes some inherent variability and stochasticity [7,8,22,23,24,25,26]. For instance, transcription of pro-inflammatory genes in an individual cell is dependent on the dynamic binding of transcription factors to a finite number of binding sites, and the anti-inflammatory hormone cortisol is released through a series of discrete, stochastic bursts rather than a constant rate of secretion. This type of stochasticity has been considered by the modeling community by developing stochastic models of pulsatile hormone release [27], models of NF-κB action that account for discrete transcriptional activation [28], and agent-based models of inflammation that inherently include stochastic behavior of individual agents [20,29,30,31,32]. Nonetheless, much interest still remains in deterministic equation-based models of inflammation [13,14,17,18,33,34,35,36,37,38,39]. While deterministic, equation-based modeling is appealing due to simplicity, elegance, wide range of established mathematical tools for model integration and analysis [8,9,40], and ability to serve as a platform for clinically translational applications such as in silico clinical trials [37,41], there is a limited ability to account for how uncertainty and stochasticity in model components can influence the output.
Since noise is an inherent characteristic of biological responses, its parametric control is an appealing method with which to regulate the inflammatory response endpoint. In the work of Kim and Sauro [42], a systematic mathematical analysis method for simultaneous control of noise and mean response levels was presented. There, noise-related phenotypes in gene promoter activity were adjusted based on a stochastic control analysis that quantified which parameters need to be controlled. This “active” noise control was applied both to regulate the mean and noise levels as well as controlling system dynamics. In the case of an inflammatory response, in which multiple components cross-talk to remove the pathogen or resolve sterile inflammation, identification of parameters that mostly account for the noise characteristics represented as response covariance are of high importance for an optimal intervention.
In the present paper, the effects of adding noise to a deterministic, ordinary differential equation (ODE)-based model of inflammation in response to infection [17] were studied. The ODEs comprising this model were converted into stochastic differential equations (SDEs), which can then be integrated at varying noise levels to determine the influence of noise on model dynamics. The behavior of the system was explored as a function of noise level and the magnitude of the pathogen challenge. Next, stochastic control analysis was performed to identify the most critical parameters for regulating responses variance as well as the mean level of the responses. These studies highlight the importance of considering the effects of noise, which is ubiquitously present in real biological systems, on the output of models of inflammation.
2. Methods
2.1. Four-Variable Model
The model presented in [17] contains four variables: a bacterial pathogen (P), activated phagocytes (N*), tissue damage (D), and anti-inflammatory mediators (CA). In Equation (1), a logistic growth function is used to model pathogen population growth followed by a saturable elimination term resulting from the quasi-steady state approximation as well as pathogen removal due to phagocytic immune cells N*. Phagocytic immune cells (N*) levels are further regulated by the pathogen (P), along with the self-induction of activating phagocytes and pro-inflammatory cytokines released by damaged tissues (R term, Equation (2)). Tissue damage (D) is induced by phagocytic immune cells (Equation (3)) and produces signals that activate both the pro-inflammatory (phagocytes in this model) and anti-inflammatory branches of the response. Finally, in Equation (4), anti-inflammatory mediators are induced through a constant source (sc) and a term representing the production of anti-inflammatory mediators from damage and activated phagocytes. All model variables maintain a first order degradation term apart from pathogen P which degradation is mediated through phagocytic immune cells.
The structure of the four-variable model is shown in Figure 1, and the ODEs driving its responses are depicted in Equations (1)–(7). For a typical simulation, specific initial conditions and parameters were identical to those in the original study [17], and are shown in Table 1 and Table 2. To investigate the effect of noise relative to the pathogen level, the initial condition of pathogen (Table 2) was also varied together with the noise level.
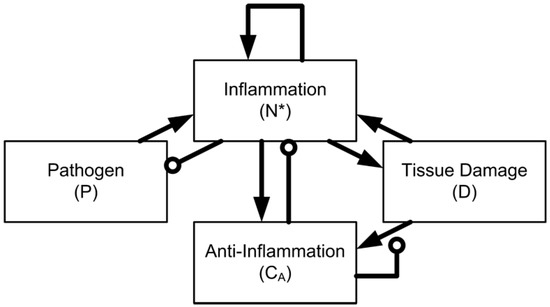
Figure 1.
Network structure of the four-variable model. The model is defined by interaction between a pathogen (P), activated phagocytes (N*), tissue damage (D), and anti-inflammatory mediators (CA).

Table 1.
Parameter values used in all model simulations, as reported in [17].

Table 2.
Initial conditions corresponding to the healthy steady state in [17].
The model shown in Equations (1)–(7) exhibits three steady states: healthy, aseptic death, and septic death [17]. The healthy response occurs when the inflammatory response is sufficient to eliminate the pathogen, and then undergoes a self-limited resolution (driven by negative feedback loops) as the inflammatory mediators and tissue damage/“danger” signals return to their baseline values. In the aseptic death state, the pathogen is eliminated but the inflammatory response does not resolve; pro-inflammatory mediators and tissue damage remain elevated. Finally, the septic death response occurs when the inflammatory response is insufficient to clear the pathogen, resulting in elevated levels of all four model variables.
2.2. SDE Formulation and Integration
There are several different approaches that can be used to model noise in a dynamical system, most notably Gillespie’s algorithm [43] and the numerous more-recent extensions of Gillespie’s work. These algorithms are based on the concept of modeling discrete, molecular-level events. However, the model given in Equations (1)–(7) is not comprised of molecular-level variables, but instead is comprised of higher-level variables representing generalized responses. Therefore, we incorporated a more general noise term to study the impact of stochasticity on Equations (1)–(7). The ODE model described in the previous section was translated to SDEs,
where fi(x,t) is the original deterministic equation and the added term represents noise. W is a Wiener process with the following properties [44]:
W(0) = 0
For 0 ≤ t0 < t1 ≤ T, W(t1) − W(t0) is normally distributed with a mean of zero and a variance of t1 − t0.
For 0 ≤ t0 < t1 < t2 < t3 ≤ T, the values W(t3) − W(t2) and W(t1) − W(t0) are independent.
σi in Equation (8) is the noise level for a given variable. In the results shown here, each σi is set equal to a constant for simplicity, but more generally the noise term could be dependent on the state of the system. This type of SDE formulation has been previously applied to other biological systems [45,46,47].
While there are several algorithms for integrating SDEs, it is much more difficult to design an efficient algorithm for solving SDEs than for ODEs. Statistical error is generally much more important than discretization error when solving SDEs, so higher-order methods introduce significant overhead without improving practicality [48]. Adaptive time step methods are extremely efficient for solving ODEs because when the system is smooth, large time steps can often be used; with SDEs, this advantage is much less apparent because local noise is always present [49]. Thus, most practical numerical applications of SDEs use a simple integrator such as the Euler-Maruyama method [48], which was the method used to perform all of the stochastic integrations in this paper.
2.3. Stochastic Control Analysis
For evaluating noise control coefficients, we adopted the concepts introduced in the work of Kim and Sauro [42]. In short, control coefficients quantify the response of a system () due to a parameter perturbation () (Equation (9))
In our work, parameters (p) of Equation (9) represent the reaction rate constants shown in Equations (1)–(7). Regarding the ultimate system responses (r) in our model, these represent the tissue damage D (Equation (3)) mean () and noise level (). The noise level is defined as variance (covariance) divided by the mean square (product of two mean values). Noise levels were computed for infinitesimally small noises. From the computed noise levels and auto-correlations, we can ultimately calculate control direction (λ) as well as control strength (κ) and efficiency (e) as following:
where dot notation (·) in Equation (10) represents dot product of the two vectors, and absolute value brackets (││) in Equations (10) and (11), the magnitude of the vectors and λ.
3. Results
The “typical” stochastic simulations shown in Figure 2 were carried out for noise levels selected to be sufficiently large that 50% of the simulations led to the same steady state as in simulations lacking noise, but the other 50% led to a different steady state. For the four-variable model, as all variables have roughly the same magnitude, all of the noise levels were set to be equal so that σi = 0.01 for all i equations (Equation (8)). Initial conditions and parameters were set equal to those used in the “healthy outcome” state described in [17] and listed in Table 1 and Table 2. In other words, under deterministic integration, the model tended toward the healthy steady state, but when a significant amount of noise was added, the model result became unpredictable: simulations could either tend towards the healthy steady state or the aseptic death steady state, as shown for two representative profiles in Figure 2.
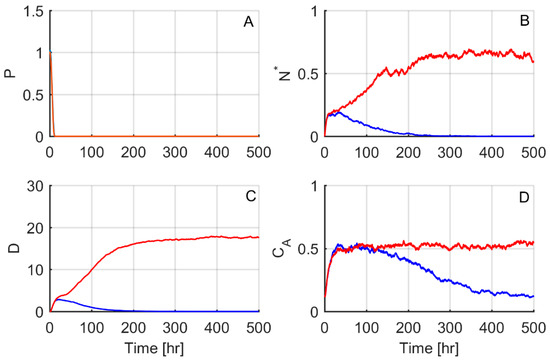
Figure 2.
A stochastic bifurcation leads to resolving and non-resolving responses. The responses of all four model variables (A–D) are shown for two different stochastic simulations, one that resolved to the healthy steady state (blue lines) and one to the aseptic death steady state (red lines). Parameters and initial conditions were set equal to the “healthy outcome” case of [17].
We next sought to further investigate why individual responses reach either the healthy or the aseptic death steady state. Figure 3A–C shows 1000 test cases where tissue damage dynamics are plotted for three different noise levels (σ). As noise increases from Figure 3A–C, inflammatory responses that ultimately lead to the aseptic death steady state (red lines) are increasing compared to responses that resolve to the healthy steady state (blue lines). In Figure 3D–F, as a representative quantity of the effect of the inflammatory response, the 24 h area under the curve (AUC) of phagocytes (N*) over AUC of anti-inflammatory mediator (CA), is plotted against the 24 h AUC of the inflammatory output of tissue damage (D). Figure 3D–F shows that the responses that ultimately reach the healthy steady state (blue circles) tend to maintain lower values, as compared to the profiles ultimately reaching the aseptic death state (red circles).
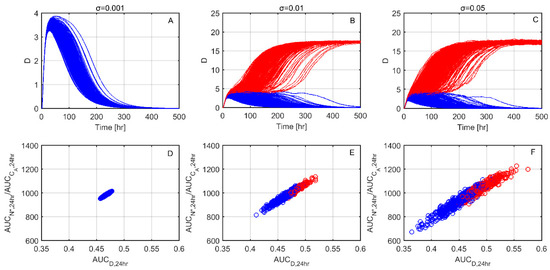
Figure 3.
Healthy vs. aseptic death dynamics for increasing noise levels (σ). (A–C) Tissue damage (D) time responses for increasing noise levels (σ). Blue lines indicate responses that reach the healthy steady state whereas red lines indicate responses that reach the aseptic death state. (D–F) 24 h AUC of phagocytes (N*) over 24 h AUC of anti-inflammatory mediators (CA) with respect to the 24 h AUC of tissue damage (D) (AUCD). In accordance with the upper panel blue circles indicate resolving profiles and red circles non-resolving.
The overall effect of noise relative to the level of the pathogen (P) introduced in the inflammatory network were investigated on Figure 4. As the representative inflammatory output, Figure 4 shows the distribution of tissue damage (D) end values at 500 h, for increasing levels of noise and inflammatory stimulus. For most scenarios tested, D end values maintain two distributions, one on high D values that represent the aseptic death steady state and one at low D values that represent the healthy outcome. For low pathogen concentrations (Figure 4A–E), increasing noise levels (σ) lead to more non-resolving steady state responses, as shown by the increasing frequency distribution on higher D values. Interestingly, for higher stimulus levels (Figure 4F–Y), an intermediate increase in noise levels (Figure 4F–H,K–M,P–R,U–X) drives more profiles to the healthy steady state. For the same stimulus, further increases in noise again drive most of the responses towards the aseptic death steady state (Figure 4H–J,M–O,R–T,X,Y). For a certain noise level, as the stimulus increases, this beneficial noise effect is diminishing, as shown by the lower D values on the lower D values distribution (Figure 4G,L,Q,V).
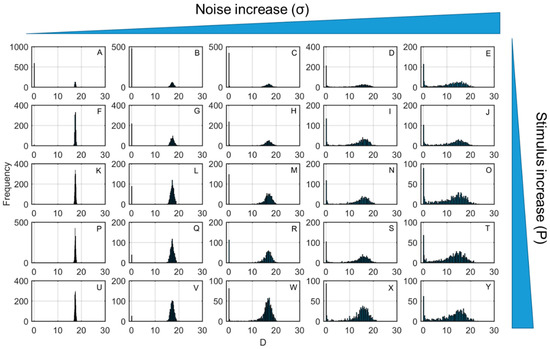
Figure 4.
Distribution of tissue damage (D) end values at 500 h for increasing levels of noise (σ) and pathogen stimulus (P). From left to right (e.g., from A to E, F to J, K to O, P to T, U to Y) noise level increases and from top to bottom (e.g., from A to U, B to V, C to W, D to X, E to Y), stimulus level (initial condition of P) increases.
Since the preceeding analysis suggests that inflammatory outcomes are highly dependent on noise, we hypothesized that controlling noise might represent a potential method by which to regulate inflammation. In Figure 5, parametric noise control was performed and values of control strength (κ) and efficiency (e) are shown. The vast majority of model parameters did not impact noise covariance and mean level signficantly. The two parameter sets that retained the highest control strength and efficiency were the maximum production rate of the anti-inflammatory mediator (kcn) with the strength of the anti-inflammatory mediator CA (cinf), as well as the maximum production rate of the anti-inflammatory mediator (kcn) with the source of resting phagocytes (snr), as shown by the larger circles and deeper blue colors in Figure 5. The activation of resting phagocytes by previously activated phagocytes and their cytokines (knp) together with most of the rest of model parameters was also shown to impact control efficiency, but their control strength values were relatively low. Other parameter sets shown to impact control efficiency and strength were (snr,μc), (snr,cinf) and (kcn,xdn).
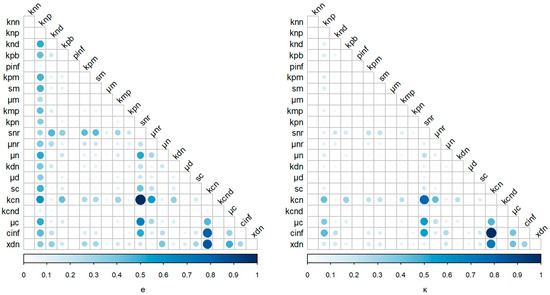
Figure 5.
Control efficiency (e) and strength (κ) values for the different parameters of the four-variable model. Circle size and color indicate the value of e and κ. Normalized units of efficiency and strength are shown for presentation purposes.
After evaluating control coefficients and calculating the parametric efficiencies and strengths, the most important set of parameters—(kcn,cinf)—was varied by ±1% and 5% and its impact as the percent of resolving profiles was investigated for three representative noise levels (Figure 6A–C). For all noise levels examined, higher kcn and lower cinf values drive more responses to the healthy steady state. Furthermore, the effect of a variation in one parameter on the “wrong” direction could be compensated by the change of the other. For example, for an intermediate noise level (σ = 0.01, Figure 6B), assuming that both parameters initially maintain their typical value, the effect on the “wrong” direction by 1% (seen as percent resolving profiles when kcn decreases) could be compensated if cinf was also decreased by 1%. As the noise level increases (Figure 6A–C), parameter adjustment becomes less efficient, as shown by the pale colors that further denote lower variation of the percent of resolving profiles.
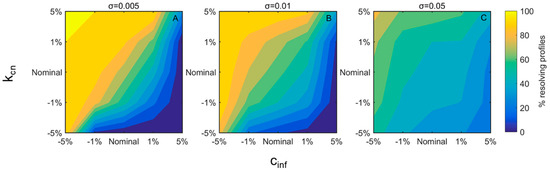
Figure 6.
Percent resolving profiles for different values of kcn and cinf at three noise levels (A–C). Parameters were varied by ±1% or ±5% of their nominal values shown in x- and y-axes. From blue to yellow the % resolving profiles are increasing. Different subplots represent different noise levels (σ).
Finally, we investigated whether adjustment of the appropriate parameters during the time of the inflammatory response could resolve some of the responses reaching the aseptic death steady state. In Figure 7, we evaluated whether adjustment of the set of parameters that retained the highest control efficiency and strength (kcn,cinf) by 10% during the progression of the inflammatory response could resolve otherwise non-resolving responses. Figure 7 shows the % of resolved responses relative to the time when parameters were adjusted. As time passes, it becomes more difficult to resolve a given profile from the aseptic death steady state. In particular, a 10% increase of kcn can recover nearly 20% of non-resolving responses when applied at 50 h, vs. 0% when applied after 200 h of the stimulus introduction. Similar results are shown for a 10% decrease of cinf, which recovers nearly 80% of the non-resolving profiles when applied at 50 h, as compared to nearly 0% again when applied at 200 h. Interestingly, orthogonal control both by kcn and cinf recovered more profiles and for an extended period of time after stimulus, suggesting a synergy between the maximum production rate of the anti-inflammatory mediator (kcn) and the strength of the anti-inflammatory mediator CA (cinf).
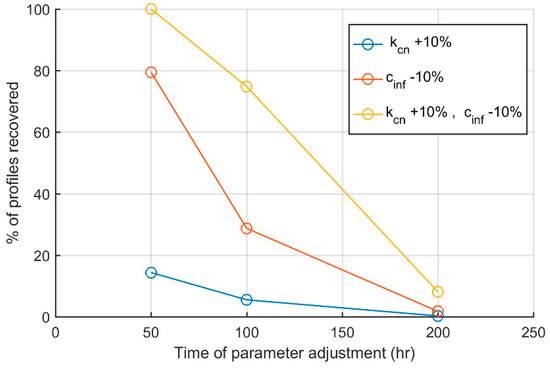
Figure 7.
Percent of profiles recovered as a function of the time when parameter adjustment was performed. Blue line indicates kcn increase by 10%, red line indicates cinf decrease by 10% and yellow a simultaneous increase of kcn and decrease of cinf by 10% for different times during the inflammatory response.
4. Discussion
Stochastic modeling can help elucidate stochastic dynamics of biological systems by revealing system behaviors which are only apparent in the presence of physiological noise [50,51,52]. Studying how inflammatory responses behave under noise is potentially critical for our overall understanding of the inflammatory response and the complexities involved [53], as well suggesting possibly non-intuitive, more effective therapeutic strategies.
Acute inflammation is a very important response of the body to infection and tissue injury, which involves highly complex cellular and molecular events associated to host defense, tissue remodeling and repair, and regulation of metabolism [1,54,55,56]. The innate immune response is initiated by the delivery of blood components to the site of infection or injury [57]. This initial recognition is mediated by production of a variety of inflammatory mediators such as cytokines and chemokines and results in a local response where plasma proteins and leukocytes access the infection and injury site. When they reach the afflicted site, neutrophils attempt to kill the invading agents by releasing toxic contents of their granules. After removal of the inflammatory agent it follows a resolution phase that is mediated mainly by tissue-resident and recruited macrophages (anti-inflammatory agents) [58]. However, activated neutrophils and their products also cause bystander tissue damage, resulting in the release of damage-associated molecular pattern (DAMP) molecules, which in turn can re-stimulate the activation of inflammatory cells and propagate further inflammation [59].
Our work in the present study shows that introducing a relatively small amount of noise to a system of the inflammatory response biases the system’s output by moving it to a different steady state. Thus, initial conditions designed to produce a healthy response [17] can lead to an unhealthy response in the presence of noise, highlighting the potential importance of taking into account stochasticity in the signaling events that govern the outcome of an inflammatory response. This transition between different steady states implies the existence of bistability, which is ultimately related to the positive feedback loops present in the inflammatory response [60]. These results are in overall agreement with prior stochastic models of inflammation that used an agent-based modeling formalism [19,20]. Due to our model’s abstraction, a quantitative characterization of noise level is difficult. We hypothesize that in the presence of biologically realistic noise, the presence of pathogen could lead to either healthy or unhealthy steady states with roughly equal probability.
To evaluate the effect of noise in the inflammatory response, in this work we used a reduced mathematical model that involves the variables of pathogen level (P), DAMP signals released from damaged tissues (D), inflammatory (N*), and anti-inflammatory agents (CA) [17]. The characteristics of bistability present in this model are related to the model structure as well as the parameter values that were either adopted from literature or estimated based on experimental evidence [18]. Despite its minimal structure that lacks explicit considerations of molecular mechanisms involved in inflammation, the model can capture qualitative dynamics of the real system such as tolerance and potentiation [18]. In particular, the health state is a fixed point with P = 0, N* = 0, D = 0, and CA = sc/mc and in aseptic death, P = 0, but N*, D, and CA are non-zero. Bistability analysis showed that the health steady state loses stability at a transcritical bifurcation when the pathogen growth rate (kpg) is 1.5. We interpret this to mean that, in the presence of realistic biological noise, infection with a bacterium whose growth rate is above a certain threshold would stimulate inflammation and lead to sepsis. This finding is in agreement with prior modeling studies which explored how different bacterial characteristics might lead to pathogenesis vs. a probiotic effect [38]. We acknowledge that the characterization of the effect of noise in the current model is only a first approximation of the real-world system. We hope to use the present study as a starting point for future studies on the impact of noise on more complex, and quantitatively realistic, models of acute inflammation in order to make specific and testable predictions.
For a constant inflammatory stimulus, our results suggest that noise regulates the inflammatory response in a level-dependent manner. For low noise levels, tissue damage tended toward the steady state at zero. However, at higher noise levels, the system tended toward the aseptic death steady state with an ever-greater probability ultimately reaching a state (noise levels σ = 0.05) at which the majority of the responses culminated in the aseptic death state. It is not immediately intuitive that adding increasingly large amounts of noise should bias the output towards one steady state at the expense of another. As random noise adds and subtracts equally from a given variable, it is not straightforward why or how this process should increase the probability of moving towards one or another steady state. Our simulations suggest that the responses that terminate in the aseptic death steady state tend to retain a higher 24-h area under the curve (AUC) of N* over CA for increasing tissue damage levels.
We may obtain some insights into this result from the field of pharmacology, in which AUC is commonly used to assess the extent of exposure of a drug in the body [61,62]. In the present work, the ratio of activated phagocytes (N*) AUC over the AUC of the level of anti-inflammatory mediators (CA), was used as a surrogate to evaluate the balance of the inflammatory response through its pro- and anti-inflammatory agents (N* and CA respectively). Up to 24 h, the response profiles for all simulations are inseparable, since the system has not yet reached the bifurcation point. However, our analysis indicates that even this time period can be informative, since responses that retain an excess of pro-inflammatory agents (higher ) tend to end up in the aseptic death steady state.
The interplay between pathogen stimulus (P) and noise introduced to the inflammatory system was also assessed. For low pathogen concentrations, increasing noise levels lead gradually more inflammatory responses to the unhealthy aseptic death steady state (Figure 4A–E). Similar behavior is observed when, for a certain noise levels, inflammatory stimulus is increased and gradually all profiles evolve to a non-resolving state (Figure 4 from top to bottom). Interestingly, for intermediate and high stimulus values, at which the majority of inflammatory responses culminate at the aseptic death state, intermediate noise increases can lead profiles towards a healthy resolution. Further increases of noise appear to reverse this beneficial effect, as again most of the inflammatory responses terminate to high tissue damages levels that signify aseptic death.
The influence of noise on biological systems has been intensively studied during recent years [63] with a particular focus on bistable systems [64]. Although the roles of noise level and network structure are appreciated as important factors for decision making [64], a theoretical understanding is still missing. Our work further indicates that depending on the level of stimulus introduced to the inflammatory network, a certain amount of intrinsic noise can be beneficial by mediating transitions from the unhealthy aseptic death state to healthy resolution (e.g., Figure 4K–M) before bistability vanishes for high noise levels. The advantageous effects of noise are already well appreciated in various scales of biological organization [63,65,66,67,68,69]. The impact of noise has been also appreciated in virus dynamics through computational modeling [70,71]. From an evolutionary perspective, the general notion is that molecular networks are designed in order to adapt to a continuously changing environment and noise facilitates their optimal function. A characteristic example is stochastic resonance, a phenomenon through which introduction of noise to a system facilitates the transmission of weak signals that are otherwise undetected [72,73]. Interestingly, this phenomenon occurs not only in artificial physical systems [74] but also naturally as has been shown on the crayfishes’ tailfans hair cells that respond optimally to stimuli when their environment retains intermediate noise [75]. Our work further underlines the potential benefits of noise in an inflammatory network where pro- and anti-inflammatory signals work in tandem to remove the pathogen and retain homeostasis.
Many current clinical practices in treating critical illness, such as mechanical ventilation, glucose control, and continuous intravenous feeding seek to reduce variability [76], and yet physiologic [77] and inflammatory [78] variability is a hallmark of a healthy response to stress [22,79]. Our simulations suggest that the ultimate outcome of clinical interventions which either add to, or take away from, a healthy degree of noise may vary based on individual factors in any given critically ill patient. Beneficial vs. detrimental outcomes appear to be dependent on the balance of pro- and anti-inflammatory mediators, which is in turn dependent both on the level of inflammatory stimulus introduced into the system as well as on the noise level.
In translational applications of inflammation modeling, the goal is to apply mechanistic models to personalized medicine, rational diagnosis, and optimization of clinical trials [40,41,80]. In that respect, control of noise inherent in physiological systems may well be critical. Attempts towards controlling variability in certain physiological systems could therefore be applied to specific areas that bias the system towards a desired response. Since the parameters of the inflammatory model used here represent certain physiological quantities, a parametric control analysis could yield insights into which physiological characteristics mostly affect noise, and ultimately impact the endpoint of the inflammatory response. Based on the work of Kim and Sauro [42], a stochastic control analysis was performed. The group of model parameters that most impacted noise levels were kcn and cinf. These parameters represent the maximum production rate of the anti-inflammatory mediators (CA) as well as the strength of the anti-inflammatory mediators. Notably, both parameters are related to the anti-inflammatory portion of the inflammatory response. An increase of kcn and concomitant decrease of cinf leads to an augmented anti-inflammatory response. snr, which represents the source of resting phagocytes, together with kcn were the second group of parameters that highly regulate noise characteristics. Overall, our analysis indicates that it is the components of the anti-inflammatory arm of the response which regulate noise characteristics. We hypothesize that at some point this property might be used to control the outcome of the inflammatory response.
In the clinical setting, patients often exhibit different outcomes even if their measurable states appear to be the same. However, appropriately controlling the amount of noise is important. Depending on the amount of noise in the system, a very small effect or a qualitatively different behavior (bifurcation to another steady state) might be observed. For a certain noise level, an increase of ani-inflammatory mediators or of the strength of the anti-inflammatory response (through decreasing cinf) leads more simulations to the healthy regime. In simulations with lower noise levels, appropriate adjustment of the inflammatory parameters prior to stimulus can drive all of the inflammatory responses to the healthy steady state. However, as noise increases, the effect of parameter adjustment becomes less efficient, being able to regulate only a portion of the simulated inflammatory responses.
Given recent interest in optimizing therapeutic strategies for inflammation [81,82] and the non-intuitive dynamics conferred on biological systems by noise [50], it is important to consider the influence of stochasticity in signaling pathways throughout the time that inflammatory response endures [83]. Our results suggest that noise early in the inflammatory response has the potential to switch the system from the unhealthy non-resolving state to the healthy resolving state. However, once the system has progressed significantly towards one steady state, away from the bifurcation point, a noise-induced switch in steady states becomes much less probable. This type of analysis, applied to more detailed, disease-specific models (e.g., [82]), could potentially identify time windows in which the physiological stability of a patient is most critical.
A challenge with this type of analysis is how to relate the noise added in this SDE formulation, via σ in Equation (8), with other types of computational models or experimental results. As the model used here is comprised of variables representing aggregate responses (such as tissue damage) rather than individual measurable quantities (such as levels of specific damage-associated molecular pattern molecules), it is difficult to derive a precise physiological meaning from the noise levels. As both experimental techniques and models become more refined, it will be increasingly plausible to have model variables whose noise levels can be measured directly. But even in the absence of this ideal, the influence of qualitatively realistic levels of noise can be assessed [45,46,47,84,85].
The results presented herein suggest that noise can exert either a healthy or unhealthy influence. It is interesting that variability in physiological signals has been found to be predictive of either positive or negative clinical outcomes, depending on the specific system and component being assessed. For instance, high variability in blood glucose levels has been linked to increased mortality in sepsis patients [86,87], yet low variability in heart rate is associated with increased morbidity in sepsis patients [76,88]. Appropriate noise adjustments through parametric control may thus ultimately help regulate inflammatory outcomes as well as enabling treatment at later times of the response.
Author Contributions
For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used I.P.A., J.D.S., P.D.M. and Y.V. conceived and designed the experiments; J.D.S. and P.D.M. performed the experiments; J.D.S. and P.D.M. analyzed the data; I.P.A., J.C.D., J.D.S., P.M. and Y.V. wrote the paper.
Funding
IPA acknowledges support from GM24211. YV acknowledges support from U.S. National Institutes of Health grants RO1-GM107231-01A1, U01EB021960-01A1, UO1-DK072146, and P50-GM-53789, as well as U.S. Department of Defense grants W81 XWH-15-1-0336, W81XWH-15-PRORP-OCRCA, W81 XWH-13-2-0061, and W911 QY-14-1-0003.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nathan, C. Points of control in inflammation. Nature 2002, 420, 846–852. [Google Scholar] [CrossRef] [PubMed]
- Reichlin, S. Neuroendocrine-immune interactions. N. Engl. J. Med. 1993, 329, 1246–1253. [Google Scholar]
- Tracey, K.J. The inflammatory reflex. Nature 2002, 420, 853–859. [Google Scholar] [CrossRef] [PubMed]
- Bone, R.C. Immunologic dissonance: A continuing evolution in our understanding of the systemic inflammatory response syndrome (SIRS) and the multiple organ dysfunction syndrome (MODS). Ann. Intern. Med. 1996, 125, 680–687. [Google Scholar] [CrossRef]
- Seely, A.J.; Christou, N.V. Multiple organ dysfunction syndrome: Exploring the paradigm of complex nonlinear systems. Crit. Care Med. 2000, 28, 2193–2200. [Google Scholar] [CrossRef] [PubMed]
- Namas, R.; Zamora, R.; Namas, R.; An, G.; Doyle, J.; Dick, T.E.; Jacono, F.J.; Androulakis, I.P.; Chang, S.; Billiar, T.R.; et al. Sepsis: Something old, something new, and a systems view. J. Crit. Care 2012, 27, 314.e1–314.e11. [Google Scholar] [CrossRef] [PubMed]
- Vodovotz, Y.; Csete, M.; Bartels, J.; Chang, S.; An, G. Translational systems biology of inflammation. PLoS Comput. Biol. 2008, 4, e1000014. [Google Scholar] [CrossRef]
- Vodovotz, Y.; Constantine, G.; Rubin, J.; Csete, M.; Voit, E.O.; An, G. Mechanistic simulations of inflammation: Current state and future prospects. Math. Biosci. 2009, 217, 1–10. [Google Scholar] [CrossRef]
- Vodovotz, Y.; Clermont, G.; Chow, C.; An, G. Mathematical models of the acute inflammatory response. Curr. Opin. Crit. Care 2004, 10, 383–390. [Google Scholar] [CrossRef]
- Prince, J.M.; Levy, R.M.; Bartels, J.; Baratt, A.; Kane, J.M., III; Lagoa, C.; Rubin, J.; Day, J.; Wei, J.; Fink, M.P. In silico and in vivo approach to elucidate the inflammatory complexity of CD14-deficient mice. Mol. Med. 2006, 12, 88. [Google Scholar] [CrossRef]
- Ben-David, I.; Price, S.E.; Bortz, D.M.; Greineder, C.F.; Cohen, S.E.; Bauer, A.L.; Jackson, T.L.; Younger, J.G. Dynamics of intrapulmonary bacterial growth in a murine model of repeated microaspiration. Am. J. Respir. Cell Mol. Boil. 2005, 33, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Chow, C.C.; Clermont, G.; Kumar, R.; Lagoa, C.; Tawadrous, Z.; Gallo, D.; Betten, B.; Bartels, J.; Constantine, G.; Fink, M.P. The acute inflammatory response in diverse shock states. Shock 2005, 24, 74–84. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Clermont, G.; Vodovotz, Y.; Chow, C.C. The dynamics of acute inflammation. J. Theor. Boil. 2004, 230, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Foteinou, P.; Calvano, S.; Lowry, S.; Androulakis, I. Modeling endotoxin-induced systemic inflammation using an indirect response approach. Math. Biosci. 2009, 217, 27–42. [Google Scholar] [CrossRef] [PubMed]
- Vodovotz, Y.; Chow, C.C.; Bartels, J.; Lagoa, C.; Prince, J.M.; Levy, R.M.; Kumar, R.; Day, J.; Rubin, J.; Constantine, G. In silico models of acute inflammation in animals. Shock 2006, 26, 235–244. [Google Scholar] [CrossRef]
- Alt, W.; Lauffenburger, D.A. Transient behavior of a chemotaxis system modelling certain types of tissue inflammation. J. Math. Boil. 1987, 24, 691–722. [Google Scholar] [CrossRef]
- Reynolds, A.; Rubin, J.; Clermont, G.; Day, J.; Vodovotz, Y.; Ermentrout, G.B. A reduced mathematical model of the acute inflammatory response: I. Derivation of model and analysis of anti-inflammation. J. Theor. Boil. 2006, 242, 220–236. [Google Scholar] [CrossRef]
- Day, J.; Rubin, J.; Vodovotz, Y.; Chow, C.C.; Reynolds, A.; Clermont, G. A reduced mathematical model of the acute inflammatory response II. Capturing scenarios of repeated endotoxin administration. J. Theor. Boil. 2006, 242, 237–256. [Google Scholar] [CrossRef]
- An, G. Agent-based computer simulation and sirs: Building a bridge between basic science and clinical trials. Shock (Augusta, GA) 2001, 16, 266–273. [Google Scholar] [CrossRef]
- An, G. In silico experiments of existing and hypothetical cytokine-directed clinical trials using agent-based modeling. Crit. Care Med. 2004, 32, 2050–2060. [Google Scholar] [CrossRef]
- Cockrell, C.; An, G. Sepsis Reconsidered: Identifying novel metrics for behavioral landscape characterization with a high-performance computing implementation of an agent-based model. J. Theor. Boil. 2017, 430, 157–168. [Google Scholar] [CrossRef] [PubMed]
- Scheff, J.D.; Mavroudis, P.D.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. Modeling autonomic regulation of cardiac function and heart rate variability in human endotoxemia. Physiol. Genom. 2011, 43, 951–964. [Google Scholar] [CrossRef] [PubMed]
- Scheff, J.D.; Mavroudis, P.D.; Calvano, S.E.; Androulakis, I.P. Translational applications of evaluating physiologic variability in human endotoxemia. J. Clin. Monit. Comput. 2013, 27, 405–415. [Google Scholar] [CrossRef] [PubMed]
- Scheff, J.D.; Mavroudis, P.D.; Foteinou, P.T.; Calvano, S.E.; Androulakis, I.P. Modeling physiologic variability in human endotoxemia. Crit. Rev. Biomed. Eng. 2012, 40, 313–322. [Google Scholar] [CrossRef] [PubMed]
- Scheff, J.D.; Mavroudis, P.D.; Foteinou, P.T.; An, G.; Calvano, S.E.; Doyle, J.; Dick, T.E.; Lowry, S.F.; Vodovotz, Y.; Androulakis, I.P. A multiscale modeling approach to inflammation: A case study in human endotoxemia. J. Comput. Phys. 2013, 244, 279–289. [Google Scholar] [CrossRef]
- Scheff, J.D.; Mavroudis, P.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. Towards in silico models of decomplexification in human endotoxemia. Comput. Aided Chem. Eng. 2011, 29, 1485–1489. [Google Scholar]
- Brown, E.N.; Meehan, P.M.; Dempster, A.P. A stochastic differential equation model of diurnal cortisol patterns. Am. J. Physiol. Endocrinol. Metab. 2001, 280, E450–E461. [Google Scholar] [CrossRef]
- Lipniacki, T.; Paszek, P.; Brasier, A.R.; Luxon, B.A.; Kimmel, M. Stochastic regulation in early immune response. Biophys. J. 2006, 90, 725–742. [Google Scholar] [CrossRef]
- Dong, X.; Foteinou, P.T.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. Agent-based modeling of endotoxin-induced acute inflammatory response in human blood leukocytes. PLoS ONE 2010, 5, e9249. [Google Scholar] [CrossRef]
- An, G. Introduction of an agent-based multi-scale modular architecture for dynamic knowledge representation of acute inflammation. Theor. Biol. Med. Model. 2008, 5, 11. [Google Scholar] [CrossRef]
- Mi, Q.; Riviere, B.; Clermont, G.; Steed, D.L.; Vodovotz, Y. Agent-based model of inflammation and wound healing: Insights into diabetic foot ulcer pathology and the role of transforming growth factor-beta1. Wound Repair Regen. 2007, 15, 671–682. [Google Scholar] [CrossRef] [PubMed]
- Ziraldo, C.; Solovyev, A.; Allegretti, A.; Krishnan, S.; Henzel, M.K.; Sowa, G.A.; Brienza, D.; An, G.; Mi, Q.; Vodovotz, Y. A computational, tissue-realistic model of pressure ulcer formation in Individuals with spinal cord injury. PLoS Comput. Biol. 2015, 11, e1004309. [Google Scholar] [CrossRef]
- Foteinou, P.T.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. A physiological model for autonomic heart rate regulation in human endotoxemia. Shock 2011, 35, 229–239. [Google Scholar] [CrossRef] [PubMed]
- Foteinou, P.T.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. Multiscale model for the assessment of autonomic dysfunction in human endotoxemia. Physiol. Genomics 2010, 42, 5–19. [Google Scholar] [CrossRef] [PubMed]
- Scheff, J.D.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. Modeling the influence of circadian rhythms on the acute inflammatory response. J. Theor. Biol. 2010, 264, 1068–1076. [Google Scholar] [CrossRef]
- Torres, A.; Bentley, T.; Bartels, J.; Sarkar, J.; Barclay, D.; Namas, R.; Constantine, G.; Zamora, R.; Puyana, J.C.; Vodovotz, Y. Mathematical modeling of posthemorrhage inflammation in mice: Studies using a novel, computer-controlled, closed-loop hemorrhage apparatus. Shock 2009, 32, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.; Namas, R.A.; Almahmoud, K.; Zaaqoq, A.; Sarkar, J.; Barclay, D.A.; Yin, J.; Ghuma, A.; Abboud, A.; Constantine, G.; et al. Trauma in silico: Individual-specific mathematical models and virtual clinical populations. Sci. Transl. Med. 2015, 7, 285ra261. [Google Scholar] [CrossRef] [PubMed]
- Arciero, J.C.; Ermentrout, G.B.; Upperman, J.S.; Vodovotz, Y.; Rubin, J.E. Using a mathematical model to analyze the role of probiotics and inflammation in necrotizing enterocolitis. PLoS ONE 2010, 5, e10066. [Google Scholar] [CrossRef] [PubMed]
- Foteinou, P.T.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. In silico simulation of corticosteroids effect on an NFkB-dependent physicochemical model of systemic inflammation. PLoS ONE 2009, 4, e4706. [Google Scholar] [CrossRef]
- Vodovotz, Y. Translational systems biology of inflammation and healing. Wound Repair Regen. 2010, 18, 3–7. [Google Scholar] [CrossRef]
- Clermont, G.; Bartels, J.; Kumar, R.; Constantine, G.; Vodovotz, Y.; Chow, C. In silico design of clinical trials: A method coming of age. Crit. Care Med. 2004, 32, 2061–2070. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.H.; Sauro, H.M. Adjusting phenotypes by noise control. PLoS Comput. Biol. 2012, 8, e1002344. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. Soc. Ind. Appl. Math. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Saarinen, A.; Linne, M.L.; Yli-Harja, O. Modeling single neuron behavior using stochastic differential equations. Neurocomputing 2006, 69, 1091–1096. [Google Scholar] [CrossRef]
- Saarinen, A.; Linne, M.L.; Yli-Harja, O. Stochastic differential equation model for cerebellar granule cell excitability. PLoS Comput. Biol. 2008, 4, e1000004. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.C.; Wang, T.Y.; Tseng, H.H.; Huang, C.Y.; Kao, C.Y. A stochastic differential equation model for quantifying transcriptional regulatory network in Saccharomyces cerevisiae. Bioinformatics 2005, 21, 2883–2890. [Google Scholar] [CrossRef]
- Higham, D.J. Stochastic ordinary differential equations in applied and computational mathematics. Univ. Strathclyde Math. Stat. Res. Rep. 2010, 7, 1–32. [Google Scholar] [CrossRef]
- Lamba, H. An adaptive timestepping algorithm for stochastic differential equations. J. Comput. Appl. Math. 2003, 161, 417–430. [Google Scholar] [CrossRef]
- Rao, C.V.; Wolf, D.M.; Arkin, A.P. Control, exploitation and tolerance of intracellular noise. Nature 2002, 420, 231–237. [Google Scholar] [CrossRef]
- Arkin, A.; Ross, J.; McAdams, H.H. Stochastic kinetic analysis of developmental pathway bifurcation in phage lambda-infected Escherichia coli cells. Genetics 1998, 149, 1633–1648. [Google Scholar] [PubMed]
- Samoilov, M.; Plyasunov, S.; Arkin, A.P. Stochastic amplification and signaling in enzymatic futile cycles through noise-induced bistability with oscillations. Proc. Natl. Acad. Sci. USA 2005, 102, 2310–2315. [Google Scholar] [CrossRef] [PubMed]
- Qian, H.; Shi, P.Z.; Xing, J. Stochastic bifurcation, slow fluctuations, and bistability as an origin of biochemical complexity. Phys. Chem. Chem. Phys. 2009, 11, 4861–4870. [Google Scholar] [CrossRef] [PubMed]
- Medzhitov, R. Origin and physiological roles of inflammation. Nature 2008, 454, 428–435. [Google Scholar] [CrossRef] [PubMed]
- Hotamisligil, G.S. Inflammation and metabolic disorders. Nature 2006, 444, 860–867. [Google Scholar] [CrossRef] [PubMed]
- Medzhitov, R.; Horng, T. Transcriptional control of the inflammatory response. Nat. Rev. Immunol. 2009, 9, 692–703. [Google Scholar] [CrossRef] [PubMed]
- Majno, G.; Joris, I. Cells, Tissues, and Disease: Principles of General Pathology; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Serhan, C.N.; Savill, J. Resolution of inflammation: The beginning programs the end. Nat. Immunol. 2005, 6, 1191–1197. [Google Scholar] [CrossRef] [PubMed]
- Andersson, U.; Tracey, K.J. HMGB1 is a therapeutic target for sterile inflammation and infection. Annu. Rev. Immunol. 2011, 29, 139–162. [Google Scholar] [CrossRef]
- Beutler, B. Microbe sensing, positive feedback loops, and the pathogenesis of inflammatory diseases. Immunol. Rev. 2009, 227, 248–263. [Google Scholar] [CrossRef]
- Krzyzanski, W.; Jusko, W.J. Integrated functions for four basic models of indirect pharmacodynamic response. J. Pharm. Sci. 1998, 87, 67–72. [Google Scholar] [CrossRef]
- Scheff, J.D.; Almon, R.R.; Dubois, D.C.; Jusko, W.J.; Androulakis, I.P. Assessment of pharmacologic area under the curve when baselines are variable. Pharm. Res. 2011, 28, 1081–1089. [Google Scholar] [CrossRef] [PubMed]
- Eldar, A.; Elowitz, M.B. Functional roles for noise in genetic circuits. Nature 2010, 467, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Balazsi, G.; van Oudenaarden, A.; Collins, J.J. Cellular decision making and biological noise: From microbes to mammals. Cell 2011, 144, 910–925. [Google Scholar] [CrossRef] [PubMed]
- Qian, H. Cooperativity in cellular biochemical processes: Noise-enhanced sensitivity, fluctuating enzyme, bistability with nonlinear feedback, and other mechanisms for sigmoidal responses. Annu. Rev. Biophys. 2012, 41, 179–204. [Google Scholar] [CrossRef] [PubMed]
- Blake, W.J.; Kærn, M.; Cantor, C.R.; Collins, J.J. Noise in eukaryotic gene expression. Nature 2003, 422, 633–637. [Google Scholar] [CrossRef] [PubMed]
- Paulsson, J.; Berg, O.G.; Ehrenberg, M. Stochastic focusing: Fluctuation-enhanced sensitivity of intracellular regulation. Proc. Natl. Acad. Sci. USA 2000, 97, 7148–7153. [Google Scholar] [CrossRef] [PubMed]
- Kærn, M.; Elston, T.C.; Blake, W.J.; Collins, J.J. Stochasticity in gene expression: From theories to phenotypes. Nat. Rev. Genet. 2005, 6, 451–464. [Google Scholar] [CrossRef]
- Kussell, E.; Leibler, S. Phenotypic diversity, population growth, and information in fluctuating environments. Science 2005, 309, 2075–2078. [Google Scholar] [CrossRef]
- Read, E.L.; Tovo-Dwyer, A.A.; Chakraborty, A.K. Stochastic effects are important in intrahost HIV evolution even when viral loads are high. Proc. Natl Acad. Sci. USA 2012, 109, 19727–19732. [Google Scholar] [CrossRef]
- Luzyanina, T.; Bocharov, G. Stochastic modeling of the impact of random forcing on persistent hepatitis B virus infection. Math. Comput. Simul. 2014, 96, 54–65. [Google Scholar] [CrossRef]
- Wiesenfeld, K.; Moss, F. Stochastic resonance and the benefits of noise: From ice ages to crayfish and SQUIDs. Nature 1995, 373, 33–36. [Google Scholar] [CrossRef] [PubMed]
- Hänggi, P. Stochastic resonance in biology how noise can enhance detection of weak signals and help improve biological information processing. ChemPhysChem 2002, 3, 285–290. [Google Scholar] [CrossRef]
- Longtin, A.; Bulsara, A.; Moss, F. Time-interval sequences in bistable systems and the noise-induced transmission of information by sensory neurons. Phys. Rev. Lett. 1991, 67, 656–659. [Google Scholar] [CrossRef] [PubMed]
- Douglass, J.K.; Wilkens, L.; Pantazelou, E.; Moss, F. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature 1993, 365, 337–340. [Google Scholar] [CrossRef] [PubMed]
- Lowry, S.F. The stressed host response to infection: The disruptive signals and rhythms of systemic inflammation. Surg. Clin. North Am. 2009, 89, 311–326. [Google Scholar] [CrossRef] [PubMed]
- Lowry, S.F.; Calvano, S.E. Challenges for modeling and interpreting the complex biology of severe injury and inflammation. J. Leukoc. Biol. 2008, 83, 553–557. [Google Scholar] [CrossRef] [PubMed]
- Mi, Q.; Constantine, G.; Ziraldo, C.; Solovyev, A.; Torres, A.; Namas, R.; Bentley, T.; Billiar, T.R.; Zamora, R.; Puyana, J.C.; et al. A dynamic view of trauma/hemorrhage-induced inflammation in mice: Principal drivers and networks. PLoS ONE 2011. [Google Scholar] [CrossRef]
- Mavroudis, P.D.; Corbett, S.A.; Calvano, S.E.; Androulakis, I.P. Circadian characteristics of permissive and suppressive effects of cortisol and their role in homeostasis and the acute inflammatory response. Math. Biosci. 2015, 260, 54–64. [Google Scholar] [CrossRef]
- Foteinou, P.T.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. Translational potential of systems-based models of inflammation. Clin. Transl. Sci. 2009, 2, 85–89. [Google Scholar] [CrossRef]
- Day, J.; Rubin, J.; Clermont, G. Using nonlinear model predictive control to find optimal therapeutic strategies to modulate inflammation. Math. Biosci. Eng. 2010, 7, 739–763. [Google Scholar] [CrossRef]
- Petersen, B.K.; Uang, J.; Grathwohl, W.S.; Cockrell, C.; Santiago, C.; An, G.; Faissol, D.M. Precision medicine as a control problem: Using simulation and deep reinforcement learning to discover adaptive, personalized multi-cytokine therapy for sepsis. arXiv, 2018; arXiv:1802.10440. [Google Scholar]
- Lestas, I.; Vinnicombe, G.; Paulsson, J. Fundamental limits on the suppression of molecular fluctuations. Nature 2010, 467, 174–178. [Google Scholar] [CrossRef] [PubMed]
- Manninen, T.; Linne, M.L.; Ruohonen, K. Developing Ito stochastic differential equation models for neuronal signal transduction pathways. Comput. Biol. Chem. 2006, 30, 280–291. [Google Scholar] [CrossRef] [PubMed]
- Steuer, R. Effects of stochasticity in models of the cell cycle: From quantized cycle times to noise-induced oscillations. J. Theor. Biol. 2004, 228, 293–301. [Google Scholar] [CrossRef] [PubMed]
- Ali, N.A.; O’Brien, J.M., Jr.; Dungan, K.; Phillips, G.; Marsh, C.B.; Lemeshow, S.; Connors, A.F., Jr.; Preiser, J.C. Glucose variability and mortality in patients with sepsis. Crit. Care Med. 2008, 36, 2316–2321. [Google Scholar] [CrossRef] [PubMed]
- Spapen, H.D. The glycemia threat in sepsis: Too high, too low, or too... variable! Crit. Care Med. 2008, 36, 2459–2460. [Google Scholar] [CrossRef] [PubMed]
- Annane, D.; Trabold, F.; Sharshar, T.; Jarrin, I.; Blanc, A.S.; Raphael, J.C.; Gajdos, P. Inappropriate sympathetic activation at onset of septic shock: A spectral analysis approach. Am. J. Respir. Crit. Care Med. 1999, 160, 458–465. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).