Extreme Multiclass Classification Criteria
Abstract
1. Introduction
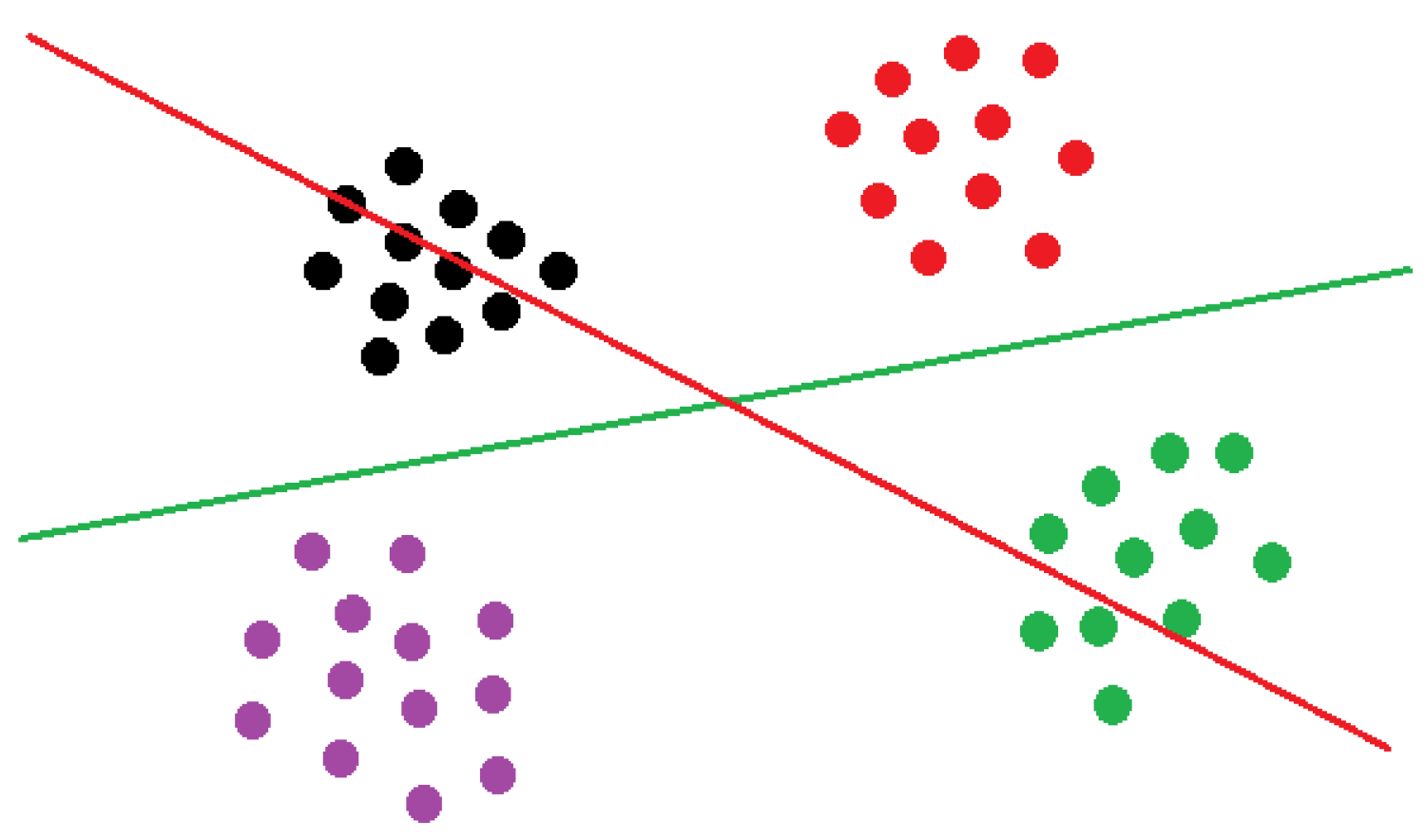
- We provide an extensive theoretical analysis of the properties of the considered objective and prove that maximizing this objective in any tree node simultaneously encourages balanced partition of the data in that node and improves the purity of the class distributions at its children nodes.
- We show a formal relation of this objective to some more standard entropy-based objectives, i.e., Shannon entropy, Gini-entropy and its modified variant, for which online optimization schemes in the context of multiclass classification are largely unknown. In particular we show that i) the improvement in the value of entropy resulting from performing the node split is lower-bounded by an expression that increases with the value of the objective and thus ii) the considered objective can be used as a surrogate function for indirectly optimizing any of the three considered entropy-based criteria.
- We present three boosting theorems for each of the three entropy criteria, which provide the number of iterations needed to reduce each of them below an arbitrary threshold. Their weak hypothesis assumptions rely on the considered objective function.
- We establish the error bound that relates maximizing the objective function with reducing the multi-class classification error.
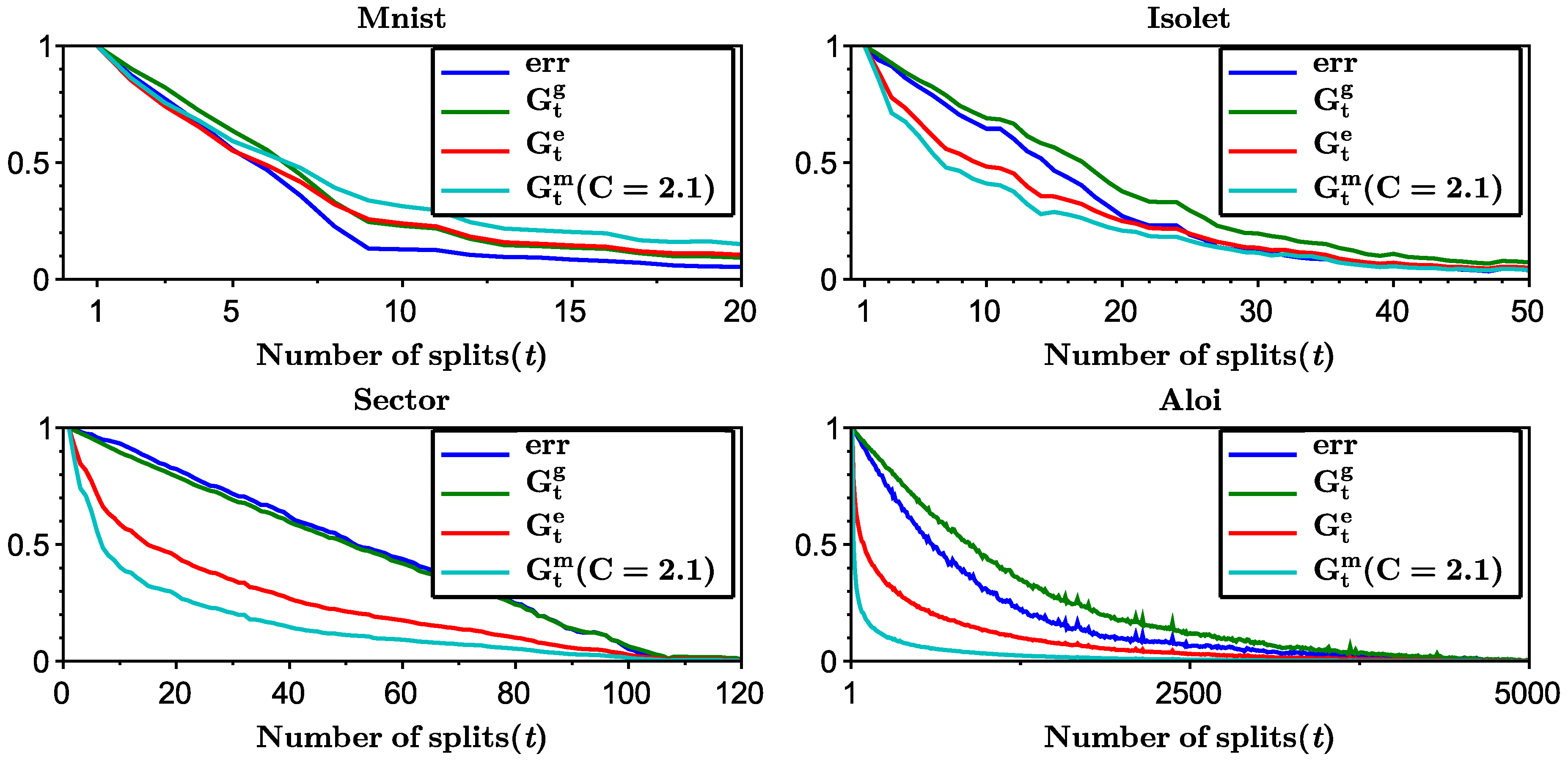
- Finally, in the Appendix A we establish an empirical connection between the multiclass classification error and the entropy criteria and show that Gini-entropy most closely resembles the behavior of the test error in practice.
2. Related Work
3. Theoretical Properties of the Objective Function
4. Main Theoretical Results
4.1. Notation
- Shannon entropy :
- Gini-entropy :
- Modified Gini-entropy :where is a constant such that .
4.2. Theorems
5. Proofs
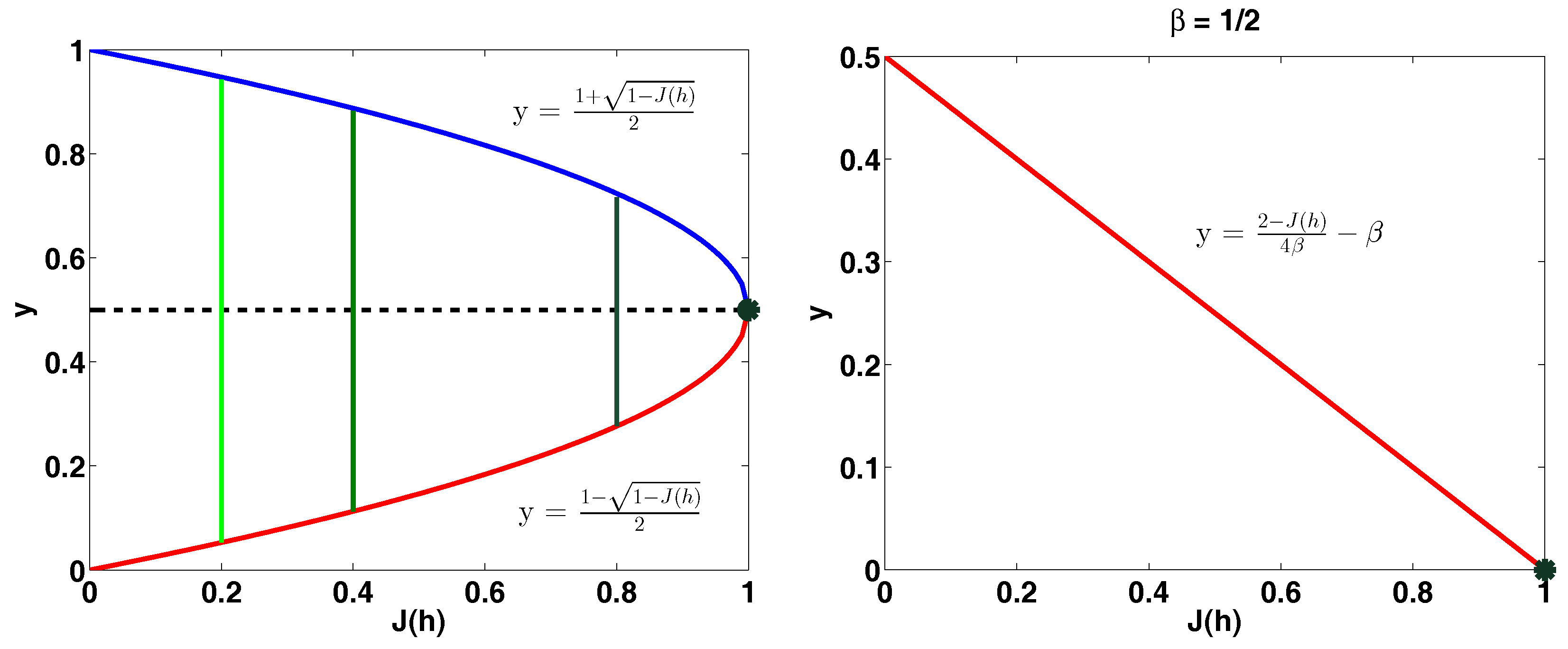
5.1. Properties of the Entropy-Based Criteria
5.1.1. Bounds on the Entropy-Based Criteria
5.1.2. Strong Concativity Properties of the Entropy-Based Criteria
5.2. Proof of Lemma 4 and Theorems 1–3
5.3. Proof of Theorem 4
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Extreme Multiclass Classification Criteria
Appendix A.1. Numerical Experiments
Appendix A.2. Additional Proofs
- Let . ThenThus which, when solved, yields the lemma.
- Let (thus ). Note that can be written assince and . Let , and . Note that and . Also note that . ThusThus as before we obtain which, when solved, yields the lemma. □
References
- Rifkin, R.; Klautau, A. In Defense of One-Vs-All Classification. J. Mach. Learn. Res. 2004, 5, 101–141. [Google Scholar]
- Daume, H.; Karampatziakis, N.; Langford, J.; Mineiro, P. Logarithmic Time One-Against-Some. arXiv, 2016; arXiv:1606.04988. [Google Scholar]
- Choromanska, A.; Langford, J. Logarithmic Time Online Multiclass prediction. In Neural Information Processing Systems 2015; Neural Information Processing Systems Foundation, Inc.: Vancouver, BC, Canada, 2015. [Google Scholar]
- Schapire, R.E.; Freund, Y. Boosting: Foundations and Algorithms; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Mukherjee, I.; Schapire, R.E. A theory of multiclass boosting. J. Mach. Learn. Res. 2013, 14, 437–497. [Google Scholar]
- Beygelzimer, A.; Langford, J.; Ravikumar, P.D. Error-Correcting Tournaments. In Algorithmic Learning Theory; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Takimoto, E.; Maruoka, A. Top-down Decision Tree Learning As Information Based Boosting. Theor. Comput. Sci. 2003, 292, 447–464. [Google Scholar] [CrossRef]
- Morin, F.; Bengio, Y. Hierarchical probabilistic neural network language model. Aistats 2005, 5, 246–252. [Google Scholar]
- Bengio, S.; Weston, J.; Grangier, D. Label Embedding Trees for Large Multi-Class Tasks. In Advances in Neural Information Processing Systems 23 (NIPS 2010); NIPS: Vancouver, BC, Canada, 2010. [Google Scholar]
- Utgoff, P.E. Incremental Induction of Decision Trees. Mach. Learn. 1989, 4, 161–186. [Google Scholar] [CrossRef]
- Domingos, P.; Hulten, G. Mining High-speed Data Streams; KDD: Boston, MA, USA, 2000. [Google Scholar]
- Gama, J.; Rocha, R.; Medas, P. Accurate Decision Trees for Mining High-speed Data Streams. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003. [Google Scholar]
- Beygelzimer, A.; Langford, J.; Lifshits, Y.; Sorkin, G.B.; Strehl, A.L. Conditional Probability Tree Estimation Analysis and Algorithms. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009. [Google Scholar]
- Madzarov, G.; Gjorgjevikj, D.; Chorbev, I. A Multi-class SVM Classifier Utilizing Binary Decision Tree. Informatica 2009, 33, 225–233. [Google Scholar]
- Weston, J.; Makadia, A.; Yee, H. Label Partitioning For Sublinear Ranking. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Deng, J.; Satheesh, S.; Berg, A.C.; Fei-Fei, L. Fast and Balanced: Efficient Label Tree Learning for Large Scale Object Recognition. In Advances in Neural Information Processing Systems 24 (NIPS 2011); NIPS: Vancouver, BC, Canada, 2011. [Google Scholar]
- Zhao, B.; Xing, E.P. Sparse Output Coding for Large-Scale Visual Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Hsu, D.; Kakade, S.; Langford, J.; Zhang, T. Multi-Label Prediction via Compressed Sensing. In Advances in Neural Information Processing Systems 22 (NIPS 2009); NIPS: Vancouver, BC, Canada, 2009. [Google Scholar]
- Agarwal, A.; Kakade, S.M.; Karampatziakis, N.; Song, L.; Valiant, G. Least Squares Revisited: Scalable Approaches for Multi-class Prediction. In Proceedings of the 31st International Conference on Machine Learning (ICML 2014), Beijing, China, 21–26 June 2014. [Google Scholar]
- Beijbom, O.; Saberian, M.; Kriegman, D.; Vasconcelos, N. Guess-Averse Loss Functions For Cost-Sensitive Multiclass Boosting. In Proceedings of the 31st International Conference on Machine Learning (ICML 2014), Beijing, China, 21–26 June 2014. [Google Scholar]
- Jernite, Y.; Choromanska, A.; Sontag, D. Simultaneous Learning of Trees and Representations for Extreme Classification and Density Estimation. arXiv, 2017; arXiv:1610.04658. [Google Scholar]
- Mnih, A.; Hinton, G.E. A Scalable Hierarchical Distributed Language Model. In Advances in Neural Information Processing Systems 21 (NIPS 2008); NIPS: Vancouver, BC, Canada, 2009. [Google Scholar]
- Djuric, N.; Wu, H.; Radosavljevic, V.; Grbovic, M.; Bhamidipati, N. Hierarchical Neural Language Models for Joint Representation of Streaming Documents and their Content. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems 26 (NIPS 2013); NIPS: Vancouver, BC, Canada, 2013. [Google Scholar]
- Kearns, M.; Mansour, Y. On the Boosting Ability of Top-Down Decision Tree Learning Algorithms. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing (STOC ’96), Philadelphia, PA, USA, 22–24 May 1996. reprinted in J. Comput. Syst. Sci. 1999, 58, 109–128. [Google Scholar] [CrossRef]
- Breiman, L. Classification Regression Trees; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Liu, W.; Tsang, I.W. Making decision trees feasible in ultrahigh feature and label dimensions. J. Mach. Learn. Res. 2017, 18, 2814–2849. [Google Scholar]
- Muñoz, E.; Nováček, V.; Vandenbussche, P.Y. Facilitating prediction of adverse drug reactions by using knowledge graphs and multi-label learning models. Brief. Bioinform. 2017, 20, 190–202. [Google Scholar] [CrossRef] [PubMed]
- Charte, F.; Rivera, A.J.; del Jesus, M.J.; Herrera, F. REMEDIAL-HwR: Tackling multilabel imbalance through label decoupling and data resampling hybridization. Neurocomputing 2019, 326, 110–122. [Google Scholar] [CrossRef]
- Koster, C.H.; Seutter, M.; Beney, J. Multi-classification of patent applications with Winnow. In International Andrei Ershov Memorial Conference on Perspectives of System Informatics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 546–555. [Google Scholar]
- Liu, W.; Tsang, I.W.; Müller, K.R. An easy-to-hard learning paradigm for multiple classes and multiple labels. J. Mach. Learn. Res. 2017, 18, 3300–3337. [Google Scholar]
- Liu, W.; Xu, D.; Tsang, I.W.; Zhang, W. Metric learning for multi-output tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 408–422. [Google Scholar] [CrossRef] [PubMed]
- Petersen, N.C.; Rodrigues, F.; Pereira, F.C. Multi-output bus travel time prediction with convolutional LSTM neural network. Expert Syst. Appl. 2019, 120, 426–435. [Google Scholar] [CrossRef]
- Langford, J.; Li, L.; Strehl, A. Vowpal Wabbit (Fast Learning). 2007. Available online: http://hunch.net/~vw (accessed on 2 February 2019).
- Bottou, L. Online Algorithms and Stochastic Approximations. In Online Learning and Neural Networks; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Shalev-Shwartz, S. Online Learning and Online Convex Optimization. Found. Trends Mach. Learn. 2012, 4, 107–194. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S. Online Learning: Theory, Algorithms, and Applications. Ph.D. Thesis, The Hebrew University of Jerusalem, Jerusalem, Israel, 2007. [Google Scholar]
- Zhukovskiy, V. Lyapunov Functions in Differential Games; Stability and Control: Theory, Methods and Applications; Taylor & Francis: London, UK, 2003. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choromanska, A.; Kumar Jain, I. Extreme Multiclass Classification Criteria. Computation 2019, 7, 16. https://doi.org/10.3390/computation7010016
Choromanska A, Kumar Jain I. Extreme Multiclass Classification Criteria. Computation. 2019; 7(1):16. https://doi.org/10.3390/computation7010016
Chicago/Turabian StyleChoromanska, Anna, and Ish Kumar Jain. 2019. "Extreme Multiclass Classification Criteria" Computation 7, no. 1: 16. https://doi.org/10.3390/computation7010016
APA StyleChoromanska, A., & Kumar Jain, I. (2019). Extreme Multiclass Classification Criteria. Computation, 7(1), 16. https://doi.org/10.3390/computation7010016




