Multi Similarity Metric Fusion in Graph-Based Semi-Supervised Learning
Abstract
1. Introduction
2. An Overview on Multi-Metric Fusion
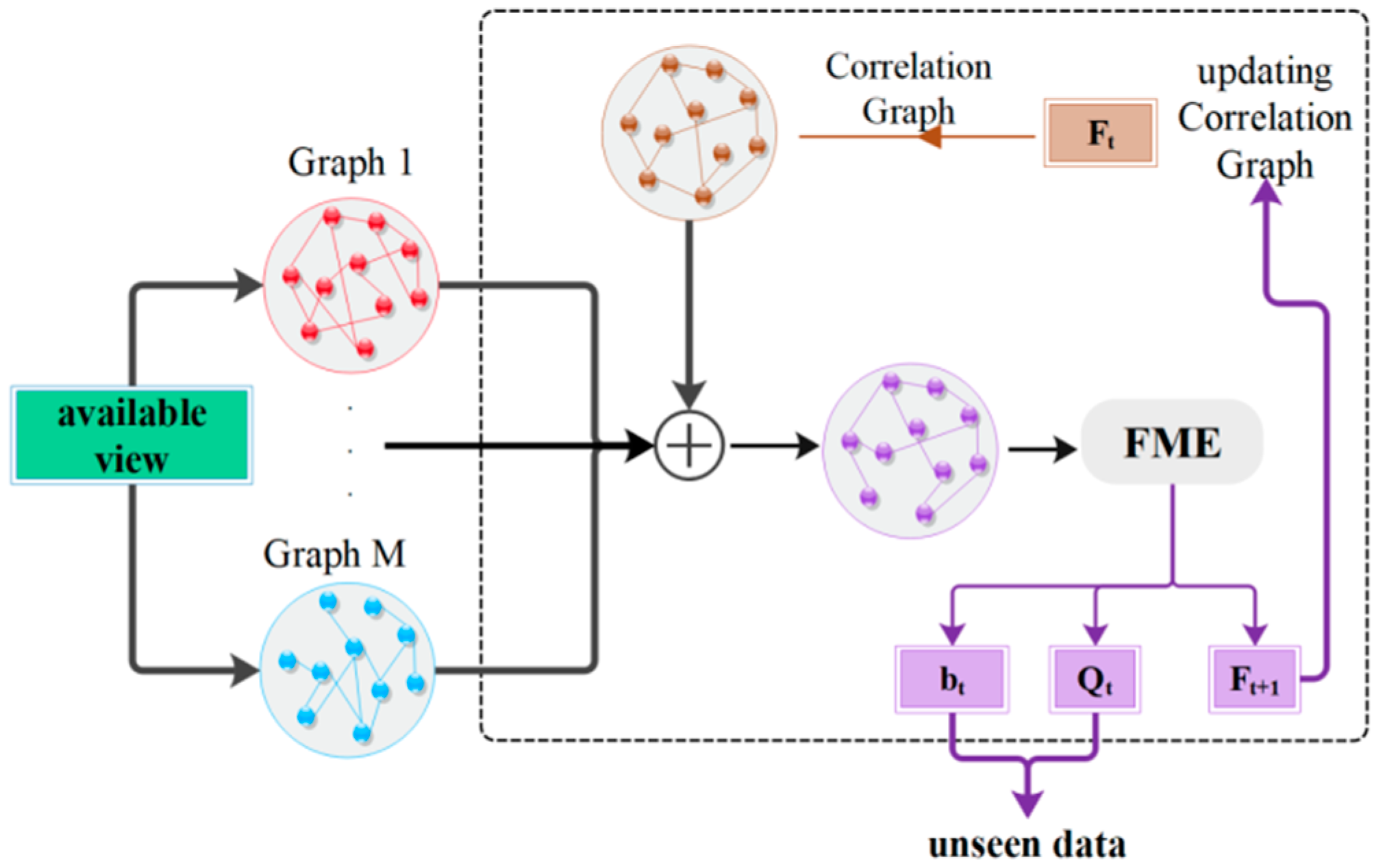
3. Proposed Method
3.1. Review of Flexible Manifold Embedding (FME)
3.2. Multi Similarity Metric Fusion
3.3. Incorporating Label Space Information
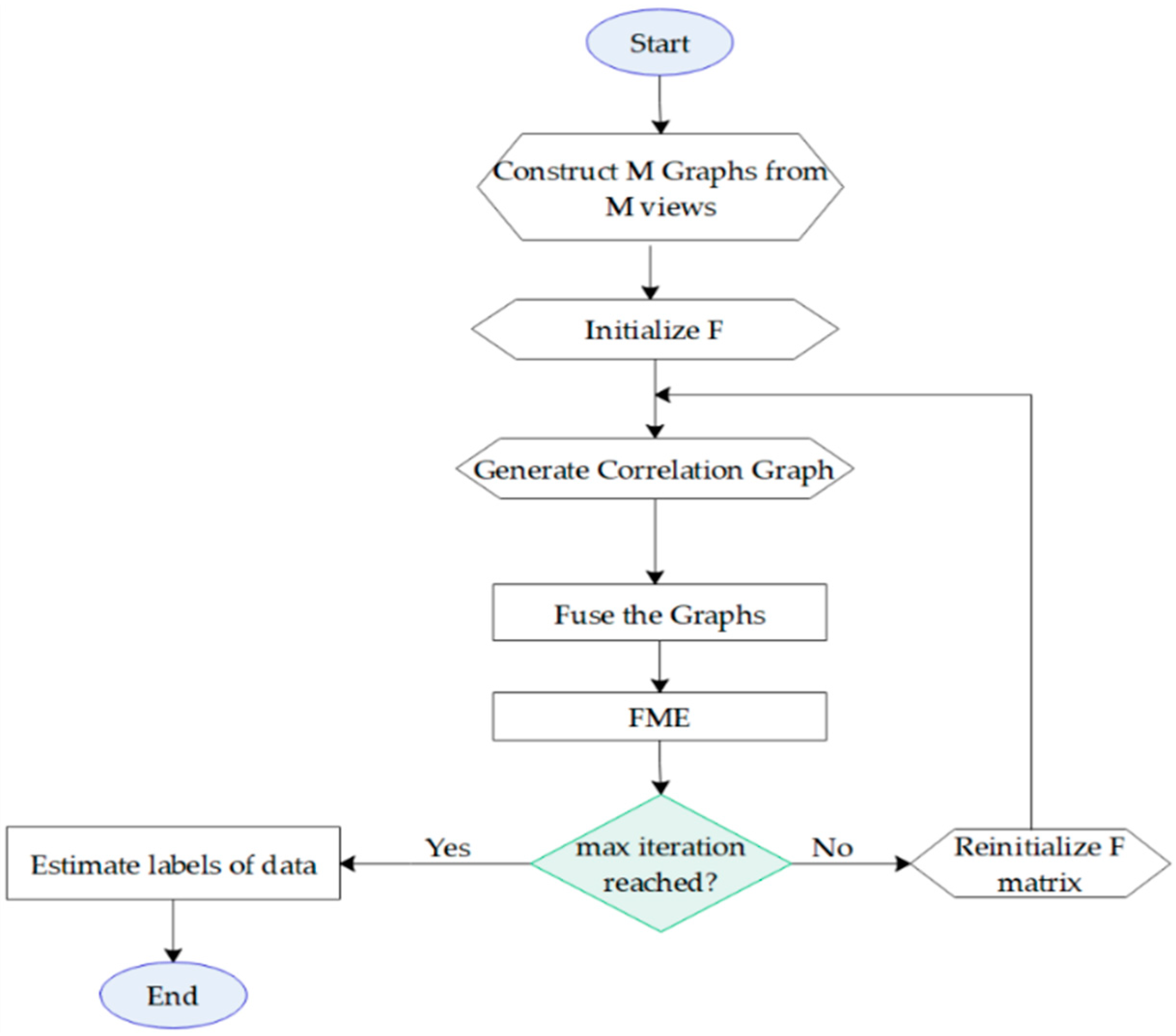
| Algorithm 1. The proposed method. |
| Input: Feature from one view X; |
| Initial label matrix Y = [Y1, Yu]; |
| Parameters μ and γ. |
| Output: Predicted label matrix F, projection matrix Q, and bias vector b. |
| 1. Construct M different graphs from the available view. |
| 2. Compute the Laplacian matrices of the graphs. |
| 3. Initialize the soft label matrix F = Y. |
| 4. for t = 1: Max iteration. |
| 5. Generate the correlation graph based on F by Equation (11). |
| 6. Fuse the M + 1 Laplacian graph to obtain adopting Equation (12). |
| 7. Feed to FME and calculate a new soft label matrix F. |
| 8. Reinitialize the part of F matrix corresponding to the labeled samples. |
| 9. end for. |
| 10. To calculate the labels of unseen samples, use the projection matrix Q and the bias vector b to predict the labels of them. |
4. Experimental Results
4.1. Experimental Setup
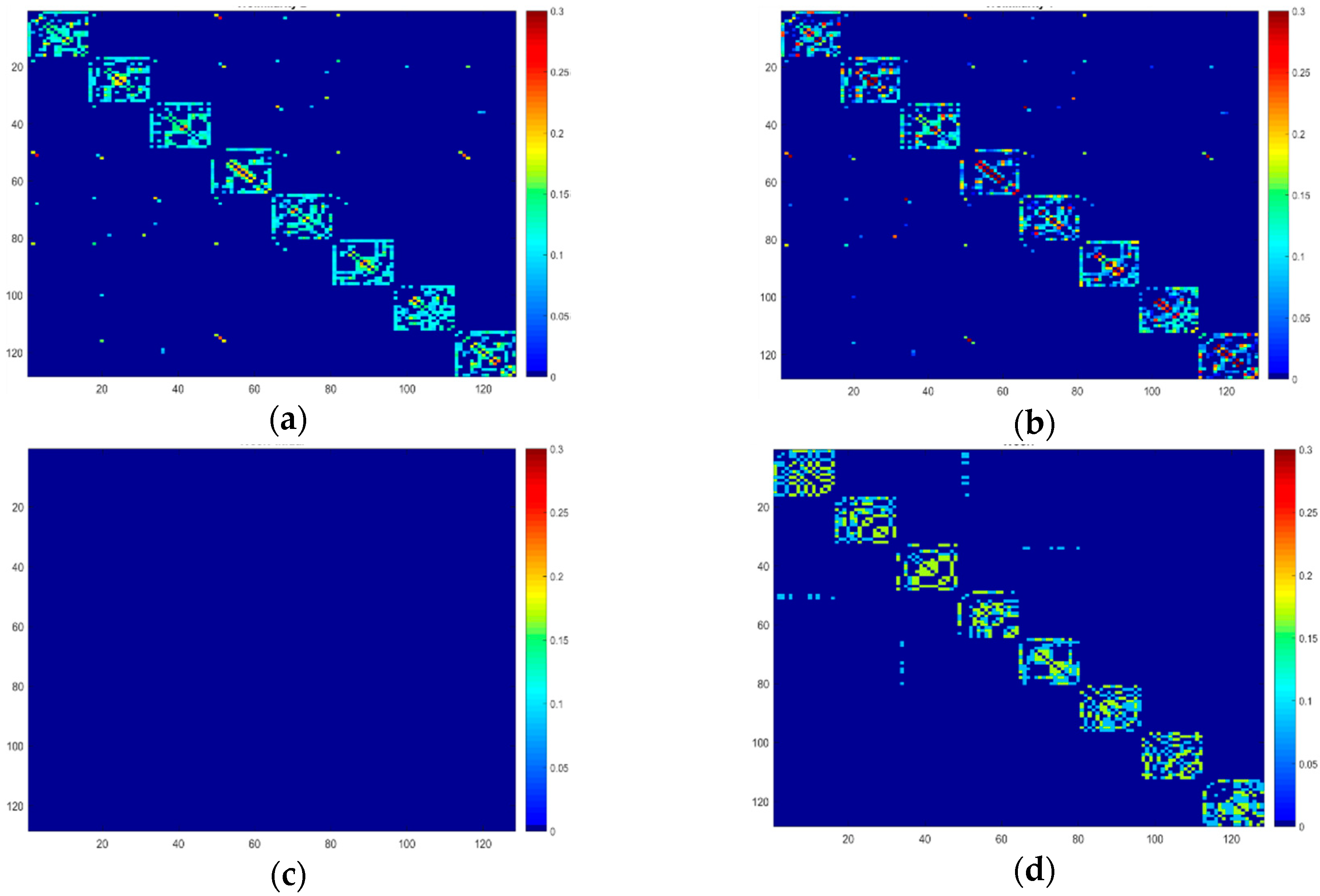
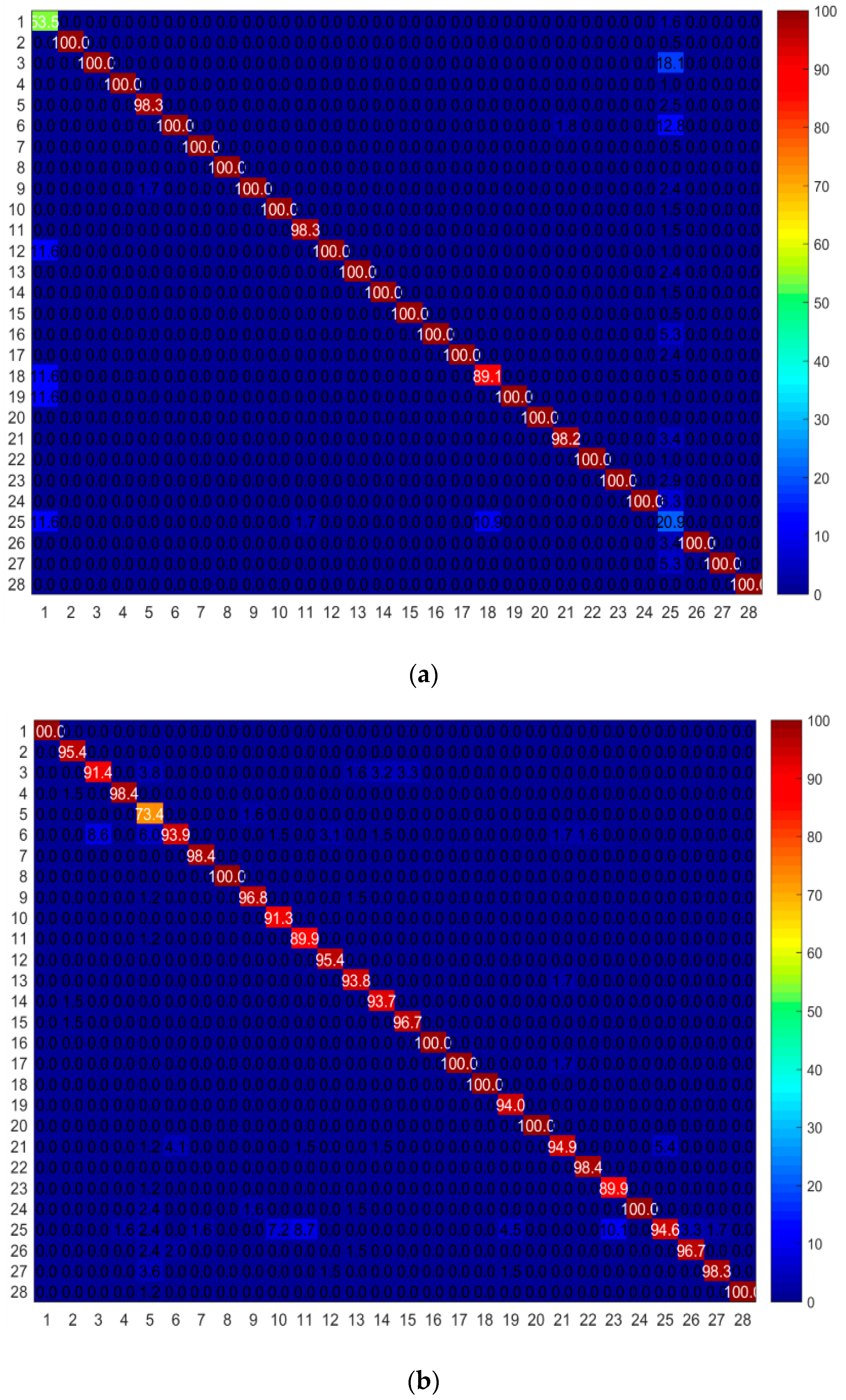
4.2. Comparison with Individual Graphs
4.3. Comparison with Other Methods
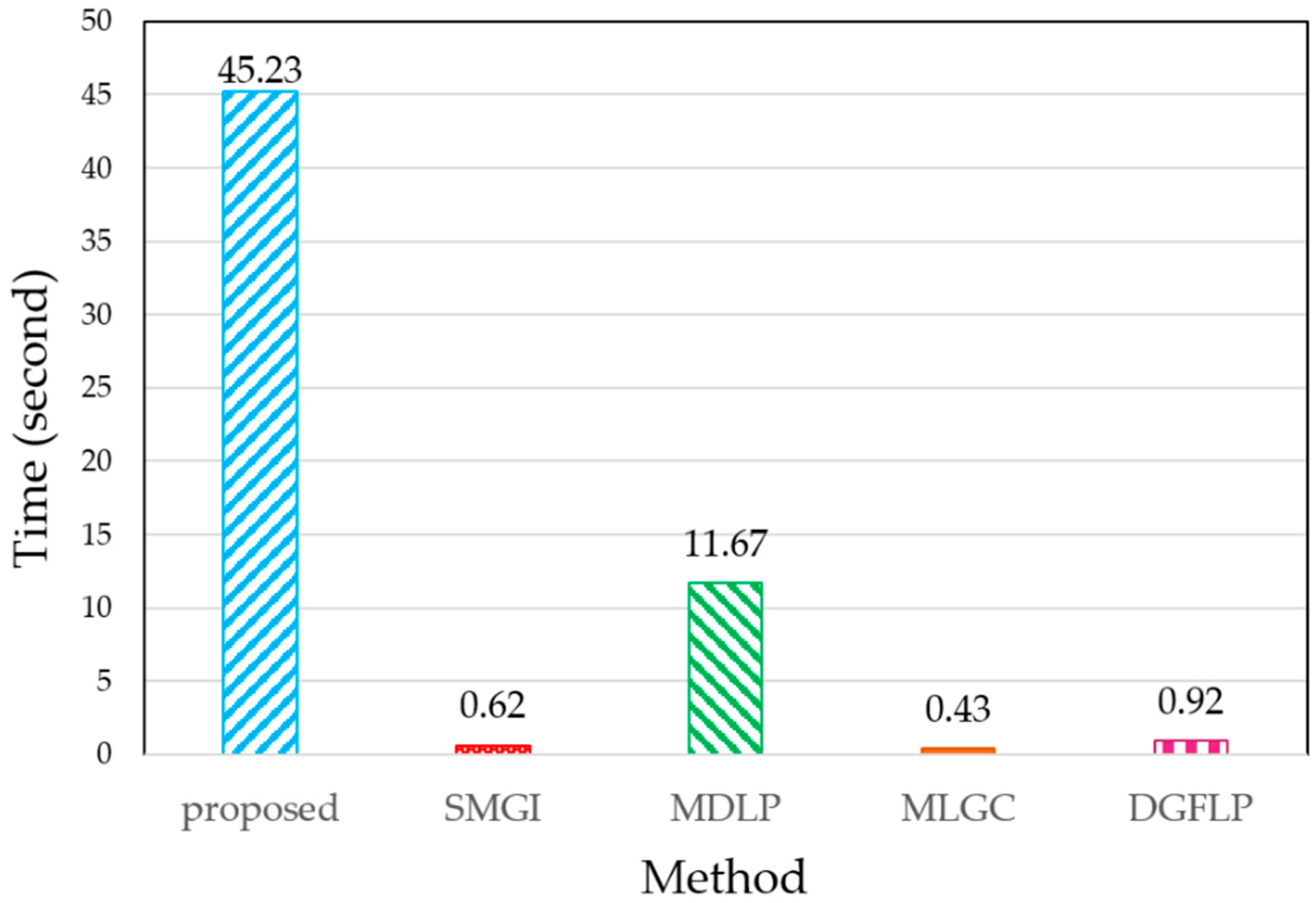
4.4. CPU-Time and Computational Complexity
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bashir, Y.; Aslam, A.; Kamran, M.; Qureshi, M.; Jahangir, A.; Rafiq, M.; Bibi, N.; Muhammad, N. On forgotten topological indices of some dendrimers structure. Molecules 2017, 22, 867. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Hu, J.; Tan, Y.-P. Discriminative deep metric learning for face and kinship verification. IEEE Trans. Image Process. 2017, 26, 4269–4282. [Google Scholar] [CrossRef] [PubMed]
- Mirmahboub, B.; Mekhalfi, M.L.; Murino, V. Person re-identification by order-induced metric fusion. Neurocomputing 2018, 275, 667–676. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, T.S.; Nasrabadi, N.M.; Zhang, Y. Heterogeneous Multi-Metric Learning for Multi-Sensor Fusion. In Proceedings of the 14th International Conference on Informatio Fusion (FUSION), Chicago, IL, USA, 5–8 July 2011; pp. 1–8. [Google Scholar]
- Zhang, L.; Zhang, D. Metricfusion: Generalized metric swarm learning for similarity measure. Inf. Fusion 2016, 30, 80–90. [Google Scholar] [CrossRef]
- Bai, J.; Xiang, S.; Pan, C. A graph-based classification method for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 803–817. [Google Scholar] [CrossRef]
- Boiman, O.; Shechtman, E.; Irani, M. In defense of nearest-neighbor based image classification. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm as 136: A k-means clustering algorithm. J. R. Stat. Soc. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, L.; Chen, S. Graph-optimized locality preserving projections. Pattern Recognit. 2010, 43, 1993–2002. [Google Scholar] [CrossRef]
- Zhou, G.; Lu, Z.; Peng, Y. L1-graph construction using structured sparsity. Neurocomputing 2013, 120, 441–452. [Google Scholar] [CrossRef]
- Tang, J.; Hong, R.; Yan, S.; Chua, T.-S.; Qi, G.-J.; Jain, R. Image annotation by k nn-sparse graph-based label propagation over noisily tagged web images. ACM Trans. Intell. Syst. Technol. 2011, 2, 14:1–14:16. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, C. Label propagation through linear neighborhoods. IEEE Trans. Knowl. Data Eng. 2008, 20, 55–67. [Google Scholar] [CrossRef]
- Gong, C.; Tao, D.; Maybank, S.J.; Liu, W.; Kang, G.; Yang, J. Multi-modal curriculum learning for semi-supervised image classification. IEEE Trans. Image Process. 2016, 25, 3249–3260. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-K.; Ren, J.; Song, C.; Jia, J.; Zhang, Q. Label propagation algorithm for community detection based on node importance and label influence. Phys. Lett. A 2017, 381, 2691–2698. [Google Scholar] [CrossRef]
- Breve, F. Interactive image segmentation using label propagation through complex networks. Expert Syst. Appl. 2019, 123, 18–33. [Google Scholar] [CrossRef]
- Seyedi, S.A.; Lotfi, A.; Moradi, P.; Qader, N.N. Dynamic graph-based label propagation for density peaks clustering. Expert Syst. Appl. 2019, 115, 314–328. [Google Scholar] [CrossRef]
- Cui, B.; Xie, X.; Hao, S.; Cui, J.; Lu, Y. Semi-supervised classification of hyperspectral images based on extended label propagation and rolling guidance filtering. Remote Sens. 2018, 10, 515–533. [Google Scholar] [CrossRef]
- Chapelle, O.; Schölkopf, B.; Zien, A. Semi-Supervised Learning; MIT Press: Cambridge, MA, USA, 2006; Chapter 11; ISBN 978-0-262-03358-9. [Google Scholar]
- Nie, F.; Xu, D.; Tsang, I.W.-H.; Zhang, C. Flexible manifold embedding: A framework for semi-supervised and unsupervised dimension reduction. IEEE Trans. Image Process. 2010, 19, 1921–1932. [Google Scholar] [PubMed]
- Zhou, D.; Bousquet, O.; Lal, T.N.; Weston, J.; Schölkopf, B. Learning with local and global consistency. In Proceedings of the 18th Conference on Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 13–16 December 2004; pp. 321–328. [Google Scholar]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 912–919. [Google Scholar]
- Karasuyama, M.; Mamitsuka, H. Multiple graph label propagation by sparse integration. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1999–2012. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.; Liao, K.; Sun, B.; Chen, Y.; Zhao, F. Dynamic graph fusion label propagation for semi-supervised multi-modality classification. Pattern Recognit. 2017, 68, 14–23. [Google Scholar] [CrossRef]
- Tong, T.; Gray, K.; Gao, Q.; Chen, L.; Rueckert, D. Alzheimer’s Disease Neuroimaging, I. Multi-modal classification of alzheimer’s disease using nonlinear graph fusion. Pattern Recognit. 2017, 63, 171–181. [Google Scholar] [CrossRef]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kains, B.; Goldenberg, A. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333:1–333:8. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Tsotsos, J. Dynamic label propagation for semi-supervised multi-class multi-label classification. Pattern Recognit. 2016, 52, 75–84. [Google Scholar] [CrossRef]
- Muhammad, N.; Bibi, N.; Qasim, I.; Jahangir, A.; Mahmood, Z. Digital watermarking using hall property image decomposition method. Pattern Anal. Appl. 2018, 21, 997–1012. [Google Scholar] [CrossRef]
- Muhammad, N.; Bibi, N. Digital image watermarking using partial pivoting lower and upper triangular decomposition into the wavelet domain. IET Image Process. 2015, 9, 795–803. [Google Scholar] [CrossRef]
- Li, S.; Liu, H.; Tao, Z.; Fu, Y. Multi-view graph learning with adaptive label propagation. In Proceedings of the IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; pp. 110–115. [Google Scholar]
- An, L.; Chen, X.; Yang, S. Multi-graph feature level fusion for person re-identification. Neurocomputing 2017, 259, 39–45. [Google Scholar] [CrossRef]
- Saeedeh, B.; Bosaghzadeh, A. Deep graph fusion for graph based label propagation. In Proceedings of the 10th Conference on Machine Vision and Image Processing (MVIP), Isfahan, Iran, 22–23 November 2017; pp. 149–153. [Google Scholar]
- Zhao, R.; Ouyang, W.; Wang, X. Person re-identification by salience matching. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2528–2535. [Google Scholar]
- Zhao, R.; Ouyang, W.; Wang, X. Unsupervised salience learning for person re-identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 23–28 June 2013; pp. 3586–3593. [Google Scholar]
- Zhang, Y.; Zhang, H.; Nasrabadi, N.M.; Huang, T.S. Multi-metric learning for multi-sensor fusion based classification. Inf. Fusion 2013, 14, 431–440. [Google Scholar] [CrossRef]
- Wang, B.; Tu, Z.; Tsotsos, J.K. Dynamic label propagation for semi-supervised multi-class multi-label classification. In Proceedings of the IEEE International Conference on Computer Vision, Sydney Conference Centre, Darling Harbour, Sydney, 1–8 December 2013. [Google Scholar]
- Cortes, C.; Mohri, M. On transductive Regression. In Proceedings of the Conference on Neural Information Processing Systems (NIPS), Hyatt Regency Vancouver, Vancouver, BC, Canada, 3–8 December 2007. [Google Scholar]
- Yang, B.; Chen, S. Sample-dependent graph construction with application to dimensionality reduction. Neurocomputing 2010, 74, 301–314. [Google Scholar] [CrossRef]
- Bang, S.; Kim, D.; Choi, S. Asian Face Image Database PF01; Intelligent Multimedia Lab, University of Science and Technology: Pohang, Korea, 2001. [Google Scholar]
- Phillips, P.J.; Moon, H.; Rauss, P.; Rizvi, S.A. The feret evaluation methodology for face-recognition algorithms. In Proceedings of the Conference on IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, USA, 17–19 June 1997. [Google Scholar]
- Parkhi, O.M.; Vedaldi, A.; Zisserman, A. Deep face recognition. In Proceedings of the BMVC, Swansea, UK, 7–10 September 2015; p. 6. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]

| Notation | Description |
|---|---|
| N | Number of samples |
| M | Number of metrics |
| X = [x1, x2, …, xN] | Data matrix |
| C | Number of classes |
| d | Sample dimension |
| Y | Initial binary label matrix |
| F | Prediction label matrix |
| W | Similarity matrix |
| L | Laplacian matrix |
| Fusion Laplacian matrix | |
| Q | Projection matrix |
| b | Bias vector |
| t | Iteration number |
| Dataset | Size | # of Classes | Features | Dimension |
|---|---|---|---|---|
| PF01 | 1819 | 107 | VGG Face-FC7 | 4096 |
| VGG Face-FC6 | 4096 | |||
| LBP | 900 | |||
| Extended_Yale | 1774 | 28 | VGG Face-FC7 | 4096 |
| VGG Face-FC6 | 4096 | |||
| LBP | 900 | |||
| PIE | 1926 | 68 | VGG Face-FC7 | 4096 |
| VGG Face-FC6 | 4096 | |||
| LBP | 900 | |||
| FERET | 1400 | 200 | VGG Face-FC7 | 4096 |
| VGG Face-FC6 | 4096 | |||
| LBP | 900 |
| Dataset | # Labeled Samples | Feature | Accuracy (Mean ± STD ) | ||
|---|---|---|---|---|---|
| k-NN graph | Adaptive k-NN Graph | Proposed Method | |||
| PF01 | 1 | FC7 | 89.63 ± 7.97 | 89.07 ± 8.39 | 92.42 ± 2.86 |
| FC6 | 90.85 ± 7.16 | 89.54 ± 8.99 | 93.99 ± 0.85 | ||
| LBP | 51.79 ± 11.64 | 49.16 ± 11.54 | 56.19 ± 8.97 | ||
| 2 | FC7 | 94.16 ± 1.09 | 93.94 ± 1 | 94.36 ± 1.19 | |
| FC6 | 94.74 ± 1.04 | 94.22 ± 1.11 | 94.75 ± 0.98 | ||
| LBP | 63.77 ± 6.82 | 61.08 ± 6.98 | 65.47 ± 5.86 | ||
| Extended_Yale | 1 | FC7 | 40.33 ± 20.86 | 40.33 ± 20.94 | 43.5 ± 19.34 |
| FC6 | 44.67 ± 22.76 | 44.32 ± 22.9 | 50.38 ± 19.27 | ||
| LBP | 91.32 ± 5.17 | 91.69 ± 5.66 | 94.25 ± 1.52 | ||
| 2 | FC7 | 54.24 ± 22 | 54.13 ± 21.99 | 55.35 ± 21.68 | |
| FC6 | 57.01 ± 22.99 | 56.81 ± 23.06 | 58.68 ± 21.77 | ||
| LBP | 96.01 ± 2.3 | 96.17 ± 2.07 | 96.73 ± 1.93 | ||
| PIE | 1 | FC7 | 77.36 ± 9.82 | 77.17 ± 9.79 | 79.04 ± 8.21 |
| FC6 | 76.52 ± 11.43 | 75.73 ± 11.7 | 79.77 ± 8.81 | ||
| LBP | 45 ± 7.71 | 44.56 ± 7.16 | 46.79 ± 7.36 | ||
| 2 | FC7 | 87.57 ± 6.41 | 87.14 ± 6.46 | 88.35 ± 5.5 | |
| FC6 | 86.24 ± 7.19 | 85.6 ± 7.26 | 87.21 ± 5.9 | ||
| LBP | 60.82 ± 6.15 | 59.22 ± 6.26 | 61.64 ± 5.99 | ||
| FERET | 1 | FC7 | 98.65 ± 0.13 | 98.63 ± 0.13 | 98.83 ± 0.08 |
| FC6 | 98.83 ± 0.14 | 98.87 ± 0.12 | 99.03 ± 0.13 | ||
| LBP | 8.41 ± 6.32 | 7.8 ± 5.88 | 8.62 ± 6.24 | ||
| 2 | FC7 | 98.96 ± 0.27 | 98.97 ± 0.29 | 98.99 ± 0.3 | |
| FC6 | 99.05 ± 0.31 | 99.1 ± 0.25 | 99.13 ± 0.26 | ||
| LBP | 15.67 ± 7.26 | 14.26 ± 6.65 | 16.04 ± 6.76 | ||
| Dataset | Method | Accuracy (Mean ± STD) | |
|---|---|---|---|
| FC7 | FC6 | ||
| PF01 1 labeled sample | SMGI | 80.33 ± 13.01 | 78.12 ± 15.87 |
| MLGC | 80.01 ± 12.84 | 77.83 ± 15.69 | |
| DGFLP | 80.54 ± 13.3 | 78.14 ± 15.72 | |
| MDLP | 76.29 ± 17.07 | 74.71 ± 19.12 | |
| Proposed method | 92.42 ± 2.86 | 93.99 ± 0.85 | |
| PF01 2 labeled samples | SMGI | 88.12 ± 2.4 | 87.31 ± 3.35 |
| MLGC | 87.79 ± 2.39 | 87.07 ± 3.39 | |
| DGFLP | 88.33 ± 2.72 | 87.4 ± 3.59 | |
| MDLP | 85.55 ± 1.82 | 85.42 ± 2.81 | |
| Proposed method | 94.36 ± 1.19 | 94.75 ± 0.98 | |
| Extended_Yale 1 labeled sample | SMGI | 37.62 ± 19.08 | 39.28 ± 18.94 |
| MLGC | 37.11 ± 17.93 | 39.56 ± 17.98 | |
| DGFLP | 37.93 ± 19.14 | 39.8 ± 19.21 | |
| MDLP | 29.21 ± 19.55 | 31.24 ± 20.2 | |
| Proposed method | 43.5 ± 19.34 | 50.38 ± 19.27 | |
| Extended_Yale 2 labeled samples | SMGI | 48.87 ± 18.32 | 51.48 ± 18.64 |
| MLGC | 47.72 ± 17.68 | 50.87 ± 18.12 | |
| DGFLP | 49.57 ± 18.61 | 51.96 ± 19.02 | |
| MDLP | 42.6 ± 18.56 | 45.57 ± 19.01 | |
| Proposed method | 55.35 ± 21.68 | 58.68 ± 21.77 | |
| PIE 1 labeled sample | SMGI | 67.71 ± 9.07 | 63.03 ± 12.48 |
| MLGC | 66.46 ± 8.72 | 62.12 ± 12.62 | |
| DGFLP | 68.96 ± 9.17 | 63.59 ± 12.22 | |
| MDLP | 63.01 ± 10.54 | 60.04 ± 12.83 | |
| Proposed method | 79.04 ± 8.21 | 79.77 ± 8.81 | |
| PIE 2 labeled samples | SMGI | 77.65 ± 6.26 | 74.57 ± 7 |
| MLGC | 76.16 ± 6.24 | 73.47 ± 6.95 | |
| DGFLP | 79.06 ± 6.65 | 75.54 ± 7.46 | |
| MDLP | 73.39 ± 6.71 | 70.11 ± 7.95 | |
| Proposed method | 88.35 ± 5.5 | 87.21 ± 5.9 | |
| FERET 1 labeled sample | SMGI | 98.38 ± 0.25 | 98.56 ± 0.24 |
| MLGC | 98.25 ± 0.3 | 98.52 ± 0.31 | |
| DGFLP | 98.43 ± 0.13 | 98.55 ± 0.13 | |
| MDLP | 96.32 ± 0.72 | 97.12 ± 0.4 | |
| Proposed method | 98.83 ± 0.08 | 99.03 ± 0.13 | |
| FERET 2 labeled samples | SMGI | 98.71 ± 0.29 | 98.9 ± 0.32 |
| MLGC | 98.49 ± 0.39 | 98.82 ± 0.31 | |
| DGFLP | 98.65 ± 0.43 | 98.8 ± 0.37 | |
| MDLP | 97.01 ± 0.49 | 97.5 ± 0.86 | |
| Proposed method | 98.99 ± 0.3 | 99.13 ± 0.26 | |
| Accuracy (Mean ± STD) | |||||
|---|---|---|---|---|---|
| SMGI | MLGC | DGFLP | MDLP | Proposed Method | |
| PF01 | 47.66 ± 10.94 | 46.55 ± 11.37 | 47.82 ± 11.1 | 17.47 ± 11.25 | 56.19 ± 8.97 |
| 1 labeled sample | |||||
| PF01 | 56.77 ± 7.16 | 55.83 ± 7.82 | 56.9 ± 7.23 | 13.7 ± 10.58 | 65.47 ± 5.86 |
| 2 labeled samples | |||||
| Extended_Yale | 73.48 ± 10.52 | 58.29 ± 11 | 80.77 ± 9.98 | 12.34 ± 20.31 | 94.25 ± 1.52 |
| 1 labeled sample | |||||
| Extended_Yale | 80.05 ± 4.79 | 65.18 ± 6.87 | 86.73 ± 5.21 | 7.01 ± 11.61 | 96.73 ± 1.93 |
| 2 labeled samples | |||||
| PIE | 36 ± 5.9 | 34 ± 5.51 | 36.09 ± 5.58 | 16.28 ± 5.12 | 46.79 ± 7.36 |
| 1 labeled sample | |||||
| PIE | 49.84 ± 7.85 | 48.06 ± 7.72 | 50.65 ± 7.63 | 30.4 ± 9.86 | 61.64 ± 5.99 |
| 2 labeled samples | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahrami, S.; Bosaghzadeh, A.; Dornaika, F. Multi Similarity Metric Fusion in Graph-Based Semi-Supervised Learning. Computation 2019, 7, 15. https://doi.org/10.3390/computation7010015
Bahrami S, Bosaghzadeh A, Dornaika F. Multi Similarity Metric Fusion in Graph-Based Semi-Supervised Learning. Computation. 2019; 7(1):15. https://doi.org/10.3390/computation7010015
Chicago/Turabian StyleBahrami, Saeedeh, Alireza Bosaghzadeh, and Fadi Dornaika. 2019. "Multi Similarity Metric Fusion in Graph-Based Semi-Supervised Learning" Computation 7, no. 1: 15. https://doi.org/10.3390/computation7010015
APA StyleBahrami, S., Bosaghzadeh, A., & Dornaika, F. (2019). Multi Similarity Metric Fusion in Graph-Based Semi-Supervised Learning. Computation, 7(1), 15. https://doi.org/10.3390/computation7010015





