Development of Simple-To-Use Predictive Models to Determine Thermal Properties of Fe₂O₃/Water-Ethylene Glycol Nanofluid

Abstract

Thermophysical properties of nanofluids play a key role in their heat transfer capability and can be significantly affected by several factors, such as temperature and concentration of nanoparticles. Developing practical and simple-to-use predictive models to accurately determine these properties can be advantageous when numerous dependent variables are involved in controlling the thermal behavior of nanofluids. Artificial neural networks are reliable approaches which recently have gained increasing prominence and are widely used in different applications for predicting and modeling various systems. In the present study, two novel approaches, Genetic Algorithm-Least Square Support Vector Machine (GA-LSSVM) and Particle Swarm Optimization- artificial neural networks (PSO-ANN), are applied to model the thermal conductivity and dynamic viscosity of Fe₂O₃/EG-water by considering concentration, temperature, and the mass ratio of EG/water as the input variables. Obtained results from the models indicate that GA-LSSVM approach is more accurate in predicting the thermophysical properties. The maximum relative deviation by applying GA-LSSVM was found to be approximately ±5% for the thermal conductivity and dynamic viscosity of the nanofluid. In addition, it was observed that the mass ratio of EG/water has the most significant impact on these properties.

1. Introduction

In recent years, the tendency to replace conventional fluids by nanofluids is increasing in many applications, such as solar energy, heat exchangers, and electronics cooling [1]. Nanofluid, characterized by a significant improvement in thermal properties compared to most of the conventional engineered fluid, is found to serve in a number of engineering applications, for example, fuel-cell industry [2], petroleum engineering [3,4,5], materials science [6], etc. These types of fluids contain flowing nanoparticles which can enhance the properties of the conventional fluid, specifically, their thermal conductivity [7,8]. This capability has attracted many researchers’ attention to study various methods which can effectively modify the physical properties of conventional fluids by adding nanoparticles with different size, shape, material, and volume concentration [9,10,11,12]. Works in this area have shown that nanofluids can improve the thermal performance both for single phase and two-phase flows in various applications depending on the operational conditions [13,14,15,16]. This enhancement is due to the liquid interfacial layering between nanoparticles and basic fluid, agglomeration of the particles, and Brownian motion [17,18].

To study nanofluids, various analytical methods and experimental setups have been utilized to measure their properties and evaluate their heat transfer performance. Most work has focused on the changes observed in the viscosity and thermal conductivity of the fluid as the major thermophysical properties [19,20,21,22]. Many correlations are proposed to predict these properties based on experimental data and physical analysis [15,16,23,24]. However, performing numerous experiments to measure the properties under different conditions is costly especially when many operational parameters, such as size, shape, and concentration of the nanoparticles, as well as the working temperature have a considerable effect on the results [25,26,27,28]. On the other hand, the accuracy of the analytical models and the data-driven correlations may not be sufficient when the operational conditions are significantly changing compared to the basic assumptions. Therefore, new approaches have been recently introduced for this purpose. Artificial neural networks (ANN) are developed learning algorithms which can be used as effective predictive tools to simulate various systems [29,30]. Recently, research has started to use these algorithms to predict the thermophysical properties of nanofluids. Nadooshen et al. [31] have used this tool to measure the dynamic viscosity of SiO2–MWCNT/10W40 engine oil by considering shear rate, concentration, and temperature as the input variables of their model. The value of R² for their proposed model was 0.9948 and their result showed an increase in dynamic viscosity when the concentration increases. Alirezaie et al. [32] also used neural network algorithms to measure the dynamic viscosity of MWCNT (COOH-functionalized)/MgO engine oil. It was reported that the viscosity was lowered by 75% when the nanofluid’s temperature was doubled from 25 °C to 50 °C Esfe et al. [33] measured the thermal conductivity of ZnO–MWCNT/EG–water and proposed a predictive artificial neural network model with temperature and concentration as the input variables. The authors monitored that their model was able to follow the experimental values very closely and the mean squares error of the presented model was 1.9585 × 10⁻⁵. In another study, Afrand et al. [34] worked on MgO/water nanofluid and obtained a correlation for thermal conductivity by using an artificial neural network. Moreover, the effect of the size of the nanoparticles has also been considered as it can have a significant effect on the thermal conductivity [29,30].

Most of the reviewed studies have studied the effects of temperature and concentration on the thermophysical properties of the used nanofluids and indicated that ANN can be utilized as a tool to predict their thermal behavior. In the present study, two novel approaches, GA-LSSVM and PSO-ANN, are used for the first time to model the thermal conductivity and dynamic viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid. These methods are selected based on their potent performance in developing high-precision models for estimating target objectives. The accuracy of the predictive algorithms has been evaluated by the correlation factor (R²), Average Absolute Relative Deviation (AARD), Root Mean Square Error (RMSE), and Margin of Deviation. The differences between the algorithms have been discussed and their accuracy is compared.

2. Methodology

2.1. Artificial Neural Network

The configuration of artificial neural networks (ANNs) is inspired by functionality and learning procedure of the human brain’s neural system. These networks are designed based on a structure of processing nodes (neurons) and inter-connections which can transmit signals between the nodes. These inter-connected elements process input information simultaneously by recognizing the links between independent and dependent parameters and are capable of adapting and learning from past patterns.

The most common ANN configuration is the multilayer feed-forward neural network in which information moves through the input, output, and hidden levels. Figure 1 shows a feed-forward ANN with one hidden layer that is used in this work. These types of neural networks are capable of analyzing non-linear functions and utilize one or more hidden layers as a learning technique to effectively transfer information through different stages. Neurons in the hidden and output layer apply a linear or non-linear transfer function as internal activation phenomenon. To feed information, a measure of strength is assigned to each interconnection which is referred to as weight. Bias is treated as an extra input which has a value of 1 at all times. All neurons within the network are responsible to use appropriate correlations to properly link the input information to the desired outputs [35,36]. The net inputs (S) for the hidden neurons are computed as [37]:

$${{\mathrm{S}}^{\mathrm{H}}}_{\mathrm{j}}={{\displaystyle \sum }}_{\mathrm{t}=1}^2{{\mathrm{w}}^{\mathrm{H}}}_{\mathrm{j},\mathrm{t}}·{\mathrm{a}}_{\mathrm{t}}+{{\mathrm{b}}^{\mathrm{H}}}_{\mathrm{j}}.$$

(1)

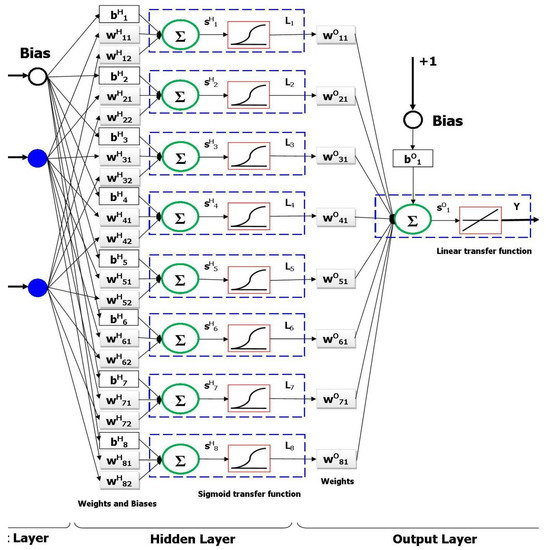
Figure 1. Structure of the proposed three layers feed-forward neural network model.

In the above equation, ${\mathrm{a}}_{\mathrm{t}}$, j and ${{\mathrm{w}}^{\mathrm{H}}}_{\mathrm{j},\mathrm{t}}$ are the input parameters vector, the index of the hidden neuron, and the interconnection weight between the input neurons with the hidden layer, respectively. In addition, ${{\mathrm{b}}^{\mathrm{H}}}_{\mathrm{j}}$ is the bias of the jth hidden neuron. Afterwards, (${\mathrm{L}}_{\mathrm{j}}$) which is the output of the hidden neurons and calculated by using a transfer function of ${\mathrm{f}}_{\mathrm{H}}$ which is related to the hidden neurons [37].

$${\mathrm{L}}_{\mathrm{j}}={\mathrm{f}}_{\mathrm{H}}\left({{\mathrm{S}}^{\mathrm{H}}}_{\mathrm{j}}\right)={\mathrm{f}}_{\mathrm{H}}\left({{\displaystyle \sum }}_{\mathrm{t}=1}^2{{\mathrm{w}}^{\mathrm{H}}}_{\mathrm{j},\mathrm{t}}·{\mathrm{a}}_{\mathrm{t}}+{{\mathrm{b}}^{\mathrm{H}}}_{\mathrm{j}}\right).$$

(2)

Computed outputs of the hidden layer are supplied as inputs for the output layers. The same approach can be also utilized to compute the final output of Y.

2.2. Least Squares Support Vector Machines

Selection of the desired function based on a set of empirical data is a subject problem which can be addressed by the statistical theory of learning and applied to a variety of applications. One of the recent learning methods based on this theory is the support vector machine (SVM) [38]. Because of its high performance, effective generalization ability, and use of kernel-induced feature spaces, it has extensively been employed to solve nonlinear functions and density estimation problems [35,36]. To improve the SVM, Suykens et al. [39] introduced the Least Squares Support Vector Machines (LSSVM) method. In LSSVM, the inequality constraints are converted to a set of equality constraints which results in solving a system of linear equations, and therefore, offers a faster and easier alternative to SVM method [40,41]. An overview of LSSVM method is described below [41,42]:

For a set of set of N training data $\left\{\left({\mathrm{x}}_1,{\mathrm{y}}_1\right), \left({\mathrm{x}}_2,{\mathrm{y}}_2\right),\dots ,\left({\mathrm{x}}_{\mathrm{N}},{\mathrm{y}}_{\mathrm{N}}\right)\right\}$, ${\mathrm{x}}_{\mathrm{k}}\in {\mathrm{ℝ}}^{\mathrm{n}}$ denotes $\mathrm{k}\mathrm{th}$ input data and ${\mathrm{y}}_{\mathrm{k}}\in \mathrm{ℝ}$ is the related output; Equation (3) is applied to estimate a model of the formula:

$$\mathrm{y}\left(\mathrm{x}\right)={𝓌}^{\mathrm{T}}\mathsf{\phi }\left(\mathrm{x}\right)+\mathrm{b}.$$

(3)

In the above equation, $\mathsf{\phi }\left(\mathrm{x}\right): {\mathrm{ℝ}}^{\mathrm{n}}\to {\mathrm{ℝ}}^{{\mathrm{n}}_{\mathrm{h}}}$ is a nonlinear mapping function. This function is employed to map the input data to a space with higher dimension features; b and $𝓌$ are the bias term and the weight vector, respectively. By minimizing the following function, Equation (4), these values are obtainable:

$$\mathcal{J}\left(𝓌,\mathrm{e}\right)=\frac{1}{2}{𝓌}^{\mathrm{T}}𝓌+\frac{1}{2}\mathsf{\gamma }{\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{N}}{\mathrm{e}}_{\mathrm{k}}^2.$$

(4)

By considering the following constraints:

$${\mathrm{y}}_{\mathrm{k}}={𝓌}^{\mathrm{T}}\mathsf{\phi }\left({\mathrm{x}}_{\mathrm{k}}\right)+\mathrm{b}+{\mathrm{e}}_{\mathrm{k}}\hspace{1em}\mathrm{k}=1, 2,\dots , \mathrm{N}.$$

(5)

In the above equations, $\mathrm{\gamma }$ is a constant to regularize and avoid over fitting and ${\mathrm{e}}_{\mathrm{k}}$ is the error of training data. To solve the constrained optimization problem, the Lagrangian function is used:

$$\mathcal{L}\left(𝓌,\mathrm{b},\mathrm{e},\mathsf{\alpha }\right)=\mathcal{J}\left(𝓌,\mathrm{e}\right)-{\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{N}}{\mathsf{\alpha }}_{\mathrm{k}}\{{𝓌}^{\mathrm{T}}\mathsf{\phi }\left({\mathrm{x}}_{\mathrm{k}}\right)+\mathrm{b}+{\mathrm{e}}_{\mathrm{k}}-{\mathrm{y}}_{\mathrm{k}}\}.$$

(6)

In the above equation, ${\mathsf{\alpha }}_{\mathrm{k}}$ are Lagrange multipliers. Performing derivative on Equation (4) with respect to $𝓌,\mathrm{b},{\mathrm{e}}_{\mathrm{k}}, \mathrm{and} {\mathsf{\alpha }}_{\mathrm{k}}$, to determine the optimal conditions resulting in:

$${\partial }_{𝓌}\mathcal{L}=𝓌-{\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{N}}{\mathsf{\alpha }}_{\mathrm{k}}\mathsf{\phi }\left({\mathrm{x}}_{\mathrm{k}}\right)=0,$$

(7)

$${\partial }_{\mathrm{b}}\mathcal{L}={\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{N}}{\mathsf{\alpha }}_{\mathrm{k}}=0,$$

(8)

$${\partial }_{{\mathrm{e}}_{\mathrm{k}}}\mathcal{L}={\mathsf{\alpha }}_{\mathrm{k}}-{\mathsf{\gamma }\mathrm{e}}_{\mathrm{k}}=0\hspace{1em}\mathrm{k}=1, \dots , \mathrm{N},$$

(9)

$${\partial }_{{\mathsf{\alpha }}_{\mathrm{k}}}\mathcal{L}=\mathsf{\phi }\left({\mathrm{x}}_{\mathrm{k}}\right)·{𝓌}^{\mathrm{T}}+\mathrm{b}+{\mathrm{e}}_{\mathrm{k}}-{\mathrm{y}}_{\mathrm{k}}=0,\hspace{1em}\mathrm{k}=1, \dots , \mathrm{N}.$$

(10)

The optimization problem can turn into a linear system if $𝓌$ and $\mathrm{e}$ are removed:

$$\left[\begin{array}{cc}0& 1_{\mathsf{\upsilon }}^{\mathrm{T}}\\ 1_{\mathsf{\upsilon }}& \mathsf{\Omega }+{\mathsf{\gamma }}^{-1}\mathrm{I}\end{array}\right]\left[\begin{array}{c}\mathrm{b}\\ \mathsf{\alpha }\end{array}\right]=\left[\begin{array}{c}0\\ \mathrm{y}\end{array}\right],$$

(11)

where $\mathrm{y}={\left[{\mathrm{y}}_1 \dots {\mathrm{y}}_{\mathrm{N}}\right]}^{\mathrm{T}}$, $1_{\mathrm{\upsilon }}={\left[1 \dots 1\right]}^{\mathrm{T}}$, $\mathrm{\alpha }={\left[{\mathrm{\alpha }}_1 \dots {\mathrm{\alpha }}_{\mathrm{N}}\right]}^{\mathrm{T}}$, $\mathrm{I}$ denotes an identity matrix and $\mathsf{\Omega }$ represents an N-dimensional symmetric matrix; ${\mathsf{\Omega }}_{\mathrm{k}\mathrm{l}}=\mathsf{\phi }{\left({\mathrm{x}}_{\mathrm{k}}\right)}^{\mathrm{T}}·\mathsf{\phi }\left({\mathrm{x}}_{\mathrm{l}}\right)=\mathrm{K}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{x}}_{\mathrm{l}}\right)\forall \mathrm{k},\mathrm{l}=1, \dots , \mathrm{N}$. $\mathrm{K}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{x}}_{\mathrm{l}}\right)$ stands for the kernel function and must meet Mercer’s theorem. The final form of the LSSVM approach for function estimation is formulated as:

$$\mathrm{y}\left(\mathrm{x}\right)={\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{N}}{\mathsf{\alpha }}_{\mathrm{k}}\mathrm{K}\left(\mathrm{x},{\mathrm{x}}_{\mathrm{k}}\right)+\mathrm{b},$$

(12)

where $\left(\mathrm{b}, \mathsf{\alpha }\right)$ is the solution to the linear system.

3. Developed Models

In the present study, two artificial intelligence methods, ANN and LSSVM, are employed to predict the dynamic viscosity and thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid based on the previously published database [43,44,45].

3.1. ANN Model

3.1.1. Data Distribution (Training and Testing Subsets)

To train a multilayer feed-forward neural network usually the data is divided into two subsets, namely, a training set and a testing set. In the training set, the network weights and biases are updated, and afterward, the accuracy of the trained neural network is evaluated in the testing set. In the current work, the main data is assumed to be the test data and 100 data points (80% of the whole data) are considered as the training data.

3.1.2. Training Method and Transfer Functions

From the several types of the transfer functions, the log-sigmoid (Logsig) transfer function is utilized for neurons in the hidden layer. The logsig transfer function is suitable for various nonlinear functions and can be expressed as [37]:

$$\mathrm{f}\left(\mathrm{S}\right)=\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{S}\right)}.$$

(13)

The logsig function is in the rage of 0 and 1. This transfer function provides favorable gain in the cases that there is a wide range of input levels [37]. Moreover, the linear transfer function (Purelin) is employed as a transfer function for the output layer. The function is represented as:

$$\mathrm{f}\left(\mathrm{S}\right)=\mathrm{S}$$

(14)

To ensure the ANN’s satisfactory performance, a training algorithm is applied to adjust the weight of the interconnections between neurons, as well as the biases. By performing these adjustments, the network can accurately predict the desired outputs for a specified set of inputs. Genetic Algorithm (GA), Back Propagation (BP), Particle Swarm Optimization (PSO), Unified Particle Swarm Optimization (UPSO), Hybrid Genetic Algorithm and Particle Swarm Optimization (HGAPSO), and Imperialist Competitive Algorithm (ICA) are examples of training algorithms which have been utilized in a variety of applications.

PSO algorithm [46] was employed as the ANN’s training algorithm due to its simplicity, robustness, adaptability, and excellent convergence features. PSO is developed by Kennedy and Eberhart [47] and is inspired by the social behavior and movement of the organisms in a bird flock, fish school, and swarm of insects. First, an initial set of solution is randomly taken as the potential solution, and then the algorithm attempts to iteratively optimize and improve the candidate solutions by updating within the search space. The swarm proceeds towards the optimal solution by moving the particles in the search space based on their local and global optimum position. Each particle’s best position is denoted as ${\mathrm{p}}_{\mathrm{i},{\mathrm{p}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}}$, and is the optimum position of particle $\mathrm{i}$ that has been achieved through applying fitness function at each iteration. The global best solution for all particles in the search space is denoted as ${\mathrm{p}}_{{\mathrm{g}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}}$ and is taken into account together with ${\mathrm{p}}_{\mathrm{i},{\mathrm{p}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}}$ to optimize the solution at each iteration. The following mathematical formulation is used to update the particles’ position and velocity in order to generate a newly optimized swarm of particles [48]:

$${{\mathrm{V}}_{\mathrm{i}}}^{\mathrm{n}+1}=\mathsf{\omega }{{\mathrm{v}}_{\mathrm{i}}}^{\mathrm{n}}+{\mathrm{c}}_1{{\mathrm{r}}_1}^{\mathrm{n}}\left[{{\mathrm{p}}_{\mathrm{i},{\mathrm{p}}_{\mathrm{best}}}}^{\mathrm{n}}-{{\mathrm{p}}_{\mathrm{i}}}^{\mathrm{n}}\right]+{\mathrm{c}}_2{{\mathrm{r}}_2}^{\mathrm{n}}\left[{{\mathrm{p}}_{{\mathrm{g}}_{\mathrm{best}}}}^{\mathrm{n}}-{{\mathrm{p}}_{\mathrm{i}}}^{\mathrm{n}}\right],$$

(15)

$${{\mathrm{p}}_{\mathrm{i}}}^{\mathrm{n}+1}={{\mathrm{p}}_{\mathrm{i}}}^{\mathrm{n}}+{{\mathrm{v}}_{\mathrm{i}}}^{\mathrm{n}+1},$$

(16)

where ${{\mathrm{v}}_{\mathrm{i}}}^{\mathrm{n}}$ and ${{\mathrm{v}}_{\mathrm{i}}}^{\mathrm{n}+1}$ are the ith particle velocities at n and n + 1 iterations, respectively. $\mathrm{v}{{\mathrm{p}}_{\mathrm{i}}}^{\mathrm{n}}$ and ${{\mathrm{p}}_{\mathrm{i}}}^{\mathrm{n}+1}$ denote ith particle positions in the mentioned iterations. $\mathsf{\omega }$ is the inertia weight which has a key role in handling the exploration and exploitation of the search space since it continuously corrects the values related to the velocity; ${\mathrm{c}}_1$ and ${\mathrm{c}}_2$ are acceleration constants representing the change of particle velocity from ${{\mathrm{p}}_{\mathrm{i},{\mathrm{p}}_{\mathrm{best}}}}^{\mathrm{n}}$ towards ${{\mathrm{p}}_{{\mathrm{g}}_{\mathrm{best}}}}^{\mathrm{n}}$; ${{\mathrm{r}}_1}^{\mathrm{n}}$ and ${{\mathrm{r}}_2}^{\mathrm{n}}$ are uniformly distributed random numbers in [0, 1]; ${{\mathrm{p}}_{{\mathrm{g}}_{\mathrm{best}}}}^{\mathrm{n}}$ is the best position in the current swarm over generation $\mathrm{n}$; and ${{\mathrm{p}}_{\mathrm{i},{\mathrm{p}}_{\mathrm{best}}}}^{\mathrm{n}}$ stands for the best position of particle $\mathrm{i}$ over generation $\mathrm{n}$ specified using the fitness function. More details of PSO are explained in [48,49].

Mean square of errors (MSE) is employed as a fitness function of the whole training data set as follows:

$$\mathrm{f}=\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({{\mathrm{y}}^{\exp }}_{\mathrm{i}}-{{\mathrm{y}}^{\mathrm{pre}}}_{\mathrm{i}}\right)}^2.$$

(17)

In the above equation, N is the total number of data used for training; ${{\mathrm{y}}^{\mathrm{p}\mathrm{r}\mathrm{e}}}_{\mathrm{i}}$ is the experimental value at point $\mathrm{i}$, ${{\mathrm{y}}^{\mathrm{pre}}}_{\mathrm{i}}$ is the $i\mathrm{t}\mathrm{h}$ output data obtained by the network. Each particle specifies a possible solution to the optimization case. Figure 2 depicts the flowchart of the procedure of training ANN model using PSO algorithm.

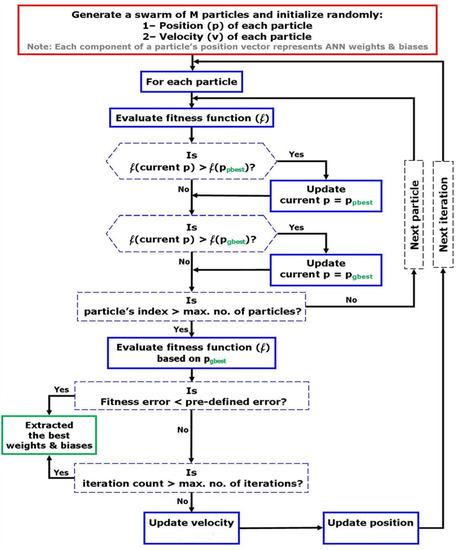
Figure 2. Flowchart of the Particle Swarm Optimization (PSO)-based optimization algorithm for evolving the weights and biases of the constructed artificial neural networks (ANN).

3.1.3. ANN Structure

The choice of optimization network structure is determined primarily by the level of complexity of the problem. Multilayer feed-forward neural networks with one hidden layer and a sufficient number of hidden neurons are capable to map any input to each output with an arbitrary level of accuracy. In the current study, 8 inputs and 1 output are assumed, and a network with one hidden layer is used accordingly. Various $2-\mathrm{x}-1$ architectures (x changes from 1 to 10) are evaluated based on their MSE and R² values to obtain the optimum number of neurons. The optimal structure has a minimum value of MSE and a maximum magnitude of R². Figure 3 shows the MSE and R² values for different examined structures. As indicated, a three-layer ANN network with a $2-8-1$ layer structure in which there are eight hidden neurons in one layer, is the most suitable structure. Figure 1 shows the final trained ANN model with eight hidden neurons. Also, the adjustable parameters used in the presented hybrid PSO-ANN approach are listed in Table 1.

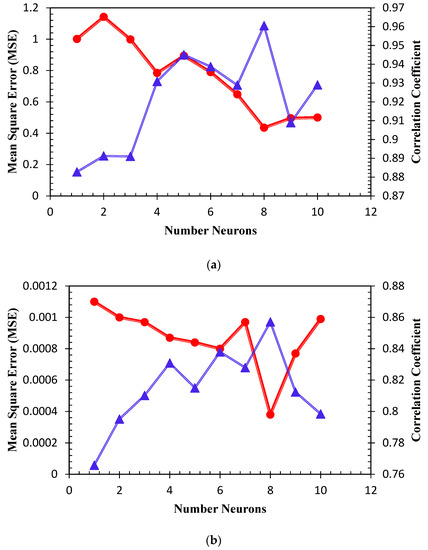
Figure 3. Effect of the number of hidden neurons on the performance of the PSO-ANN model in terms of R² and MSE values for (a) viscosity (b) thermal conductivity.

Table 1. Details of trained ANNs with PSO for the prediction of viscosity and thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

Type	Value/Comment
Input layer	3
Hidden layer	8
Output layer	2
Hidden layer activation function	Logsig
Output layer activation function	Purelin
Number of datum used for training	100
Number of datum used for testing	26
Number of max iterations	1000
c1 and c2 in Equation (15)	2
Number of particles	25

3.2. LSSVM Model

3.2.1. Data Distribution (Training and Testing Subsets)

Just as the case for ANNs, to improve the performance and effectiveness of the LSSVM model, training and testing subsets are created from the database. From 126 data points, 100 data sets are selected for the training subset, and the rest are used for testing the model.

3.2.2. Kernel Function

It is necessary to select a proper kernel function. Several kernel functions exist; however, there are three types which are more common as listed below:

• $\mathrm{K}\left(\mathrm{x},{\mathrm{x}}_{\mathrm{k}}\right)={\mathrm{x}}_{\mathrm{k}}^{\mathrm{T}}\mathrm{x} \left(\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r} \mathrm{k}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{l}\right)$
• $\mathrm{K}\left(\mathrm{x},{\mathrm{x}}_{\mathrm{k}}\right)={(\mathrm{\tau }+{\mathrm{x}}_{\mathrm{k}}^{\mathrm{T}}\mathrm{x})}^{\mathrm{d}} \left(\mathrm{P}\mathrm{o}\mathrm{l}\mathrm{y}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{k}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{l} \mathrm{o}\mathrm{f} \mathrm{d}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e} \mathrm{d}\right)$
• $\mathrm{K}\left(\mathrm{x},{\mathrm{x}}_{\mathrm{k}}\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-{\Vert \mathrm{x}-{\mathrm{x}}_{\mathrm{k}}\Vert }^2/{\mathrm{\sigma }}^2) \left(\mathrm{R}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{i}\mathrm{s} \mathrm{f}\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{R}\mathrm{B}\mathrm{F} \mathrm{k}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{l}\right)$

Several studies have focused on the comparison between these common kernels [39,46,50]. In the present study, RBF is applied as the kernel function due to its ability in producing precise results [50,51].

3.2.3. Optimization Approach to Tune the Embedded Parameters ($\mathsf{\gamma }$ and ${\mathsf{\sigma }}^2$)

To optimize the values of the kernel (σ²) and regulation (γ) parameters in the training stage, a genetic algorithm (GA) is linked to the LSSVM model in this work. The genetic algorithm is an optimization method and is extensively utilized to solve constrained and unconstrained problems by simulating the natural selection process in biological evolution. A population of candidate solutions is moved towards the optimum solution through an iterative process in which generations are evolved based on the objective function and selection, crossover, and mutation rules. An optimal solution is obtained after successive generations. Figure 4 shows the flowchart of the hybrid GA-LSSVM model used in the current study. The procedure of utilizing this approach to optimize $\mathsf{\gamma }$ and ${\mathsf{\sigma }}^2$ is briefly described below.

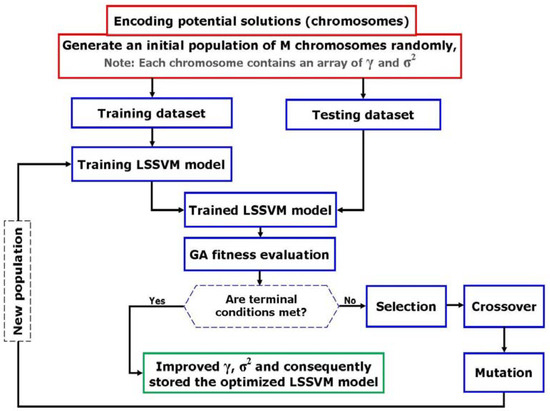
Figure 4. Flowchart of GA-based optimization algorithm to adjust the embedded parameters of LSSVM model.

• Encoding and generating Initial population: First, an array of variables called a chromosome (or a unique solution) is considered to be optimized. Two variables of $\mathsf{\gamma }$, ${\mathsf{\sigma }}^2$ are assigned to the chromosome and a mapping practice named encoding is applied between the chromosome and the solution space. An initial population of chromosomes is randomly created after the representation of the candidate solutions.
• Fitness assignment: The mean squared error of all data set used for training is employed as a fitness function to evaluate each chromosome in the population.
• Selection: In this step, the most available triumphant individuals in a population are repeated. The rate of repeat is proportional to their relative quality. In fact, chromosomes which have more appropriate fitness have a higher chance to be chosen.
• Crossover: In this stage, two various solutions are putrefied; afterward, the components are randomly combined in order to generate new solutions.
• Mutation: Using a random way to alter a potential solution.
• Replace: New generated population is utilized for the following generation.
• Stop criterion: This procedure will continue until an acceptable solution is obtained.

Table 2 lists the settings and parameters used in the current hybrid GA-LSSVM model. The final values of γ and σ² are 6765.87641 and 0.210787768 for viscosity, and 8765.56465 and 0.06587768 for thermal conductivity, respectively. These values of γ and σ² suggest that the current model is fairly reliable to be employed as a predictive model.

Table 2. Basic parameter values of GA-LSSVM model for the prediction of viscosity and thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

Type	Value/Comment
Input layer	2
Output layer	1
Kernel function	RBF kernel function
Number of datum used for training	100
Number of datum used for testing	26
GA Population size	1000
Max. number of generations	1000
Crossover rate	0.82
Mutation rate	0.02

4. Results and Discussion

In this section, the results obtained for the viscosity and thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid using the GA-LSSVM and PSO-ANN models are presented and compared to the actual experimental values which are extracted from the references [43,44,45]. Performance of each model in predicting the thermophysical properties is evaluated using various criteria. First, to get a better insight into the general effects that concentration has on the viscosity and thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid, their variation versus the concentration are shown in Figure 5. As can be seen, for the considered range of concentration, viscosity and thermal conductivity increase by volume fraction at both temperatures of 20 °C and 50 °C, and both EG/Water ratios of 0.2 and 0.4. Moreover, for the case of EG/Water = 0.2, when the temperature increases from 20 °C to 50 °C, the viscosity of the nanofluid decreases while the thermal conductivity increases. These effects of the volume fraction on the viscosity and thermal conductivity are well discussed in the literature using experimental and numerical methods. Here, the performance of the GA-LSSVM and PSO-ANN models are investigated to evaluate how well these predictive models can follow the same trend observed in experiments for each parameter.

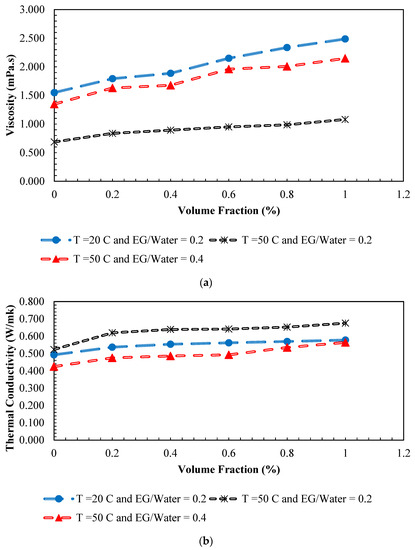
Figure 5. Variation of viscosity (a) and thermal conductivity (b) versus volume fraction at different temperatures.

4.1. Viscosity

4.1.1. GA-LSSVM Model for Viscosity

Figure 6 represents a regression plot between the estimated values for the viscosity using LSSVM approach and the experimental data. As can be seen, the obtained values by the model and actual data are very close which indicates the high accuracy of the proposed model. To further evaluate the accuracy of the LSSVM model, values of mean squared errors (MSE), average absolute relative deviations (AARD), and determination coefficients (R²) are represented in Table 3. As indicated, R² > 0.998, AARD < 2.9, and MSE < 0.5 are achieved for all data sets. In Figure 7, actual values and model output for each data index are compared for the viscosity of the nanofluid. It can be seen that the outputs of the model are reliable since they are in good agreement with experimental data. Furthermore, the absolute relative deviation of the obtained results from LSSVM versus actual data for viscosity is shown in Figure 8. As shown in Figure 8, the highest relative deviation of the model output from experimental data is approximately ±5%. In addition, the estimated and experimental data of dynamic viscosity of the nanofluid versus volumetric concentration at various temperatures are shown in Figure 9. All presented results for various criteria demonstrate that the outputs of the model match well with the experimental data for this specific system. In order to evaluate the importance of the used variables on the viscosity of the nanofluid, a rigorous statistical approach is used which is known as “analysis of variance (ANOVA)”. The results of this method are represented in Figure 10. It can be concluded that the mass ratio of EG/water has a positive effect on the viscosity while the temperature has the maximum negative effect. The same effects for temperature and volume fraction can be seen in Figure 5 which has been discussed before.

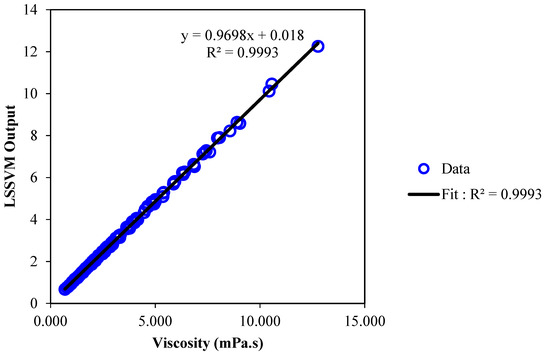
Figure 6. Regression plot of the proposed vector machine model versus actual viscosity of /ethlyene glycol-water nanofluid.

Table 3. Statistical parameters of the evolved LSSVM approach for determination of viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

Training Set
R2	0.9995
Average absolute relative deviation	2.8194
mean square error	0.01387
N	100
Test Set
R2	0.9985
Average absolute relative deviation	2.1923
mean square error	0.433
N	26
Total
R2	0.9993
Average absolute relative deviation	2.7828
mean square error	0.0156
N	126

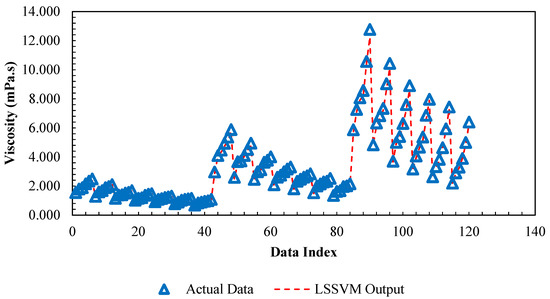
Figure 7. Comparison between actual viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid and predicted values by Least Square Support Vector Machine (LSSVM) model versus relevant data index.

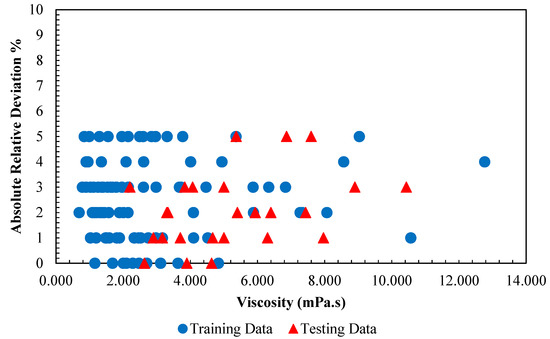
Figure 8. Absolute relative error distribution of the obtained outputs from LSSVM model versus corresponding viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid data points.

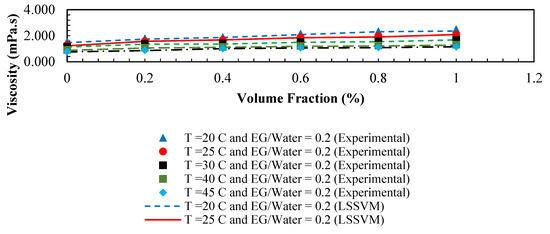
Figure 9. Comparison between predicted and experimental viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid, versus volume fraction (%) at different condition.

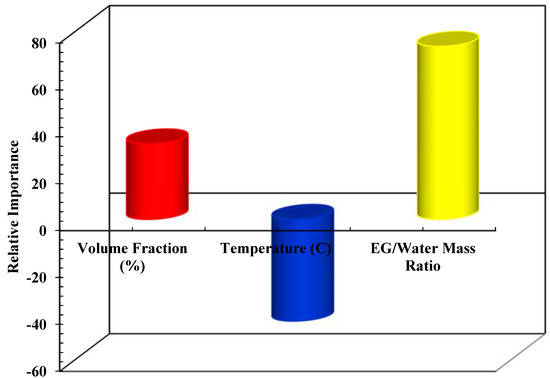
Figure 10. Relative importance of each input variables on the viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

4.1.2. PSO-ANN Model for Viscosity

Performance of the PSO-ANN model in predicting viscosity is presented in this section and has been compared with the GA-LSSVM model. In Figure 11, a regression plot between obtained data using PSO-ANN model and actual data is represented. As can be seen, there are not sufficient data are around the diagonal line (Y = X) which demonstrates that the model is not very accurate. Similar to the previous section, the statistical criteria are used to assess the accuracy of the model. The values of mean squared errors (MSE), average absolute relative deviations (AARD), and determination coefficients (R²) are represented in Table 4. The superior performance of the LSSVM model in predicting viscosity can be specifically seen when comparing the MSE and AARD values. In Figure 12, the obtained data by applying the PSO-ANN model and the experimental data for each data index is compared. By comparing Figure 12 to Figure 7, it can be concluded that to predict the viscosity, the accuracy of PSO-ANN model is lower compared to the LSSVM model. Relative deviations of the PSO-ANN model outputs versus actual data are shown in Figure 13. The highest relative error is approximately ±50% which is not acceptable. In Figure 14, the comparison between PSO-ANN outputs and the experimental data for dynamic viscosity is represented for various concentrations at different temperatures. Based on the results in Figure 14, it can be seen more clearly that the outputs of the model do not follow the actual data as accurate as the LSSVM model.

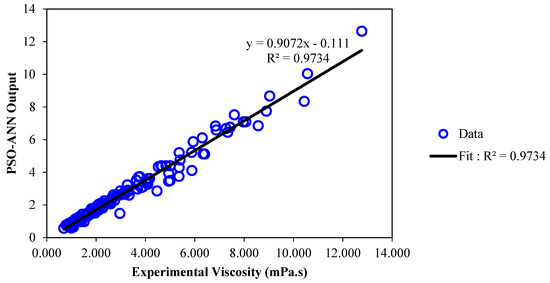
Figure 11. Regression plot of the proposed PSO-ANN model versus actual viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

Table 4. Calculated statistical indexes of the implemented intelligence-based approaches for the viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water mixture determination.

Statistical Parameter	LSSVM	PSO-ANN
(MSE)	0.0156	0.3541
R2	0.9993	0.9734
AARD	2.7828	13.492

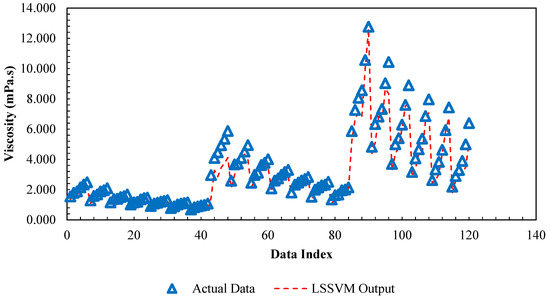
Figure 12. Comparison between actual viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid and predicted values by PSO-ANN model versus relevant data index.

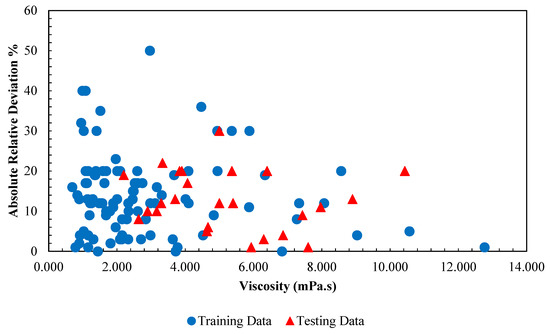
Figure 13. Absolute relative error distribution of the obtained outputs from PSO-ANN model versus corresponding viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid data points.

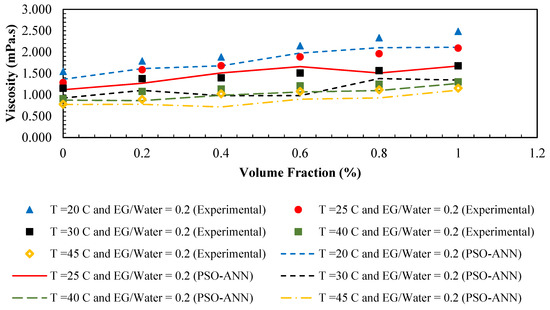
Figure 14. Comparison between PSO-ANN outputs and experimental viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid, versus volume fraction (%) at different condition.

4.2. Thermal Conductivity

4.2.1. GA-LSSVM Model for Thermal Conductivity

Similar to the approach used in the previous sections to evaluate the performance of the models in predicting viscosity, the results for thermal conductivity are investigated in this section. The regression plot between the estimated values of the thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid obtained by the GA-LSSVModel and the actual values are illustrated in Figure 15. Sufficient accuracy is observed as the majority of the data are in the vicinity of the diagonal line. To further assess this accuracy, the major statistical criteria are represented in Table 5. Values of R² > 0.94, AARD < 2.5, and MSE < 0.00025 are achieved for all data sets. In Figure 16, the obtained data by the model and experimental values are compared for each data index. As shown, the proposed model is accurate and reliable since the outputs of the model follow the actual data precisely. The absolute relative deviation of the model is presented in Figure 17 to get better insight into the deviation of output data versus actual data for the thermal conductivity of the nanofluid. Based on the results, as the case for viscosity, the highest relative deviation by the proposed model is approximately ±5%. Moreover, in Figure 18, model outputs and experimental data are depicted at various temperatures versus concentration. The results are matched appropriately with experimental data. In the same approach used for viscosity, to assess the relative importance of each input variable, the ANOVA technique is applied for the thermal conductivity of the nanofluid. Obtained results, as shown in Figure 19, show that the mass ratio of EG/water has the highest effect compared to other input variables.

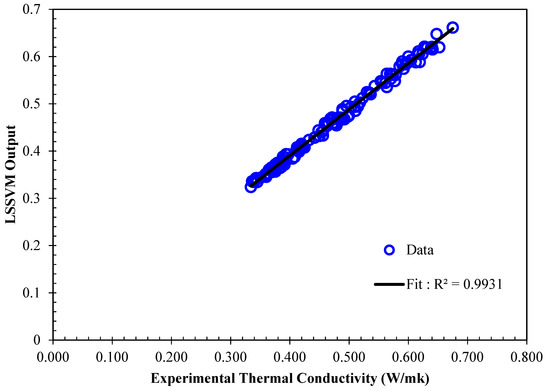
Figure 15. Regression plot of the proposed vector machine model versus actual thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

Table 5. Statistical parameters of the evolved LSSVM approach for calculating thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

Training Set
R2	0.9921
Average absolute relative deviation	2.43
mean square error	0.00021
N	100
Test Set
R2	0.942
Average absolute relative deviation	2.192
mean square error	0.0001
N	26
Total
R2	0.9931
Average absolute relative deviation	2.3809
mean square error	0.00019
N	126

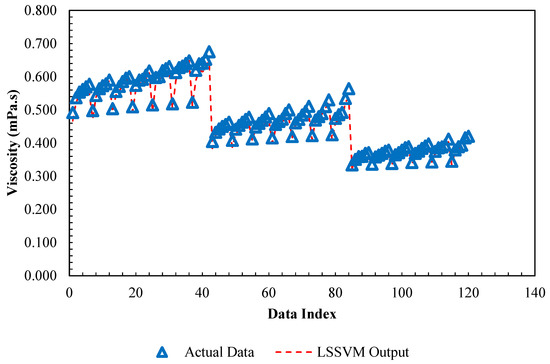
Figure 16. Comparison between actual thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid and predicted values by LSSVM model versus relevant data index.

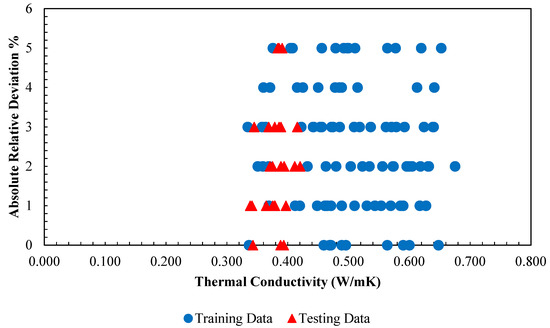
Figure 17. Absolute relative error distribution of the obtained outputs from LSSVM model versus corresponding thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid data points.

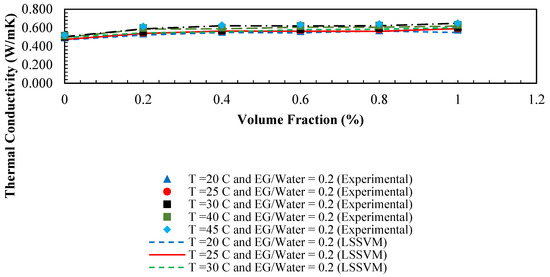
Figure 18. Comparison between predicted and experimental thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water mixture, versus volume fraction (%) at different condition.

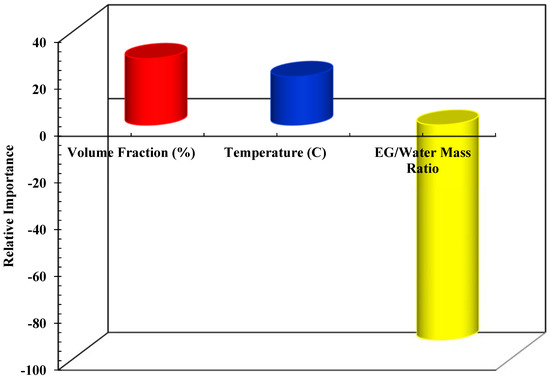
Figure 19. Relative importance of each input variables on the thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

4.2.2. PSO-ANN Model for Thermal Conductivity

Similar to dynamic viscosity, PSO-ANN approach is also applied to model the thermal conductivity of the nanofluid. The regression plot between the model outputs and experimental data is depicted in Figure 20. In comparison with the LSSVM approach, the share of data points which are in the vicinity of the diagonal line is lower which shows that the model is not as precise as GA-LSSVM. In Figure 21, both values, including experimental data and model outputs, are depicted for each data index. By comparing this figure to Figure 16, it can be concluded that the differences between model outputs and actual data are higher when using the PSO-ANN model. Absolute deviation of the PSO-ANN model outputs versus experimental data is shown in Figure 22. The maximum relative deviation is in the range of ±20% which is much higher compared with the GA-LSSVM model. Moreover, outputs of PSO-ANN model and experimental data for various concentrations are represented in Figure 23. It is clear that the accuracy of the obtained results is not acceptable. Major statistical criteria to evaluate the accuracy of the PSO-ANN model in predicting thermal conductivity is presented in Table 6. The considerable difference can be seen in the MSE, R², and AARD values. Therefore, it can be concluded that the PSO-ANN model is not as precise as LSSVM in predicting thermal conductivity of the nanofluid.

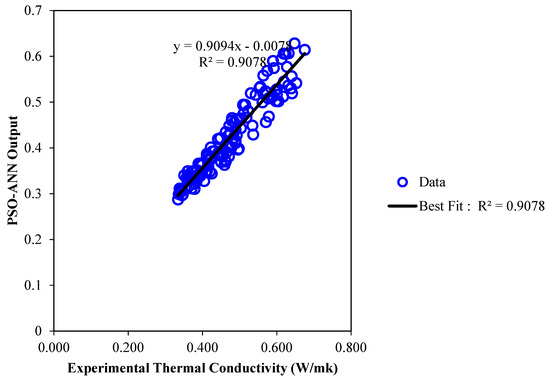
Figure 20. Regression plot of the proposed PSO-ANN model versus actual thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid.

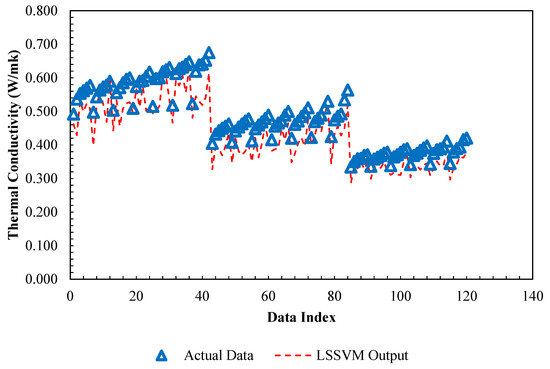
Figure 21. Comparison between actual thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid and predicted values by PSO-ANN model versus relevant data index.

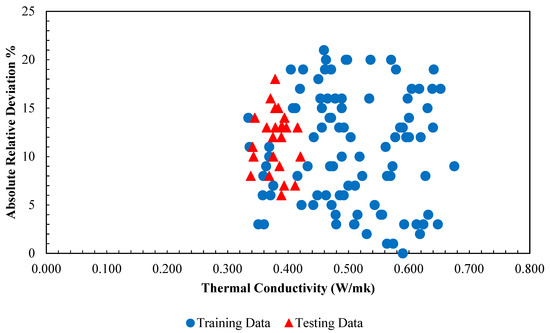
Figure 22. Absolute relative error distribution of the obtained outputs from PSO-ANN model versus corresponding thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid data points.

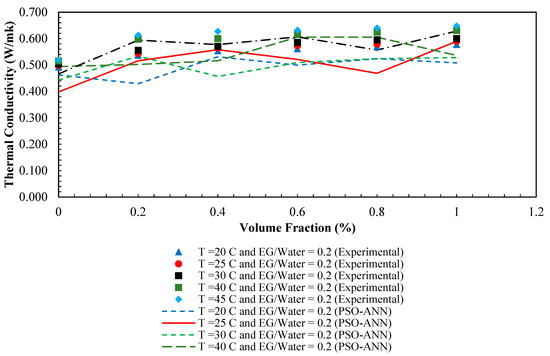
Figure 23. Comparison between PSO-ANN outputs and experimental thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid, versus volume fraction (%) at different condition.

Table 6. Calculated statistical indexes of the implemented intelligence-based approaches for thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid determination.

Statistical Parameter	LSSVM	PSO-ANN
(MSE)	0.00019	0.00338
R2	0.9931	0.9078
AARD	2.3809	10.761

4.3. Leverage Approach

It is crucial to determine the outlier of the proposed models for viscosity and thermal conductivity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid to see the effects of uncertainties on the capability of these methods. In order to achieve this goal, the approach of Leverage Value Statistics is used. The Graphical Williams plot is used to determine the outliers using the determined H values from the outputs of the GA-LSSVM approach. More details about the procedure of this method can be found in the literature. The Williams plot is shown in Figure 24 for the obtained results by applying GA-LSSVM and PSO-ANN approaches. As can be seen, GA-LSSVM model shows higher performance based on accuracy and applicability range since the majority of the data are in the range of H [0, 0.12] and R [−3, 3]. Moreover, it shows that all the applied data in the modelling are in the acceptable ranges.

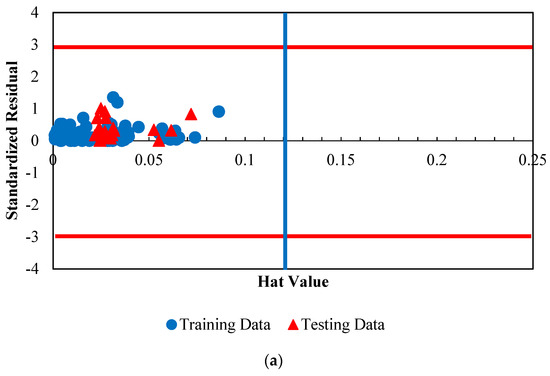
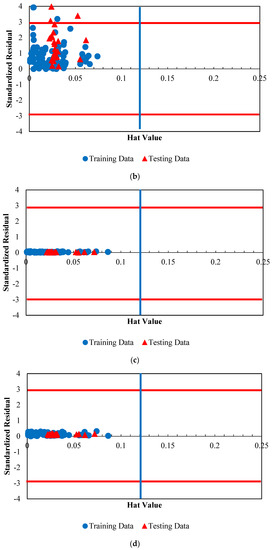
Figure 24. Detection of the probable doubtful measured viscosity and thermal conductivity data and the applicability domain of the suggested approaches for the viscosity of $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$/ethylene glycol-water nanofluid. (a) GA-LSSVM model for viscosity prediction (b) PSO-ANN model for viscosity prediction (c) GA-LSSVM model for thermal conductivity prediction (d) PSO-ANN model for thermal conductivity prediction (the H* value is 0.12).

5. Conclusions

In the present study, two novel approaches, namely, GA-LSSVM and PSO-ANN are utilized to predict the thermal conductivity and dynamic viscosity of Fe₂O₃/ethylene glycol-water nanofluids. Various statistical tools are used to thoroughly evaluate the performance of each model in predicting each thermophysical property. Regression plots, R², MSE, AARD, absolute relative deviation, and one by one comparison of the outputs and actual data are presented in each section. Based on all evaluations:

• Results indicate that the accuracy of the GA-LSSVM model in predicting both thermal conductivity and dynamic viscosity is much higher compared to the PSO-ANN model.
• The highest relative deviations of the proposed GA-LSSVM model $\mathrm{F}{\mathrm{e}}_2{\mathrm{O}}_3$ viscosity and thermal conductivity are approximately ±5%.
• The R², MSE, and AARD values for the GA-LSSVM model are in satisfactory range in predicting the viscosity and conductivity.
• ANOVA technique implementation demonstrates that among various input variables, including temperature, concentration, and the mass ratio of EG/water, the mass ratio has the most significant effect on both thermal conductivity and dynamic viscosity.

Overall, based on the obtained results, it can be concluded that GA-LSSVM approach has a better performance compared to the PSO-ANN models, and is a reliable tool for predicting the thermal conductivity and dynamic viscosity of nanofluids.