Numerical Investigation of Film Cooling Enhancement Using an Upstream Sand-Dune-Shaped Ramp
Abstract
:1. Introduction
2. Numerical Modelling
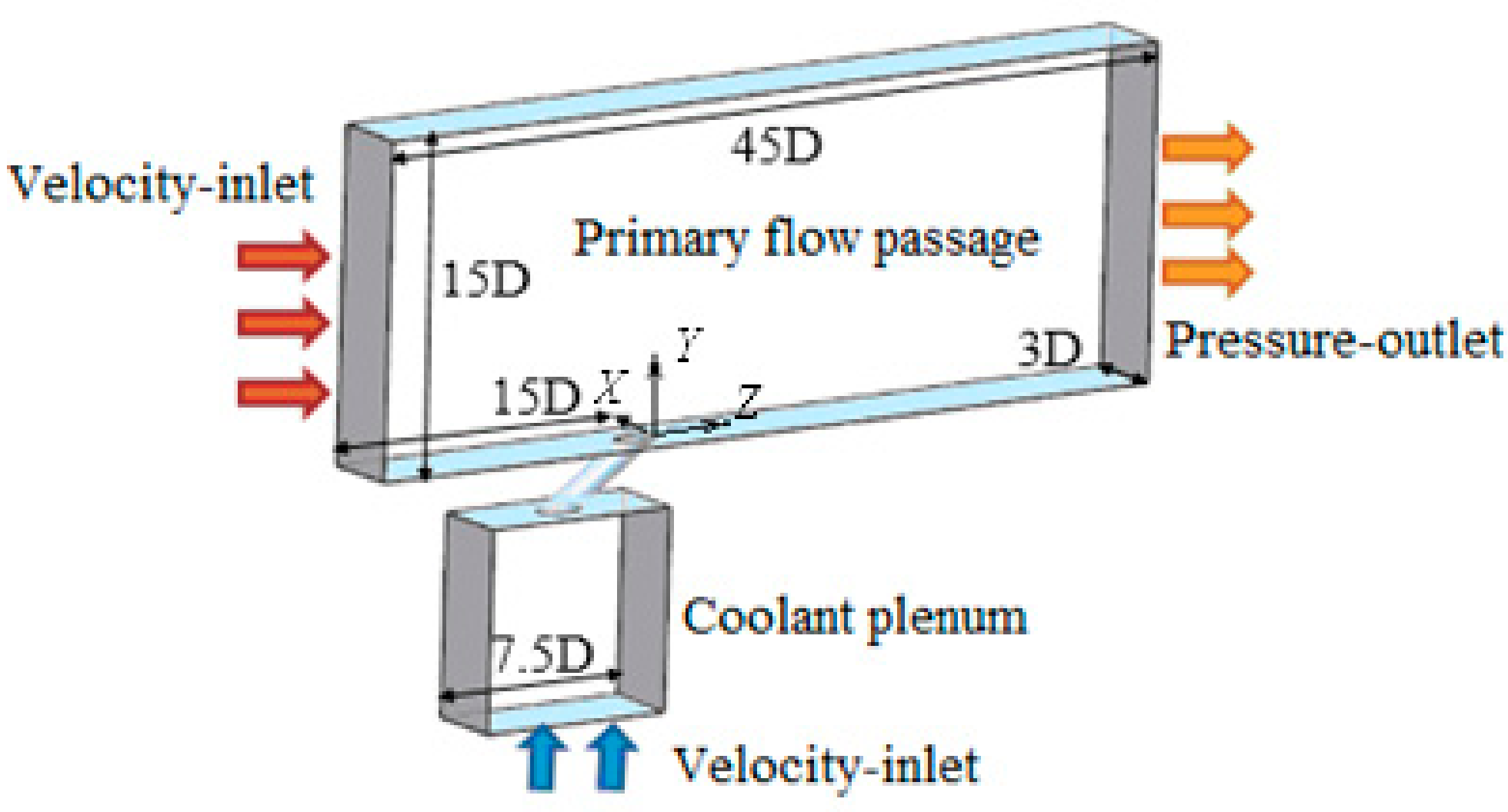
2.1. Computational Domain
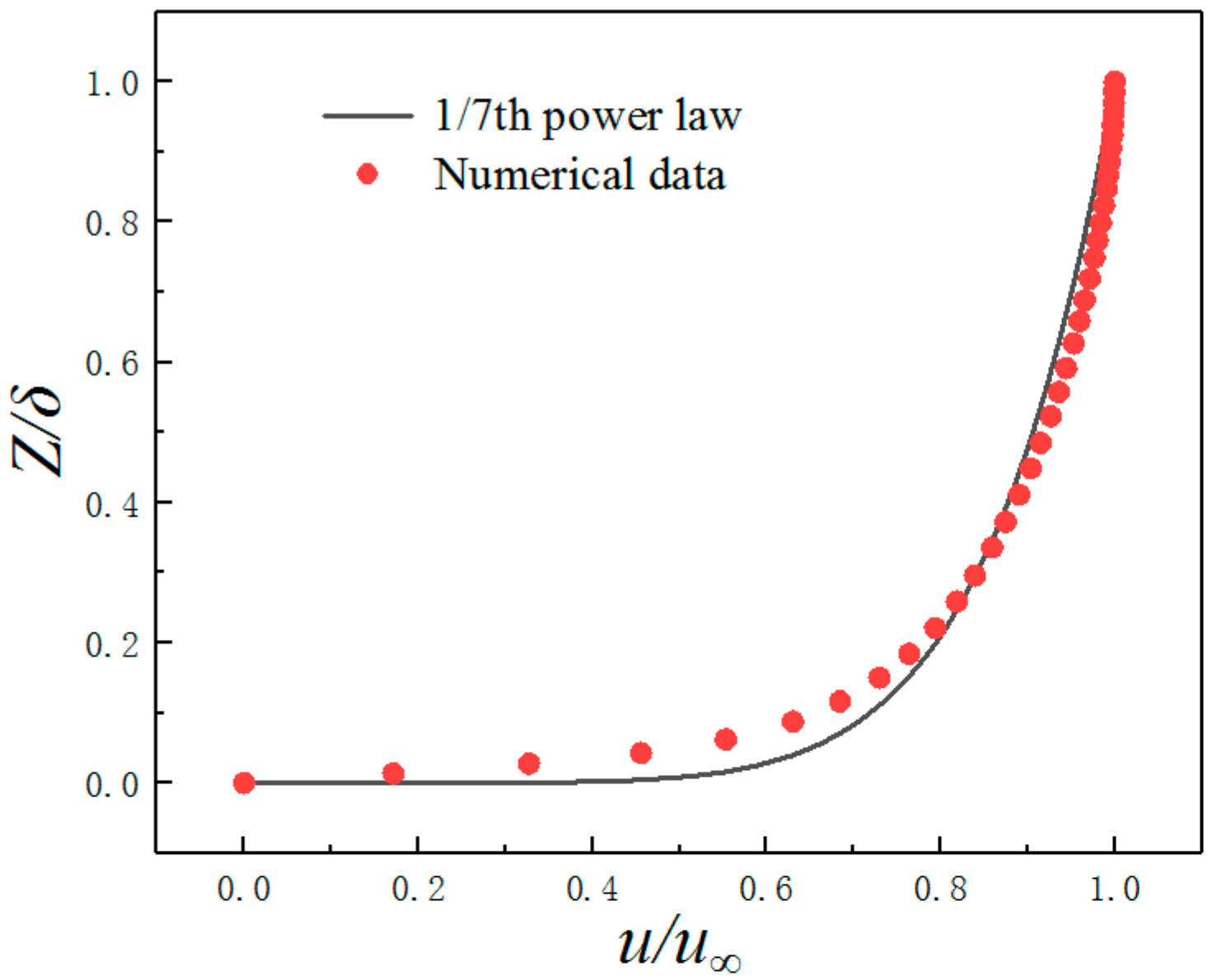
2.2. Boundary Conditions
2.3. Computational Scheme
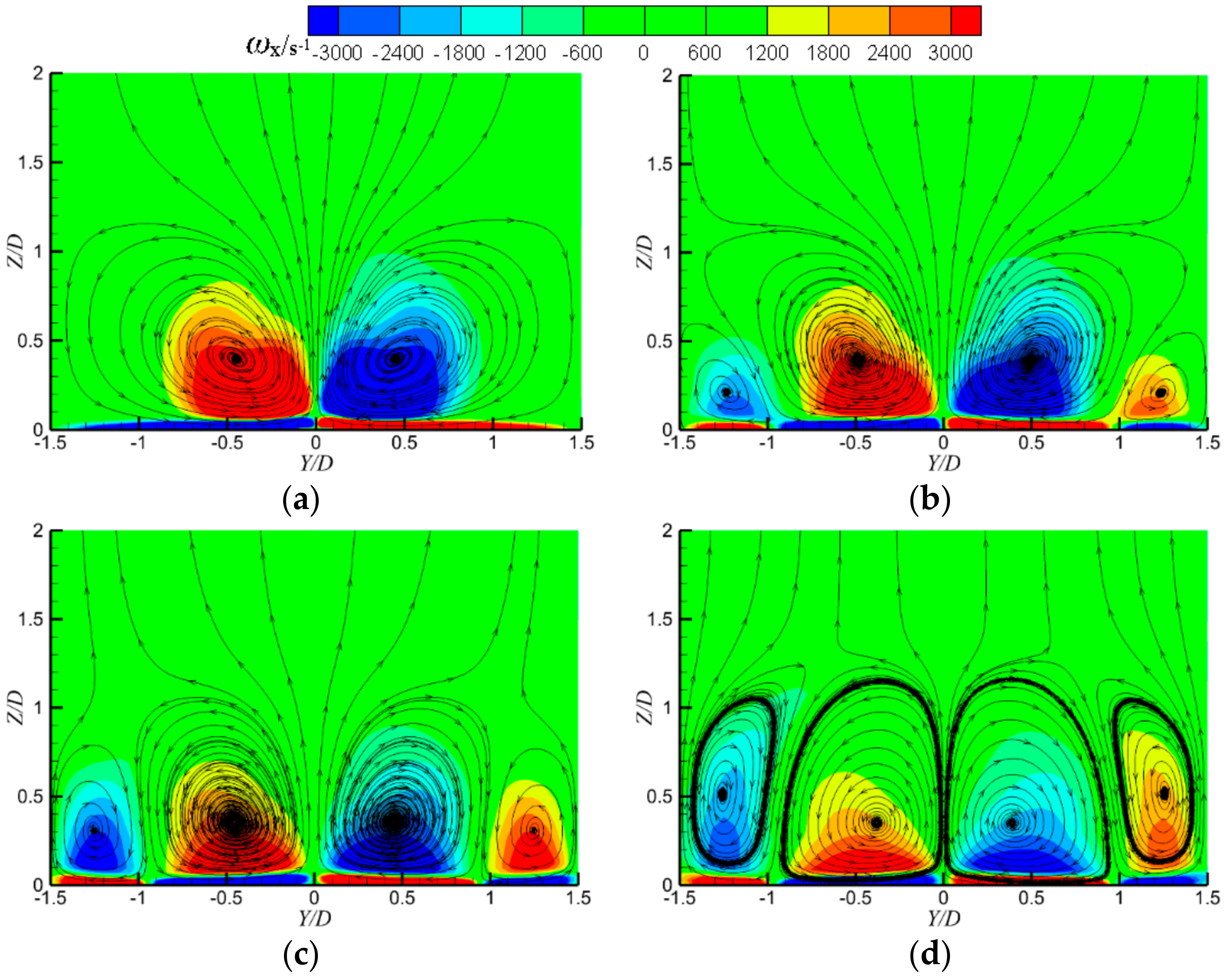
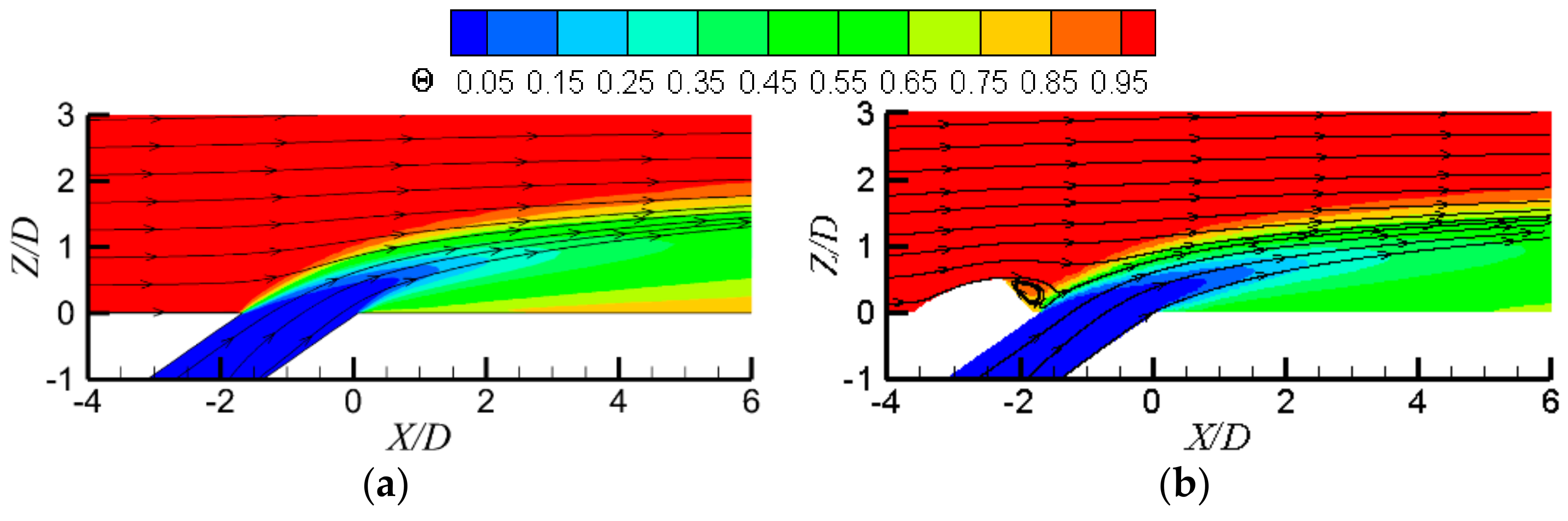
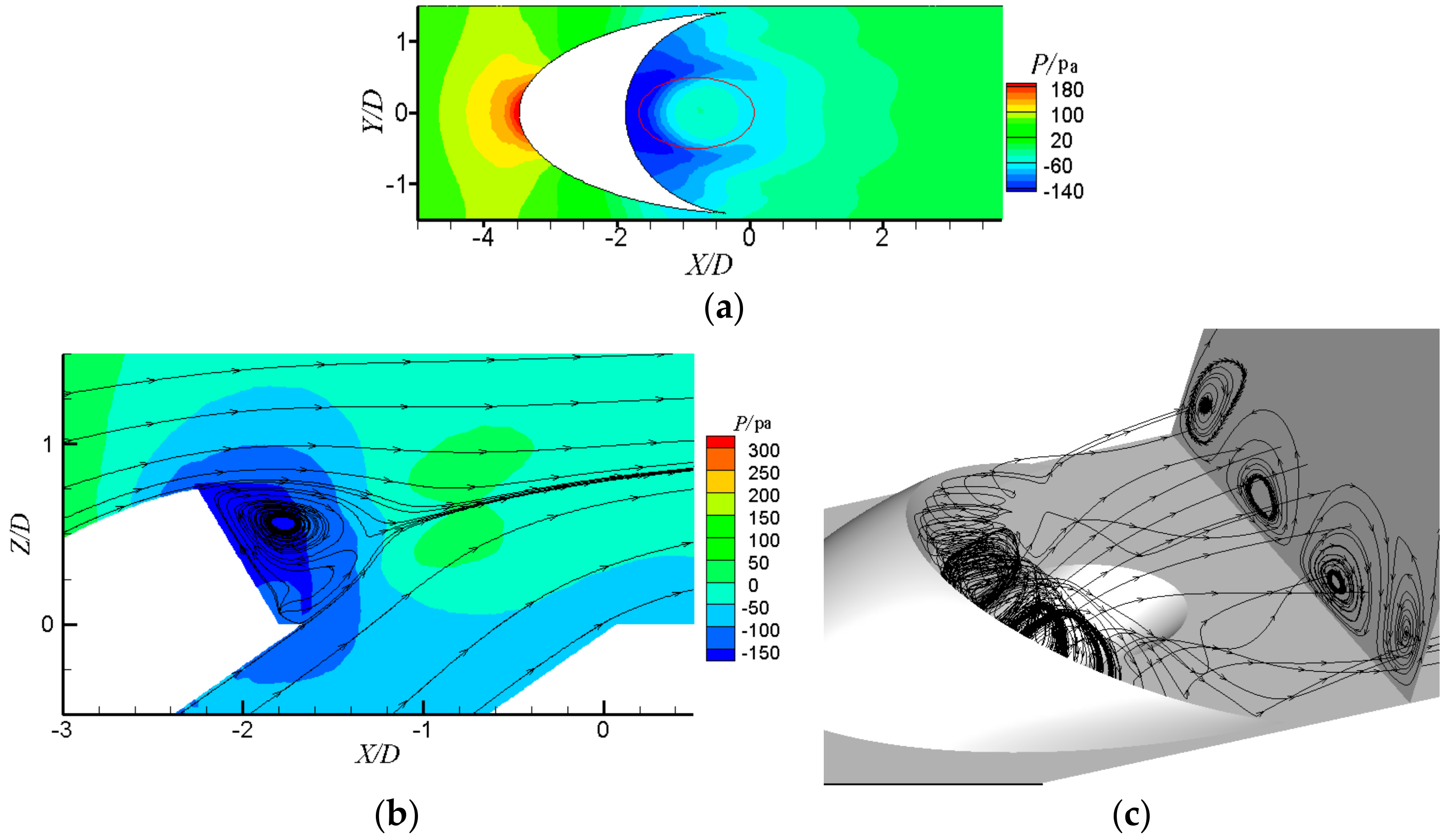
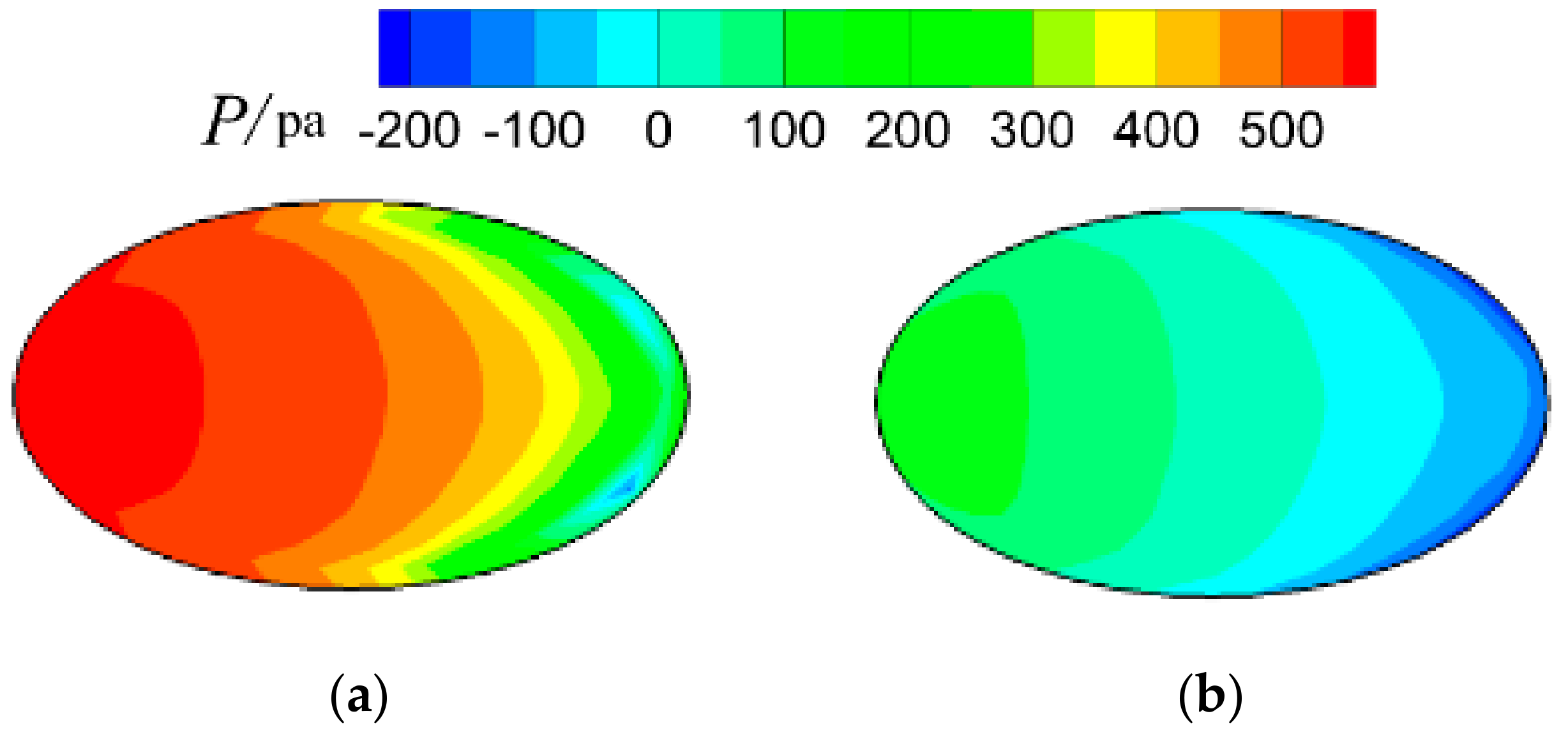
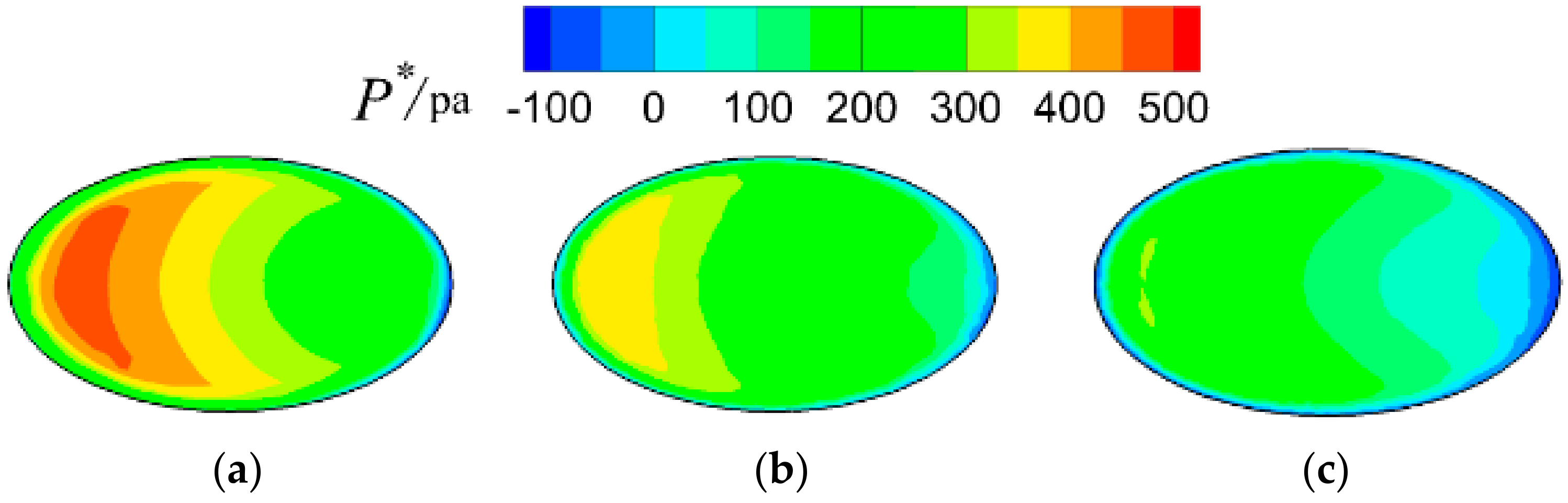
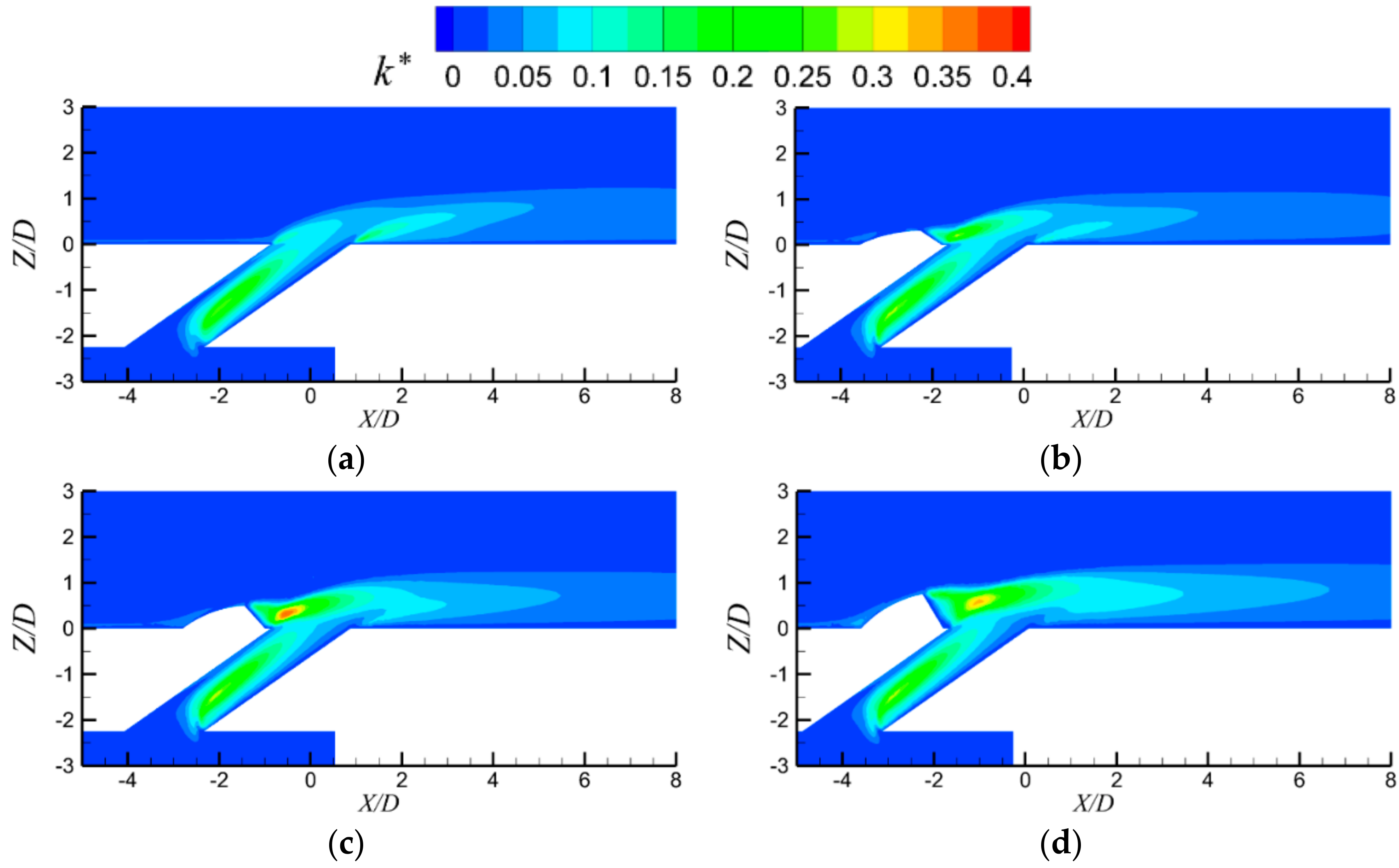
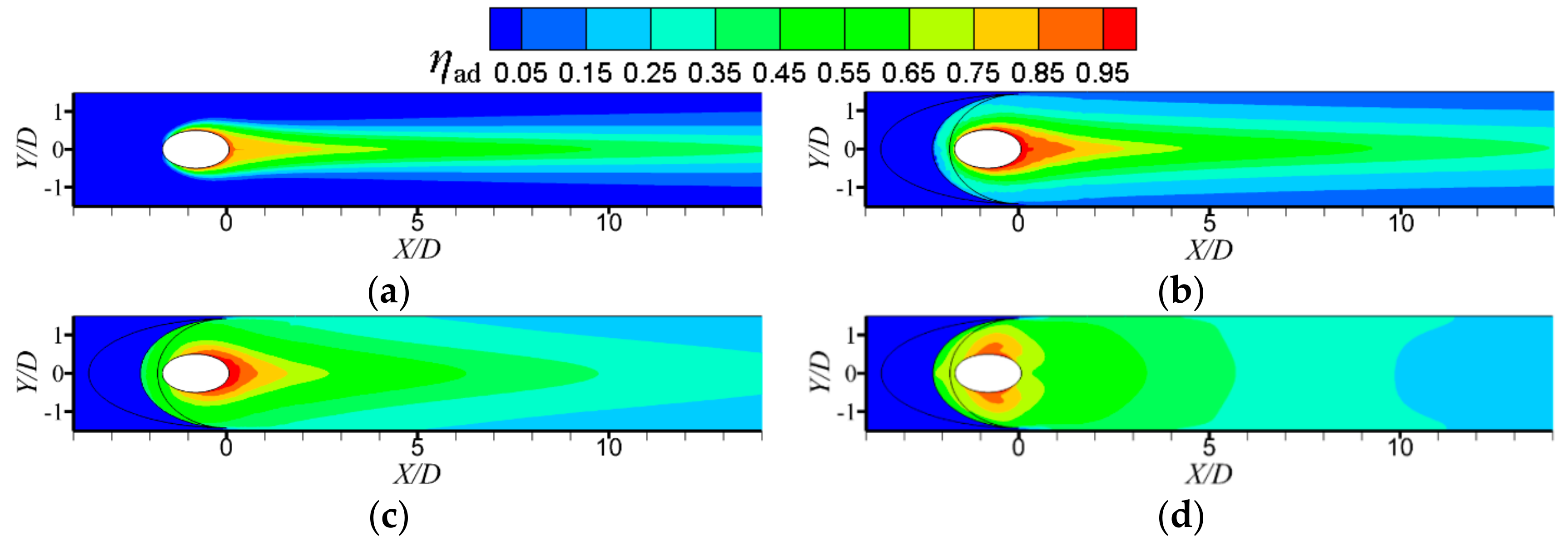
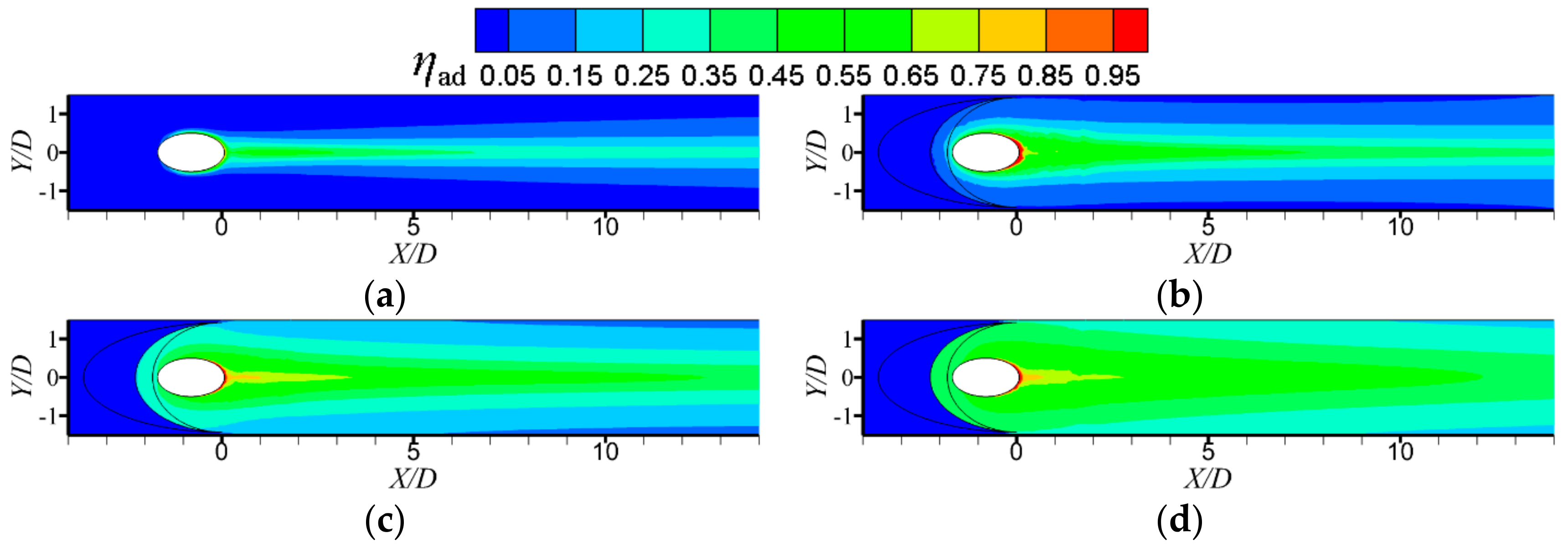
3. Results and Discussion
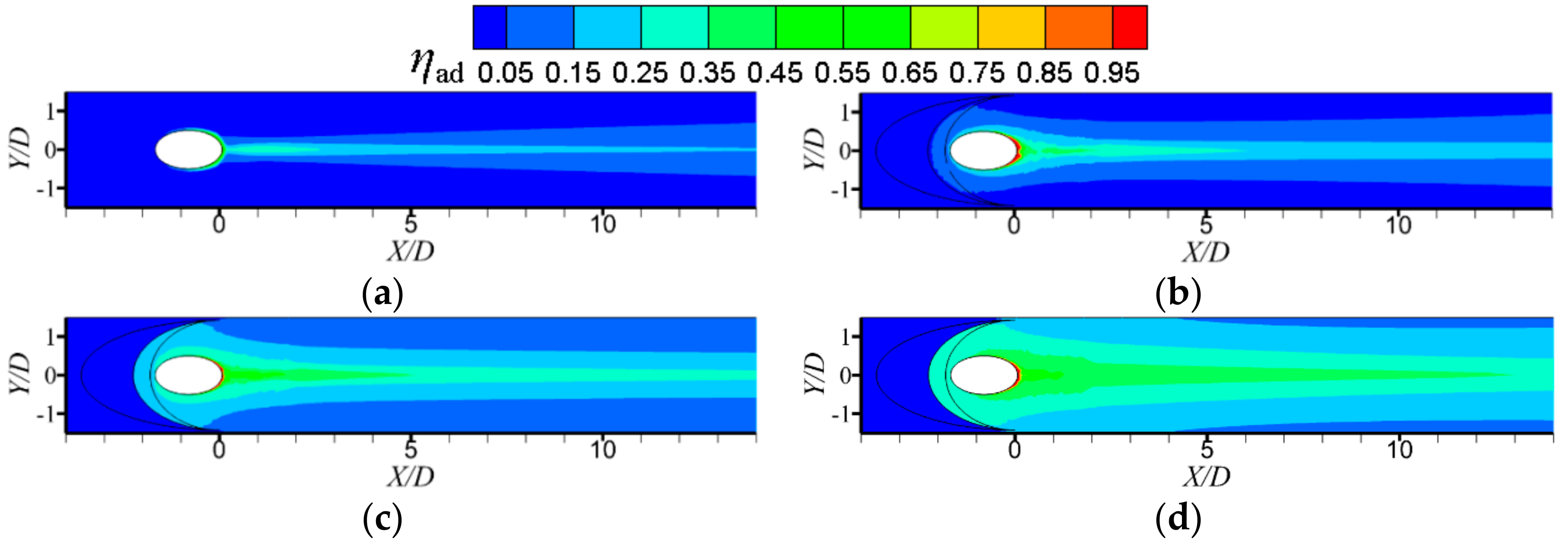
3.1. Detailed Flow Fields
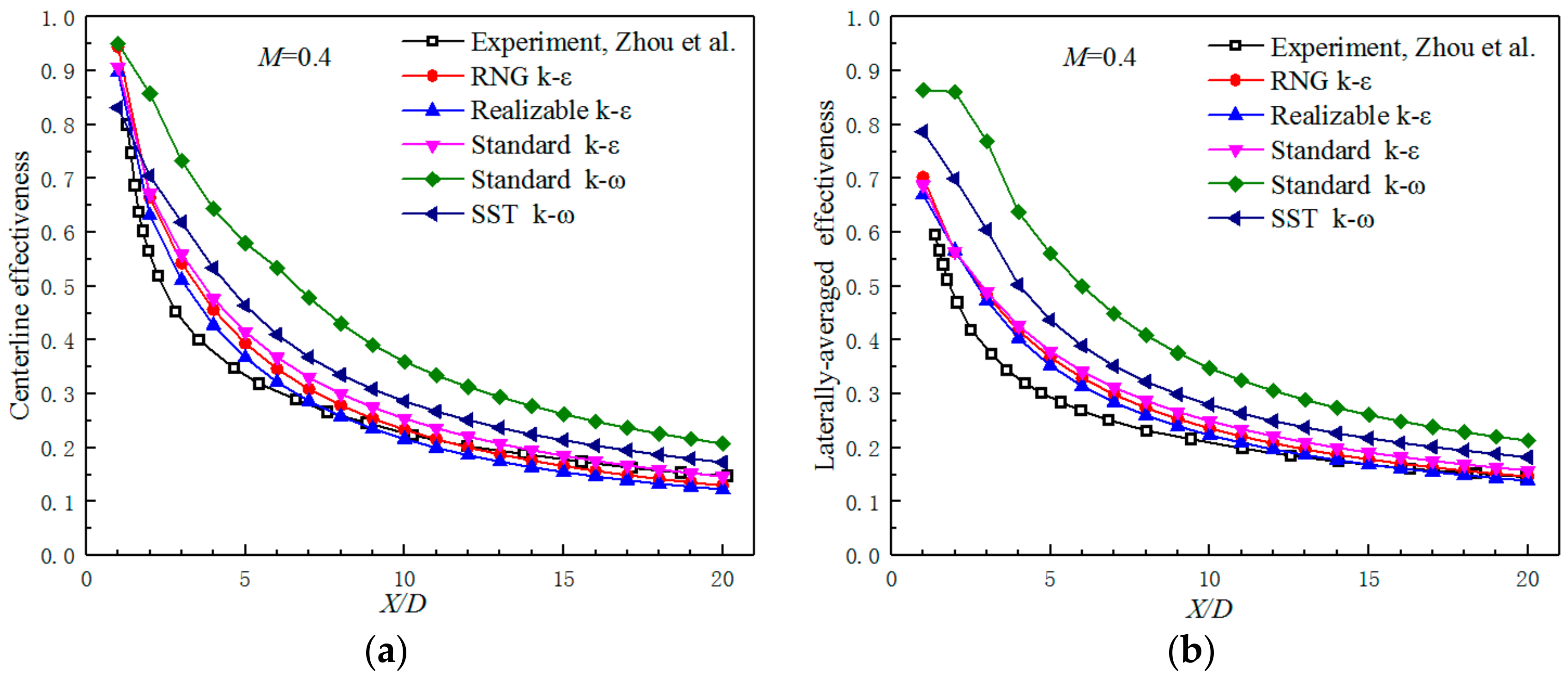
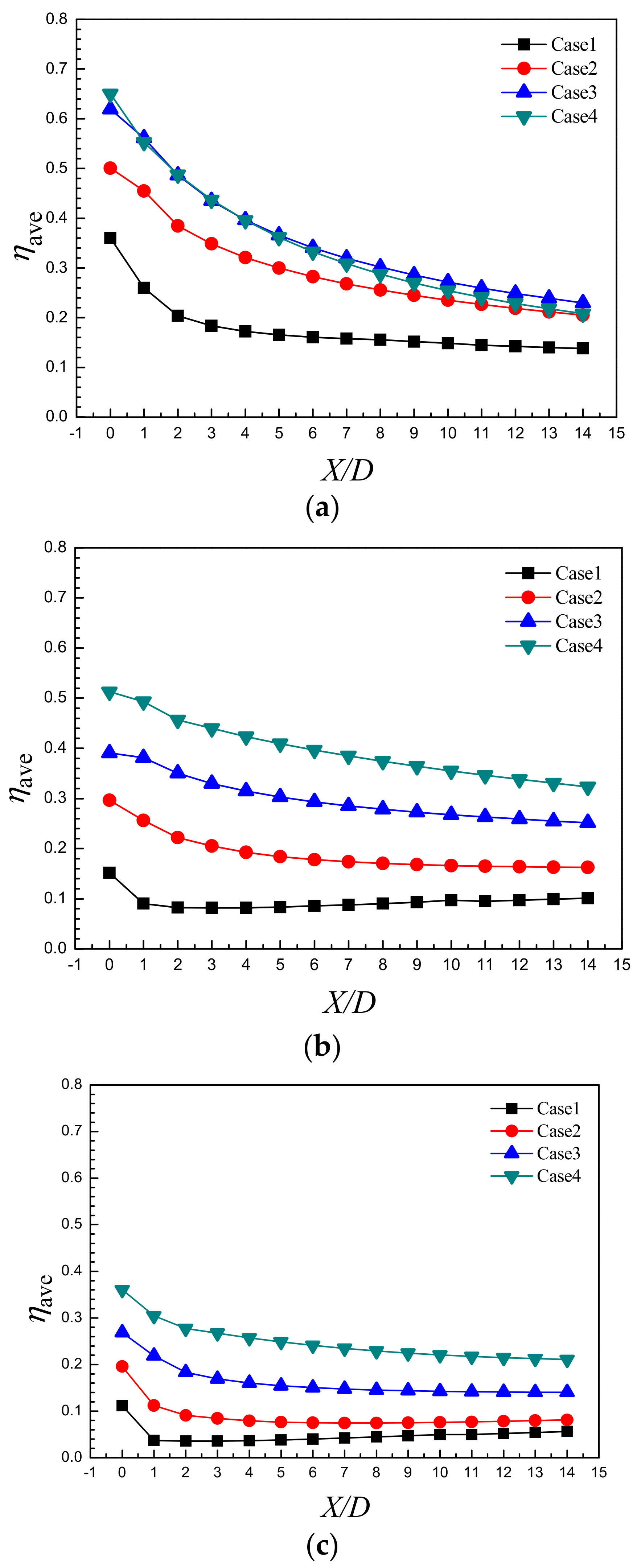
3.2. Adiabatic Film Cooling Effectiveness
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bunker, R.S. Gas Turbine Heat Transfer: Ten Remaining Hot Gas Path challenges. ASME J. Turbomach. 2007, 129, 193–210. [Google Scholar] [CrossRef]
- Bell, C.M.; Hamakawa, H.; Ligrani, P.M. Film Cooling from Shaped Holes. ASME J. Heat Transf. 2000, 122, 224–232. [Google Scholar] [CrossRef]
- Bunker, R.S. A review of Turbine Shaped Film Cooling Technology. ASME J. Heat Transf. 2005, 127, 441–453. [Google Scholar] [CrossRef]
- Na, S.; Shih, T.I.-P. Increasing Adiabatic Film-Cooling Effectiveness by Using an Upstream Ramp. ASME J. Heat Transf. 2007, 129, 464–471. [Google Scholar] [CrossRef]
- Barigozzi, G.; Franchini, G.; Perdichizzi, A. The Effect of an Upstream Ramp on Cylindrical and Fan-Shaped Hole Film Cooling: Part I—Aerodynamic Results. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007. ASME Paper GT2007-27077. [Google Scholar]
- Barigozzi, G.; Franchini, G.; Perdichizzi, A. The Effect of an Upstream Ramp on Cylindrical and Fan-Shaped Hole Film Cooling: Part II—Adiabatic Effectiveness Results. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007. ASME Paper GT2007-27079. [Google Scholar]
- Chen, S.P.; Chyu, M.K.; Shih, T.I.-P. Effects of Upstream Ramp on the Performance of Film Cooling. Int. J. Therm. Sci. 2011, 50, 1085–1094. [Google Scholar] [CrossRef]
- Rallabandi, A.P.; Grizzle, J.; Han, J.C. Effect of Upstream Step on Flat Plate Film Cooling Effectiveness Using PSP. ASME J. Turbomach. 2011, 133, 041024. [Google Scholar] [CrossRef]
- Yan, W.S.; Pu, J.; Wang, J.H. The Combined Effects of an Upstream Ramp and Swirling Coolant Flow on Film Cooling Characteristics. ASME J. Turbomach. 2016, 138, 111008. [Google Scholar]
- Abdala, A.M.; Elwekeel, F.N. An Influence of Novel Upstream Steps on Film Cooling Performance. Int. J. Heat Mass Transf. 2016, 93, 86–96. [Google Scholar] [CrossRef]
- Abdala, A.M.; Elwekeel, F.N.; Huang, D.G. Film Cooling Effectiveness and Flow Structures for Novel Upstream Step. Appl. Therm. Eng. 2016, 105, 397–410. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, H. Improvements of Film Cooling Effectiveness by Using Barchan Dune Shaped Ramps. Int. J. Heat Mass Transf. 2016, 103, 443–456. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, H. A Novel Sand-Dune-Inspired Design for Improved Film Cooling Performance. Int. J. Heat Mass Transf. 2017, 110, 908–920. [Google Scholar] [CrossRef]
- Keller, M.A.; Kloker, M.J. Direct Numerical Simulation of Foreign-Gas Film Cooling in Supersonic Boundary-Layer Flow. AIAA J. 2016, 55, 1–13. [Google Scholar] [CrossRef]
- Keller, M.A.; Kloker, M.J. Effusion Cooling and Flow Tripping in Laminar Supersonic Boundary-Layer Flow. Res. Vet. Sci. 2015, 59, 10–16. [Google Scholar] [CrossRef]
- Harrison, K.; Bogard, D. Comparison of RANS Turbulence Models for Prediction of Film Cooling Performance. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008. ASME Paper GT2008-50366. [Google Scholar]
- Silieti, M.; Kassab, A.J.; Divo, E. Film Cooling Effectiveness: Comparison of Adiabatic and Conjugate Heat Transfer CFD Models. Int. J. Therm. Sci. 2009, 48, 2237–2248. [Google Scholar] [CrossRef]
- Fly, M.J.; Jubran, B.J. A Numerical Evaluation on the Effect of Sister Holes on Film Cooling Effectiveness and the Surrounding Flow Filed. Heat Mass Transf. 2009, 45, 1435–1446. [Google Scholar]
- Nikparto, A.; Schobeiri, M.T. Combined numerical and experimental investigations of heat transfer of a highly loaded low-pressure turbine blade under periodic inlet flow condition. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018. [Google Scholar] [CrossRef]
- Nikparto, A.A.; Rice, T.T.; Schobeiri, M.T. Experimental and Numerical Investigation of Heat Transfer and Film Cooling Effectiveness of a Highly Loaded Turbine Blade Under Steady and Unsteady Wake Flow Condition. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Charlotte, NC, USA, 26–30 June 2017; ASME: New York, NY, USA, 2017. [Google Scholar]
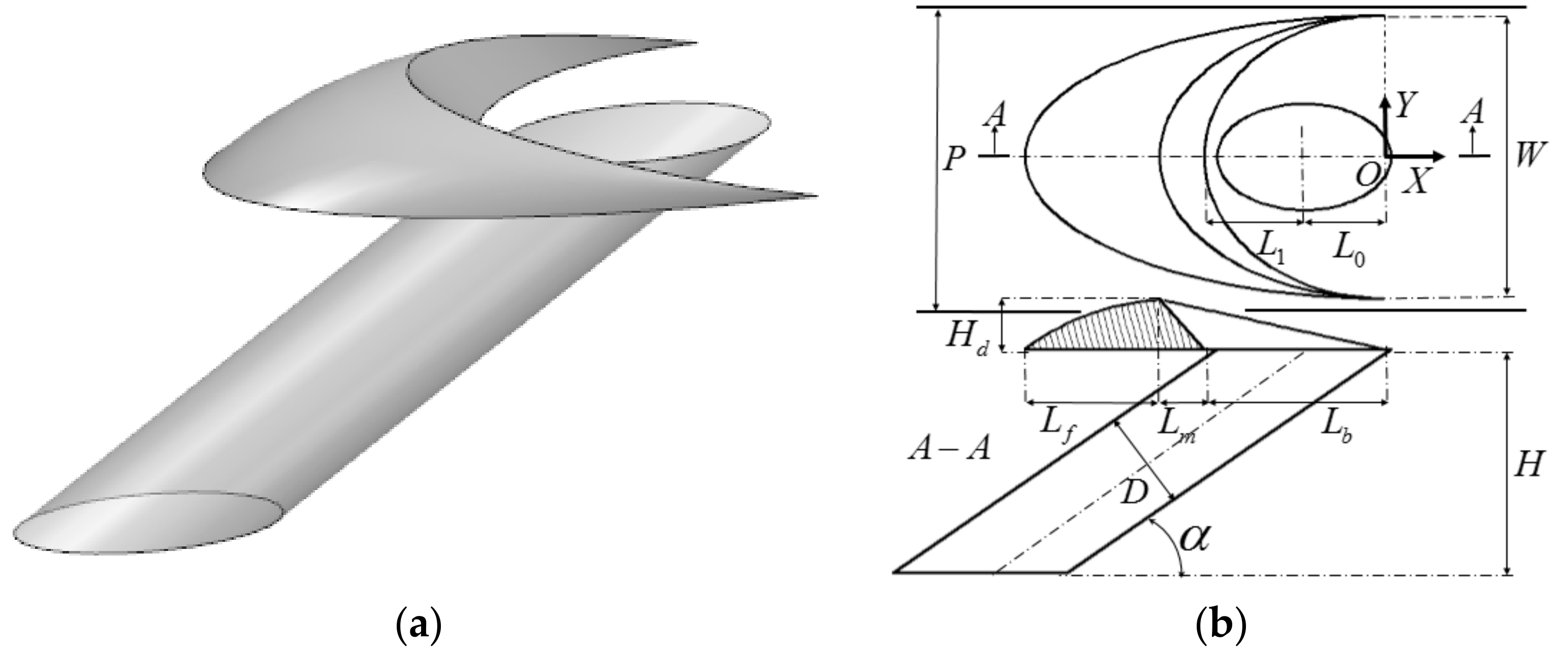


| Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|
| L0 | 3.2 | Lf | 5.4 |
| L1 | 4.0 | Lm | 1.8 |
| Lb | 7.2 | W | 11.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.-C.; Zhang, J.-Z.; Tan, X.-M. Numerical Investigation of Film Cooling Enhancement Using an Upstream Sand-Dune-Shaped Ramp. Computation 2018, 6, 49. https://doi.org/10.3390/computation6030049
Zhang S-C, Zhang J-Z, Tan X-M. Numerical Investigation of Film Cooling Enhancement Using an Upstream Sand-Dune-Shaped Ramp. Computation. 2018; 6(3):49. https://doi.org/10.3390/computation6030049
Chicago/Turabian StyleZhang, Sheng-Chang, Jing-Zhou Zhang, and Xiao-Ming Tan. 2018. "Numerical Investigation of Film Cooling Enhancement Using an Upstream Sand-Dune-Shaped Ramp" Computation 6, no. 3: 49. https://doi.org/10.3390/computation6030049
APA StyleZhang, S.-C., Zhang, J.-Z., & Tan, X.-M. (2018). Numerical Investigation of Film Cooling Enhancement Using an Upstream Sand-Dune-Shaped Ramp. Computation, 6(3), 49. https://doi.org/10.3390/computation6030049




