Determination of Aerosol Size Distribution from Angular Light-Scattering Signals by Using a SPSO-DE Hybrid Algorithm

Abstract

The comparison of the angular light-scattering method (ALSM) and the spectral extinction method (SEM) in solving the inverse problem of aerosol size distribution (ASD) are studied. The inverse problem is solved by a SPSO-DE hybrid algorithm, which is based on the stochastic particle swarm optimization (SPSO) algorithm and differential evolution (DE) algorithm. To improve the retrieval accuracy, the sensitivity analysis of measurement signals to characteristic parameters in ASDs is studied; and the corresponding optimal measurement angle selection region for ALSM and optimal measurement wavelength selection region for SEM are proposed, respectively. Results show that more satisfactory convergence properties can be obtained by using the SPSO-DE hybrid algorithm. Moreover, short measurement wavelengths and forward measurement angles are beneficial to obtaining more accurate results. Then, common monomodal and bimodal ASDs are estimated under different random measurement errors by using ALSM and SEM, respectively. Numerical tests show that retrieval results by using ALSM show better convergence accuracy and robustness than those by using SEM, which is attributed to the distribution of the objective function value. As a whole, considering the convergence properties and the independence on prior optical information, the ALSM combined with SPSO-DE hybrid algorithm provides a more effective and reliable technique to obtain the ASDs.

1. Introduction

Atmospheric aerosols are important drivers of air quality, atmospheric heat radiative balance, human health and climate, etc. Generally, there are three vitally important properties of aerosols, i.e., aerosol size distributions (ASDs), aerosol optical depths (AODs) and Ångström exponents [1,2]. The knowledge of ASDs is essential to a better understanding of their potential contributions to climate change, source identification and environmental quality, necessary to control pollution and preserve citizen health. Therefore, in situ measuring the ASDs presented in the atmosphere is of great necessity [3,4]. Nowadays, although there are several global ground-based aerosol observation networks and satellite instrument networks that have been established to study the properties of the atmospheric aerosols, e.g., AERONET, MODIS [5,6,7,8], determining the ASDs accurately is still regarded as an unsolved problem and needs further research.

During the past several years, various types of methods have been proposed to study the ASDs, e.g., the aerodynamic method, the optical measurement method, electrical mobility and condensation method, electrical sensing zone method and the electron microscopy method [9]. Owing to offering a useful and effective approach, reliable measurement results and broad size ranges, the optical measurement method coupled with inverse methods has drawn much attention in the field of determining the ASDs [10]. Usually the optical measurement method could be divided into several categories, such as spectral extinction method (SEM), angular light-scattering method (ALSM) and optical depth measurement method, etc. During our previous work, the ASDs were reconstructed effectively by using SEM, and the retrieval accuracy was improved by increasing the number of measurement wavelengths [11]. However, all the satisfactory results obtained by using SEM were based on having sufficient spectral measurement information about the aerosol dispersion system beforehand, e.g., the multi-spectral transmittance signals. To obtain these information measurements, the multi-spectral light source and detector should be needed, and the multi-spectral optical constants of aerosol should be known, which may increase the difficulty and the cost of experiment. Unlike the SEM, only single spectral information of aerosol is required by using ALSM, and the ASDs can be recovered by measuring multi-angle light-scattering signals [12,13].

In the present study, the comparison of ALSM and SEM in retrieval of ASDs are studied. The inverse problem is solved by using a SPSO-DE hybrid algorithm, which is based on the stochastic particle swarm optimization (SPSO) algorithm and differential evolution (DE) algorithm. The research is organized as follows. First, the principles of ALSM and SPSO-DE hybrid algorithm are introduced, and that of SEM, available in Reference [14], is not repeated here. Then, the sensitivity analysis of optical measurement signals to characteristic parameters in ASDs is studied, and the corresponding optimal measurement angle selection region for ALSM and optimal measurement wavelength selection region for SEM are proposed. Finally, common monomodal and bimodal ASDs are retrieved by SEM and ALSM, respectively, and the main conclusions and perspectives are provided.

2. Methodology

2.1. The principle of the ALSM

According to the principle of the ALSM, when a suspension particle system is illuminated by a parallel light beam with intensity $I_0$ and the refractive index of the particle is different from those of the surrounding medium, the angular light-scattering intensity $I(\theta )$ can be written as:

$$I(\theta )=\frac{\pi N_0}{\lambda }{\displaystyle {\int }_{D_{\min }}^{D_{\max }}i(\theta ,m_{\lambda },D,\lambda )f(D)dD}$$

(1)

$$i(\theta ,m_{\lambda },D,\lambda )=\frac{i_1(\theta ,m_{\lambda },D,\lambda )+i_2(\theta ,m_{\lambda },D,\lambda )}{8{\pi }^2}{\lambda }^2{I}_0$$

(2)

where $i_1(\theta ,m_{\lambda },D,\lambda )$ and $i_2(\theta ,m_{\lambda },D,\lambda )$ can be derived in terms of the Mie scattering functions [12,15]. Detailed information about the ALSM can be found in References [12,13,16].

2.2. The Principle of the SPSO

The standard PSO algorithm, introduced by Eberhart and Kennedy [17] in 1995, firstly, can be easily implemented by adjusting a small number of parameters. However, in the standard PSO algorithm, there is only one term which regulates historic velocity during the evolution process, and therefore the particle can only fly along one direction until it finds a better position, which will result in premature convergence. To overcome the difficulty, the SPSO algorithm was introduced, and showed better retrieval accuracy in solving the problem of estimating the ASD and other inverse radiation problems [18,19,20].

In the SPSO algorithm, the velocity-update formula and the position-update formula can be described as [18]:

$$V_i(t+1)=C_1\cdot ran{d}_1\cdot \left[P_i(t)-X_i(t)\right]+C_2\cdot ran{d}_2\cdot \left[P_{\mathrm{g}}(t)-X_i(t)\right]$$

(3)

$$X_i(t+1)=X_i(t)+V_i(t+1)$$

(4)

where $C_1$ and $C_2$ denote the positive acceleration coefficients; $ran{d}_1$ and $ran{d}_2$ are the random numbers selected within [0, 1]; $P_i(t)$ and $P_{\mathrm{g}}(t)$ denote the personal best position and global best position at the $t\mathrm{th}$ iteration, respectively; $X_i(t)$ denotes the $t\mathrm{th}$ iteration for old position, while $X_i(t+1)$ is the $\left(t+1\right)\mathrm{th}$ iteration for the new one. Detailed information of the SPSO is available in Reference [18].

2.3. The Principle of the SPSO-DE Hybrid Algorithm

In this study, to avoid the swarm diversity declining rapidly and the local optima, the Differential Evolution (DE) algorithm is proposed to modify the personal best food source positions. The detail of the DE is available in Reference [21,22,23]. During the DE algorithm, the mutant vector can be derived as [23]:

$${\mathbf{P}}_{i,\mathrm{mut}}(t)={\mathbf{P}}_k(t)+F·\left[{\mathbf{P}}_j(t)-{\mathbf{P}}_m(t)\right]$$

(5)

where $k,l,m$ are random integers uniformly selected from $\left[1,N_{\mathrm{s}}\right]$, which are different from each other; $F\in \left[0,2\right]$, a real and constant value, denotes the mutant factor. After the crossover process, the trial vector ${\mathbf{P}}_{i,\mathrm{tri}}(t)=(p_{i1,\mathrm{tri}},p_{i2,\mathrm{tri}},p_{i3,\mathrm{tri}}\dots ,p_{i{N}_{\mathrm{p}},\mathrm{tri}})$ can be expressed as [23]:

$$p_{ij,\mathrm{tri}}(t)=\{\begin{array}{l}{p}_{ij,\mathrm{mut}}(t)\mathrm{if}ran{d}_3(j)\le C_R\mathrm{or}j=rnbr(i)\\ p_{ij}(t)\mathrm{if}ran{d}_3(j)>C_R\mathrm{or}j\ne rnbr(i)\end{array}$$

(6)

where $ran{d}_3$, a uniform random number, is selected within [0, 1]; $C_R\in \left[0,1\right]$ is the user-defined crossover constant; $rnbr\in \left[1,N_{\mathrm{s}}\right]$ is a random integer. The detailed search procedures of the SPSO-DE hybrid algorithm are shown below.

Step 1.

Initialize the system control variables of SPSO-DE hybrid algorithm, such as $N_{\mathrm{s}}$, $N_{\mathrm{c}}$, $N_{\mathrm{p}}$, $\epsilon$, $C_1$, $C_2$, $F$ and $C_R$.

Step 2.

Obtain the initial particles’ position and velocity for all the swarm randomly; calculate and evaluate the corresponding objective function value $F_{\mathrm{obj},}{}_i$ of each particle; record the initial personal best position ${\mathbf{P}}_i$ and objective function value $pbes{t}_i$ of each particle; record the global best position ${\mathbf{P}}_{\mathrm{g}}$ and objective function value $gbest$ of the swarm.

Step 3.

Finish the iteration, if the calculation and iteration satisfy the stop criteria:

(i)

$gbest$ is less than the tolerance ε;

(ii)

iteration number is not less than the user-defined iteration limit $N_{\mathrm{c}}$.

Step 4.

Update and obtain the new particle velocity and position according to Equations (3) and (4).

Step 5.

Calculate new $F_{\mathrm{obj},}{}_i$ and evaluate the new positions for each particle.

Step 6.

Compare the old $F_{\mathrm{obj},}{}_i$ with the new one for each particle. Update the corresponding particle information if the new $F_{\mathrm{obj},}{}_i$ is superior

Step 7.

Use the DE algorithm to modify the personal best food source positions according to Equations (5) and (6).

Step 8.

Determine if the current personal best position and global best position are superior than the old ones, if so, update them. Loop to Step 3.

3. The Aerosol Size Distribution and Optical Constants

The mathematical representations of particle size distribution functions studied here are shown below [11]:

$$f_{\mathrm{L}-\mathrm{N}}^{\mathrm{mono}}(D)=\frac{1}{\sqrt{2\pi }D\ln \sigma }\times \exp \left[-\frac{1}{2}{\left(\frac{\ln D-\ln \overline{D}}{\ln \sigma }\right)}^2\right]$$

(7)

$$f_{\mathrm{Gamma}}^{\mathrm{mono}}(D)=D^{\alpha }\times \exp \left(-\beta D^{\gamma }\right)$$

(8)

$$f_{\mathrm{L}-\mathrm{N}}^{\mathrm{bi}}(D)=n\times \frac{1}{\sqrt{2\pi }D\ln {\sigma }_1}\times \exp \left[-\frac{1}{2}{\left(\frac{\ln D-\ln {\overline{D}}_1}{\ln {\sigma }_1}\right)}^2\right]+(1-n)\times \frac{1}{\sqrt{2\pi }D\ln {\sigma }_2}\times \exp \left[-\frac{1}{2}{\left(\frac{\ln D-\ln {\overline{D}}_2}{\ln {\sigma }_2}\right)}^2\right]$$

(9)

$$f_{\mathrm{Gamma}}^{\mathrm{bi}}(D)=n\times D^{{\alpha }_1}\times \exp \left(-{\beta }_1{D}^{{\gamma }_1}\right)+(1-n)\times D^{{\alpha }_2}\times \exp \left(-{\beta }_2{D}^{{\gamma }_2}\right)$$

(10)

where the superscript ‘mono’ and ‘bi’ denote the monomodal and bimodal distributions; the superscript ‘L-N’ and ‘Gamma’ denote the Logarithmic Normal distribution and the Gamma distribution. The detailed description of these functions is available in our previous work [11]. To meet the need of optical measurement methods, the particle size range is set within [0.001, 10.0] μm [24].

Table 1. The true values of characteristic parameters of ASDs.

Function Types		Parameters	True Values
Monomodal	L-N	$(\overline{D},\sigma )$	$(1.0,2.99)$
	Gamma	$(\alpha ,\beta )$	$(6.0,3.0)$
Bimodal	L-N	$({\overline{D}}_1,{\sigma }_1,{\overline{D}}_2,{\sigma }_2,n)$	$(2.5,1.1,6.0,1.2,0.2)$
	Gamma	$({\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2,n)$	$(6.0,2.2,0.8,2.0,0.15)$

lists the true values of the ASDs mentioned above.

According to the standard radiation atmospheric model (SRA) of atmospheric aerosols, which was recommended by the radiation committee of the International Association of Meteorology and Atmospheric Physics (IAMAP) in 1983, the atmospheric aerosols with different composition were divided into six categories, i.e., dust-like aerosol, water-soluble aerosol, oceanic aerosol, soot aerosol, volcanic ash aerosol and sulfuric acid aerosol [25]. Later, D’Almeida and coworkers [26] proposed a new kind of global aerosol model and added the mineral aerosol into the model, which represents the aerosol of one-third of global terrestrial deserts and grassland (arid or semi-arid) areas. 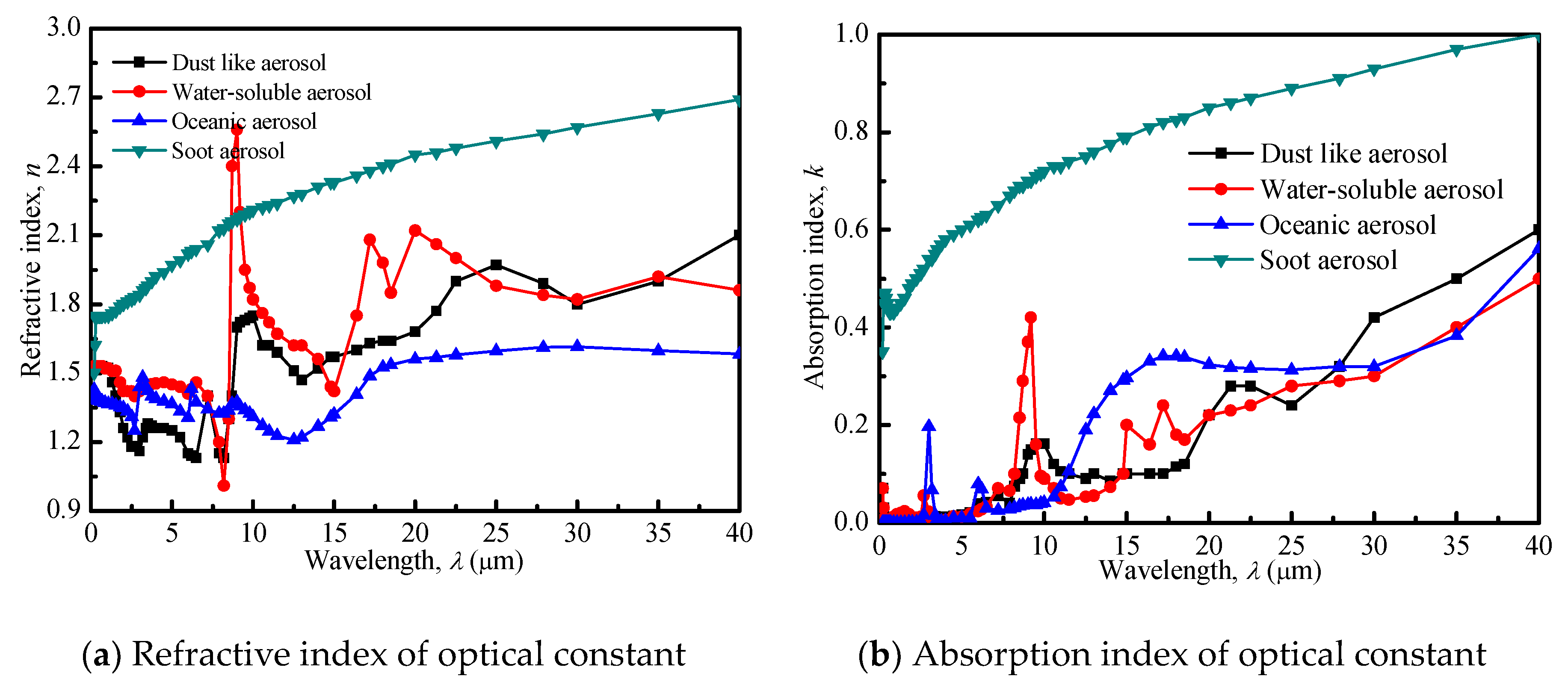Figure 1 depicts the spectral optical constants of four kinds of common aerosols, i.e., dust-like aerosol, water-soluble aerosol, oceanic aerosol and soot aerosol, which are available in Reference [25,26]. In the present work, the spectral optical constants are selected according to soot aerosol.

4. Sensitivity Analysis of Optical Measurement Signals to Characteristic Parameters in ASDs

Because the inverse accuracy of ASDs is relevant to the information obtained from the optical measurement signals, i.e., spectral transmittance signals or angular light-scattering signals, it is necessary to optimize the measurement signals.

Generally, to improve retrieval accuracy, the optical measurement signals are usually selected irrelevant to each other and sensitive to changes of inverse parameters. With this idea, the sensitivity analysis of optical measurement signals to unsolved characteristic parameters in ASDs at a different measurement wavelength or angle is employed to find the optimal measurement wavelength selection region for SEM and optimal measurement angle selection region for ALSM. The sensitivity coefficient is one of the most important characteristic parameters in the sensitivity analysis, which is the first derivative of the optical measurement signals, i.e., $\tau (\lambda )$ or $I(\theta )$, to a certain inverse characteristic parameter. The sensitivity coefficient at every wavelength or angle ${\chi }_a(\eta )$ is defined as [27]:

$${\chi }_a(\eta )=\frac{\partial \varphi (a,\eta )}{\partial a}=\frac{\varphi \left(a+\Delta a,\eta \right)-\varphi \left(a-\Delta a,\eta \right)}{2\Delta a},\varphi =\tau \mathrm{or}I,\eta =\lambda \mathrm{or}\theta$$

(11)

where a denotes the inverse characteristic parameters in ASDs; $\Delta$ represents a tiny change and is set at 0.5% in this study, $\Delta \lambda ,\Delta \theta >0$; $I(\theta )$ is the angular light-scattering measurement signals; $\tau (\lambda )$ is the spectral transmittance obtained in the SEM. It is obvious that to improve the retrieval accuracy, the optical measurement signals with larger absolute values of sensitivity coefficient should better be selected.

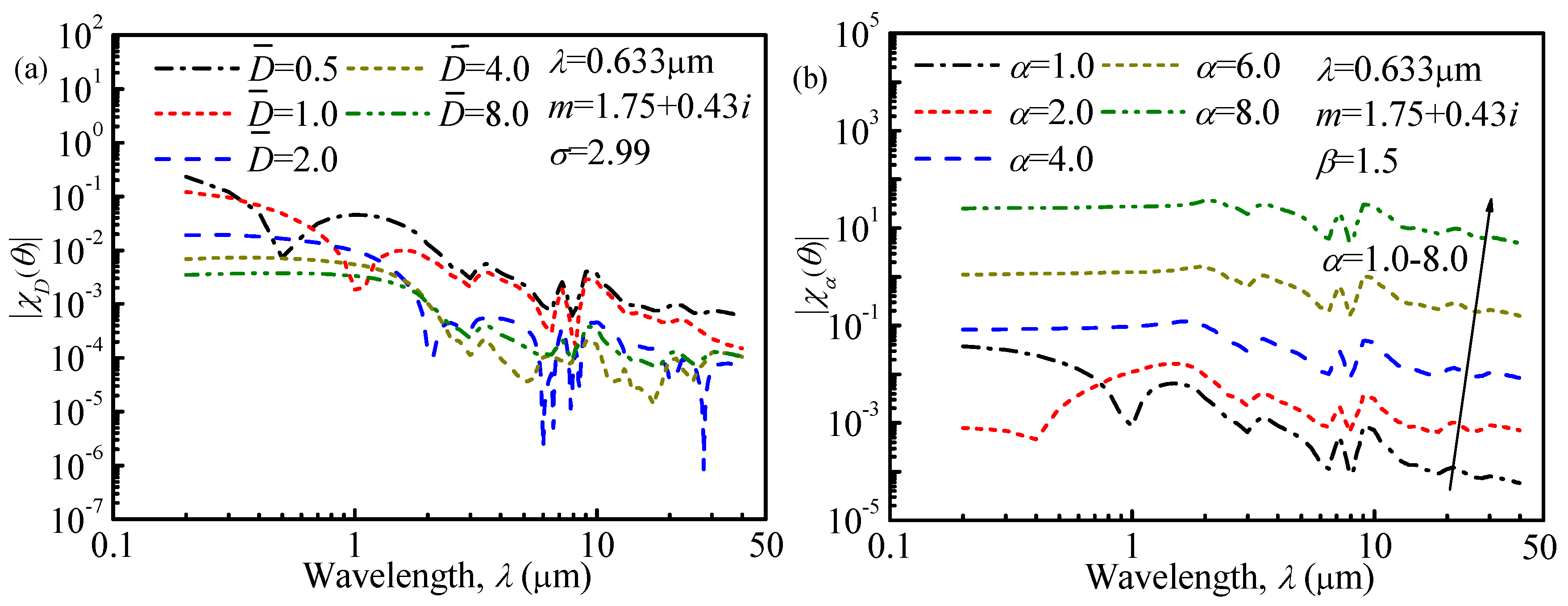
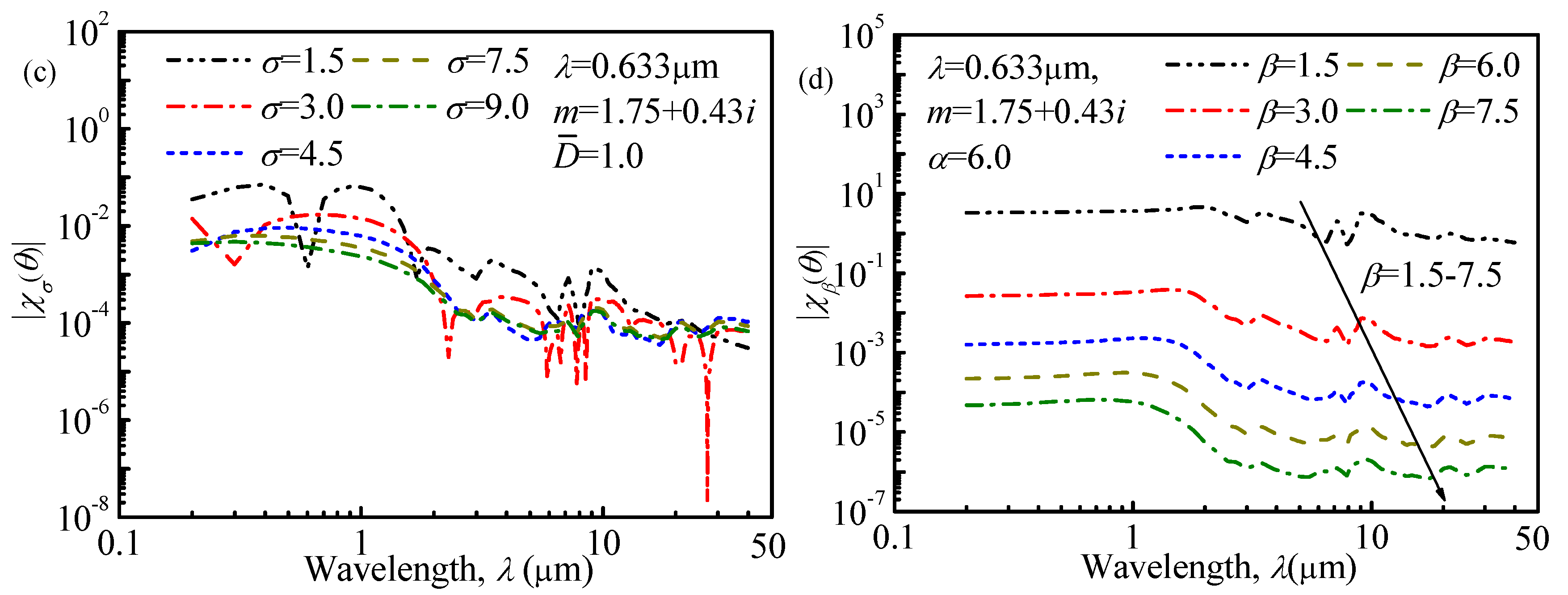
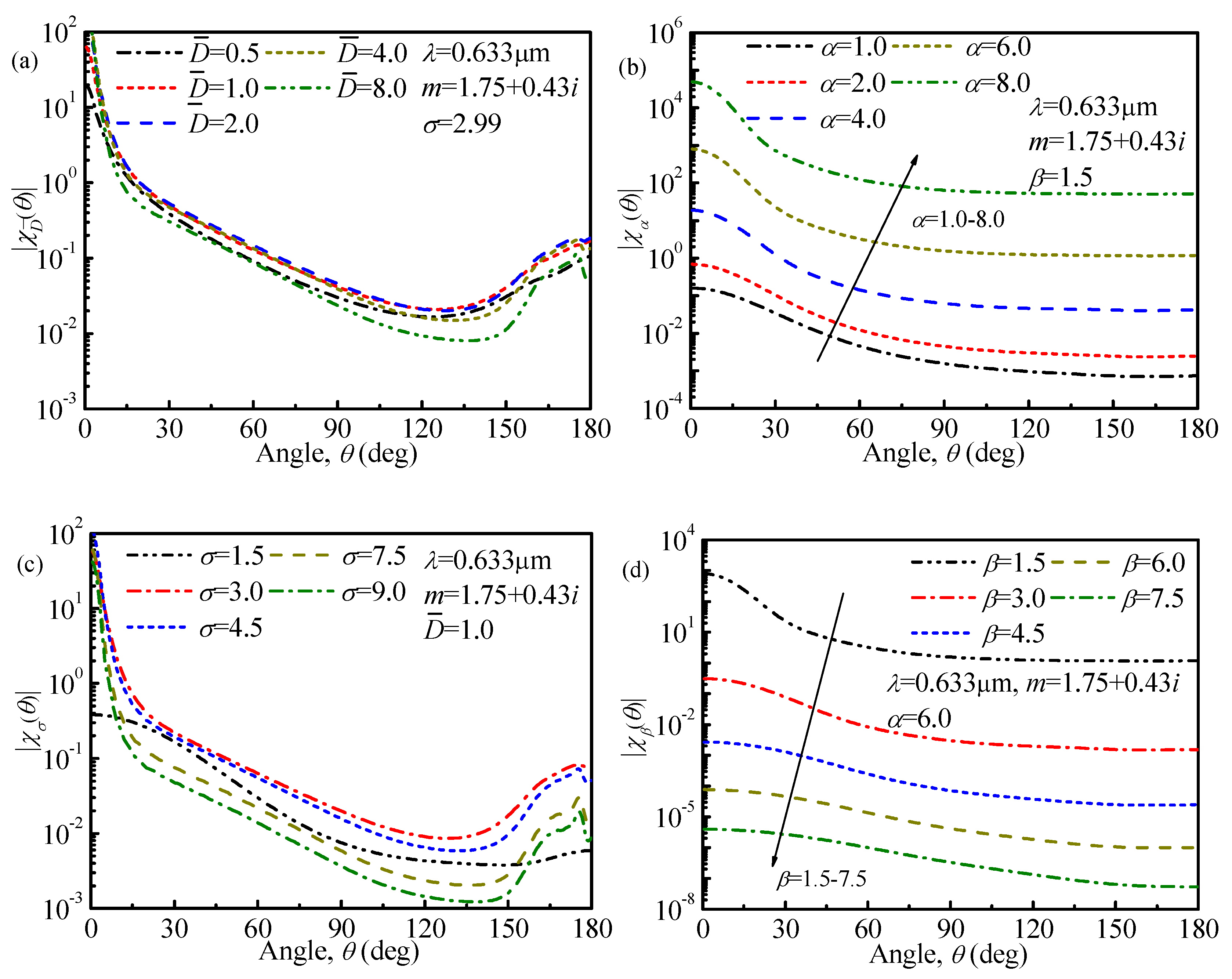
Figure 2 and Figure 3 depict the sensitivity coefficient for different monomodal ASDs with respect to spectral transmittance signals and angular light-scattering signals, respectively. From Figure 2, it can be found that increasing the measurement wavelength will reduce the sensitivity coefficient in general, so to ensure the retrieval accuracy, the measurement wavelengths in this study are selected from $[0.2,1.4]\mathsf{\mu }\mathrm{m}$. From Figure 3, it is obvious that the value of the sensitivity coefficient will decline with an increase in the measurement angles. According to References [28,29], for a small angle, the scattered intensities are weakly dependent upon the particle’s composition but strongly dependent upon the particle’s roughness and size, so the measurement angles in this study are selected from $[0,30]\mathrm{deg}$ to obtain more accurate retrieval results. Similar conclusions can be obtained in studying bimodal ASDs, and the measurement wavelengths and angles are also selected from $[0.2,1.4]\mathsf{\mu }\mathrm{m}$ and $[0,30]\mathrm{deg}$, respectively. The details in studying the bimodal ASDs are not shown here and interested readers can contact us.

5. Numerical Simulation

The true values of characteristic parameters of monomodal and bimodal ASDs in this study are listed in Table 1. According to our former studies [11], the number of measurement wavelengths and angles are set as 4 for monomodal ASDs and 7 for bimodal ASDs to make sure the retrieval accuracy, and the corresponding measurement wavelengths and angles are listed in

Table 2. The measurement wavelengths and angles for retrieval of ASDs.

Function Types		Spectral Extinction Method, λ (μm)	Angular Light-Scattering Method, θ (deg)
Monomodal	L-N	$(0.2,0.4,0.6,0.8)$	$(5,10,15,20)$
	Gamma	$(0.2,0.4,0.6,0.8)$	$(5,10,15,20)$
Bimodal	L-N	$(0.2,0.4,0.6,0.8,1.0,1.2,1.4)$	$(4,8,12,16,20,24,28)$
	Gamma	$(0.2,0.4,0.6,0.8,1.0,1.2,1.4)$	$(4,8,12,16,20,24,28)$

.

The retrieval of the ASDs is solved by minimizing the objective function value, which is the sum of the square residuals between the estimated and measured transmittance:

$$F_{obj}={\displaystyle \sum _{i=1}^M{\left\{\frac{{\left[\varphi (\eta )\right]}_{\mathrm{est}}-{\left[\varphi (\eta )\right]}_{\mathrm{mea}}}{{\left[\varphi (\eta )\right]}_{\mathrm{mea}}}\right\}}^2,\varphi =\tau \mathrm{or}I,\eta =\lambda \mathrm{or}\theta }.$$

(12)

where ${\left[\varphi (a,\eta )\right]}_{\mathrm{est}}$ and ${\left[\varphi (a,\eta )\right]}_{\mathrm{mea}}$ denote the estimated and measured optical measurement signals, respectively. For the algorithm is a stochastic optimization method and all optimizations have certain randomness, all the calculations are repeated 30 times. Moreover, the relative deviation of ASDs δ is used to evaluate the quality of estimated results:

$$\delta =\frac{{\left\{{\displaystyle \sum _{i=1}^N{\left[f_{\mathrm{est}}({\tilde{D}}_i)-f_{\mathrm{true}}({\tilde{D}}_i)\right]}^2}\right\}}^{1/2}}{{\left\{{\displaystyle \sum _{i=1}^N{\left[f_{\mathrm{true}}({\tilde{D}}_i)\right]}^2}\right\}}^{1/2}}$$

(13)

where $N$ denotes the number of subintervals which the particle size range [$D_{\min }$, $D_{\max }$] is divided into; ${\tilde{D}}_i$ is the midpoint of the ith subinterval [$D_i$, $D_{i+1}$]; $f_{\mathrm{true}}({\tilde{D}}_i)$ is the true volume frequency distribution in the ith subinterval; and $f_{\mathrm{est}}({\tilde{D}}_i)$ is the estimated volume frequency distribution in the ith subinterval.

5.1. Comparison of SPSO and Hybrid SPSO-DE Algorithms

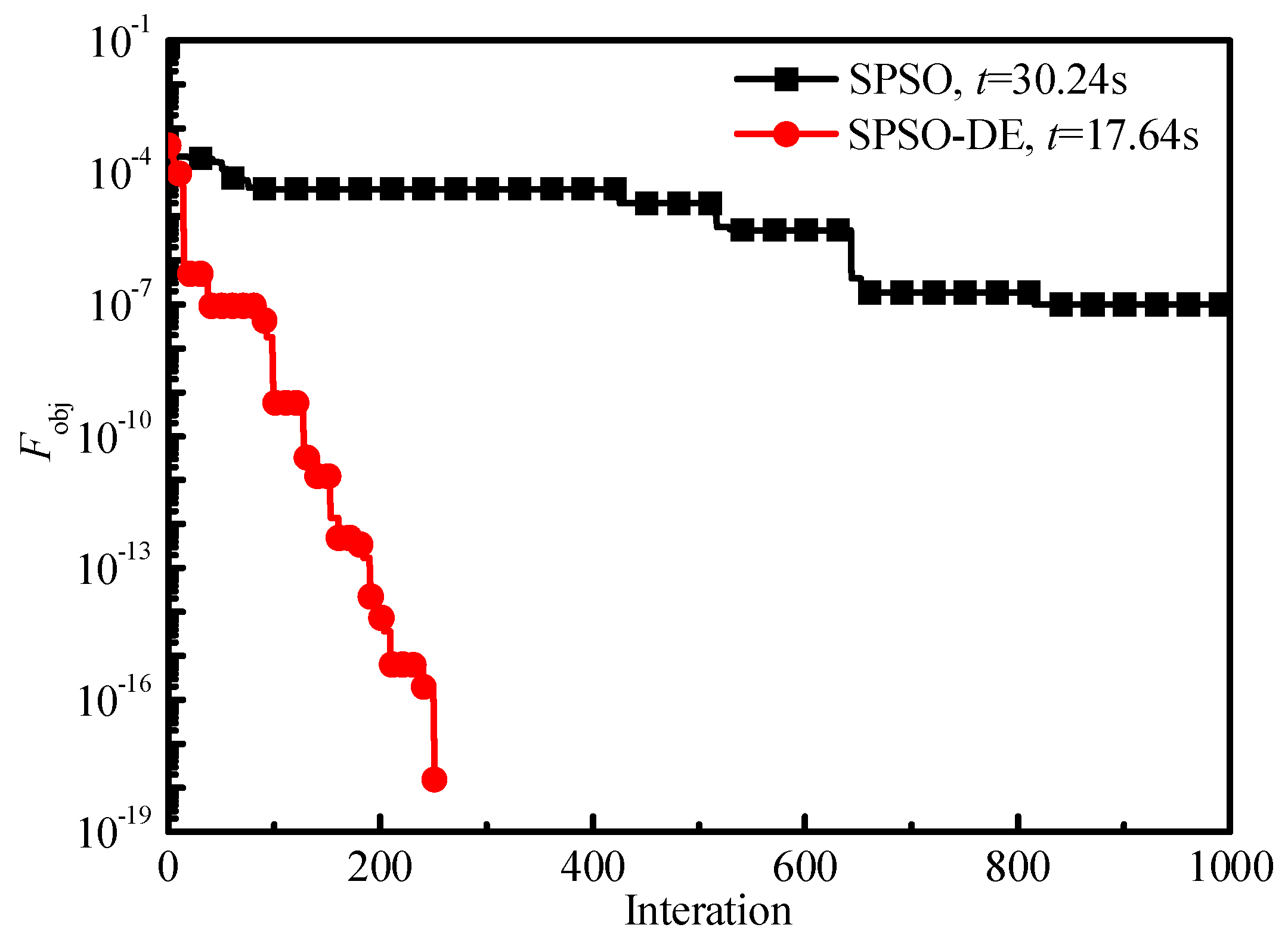
At first, the performance of the hybrid SPSO-DE algorithm is investigated through comparison with the SPSO algorithm in retrieving the monomodal Gamma distribution by using an angular light-scattering method (See Figure 4).

Table 3. System control parameters of the SPSO and hybrid SPSO-DE algorithms in retrieving monomodal Gamma distribution.

Parameters	Ns	Np	Nc	$\mathit{\epsilon }$	C1	C2	F	CR
SPSO	50	2	1000	10−16	1.0	1.0	$—$	$—$
SPSO-DE	50	2	1000	10−16	1.0	1.0	0.5	0.4

lists the system control parameters. When the objective function value is less than 10⁻¹⁶ or the iteration number is larger than 1000, finish the calculation and output the results. The investigation shows that the convergence speed and the value of the objective function of the SPSO-DE hybrid algorithm are superior to the SPSO algorithm, which means the local optima and low convergence accuracy exiting in the SPSO can be avoided in the hybrid SPSO-DE algorithm.

5.2. Retrieval of the Aerosol Size Distribution

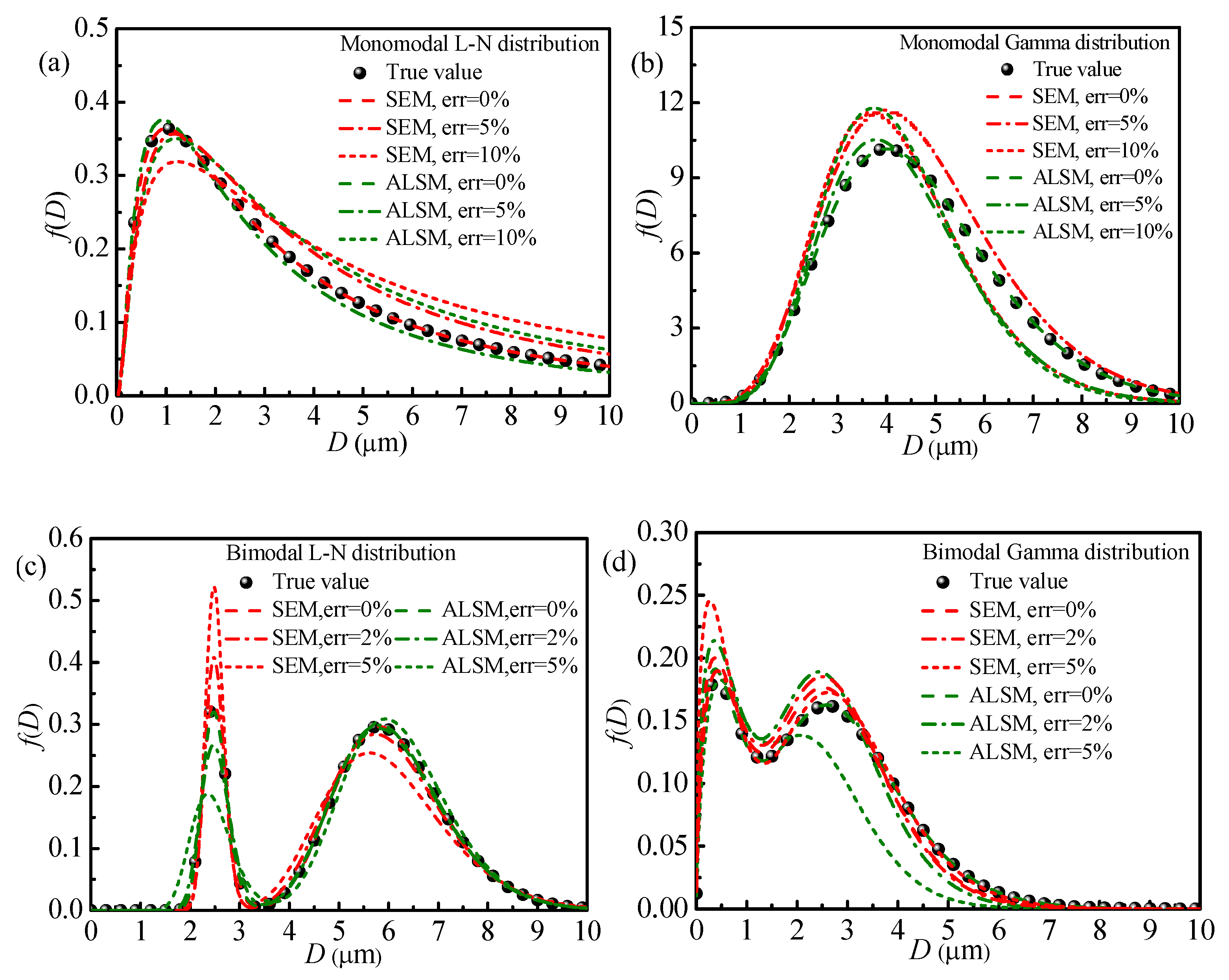
With the help of hybrid SPSO-DE algorithm, the ASDs mentioned above are reconstructed under different random measurement errors by using the SEM and ALSM, respectively, which are showed in

Table 4. Retrieval results of ASDs under different optical measurement methods.

Different Functions		Random Error	SEM	ASLM
			Retrieval Error, δ	Retrieval Error, δ
Monomodal	L-N	0%	0.000125	0.000312
		5%	0.130401	0.064109
		10%	0.215168	0.162801
		20%	0.387621	0.265412
	Gamma	0%	0.000322	0.000545
		5%	0.162721	0.144108
		10%	0.187542	0.169336
		20%	0.365729	0.287532
Bimodal	L-N	0%	0.000156	0.003148
		2%	0.096542	0.085159
		5%	0.244494	0.232532
		10%	0.356279	0.328765
	Gamma	0%	0.025242	0.090019
		2%	0.145623	0.110330
		5%	0.181529	0.144053
		10%	0.319732	0.298621

and Figure 5. Satisfactory retrieval accuracy can be obtained by both SEM and ASLM without measurement errors. The retrieval accuracy deteriorates with more random measurement errors, but are still reasonable even with 10% errors. Comparing the convergence accuracy of retrieval results by using the SEM with that by using the ALSM, it can be found that the robustness of retrieval results by using the ASLM is better than those by using the SEM. Moreover, in studying the bimodal ASDs, there is more satisfactory agreement between the estimated results and the true values of the major peak than those of the other peak.

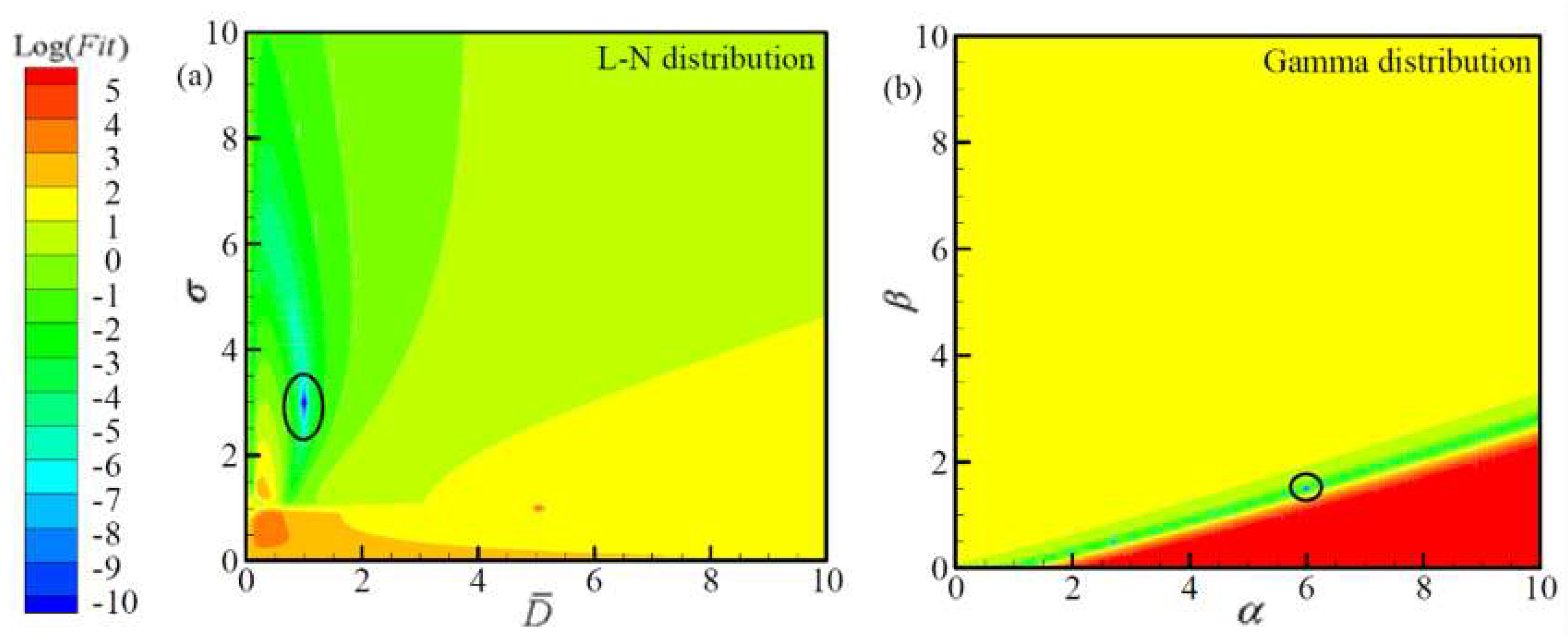
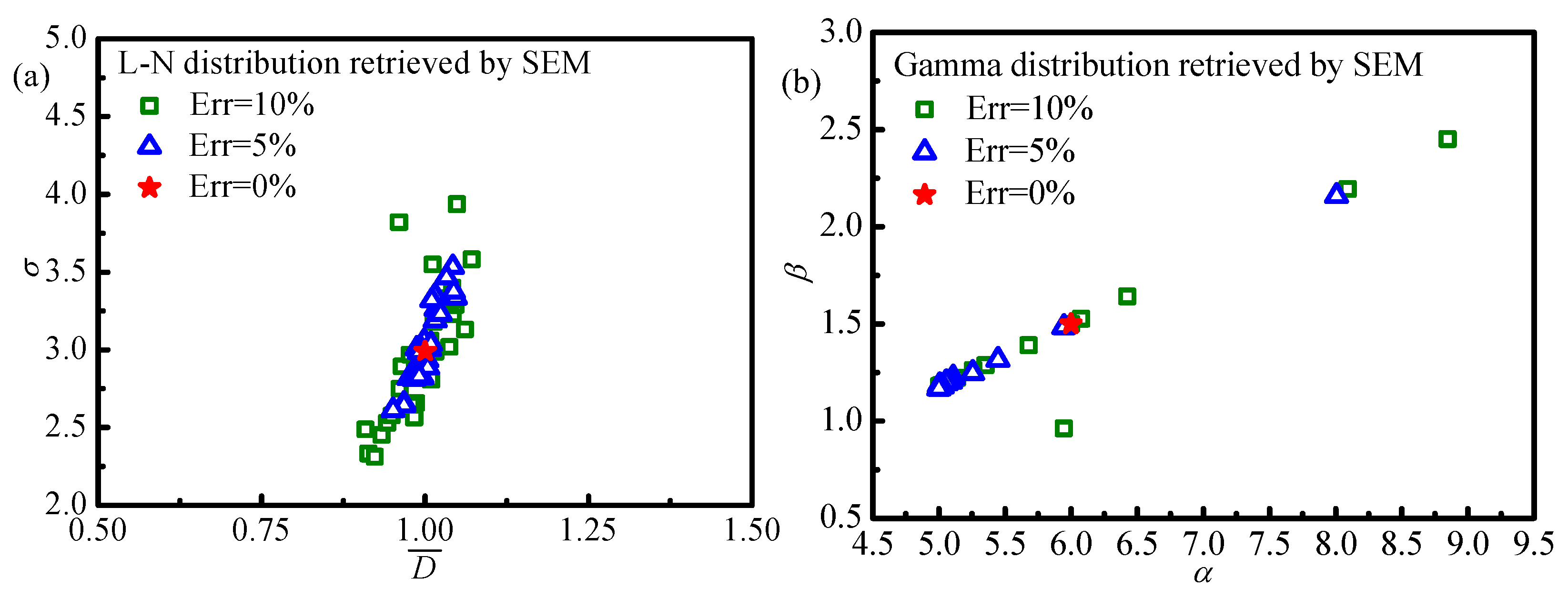
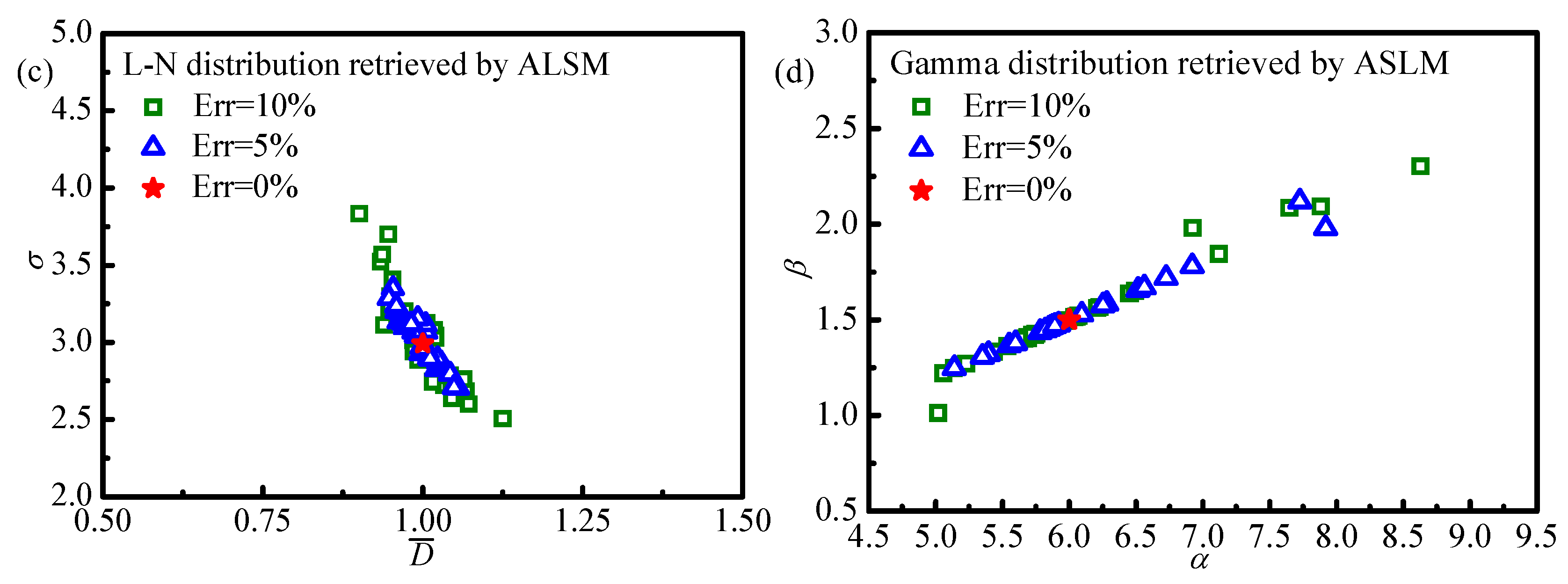
Figure 6 and Figure 7 depict the distributions of the objective function values for monomodal ASDs by using two different type of optical measurement methods. Figure 8 shows the corresponding distributions of estimated results. From Figure 6 and Figure 7, it is obvious that the minimum value region of the objective function is a point, which means the optimal retrieval result is unique, especially for the monomodal Gamma distribution. Moreover, comparing the distributions of objective function by using the SEM and that by using the ALSM, it is obvious that the objective function value by using the SEM is smaller than that by using the ALSM. So, to obtain more accurate retrieval results by using the SEM, the lower objective function value should be obtained during inverse calculation, which will increase the convergence difficulty and time. This phenomenon can explain the reason for the better retrieval accuracies by using the ALSM than those by using the SEM. From Figure 8, it can be found that the distributions of the results retrieved by using the SEM show more dispersion than those retrieved by using ALSM, which also confirms the results obtained above.

6. Conclusions

Combined with a SPSO-DE hybrid algorithm, the convergence properties of angular light-scattering method (ALSM) and spectral extinction method (SEM) in retrieving ASDs are studied. Moreover, the sensitivity analysis of measurement signals to characteristic parameters in ASDs is also studied. Compared with the SEM, there are several advantages of using ALSM. The following conclusions can be drawn:

(1)

To obtain more accurate results, the measurement wavelengths should be better selected from the short wavelength region for SEM (e.g., $\lambda \in \left[0.2,1.4\right]\mathsf{\mu }\mathrm{m}$ in this study), and the measurement angles should better be selected from the forward angle region for ALSM (e.g., $\theta \in \left[0,30\right]\mathrm{deg}$ in this study).

(2)

The SPSO-DE hybrid algorithm can converge much faster and obtain a lower fitness function value within a smaller number of generations than the SPSO algorithm in retrieving the ASDs.

(3)

The retrieval results by using ALSM show better convergence accuracy and robustness than those by using SEM, which attributes to the different distributions of objective function value for these methods. Moreover, considering only single spectral information of aerosol is required, the ALSM provides a more effective and reliable technique to obtain spherical ASDs. Future research will focus on the application of ALSM in studying spheroidal ASDs.