Implicit Large Eddy Simulation of Flow in a Micro-Orifice with the Cumulant Lattice Boltzmann Method

Abstract

A detailed numerical study of turbulent flow through a micro-orifice is presented in this work. The flow becomes turbulent due to the orifice at the considered Reynolds numbers (∼${10}^4$). The obtained flow rates are in good agreement with the experimental measurements. The discharge coefficient and the pressure loss are presented for two input pressures. The laminar stress and the generated turbulent stresses are investigated in detail, and the location of the vena contracta is quantitatively reproduced.

1. Introduction

Flow through orifices is observed in many industrial applications. One example is the orifice meter used for measuring flow rates via the pressure drop induced by the constriction of the flow [1,2,3,4]. The main characteristic of flow through an orifice is that the flow velocity increases by substantially decreasing the cross-sectional flow area. Turbulent shear stresses are created downstream of the orifice. A “vena contracta” is formed inside the orifice. Turbulent eddies and recirculation of flow occur both upstream and downstream of the orifice. Theory and applications of orifice meters for measurement purposes can be found in [5,6,7,8,9].

Orifices can be used for increasing the shear stress in the flow (e.g., in order to break up suspended particles). The geometry studied in this paper was designed for this purpose, but the methodology used here applies in the same way for any kind of turbulent flow through an orifice at subsonic speeds [10,11].

Few studies have been conducted to simulate an orifice with the help of computational fluid dynamics (CFD) [12,13,14,15,16,17], and are usually focused on experimental investigations. However, measurements are not possible under all conditions (e.g., due to high pressure), and some quantities like local shear stress distributions are difficult to obtain experimentally. Most of the above-cited CFD studies considered laminar flow in the orifice or they used explicit turbulence modeling in order to capture turbulent eddies. These simplifications may reduce the overall accuracy of the CFD approach [13,18,19]. The advancement in CFD theory and in high performance computing motivates us to study orifice flow with a high-fidelity CFD method that resolves the relevant flow features in space and time. Here we use the cumulant lattice Boltzmann method (LBM) that allows the simulation of time-resolved turbulent flows at acceptable cost [20,21,22,23].

2. Aim of This Work

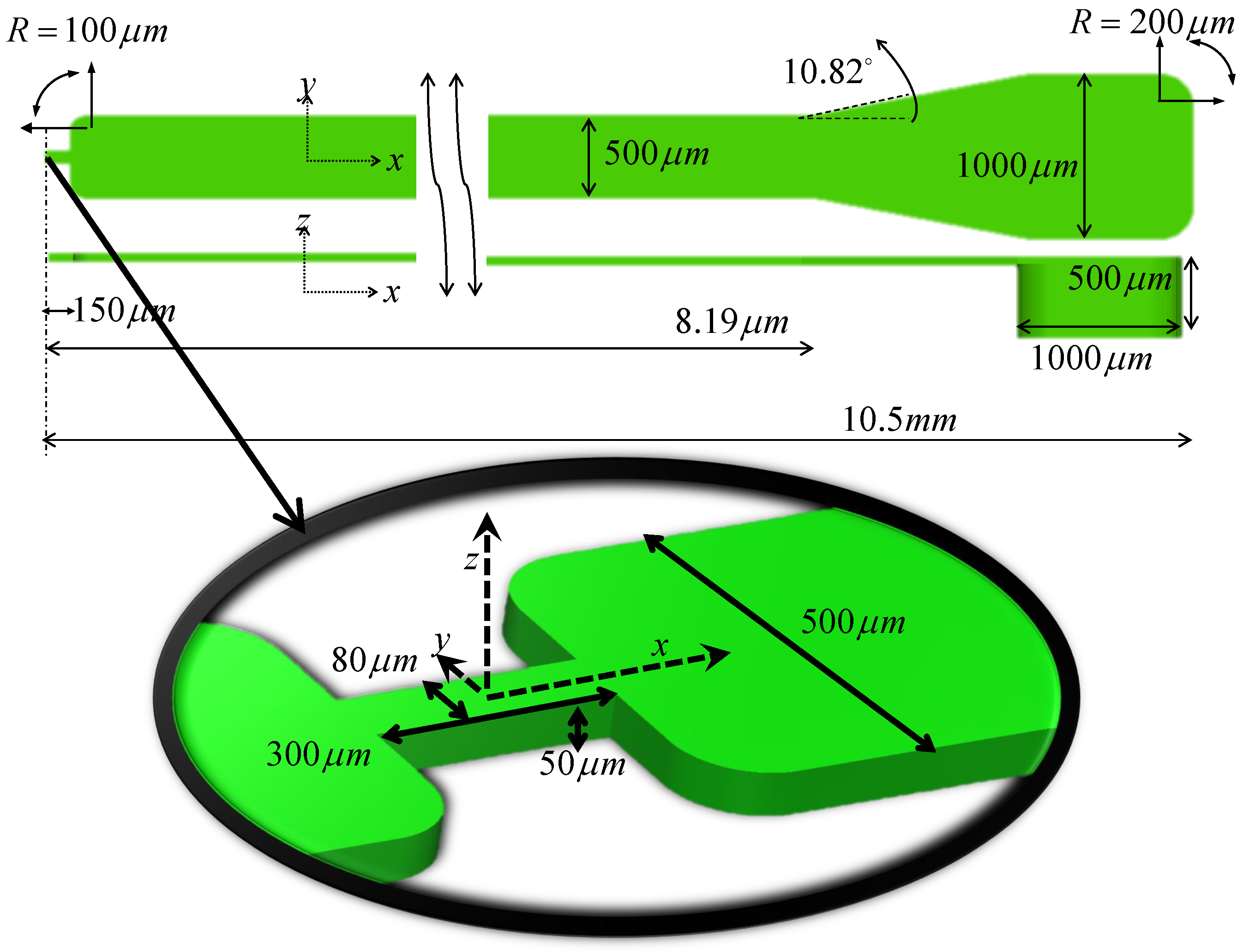
The aim of this work is to simulate turbulent flow in a micro-orifice [24] while resolving all essential flow features. The micro-orifice has a width of 80 μm, a height of 50 μm, and a length of 300 μm (Figure 1). It is located in the center of a channel of two centimeters in length. Only half of the geometry is displayed, since the shape is symmetric in the x-direction (however, the simulation included the full geometry). There is an asymmetry in the z-direction. Pressure, velocity, and stress distributions are studied for this special orifice. The laminar and turbulent stresses in the orifice are calculated and presented in detail.

Three input pressures corresponding to pressure drops of 100 bar, 200 bar, and 500 bar, respectively, between the entrance and the exit of the device are considered in this study. All pressures and stresses in this paper are given in bar, with 1 bar = ${10}^5$ Pa. All pressures are measured with reference to the pressure at the outlet, where we assume the pressure to be zero. In the real device, a sufficiently high pressure was applied at the outlet to suppress cavitation inside the device. This absolute pressure at the outlet can be determined a posteriori from the simulation results, and is hence no input parameter to the simulation itself. The flow setup was chosen to accurately simulate the pressure drop of 200 bar by adjusting the resolution to the boundary layer thickness.

In CFD simulations, more resolution is required when higher pressure drops are imposed, leading to larger mass fluxes and thinner boundary layers. The simulation for a pressure drop of 500 bar is already slightly under-resolved. Therefore, the results for this case have to be used with some caution, as they are expected to be less accurate than the results for the pressure drop of 200 bar.

3. The Cumulant Lattice Boltzmann Method

This study applies the cumulant lattice Boltzmann method [20]. Turbulent flow can be simulated accurately with the use of this method, as long as the computational domain is resolved adequately. The classical lattice Boltzmann equation without an external force can be written as follows:

$$f_i(x+e_{xi}c\Delta t,y+e_{yi}c\Delta t,z+e_{zi}c\Delta t,t+\Delta t)-f_i(x,y,z,t)={\Omega }_i$$

(1)

where $f_i$ and ${\Omega }_i$ are the discrete momentum distribution function and the collision operator, respectively. Here x, y, and z are positions of the lattice nodes. The lattice speed $c=\frac{\Delta x}{\Delta t}$ is defined as the ratio of the lattice spacing to the time step such that the distributions are shifted by $e_{xi}c\Delta t$ from one lattice node to another on a Cartesian grid during one time step.

In order to obtain the lattice Boltzmann equation in the cumulant space, we have to transform the distribution functions into cumulants [20,25]. The lattice Boltzmann equation in cumulant space is:

$$c_{{}_{{\xi }^m{\upsilon }^n{\zeta }^l}}^{*}=c_{{\xi }^m{\upsilon }^n{\zeta }^l}+{\omega }_{{\xi }^m{\upsilon }^n{\zeta }^l}(c_{{}_{{\xi }^m{\upsilon }^n{\zeta }^l}}^{eq}-c_{{}_{{\xi }^m{\upsilon }^n{\zeta }^l}}^{})$$

(2)

where $c_{eq}$ is the cumulant for the equilibrium state and $\xi$, $\upsilon$, and $\zeta$ are three discrete random variables corresponding to the normalized microscopic velocities in x, y, and z directions.

4. Simulation Results

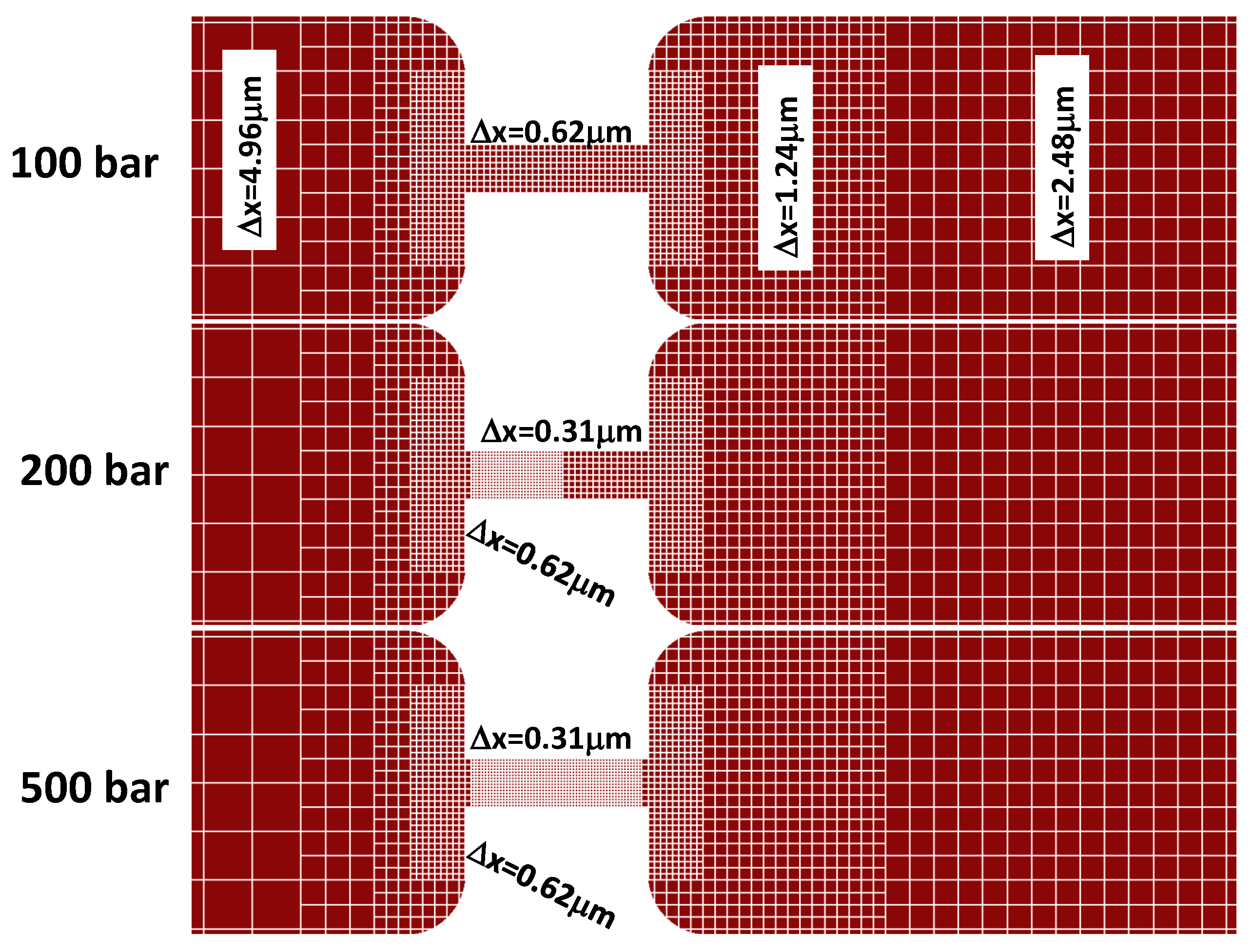
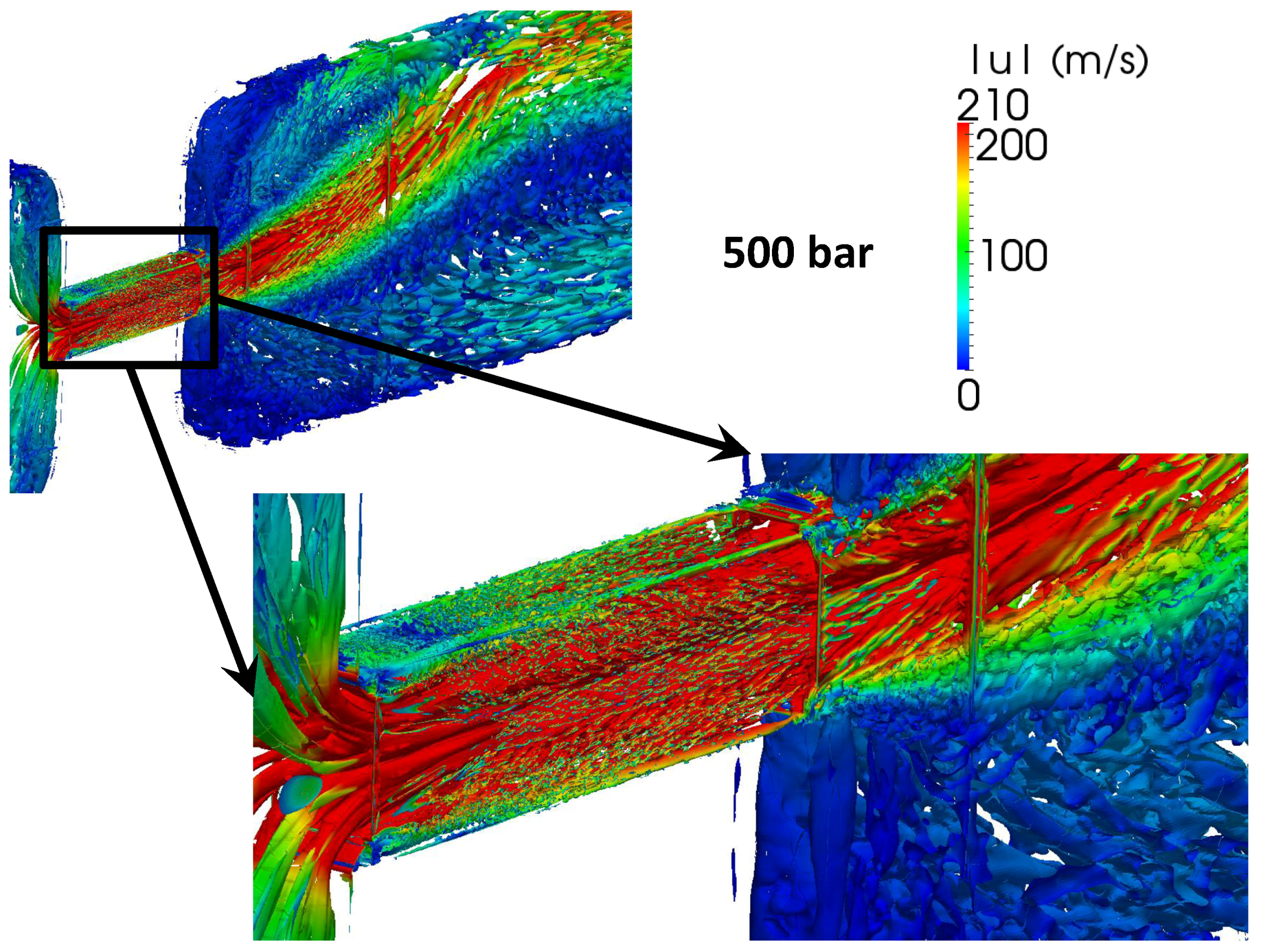
The simulation domain was discretized with nested Cartesian grids [26,27] using a block-structured code based on Esoteric Twist [28] with resolution varying from 4.96 μm to 0.62 μm for the 100 bar case and down to 0.31 μm in the 200 bar and 500 bar cases. The grid for the 100 bar case contained approximately 57 million grid nodes, the one for the 200 bar case had 65 million grid nodes, and the grid for the 500 bar case had 79 million grid nodes. The setup is shown in Figure 2, and further details are given in [21]. Turbulence emerges naturally in the cumulant lattice Boltzmann method. No fluctuations were added to the flow field. In general, high velocity gradients are observed close to the wall, which is why the highest grid resolution has to be spent there. A commonly-used grid independence criterion for CFD simulations is that the $y+$ value is on the order of one or smaller [29]. For that reason, one additional grid level was spent for the pressure drops of 200 bar and 500 bar in comparison to the 100 bar case in order to keep the $y+$ value close to one. The simulation required about 15 days on 120 Intel Nehalem compute nodes (2.6 GHz) with eight cores each to simulate 655 μs real time for the 200 bar case. Due to the different numbers of lattice nodes, the 100 bar case required about half the compute time of the 200 bar case, and the 500 bar case required about 1.5 times the time of the 200 bar case to reach the same real time.

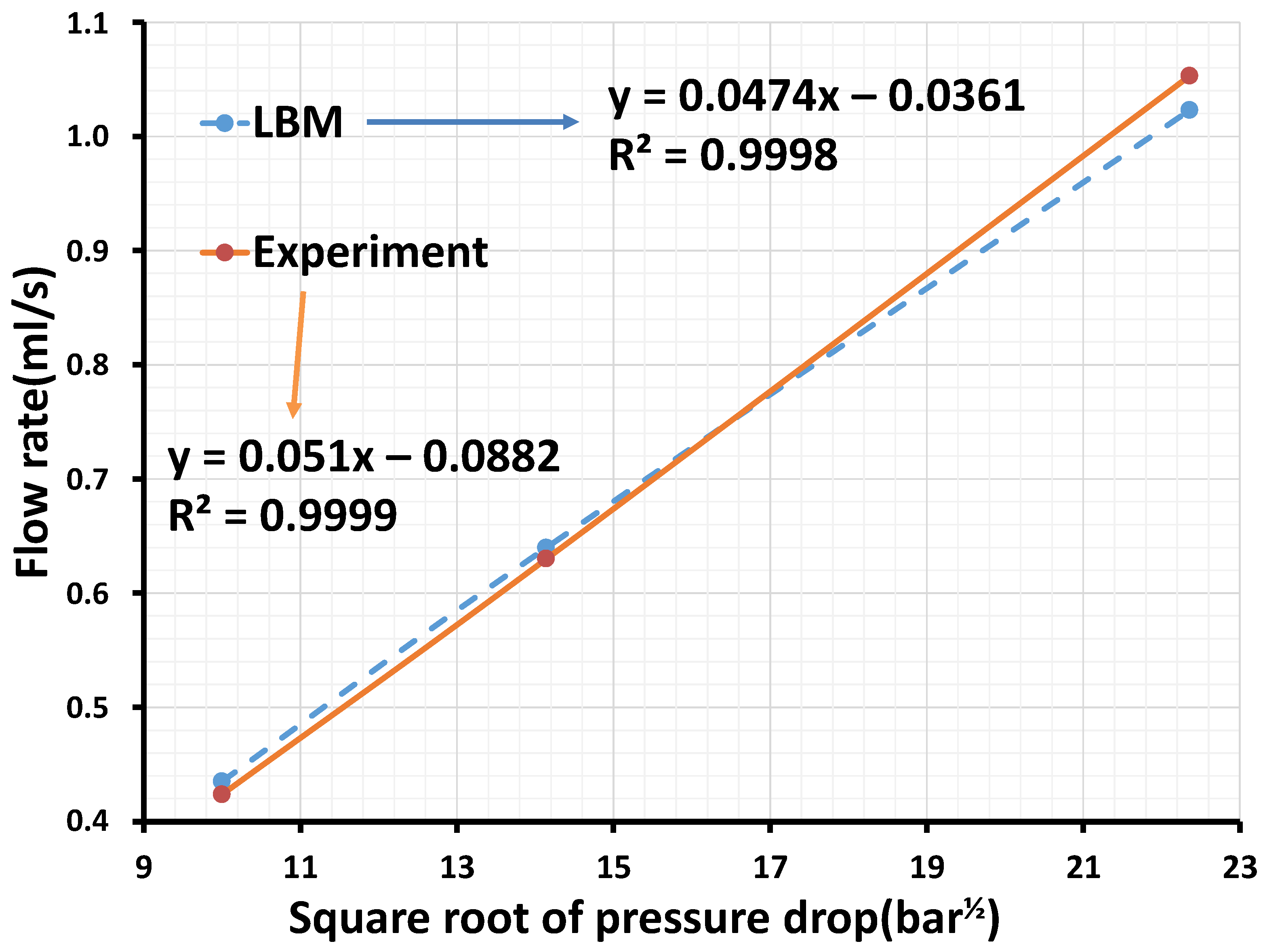
The flow rates acquired by our simulations are compared with the experimental measurement to validate our results [11]. The deviations between the LBM simulation and the experiment for the 100 bar, 200 bar, and 500 bar pressure drops are 1.57%, 1.51%, and 2.84%, respectively. It is observed that our results are in close agreement with the experimental results (see Figure 3).

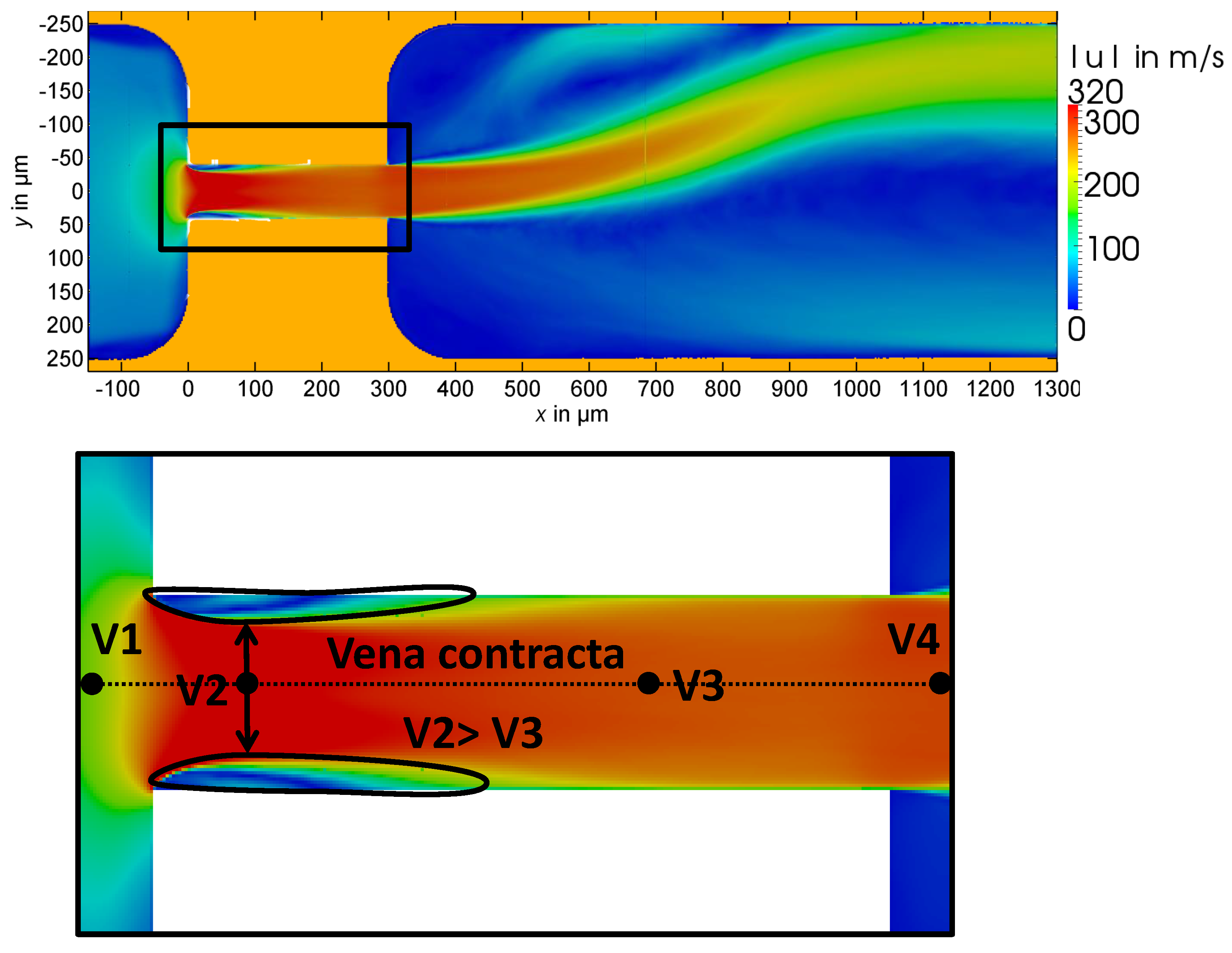
In addition to the averaged velocity, Figure 4 demonstrates the vena contracta effect. The vena contracta reduces the effective area and increases the velocity. Thus, it is observed that the velocity in position 2, $V_2$, is greater than the velocity in position 3, $V_3$. This phenomenon is a classical problem in fluid mechanics, and researchers try to eliminate it in some ways, such as by rounding the entrance region [30]. An orifice usually has two loss coefficients: the loss coefficient due to a sudden contraction, and the loss coefficient due to a sudden expansion. Streeter [31] calculated the loss coefficient for both a sudden contraction and a sudden expansion, and provided approximations for these coefficients in relation to the ratios of the cross-sections. For example, for a cylindrical orifice, the loss coefficients extracted from his plot are 0.42 and 0.68 for the sudden expansion and the sudden contraction, respectively. In general, these loss coefficients are related to the pressure loss calculated from the energy equation between points 1 and 2 and points 3 and 4 [30].

The center line magnitude velocities for three different pressure drops of 100 bar, 200 bar, and 500 bar are shown in Figure 5. The plot area covers a distance from 50 μm before the orifice entrance to 50 μm after the orifice exit. The position $x=0$ coincides with the entrance of the orifice. The velocity in each case reaches the maximum value at point $V_2$ (Figure 4).

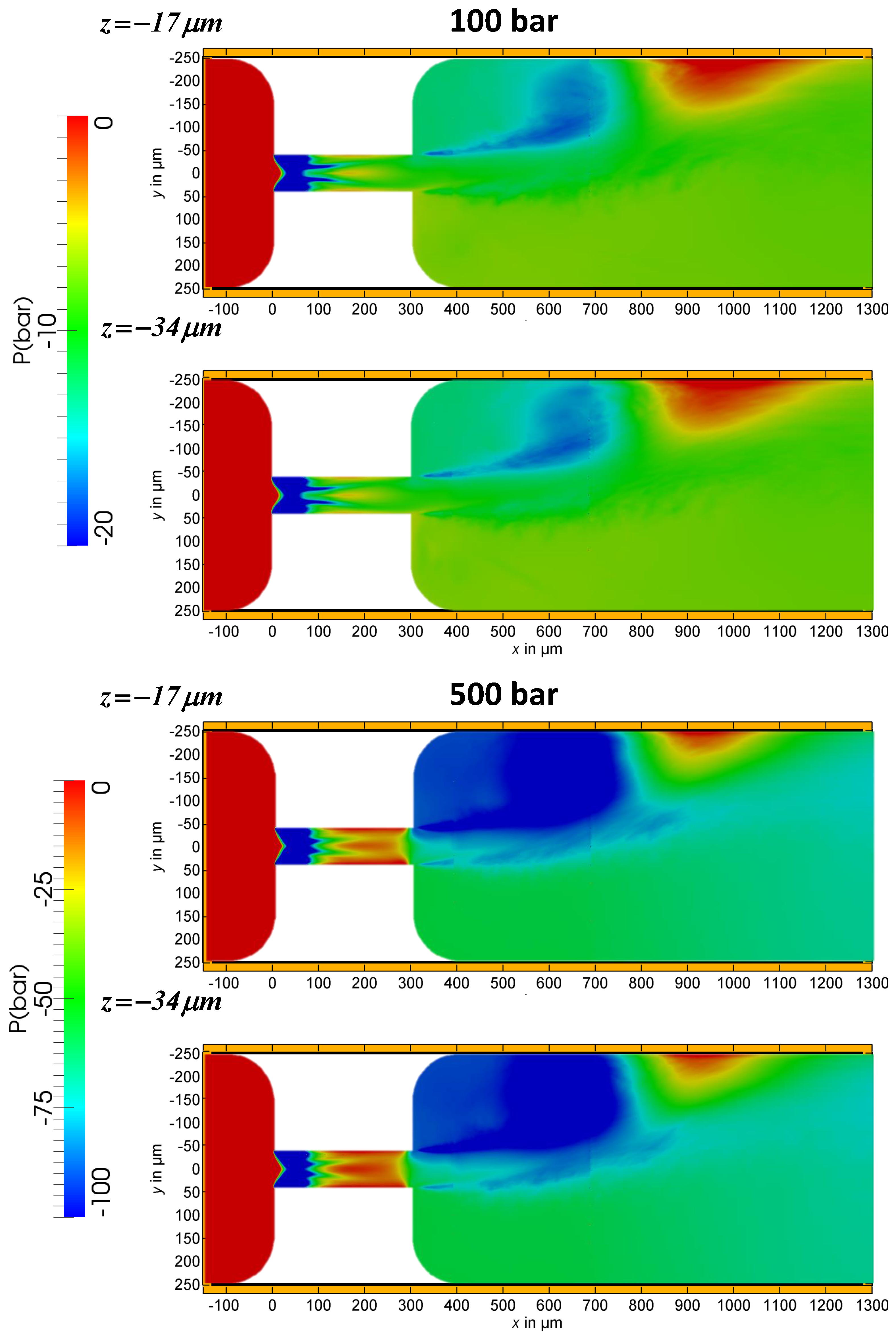
The time-averaged pressure in and behind the orifice is depicted for the 100 bar and 500 bar cases in Figure 6. It is shown for two different planes: $z=-17$ μm and $z=-34$ μm, according to Figure 1.

The pressure is seen to have negative values in comparison to the pressure at the outlet of the device (assumed to be zero). The device is susceptible to cavitation, which is undesired since it leads to the erosion and eventually to the destruction of the device. Cavitation is suppressed in the operation of the device by applying a sufficiently high absolute pressure at the outlet such that the minimal absolute pressure inside the device does not drop below the vapor pressure of water. Part of the purpose of the simulation was to determine the minimum pressure required at the outlet to suppress the cavitation. Since this can be done a posteriori, it was not required to consider the cavitation in the simulation itself. We note here that cavitation can be simulated with the lattice Boltzmann method, if required [32].

Figure 6 shows the reason why the jet is attached to the wall after leaving the orifice. In the volume confined by the jet and the wall in negative y direction, the pressure decreases due to the suction effect of the moving jet. This lowers the pressure in the confined volume relative to the pressure in the open volume on the other side of the jet. The pressure difference between the confined and the open volume drives the jet towards the confined volume. While the jet oscillates downstream of the orifice, it was never observed in the simulation or the experiment that the jet would switch to the other wall once it was attached.

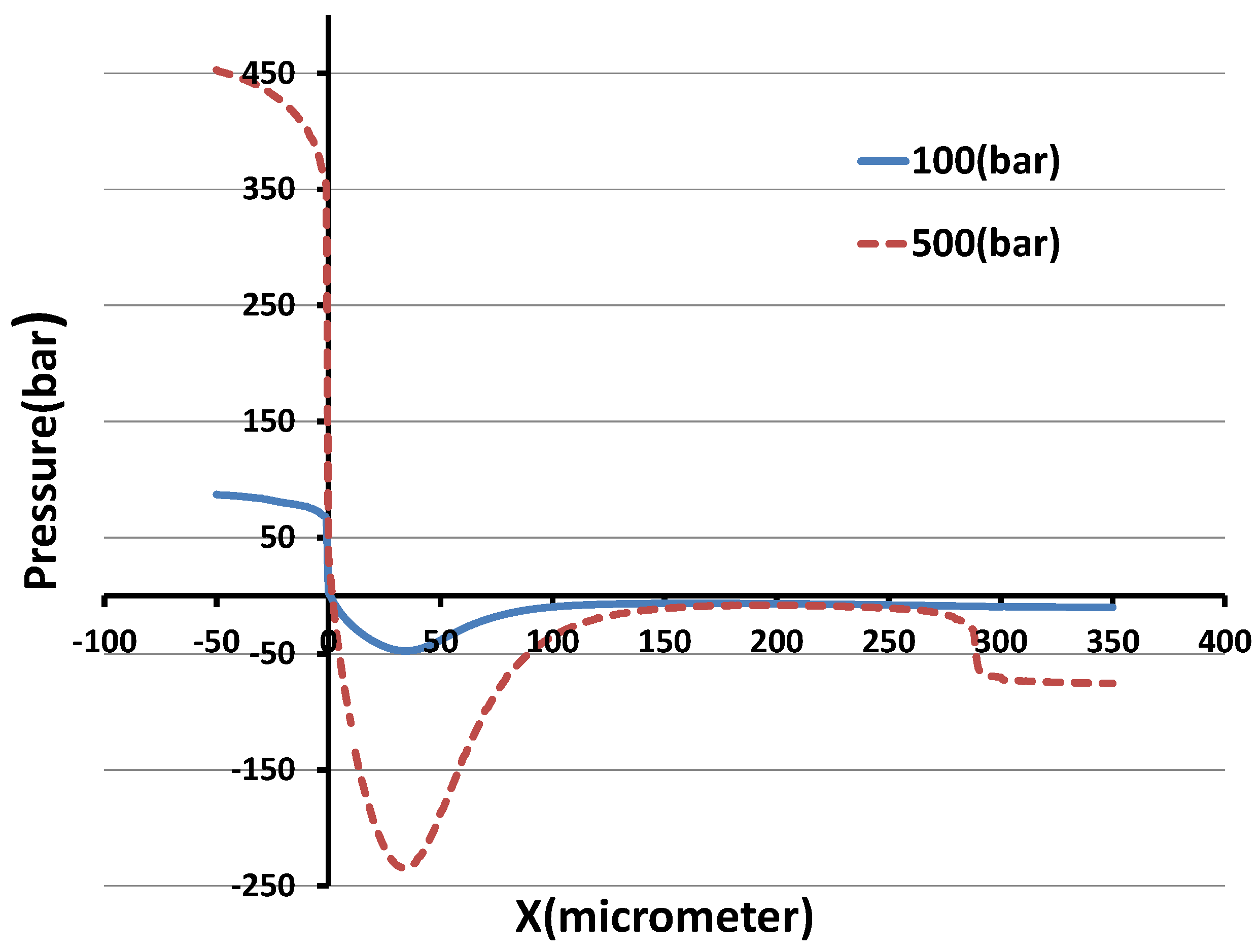
The time-averaged pressure is averaged again over the $y-z$ planes and plotted along the main flow direction (x direction) for the 100 bar and 500 bar cases in Figure 7. The orifice entrance is located at $x=0$. The pressure drops suddenly at the entrance, and reaches its minimum value where the velocity has its maximum. The pressure drops further at the exit of the orifice. This effect is much more pronounced in the 500 bar case than in the 100 bar case. The plot displayed in Figure 7 is used to calculate the pressure loss between two points along the x direction [30]. With the flow rate known, the only required parameter for the energy equation is the pressure drop between the two points, and the discharge coefficient can be calculated (defined as the ratio of the actual flow to the theoretical flow—mean velocity × cross-section × density). The following equation has been used to calculate $C_D$ [33]:

$$C_D=\frac{V\sqrt{(1-{\beta }^4)}}{\sqrt{\Delta p/\rho }}$$

(3)

where V is the averaged velocity in the orifice and $\Delta p$ is the pressure difference between upstream of the orifice and the vena contracta—at which the wall pressure is at its minimum. The ratio of the orifice diameter to the channel diameter is termed $\beta$. In our case, it is determined as $\beta =80\mathsf{\mu }\mathrm{m}/500\mathsf{\mu }\mathrm{m}=0.16$. The discharge coefficients for pressure drops 100 bar and 500 bar are $C_D=0.8855$ and $C_D=0.9432$, respectively. The actual location of the vena contracta changes with the flow rate, and this location can be obtained from Figure 5 or Figure 7.

Tables in hydraulic handbooks list the loss coefficient only for a limited number of specific geometries. In other cases, CFD simulations as presented in this work can be used to obtain this coefficient. The averaged pressure and velocity can be extracted from Figure 3 and Figure 7, respectively. The pressure loss can be easily calculated by inserting the obtained pressures and velocities into the energy equation.

The pressure loss per length l can be calculated by the use of the following equation [34]:

$$\frac{\Delta p}{l}=\lambda \left(\frac{V^2}{2D_h}\right)$$

(4)

where the mean velocity V is calculated from the numerically-determined mass flow, $\rho$ is the density of water, and $\lambda$ is the friction factor. Since the studied orifice has a rectangular shape, the hydraulic diameter must be considered, $D_h$. The Reynolds number $Re$ at the smallest cross-sectional areas of the orifice is defined as:

$$Re=\frac{V{D}_h\rho }{\mu }$$

(5)

here $\mu$ is the dynamic viscosity. When the device simulated here was designed, no simulations were available and the geometry was chosen based on simple considerations using the Blasius equation for round channels [10], even though the orifice is neither round nor a channel in the sense used by Blasis [35]. The roughness of the orifice is below 20 nm [10,11]; thus, the friction factor of hydraulically smooth channels at the respective Reynolds numbers ($2320<Re<{10}^5$) was chosen [35]:

$$\lambda =0.3164{\left(Re\right)}^{-1/4}$$

(6)

The calculated pressure losses per millimeter in the orifice segments with the smallest cross-sectional area are 33.00 bar/mm and 150.12 bar/mm for the two pressure drops 100 bar and 500 bar, respectively.

4.1. Fluid Flow Intensity

The stresses are calculated by the velocity-gradient components. The strain rate tensor is composed of the nine velocity-gradient components, of which three are normal strain components and six are tangential strains components. The magnitude of the strain rate tensor can be written in terms of velocity gradients, as:

$$\begin{array}{c}{S}^2=\left[\frac{\partial u}{\partial x}\left(\frac{\partial u}{\partial x}+\frac{\partial u}{\partial x}\right)+\frac{\partial u}{\partial y}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)+\frac{\partial u}{\partial z}\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)\right]+\hfill \\ \left[\frac{\partial v}{\partial x}\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)+\frac{\partial v}{\partial y}\left(\frac{\partial v}{\partial y}+\frac{\partial v}{\partial y}\right)+\frac{\partial v}{\partial z}\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right)\right]+\hfill \\ \left[\frac{\partial w}{\partial x}\left(\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\right)+\frac{\partial w}{\partial y}\left(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\right)+\frac{\partial w}{\partial z}\left(\frac{\partial w}{\partial z}+\frac{\partial w}{\partial z}\right)\right]\hfill \end{array}$$

(7)

In order to obtain the velocity-gradients in this equation, a finite difference scheme is implemented in common CFD methods. Thus, each grid node needs information from its neighbors. In the LBM, the strain rate can be computed locally from the non-equilibrium part of the distribution function. The above equation is rewritten according to the strain rate instead of the velocity gradients as:

$$S^2=2({s_{xx}}^2+{s_{yy}}^2+{s_{zz}}^2+2{s_{xy}}^2+2{s_{xz}}^2+2{s_{yz}}^2)$$

(8)

By convention, the magnitude of the strain rate tensor is defined as [36,37]:

$$S^2=2s:s=2s_{ij}{s}_{ji}$$

(9)

where the strain rate component $s_{ij}$ is:

$$s_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$$

(10)

The dissipation rate is a useful parameter for the characterization of the local hydrodynamic conditions and flow field intensities.

$$ϵ=\nu S^2$$

(11)

The total dissipation can be split up into the averaged energy dissipation rate and the turbulent dissipation rate according to the following equation [38]:

$${ϵ}_{total}={ϵ}_{fluctuation}+{ϵ}_{mean}=2\nu \overline{s_{ij}^{\prime }{s}_{ij}^{\prime }}+2\nu {\overline{s}}_{ij}{\overline{s}}_{ij}$$

(12)

This is often done in the CFD literature due to the prevalence of Reynolds-averaged Navier–Stokes (RANS) methods. In such methods, only the average energy dissipation rate is directly accessible, and the turbulent dissipation rate must be estimated with some turbulence model. Our method provides the full information on the dissipation rate.

The corresponding stress can be acquired from:

$$\tau =\mu \sqrt{ϵ/\nu }$$

(13)

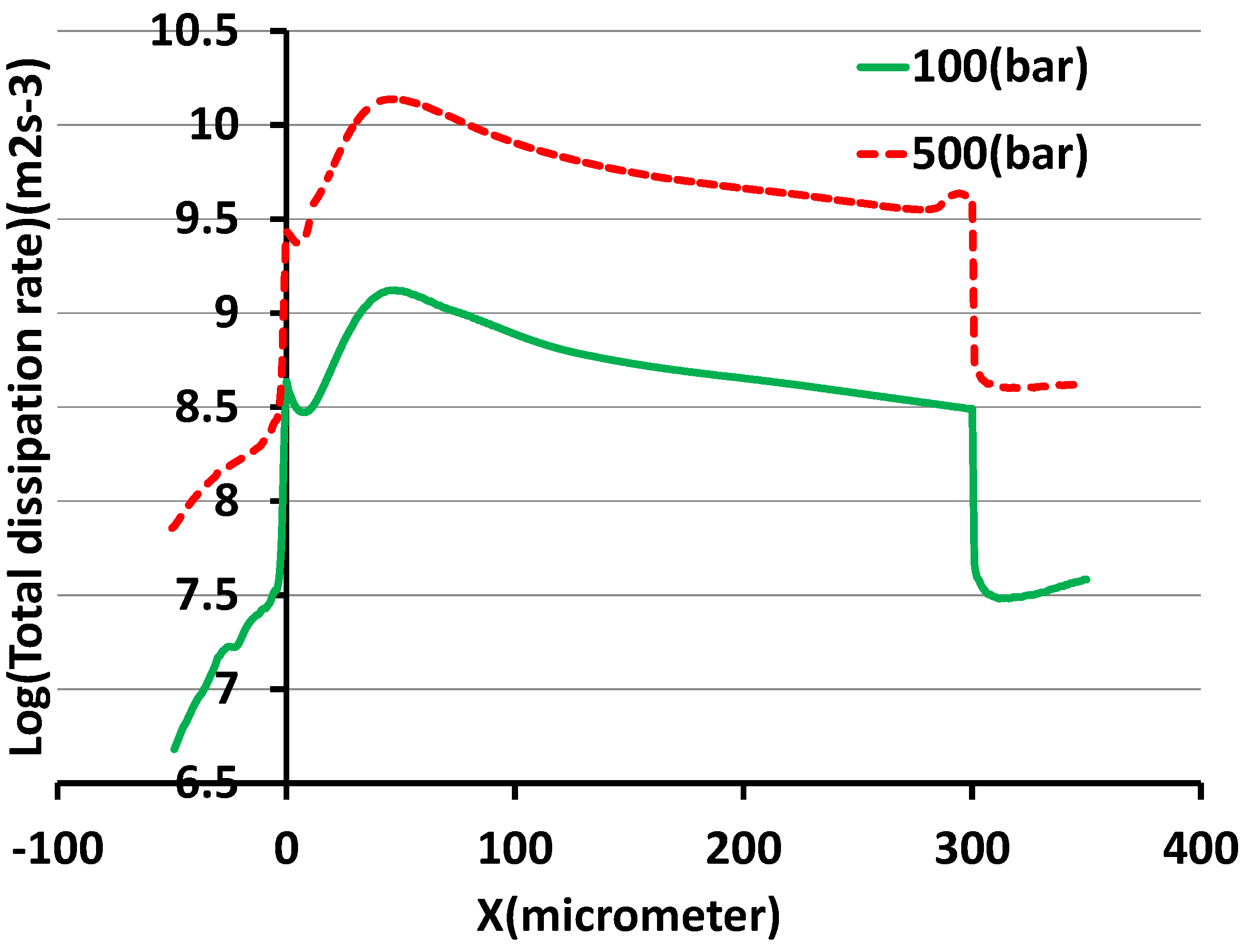
Figure 8 shows the logarithm of the dissipation rates for the 100 bar and 500 bar cases from 50 μm before to 50 μm after the orifice. There is a substantial increase in the dissipation rate at the entrance of the orifice in comparison to 50 μm in front of the entrance. Two peaks are observed in the dissipation; one is exactly at the entrance, and another one is at position $x=46$ μm. It is the same position where the maximal velocity and the minimal pressure are observed.

4.1.1. Q-Criterion

Both Eulerian and Lagrangian methods are available to detect coherent structures (eddies) in a flow [39,40]. Many of the Eulerian methods are based on the velocity gradient tensor [40,41,42]. One prominent example of such indicators is the Q-criterion [43], which is determined from the second invariant of the velocity gradient tensor, and is given by:

$$Q=\frac{1}{2}{\left[\right|\Omega |}^2-{\left|s\right|}^2]$$

(14)

where the antisymmetric part or the vorticity tensor is:

$${\Omega }_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}-\frac{\partial u_j}{\partial x_i}\right)$$

(15)

The Q-criterion is applied to detect the dominance of the vorticity over the strain. Vorticity is dominant when $Q>0$, while strain is dominant for $Q<0$. A zero contour of Q can be used to visualize vortices.

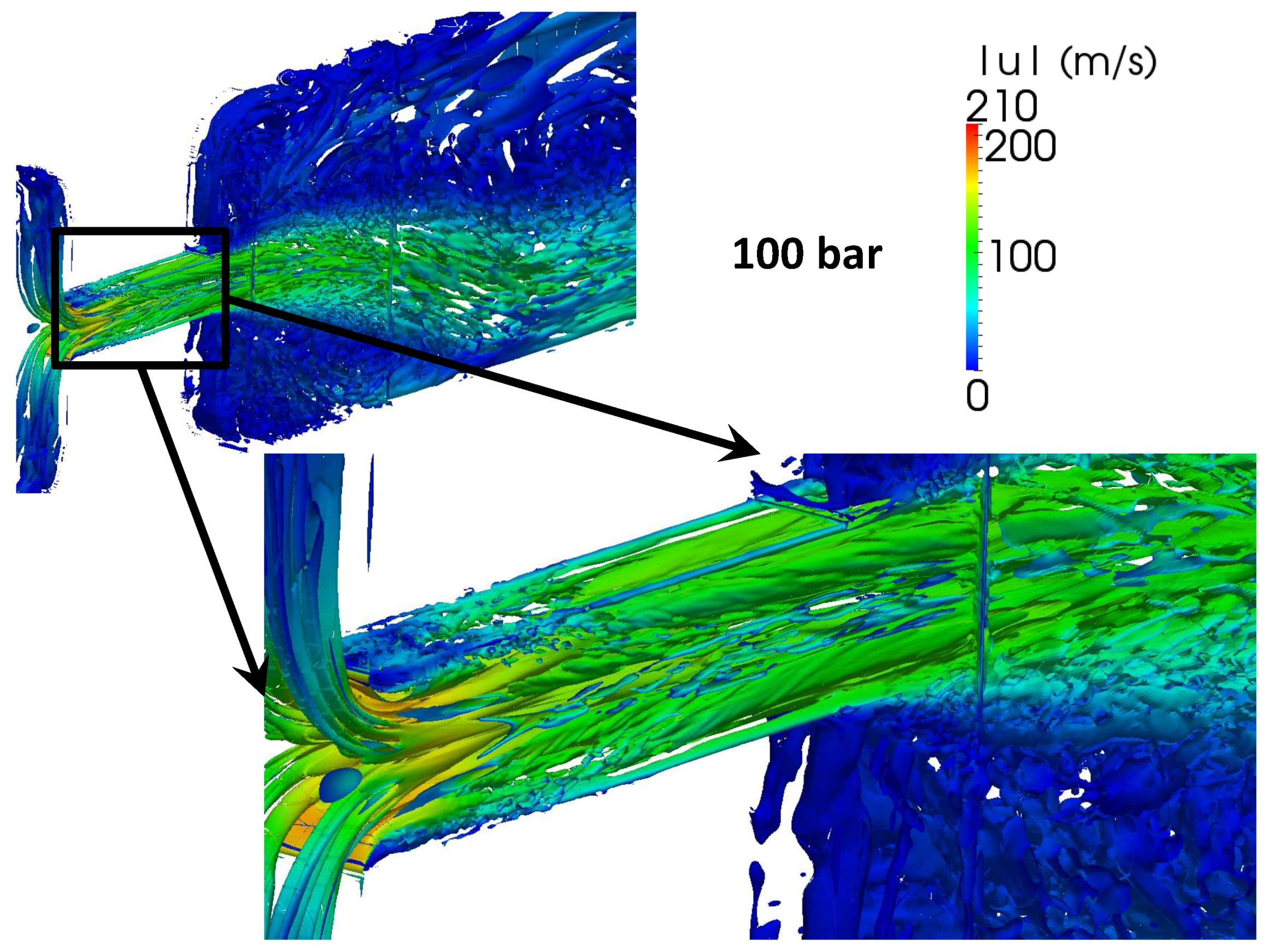
Figure 9, Figure 10 and Figure 11 show contours for $Q=0$ for the three cases. Q is calculated for the averaged velocity fields in these figures. Stretched vortex tubes are observed at the entrance of the orifice. With increasing pressure drop and Reynolds number, finer vortex structures develop in the orifice.

4.1.2. Laminar and Turbulent Stresses

As with dissipation, the stresses generated by the fluid flow can be divided into laminar stresses and turbulent stresses [44,45,46,47].

$$\tau ={\tau }_l+{\tau }_t$$

(16)

where ${\tau }_l$ and ${\tau }_t$ are the laminar stress tensor and turbulent stress tensor, respectively. The stress tensor is given by:

$$\tau =\left[\begin{array}{ccc}{\tau }_{xx}& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\tau }_{yy}& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\tau }_{zz}\end{array}\right]$$

(17)

The laminar stress tensor consists of the average velocity derivatives [44]:

$${\tau }_l=\mu \left[\begin{array}{ccc}{\tau }_{xx}& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\tau }_{yy}& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\tau }_{zz}\end{array}\right]=\mu \left[\begin{array}{ccc}\frac{\partial \overline{u}}{\partial x}+\frac{\partial \overline{u}}{\partial x}& \frac{\partial \overline{u}}{\partial y}+\frac{\partial \overline{v}}{\partial x}& \frac{\partial \overline{u}}{\partial w}+\frac{\partial \overline{w}}{\partial x}\\ \frac{\partial \overline{v}}{\partial x}+\frac{\partial \overline{u}}{\partial y}& \frac{\partial \overline{v}}{\partial y}+\frac{\partial \overline{v}}{\partial y}& \frac{\partial \overline{v}}{\partial z}+\frac{\partial \overline{w}}{\partial y}\\ \frac{\partial \overline{w}}{\partial x}+\frac{\partial \overline{u}}{\partial z}& \frac{\partial \overline{w}}{\partial y}+\frac{\partial \overline{v}}{\partial z}& \frac{\partial \overline{w}}{\partial z}+\frac{\partial \overline{w}}{\partial z}\end{array}\right]$$

(18)

The turbulent stress tensor is identical to the Reynolds stress tensor (${\tau }_{ij}^R=-\rho \overline{u_i^{\prime }{u}_j^{\prime }}$) [38,48]:

$${\tau }_t=\left[\begin{array}{ccc}{\tau }_{xx}& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\tau }_{yy}& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\tau }_{zz}\end{array}\right]=-\rho \left[\begin{array}{ccc}\overline{u^{\prime }{u}^{\prime }}& \overline{u^{\prime }{v}^{\prime }}& \overline{u^{\prime }{w}^{\prime }}\\ \overline{u^{\prime }{v}^{\prime }}& \overline{v^{\prime }{v}^{\prime }}& \overline{v^{\prime }{w}^{\prime }}\\ \overline{u^{\prime }{w}^{\prime }}& \overline{v^{\prime }{w}^{\prime }}& \overline{w^{\prime }{w}^{\prime }}\end{array}\right]$$

(19)

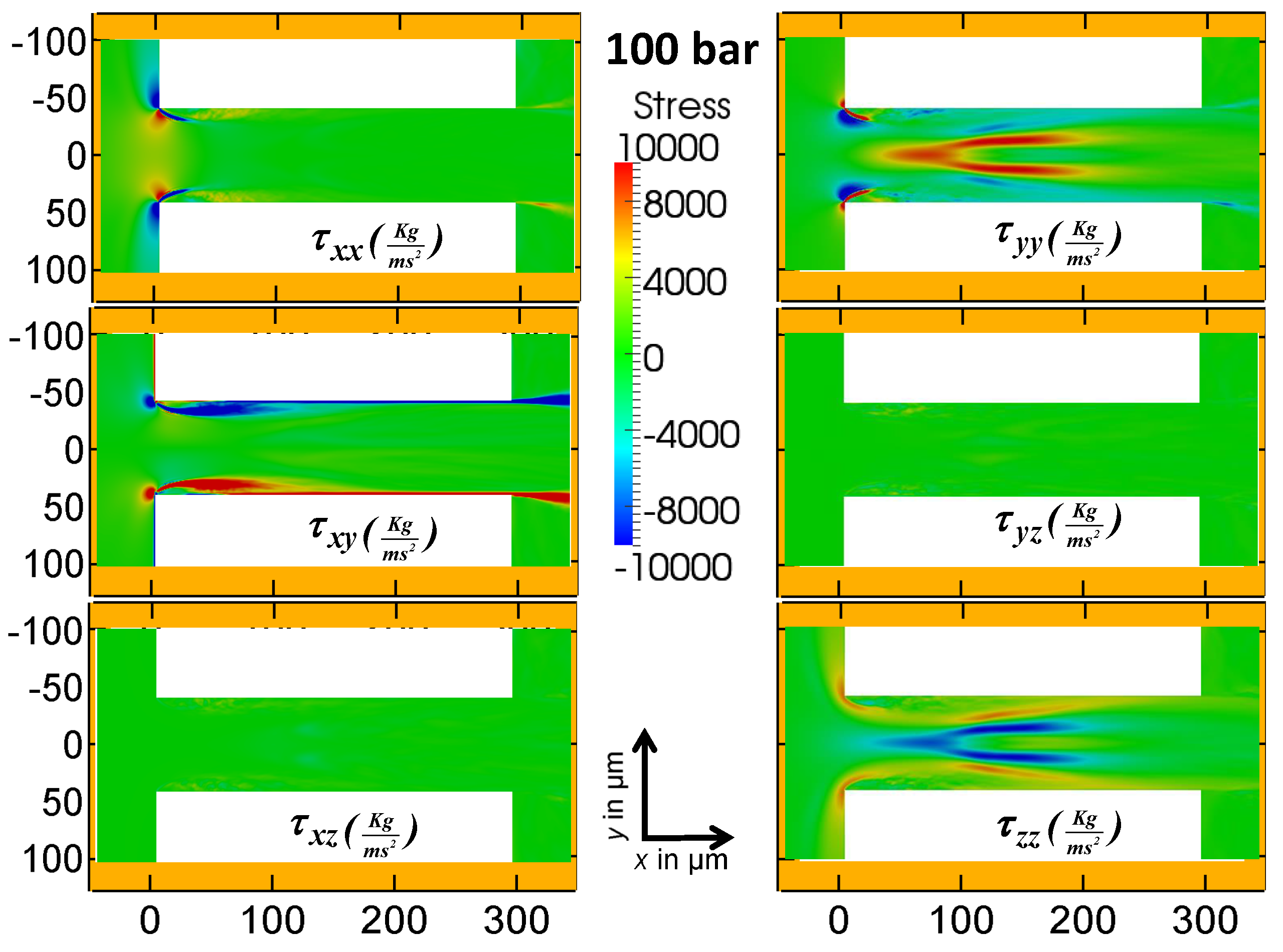
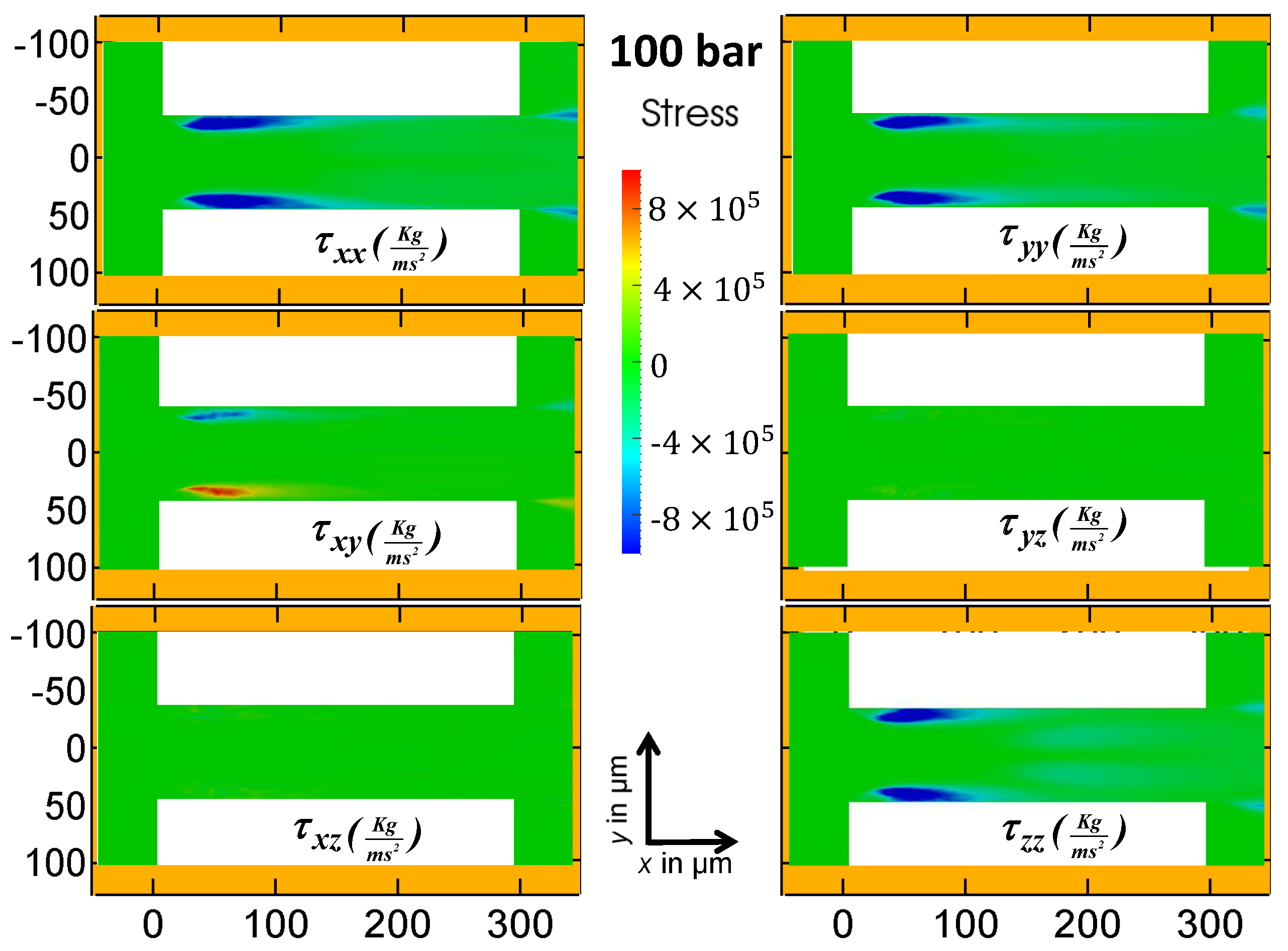
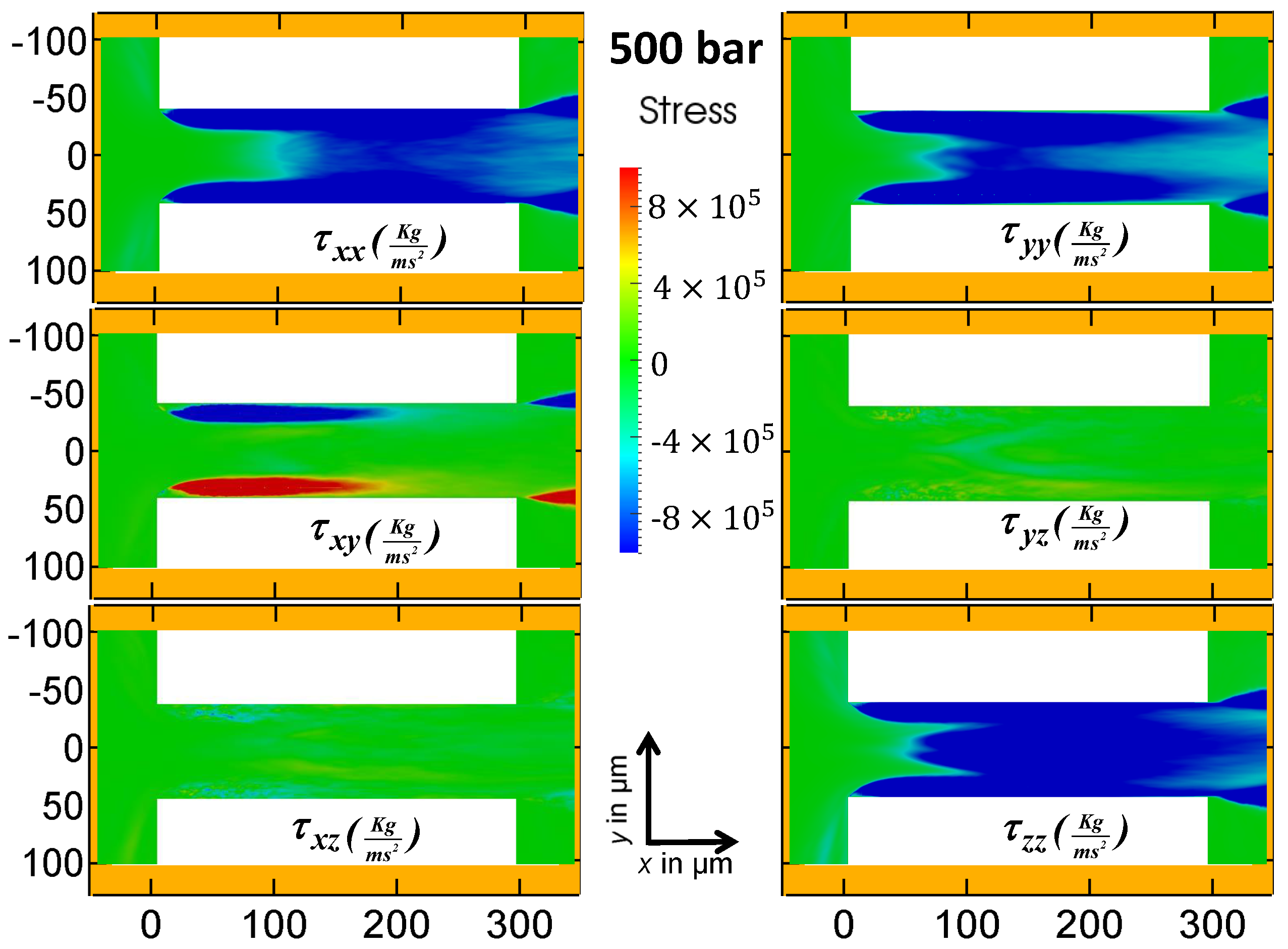
The laminar stresses produced in the orifice for the 100 bar and 500 bar cases in the mid-plane are shown in Figure 12 and Figure 13. The six independent stress components are depicted in each figure. In general, if the coordinate system is aligned with the flow direction, the diagonal components of the stress tensor cause a fluid element to be elongated. The diagonal components of the stress tensor in Figure 12 and Figure 13 are dominant. From the non-diagonal components, only ${\tau }_{xy}$ has a significant contribution to the stress in the mid plane. However, the non-diagonal parts of the stress tensor become dominant closer to the wall, as depicted in Figure 14.

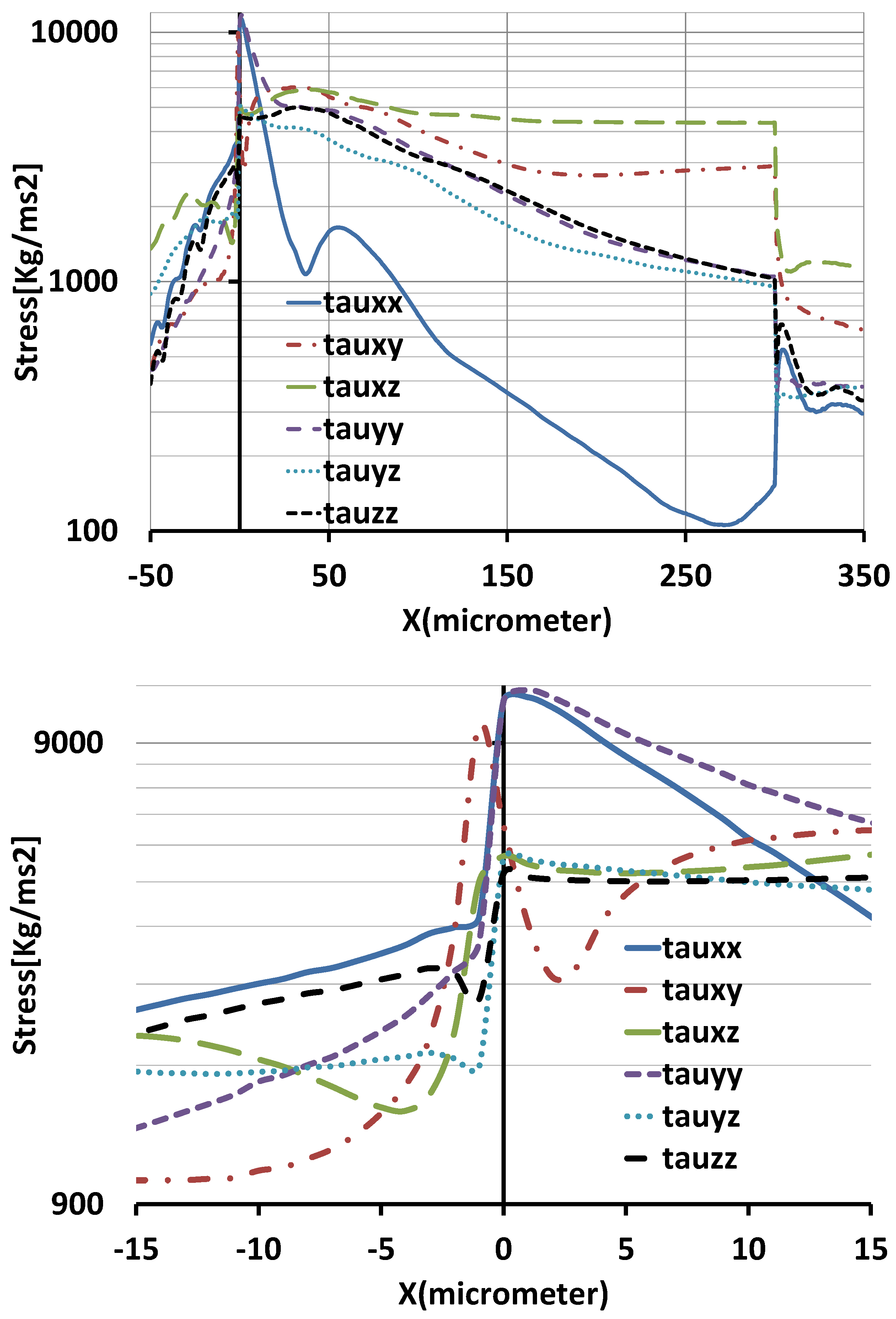
In order to quantitatively compare the effects of each stress component, the magnitude of the stress is averaged over $y-z$ planes and plotted along the length of the orifice (Figure 15). The upper figure shows the stress components from 50 μm before to 50 μm after the orifice. The lower figure shows a close-up of the upper figure. At the entrance, the diagonal components of the stress tensor ${\tau }_{xx}$ and ${\tau }_{yy}$ are dominant. The stress component ${\tau }_{xx}$ decreases along the orifice. The stress component ${\tau }_{xy}$ shows a complicated behavior. It starts from a low value and reaches its maximum a short distance in front of the entrance. After a short distance from the entrance, it reaches a local minimum.

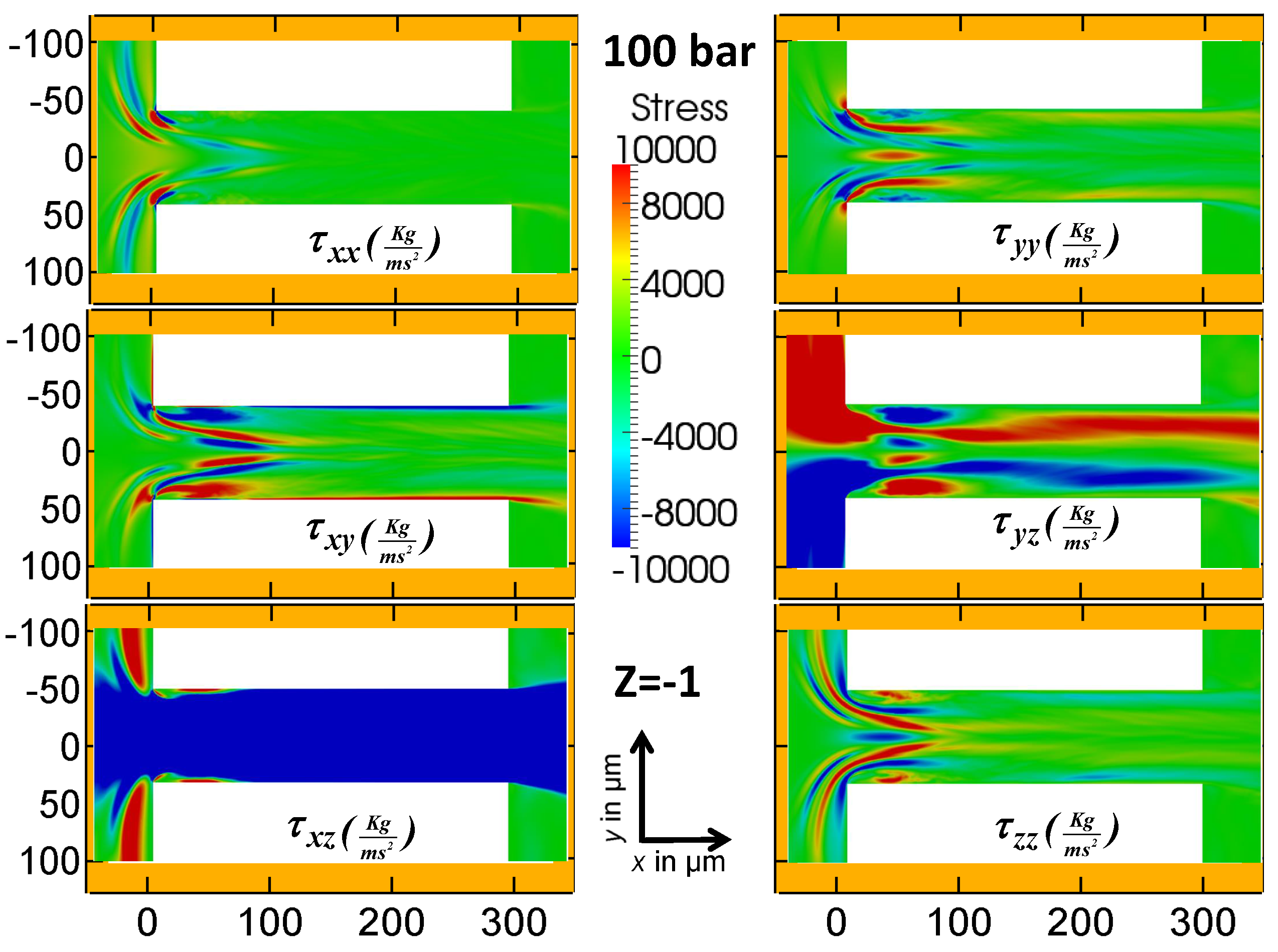
The components of the turbulent stress tensor for the 100 bar and 500 bar cases are shown in Figure 16 and Figure 17. These figures are taken in the mid-plane of the orifice. The trace of the turbulent stress tensor constitutes the turbulent kinetic energy of the fluid flow. The magnitude of the diagonal components is considerably larger than the non-diagonal components in the mid-plane. As for the laminar stresses, only ${\tau }_{xy}$ has a significant contribution among the non-diagonal stresses.

Unlike the laminar stresses, turbulent stresses play no role at the entrance of the orifice. The turbulence is produced where the laminar stresses are high, and moves downstream with the flow. The turbulent flow near the wall in the plane $z=-1$ is shown in Figure 18. The values for the turbulent stresses are seen to be smaller close to the wall than in the mid-plane. The diagonal components of the turbulent stress tensor are dominant before, after, and inside of the orifice. This behavior can be seen in Figure 19. The upper figure shows the average magnitude of the turbulence stress for each component. The lower figure is a close-up of the upper figure.

The maximum of the turbulent stress is observed where the velocity obtains its peak value at about 50 μm behind the entrance of the orifice.

From comparing the turbulent stress in Figure 19 to the laminar stress in Figure 15, we see that the turbulent stress is generally one order of magnitude larger than the maximum of the laminar stress. Our result is therefore in disagreement with the result by Beinert et al. [49], who simulated the same device at the same pressure drop values and obtained turbulent stresses one order of magnitude larger than we did while simultaneously reporting laminar stresses one order of magnitude lower than ours. This difference merits some further discussion. Beinert et al. obtained their result by applying the commercial software ANSYS Fluent 14.0 using a Reynolds-stress model. The turbulent stresses in this software are obtained from empirical closure relations, which are not primarily designed to obtain microscopic stresses. Their approach is therefore based on the assumption that the modeled Reynolds-stresses are valid substitutes of the turbulent stresses. On the other hand, our approach does not rely on explicit turbulence models. The turbulent stresses in our model are essentially obtained by direct simulation of the Navier–Stokes equation. Yet, this does not prove that our result is correct. In order to check for the plausibility of their result, Beinert et al. estimated the size of the eddies necessary to comply with the stresses obtained from their turbulence model. For this, they had to estimate the velocity at which the eddy rotates; they chose the maximum velocity measured in the flow, which they give as 250 m/s for the case of 200 bar (we obtained a similar maximum velocity). With this, they obtained eddy sizes of 154 nm. This was compared to an estimate of the Kolmogorov scale obtained from the dissipation, which was estimated as $v_{max}^3/l$, with $v_{max}=250$ m/s being the maximal velocity observed in the flow and l being the size of the largest eddies, corresponding to the diameter of the orifice. Under those assumptions, the Kolmogorov scale was estimated to be 33 nm, which was judged to be sufficiently smaller than the smallest estimated eddy size computed from the Reynolds-stress model to support the validity of their result. As our result for the same test case was different, we have re-examined this procedure. First of all, the hypothesis that the smallest eddies would rotate with a velocity equal to the global maximum in the flow does not appear to be very plausible. It should be noted that the argument depends crucially on this point, as the size of the smallest eddies required for their dissipation is inversely proportional to the assumed velocity. Under the assumption that the velocity of the smallest eddies would be five times smaller than the global maximum, the obtained eddies would already be smaller than the Kolmogorov length scale, which would render the results unphysical according to the criterion of Beinert et al. Another crucial point is that the estimates of Beinert et al. require that the smallest eddies are responsible for the largest stress, which is also only plausible under the assumption that the velocity of the smallest eddies was very high. Now we return to our own results and try to estimate Kolmogorov length. The Kolmogorov length $\eta$ is computed from the turbulent dissipation $ϵ$ and the kinematic viscosity of water $\nu$ as:

$$\eta ={\left(\frac{{\nu }^3}{ϵ}\right)}^{1/4}$$

(20)

The dissipation in the orifice according to our results is depicted in Figure 8. If we pick, e.g., a value of $ϵ=5.6\times {10}^8{\mathrm{m}}^2{\mathrm{s}}^{-3}$ for the 100 bar case, we obtain a Kolmogorov scale of $\eta =206$ nm, which is three times smaller than the smallest grid spacing in our simulation. In order to check the plausibility of this value, we also estimate the dissipation in another way. The global energy dissipation of the flow in the device is easily obtained from the measurement in Figure 3. It is calculated as the volume flux times the pressure drop; i.e., $Q\times \Delta p=4.3$ W for the 100 bar case. In order to compute the dissipation rate, we have to specify a volume in which the dissipation takes place. Here we assume that all dissipation is confined to the orifice, which gives us:

$$ϵ=\frac{4.3\mathrm{W}}{80\mathsf{\mu }\mathrm{m}\times 50\mathsf{\mu }\mathrm{m}\times 300\mathsf{\mu }\mathrm{m}\times 1000\mathrm{kg}{\mathrm{m}}^{-3}}=3.58\times {10}^9{\mathrm{m}}^2{\mathrm{s}}^{-3}$$

(21)

We see that this value is six times larger than the dissipation obtained directly from the simulation. This rough estimate neglects the fact that the jet behind the orifice participates in the dissipation, and that the remainder of the device is 30 times larger than the orifice itself. This estimate must therefore over-predict the real dissipation, which is compatible with the observation that the previous estimate is smaller. The corresponding Kolmogorov length obtained from this estimate is expected to under-predict the the real Kolmogorov scale. We obtain $\eta =129$ nm. Note in particular that the last estimate of the Kolmogorov length was obtained entirely from the experimentally-measured flow rate, and did not use any data obtained from the simulation. The so-obtained Kolmogorov length—which underpredicts the real Kolmogorov length—is larger than the one estimated by Beinert et al. Thus, we conclude that the turbulent stresses and the associated dissipation rate is physically more plausible than the results obtained by Beinert et al.

5. Conclusions

We used a high-fidelity implicit large eddy simulation code based on the cumulant lattice Boltzmann method to simulate the turbulent flow through a mirco-orifice. In this paper, we especially focused on turbulent quantities like turbulent stresses and dissipation. In particular, we compare our results to the state-of-the-art approach to obtain turbulent stresses from the empirical Reynolds-stresses of standard turbulence models. It is found that our results for turbulent stresses disagree with published results obtained from RANS equations. The plausibility of our results is checked with the Kolmogorov theory, and it is found that the RANS model predictions for the smallest eddy sizes appear inconsistent. We conclude that our approach of a direct simulation without an explicit turbulence model is a priori more sound in terms of the underlying physics of the problem considered. The resolution in our simulation could support eddies up to about three times the Kolmogorov size, such that it can be considered as a very highly resolved LES. It is not possible to obtain turbulent shear stresses from experiments directly such that time- and space-resolved simulations such as the ones presented here are the only practical means to check the plausibility of RANS results in this regard. Since such resolved simulations are very expensive in terms of compute time, the results from RANS models are rarely challenged. Here we observed a clear indication that standard RANS turbulence models might have deficiencies in obtaining quantitative turbulent stresses for the problem class under consideration.