Abstract
This article gives an overview of the diverse range of teaching applications that can be realized using an interactive lattice Boltzmann simulation tool in fluid mechanics instruction and outreach. In an inquiry-based learning framework, examples are given of learning scenarios that address instruction on scientific results, scientific methods or the scientific process at varying levels of student activity, from consuming to applying to researching. Interactive live demonstrations on portable hardware enable new and innovative teaching concepts for fluid mechanics, also for large audiences and in the early stages of the university education. Moreover, selected examples successfully demonstrate that the integration of high-fidelity CFD methods into fluid mechanics teaching facilitates high-quality student research work within reach of the current state of the art in the respective field of research.
1. Introduction
The highlight of fluid mechanics instruction is often time spent at wind tunnels or wave tanks, where students can observe phenomena in action that they typically only encounter using complex mathematical tools and abstract theories. Ideally, those facilities would be accessible to students for self-guided inquiry and experiments, so that they can experience how researchers of fluid mechanics historically come to form their theories. However, time at such research facilities is, for typical teaching contexts, prohibitively expensive for more than fleeting visits, and time away from the university campus always implies logistical challenges. With the exponential increase of calculating power over recent years, an attractive alternative to classical fluid mechanics experiments has emerged for both research and teaching purposes. Nowadays, simulations can provide physically-accurate results in (or near) real-time and, additionally, interactively respond to user input, under the condition that a sufficiently accurate and fast numerical method is used. This presents a great opportunity for instruction in diverse fields like mechanical engineering, water management, energy management or geophysical fluid dynamics. We here present the successful application of an interactive lattice Boltzmann-based simulation tool for a wide range of teaching purposes such as lectures, tutorials or self-study. The lattice Boltzmann method (LBM) is a viable alternative to conventional computational fluid dynamics approaches that approximate continuum physics equations, mostly Navier–Stokes. Thanks to a number of model-specific advantages, particularly concerning data locality and parallel computing, the method scales very well on recent high-performance computing hardware and provides numerical solutions in a very competitive computational time. This is beneficial for numerous scientific and industrial applications and at the same time enables innovative and interactive ways of teaching, primarily in the field of fluid mechanics. After a brief review of the state of the art in fluid mechanics instruction in Section 2, the basics of the employed LBM solver ELBE are presented in Section 3. In Section 4, the use of ELBE for instructional purposes is discussed within an inquiry-based learning framework; in Section 5 in light of student feedback; and finally, in Section 6 conclusions are drawn and an outlook is given.
2. Motivation
The science of fluid mechanics studies the behavior of liquids and gases if subjected to forces or displacements and their interaction with their surroundings. Typically, problems considered in fluid mechanics are large-scale problems in violent environments, like the impact of wave action on coastlines or the interaction between a ship and an ice-covered ocean. Observations of these phenomena in situ might be possible in some cases, but even for very simple flow problems, for example, a cylinder in a flow shedding eddies (Figure 1, top left panel), precisely measuring the acting forces is extremely difficult. Furthermore, reproducing conditions in situ in order to run repeated measurements is impossible.

Figure 1.
Comparison of a fluid mechanics problem, a Kármán vortex street, in situ, in two different laboratory realizations and in an ELBE simulation. (a) Periodically shedding, alternating eddies downstream of a cylinder in the Elbe river. (b) Same as (a), but the direction of flow (yellow) and the structures of eddies (red) are indicated. (c) Vortex shedding behind a cylinder in a water tunnel. The flow field is visualized using food coloring diluted in water. Picture by courtesy of Sarwesh Narayan Parbat. (d) “Kitchen experiment” of the same situation as in the other figures. A paint brush is moved through sugar water dyed with metallic water colors to simulate the above situation. (e,f) ELBE simulation results of a similar situation: (e) adding “dye” yields a visualization similar to the water tunnel; (f) velocity magnitude.
2.1. Laboratory Experiments for Fluid Mechanics Instruction
Laboratory experiments, which are easier to control than measurements in situ, have therefore always been an important method of knowledge generation in fluid mechanics. Elaborate experiments are being conducted in research facilities around the world. For scaling reasons, experiments often require very large wave tanks, wind channels or water tunnels. For example, models of container ships have to be several meters long, and the towing tanks to investigate their behavior moving through water have to be accordingly long and wide: the large towing tank at The Hamburg Ship Model Basin (HSVA) is 300 m long, 18 m wide and 6 m deep. Research questions on static structures in moving water are arguably as difficult to represent in a laboratory. For example, the problem of a cylinder shedding eddies in a flow requires large volumes of water (especially if dye is added to visualize the flow field; see Figure 1, middle left panel) in a very well-controlled flow field throughout the experimental chamber.
Because of their importance in research, laboratory experiments play an important role in instruction in science, technology, engineering and mathematics subjects (STEM) [1], where they can accommodate many desirable learning outcomes [2]. Ideally, one would expose students of fluid mechanics to real research facilities and let them run self-guided, inquiry-based experiments, thereby providing realistic research contexts and preparing them for future research careers [3,4]. However, due to the issues sketched above, fluid mechanics research facilities are prohibitively expensive to use in fluid mechanics instruction for more than the occasional visit during a field day, where students look at carefully-prepared experiments, rather than having the opportunity to plan and conduct experiments themselves, making and learning from their own mistakes. Many of the experiments run at large research facilities are documented and shared, for example via videos shared on online platforms, in addition to conventional publication channels to the scientific community. Presenting experiments in teaching, however exciting, always leaves something to be desired, since students are restricted to passively watching and have no way of interacting with the experiment.
In some cases, it is possible to run very simplified versions of experiments in teaching labs or even at home. For example, in the case of the cylinder in a flow, the problem could be turned upside down by moving the cylinder relative to the water, rather than the water relative to the cylinder (see Figure 1d). However, for obvious reasons, such simplified experiments can only ever give a qualitative taste of what could be observed and never provide the opportunity to engage with real instrumentation or achieve authentic measurements that can be used in further analysis. This deprives students of the opportunity to learn many of the skills they could acquire working with “real” experiments.
2.2. (Interactive) Simulations for Fluid Mechanics Instruction
Luckily, a new alternative has emerged over the last couple of years, made possible by the exponential increase of computing power: numerical simulations. An interactive simulation can give students the opportunity to manipulate the experiment and experience in real time how the system reacts to their interventions. This way, classical, as well as novel fluid mechanics experiments can be simulated, but with many advantages over the laboratory experiment: fewer resources are needed; the experiment can be repeated as often as desired; and the experiment can be conducted in a lecture theater, as well as in an office instead of only at specialized facilities. Figure 1e and Figure 1f show examples of this: an obstacle of any shape, in this case representing a cylinder as in the other examples above, was drawn into a homogeneous flow field by a student, and the flow interactively adjusted to this disturbance in real time. Watching this simulation is therefore much like observing what happens when putting a physical obstacle into a stream of water, except that simulations provide the opportunity for extended visualizations that are extremely difficult or impossible in physical experiments. Simulations therefore are a highly beneficial addition to conventional teaching. Successful examples include, e.g., the software packages TeachFlow [5], CFD Studio [6], FlowLab [7,8], VirtualFlowLab [9] (http://users.metu.edu.tr/csert/virtualFlowLab) and jFlowSim (https://github.com/ChristianFJanssen/jflowsim). More recently, implementations based on high-performance hardware have emerged, as discussed in the next section on LBMs. When embedded in blended-learning scenarios, i.e., integrated in face-to-face learning, simulations or remote experiments can lead to similar learning gains as laboratory experiments [10].
When designing learning opportunities using blended scenarios, as is the case in all instructional designs, the desired characteristics of the learning process (see for example [11]) have to be adequately addressed. In general, experiments are most beneficial in student-centered teaching scenarios, where students take on the responsibility for their learning and follow their interests: inquiry-based learning aims at designing learning situations in which students experience the research process, as a whole or in parts. One characteristic of inquiry-based learning is therefore that new knowledge is gained which is interesting not only to the student/researcher himself/herself. However, this does not mean that inquiry-based learning has to lead to cutting-edge research results. Knowledge is also considered as “new”, even though not new to the scientific community, if it is new and interesting to the students’ peer group, i.e., other students of the same course or of other courses, where the results might be presented [12]. Indeed, it is important to include presenting and other typical social practices and norms in authentic science learning [13].
3. LBM for Interactive Monitoring and Steering
Compared to other fields of numerical simulations, simulation of fluid mechanical problems is computationally very demanding. Due to the large scale of the problems under consideration and the highly turbulent nature of the flows that require a high temporal and spatial resolution, a large number of operations is required. Efficient software and hardware concepts have to be harmonized in order to obtain numerical results in a reasonable amount of time. Concerning the numerical back-end, this motivates the use of lattice Boltzmann methods, mainly due to the following four reasons: 1. The LBM is a valid discretization and approximation of the weakly compressible Navier–Stokes equations. 2. The LBM features solver-specific advantages in terms of data locality and parallel computing, which allow for very efficient simulations on massively-parallel hardware. 3. The LBM allows for a parallelization on GPUs, bringing massive computing power to the lecture room, as one single GPU offers the performance of approximately 4–5 recent CPUs, but with a significantly higher energy efficiency and a lower price. 4. Grid generation is rather simple, as it does not involve a change in topology, and wall boundary conditions can be adapted easily, opposite to, e.g., finite-volume-based solvers.
3.1. State of the Art
Real-time rendering and interactive simulations in the realm of scientific high performance computing (HPC) and computational fluid dynamics (CFD) are comparably young fields of research. The complexity of most fluid mechanics problems with engineering relevance requires such detailed simulations of both time and space that an apparent change in intermediate results, obtained by current methods that simulate viscous flows, occurs in time frames that do not coincide with the human time frame defined by practicality and patience.
A very early approach to visualize and interact with a computational fluid dynamics simulation in real time was implemented by Kreylos et al. [14]. It included rudimentary 2D visualization, but also allowed for a dynamic remeshing of the fluid domain, as required for potentially interactive simulations. Höfler [15] presented a real-time visualization technique for unstructured data employing a shading language to program graphics cards. A more recent implementation by De Vuyst et al. [16] showcases the current processing and visualization capabilities of modern graphics cards. With the recent advances of GPU computing and its application in the field of computational fluid dynamics, it is possible to compute complex simulations of reasonable resolution even in a time frame that relates to the human perception of real time. Mawson et al. [17] present an interactive LBM solver that, on top of the conventional input of 2D geometry using a mouse or stylus, offers input based on the Kinect sensor, yielding 2D silhouettes or even 3D topologies. Harwood and Revell [18] take another step forward and develop an interactive LBM flow solver on Android-powered mobile devices.
3.2. LBM Bulk Scheme
The visualization suite that is used in our work utilizes the highly parallelized ELBE [19] code, which is optimized for execution on graphics processing units (GPUs). Tölke and Krafczyk [20] among others [21,22,23] have already demonstrated the immense performance capabilities and, therefore, the suitability for real-time visualization of LBM implementations on GPUs. The method’s inherently explicit character in time allows unlimited parallelization and yields simulation times that fit the human time frame. For some engineering problems, computations in real-time are possible, even on one single GPGPU board only.
ELBE is based on the second author’s PhD thesis work at Braunschweig University of Technology, where he developed first GPU-accelerated free surface flow kernels [23]. Since the completion of his PhD, he is leading the development of ELBE, an object-oriented and efficient C++ and CUDA-based framework for GPU-accelerated free surface flow simulations, first at the University of Rhode Island (2011) and since 2012 at Hamburg University of Technology. ELBE supports 1D, 2D and 3D simulations of shallow water flows, single-phase flows, flows with a free surface and fluid-structure interactions. For the bulk flow solution, both conventional single-relaxation-time (SRT) and multiple-relaxation-time (MRT) collision operators and more sophisticated, very low-diffusive Cumulant operators are applied, as elaborately discussed for turbulent channel flows in [24]. Rigid-body motions are modeled with quaternion-based motion solvers or a collision-resolving physics engine, as detailed in [25,26]. The code permits simulations on (10,000) CUDA cores on multiple GPUs in a shared memory system. The code was carefully validated, e.g., for sloshing and slamming, wave run-up [27], internal floodwater dynamics in partly filled tanks [28] and for three-dimensional free-surface flows with fluid-structure interactions [29,30]. Several applications related to ocean engineering were also addressed, e.g., wave propagation and wave run-up [27], steady streaming in boundary layers of progressive waves [31] and air-sea interaction and sea spray generation [32,33,34]. An efficient on-device grid generator serves to map complex geometries to the computational grid [30] and was recently extended to second-order accuracy [35].
ELBE is using mainly weakly compressible lattice Boltzmann models, for which single-precision arithmetics have been shown to be sufficiently accurate. The following performance estimates were obtained on an NVIDIA Quadro M6000 device. Performance is reported in terms of million node updates per second (MNUPS). For 2D single-phase flows, the performance is in the order of 1000 MNUPS and above, e.g., for a lid-driven cavity simulation on a 512 × 512 grid. With additional consideration of fluid-structure interactions, e.g., for the simulation of an oscillating cylinder in a transient flow, the performance is slightly reduced and in the order of 700–800 MNUPS, for a 1024 × 512 node grid. In case the VOF free surface tracking is activated, the resulting performance is further reduced. For a 2D numerical wave tank with inlet and outlet boundary conditions on a 1300 × 218 node grid, we end up with node update rates in the order of 550 MNUPS. In 3D, performance naturally is slightly lower. For 3D lid-driven cavity flows (on a grid and finer), we obtain node update rates in the order of 700 MNUPS. If again free surface capturing and the bidirectional fluid-structure interaction interface are activated, we end up with 450 MNUPS, as tested for the simulation of the water entry of a solid cube on a 300 × 195 × 121 node grid. All in all, the performance is found to be very competitive and sufficiently high for the application of ELBE as a tool for interactive teaching.
3.3. Online Visualization: The Key to Success for Teaching Purposes
For the teaching applications presented in this work, the ELBE solver is used in combination with the visualizer interface ELBEvis [36]. The primary objective of all added functionality for visualization and interaction purposes is to maintain the high update rates of the main computation. The resulting tool uses CUDA and OpenGL interoperability to avoid the bottleneck of device-to-host data transfers and to visualize the results directly from the GPU memory. The visualization features are realized directly on the GPU so that no additional and comparatively slow data transfer have to be performed. The easy and direct control of these features is realized with a graphical user interface that can be started as a separate process and communicates with ELBEvis through a shared memory segment. The details of ELBEvis are elaborately discussed in [36]. The performance of the fully-coupled ELBE-ELBEvis solver yields still more than 90% of the performance of the standalone ELBE simulation for both 2D and 3D simulations (Tables 1 and 2 in [36]). Only for two very compute-intensive visualizer features, the performance is significantly reduced, down to 76% for the isolines filter and down to 38% for the streamline filter (which requires a time-integration of a frozen velocity field).
Selected visualizer features are shown in the following, for two standard fluid dynamics test cases, the Kármán vortex street and a dam break setup. The Kármán vortex street is simulated as a two-dimensional single phase channel flow around a cylinder. A dam break test case is used to demonstrate the three-dimensional visualizer features. Figure 2 shows the colored-slice feature applied to both test cases. The local distribution of flow velocities in the whole computational domain can be observed. Figure 3a shows the reconstructed free water surface for the dam break case. The isosurface feature can not only be used to reconstruct the free surface, but can also be applied to the velocity or density field to acquire information about thevalues within the fluid. Thanks to the GPU acceleration, the surface can be reconstructed with almost no computational overhead, while a similar reconstruction on the CPU would significantly slow down the simulations. For complex three-dimensional fluid flow problems, the visualization of field values throughout the entire domain can be very useful, as similar information would not be accessible with experiments at all. Figure 3b shows the dam break’s velocity magnitude distribution. Lattice nodes are transparently blended with their opacity and color adjusted in accordance with the applied data range and color map. Lattice nodes with vanishing velocities are discarded entirely.
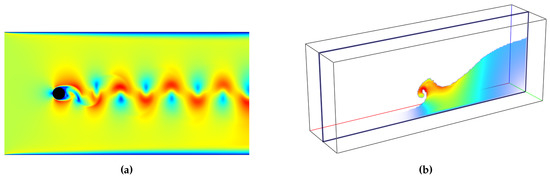
Figure 2.
Colored slice applied to (a) a flow around a cylinder and (b) the dam break test case.

Figure 3.
Two sophisticated three-dimensional visualizer features: (a) a free-surface dynamically computed with the marching cubes algorithm; (b) volume rendering applied to the dam break’s velocity magnitude field.
3.4. Hardware Concepts: Bringing the Computing Power to the Lecture Room
The usage of GPUs is essential for the interactive monitoring environment of ELBE. Moreover, running computations on GPUs allows to run computationally-expensive simulations on the desktop, without tedious access to remote supercomputers. This also allows to bring HPC-based simulations to the lecture room, e.g., with GPU-accelerated laptops and workstations or remote access to local GPU-based HPC hardware. The hardware that is used for the simulations presented here is summarized in Table 1, and selected devices are depicted in Figure 4. In addition to its portability, the hardware is found to be rather inexpensive, in comparison to other state of the art high-performance computing hardware. The hardware demonstrator ELBE2go (Figure 4a), which is used for interactive live demos in lectures, at exhibitions, or science nights, costs only around 1500 Euros (approximately 1680 USD). The machine can be connected to any projector, smart board or conventional screen, as required by the particular audience. Note that the machine is equipped with the most powerful NVIDIA gaming GPU, which allows for very demanding simulations. In case that slightly less computing power and even more portability is required, a laptop solution can be used: the ELBEbook; see Figure 4b. The device formally cannot be distinguished from a conventional office laptop. As it is equipped with a portable NVIDIA GTX 970M GPU, it can, however, be used to run ELBE and ELBEvis, with approximately half the performance of its stationary equivalent. This is more than sufficient for most of the live demos and the interactive test cases.

Table 1.
Hardware resources that were used for the results presented here.

Figure 4.
Hardware used for the present work. (a) ELBE2go, portable Mini-ITX machine with an NVIDIA GTX Titan GPU, mainly used for lectures, science nights and presentations. (b) ELBEbook, gaming notebook with a portable NVIDIA GTX 970M device.
Note that this sort of portable performance is available to the teaching personnel only. The hardware that is commonly used by students (standard tablets or notebooks) is not necessarily equipped with (efficient) GPU hardware. Right now, there are no intentions to provide access to GPUs to a broad range of students. If students already have achieved a reasonable base knowledge of ELBE and are able to run their own simulations, they typically get access to the institute’s standard workstations in the student pool. These workstations are equipped with recent NVIDIA gaming GPUs that provide sufficient compute power to run both simple validation cases and one’s own, more demanding, simulations. In case that in-depth analyses and more time-/memory-consuming simulations are needed, the students can also access our in-house server infrastructure, with professional NVIDIA Tesla boards (C2075, K40 and K80 configurations). For a more interactive solution, we are currently discussing porting ELBE to a tablet-based version using NVIDIA’s own tablet series. From an economical point of view, the use of less scientific tools (such as apps for conventional cell phones) would also be an appealing alternative, even though they do not offer the possibility of scientific, research-oriented simulations at all.
4. Inquiry-Based Learning Scenarios with the LBM Solver ELBE
We use the Rueß (2013, [37]) framework to describe how a tool like ELBE can be used in student-centered teaching as successfully demonstrated at Hamburg University of Technology (TUHH). In this framework, different inquiry-based learning activities are presented as a function of the student activity (i.e., consuming, applying or researching) and the topic of the activity (scientific results, scientific methods or scientific processes; Table 2). Student activity can range from more or less passive consumption of the application, to active engagement in different kinds of research activities. The type of content can be broken down into content with a focus on research results (“learning about research”), research methods (“learning for research”) or the research process itself (“learning through research”) [38]. Depending on the desired learning outcomes, each of the nine fields, or any combination thereof, can inform design choices for any part of an instructional unit, for all of it or even for a whole course or study program. We present examples of different teaching scenarios and explain how they let students gain familiarity with aspects of the research process and, combined with each other, prepare students for active participation in the research process.

Table 2.
Example tasks for different flavors of inquiry-based learning (based on Rueß (2013, [37]) and personal communication with Klaus Vosgerau and Timo Lüth (2014)).
The research process consists of many individual steps that are conducted in a distinct sequence (Figure 5). Sometimes, it becomes necessary to repeat one or several of those steps, while maintaining their order. When educating future researchers, the final goal for students is to be able to independently conduct a full research process. This can be scaffolded by first teaching about research processes, then discussing and practicing the design of research questions and then, finally, conducting research, now using skills learned on all other aspects of research mentioned in Table 2. Consequently, fluid mechanics teaching can either focus on one of the key ingredients or address the full loop. ELBE is used as a tool to support the situatedness of learning, demonstrating the relevance of each individual task to the larger research questions of the ELBE community. In order for this to work well, it is important to communicate where each task fits, and where it is relevant and important in the large research process.

Figure 5.
Schematic view of a scientific process. Shown is a linear model; in practice, it often is necessary to repeat one or several steps. On the right, an example is given, based on a master thesis project with ELBE that is aiming at analyzing violent pool sloshing aboard cruise ships.
Whether tasks then resemble authentic research can be evaluated using the Chinn and Malhotra (2015, [39]) framework. One drawback that they typically find with computer simulated experiments used in teaching is, for example, that students are asked to make choices about variables that they would otherwise not consider and that they are limited to the theories included in the model and cannot invent and include theories or variables on their own. While this is likely true for many instances, we suggest how to overcome this specific limitation and let students experience authentic research in the ELBE framework.
Even though the presentation in the following might seem to imply a preferred sequence of instructional activities, the different aspects of the research process are presented in only one of many feasible orders. However, any other order might be more appropriate for planned overarching learning progressions. Arranging by topic of the student task and increasing level of student activity is, most generally speaking, an order that makes sense in terms of scaffolding and is traditionally followed (more or less closely) in teaching. Learning about results, then methods, then processes can be a sensible progression, as well, if a context is first motivated, and students then dig into the topic more and more deeply. Additionally, many of the tasks will lead to students wanting to expand on them, leading to new questions that extend into different fields of the Rueß (2013, [37]) framework, towards conducting a full research process. However, even addressing only selected fields of the matrix in individual lessons or even courses might be most suitable for a given learning outcome as long as care is taken that interested students are not hindered from pursuing goals larger than the learning outcomes of that course.
In the following, we have grouped aspects of the Rueß (2013, [37]) matrix together under four headings to draw a picture from getting a taste of fluid mechanics and CFD (Section 4.1), of working with literature (Section 4.2) and learning aspects of simulation (Section 4.3) to authentic, full research processes (Section 4.4).
4.1. Getting a Taste of Fluid Mechanics and CFD
ELBE provides a great opportunity to give a first taste of fluid mechanics, as well as CFD to both students and the general public: its easy visualization and interactivity make it hugely attractive to use in introductory lectures or for demonstration and PR purposes at conferences, fairs, open days and numerous other events when faced with large groups of dozens to hundreds of people to be taught simultaneously with one or very few instructors (compare Figure 6). Even though large lecture theaters or online learning scenarios are, at first glance, not conducive to actively experiencing the research process, inquiry-based learning can still happen in those settings and in a way that is similar to the parts of the research process as described above.

Figure 6.
Two examples of students (and other interested audience) consuming scientific results: (a) Preparations for a lecture in the Audimax II, the TUHH’s second-largest lecture theater. ELBE2go can be seen standing on the desk. (b) ELBE in action at the TUHH science night. Again, the computations are run on ELBE2go, this time in combination with the smart board interface.
4.1.1. Students Consume Scientific Results
When the desired learning outcome is to familiarize an audience with scientific results, ELBE is used to visualize and explain basic fluid mechanics phenomena that would otherwise not be presented at all or as purely theoretical constructs (e.g., turbulence, drag, vortex shedding, boundary layers, and so on). By varying parameters in the input to the simulation, the influence of those parameters on given properties can be directly “experienced” by way of real-time simulation rather than just calculated. Streamlines around bodies or dispersion of tracer particles become tangible, and scientific results therefore approachable and much more easily recognized when later encountered “in the wild”. In such teaching scenarios, the interaction with the ELBE tool is mainly done by the lecturer or one or a few volunteers, possibly reacting to audience’s suggestions. If interactive input devices (such as smart boards) are used with the ELBE tool, the interested audience can get in touch with a real CFD simulation easily, e.g., by writing or drawing shapes that act as obstacles to the flow and observing the real-time changes in the flow fields, and depending on group size, as many as possible of the participants are encouraged to try and gain first-hand experience.
As a concrete example, such a teaching scenario was used in the lecture Fluid Mechanics and the corresponding exercise. The course is scheduled for the fourth semester of the bachelor degrees in Naval Engineering and Mechanical Engineering. Weekly lectures are accompanied by weekly exercises to practice solving actual fluid mechanics problems. This mostly involves analytical solutions of the previously-introduced equations. In this context, ELBE was tested in the lecture room as an alternative to conventional equation-solving. The question that the students had to answer was, which of the two wings of a double-decker airplane (the upper or the lower one) generates more lift. Typically, this question is answered by a theoretical analysis with the help of inviscid potential flow theory. After a quick introduction to ELBE and showing standard live simulations of, e.g., vortex shedding behind cylindrical obstacles (see Figure 1), the audience was asked to answer this question with an interactive analysis. The group size was approximately 25. A couple of volunteers drew simple profile-like shapes in the numerical ELBE wind-tunnel. ELBE generated the resulting velocity and pressure fields on the fly. By analyzing the pressure distribution along the two NACA profiles, the students finally were able to answer the question: the upper NACA profile creates significantly more lift than the lower one. Instead of a conventional analysis based on equations, a more playful, interactive and memorable explanation was obtained. On the technical side, the simulation was addressed with a 2D LBM single-phase simulation with MRT collision operator and LES turbulence closure. Standard results of a predefined simulation are shown in Figure 7. This scenario was used after the students interactively drew their own test shapes.
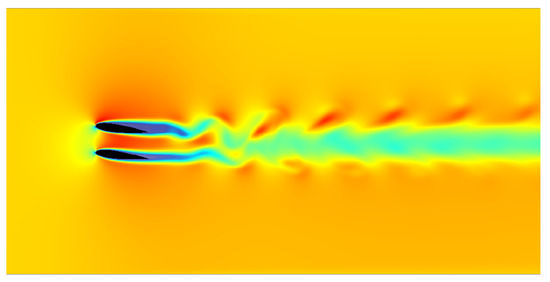
Figure 7.
ELBE simulation of two NACA profiles to answer the question which of the two profiles generates more lift. The flow is coming from the left (velocity boundary condition). 512 times 256 lattice nodes were used, yielding a total of 131,072 lattice nodes.
4.1.2. Students Consume Scientific Methods
A learning outcome that focuses on familiarizing students with scientific methods can, in the spirit of inquiry-based learning, mean many different things, for example students attending presentations on methodological topics or watching videos explaining a specific method. ELBE can be used here to demonstrate the influence of different resolutions on run speeds that change from real time to visually slower or that have effects on the solution the simulation findings. Doing this, students experience an important part of the scientific process: participation in scientific conferences and browsing of scientific presentations, which are common occurrences in the life of a scientist and where being part of a large, mainly passive, audience is part of the experience. Moving from passive consumption to active engagement with the topic can be supported by interactive formats that engage students in discussions or quizzes.
4.1.3. Students Consume Scientific Process
Consuming the scientific process will, as consuming in the two previously mentioned fields, likely mean listening to a presentation, for example on the history of ELBE. However, it can also mean to go on a field trip to a fluid mechanics research facility where experiments are presented and the results compared to results of ELBE simulations. Even though this counts as “consuming” the scientific processes, this should not be a passive endeavor. Even though they are not producing scientific results themselves, students should still be actively engaging in the learning process.
4.2. Working with the Literature
Reading articles written by authors personally known to the students (e.g., their professors, instructors, even fellow students at master’s or Ph.D. level) is highly motivating, as is working with literature in order to solve an authentic problem of the ELBE community. Therefore, practicing skills related to literature search in the context of ELBE provides situatedness of learning. This refers to the gray-shaded cells of Table 2.
4.2.1. Students Apply Scientific Results
When the desired learning outcome for students is to be able to apply scientific results, a task could be to search the scientific literature for specific topics of interest, to discuss scientific results critically and then to add a synthesis to the ELBE wiki, corresponding to early steps in the research process concerned with reviewing the literature for state of the art solutions. Alternatively, students can analyze results of ELBE simulations to draw conclusions about related, real-life problems they are interested in: They can for example use simulations of rigid wing profiles in a flow field to improve their own sailing skills by considering the difference between lift and drag and different downwind turbulence fields or simulations of tracer dispersion in a flow to determine at which location relative to a source of pollution they would draw drinking water from a creek. This would correspond to the “formulating a hypothesis” step in the scientific process. This organically leads to students wanting to conduct other steps of the scientific process, as well, e.g., testing the hypothesis they just generated.
Although it is more difficult to instruct this kind of tasks when audiences are large, it is possible to make this kind of learning available to the public, for example by having interfaces to the tools available online and then collecting answers via social media and engaging participants in discussions there. An interactive web interface is currently under construction for ELBE, but successful examples include the dispersion of surface drifters in the world oceans (adrift.org.au) or a simple climate model (http://mscm.dkrz.de).
4.2.2. Students Research Scientific Results
When students are asked to research scientific results, this can mean a classical literature study, as well as interviewing experts on a topic. This is motivated by the direct relevance to the further development of ELBE and the contribution to the ELBE community, and questions can be given by the instructor or developed by the students themselves. A current example is project work on the topic of wind turbines in the form of a literature study. This study will directly influence the ELBE community’s future research directions and is therefore in itself an important part of an authentic research process.
This kind of task is easiest to implement in the form of students working on their own projects or with small groups in which students can share and discuss the results of their literature searches with others. Getting large groups of people to engage in such a task requires high levels of motivation on the participants’ part and will most likely occur as self-directed rather than instructed, unless extrinsically-motivating mechanisms like homework and feedback are in place.
4.3. Learning about (Aspects of) Simulation
In many study programs, important learning outcomes are skills in applying, sometimes predefined, scenarios of simulations as a prerequisite for future independent work with numerical models. The following two sections refer to the orange cells of Table 2.
4.3.1. Students Apply Scientific Methods
When students “apply scientific methods”, they use one specific scientific method to carry out a given task. Applying scientific methods in an inquiry-based learning sense can mean, for example, to run a predefined ELBE test scenario. In those scenarios, sensible parameters are suggested, and the setup is guaranteed to work; however, students can practice running a numerical model in a low-stakes environment and gain experience applying this specific scientific method. Furthermore, the discussion of the advantages and disadvantages of scientific methods is an application that is a very real part of the research process and an important part of the learning process.
Current examples of students applying scientific methods related to the ELBE project, e.g., include project tasks in several lectures at TUHH (InnoCFD and ASM; see Section A.1), where students are asked to determine the relationship between the frequency with which vortices are shed and the Reynolds number. This task is addressed by each participant by running individual numerical simulations and developing individual routines to analyze the flow field to extract the vortex shedding frequency. Another example, currently part of a master’s project, is the design of the aerodynamics package of an electronic race car using ELBE simulations of wings (master thesis of Reichert, elbe-2015-17, Table 3).

Table 3.
List of completed ELBE thesis projects: bachelor theses (B.Sc.), master theses (M.Sc.) and project theses (P.Th.). Note that most of the titles were translated from German to English. An up-to-date list can also be found online: https://www.tuhh.de/elbe/education/thesis-projects.html.
A typical example for such an application-oriented example is the ASM project task on flooding (Budde, Conradi and Lüke, 2014). The students were asked to validate ELBE for flooding and sloshing scenarios of ships and were provided with a set of experimental data (free surface elevations and force time series). The group started using ELBE, implemented several minor code extensions and, finally, validated the code with the help of experimental data; see Figure 8.
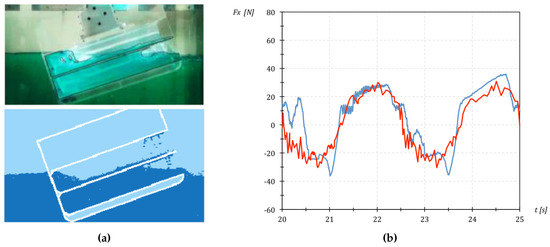
Figure 8.
Selected figures from the ASM project work of Budde, Conradi and Lüke on flooding simulations with ELBE: (a) comparison of experimental (top) and numerical (bottom) results for a damaged car deck; (b) comparison of fluid forces of experiment (red) and simulation (blue). A grid with 1280 times 256 nodes was used. Twenty six seconds of real-time sloshing were simulated in less than one hour on a single GPU.
Adapting this setup for large groups is challenging, but can, as discussed in Section 4.2.1, be managed through web-based or app-based approaches. It is important to give participants a reason to participate, for example by letting them contribute to discussions with experts.
4.3.2. Students Apply Scientific Processes
When the aim is for students to apply scientific processes, they can be asked to discuss research designs or practice developing research questions or designs. This can, for example, mean making decisions on questions like which grid resolution is suitable for a given research question or how to design an experiment for another question; or, as currently in the seminar InnoCFD/ASM (see Section A.1), students can do analyses of the convergent behavior in space and time for a simple, two-dimensional academic test case. With large groups, it can mean discussing research designs and actively encouraging suggestions.
4.4. Research
The goal of academic education is to enable students to do independent research, whether in industry, in academia or elsewhere. The corresponding cells in Table 2 are colored in red.
4.4.1. Students Research Scientific Methods
When students “research scientific methods”, they are very active in the way a researcher would be, except that they are only doing one specific part of the research process: they do literature searches, talk to colleagues or attend presentations, all with the goal to find a scientific method that can be used to address a specific question. This question can both be their own or prescribed; however, students’ own questions usually are better motivators. Current examples of students researching their own questions in the ELBE team include master’s projects on finding and implementing a new LBM model for the simulation of turbulent channel flows, finding and implementing an overset grid model in ELBE and the implementation of a suitable visualization.
The latter is essentially the basis of the current work: Koliha (elbe-2013-06, Table 3) implemented and validated the basic ELBE visualizer interface, which is now the basis of the present publication and most of the ELBE applications in teaching. He started with a sound literature review, followed by a technical analysis of the requirements and technical options for a visualizer interface In the second part of his work, he implemented and validated the visualization environment.
Similarly, much progress was made with ELBE in the actual LBM- and CFD-based research. Gehrke presented a new model for simulations of turbulent channel flows, which is currently part of an international, peer-reviewed journal publication (elbe-2015-12, Table 3, [24]). Similarly, Asmuth very recently implemented and tested a new overset grid approach for LBM methods (elbe-2016-21, Table 3). Both theses would not have been possible without proper and fast online visualization and GPU acceleration of the code.
4.4.2. Students Research Scientific Processes
When “students research scientific processes” in the sense of the inquiry-based learning framework, they are actively participating in the full research process. It is not difficult to see that this is inquiry-based learning in its most obvious sense. This happens in many different scenarios ranging from courses where ELBE is used to answer smaller research questions, over bachelor’s and master’s theses, to fully-developed research projects and Ph.D. theses on very challenging topics, such as three-dimensional ship-ice interactions, tsunami propagation and inundation modeling and transition from laminar to turbulent flow.
A typical example for the full implementation of the research cycle (as depicted in Figure 5) is the master’s project of Budde (elbe-2016-22, Table 3). Focusing on pool-sloshing onboard of mega-yachts, the first part of his thesis was concerned with analyzing the actual problem by field observations and evaluating experimental field data taken from model tests. He then came up with a hypothesis on the influence of the shape of the pool on the eigenfrequency and sloshing behavior, which then was tested with a whole set of ELBE simulations (Figure 9). In the end, he was able to derive simple relations of swimming pool shapes aboard mega yachts on the sloshing behavior. The numerical simulations of the complex three-dimensional sloshing process were run overnight on one of the ELBE rack servers (see Table 1). Also note that he first got in touch with ELBE in the scope of the ASM lectures and the related project tasks that were mentioned in Section 4.3.1.

Figure 9.
Two different pool geometries that were part of the analysis of Budde: (a) original pool with large sloshing amplitudes; (b) optimized pool with an irregular bottom elevation in the form of a bump with significantly lower sloshing amplitudes. Each simulation took only two hours on a single GPU.
5. Feedback and Evaluation
In order to give an impression of the success of ELBE in the instructional context at TUHH, we have added information on the amount of student research projects at our institute, which can serve as approximation for the attractiveness of the tool, and we have additionally asked selected ELBE team members, who attended the ELBE lectures years ago, for personal feedback.
5.1. Statistics
The Institute for Fluid Dynamics and Ship Theory (FDS) is responsible for research and teaching in the field of fluid dynamics in general and ship hydrodynamics specifically. The team of approximately 40 Ph.D. students is led by two professors that are supported by 2–3 postdoctoral researchers (https://www.tuhh.de/fds/staff.html). The development of ELBE and the visualizer interface ELBEvis was initiated and led by the second author (C.F.J.) and is associated with the team of Prof. Rung. Martin Gehrke, the first regular ELBE Ph.D. student, joined the team in 2015. Since then, the team is growing continuously. Currently, as of July 2017, the ELBE team consists of five employees, corresponding to ≈12.5% of the whole team size. In the last five years, a total of 150 theses at the bachelor’s and master’s level were advised by members of the FDS. Thirty of these 150 theses were associated with ELBE (see Table 3), approximately 20% of the total lab contribution, despite having significantly lower human resources. This gives a strong indication that the actual teaching style and the interactive, versatile combination of ELBE and ELBEvis is at least one of the reasons for the high popularity and mid-term success.
5.2. Personal Feedback
In addition, we have asked three selected ELBE team members for detailed personal feedback. All three team members have experienced ELBE and ELBEvis during their university education and are now permanent members of the ELBE research team at the FDS.
Huisman is working for the European research project PRICE. He joined the team in 2016 and already attended a couple of international conferences and published his work with ELBE in peer-reviewed conference proceedings [40,41].After attending the lecture ”Application of Numerical Methods in Marine Engineering” (ASM) and the project that was part of the course, I had a clear overview of the research code ELBE and its application spectrum. The possibility of quick implementation of new code snippets and the fast computation and post-processing times enables the user to get a fast response to his own code developments. This makes it possible to quickly generate working simulations, even for beginners without distinct programming skills. When I started my master thesis (simulation of fluid-ship-ice interaction) I already had a good sense of the functionalities and possibilities of ELBE. Now I am working as part of the ELBE developer team in a research project following my master degree. This project is based on the topic of my master thesis and therefore good example for student work leading to new research activities.Michael Huisman, Ph.D. student, TUHH
Überrück joined the FDS in 2016. Even though he is not part of the ELBE team anymore, he’s occasionally using ELBE for gaining additional fluid mechanical insight for his current research project, or for demonstration purposes. Moreover, he published his work for the above-mentioned research project in three different journal publications [30,42,43]. On top, he presented the results in front of a large audience at an international conference.My first contact with the lattice Boltzmann Method was in a lecture during my master program. During the practical part of the course, I was impressed by the performance and simplicity of the code, also in the case of flow problems with a free surface, which are very important for me as a naval architect. I decided to write my project thesis and also later on my master thesis in this research field. Moreover, I was involved in a research project as student research assistant. The project was concerned with the analysis of the sloshing behavior in LNG tanks and was funded by a big aircraft manufacturer. I ran all the simulations on campus and later on presented the results at the customer’s site, including a live demo of ELBEvis. All in all, the research on this method and the cooperation with the company motivated me to become a research assistant at the FDS.Micha Überrück, Ph.D. student, TUHH
Mierke is working as a Ph.D. student for the ProEis project. He also contributed to a couple of papers already [25,26,30,35]. Moreover, he won the “Best GPU-related talk” award at the 13th International Conference for Mesoscopic Methods in Engineering and Science (ICMMES 2016, 18–22 July, Hamburg, Germany) and was awarded a recent NVIDIA GPU.I had the chance to participate in the lecture ASM in summer 2013. From the very beginning, I was fascinated by the innovative style of teaching. Advantages and disadvantages, as well as challenges of fluid simulation approaches based on the lattice Boltzmann method (LBM) were demonstrated in a modern and playful way. Furthermore, the development and implementation of the new algorithms on many-core hardware systems like GPUs together with other students resulted in very efficient simulation tools. This has allowed us to visualize the numerical results and even to interact with the fluid simulation during runtime, which was very interesting, fascinating and helpful to understand complex fluid mechanics. Later on, my curiosity for the LBM increased even more. In my project and my master thesis at the FDS, I’ve focused on algorithmic and numerical details of the LBM and developed a valuable new method that I later presented on a notable LBM conference as well as in a publication. Thanks to the inspiring ASM lecture, which has caught my attention and triggered my interest in LBM, I’m now working as a Ph.D. student at the FDS, focusing on numerical and algorithmic details of complex LBM schemes for large engineering applications.Dennis Mierke, Ph.D. student, TUHH
6. Conclusions
In this article, we presented a variety of inquiry-based learning activities using the ELBE simulation tool. Thanks to innovative hardware and software concepts and an inquiry-based approach to teaching and learning, even complex numerical simulations were successfully embedded into various teaching and learning activities at TUHH and beyond. This presents an alternative to conventional laboratory experiments and gives students the opportunity to actively experience (parts of) research processes. Since teaching activities are often part of the larger ELBE research strategy, this provides situated learning opportunities, which are highly motivating to students. The long list of successful ELBE research projects (Table 3) shows that the integration of high-fidelity CFD methods into fluid mechanics teaching facilitates high-quality student research work within reach of the current state of the art in the respective field of research. Moreover, interactive live demonstrations on portable hardware enable new and innovative teaching concepts for fluid mechanics, also for large audiences and in the early stages of the university education.
Future work will address further increased levels of student participation and student interest-led inquiry-based learning. On the technical side, further improvements of the visualizer interface ELBEvis will allow enriched interactions and self-study. In this context, an open-source release of the ELBEvis framework is currently up for discussion.
Acknowledgments
The authors would like to thank NVIDIA for supporting the ELBE-related research in the scope of the Academic Partnership Program and the more recent GPU Research Center initiative. The authors would also like to thank Sarwesh Narayan Parbat for permission to use a screenshot of his video in this article (https://www.youtube.com/watch?v=XF4KzAWSyMk).
Author Contributions
M.S.G. is a physical oceanographer and researcher in physics education and ocean/climate outreach. C.F.J. is the chief developer of the efficient lattice Boltzmann environment (ELBE), which is the basis for the numerical simulations presented here. Both authors contributed equally to this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A List of ELBE Teaching Activities
Appendix A.1. List of ELBE-related lectures and presentations
- Lecture “Application of Numerical Methods in Marine Engineering (ASM)”
- Application of ELBE for individual student research projects. Lecture given by C. Janßen, 2012 – 2015.
- Lecture “Innovative Numerical Methods for Computational Fluid Mechanics (InnoCFD)”
- Application of ELBE for demos in the lecture room and individual student research projects. Lecture given by T. Rung and C. Janßen, since 2015.
- Lecture “Fluid Mechanics”
- Application of ELBE for interactive demos in the lecture room. Lecture given by T. Rung, since 2015.
- Event “TUHH Science Night”
- Application of ELBE for interactive demos with smart board input for a public audience. Demos given by T. Rung and C. Janßen. November 2015 and November 2017 (scheduled).
Appendix A.2. List of ELBE-Related Project Works in ASM
- “LBM, VOF, FSI and GPU”, Detlefsen, Gäbler, Nagrelli, Schimonek. 2012.
- “Analysis of a stirring unit”, Feder, Kömpe, Tobies, 2013.
- “Sloshing in partly filled tanks”, Gehrke, Huisman, Willing, 2013.
- “Analysis of a waterbike in the numerical towing tank”, Herting, v. Meyerinck, Überrück, 2013.
- “Cavitation Modeling”, Brüdigam and Hartmann, 2014.
- “Flooding of generic ship sections”, Budde, Conradi and Lüke, 2014.
- “Sloshing Simulations for various testcase setups”, Rudaa and Olivucci, 2015.
- “The Potsdam Propeller Test Case (PPTC)”, Angerbauer, 2015.
- “LBM for aeroacoustics”, Worst, 2016.
References
- Hart, C.; Mulhall, P.; Berry, A.; Loughran, J.; Gunstone, R. What is the purpose of this experiment? Or can students learn something from doing experiments? J. Res. Sci. Teach. 2000, 7, 655–675. [Google Scholar] [CrossRef]
- Feisel, L.D.; Rosa, A.J. The role of the laboratory in undergraduate engineering education. J. Eng. Educ. 2005, 1, 121–130. [Google Scholar] [CrossRef]
- Weaver, G.C.; Russell, C.B.; Wink, D.J. Inquiry-based and research-based laboratory pedagogies in undergraduate science. Nat. Chem. Biol. 2008, 4, 577–580. [Google Scholar] [PubMed]
- Crouch, C.; Fagen, A.P.; Callan, J.P.; Mazur, E. Classroom demonstrations: Learning tools or entertainment? A. J. Phys. 2004, 6, 835–838. [Google Scholar] [CrossRef]
- Krafczyk, M. Gitter-Boltzmann-Methoden: Von der Theorie zur Anwendung; Technical University of Munich (TUM): MÜnchen, Germany, 2001. [Google Scholar]
- Pieritz, R.A.; Mendes, R.; da Silva, R.F.A.F.; Maliska, C.R. CFD studio: An educational software package for CFD analysis and design. Comput. Appl. Eng. Educ. 2004, 12, 20–30. [Google Scholar]
- LaRoche, R.; Muralikrishnan, R.; Hutchings, B. FlowLab: Computational fluid dynamics (CFD) framework for undergraduate education. In Proceedings of the 2002 ASEE/SEFI/TUB Colloquium, Montreal, Canada, 16–19 June 2002; pp. 1235–1238. Available online: https://peer.asee.org/10204 (accessed on 28 July 2017).
- Parihar, A.; Kulkarni, A.; Stern, F.; Xing, T.; Moeykens, S. Using FlowLab: An educational computational fluid dynamics tool: To perform a comparative study of turbulence models. Comput. Fluid Dyn. J. 2006, 15, 175. [Google Scholar]
- Nakiboglu, G. Development of an Educational CFD Software for Two-Dimensional Incompressible Flows. Master’s thesis, Department of Mechanical Engineering, METU, Ankara, Turkey, 2007. [Google Scholar]
- Corter, J.E.; Esche, S.K.; Chassapis, C.; Ma, J.; Nickerson, J.V. Process and learning outcomes from remotely-operated, simulated, and hands-on student laboratories. Comput. Educ. 2011, 57, 2054–2067. [Google Scholar] [CrossRef]
- Reinmann-Rothmeier, G.; Mandl, H. Unterrichten und Lernumgebungen gestalten. In Pädagogische Psychologie. Ein Lehrbuch; Krapp, A.W., Ed.; Beltz Psychologie Verlags Union: Weinheim, Germany, 2001; pp. 601–646. [Google Scholar]
- Huber, L.; Hellmer, J.; Schneider, F. Forschendes Lernen im Studium, 2nd ed.; UVW Universitäts Verlag: Bielefeld, Germany, 2009. [Google Scholar]
- Edelson, D.C. Realising authentic science learning through the adaptation of scientific practice. Int. Handb. Sci. Educ. 1998, 1, 317–331. [Google Scholar]
- Kreylos, O.; Tesdall, A.; Hamann, B.; Hunter, J.; Joy, K. Interactive visualization and steering of CFD simulations. In Proceedings of the Symposium on Data Visualisation 2002, Barcelona, Spain, 2002; pp. 25–34. [Google Scholar]
- Höfler, M. Real-time visualization of unstructured volumetric CFD data sets on GPUs. 2006. Available online: https://pdfs.semanticscholar.org/9ab5/9f46c79fc5ae214a43bd04692bd9673c8c57.pdf (accessed on 28 July 2017).
- De Vuyst, F.; Labourdette, C.; Rey, C. GPU-accelerated real-time visualization and interaction for coupled fluid dynamics. 2013. Available online: http://documents.irevues.inist.fr/handle/2042/52817 (accessed on 28 July 2017).
- Mawson, M.; Leaver, G.; Revell, A. Real-time flow computations using an image based depth sensor and GPU Acceleration. In Proceedings of the NAFEMS World Congress 2013, Salzburg, Austria, 9–12 June 2013. [Google Scholar]
- Harwood, A.; Revell, A. Parallelisation of an interactive Lattice-Boltzmann method on an Android-powered mobile device. Adv. Eng. Softw. 2017, 104, 38–50. [Google Scholar] [CrossRef]
- Janßen, C.F. The efficient lattice boltzmann environment ELBE. Available online: http://www.tuhh.de/elbe (accessed on 28 July 2017).
- Tölke, J.; Krafczyk, M. TeraFLOP computing on a desktop PC with GPUs for 3D CFD. Int. J. Comput. Fluid Dyn. 2008, 22, 443–456. [Google Scholar] [CrossRef]
- Linxweiler, J.; Krafczyk, M.; Tölke, J. Highly interactive computational steering for coupled 3D flow problems utilizing multiple GPUs. Comput. Vis. Sci. 2010, 13, 299–314. [Google Scholar] [CrossRef]
- Delbosc, N.; Summers, J.; Khan, A.; Kapur, N.; Noakes, C. Optimized implementation of the lattice Boltzmann Method on a graphics processing unit towards real-time fluid simulation. Comput. Math. Appl. 2014, 67, 462–475. [Google Scholar] [CrossRef]
- Janßen, C.; Krafczyk, M. Free surface flow simulations on GPUs using the LBM. Comput. Math. Appl 2011, 61, 3549–3563. [Google Scholar] [CrossRef]
- Gehrke, M.; Janßen, C.F.; Rung, T. Scrutinizing Lattice Boltzmann methods for direct numerical simulations of turbulent channel flows. Comput. Fluids 2017. [CrossRef]
- Mierke, D.; Janßen, C.; Rung, T. GPU-accelerated large-eddy simulation of ship-ice interactions. In Proceedings of the 6th International Conference on Computational Methods in Marine Engineering (MARINE 2015), Rome, Italy, 15–17 June 2015; pp. 229–240. [Google Scholar]
- Janßen, C.F.; Mierke, D.; Rung, T. On the development of an efficient numerical ice tank for the simulation of fluid-ship-rigid-ice interactions on graphics processing units. Comput. Fluids 2017. [CrossRef]
- Janßen, C.F.; Grilli, S.; Krafczyk, M. Efficient simulations of long wave propagation and runup using a LBM approach on GPGPU hardware. In Proceedings of the 22nd International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; pp. 145–152. [Google Scholar]
- Janßen, C.; Bengel, S.; Rung, T.; Dankowski, H. A fast numerical method for internal flood water dynamics to simulate water on deck and flooding scenarios of ships. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Janßen, C.; Nagrelli, H.; Rung, T. GPGPU-accelerated simulation of wave-ship interactions using LBM and a quaternion-based motion modeler. In Proceedings of the 5th International Conference on Computational Methods in Marine Engineering (MARINE 2013), Hamburg, Germany, 29–31 May 2013; pp. 229–240. [Google Scholar]
- Janßen, C.F.; Mierke, D.; Überrück, M.; Gralher, S.; Rung, T. Validation of the GPU-accelerated CFD solver ELBE for free surface flow problems in civil and environmental engineering. Computation 2015, 3, 354–385. [Google Scholar] [CrossRef]
- Janßen, C.; Grilli, S. Modeling of wave breaking and wave-structure interactions by coupling of fully nonlinear potential flow and Lattice-Boltzmann models. In Proceedings of the 20th International Offshore and Polar Engineering, Beijing, China, 20–25 June 2010. [Google Scholar]
- Banari, A.; Janßen, C.; Krafczyk, M.; Grilli, S.T. Efficient GPGPU implementation of a lattice Boltzmann Model for multiphase flows with high density ratios. Comput. Fluids 2014, 93, 1–11. [Google Scholar] [CrossRef]
- Banari, A.; Janßen, C.; Grilli, S. An efficient lattice Boltzmann multiphase model for 3D flows with large density ratios at high Reynolds numbers. Comput. Math. Appl. 2014, 68, 1819–1843. [Google Scholar] [CrossRef]
- Banari, A.; Mauzole, Y.; Hara, T.; Grilli, S.T.; Janßen, C.F. The simulation of turbulent particle-laden channel flow by the lattice Boltzmann method. Int. J. Numer. Methods Fluids 2015, 79, 491–513. [Google Scholar] [CrossRef]
- Mierke, D.; Rung, T.; Janßen, C.F. An effcient algorithm for the calculation of sub-grid distances for higher-order LBM boundary conditions in a GPU simulation environment. Comput. Math. Appl. 2017. under review. [Google Scholar]
- Koliha, N.; Janßen, C.F.; Rung, T. Towards online visualization and interactive monitoring of real-time CFD simulations on commodity hardware. Computation 2015, 3, 444–478. [Google Scholar] [CrossRef]
- Rueß, J.; Gess, C.; Deicke, W. Schärfung des Konzepts Forschenden Lernens im Kontext forschungsorientierter Lehre. 2013. Available online: https://www.hu-berlin.de/de/einrichtungen-organisation/verwaltung/bolognalab/aktuelles/archiv/ wiss_beitrag/schaerfung-des-konzeptes-forschenden-lernen (accessed on 28 July 2017).
- Reinmann, G. Gestaltung akademischer Lehre: semantische Klärungen und theoretische Impulse zwischen Problem- und Forschungsorientierung. 2016. Available online: http://www.zfhe.at/index.php/zfhe/article/view/983 (accessed on 28 July 2017).
- Chinn, C.A.; Malhotra, B.A. Epistemologically authentic inquiry in schools: A theoretical framework for evaluating inquiry tasks. Sci. Educ. 2002, 86, 175–218. [Google Scholar] [CrossRef]
- Huisman, M.; Janßen, C.F.; Rung, T.; Ehlers, S. Numerical simulation of ship-ice interactions with physics engines under consideration of ice breaking. In Proceedings of the 26nd Offshore and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- Ehlers, S.; Leira, B.; Hahn, M.; Dankowski, H.; Ergec, S.; Rung, T.; Huisman, M.; Sjoblom, H.; Chai, W. Numerical Prediction of Ship-Ice Interaction (OMAE2017 61814). In Proceedings of the 36th International Conference on Ocean, Offshore & Arctic Engineering (OMAE), Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Janßen, C.F.; Überrück, M.; Rung, T.; Behruzi, P. Real-time simulation of impact waves in LNG ship tanks with Lattice Boltzmann single-phase models. In Proceedings of the 26nd Offshore and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- Überrück, M.; Janßen, C.F. On the applicability of Lattice Boltzmann single-phase models for the simulation of wave impact in LNG tanks. Int. J. Offshore Polar Eng. 2017. accepted. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



