Scatter Search Applied to the Inference of a Development Gene Network
Abstract
:1. Introduction
2. Materials and Methods
2.1. Scatter Search Method
2.2. Parallel Simulated Annealing
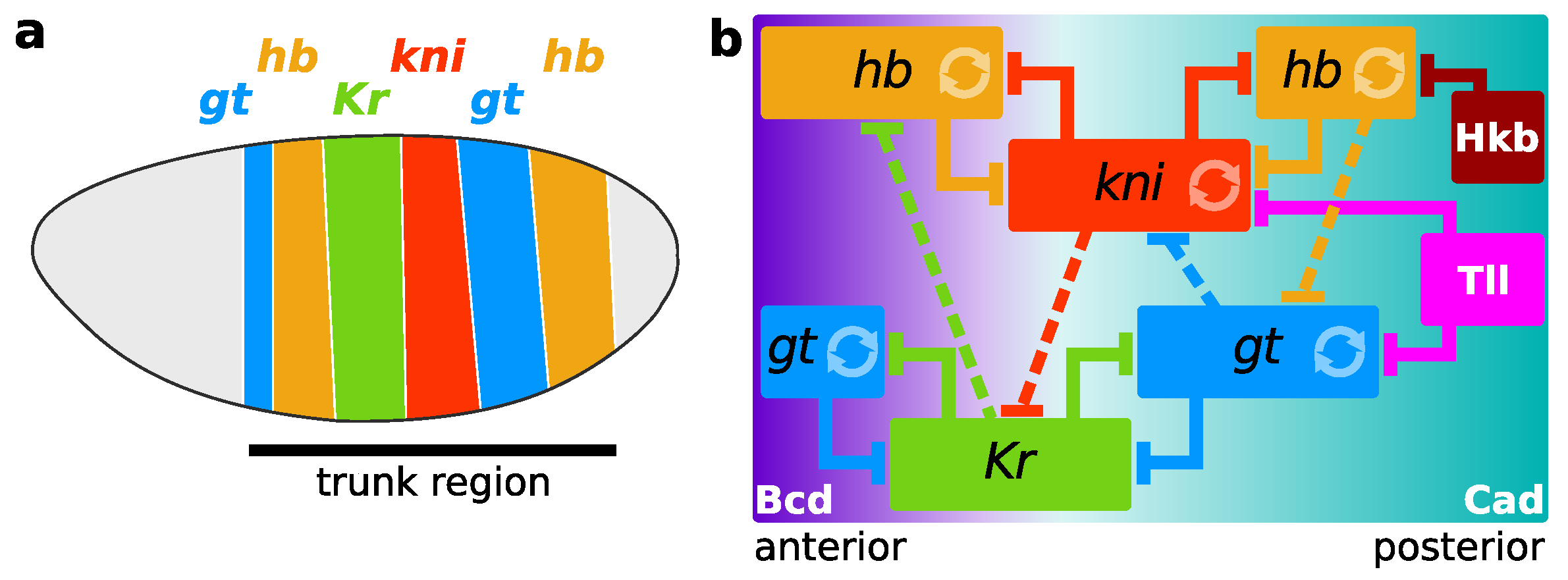
2.3. Gene Circuits, Simulation, and Analysis
3. Results
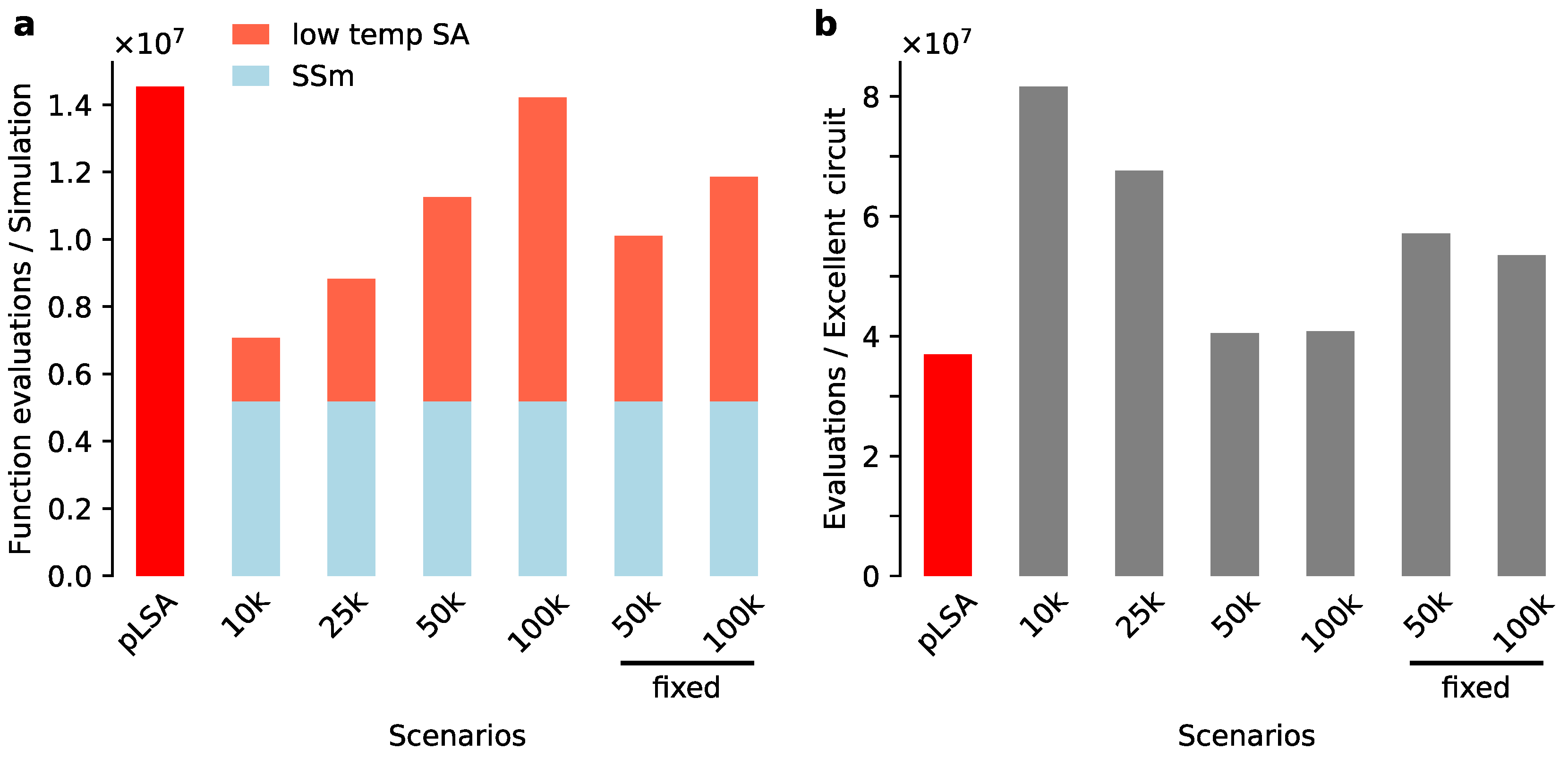
3.1. Scatter Search Efficiently Explores Parameter Space
3.2. Exploiting the Exploration Done by Scatter Search
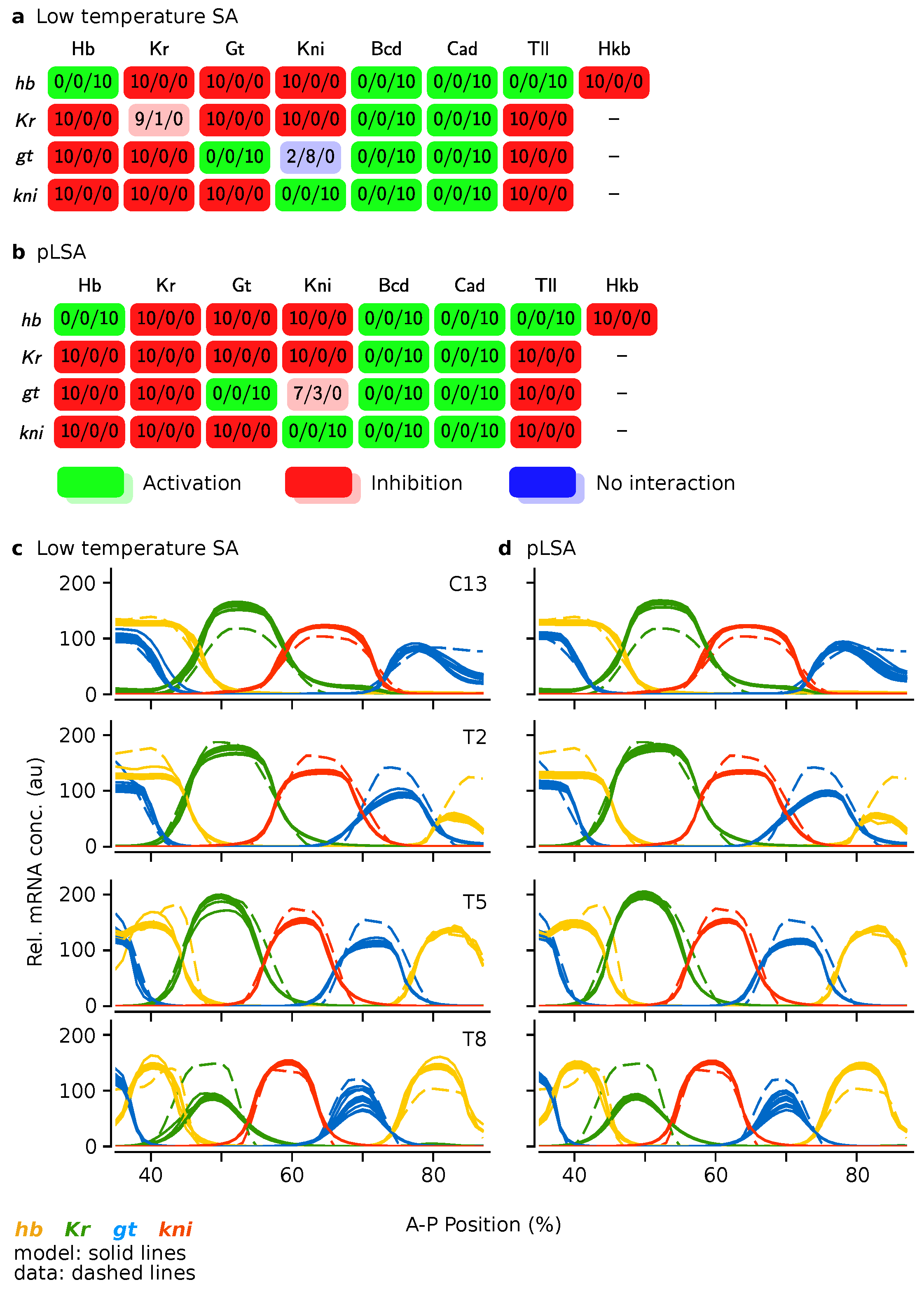
3.3. Low Temperature Simulated Annealing Refines Good Solutions into Excellent Ones
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Villaverde, A.F.; Banga, J.R. Reverse engineering and identification in systems biology: Strategies, perspectives and challenges. J. R. Soc. Interface 2013, 11, 20130505. [Google Scholar] [CrossRef] [PubMed]
- Heavner, B.D.; Smallbone, K.; Price, N.D.; Walker, L.P. Version 6 of the consensus yeast metabolic network refines biochemical coverage and improves model performance. Database 2013, 2013, bat059. [Google Scholar] [CrossRef] [PubMed]
- Borodina, I.; Nielsen, J. Advances in metabolic engineering of yeast Saccharomyces cerevisiae for production of chemicals. Biotechnol. J. 2014, 9, 609–620. [Google Scholar] [CrossRef] [PubMed]
- Costa, R.S.; Hartmann, A.; Vinga, S. Kinetic modeling of cell metabolism for microbial production. J. Biotechnol. 2016, 219, 126–141. [Google Scholar] [CrossRef] [PubMed]
- Selvarasu, S.; Ho, Y.S.; Chong, W.P.K.; Wong, N.S.C.; Yusufi, F.N.K.; Lee, Y.Y.; Yap, M.G.S.; Lee, D.Y. Combined in silico modeling and metabolomics analysis to characterize fed-batch CHO cell culture. Biotechnol. Bioeng. 2012, 109, 1415–1429. [Google Scholar] [CrossRef] [PubMed]
- Saraiva, I.; Vande Wouwer, A.; Hantson, A.L. Parameter identification of a dynamic model of CHO cell cultures: An experimental case study. Bioprocess Biosyst. Eng. 2015, 38, 2231–2248. [Google Scholar] [CrossRef] [PubMed]
- López-Meza, J.; Araíz-Hernández, D.; Carrillo-Cocom, L.M.; López-Pacheco, F.; Rocha-Pizaña, M.D.R.; Alvarez, M.M. Using simple models to describe the kinetics of growth, glucose consumption, and monoclonal antibody formation in naive and infliximab producer CHO cells. Cytotechnology 2016, 68, 1287–1300. [Google Scholar] [CrossRef] [PubMed]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI—A COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [PubMed]
- Hucka, M.; Finney, A.; Sauro, H.M.; Bolouri, H.; Doyle, J.C.; Kitano, H.; Arkin, A.P.; Bornstein, B.J.; Bray, D.; Cornish-Bowden, A.; et al. The systems biology markup language (SBML): A medium for representation and exchange of biochemical network models. Bioinformatics 2003, 19, 524–531. [Google Scholar] [CrossRef] [PubMed]
- Miller, A.K.; Marsh, J.; Reeve, A.; Garny, A.; Britten, R.; Halstead, M.; Cooper, J.; Nickerson, D.P.; Nielsen, P.F. An overview of the CellML API and its implementation. BMC Bioinform. 2010, 11, 178. [Google Scholar] [CrossRef] [PubMed]
- Karr, J.R.; Williams, A.H.; Zucker, J.D.; Raue, A.; Steiert, B.; Timmer, J.; Kreutz, C.; DREAM8 Parameter Estimation Challenge Consortium; Wilkinson, S.; Allgood, B.A.; et al. Summary of the DREAM8 parameter estimation challenge: Toward parameter identification for whole-cell models. PLoS Comput. Biol. 2015, 11, e1004096. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, J.; Surkova, S.; Blagov, M.; Janssens, H.; Kosman, D.; Kozlov, K.N.; Myasnikova, E.; Vanario-Alonso, C.E.; Samsonova, M.; Sharp, D.H.; et al. Dynamic control of positional information in the early Drosophila embryo. Nature 2004, 430, 368–371. [Google Scholar] [CrossRef] [PubMed]
- Ashyraliyev, M.; Siggens, K.; Janssens, H.; Blom, J.; Akam, M.; Jaeger, J. Gene circuit analysis of the terminal gap gene huckebein. PLoS Comput. Biol. 2009, 5, e1000548. [Google Scholar] [CrossRef] [PubMed]
- Crombach, A.; Wotton, K.R.; Cicin-Sain, D.; Ashyraliyev, M.; Jaeger, J. Efficient reverse-engineering of a developmental gene regulatory network. PLoS Comput. Biol. 2012, 8, e1002589. [Google Scholar] [CrossRef] [PubMed]
- Crombach, A.; Garcia-Solache, M.A.; Jaeger, J. Evolution of early development in dipterans: Reverse-engineering the gap gene network in the moth midge Clogmia albipunctata (Psychodidae). Biosystems 2014, 123, 74–85. [Google Scholar] [CrossRef] [PubMed]
- Crombach, A.; Wotton, K.R.; Jimenez-Guri, E.; Jaeger, J. Gap gene regulatory dynamics evolve along a genotype network. Mol. Biol. Evol. 2016, 33, 1293–1307. [Google Scholar] [CrossRef] [PubMed]
- Leclère, L.; Rentzsch, F. RGM regulates BMP-mediated secondary axis formation in the sea anemone Nematostella vectensis. Cell Rep. 2014, 9, 1921–1930. [Google Scholar] [CrossRef] [PubMed]
- Sheth, R.; Marcon, L.; Bastida, M.F.; Junco, M.; Quintana, L.; Dahn, R.; Kmita, M.; Sharpe, J.; Ros, M.A. Hox genes regulate digit patterning by controlling the wavelength of a Turing-type mechanism. Science 2012, 338, 1476–1480. [Google Scholar] [CrossRef] [PubMed]
- Raspopovic, J.; Marcon, L.; Russo, L.; Sharpe, J. Modeling digits. Digit patterning is controlled by a Bmp- Sox9-Wnt Turing network modulated by morphogen gradients. Science 2014, 345, 566–570. [Google Scholar] [CrossRef] [PubMed]
- Hoyos, E.; Kim, K.; Milloz, J.; Barkoulas, M.; Pénigault, J.B.; Munro, E.; Félix, M.A. Quantitative variation in autocrine signaling and pathway crosstalk in the Caenorhabditis vulval network. Curr. Biol. 2011, 21, 527–538. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Fernandez, M.; Egea, J.A.; Banga, J.R. Novel metaheuristic for parameter estimation in nonlinear dynamic biological systems. BMC Bioinform. 2006, 7, 483. [Google Scholar] [CrossRef] [PubMed]
- Egea, J.A.; Rodríguez-Fernández, M.; Banga, J.R.; Martí, R. Scatter search for chemical and bio-process optimization. J. Glob. Optim. 2007, 37, 481–503. [Google Scholar] [CrossRef]
- Neumaier, A.; Shcherbina, O.; Huyer, W.; Vinkó, T. A comparison of complete global optimization solvers. Math. Program. 2005, 103, 335–356. [Google Scholar] [CrossRef]
- Reinitz, J.; Sharp, D.H. Mechanism of eve stripe formation. Mech. Dev. 1995, 49, 133–158. [Google Scholar] [CrossRef]
- Fomekong-Nanfack, Y.; Kaandorp, J.A.; Blom, J. Efficient parameter estimation for spatio-temporal models of pattern formation: Case study of Drosophila melanogaster. Bioinformatics 2007, 23, 3356–3363. [Google Scholar] [CrossRef] [PubMed]
- Jostins, L.; Jaeger, J. Reverse engineering a gene network using an asynchronous parallel evolution strategy. BMC Syst. Biol. 2010, 4, 17. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, K.; Samsonov, A. DEEP-differential evolution entirely parallel method for gene regulatory networks. J. Supercomput. 2011, 57, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, J. The gap gene network. Cell. Mol. Life Sci. 2011, 68, 243–274. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, L.; Thieffry, D. A logical analysis of the Drosophila gap-gene system. J. Theor. Biol. 2001, 211, 115–141. [Google Scholar] [CrossRef] [PubMed]
- Perkins, T.J.; Jaeger, J.; Reinitz, J.; Glass, L. Reverse engineering the gap gene network of Drosophila melanogaster. PLoS Comput. Biol. 2006, 2, e51. [Google Scholar] [CrossRef] [PubMed]
- Perkins, T.J. The gap gene system of Drosophila melanogaster: Model-fitting and validation. Ann. N. Y. Acad. Sci. 2007, 1115, 116–131. [Google Scholar] [CrossRef] [PubMed]
- Wunderlich, Z.; DePace, A.H. Modeling transcriptional networks in Drosophila development at multiple scales. Curr. Opin. Genet. Dev. 2011, 21, 711–718. [Google Scholar] [CrossRef] [PubMed]
- Wunderlich, Z.; Bragdon, M.D.; Eckenrode, K.B.; Lydiard-Martin, T.; Pearl-Waserman, S.; DePace, A.H. Dissecting sources of quantitative gene expression pattern divergence between Drosophila species. Mol. Syst. Biol. 2012, 8, 604. [Google Scholar] [CrossRef] [PubMed]
- Becker, K.; Balsa-Canto, E.; Cicin-Sain, D.; Hoermann, A.; Janssens, H.; Banga, J.R.; Jaeger, J. Reverse-engineering post-transcriptional regulation of gap genes in Drosophila melanogaster. PLoS Comput. Biol. 2013, 9, e1003281. [Google Scholar] [CrossRef] [PubMed]
- Chertkova, A.A.; Schiffman, J.S.; Nuzhdin, S.V.; Kozlov, K.N.; Samsonova, M.G.; Gursky, V.V. In silico evolution of the Drosophila gap gene regulatory sequence under elevated mutational pressure. BMC Evol. Biol. 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Mjolsness, E.; Sharp, D.H.; Reinitz, J. A connectionist model of development. J. Theor. Biol. 1991, 152, 429–453. [Google Scholar] [CrossRef]
- Reinitz, J.; Mjolsness, E.; Sharp, D.H. Model for cooperative control of positional information in Drosophila by bicoid and maternal hunchback. J. Exp. Zool. 1995, 271, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, J.; Blagov, M.; Kosman, D.; Kozlov, K.N.; Myasnikova, E.; Surkova, S.; Vanario-Alonso, C.E.; Samsonova, M.; Sharp, D.H.; Reinitz, J. Dynamical analysis of regulatory interactions in the gap gene system of Drosophila melanogaster. Genetics 2004, 167, 1721–1737. [Google Scholar] [CrossRef] [PubMed]
- Genikhovich, G.; Fried, P.; Prünster, M.M.; Schinko, J.B.; Gilles, A.F.; Fredman, D.; Meier, K.; Iber, D.; Technau, U. Axis patterning by BMPs: Cnidarian network reveals evolutionary constraints. Cell Rep. 2015, 10, 1646–1654. [Google Scholar] [CrossRef] [PubMed]
- Botman, D.; Jansson, F.; Röttinger, E.; Martindale, M.Q.; de Jong, J. Analysis of a spatial gene expression database for sea anemone Nematostella vectensis during early development. BMC Syst. Biol. 2016, 9, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Glover, F. A template for scatter search and path relinking. In Artificial Evolution; Springer: Berlin/Heidelberg, Germany, 1997; pp. 1–51. [Google Scholar]
- Mendes, P.; Kell, D. Non-linear optimization of biochemical pathways: applications to metabolic engineering and parameter estimation. Bioinformatics 1998, 14, 869–883. [Google Scholar] [CrossRef] [PubMed]
- Aarts, E.H.; Lenstra, J.K. Local Search in Combinatorial Optimization; Wiley: Hoboken, NJ, USA; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Chu, K.W.; Deng, Y.; Reinitz, J. Parallel simulated annealing by mixing of states. J. Comput. Phys. 1999, 148, 646–662. [Google Scholar] [CrossRef]
- Lam, J.; Delosme, J. An Efficient Simulated Annealing Schedule: Derivation; Technical Report 8816; Electrical Engineering Department, Yale: New Haven, CT, USA, 1988. [Google Scholar]
- Lam, J.; Delosme, J. An Efficient Simulated Annealing Schedule: Implementation and Evaluation; Technical Report 8817; Electrical Engineering Department, Yale: New Haven, CT, USA, 1988. [Google Scholar]
- Surkova, S.; Spirov, A.V.; Gursky, V.V.; Janssens, H.; Kim, A.R.; Radulescu, O.; Vanario-Alonso, C.E.; Sharp, D.H.; Samsonova, M.; Reinitz, J. Canalization of gene expression in the Drosophila blastoderm by gap gene cross regulation. PLoS Biol. 2009, 7, e1000049. [Google Scholar]
- Gursky, V.V.; Panok, L.; Myasnikova, E.M.; Manu, M.; Samsonova, M.G.; Reinitz, J.; Samsonov, A.M. Mechanisms of gap gene expression canalization in the Drosophila blastoderm. BMC Syst. Biol. 2011, 5, 118. [Google Scholar] [CrossRef]
- Penas, D.R.; González, P.; Egea, J.A.; Doallo, R.; Banga, J.R. Parameter estimation in large-scale systems biology models: A parallel and self-adaptive cooperative strategy. BMC Bioinform. 2017, 18, 52. [Google Scholar] [CrossRef] [PubMed]
- Lou, Z.; Reinitz, J. Parallel simulated annealing using an adaptive resampling interval. Parallel. Comput. 2016, 53, 23–31. [Google Scholar] [CrossRef] [PubMed]




| Name | Value | Description |
|---|---|---|
| iterations | 10,000 | Maximum number of iterations |
| reference set size | 22 | Number of individuals in set |
| scatter set size | 1000 | Number of individuals in set |
| local search frequency | 25 | Do search every n iterations |
| local search score | Cost must be lower than x | |
| regenerate reference set | 50 | Refresh set every n iterations |
| stop criterion | Maximum number of iterations is reached |
| Name | Value | Description |
|---|---|---|
| initial moves | 96,000 | Initial moves to establish unbiased Boltzmann distribution |
| processing nodes | 64 | Number of CPU cores used |
| moves per iteration | 41 | One move per gene circuit parameter |
| mixing interval | 25 | Synchronization every n iterations |
| start temperature | High starting temperature | |
| stop criterion | 0.0001 | Cost change in last 5 moves less than value |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdol, A.M.; Cicin-Sain, D.; Kaandorp, J.A.; Crombach, A. Scatter Search Applied to the Inference of a Development Gene Network. Computation 2017, 5, 22. https://doi.org/10.3390/computation5020022
Abdol AM, Cicin-Sain D, Kaandorp JA, Crombach A. Scatter Search Applied to the Inference of a Development Gene Network. Computation. 2017; 5(2):22. https://doi.org/10.3390/computation5020022
Chicago/Turabian StyleAbdol, Amir Masoud, Damjan Cicin-Sain, Jaap A. Kaandorp, and Anton Crombach. 2017. "Scatter Search Applied to the Inference of a Development Gene Network" Computation 5, no. 2: 22. https://doi.org/10.3390/computation5020022
APA StyleAbdol, A. M., Cicin-Sain, D., Kaandorp, J. A., & Crombach, A. (2017). Scatter Search Applied to the Inference of a Development Gene Network. Computation, 5(2), 22. https://doi.org/10.3390/computation5020022






