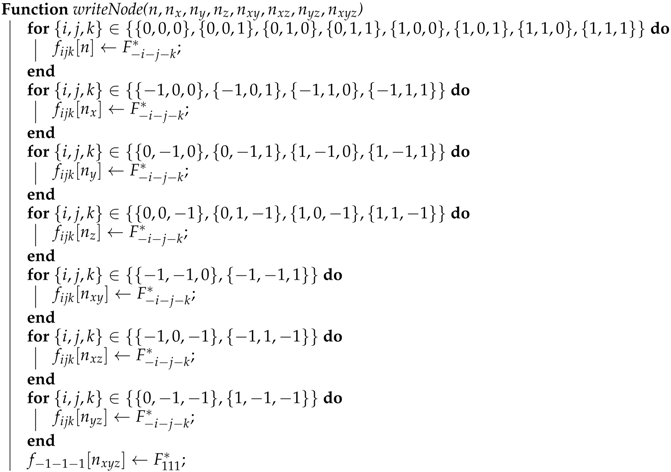Esoteric Twist: An Efficient in-Place Streaming Algorithmus for the Lattice Boltzmann Method on Massively Parallel Hardware

Abstract

We present and analyze the Esoteric Twist algorithm for the Lattice Boltzmann Method. Esoteric Twist is a thread safe in-place streaming method that combines streaming and collision and requires only a single data set. Compared to other in-place streaming techniques, Esoteric Twist minimizes the memory footprint and the memory traffic when indirect addressing is used. Esoteric Twist is particularly suitable for the implementation of the Lattice Boltzmann Method on Graphic Processing Units.

1. Introduction

The lattice Boltzmann method (LBM) is a simple algorithm used in computational fluid dynamics for solving the Navier–Stokes equations. The efficient implementation of the lattice Boltzmann method has received considerable attention from the computer scientist community [1,2,3]. The LBM has several properties that make it interesting from a performance oriented algorithmic point of view. The ratio of floating point operations to memory access is relatively low so that the performance of the method is usually bandwidth limited. The LBM uses more variables than mathematically necessary for solving the Navier–Stokes equation, which adds to the relatively large data traffic. Still, the LBM is often considered to be efficient if implemented correctly. The algorithm is perfectly suitable for massively parallel implementation [4]. The time integration is second order accurate even though it depends only on the previous time step [5]. A particular feature of the LBM in distinction to finite difference schemes is that the number of input variables of the local (i.e., node-wise) time integration scheme equals the number of output variables. This is important as it implies that each input datum is required only once. In a finite difference scheme, functional values usually have to be gathered in a finite neighborhood of a grid node and the same datum is required to update several grid nodes. Most algorithmic and hardware optimizations of recent years focused on the reuse of data. Spatial blocking and scan-line algorithms are prominent examples developed for accelerating finite differences methods [6]. Caching is a generic hardware optimization meant to improve performance for repeatedly used data. It is interesting to note that the LBM does not benefit from such optimizations because it does not reuse data in a single time step. The LBM benefits from hardware cache only indirectly or when the cache is so large that it can hold the state variables until they are reused in the next time step. This zero-data-redundancy is not necessarily a disadvantage of the LBM. For example, it has been argued by Asinari et al. [7] that the LBM was inefficient due to the utilization of the distribution functions which increase the memory requirements and should intuitively increase traffic between the CPU and the main memory. Asinari et al. [8] proposed replacing the distribution functions with macroscopic variables, which reduced the memory footprint but counter-intuitively increased the memory traffic since data had to be read repeatedly for the computation of finite differences [7]. In addition, the savings in memory turned out to be smaller than naively assumed: the LBM can overwrite each input datum with the output datum while the finite difference method requires a source and a destination array to avoid the overwriting of data that is still required for neighboring grid nodes. In addition to these purely algorithmic differences, there are differences in accuracy between finite difference and LBM implementations. Depending on the details of the model and the validation example, either the finite difference method [9] or the LBM [10] excels over the other. In the current paper, we will not discuss the numerical modeling underlying the LBM. Instead, we focus entirely on its efficient implementation. By doing so, we exploit the features of the method and arrive at a result that is very different from what one should do to implement a finite difference method efficiently.

2. Lattice Boltzmann Method

In this section, we describe the LBM from a purely algorithmic point of view without considering the details of the modeling. We direct the reader to various text books for an introduction to the method [11,12,13,14].

The LBM is a computational method to solve the lattice Boltzmann equation which can be written in three dimensions as:

$$f_{ijk(x+i)(y+j)(z+k)(t+1)}=f_{ijkxyzt}+{\mathrm{\Omega }}_{ijkxyzt}.$$

(1)

Here, the indexes i, j and k are integer values indicating the direction in which the distribution $f_{ijkxyzt}$ moves on a Cartesian lattice with the nodes being located at positions x, y and z. The time step is indicated by t. The so-called collision operator ${\mathrm{\Omega }}_{ijkxyzt}$ is a function of all local distributions $f_{ijkxyzt}$ but neither depends on the state of any other lattice node nor on the state of the same node at any time other than t. It is hence seen that communication between lattice nodes happen only on the left-hand side of (1), the so-called streaming. The right-hand side, the so-called collision, is entirely local. It is also seen that the lattice Boltzmann equation is a local mapping from $Q\to Q$ variables. Each datum is used only once.

The LBM can be implemented for different velocity sets where the indexes i, j and k take different values. Without loss of generality, we restrict us here to the technically most relevant case with 27 velocities and i, j, $k\in \{-1,0,1\}$.

3. Implementation of the Lattice Boltzmann Method

The LBM has a superficial algorithmic similarity to a finite difference time domain technique and it is admissible to implement it in a likewise fashion. A naive approach would utilize two data arrays $f_{ijkxyzt}$ and $f_{ijkxyzt}^{*}$ and rewrite (1) as:

$$f_{ijk(x+i)(y+j)(z+k)t}^{*}=f_{ijkxyzt}+{\mathrm{\Omega }}_{ijkxyzt}.$$

(2)

After completing one time step, the post-collision distributions might be redefined as the new pre-collision distributions:

$$f_{ijkxyz(t+1)}=f_{ijkxyzt}^{*}.$$

(3)

This updated algorithm is denoted as AB-pattern [15,16]. In a finite difference time domain method, such an update was necessary in order to avoid the overwriting of data at the neighboring node. In the LBM, this is not necessary because the collision maps a set of inputs to the same number of outputs. It is hence admissible to overwrite the input directly by the output and a secondary array is never required. A naive implementation of this concept would require moving the distributions in a separate step:

$$\begin{array}{ccc}\hfill f_{ijkxyzt}^{*}& =& f_{ijkxyzt}+{\mathrm{\Omega }}_{ijkxyzt},\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill f_{ijk(x+i)(y+j)(z+k)(t+1)}& =& f_{ijkxyzt}^{*}.\hfill \end{array}$$

(5)

It is desired to implement the LBM in such a way that only one array is required while both streaming and collision are combined in a single step, i.e., we are looking for an algorithm that requires only a single array to hold the distributions and reads and writes each datum only once in each time step. Such a technique is called in-place streaming and several methods have been proposed in literature. An early example of an in-place streaming algorithm is the swap algorithm of Mattila et al. [17] and Latt [18]. The swap algorithm combines the streaming and the collision in a single step, but it does not overwrite the input of the local collision by the output. As a result, the swap algorithm requires a certain order in which the lattice nodes have to be processed. This is a severe disadvantage, as it limits the application of the algorithm to serial computations with a clear order of the instructions. The method is not applicable to massively parallel computations.

An alternative approach to in-place streaming is the compressed grid that approximately saves half the memory [19]. The idea behind the compressed grid is to extend a rectangular simulation domain by one line of nodes in all directions and keep a certain order in the processing of the grid nodes, which, after the update of the first line of nodes, are written to spare line of nodes. Once the nodes in the first line are processed, they are no longer required and the second line of nodes can be written to the first line of nodes and so on until all lines have been processed. The compressed grid method works only for a rectangular domain and requires a fixed order of updating the nodes.

Bailey [16] studied the implementation of the LBM on Graphics Cards where lattice nodes are updated in random order by thousands of threads in parallel. He proposed an algorithm called AA-pattern that overwrites the input with the output by distinguishing between odd and even time steps (see Figure 1). In the odd time step, the distributions are not streamed and the local distribution are directly overwritten. In the even time step, the distributions are fetched from the neighboring nodes and written back to the neighboring nodes in an opposite direction after collision. In such a way, the distributions move two lattice spacings every second time step. The AA-pattern requires the code to be implemented twice, once for the even and once for the odd time steps.

The AA-pattern solves the concurrency problem of the swap algorithm, but it was designed to run on a full matrix implementation. Real world applications of computational fluid dynamics usually require a higher geometrical flexibility and local grid-refinement. For this purpose, it is usually desired to implement the LBM as a sparse matrix method. The AA-pattern permits an implementation on sparse matrices, but it requires pointers to all neighboring nodes, which implies a relatively large memory footprint. In the reminder of this paper, we present and discuss the properties of the Esoteric Twist data structure that solves the concurrency problem similar to the AA-pattern but leads to substantial savings in memory when indirect addressing is used.

4. Esoteric Twist

The Esoteric Twist, or short EsoTwist, algorithm combines the following desired features:

• Streaming and collision are combined in one step.
• Each datum is read once and written once in each time step.
• The method is thread safe; all nodes can be processed in arbitrary order or entirely in parallel.
• The method is well suitable for indirect addressing, i.e., has a small memory footprint.

The swap algorithm fulfills all but the last two features, and the AA-pattern fulfills all but the last feature. The AA-pattern has to access all neighboring nodes in every second time step, which implies that it first has to read the pointer to all neighbors from an index array if indirect addressing is used. We show below that the EsoTwist method is more economical in terms of memory footprint and memory reads for indirect addressing. In this section, we first introduce the EsoTwist method for the general case.

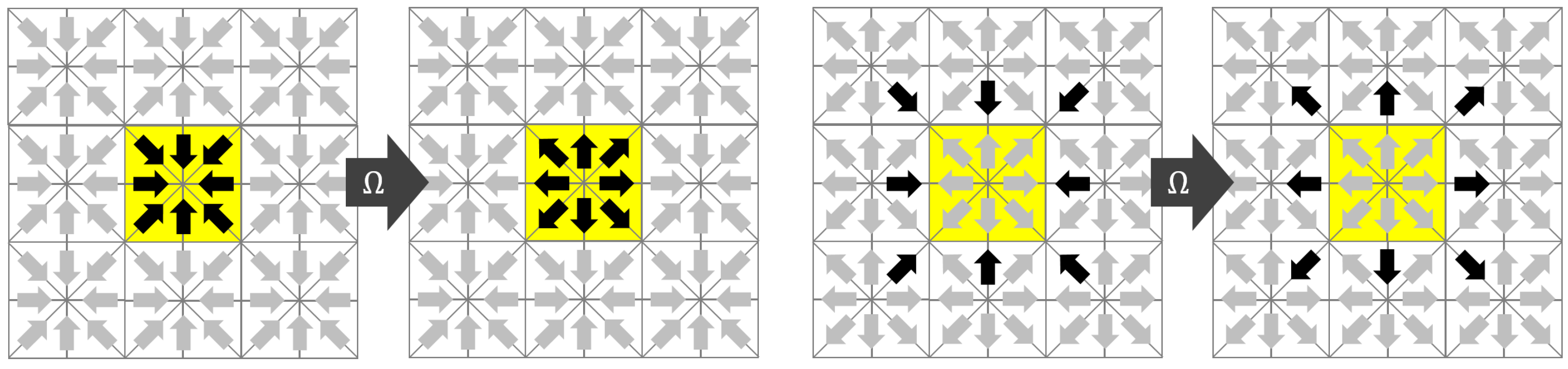
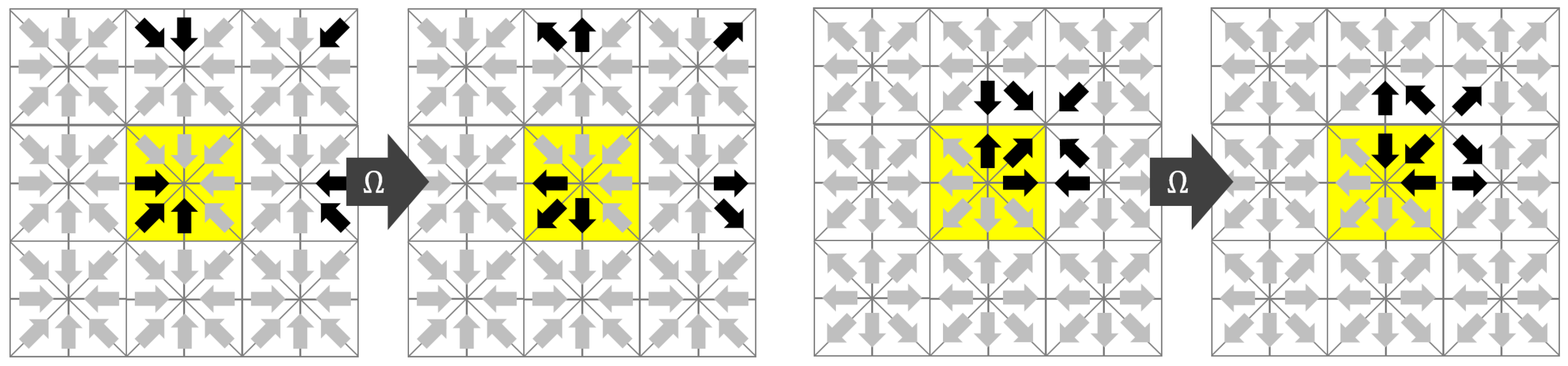
The name Esoteric Twist originates from the unintuitive (esoteric) observation that the streaming step can be eliminated if the distributions are written back in opposite (twisted) order compared to the reading before collision. As in the case of the AA-pattern, the key to a thread safe in-place streaming is that the collision operator writes only to the memory from which it draws its inputs. We assume that modern computers have access to a slow but vast memory that holds all the distributions of all nodes and a fast but small memory in which all operations associated with a collision at a single node can be executed. We will call the former the main memory and the latter the registers. We assume, as in the AA-pattern, that the distributions belonging to one node are transferred from the main memory to the registers before collision and written back to the main memory after collision. We assume that the transfer between main memory and registers is expensive and should be minimized. Since the distributions ought to move, they either need to be drawn from the neighboring nodes (pull-scheme) before collision or they have to be sent to the neighboring nodes after collision (push-scheme). In the EsoTwist approach, all distributions that move in negative direction with i, j, $k<0$ are pulled while all distributions moving in positive directions with i, j, $k>0$ are pushed. The procedure is depicted in Figure 2 for the two-dimensional case. The yellow node in Figure 2 is the one for which we consider one update step. The collision on the node depends on all Q incoming distributions and it returns Q outgoing distributions. Only the incoming distributions moving in positive x- and y-directions are read from the yellow node itself. The distributions moving in negative directions are read from the respective neighbors in the positive directions as depicted in the figure. After collision, the distributions are written back to the places where the distributions moving in the opposite direction were read from. As is the case in the AA-pattern, each distribution swaps places with the distribution moving in the opposite direction after collision. For the movement of the distribution to happen, the method has to distinguish between odd and even time steps, as depicted in Figure 2. This can be realized in different ways. Unlike in the case of the AA-pattern, EsoTwist does not necessarily require two implementations of the method for odd and even time steps. A much simpler realization of the method is obtained by storing the distributions in a structure of arrays, i.e., by grouping the distributions in arrays according to the direction in which they are moving. After one time step is completed, all pointers to the arrays are swapped with the pointers to the arrays moving in the opposite direction. Then, the next time step is executed as before. However, a structure of arrays is not necessarily desired. The EsoTwist method can also be implemented like the AA-pattern by explicitly distinguishing between odd and even time steps. Algorithm 1 shows the concept of the EsoTwist algorithm in one dimension. The complete algorithm in three dimensions is shown in the Appendix A.

It is of note here that an algorithm almost identical to EsoTwist was presented in [20]. However, the authors apparently missed the fact that they could simply combine collision and swapping the directions into a single step. Instead, they swapped the distributions in a separate step, which unnecessarily doubles the data traffic.

Algorithm 1: The basic EsoTwist Algorithm for a one-dimensional LBM with three speeds in a structure of arrays format. The asterisk marks the post-collision distribution. The capital F denotes a register to which the distribution is read from the distributions in main memory f for the collision. The distribution $f_1$ moving in a positive direction and the stationary distribution $f_0$ are read at the index n while the distribution $f_{-1}$ moving in a negative direction is read from the neighbor in a positive direction. After collision, the distribution moving in positive direction $F_1^{*}$ is written to the neighbor in a positive direction at the slot where the distribution going to the opposite direction was originally read. The distribution going in negative direction $F_{-1}^{*}$ is now written to location n. In that way, both the distribution going in a negative direction and the distribution going in a positive direction moved a distance of one node during the time step. After all nodes have been collided, it is sufficient to swap the pointers to the arrays $f_{-1}$ and $f_1$ to execute the streaming of all nodes.

4.1. Indirect Addressing

In almost all real-world applications of computational fluid dynamics, it would be unpractical to discretize the computational domain with a rectangular Cartesian grid. To discretize domains of arbitrary shape, sparse matrices are the most flexible choice. In a sparse matrix implementation, each node has to access its neighbors via a pointer, or equivalently via an index which has to be stored in an additional array. For example, if a three-dimensional LBM with 27 velocities is implemented on a sparse matrix using the AA-pattern, each node has to find the 26 neighbors of the node in the even time step. The AA-pattern is efficient in the sense that it has to find the neighbors only every other time step. Still, it has to store the pointer to these neighbors. A pointer usually occupies the same amount of memory as a scalar datum such that 26 pointers basically occupy almost as much memory as the distributions themselves. This memory can be substantially reduced by applying pointer chasing. For example, using the AA-pattern, it would be sufficient to store pointers in the six axial directions and access the diagonal neighbors by querying, for example, the neighbor in the positive x-direction for its neighbor in the negative y-direction. Applying this technique reduces the number of pointers per node from 26 to 6. This number can be reduced further to four if the nodes are aligned in one of the cardinal directions along the array. However, each of these optimizations reduce the flexibility of the method. The alignment of the grid along one of the cardinal axes in connection with indirect addressing usually means that the grid cannot be modified after its generation, which is an obstacle for adaptive simulations. That is to say, the feature that nodes on a sparse matrix gird can be inserted and deleted ad libitum is lost once the nodes are aligned along one dimension in order to eliminate the pointers in this direction. We will hence not consider the alignment of the data along one of the cardinal directions in our analysis for sparse matrix grids.

Using pointer chasing, the AA-pattern has to store links to six neighbors at each node ($6\times N$ data values for N nodes). The total memory requirement without further meta data for an LBM with 27 discrete speeds is $33\times N$ data values. Since the AA-pattern streams data only every other time step, it requires $(27+26/2)\times N=40\times N$ reads and $27\times N$ writes from and to the main memory in every time step with $27\times N$ reads in the odd and $53\times N$ reads in the even time steps. It is interesting to note that, while pointer chasing reduces the memory footprint, it does not reduce the number of reads. All 26 pointers to all neighbors have to be read every other time step.

In comparison to the AA-pattern, EsoTwist reduces both the memory footprint and the number of reads. This is due to EsoTwist being asymmetric in space. Only neighbors in positive directions in either dimension have to be accessed. In three dimensions, using 27 speeds, all distributions accessed by a node are stored at the indexes of the node and the seven neighbors in the upper octant of the surrounding cube. Thus, by applying pointer chasing, $3\times N$ links have to be stored and each time step requires $(27+7)\times N=34\times N$ reads and $27\times N$ writes. The total memory requirement is hence $30\times N$ (9% less then for the AA-pattern). The data reads are even 25% less than for the AA-pattern and the data writes are the same. In their analysis, Wittmann et al. [3] conclude that the AA-pattern and EsoTwist have the lowest data traffic for the known streaming algorithm, but their analysis ignores that EsoTwist requires fewer pointers and fewer reads than the AA-pattern.

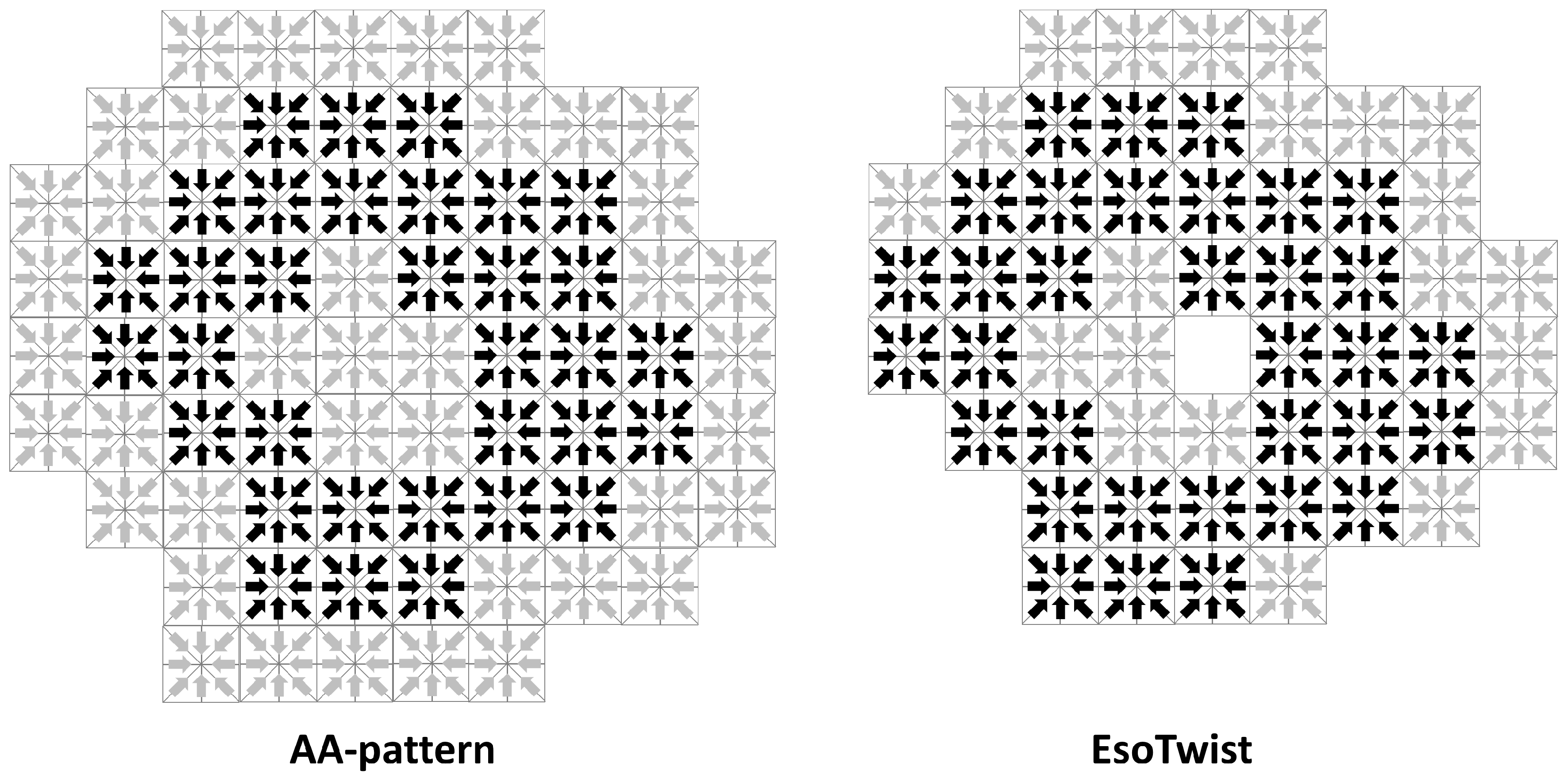
In addition to those direct savings in memory, there is also an indirect savings compared to the AA-pattern due to the fact that the fewer ghost nodes are required when indirect addressing is used (see Figure 3). Both EsoTwist and the AA-pattern store part of the distributions associated with each node at some neighboring nodes. The memory for these nodes has to be allocated even if the node itself is not part of the simulation domain. In the AA-pattern, all 26 neighbors of an existing node have to be allocated while, in EsoTwist, only the seven neighbors in the upper octant of the surrounding cube have to be allocated. Depending on the complexity of the geometry, this can result in considerable savings through a smaller number of ghost nodes.

It should be noted that the above analysis ignores the effect of caching for the number of reads and writes such that no general conclusion on performance can be drawn at this stage. Modern CPUs usually read complete cache lines at once and this enhances performance when data is aligned. However, since, in the current subsection, we consider sparse matrix grids, we have no general guarantee that our nodes are arranged in any favorable ordering and that we would benefit from caching. The above analysis is valid for the worst case scenario of completely unaligned data.

4.2. Variants

Even though pointers are an indispensable element of all software on the machine level, several popular programming languages (e.g., Fortran) do not support pointers explicitly. This is very unfortunate since a simple operation that is efficiently executed by the hardware in nano-seconds has to be mimicked by more complicated and certainly less efficient operations. Still, it is possible to implement EsoTwist without pointers. One possibility is to combine the arrays for distributions moving in opposite directions into one array of twice the length. Staying with our example of the D3Q27 velocity set, we would have one array of length N for the distributions $f_{000}$ and thirteen arrays of length $2N$ for the other distributions. For example, let $g_{1-10}[n]$ be the array for the distributions $f_{1-10}$ and $f_{-110}$. Now, let $odd=1$ and $even=0$ for odd time steps and $odd=0$ and $even=1$ for even time steps. It is possible to access the distributions without pointer exchange trough:

$$\begin{array}{ccc}\hfill f_{1-10}[n]& =& g_{1-10}[n+odd*N],\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill f_{-110}[n]& =& g_{1-10}[n+even*N].\hfill \end{array}$$

(7)

Thus, it is also possible to implement EsoTwist in a programming language that does not support pointers.

Another consideration concerns the structure of arrays data type. On massively parallel hardware like GPGPUs that apply single instruction multiple data operations, it is beneficial to store the data in different arrays according to the directions. However, this is not the optimal data layout for serial computing since all 27 distributions are stored in different locations of the main memory and none of them would share a single cache line. On those machines, storing all data belonging to a node together would be optimal. Geller [21] proposed a compromise that enhanced the performance of EsoTwist on serial computers. He suggested to use two containers, one for the local distributions and one for the distributions at neighboring nodes. In this way, half the data required for the collision could always be accessed together. Only the static distribution was stored separately.

EsoTwist has also been implemented successfully for block structured grids [22,23]. Block structuring can be used to increase locality of the data and is useful for load balancing parallel codes. Inside a block, no pointers to neighboring nodes are required. In connection with EsoTwist, each block needs only to access its seven neighboring blocks in the upper octant of the surrounding cube for data exchange. Hence, each block would require only three links to neighboring blocks if pointer chasing is used. Block structured grids might increase performance through high data locality, and they largely simplify the parallelization of the method, but they also have some disadvantages compared to the application of EsoTwist on sparse matrix grids. The data transfer at the interfaces between the blocks does not happen automatically and requires an explicit step of data exchange. Usually, also at least one additional layer of nodes is required to facilitate the exchange of data. In terms of memory occupation for a cubic block in three dimensions with $N\times N\times N$ nodes, ${(N+1)}^3-N^3$ ghost nodes are usually required. Using pointer chasing, only three links to neighboring blocks are required per block. In contrast, sparse matrices require three links per node and ghost cells only on the domain boundaries. Assuming that each datum (distributions and pointers) occupies the same size in memory, we can determine the breakeven point in memory consumption when block structured grids occupy less memory than a sparse matrix representation. For a method with 27 speeds, we have to equate the three pointers with the average amount of additional data required for the block structured grids:

$$3=\frac{27({(N+1)}^3-N^3)+3}{N^3}.$$

(8)

This solves to $N\approx 27.98$. We hence see that a block size of at least $28\times 28\times 28$ nodes is required to occupy less memory on a block structured grid compared to a sparse matrix. This analysis does not take into account that block structured grids usually contain nodes which do not belong to the domain. In principle, a block has to be allocated completely whenever at least one node in the block is located in the fluid domain. It is hence seen that memory economy is usually a poor motivation for the use of block structured grids, at least when combined with EsoTwist.

The EsoTwist data structure has also been implemented in a variant that secures memory alignment of all distributions [24]. This was historically important for the implementation of the lattice Boltzmann method on Nvidia GPUs of older generations [25] where data was always read in form of sixteen adjacent four byte values. The trick in this EsoStripe called variant is that the distributions of adjacent points are stored in a distance of sixteen, such that whenever sixteen nodes are processed simultaneously by the vector processor, the data access is completely aligned. While this leads to more than a 25% performance increase on GeForce GTX 465, no performance gain was observed on newer hardware when compared to non-aligned reads and writes [24]. In that case, data alignment was found to not be essential for newer hardware.

4.3. Implicit Bounce Back

EsoTwist has an interesting feature concerning lattice nodes which are excluded from the computation. If a lattice node is not touched, i.e., if no distributions are read and no distributions are written, the direction in which the populations on this node move is reversed through the pointer exchange. In the LBM, a reversal of the directions of the distributions is used to model solid walls in the so-called simple bounce back scheme. Using EsoTwist bounce back is implicitly applied to all nodes skipped during the update, and these nodes will thus behave like solid walls. Applying simple bounce back in EsoTwist is entirely for free since the respective nodes do not even need to be touched. This way of imposing bounce back by omission of the node is called implicit bounce back. This property is shared by other swap methods like the one proposed by Mattila et al. [17] and Latt [18] and by the AA-pattern [16].

5. Results

The EsoTwist data structure has been successfully implemented both on parallel CPU systems [22,23] and on GPUs [26,27,28]. Here, we focus on the implementation for GPUs in connection with indirect addressing.

5.1. Performance Model

Our performance model is based on the observation that the LBM is typically a memory bandwidth limited algorithm [3,29,30,31,32]. The EsoTwist method for a 27 speed lattice requires 27 distributions that have to be read and written in every time step. Even though only three pointers to neighbors are stored with every node, we still need to read seven such pointers per node and time step through pointer chasing. One additional number is used to indicate the type of the node. Since this indicator is also used as a pointer to an array of boundary conditions (each node can have its individual boundary condition), this number must also have at least four bytes. In total, our method requires 27 + 7 + 1 = 35 reads and 27 writes per node and time step which sums to $\#Bytes$ = 62 × 4 Bytes = 248 Bytes. The performance of our code is measured in Million Node Updates Per Second (MNUPS). The bandwidth occupancy P is calculated by:

$$P=\frac{\#MNUPS\times \#Bytes}{bandwidth}\times 100\%.$$

(9)

When comparing results of EsoTwist to results from a full matrix code, we have to take into account that the full matrix code does not require any pointers such that it has only 28 reads and 27 writes in every time step per node.

5.2. Comparison to Full Matrix Implementation

Here, we compare the performance of EsoTwist on sparse matrices with a full matrix implementation. In order to make the setup comparable, we chose a cubic domain with $128\times 128\times 128$ nodes. In the first example, we simulate duct flow with implicit bounce back boundary condition and use the Bhatnagar Gross Krook collision model [33]. This example is run on an old Nvidia Tesla C1060 GPU with a bandwidth of 102 GBytes/s. The full matrix implementation obtains 205 MNUPS (41.2% bandwidth) and the sparse matrix implementation obtains 191 MNUPS (43.2% bandwidth).

In our second example, we compare the performance of a simulation with the same grid size but with a cascaded collision kernel [34] on a GeForce GTX Titan X (Maxwell GM200), which is a much more recent GPU than the Tesla C1060. The theoretical peak bandwidth of the GeForce GTX Titan X is $336.6$ GBytes/s. The full matrix version of the code uses the AB-pattern [15,16]. Despite the fact that the cascaded kernel is computationally more intensive, we obtain much better performance figures on this newer hardware. The full matrix version runs with 999.425 MNUPS (60.8% bandwidth), and the sparse matrix version runs with 993.514 MNUPS (68.2% bandwidth).

It is observed in both cases that, while the performance on the full matrix is higher in terms of lattice updates, the sparse matrix version makes better use of the bandwidth. The differences in execution speed are marginal. The sparse matrix version obtains 93.2% of the execution speed of the full matrix version on the outdated Tesla C1060 and 99.4% on the more recent GeForce GTX Titan X. This result is a further confirmation of the observation by Linxweiler [24] that progress in hardware reduces the advantage of highly optimized full matrix codes over more flexible codes.

5.3. Isotropy

We probe the isotropy of the EsoTwist method by comparing the execution speed of a simulation of the same geometry under three different orientations. This is done because the nodes on this grid are filled along one of the cardinal directions first, depending on whether the orientation of the geometry neighboring nodes are either close together or far apart. The problem hence probes how the method reacts to different levels of data locality. The geometry is shown in Figure 4. It is composed of three rectangular pipes with different cross sections. Each pipe is 128 grid nodes long. The cross-sections of the pipes are $5\times 5$, $10\times 10$ and $20\times 20$ grid nodes, respectively. Simulations are executed on a Nvidia GeForce GTX Titan GPU running with device driver version 331.82 and the CUDA (Compute Unified Device Architecture) toolkit version 6.0. The theoretical bandwidth of this GPU is $288.4$ GBytes/s [35]. The computational model used was the BGK collision kernel in single precision. We observe similar performance regardless of the orientation of the domain in space. For the larger pipe oriented along the x-axis, we obtain 738.5 MNUPS (59.1% peak bandwidth); for the larger pipe oriented along the y-axis, we obtain 729.8 MNUPS (58.4% peak bandwidth) and, for the z direction, we obtain 727.3 MNUPS (58.2% peak bandwidth). Our performance figures compare to between 407 and 684 MNUPS reported for the GeForce GTX Titan by Tomczak and Szafran [36] using a lattice Boltzmann method with nineteen speeds (D3Q19 lattice) in double precision in a tiling layout (similar to block structuring) and two data sets (AB-pattern), which corresponds to between 48% and 72.6% bandwidth (the numbers are taken directly from [36] as our performance model does not apply directly to their code). The relatively wide range in the performance of [36] is due to differences in the data locality in the different test cases.

5.4. Porous Material

Our implementation of the LBM using EsoTwist with indirect addressing on GPUs participated in a comparative study between different Computational Fluid Dynamics (CFD) methods. Simulation results were presented in [27]. Our method was found to be the most efficient when compared to the competing methods to solve the Navier–Stokes equations in porous media. Here, we present only performance values.

We discretize a random packing of 6864 mono-disperse spheres (beads) with radius $0.5$ mm as depicted in Figure 5. The bead pack is discretized with Cartesian grids using two different resolutions: 40 $\mathsf{\mu }$m (Figure 6) and 20 $\mathsf{\mu }$m (Figure 7). The full matrix representation of the grids would contain $1.74\times {10}^7$ and $1.39\times {10}^8$ grid nodes for the 40 $\mathsf{\mu }$m and the 20 $\mathsf{\mu }$m case, respectively. By the use of indirect addressing, the number of nodes is reduced to $9.05\times {10}^6$ (52%) and $6.465\times {10}^7$ (46.5%), respectively. We hence see that indirect addressing eliminates about half of the grid nodes in this case. It is interesting to note that, in the case of the AA-pattern without pointer chasing, there would hardly be any advantage of the sparse data structure over the full matrix in this case since the number of pointers required for indirect addressing is almost as large as the memory required to store the distributions. In the case of EsoTwist combined with pointer chasing, only three pointers have to be stored with each grid node. The 20 $\mathsf{\mu }$m case was simulated for 72 s in real time, which translates to 1,600,000 time steps. Other than in the previous simulation, the current test case applied second order accurate boundary conditions to capture the curvature of the beads and the simulation domain was decomposed and distributed over several GPUs. On two Nvidia K40c GPUs, we obtained a performance of 525.2 MNUPS and on six Tesla C1060 we obtained 448.6 MNUPS. The 40 $\mathsf{\mu }$m test case was simulated on a single K40c GPU and run for 400.000 time steps. It obtained a performance of 233.3 MNUPS. However, these performance figures do not include the fact that the simulation of a porous medium is boundary dominated and that the application of the second order accurate interpolation boundary condition [26] is done in a separate step. In addition, it must be taken into account that the complex cumulant collision kernel [26] was used. The application of the second order boundary conditions produce about the same data traffic as one collision. In the case of the 40 $\mathsf{\mu }$m simulation, we had about $4.26\times {10}^6$ boundary nodes such that the bandwidth occupancy including the application of the boundary conditions is calculated as 27.5%. These performance figures hence show that, even though the optimal performance is never obtained in real-world applications with complex boundary conditions, the performance remains comparable to the optimal case.

6. Conclusions

We presented the Esoteric Twist data structure for efficient thread safe execution of the LBM on massively parallel hardware. EsoTwist requires only a single read and write operation for each datum in each time step and only a single place in main memory. When combined with indirect addressing, EsoTwist requires the smallest number of pointers to neighboring nodes of any LBM algorithm using sparse matrices known to us. To our knowledge, EsoTwist has the smallest memory footprint of any sparse matrix LBM implementations, and it requires the smallest number of reads of any known LBM algorithm using sparse matrices. These claims are also confirmed by comparing to a recent analysis of Wittmann et al. [3]. Ignoring that EsoTwist requires, in fact, less pointers and reads than the AA-pattern, Wittmann et al. concluded that the AA-pattern and EsoTwist have the lowest data traffic of the known streaming algorithms. While being efficient, EsoTwist is also very flexible and is easily applied to real-world applications with complex boundaries. It also combines very favorably with local grid refinement techniques as shown in several publications [22,23,26,28].

Our results show comparable performance in terms of memory bandwidth (up to ∼68.2% peak bandwidth) to a block structured code with two distributions on recent Nvidia GPUs [36] and to full matrix codes. In terms of execution time, the sparse matrix EsoTwist method was found to obtain 99.4% of the performance of the AB-pattern on a recent GPU. It is of note that the ratio on older hardware was found to be inferior (93.2% for a Tesla C1060). It is hence seen that progress in hardware allows for more flexibility of the code without severe performance penalty.