Abstract
Our study investigates the interaction of dislocations with hexagonal close-packed (hcp) and chi-phase (χ) particles in body-centred cubic (bcc) tungsten (W) using molecular dynamics simulations. The research aims to understand how these interactions influence the mechanical properties of W, particularly in the context of neutron irradiation environments. The simulations were conducted with spherical and cylindrical particles at various temperatures and cell sizes to observe the effects on critical shear stress. Results indicate that the shape and size of the particles significantly affect the critical shear stress required for dislocation movement, with cylindrical particles requiring higher stresses than spherical ones. Additionally, the study found that temperature variations have a more pronounced effect on χ-phase particles compared to hcp-phase particles. Our findings provide insights into the strengthening mechanisms in W-Re alloys and suggest potential pathways for enhancing the material’s performance under extreme conditions.
1. Introduction
Tungsten (W) is widely used in modern industries due to its unique properties including a very high melting point, high density, good electrical and thermal conductivity, and low reactivity. These unique properties make W an indispensable material for cutting, wear-resistant, high-temperature, and high-strength applications. For example, thanks to these features, W is considered as a good candidate as a plasma-facing component for future fusion reactors [1].
However, W and some of its alloys are often susceptible to embrittlement from both thermal overload and neutron irradiation damage [2,3]. Irradiation can lead to the formation of defects that significantly reduce the fracture toughness, leading to the embrittlement of W [4].
It is believed that one of the possible solutions for improving the ductility and high-temperature creep resistance of W is obtaining a solid solution of W with rhenium (Re). During neutron irradiation, under extremely high temperatures, the nuclear reaction of W isotopes with neutrons can lead to the formation of Re isotopes [5,6]. Such a nuclear transmutation reaction can also lead to the formation of Re-rich precipitates in W alloys [7]. The precipitates can be coherent and represent relatively weak obstacles for moving dislocations. However, the incoherent precipitation in W-Re alloys can significantly impact the mechanical properties and result in high work-hardening rates [8,9]. Dislocations in W can interact with both vacancy-type defects and dispersed particles. As a result, they can undergo bowing, bypassing, and pinning, which can contribute to the strengthening of W-based materials.
The behaviour and properties of nano-objects can be difficult and sometimes impossible to explain based on experimental data alone. And computer modelling helps to fill these gaps. There are various modelling methods; among them, molecular dynamics (MD) is a fundamental and universal tool that allows us to study the mechanical, chemical, and thermodynamic properties of materials at the atomic-molecular level, thus helping to predict and understand macroscopic properties.
The interaction of dislocations with various obstacles or pores in metallic materials was extensively studied using MD as it provides valuable insights into the atomic-scale mechanisms of this phenomenon. Thus, it was demonstrated that the formation of Lomer–Cottrell and Hirth locks or clusters can enhance the flow stress and strain hardening in high-entropy alloys because the dislocation motion is suppressed due to the strong interaction with these obstacles [10,11]. Earlier, this approach helped to reveal that stacking fault tetrahedra induced by irradiation in face-centred cubic copper acts as a strong obstacle to dislocation motion [12]. The authors concluded that the shearing is the dominant mechanism for such interactions. Moreover, they found that when we deal with a void in body-centred cubic (bcc) Mo, dislocation first annihilates and then re-nucleates on the void surface, resulting in its simple shear. In this case, the void having a diameter greater than 3 nm resulted in a much higher critical resolved shear stress level for overcoming the obstacle. The authors of [13] determined the maximum size of the Ni3Nb precipitate (~20 nm) in the Ni matrix that can be sheared by dislocation. The interaction of dislocations with Fe-V particles with different V concentrations was studied in [14]. Increasing the concentration of V in the precipitate resulted in a stronger interaction and reduced the particle amorphisation caused by its cutting by dislocation. In general, there are plenty of factors affecting the interaction of dislocations with obstacles, including the deformation condition applied, size of obstacles, their chemical composition and shape, and so on, and, therefore, for each considered case, a detailed analysis must be carried out.
There are several works where MD was used to study the porosity effect on the dislocation structure evolution and mechanical properties of W. For example, the interaction of dislocations with voids in single-crystal W was analysed in [15]. Another study used this approach to investigate the interaction between an interstitial dislocation loop and vacancy-type defects, including vacancies, di-vacancies, and vacancy clusters, in W [16]. The results showed that the loops can be pinned by vacancy-type defects.
However, the known information is more general and focuses mostly on dislocations interacting with voids and vacancy-type defects. There are not many works devoted to the interaction of dislocations with precipitates in the W-Re alloys. Among them, the work by Bonny et al. [17] studied the interaction of dislocations with incoherent σ, χ, and hcp phase particles in bcc W in the quasi-static limit. They analysed the interaction mechanisms and defined the obstacle strength of the particles by the rigid displacement of the upper and lower parts of the computational cells. The interaction with the dislocation reduced the effective diameter of the obstacle pinning dislocations, thus affecting the obstacle strength. However, additional studies are needed to fully characterise the effect of incoherent Re and W-Re particles on the mechanical properties of W alloys.
2. Materials and Methods
The molecular dynamics modelling is performed with the widely used Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [18]. The interaction between atoms is described by the EAM potential for the W-Re system developed by Bonny et al. [19]. This potential demonstrates relatively good accuracy compared to other available potentials [20]. For the visualisation of the atomic structure, the Open Visualisation Tool was adopted [21]. Figure 1 shows the top view of the considered hcp- and χ-particles.
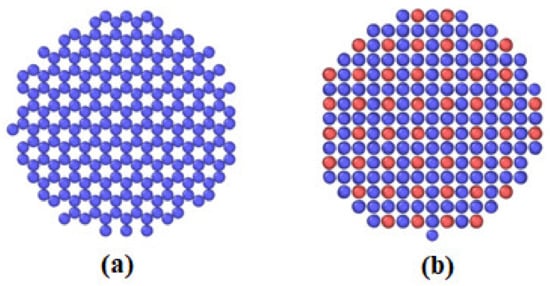
Figure 1.
The z-axis view of the cylindrical hcp- (a) and χ-particles (b), where W and Re atoms are given in blue and red colours, respectively.
In the simulation, single crystalline computational cells filled with W atoms forming the bcc structure with the lattice constant a = 3.16 Å are utilised. In addition, the spherical or cylindrical shape particles (see Figure 1) of the χ- and hcp-phases were introduced into the cell to investigate the interaction of dislocations with these particles in W. The hcp-phase consists of Re atoms only, while the χ-phase, having an L12 structure, includes two different elements. The crystal lattice of the L12 phase is similar to a simple body-centred cubic (bcc) lattice, but it is formed by two different elements, namely W and Re, in the ratio 1:3. This is why, to create the χ-phase particles, 75% of the W atoms in the bcc structure were replaced with Re. MD simulation results demonstrate the good stability of the L12 χ-phase. According to the ab initio data provided in [19], the lattice constant of this phase is 3.9272 Å.
The ½ [111] edge dislocation, having the Burgers vector b = a√3/2 = 2.736 Å, are introduced into the cells; see Figure 2. Its linear dimensions vary along the x- (Lx) and y-axes (Ly) from 10 to 40 nm and from 15 to 55 nm, respectively, affecting the dislocation density in the structure, while in the z-axis, the size is kept the same (38 nm). The x-, y-, and z-axes of the cells correspond to the crystallographic directions [111], [], and [], respectively. In Table 1, the sizes of the hcp-phase particles, as well as the dimensions of the simulation cells, are listed. The corresponding data for the χ-phase particles are listed in Table 2. These values, including those for the hcp-phase, are chosen to be consistent with the available experimental data [22,23,24,25,26,27].
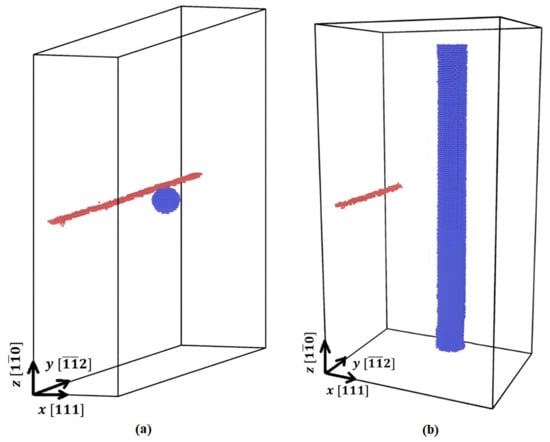
Figure 2.
An example of the computational cells with spherical (a) and cylindrical (b) particles interacting with the edge dislocations (shown in red colour).

Table 1.
The size of hcp-phase particles and corresponding dimensions of the cells along the x- and y-axes.

Table 2.
The size of the χ-phase particles and the corresponding dimensions of the cells along the x- and y-axes.
To investigate the particle–dislocation interaction, the strain control shear loading with a strain rate of = 108 s−1 is applied [28,29]. Structure relaxation and shear loading processes have been performed in the NPT ensemble (constant number of atoms, pressure, and temperature). All the stress components except for σxz are controlled to be zero. The timestep of the simulation is set as 2 fs. The fixed boundary conditions are imposed along the z-axis, while in the other two directions, periodic boundary conditions are adopted.
3. Results and Discussion
Let us first consider incoherent hcp-phase particles. The interaction of dislocations with the spherical particles is similar to that demonstrated by samples with cylindrical particles; the shear stress–strain curves for the considered cases look quite similar. Therefore, the detailed analysis will be given only for the interaction with cylindrical shape particles. Figure 3 shows the curves obtained for the cases from NO 8 to NO 11 of Table 1 with different Lx and Ly to compare the cell size effect.
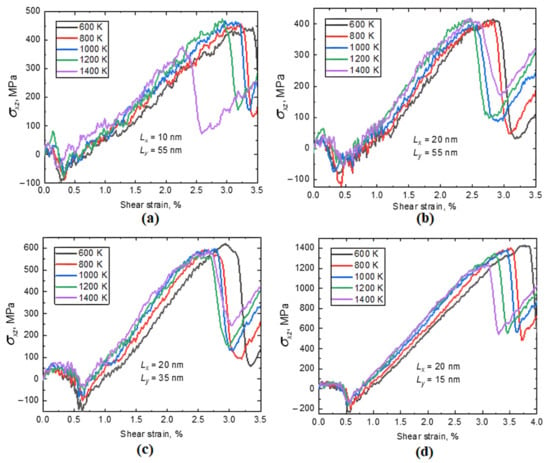
Figure 3.
Shear deformation stress–strain curves for the cells with cylindrical hcp-phase particles. The corresponding deformation temperatures and cell sizes are shown in each panel. Panels (a–d) correspond to simulation cell sizes for cases № 8–11, respectively, as described in Table 1.
There are two main regions on the plots that should be highlighted. The first one is when an abrupt decrease in stresses happens, and they decrease to negative values. This means that dislocation approaches the precipitate and comes into contact with it. The negative values of the shear stresses can be explained by the fact that we use fixed boundary conditions, which results in uncompensated shear stress in the simulation cell. This phenomenon refers to the peculiarities of the modelling process, and the current study does not address this issue. The features of modelling with and without fixed boundary conditions have been discussed in detail in a previous paper [15]. In the second region, the stress reaches a maximum value at ~2.5–3.0% strain (see Figure 3), which is called the critical shear stress, followed by an even sharper drop. At this step, the dislocation goes through the particle by cutting it. This is accompanied by a decrease in stress to minimum values at a shear strain of about 3.0–3.5%. The samples are deformed by up to 4% shear strain, which is sufficient for one full cycle of the interaction process. Figure 4 shows the interaction of dislocation with the particle at the moments when the dislocation comes into contact with it (a) and then detaches from it (b). In (c), the spherical and cylindrical particles cut by dislocation are represented.
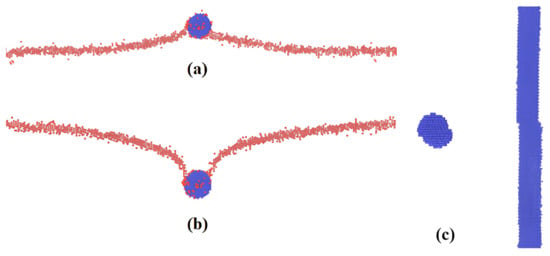
Figure 4.
(a) Dislocation comes into contact with the particle and (b) detaches from it. In (c), spherical and cylindrical particles cut by dislocation are presented. Atoms around the dislocation core are shown in red while the precipitates are given in blue.
Looking ahead, we note that such a scenario of the dislocation–particle interaction is true not only for the hcp-phase but also for the χ-phase, and works for both spherical and cylindrical particles. Referring to Figure 3, we can analyse the effect of temperature, the parameter Lx (free passage between dislocation and particle), and the parameter Ly (distance between obstacles). It is clearly seen in Figure 3 that, in general, at higher temperatures, lower shear stresses are required for the dislocation to overcome the particle, since the interaction is a thermally activated process. However, the decrease in stress values with temperature is not very obvious, except for the case of NO 11, as it also depends on the thermal fluctuations of atoms. In this case, the dislocation passes through the particle at lower strains. As for the computational cell size effect, one can see that with increases in Lx, the critical stress and corresponding strain values slightly decrease, except for 1400 K (Figure 3a,b). Regarding the Ly effect, decreasing the distance between particles leads to an increase in the critical shear stresses (Figure 3c,d). This effect can be described by the Bacon–Kocks–Scattergood (BKS) theory [30], which explains how decreasing the distance between particles leads to an increase in critical shear stresses. This effect is due to three main factors: increased linear tension along the dislocation lines, the greater curvature of dislocations as they bow between closely spaced particles, and higher interaction energy between dislocations and particles. These factors collectively raise the stress required to initiate dislocation movement, thereby increasing the material’s strength as observed in Figure 3c,d. The critical shear stress values for all the considered cases are listed in Table 3. The data from this table correspond well with the above description of the effect.

Table 3.
The critical shear stresses for the interaction of dislocation with hcp-phase particles.
As we said before, both the temperature effect and the size effect, namely Lx, are relatively negligible. However, reducing Ly from 55 nm to 35 nm results in an increase in the critical shear stress, approximately from 410 MPa to 580 MPa, and further lowering this parameter down to 15 nm causes the stresses to raise up to 1300 MPa. It should be noted that as the particle diameter increases, the critical shear stress also increases, and this correlation is almost linear.
The shape of particles affects the stresses as well. It can be concluded that the cutting cylindrical particles requires around 20% higher stresses than for the spherical particles. This can be explained by the fact that thermal fluctuations may cause dislocation to cut the sphere not right in the middle of the particle, but slightly off-centre. Such thermal fluctuations have the greatest impact on the relative displacement of the dislocation and the particle during relaxation at different simulation temperatures and precipitation sizes before the dislocation–particle interaction. In the case of cylindrical phases, this displacement does not affect the interaction. On the other hand, in the case of a spherical particle, the effective diameter can be smaller than the initial particle size and, obviously, overcoming the particle by dislocation becomes easier and requires lower stresses. These observations correlate well with the previous works [15,31].
Now let us consider the interaction of dislocations with χ-phase particles. Similar to the previous situation, as the deformation curves look similar, only those corresponding to the cases NO 7–10 in Table 2 are presented in Figure 5.
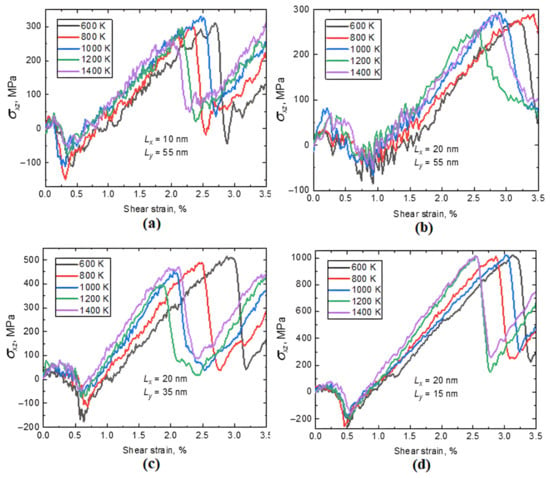
Figure 5.
Shear deformation stress–strain curves for the cells with the cylindrical χ-phase particles. The corresponding deformation temperatures and cell sizes are shown in each panel. Panels (a–d) correspond to simulation cell sizes for cases № 7–10, respectively, as described in Table 2.
The results show that in the case of χ-phase particles, in contrast to hcp-phase particles, the influence of temperature is more pronounced. In general, both the critical shear stress and the corresponding shear strain decrease with increasing temperature, which is especially evident when comparing the values for the highest and lowest temperatures considered (Figure 5a–c). However, it is difficult to see the difference in stresses when the cell size along the y-axis Ly is only 15 nm (Figure 5d). The cell size effect (Lx and Ly), as well as the effect of the particle shape and diameter, is very similar to those we observed for the hcp-phase particles. The critical shear stresses for the interaction of dislocations with χ-phase particles are given in Table 4.

Table 4.
The critical shear stresses for the interaction of dislocations with χ-phase particles.
If we were to compare the interaction with χ- and hcp-phase particles at the same simulation conditions, namely the computational cell size along the x- and y-axes and the particle diameter, it can be clearly seen that dislocations overcome hcp-phase particles at about 15–30% higher shear stresses (Table 3 and Table 4). We explain this phenomenon by the difference in the chemical composition of the particles. The hcp-phase is entirely formed by Re atoms, while in the χ-phase, there are 25% of W atoms. Both phases are incoherent with the matrix; however, the amount of local lattice distortion around the hcp-phase particles is higher than around the χ-phase particles because the Re atom has a larger atomic radius and more atomic mass compared to W. One can conclude that the obstacle strength of the particles can be increased by increasing the content of Re atoms in particles, and this agrees well with the molecular statics simulation results obtained earlier in [17].
In general, the stresses required for a dislocation to cut a particle are determined by various factors, such as the distance between neighbouring particles when periodic boundary conditions are used and their shear moduli. As the distance decreases, the stress required to push the dislocations between neighbouring particles increases. An increase in temperature facilitates the movement of dislocations and, at the same time, leads to a decrease in the shear moduli of the particles, which leads to a decrease in the values of critical stresses. The results obtained in the present study are in good agreement with these statements.
4. Conclusions
This study has elucidated the mechanisms by which dislocations interact with hcp- and χ-phase particles in bcc tungsten, revealing several key findings as follows:
- Particle Shape and Size Effects: Cylindrical particles require approximately 20% higher critical shear stresses compared to spherical particles, indicating that particle shape significantly influences dislocation behaviour. The critical shear stress increases almost linearly with particle diameter.
- Temperature Effects: The influence of temperature on critical shear stress is more pronounced for χ-phase particles than for hcp-phase particles. Higher temperatures generally reduce the critical shear stress required for dislocation movement, highlighting the thermally activated nature of these interactions.
- Cell Size Effects: Reducing the cell size along the y-axis increases the critical shear stress, demonstrating the importance of spatial constraints on dislocation dynamics.
- Material Composition: The study confirms that hcp-phase particles, composed entirely of Re atoms, present stronger obstacles to dislocations than χ-phase particles, which contain a mix of W and Re atoms. This is attributed to the greater local lattice distortion around hcp-phase particles.
In general, these results agree well with those obtained earlier in molecular statics, where the influence of the Re content as well as the effect of such modelling parameters as the particle and computational cell sizes were reported [17]. However, the use of the MD approach and the consideration of the temperature effect in the current study deepens the scientific value of the work from an experimental point of view.
These findings contribute to a deeper understanding of the strengthening mechanisms in W-Re alloys, particularly under conditions of neutron irradiation. Future research should focus on exploring the long-term stability of these interactions and their implications for the design of radiation-resistant materials.
Author Contributions
Conceptualisation, Y.R.S.; methodology, A.M.K.; software, A.M.K.; validation, R.I.B. and A.A.I.; formal analysis, R.I.B.; investigation, E.A.K.; data curation, A.S.S.; project administration, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
For E.A.K., the work was funded by the Ministry of Science and Higher Education of the Russian Federation as part of the World-class Research Center programme: Advanced Digital Technologies (contract No. 075-15-2022-311 dated 20 April 2022).
Data Availability Statement
The datasets are available from the authors upon reasonable request (arseny.m.kazakov@gmail.com).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Knaster, J.; Moeslang, A.; Muroga, T. Materials research for fusion. Nat. Phys. 2016, 12, 424–434. [Google Scholar] [CrossRef]
- Riesch, J.; Feichtmayer, A.; Coenen, J.; Curzadd, B.; Gietl, H.; Hoeschen, T.; Manhard, A.; Schwarz-Selinger, T.; Neu, R. Irradiation effects in tungsten—From surface effects to bulk mechanical properties. Nucl. Mater. Energy 2021, 30, 101093. [Google Scholar] [CrossRef]
- Terentyev, D.; Zinovev, A.; Khvan, T.; You, J.-H.; Van Steenberge, N.; Zhurkin, E.E. Irradiation embrittlement in pure chromium and chromium-tungsten alloy in a view of their potential application for fusion plasma facing components. J. Nucl. Mater. 2021, 554, 153086. [Google Scholar] [CrossRef]
- Terentyev, D.; Rieth, M.; Pintsuk, G.; Riesch, J.; Von Müller, A.; Antusch, S.; Mergia, K.; Gaganidze, E.; Schneider, H.C.; Wirtz, M.; et al. Recent progress in the assessment of irradiation effects for in-vessel fusion materials: Tungsten and copper alloys. Nucl. Fusion 2021, 62, 026045. [Google Scholar] [CrossRef]
- Li, Y.-H.; Ma, F.-F.; Yue, F.-Y.; Ren, Q.-Y.; Zhou, H.-B.; Hong, L. Radiation-induced precipitation of transmutation elements rhenium/osmium and their effects on hydrogen behavior in tungsten. Prog. Nat. Sci. Mater. Int. 2019, 29, 285–294. [Google Scholar] [CrossRef]
- Yokoyama, T.; Ozawa, M. Production of Low Activity Rhenium by Transmuting Tungsten Metal in Fast Reactors with Moderator. Int. J. At. Nucl. Phys. 2019, 4, 12. [Google Scholar] [CrossRef]
- Osetsky, Y. Strengthening of tungsten by coherent rhenium precipitates formed during low fluence irradiation. Tungsten 2022, 4, 20–27. [Google Scholar] [CrossRef]
- Liu, M.; Cowley, J. Particle/dislocation interactions in a dispersion strengthened tungsten alloy at ultrahigh temperatures. Scr. Metall. Mater. 1993, 28, 307–312. [Google Scholar] [CrossRef]
- Mihajlović, A.; Jovanović, M.; Nešić, O. Interaction of dislocations with precipitates in a Cu–Be–Ni–Zr alloy. Met. Technol. 1979, 6, 190–193. [Google Scholar] [CrossRef]
- Jarlöv, A.; Ji, W.; Babicheva, R.; Tian, Y.; Hu, Z.; Seet, H.L.; Tan, L.; Liu, F.; Liu, Y.; Nai, S.M.L.; et al. Tailoring short-range order and dislocation evolution in Cr–Co–Ni medium-entropy alloys: A molecular dynamics study. Mater. Des. 2024, 240, 112840. [Google Scholar] [CrossRef]
- Jarlöv, A.; Ji, W.-M.; Zhu, Z.; Tian, Y.; Babicheva, R.; An, R.; Seet, H.; Nai, M.L.S.; Zhou, K. Molecular dynamics study on the strengthening mechanisms of Cr-Fe-Co-Ni high-entropy alloys based on the generalized stacking fault energy. J. Alloys Compd. 2022, 905, 164137. [Google Scholar] [CrossRef]
- Lee, H.; Shim, J.; Wirth, B. Molecular Dynamics Simulation of Dislocation-Obstacle Interactions in Irradiated Materials. Key Eng. Mater. 2007, 345–346, 947–950. [Google Scholar] [CrossRef]
- Wan, C.-F.; Sun, L.-G.; Qin, H.-L.; Bi, Z.-N.; Li, D.-F. A Molecular Dynamics Study on the Dislocation-Precipitate Interaction in a Nickel Based Superalloy during the Tensile Deformation. Materials 2023, 16, 6140. [Google Scholar] [CrossRef] [PubMed]
- Yazdani, S.; Mesbah, M.; Vitry, V. Molecular Dynamics Simulation of the Interaction between Dislocations and Iron–Vanadium Precipitates in Alpha Iron: Effect of Chemical Composition. Crystals 2023, 13, 1247. [Google Scholar] [CrossRef]
- Kazakov, A.; Babicheva, R.; Zinovev, A.; Terentyev, D.; Zhou, K.; Korznikova, E.; Dmitriev, S. Interaction of edge dislocations with voids in tungsten. Tungsten 2024, 6, 633–646. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.; Xu, K.; Li, B.; Jin, S.; Li, X.-C.; Shu, X.; Liang, L.; Lu, G.-H. Atomic Simulations of the Interaction between a Dislocation Loop and Vacancy-Type Defects in Tungsten. Metals 2022, 12, 368. [Google Scholar] [CrossRef]
- Bonny, G.; Bakaev, A.; Terentyev, D. Assessment of hardening due to non-coherent precipitates in tungsten-rhenium alloys at the atomic scale. Sci. Rep. 2019, 9, 16215. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Bonny, G.; Bakaev, A.; Terentyev, D.; Mastrikov, Y. Interatomic potential to study plastic deformation in tungsten-rhenium alloys. J. Appl. Phys. 2017, 121, 165107. [Google Scholar] [CrossRef]
- Kosarev, I.; Shcherbinin, S.; Kistanov, A.; Babicheva, R.; Korznikova, E.; Dmitriev, S. An approach to evaluate the accuracy of interatomic potentials as applied to tungsten. Comp. Mater. Sci. 2024, 231, 112597. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Fukuda, M.; Yabuuchi, K.; Nogami, S.; Hasegawa, A.; Tanaka, T. Microstructural development of tungsten and tungsten–rhenium alloys due to neutron irradiation in HFIR. J. Nucl. Mater. 2014, 455, 460–463. [Google Scholar] [CrossRef]
- Nemoto, Y.; Hasegawa, A.; Satou, M.; Abe, K. Microstructural development of neutron irradiated W–Re alloys. J. Nucl. Mater. 2000, 283–287, 1144–1147. [Google Scholar] [CrossRef]
- Tanno, T.; Hasegawa, A.; Fujiwara, M.; He, J.C.; Nogami, S.; Satou, M.; Shishido, T.; Abe, K. Precipitation of solid transmutation elements in irradiated tungsten alloys. Mater. Trans. 2008, 49, 2259–2264. [Google Scholar] [CrossRef]
- Hwang, T.; Hasegawa, A.; Tomura, K.; Ebisawa, N.; Toyama, T.; Nagai, Y.; Fukuda, M.; Miyazawa, T.; Tanaka, T.; Nogami, S. Effect of neutron irradiation on rhenium cluster formation in tungsten and tungsten-rhenium alloys. J. Nucl. Mater. 2018, 507, 78–86. [Google Scholar] [CrossRef]
- Fukuda, M.; Tanno, T.; Nogami, S.; Hasegawa, A. Effects of Re content and fabrication process on microstructural changes and hardening in neutron irradiated tungsten. Mater. Trans. 2012, 53, 2145–2150. [Google Scholar] [CrossRef]
- Tanno, T.; Fukuda, M.; Nogami, S.; Hasegawa, A. Microstructure Development in Neutron Irradiated Tungsten Alloys. Mater. Trans. 2011, 52, 1447–1451. [Google Scholar] [CrossRef]
- Morkina, A.Y.; Babicheva, R.I.; Korznikova, E.A.; Enikeev, N.A.; Edalati, K.; Dmitriev, S.V. A Molecular Dynamics Simulation to Shed Light on the Mechanical Alloying of an Al-Zr Alloy Induced by Severe Plastic Deformation. Metals 2023, 13, 1595. [Google Scholar] [CrossRef]
- Peng, Q.; Huang, Z.; Chen, G.; Zhang, Y.; Zhang, X.; Chen, X.-J.; Hu, Z. Effect of Strain Rate, Temperature, Vacancy, and Microcracks on Mechanical Properties of 8-16-4 Graphyne. Nanomaterials 2024, 14, 556. [Google Scholar] [CrossRef] [PubMed]
- Bacon, D.J.; Kocks, U.F.; Scattergood, R.O. The effect of dislocation self-interaction on the Orowan stress. Philos. Mag. 1973, 28, 1241–1263. [Google Scholar] [CrossRef]
- Haghighat, H.S.M.; Lucas, G.; Schäublin, R. State of a pressurized helium bubble in iron. Europhys. Lett. 2009, 85, 60008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).