Methods for Detecting the Patient’s Pupils’ Coordinates and Head Rotation Angle for the Video Head Impulse Test (vHIT), Applicable for the Diagnosis of Vestibular Neuritis and Pre-Stroke Conditions
Abstract
1. Introduction
- The position of the glasses on the patient;
- The instructions given to the patient;
- The reproducibility of the results;
- The speed of the patient’s head during the test;
- The quality of the verification of the results;
- The age of the patient;
- The illumination of the patient’s face.
2. Methods of Estimating the Position of the Human Head
2.1. Classical Machine Learning
- The data from the sensors is subjected to pre-filtering, normalization, and segmentation in time.
- A set of features is extracted from the segments, which serve as the basis for head orientation classification. The data are partitioned manually.
- Nine classifiers are trained and tested using the available data.
- We feed a face photo as input, and a landmark detector extracts the coordinates of 68 landmarks of the face;
- The WSM draws a virtual web on the face, and a descriptive array of facial poses is extracted based on the position of landmarks.
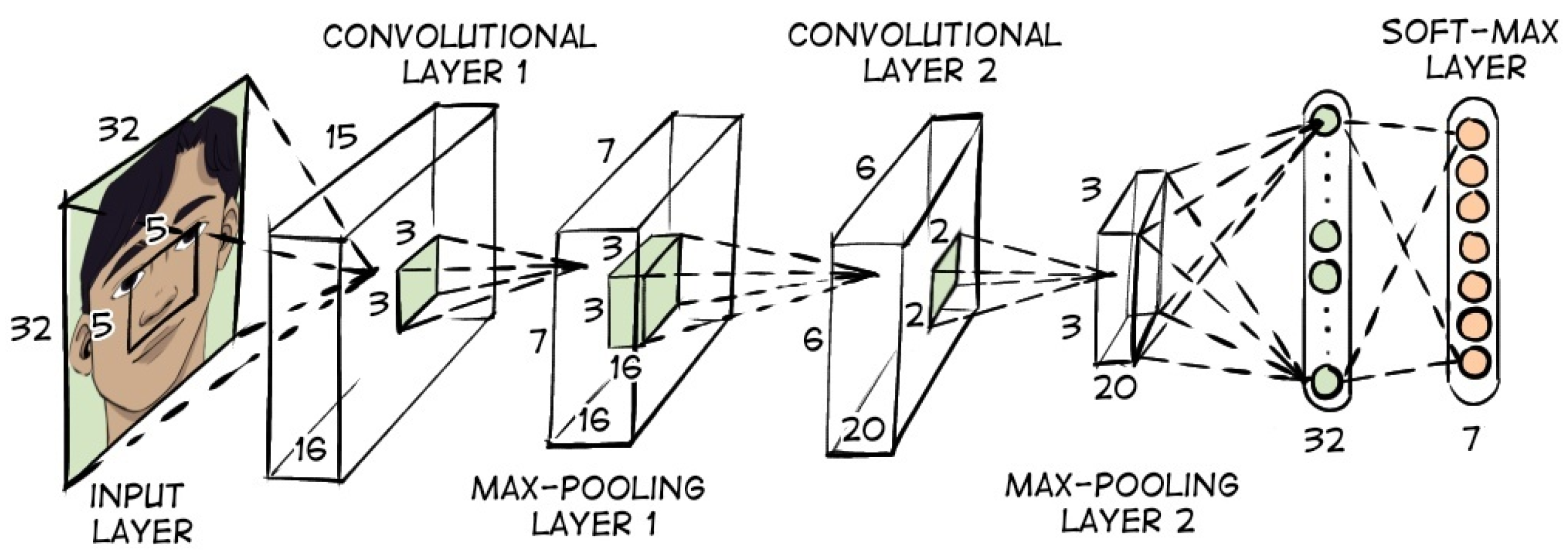
2.2. Deep Learning Methods
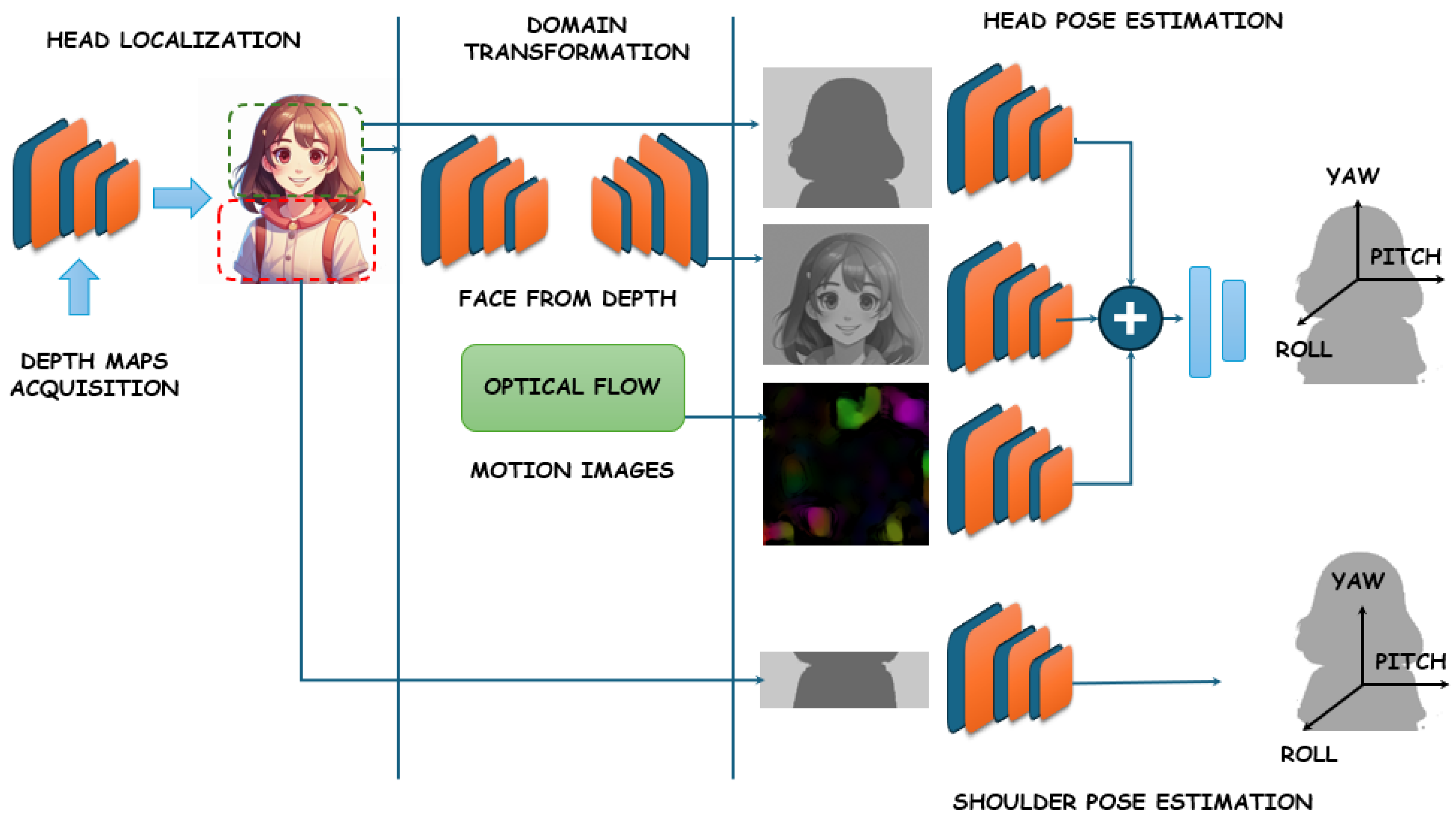
2.3. Attention Networks
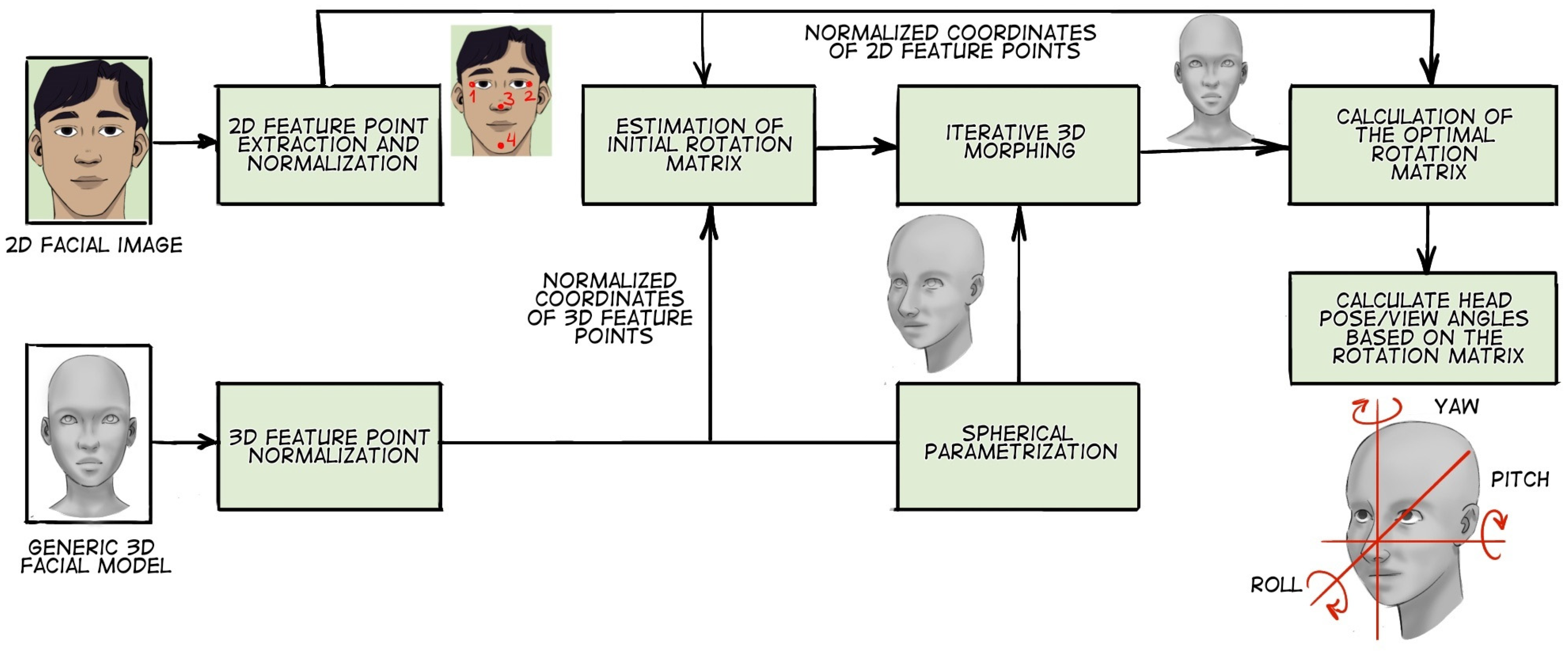
2.4. Geometric Transformations
2.5. Decision Trees
2.6. Search by Template Matching
2.7. Viola–Jones Algorithm
- Face recognition using an optimized Viola–Jones algorithm;
- Nose position recognition;
- Eye position recognition;
- The overall head position (roll, yaw, and pitch angle) is calculated from the nose and eye positions.
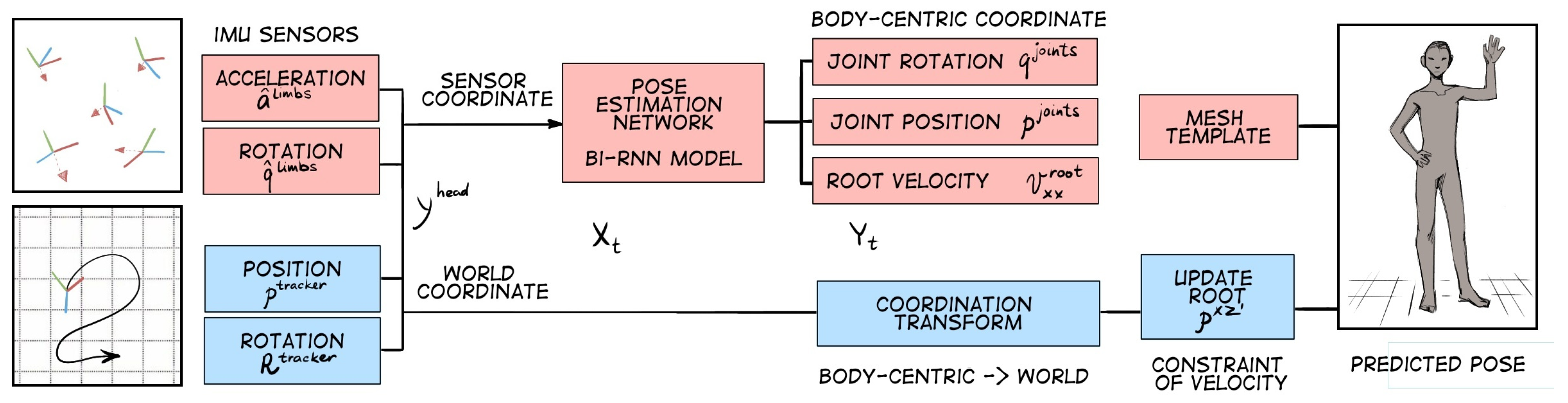
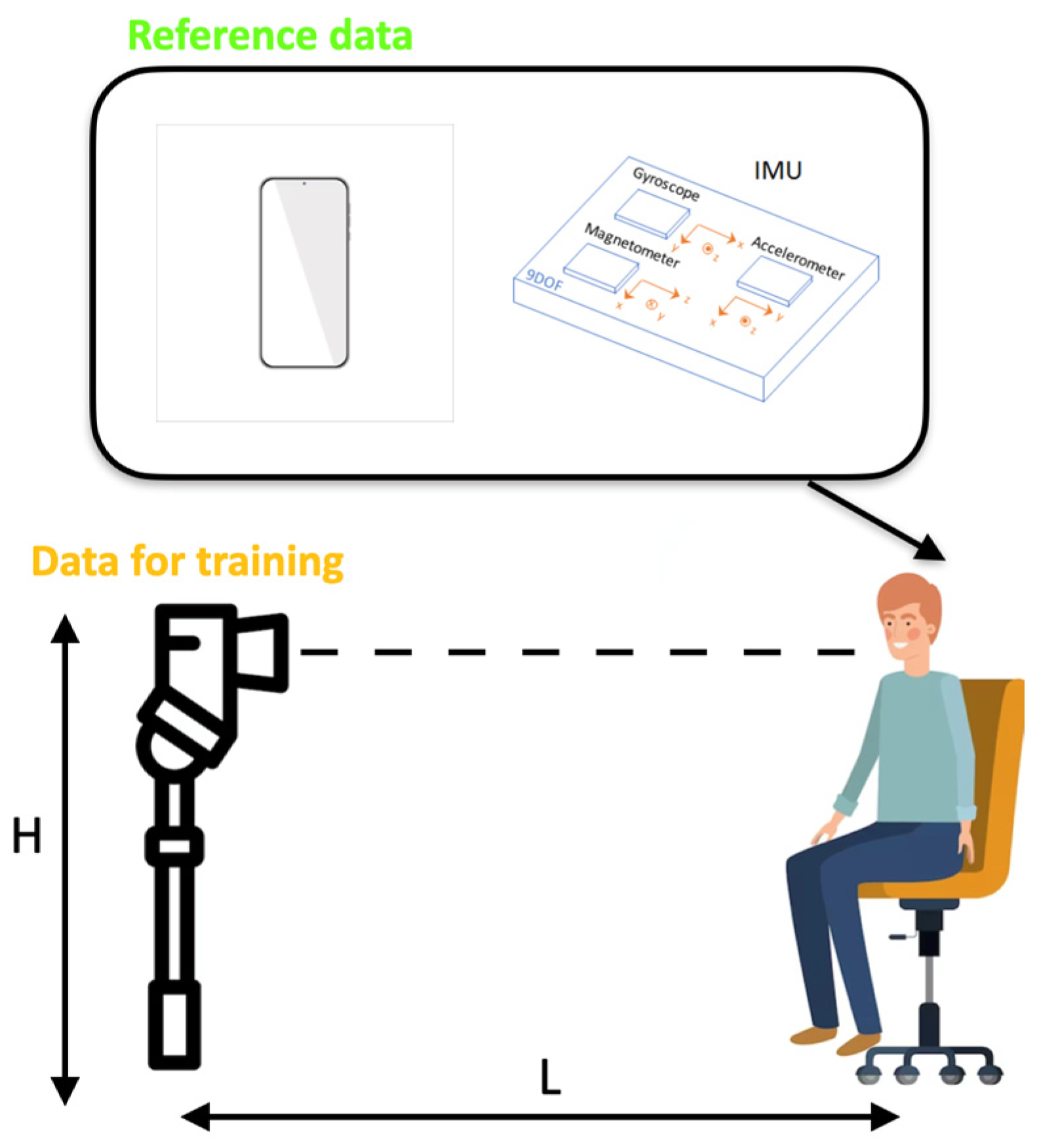
2.8. IMU Sensor Usage for Head Position Estimation
- The initial step is to calibrate the readings of all sensors (accelerometer, gyroscope, and magnetometer) to ensure that all measurements are close to zero when the system is at rest;
- The next step is to apply a Butterworth low-pass filter. The accelerometer reading is utilized to eliminate high-frequency additive noise;
- An additional filter is employed to enhance the response time and ensure the absence of noise in the measurement;
- Using the magnetometer in conjunction with the accelerometer and gyroscope to detect head rotation.
2.9. EMG Sensors Usage for Head Position Estimation
2.10. Optical Fiber Use for Head Position Estimation
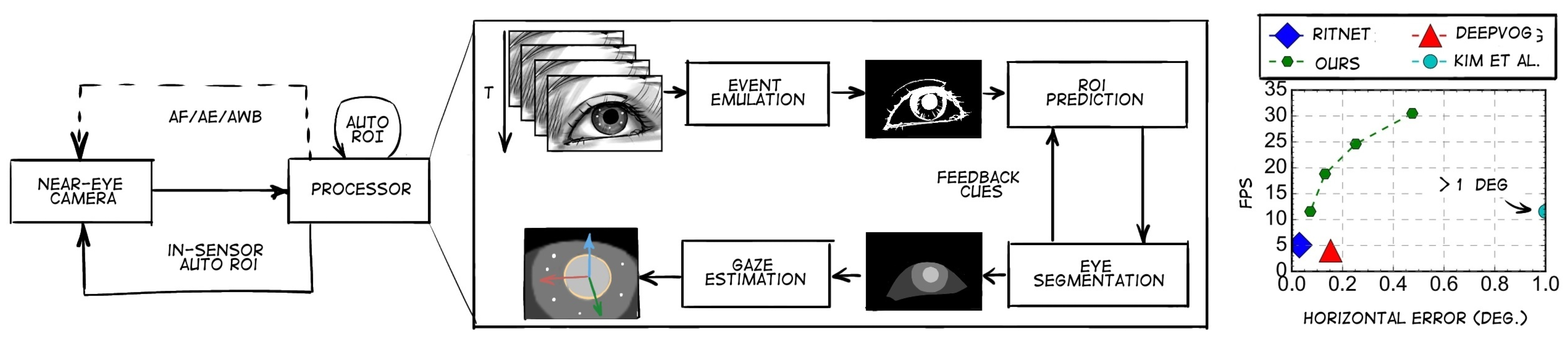
3. Methods of Detecting the Human Pupils’ Position
- Pupil detection using scleral search coils;
- Infrared oculography;
- Electro-oculography;
- Video oculography.
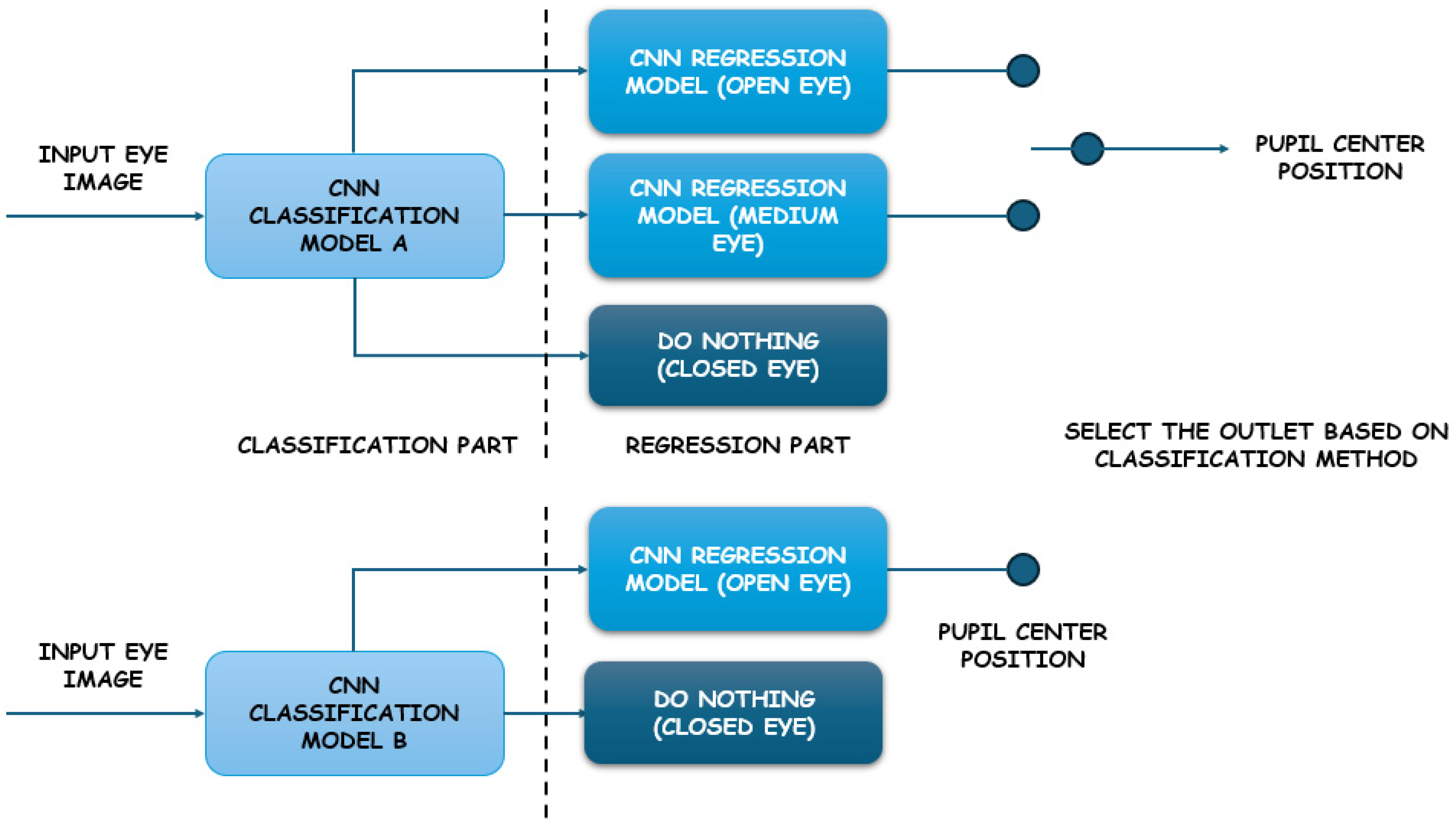
3.1. Deep Learning Techniques
3.2. SVM Algorithms
3.3. Color Histograms, Template Matching
3.4. Geometric Transformations
3.5. Decision Trees
3.6. Viola–Jones Algorithm
3.7. Classical Machine Learning Methods
3.8. CHT Algorithm
- Obtaining an image of the eye;
- Image filtering;
- Calibration of the system by nine reference points;
- Detecting the coordinates of the pupil center in each frame provided by the IR video camera;
- Matching the detected pupil center of the eye image with the cursor movement on the user’s screen;
- Optimization of the algorithm in order to stabilize the cursor movement on the user’s screen using different techniques: real-time filtering and burst removal.
3.9. RASNAC Algorithm
4. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Strupp, M.; Bisdorff, A.; Furman, J.; Hornibrook, J.; Jahn, K.; Maire, R.; Newman-Toker, D.; Magnusson, M. Acute unilateral vestibulopathy/vestibular neuritis: Diagnostic criteria. J. Vestib. Res. 2022, 32, 389–406. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Newman-Toker, D.E.; Kerber, K.A.; Jahn, K.; Bertholon, P.; Waterston, J.; Lee, H.; Bisdorff, A.; Strupp, M. Vascular vertigo and dizziness: Diagnostic criteria. J. Vestib. Res. 2022, 32, 205–222. [Google Scholar] [CrossRef]
- Parfenov, V.A.; Kulesh, A.A.; Demin, D.A.; Guseva, A.L.; Vinogradov, O.I. Vestibular vertigo in stroke and vestibular neuronitis. S.S. Korsakov J. Neurol. Psychiatry 2021, 121, 41–49. [Google Scholar] [CrossRef]
- Kulesh, A.A.; Dyomin, D.A.; Guseva, A.L.; Vinogradov, O.I.; Parfyonov, V.A. Vestibular vertigo in emergency neurology. Russ. Neurol. J. 2021, 26, 50–59. [Google Scholar] [CrossRef]
- Newman-Toker, D.E.; Curthoys, I.S.; Halmagyi, G.M. Diagnosing Stroke in Acute Vertigo: The HINTS Family of Eye Movement Tests and the Future of the “Eye ECG”. In Semin Neurology; Thieme Medical Publishers: New York, NY, USA, 2015; Volume 35, pp. 506–521. [Google Scholar] [CrossRef]
- Nham, B.; Wang, C.; Reid, N.; Calic, Z.; Kwok, B.Y.C.; Black, D.A.; Bradshaw, A.; Halmagyi, G.; Welgampola, M.S. Modern vestibular tests can accurately separate stroke and vestibular neuritis. J. Neurol. 2023, 270, 2031–2041. [Google Scholar] [CrossRef]
- Ulmer, E.; Chays, A. «Head impulse test de curthoys & halmagyi»: Un dispositif d’analyse. In Annales d’Otolaryngologie et de Chirurgie Cervico-Faciale; Elsevier Masson: Paris, Fance, 2005; Volume 122, pp. 84–90. [Google Scholar]
- Rasheed, Z.; Ma, Y.-K.; Ullah, I.; Al-Khasawneh, M.; Almutairi, S.S.; Abohashrh, M. Integrating Convolutional Neural Networks with Attention Mechanisms for Magnetic Resonance Imaging-Based Classification of Brain Tumors. Bioengineering 2024, 11, 701. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, I.; Yao, C.; Ullah, I.; Li, L.; Chen, Y.; Liu, Z.; Chen, S. An efficient feature selection and explainable classification method for EEG-based epileptic seizure detection. J. Inf. Secur. Appl. 2024, 80, 103654. [Google Scholar] [CrossRef]
- Ghaderzadeh, M.; Asadi, F.; Ghorbani, N.R.; Almasi, S.; Taami, T. Toward artificial intelligence (AI) applications in the determination of COVID-19 infection severity: Considering AI as a disease control strategy in future pandemics. Iran. J. Blood Cancer 2023, 15, 93–111. [Google Scholar] [CrossRef]
- Fasihfar, Z.; Rokhsati, H.; Sadeghsalehi, H.; Ghaderzadeh, M.; Gheisari, M. AI-driven malaria diagnosis: Developing a robust model for accurate detection and classification of malaria parasites. Iran. J. Blood Cancer 2023, 15, 112–124. [Google Scholar] [CrossRef]
- Jiang, Y.; Sadeqi, A.; Miller, E.L.; Sonkusale, S. Head motion classification using thread-based sensor and machine learning algorithm. Sci Rep. 2021, 11, 2646. [Google Scholar] [CrossRef]
- Abate, A.F.; Barra, P.; Pero, C.; Tucci, M. Head pose estimation by regression algorithm. Pattern Recognit. Lett. 2020, 140, 179–185. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, Y. Head pose estimation algorithm based on deep learning. In Proceedings of the AIP Conference Proceedings, Hangzhou, China, 8 May 2017; Volume 1839, p. 020144. [Google Scholar] [CrossRef]
- Zhou, Y.; Gregson, J. WHENet: Real-time Fine-Grained Estimation for Wide Range Head Pose. arXiv 2020, arXiv:2005.10353. [Google Scholar]
- Ruiz, N.; Chong, E.; Rehg, J.M. Fine-Grained Head Pose Estimation Without Keypoints. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; Georgia Institute of Technology: Atlanta, GA, USA, 2018. [Google Scholar]
- Yu, J.; Scheck, T.; Seidel, R.; Adya, Y.; Nandi, D.; Hirtz, G. Human Pose Estimation in Monocular Omnidirectional Top-View Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; Chemnitz University of Technology: Chemnitz, Germany. [Google Scholar]
- Khan, K.; Mauro, M.; Migliorati, P.; Leonardi, R. Head pose estimation through multi-class face segmentation. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), Hong Kong, China, 10–14 July 2017. [Google Scholar] [CrossRef]
- Xu, X.; Kakadiaris, I.A. Joint Head Pose Estimation and Face Alignment Framework Using Global and Local CNN Features. In Proceedings of the 12th IEEE Conference on Automatic Face and Gesture Recognition, Washington, DC, USA, 30 May–3 June 2017. [Google Scholar] [CrossRef]
- Song, H.; Geng, T.; Xie, M. An multi-task head pose estimation algorithm. In Proceedings of the 5th Asian Conference on Artificial Intelligence Technology (ACAIT), Haikou, China, 29–31 October 2021. [Google Scholar] [CrossRef]
- Khan, K.; Ali, J.; Ahmad, K.; Gul, A.; Sarwar, G.; Khan, S.; Ta, Q.T.H.; Chung, T.-S.; Attique, M. 3D Head Pose Estimation through Facial Features and Deep Convolutional Neural Networks. Comput. Mater. Contin. 2021, 66, 1745–1755. [Google Scholar] [CrossRef]
- Borghi, G.; Fabbri, M.; Vezzani, R.; Calderara, S.; Cucchiara, R. Face-from-Depth for Head Pose Estimation on Depth Images. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 596–609. [Google Scholar] [CrossRef]
- Paggio, P.; Gatt, A.; Klinge, R. Automatic Detection and Classification of Head Movements in Face-to-Face Conversations. In Proceedings of the Workshop on People in Language, Vision and the Mind, Marseille, France, 11–16 May 2020; pp. 15–21. [Google Scholar]
- Han, J.; Liu, Y. Head posture detection with embedded attention model. IOP Conf. Ser. Mater. Sci. Eng. 2020, 782, 032003. [Google Scholar] [CrossRef]
- La Cascia, M.; Sclaroff, S.; Athitsos, V. Head posture detection with embedded attention model. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 322–336. [Google Scholar] [CrossRef]
- Wenzhu, S.; Jianping, C.; Zhongyun, S.; Guotao, Z.; Shisheng, Y. Head Posture Recognition Method Based on POSIT Algorithm. J. Phys. Conf. Ser. 2020, 1642, 012017. [Google Scholar] [CrossRef]
- Yuan, H.; Li, M.; Hou, J.; Xiao, J. Single Image based Head Pose Estimation with Spherical Parameterization and 3D Morphing. Pattern Recognit. 2020, 103, 107316. [Google Scholar] [CrossRef]
- Fanelli, G.; Weise, T.; Gall, J.; Van Gool, L. Real Time Head Pose Estimation from Consumer Depth Cameras. In Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2011; pp. 101–110. [Google Scholar]
- Kim, H.; Lee, S.-H.; Sohn, M.-K.; Kim, D.-J. Illumination invariant head pose estimation using random forests classifier and binary pattern run length matrix. Hum.-Centric Comput. Inf. Sci. 2014, 4, 9. [Google Scholar] [CrossRef]
- Li, X.; Chen, H.; Chen, Q. A head pose detection algorithm based on template match. In Proceedings of the 2012 IEEE Fifth International Conference on Advanced Computational Intelligence (ICACI), Nanjing, China, 18–20 October 2012. [Google Scholar] [CrossRef]
- Lavergne, A. Computer Vision System for Head Movement Detection and Tracking. Master’s Thesis, University of British Columbia, Kelowna, BC, Canada, 1999. [Google Scholar]
- Chen, S.; Bremond, F.; Nguyen, H.; Thomas, H. Exploring Depth Information for Head Detection with Depth Images. In Proceedings of the AVSS 2016-13th International Conference on Advanced Video and Signal-Based Surveillance, Colorado Springs, CO, USA, 23–26 August 2016; ffhal-01414757. [Google Scholar]
- Saeed, A.; Al-Hamadi, A.; Handrich, S. Advancement in the head pose estimation via depth-based face spotting. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016. [Google Scholar]
- Neto, E.N.A.; Barreto, R.M.; Duarte, R.M.; Magalhaes, J.P.; Bastos, C.A.; Ren, T.I.; Cavalcanti, G.D. Real-Time Head. Pose Estimation for Mobile Devices. In Intelligent Data Engineering and Automated Learning-IDEAL 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 467–474. [Google Scholar]
- Al-Azzawi, S.S.; Khaksar, S.; Hadi, E.K.; Agrawal, H.; Murray, I. HeadUp: A Low-Cost Solution for Tracking Head Movement of Children with Cerebral Palsy Using IMU. Sensors 2021, 21, 8148. [Google Scholar] [CrossRef] [PubMed]
- Benedetto, M.; Gagliardi, A.; Buonocunto, P.; Buttazzo, G. A Real-Time Head-Tracking Android Application Using Inertial Sensors. In Proceedings of the MOBILITY 2016-6th International Conference on Mobile Services, Resources, and Users, Valencia, Spain, 22–26 May 2016. [Google Scholar]
- Kim, M.; Lee, S. Fusion Poser: 3D Human Pose Estimation Using Sparse IMUs and Head Trackers in Real Time. Sensors 2022, 22, 4846. [Google Scholar] [CrossRef] [PubMed]
- Morishige, K.-I.; Kurokawa, T.; Kinoshita, M.; Takano, H.; Hirahara, T. Prediction of head-rotation movements using neck EMG signals for auditory tele-existence robot “TeleHead”. In Proceedings of the RO-MAN 2009-The 18th IEEE International Symposium on Robot and Human Interactive Communication, Toyama, Japan, 27 September–2 October 2009. [Google Scholar]
- Brodie, F.L.; Woo, K.Y.; Balakrishna, A.; Choo, H.; Grubbs, R.H. Validation of sensor for postoperative positioning with intraocular gas. Clin. Ophthalmol. 2016, 10, 955–960. [Google Scholar] [CrossRef] [PubMed]
- Ba, S.O.; Odobez, J.M. Head Pose Tracking and Focus of Attention Recognition Algorithms in Meeting Rooms. In Proceedings of the Multimodal Technologies for Perception of Humans, First International Evaluation Workshop on Classification of Events, Activities and Relationships, CLEAR 2006, Southampton, UK, 6–7 April 2006. [Google Scholar]
- Lunwei, Z.; Jinwu, Q.; Linyong, S.; Yanan, Z. FBG sensor devices for spatial shape detection of intelligent colonoscope. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar] [CrossRef]
- Park, Y.L.; Elayaperumal, S.; Daniel, B.; Ryu, S.C.; Shin, M.; Savall, J.; Black, R.J.; Moslehi, B.; Cutkosky, M.R. Real-Time Estimation of Three-Dimensional Needle Shape and Deflection for MRI-Guided Interventions. IEEE ASME Trans. Mechatron. 2010, 15, 906–915. [Google Scholar] [PubMed]
- Wang, H.; Zhang, R.; Chen, W.; Liang, X.; Pfeifer, R. Shape Detection Algorithm for Soft Manipulator Based on Fiber Bragg Gratings. IEEE/ASME Trans. Mechatron. 2016, 21, 2977–2982. [Google Scholar] [CrossRef]
- Freydin, M.; Rattner, M.K.; Raveh, D.E.; Kressel, I.; Davidi, R.; Tur, M. Fiber-Optics-Based Aeroelastic Shape Sensing. AIAA J. 2019, 57, 5094–5103. [Google Scholar] [CrossRef]
- MacPherson, W.N.; Flockhart, G.M.H.; Maier, R.R.J.; Barton, J.S.; Jones, J.D.C.; Zhao, D.; Zhang, L.; Bennion, I. Pitch and roll sensing using fibre Bragg gratings in multicore fibre. Meas. Sci. Technol. 2004, 15, 1642–1646. [Google Scholar] [CrossRef]
- Botsis, J.; Humbert, L.; Colpo, F.; Giaccari, P. Embedded fiber Bragg grating sensor for internal strain measurements in polymeric materials. Opt. Lasers Eng. 2005, 43, 491–510. [Google Scholar] [CrossRef]
- Barrera, D.; Madrigal, J.; Sales, S. Long Period Gratings in Multicore Optical Fibers for Directional Curvature Sensor Implementation. J. Light. Technol. 2017, 36, 1063–1068. [Google Scholar] [CrossRef]
- Duncan, R.G.; Froggatt, M.E.; Kreger, S.T.; Seeley, R.J.; Gifford, D.K.; Sang, A.K.; Wolfe, M.S. High-accuracy fiber-optic shape sensing. In Proceedings of the Sensor Systems and Networks: Phenomena, Technology, and Applications for NDE and Health Monitoring 2007, San Diego, CA, USA, 19–21 March 2007. [Google Scholar]
- Lally, E.M.; Reaves, M.; Horrell, E.; Klute, S.; Froggatt, M.E. Fiber optic shape sensing for monitoring of flexible structures. In Proceedings of the SPIE, San Diego, CA, USA, 6 April 2012; Volume 8345. [Google Scholar]
- Brousseau, B.; Rose, J.; Eizenman, M. Hybrid Eye-Tracking on a Smartphone with CNN Feature Extraction and an Infrared 3D Model. Sensors 2020, 20, 543. [Google Scholar] [CrossRef]
- Valliappan, N.; Dai, N.; Steinberg, E.; He, J.; Rogers, K.; Ramachandran, V.; Xu, P.; Shojaeizadeh, M.; Guo, L.; Kohlhoff, K.; et al. Accelerating eye movement research via accurateand affordable smartphone eye tracking. Sensors 2020, 20, 543. [Google Scholar]
- Feng, Y.; Goulding-Hotta, N.; Khan, A.; Reyserhove, H.; Zhu, Y. Real-Time Gaze Tracking with Event-Driven Eye Segmentation. In Proceedings of the 2022 IEEE Conference on Virtual Reality and 3D User Interfaces (VR), Christchurch, New Zealand, 12–16 March 2022; University of Rochester: Rochester, NY, USA, 2022. [Google Scholar]
- Ji, Q.; Zhu, Z. Eye and gaze tracking for interactive graphic display. Machine vision and applications. In Proceedings of the 2nd International Symposium on Smart Graphics, New York, NY, USA, 8 June 2004; Volume 15, pp. 139–148. [Google Scholar]
- Li, B.; Fu, H. Real Time Eye Detector with Cascaded Convolutional Neural Networks. Appl. Comput. Intell. Soft Comput. 2018, 2018, 1439312. [Google Scholar] [CrossRef]
- Chinsatit, W.; Saitoh, T. CNN-Based Pupil Center Detection for Wearable Gaze Estimation System. Appl. Comput. Intell. Soft Comput. 2017, 2017, 8718956. [Google Scholar] [CrossRef]
- Fuhl, W.; Santini, T.; Kasneci, G.; Kasneci, E. Convolutional Neural Networks for Robust Pupil Detection. Computer Vision and Pattern Recognition. arXiv 2016, arXiv:1601.04902. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. Comput. Vis. Pattern Recognit. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Navaneethan, S.; Sreedhar, P.S.S.; Padmakala, S.; Senthilkumar, C. The Human. Eye Pupil Detection System Using. BAT Optimized Deep Learning Architecture. Comput. Syst. Sci. Eng. 2023, 46, 125–135. [Google Scholar]
- Li, Y.-H.; Huang, P.-J.; Juan, Y. An Efficient and Robust Iris Segmentation Algorithm UsingDeep Learning. Mobile Inf. Syst. 2019, 2019, 4568929. [Google Scholar]
- Wang, C.; Muhammad, J.; Wang, Y.; He, Z.; Sun, Z. Towards Complete and Accurate Iris SegmentationUsing Deep Multi-task Attention Network forNon-Cooperative Iris Recognition. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2944–2959. [Google Scholar] [CrossRef]
- Biradar, V. Neural Network Approach for Eye Detection. Comput. Sci. Inf. Technol. 2012, 2, 269–281. [Google Scholar] [CrossRef]
- Han, Y.J.; Kim, W.; Park, J.S. Efficient eye-blinking detection on smartphones: A hybrid approach based on deep learning. Mob. Inf. Syst. 2018, 2018, 6929762. [Google Scholar] [CrossRef]
- Zhu, Z.; Ji, Q.; Fujimura, K.; Lee, K. Combining Kalman Filtering and Mean Shift for Real Time Eye Tracking Under Active IR Illumination. In Proceedings of the International Conference on Pattern Recognition, Quebec City, QC, Canada, 1–15 August 2002; Department of CS, UIUC: Urbana, IL, USA, 2002. [Google Scholar]
- Yu, M.; Lin, Y.; Wang, X. An efficient hybrid eye detection method. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 1586–1603. [Google Scholar] [CrossRef]
- Kim, H.; Jo, J.; Toh, K.-A.; Kim, J. Eye detection in a facial image under pose variation based on multi-scale iris shape feature. Image Vis. Comput. 2017, 57, 147–164. [Google Scholar] [CrossRef]
- Sghaier, S.; Farhat, W.; Souani, C. Novel Technique for 3D Face Recognition Using Anthropometric Methodology. Int. J. Ambient. Comput. Intell. 2018, 9, 60–77. [Google Scholar] [CrossRef]
- Tresanchez, M.; Pallejà, T.; Palacín, J. Optical Mouse Sensor for Eye Blink Detection and Pupil Tracking:Application in a Low-Cost Eye-Controlled Pointing Device. J. Sensors 2019, 2019, 3931713. [Google Scholar] [CrossRef]
- Raj, A.; Bhattarai, D.; Van Laerhoven, K. An Embedded and Real-Time Pupil Detection Pipeline. arXiv 2023, arXiv:2302.14098. [Google Scholar]
- Javadi, A.-H.; Hakimi, Z.; Barati, M.; Walsh, V.; Tcheang, L. SET: A pupil detection method using sinusoidal approximation. Front. Neuroeng. 2015, 8, 4. [Google Scholar] [CrossRef]
- Gautam, G.; Mukhopadhyay, S. An adaptive localization of pupil degraded by eyelash occlusion and poor contrast. Multimed. Tools Appl. 2019, 78, 6655–6677. [Google Scholar] [CrossRef]
- Hashim, A.T.; Saleh, Z.A. Fast Iris Localization Based on Image Algebra and Morphological Operations. J. Univ. Babylon Pure Appl. Sci. 2019, 27, 143–154. [Google Scholar] [CrossRef]
- Jan, F.; Usman, I. Iris segmentation for visible wavelength and near infrared eye images. Optik 2014, 125, 4274–4282. [Google Scholar] [CrossRef]
- Perumal, R.S.; Mouli, P.C. Pupil Segmentation from IRIS Images using Modified Peak Detection Algorithm. Int. J. Comput. Appl. 2011, 37, 975–8887. [Google Scholar]
- Wang, J.; Zhang, G.; Shi, J. Pupil and Glint Detection Using Wearable CameraSensor and Near-Infrared LED Array. Sensors 2015, 15, 30126–30141. [Google Scholar] [CrossRef]
- Khan, T.M.; Khan, M.A.; Malik, S.A.; Khan, S.A.; Bashir, T.; Dar, A.H. Automatic localization of pupil using eccentricity and iris using gradient based method. Opt. Lasers Eng. 2011, 49, 177–187. [Google Scholar] [CrossRef]
- Shah, S.; Ross, A. Iris Segmentation Using Geodesic Active Contours. IEEE Trans. Inf. Forensics Secur. 2009, 4, 824–836. [Google Scholar] [CrossRef]
- Basit, A.; Javed, M. Localization of iris in gray scale images using intensity gradient. Opt. Lasers Eng. 2007, 45, 1107–1114. [Google Scholar] [CrossRef]
- Su, M.-C.; Wang, K.-C.; Chen, G.-D. An eye tracking system and its application in aids for people with severe disabilities. Biomed. Eng. Appl. Basis Commun. 2006, 18, 319–327. [Google Scholar] [CrossRef]
- Peng, K.; Chen, L.; Ruan, S.; Kukharev, G. A Robust Algorithm for Eye Detection on Gray Intensity Face without Spectacles. J. Comput. Sci. Technol. 2005, 5, 127–132. [Google Scholar]
- Timm, F.; Barth, E. Accurate Eye Centre Localisation By Means Of Gradients. In Proceedings of the VISAPP 2011-Sixth International Conference on Computer Vision Theory and Applications, Vilamoura, Algarve, Portugal, 5–7 March 2011. [Google Scholar]
- Araujo, G.M.; Ribeiro, F.M.L.; Silva, E.A.B.; Goldenstein, S.K. Fast eye localization without a face model using inner product detectors. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014. [Google Scholar] [CrossRef]
- Ghazali, K.H.; Jadin, M.S.; Jie, M.; Xiao, R. Novel automatic eye detection and tracking algorithm. Opt. Lasers Eng. 2015, 67, 49–56. [Google Scholar] [CrossRef]
- Leo, M.; Cazzato, D.; De Marco, T.; Distante, C. Unsupervised approach for the accurate localizationof the pupils in near-frontal facial images. J. Electron. Imaging 2013, 22, 033033. [Google Scholar] [CrossRef]
- Fisunov, A.V.; Beloyvanov, M.S.; Korovin, I.S. Head-mounted eye tracker based on android smartphone. Proc. E3S Web Conf. 2019, 104, 02008. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, G.; Zheng, K.; Mazhar, S. Pupil Detection Based on Oblique Projection Using a Binocular Camera. IEEE Access 2020, 8, 105754–105765. [Google Scholar] [CrossRef]
- Cazzato, D.; Dominio, F.; Manduchi, R.; Castro, S.M. Real-time gaze estimation via pupil center tracking. J. Behav. Robot. 2018, 9, 6–18. [Google Scholar] [CrossRef]
- Kang, S.; Kim, S.; Lee, Y.-S.; Jeon, G. Analysis of Screen Resolution According to Gaze Estimation in the 3D Space. In Proceedings of the Convergence and Hybrid Information Technology: 6th International Conference, ICHIT 2012, Daejeon, Republic of Korea, 23–25 August 2012; pp. 271–277. [Google Scholar]
- De Santis, A.; Iacoviello, D. A Robust Eye Tracking Procedure for Medical and Industrial Applications. In Advances in Computational Vision and Medical Image Processing; Springer Netherlands: Dordrecht, The Netherlands, 2009; pp. 173–185. [Google Scholar]
- Kacete, A.; Seguier, R.; Royan, J.; Collobert, M.; Soladie, C. Real-time eye pupil localization using Hough regression forest. In Proceedings of the 2016 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Placid, NY, USA, 7–10 March 2016. [Google Scholar] [CrossRef]
- Mosa, A.H.; Ali, M.; Kyamakya, K. A Computerized Method to Diagnose Strabismus Based on a Novel Method for Pupil Segmentation. In Proceedings of the ISTET 2013: International Symposiumon Theoretical Electrical Engineering, Pilsen, Czech Republic, 24–26 June 2013. [Google Scholar]
- Markuš, N.; Frljak, M.; Igor; Pandžić, S.; Ahlberg, J.; Forchheimer, R. A Computerized Method to Diagnose Strabismus Based on a Novel Method for Pupil Segmentation. Pattern Recognit. 2014, 47, 578–587. [Google Scholar] [CrossRef]
- Goua, C.; Wub, Y.; Wang, K.; Wanga, K.; Wanga, F.-Y.; Ji, Q. A joint cascaded framework for simultaneous eye detection and eye state estimation. Pattern Recognit. 2017, 67, 23–31. [Google Scholar] [CrossRef]
- Ibrahim, F.N.; Zin, Z.M.; Ibrahim, N. Eye Feature Extraction with Calibration Model using Viola-Jones and Neural Network Algorithms. Adv. Sci. Technol. Eng. Syst. J. 2018, 4, 208–215. [Google Scholar] [CrossRef]
- Haq, Z.A.; Hasan, Z. Eye-Blink rate detection for fatigue determination. In Proceedings of the 2016 1st India International Conference on Information Processing (IICIP), Delhi, India, 12–14 August 2016. [Google Scholar] [CrossRef]
- He, H.; She, Y.; Xiahou, J.; Yao, J.; Li, J.; Hong, Q.; Ji, Y. Real-Time Eye-Gaze Based Interaction for Human Intention Prediction and Emotion Analysis. In Proceedings of the CGI 2018: Proceedings of Computer Graphics International 2018, New York, NY, USA, 11–14 June 2018. [Google Scholar] [CrossRef]
- Swirski, L.; Bulling, A.; Dodgson, N. Robust real-time pupil tracking in highly off-axis images. In Proceedings of the ETRA ‘12: Proceedings of the Symposium on Eye Tracking Research and Applications, Santa Barbara CA, USA, 28–30 March 2012. [Google Scholar] [CrossRef]
- Raudonis, V.; Simutis, R.; Narvydas, G. Discrete eye tracking for medical applications. In Proceedings of the 2009 2nd International Symposium on Applied Sciences in Biomedical and Communication Technologies, Bratislava, Slovakia, 24–27 November 2009. [Google Scholar] [CrossRef]
- Bozomitu, R.G.; Păsărică, A.; Cehan, V.; Lupu, R.G.; Rotariu, C.; Coca, E. Implementation of Eye-tracking System Based on Circular Hough Transform Algorithm. In Proceedings of the 2015 E-Health and Bioengineering Conference, EHB 2015, Iasi, Romania, 19–21 November 2015. [Google Scholar] [CrossRef]
- Thomas, T.; George, A.; Devi, K.P.I. Effective Iris Recognition System. Procedia Technol. 2016, 25, 464–472. [Google Scholar] [CrossRef][Green Version]
- Halmagyi, G.M.; Chen, L.; MacDougall, H.G.; Weber, K.P.; McGarvie, L.A.; Curthoys, I.S. The Video Head Impulse Test. Front. Neurol. 2017, 8, 258. [Google Scholar] [CrossRef] [PubMed]
- Krivosheev, A.I.; Konstantinov, Y.A.; Barkov, F.L. Comparative Analysis of the Brillouin Frequency Shift Determining Accuracy in Extremely Noised Spectra by Various Correlation Methods. Gen. Exp. Tech. 2021, 64, 715–719. [Google Scholar] [CrossRef]
- Konstantinov, Y.A.; Kryukov, I.I.; Pervadchuk, V.P.; Toroshin, A.Y. Polarisation reflectometry of anisotropic optical fibres. Quantum Electron. 2009, 39, 1068. [Google Scholar] [CrossRef]
- Turov, A.T.; Barkov, F.L.; Konstantinov, Y.A.; Korobko, D.A.; Lopez-Mercado, C.A.; Fotiadi, A.A. Activation Function Dynamic Averaging as a Technique for Nonlinear 2D Data Denoising in Distributed Acoustic Sensors. Algorithms 2023, 16, 440. [Google Scholar] [CrossRef]
- Turov, A.T.; Konstantinov, Y.A.; Barkov, F.L.; Korobko, D.A.; Zolotovskii, I.O.; Lopez-Mercado, C.A.; Fotiadi, A.A. Enhancing the Distributed Acoustic Sensors’ (DAS) Performance by the Simple Noise Reduction Algorithms Sequential Application. Algorithms 2023, 16, 217. [Google Scholar] [CrossRef]
- Nordin, N.D.; Abdullah, F.; Zan, M.S.D.; Bakar, A.A.A.; Krivosheev, A.I.; Barkov, F.L.; Konstantinov, Y.A. Improving Prediction Accuracy and Extraction Precision of Frequency Shift from Low-SNR Brillouin Gain Spectra in Distributed Structural Health Monitoring. Sensors 2022, 22, 2677. [Google Scholar] [CrossRef]
- Azad, A.K.; Wang, L.; Guo, N.; Tam, H.-Y.; Lu, C. Signal processing using artificial neural network for BOTDA sensor system. Opt. Express 2016, 24, 6769–6782. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, Z.; Tang, M. Advances in Multicore Fiber Interferometric Sensors. Sensors 2023, 23, 3436. [Google Scholar] [CrossRef] [PubMed]
- Cuando-Espitia, N.; Fuentes-Fuentes, M.A.; Velázquez-Benítez, A.; Amezcua, R.; Hernández-Cordero, J.; May-Arrioja, D.A. Vernier effect using in-line highly coupled multicore fibers. Sci. Rep. 2021, 11, 18383. [Google Scholar] [CrossRef] [PubMed]
- Guo, D.; Wu, L.; Yu, H.; Zhou, A.; Li, Q.; Mumtaz, F.; Du, C.; Hu, W. Tapered multicore fiber interferometer for refractive index sensing with graphene enhancement. Appl. Opt. 2020, 59, 3927–3932. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Bai, Q.; Yan, M.; Wang, Y.; Zhang, H.; Jin, B. A Comprehensive Study of Optical Frequency Domain Reflectometry. IEEE Access 2021, 9, 41647–41668. [Google Scholar] [CrossRef]
- Belokrylov, M.E.; Kambur, D.A.; Konstantinov, Y.A.; Claude, D.; Barkov, F.L. An Optical Frequency Domain Reflectometer’s (OFDR) Performance Improvement via Empirical Mode Decomposition (EMD) and Frequency Filtration for Smart Sensing. Sensors 2024, 24, 1253. [Google Scholar] [CrossRef] [PubMed]
- Belokrylov, M.E.; Claude, D.; Konstantinov, Y.A.; Karnaushkin, P.V.; Ovchinnikov, K.A.; Krishtop, V.V.; Gilev, D.G.; Barkov, F.L.; Ponomarev, R.S. Method for Increasing the Signal-to-Noise Ratio of Rayleigh Back-Scattered Radiation Registered by a Frequency Domain Optical Reflectometer Using Two-Stage Erbium Amplification. Instrum. Exp. Tech. 2023, 66, 761–768. [Google Scholar] [CrossRef]
- Fu, C.; Xiao, S.; Meng, Y.; Shan, R.; Liang, W.; Zhong, H.; Liao, C.; Yin, X.; Wang, Y. OFDR shape sensor based on a femtosecond-laser-inscribed weak fiber Bragg grating array in a multicore fiber. Opt. Lett. 2024, 49, 1273–1276. [Google Scholar] [CrossRef]
- Monet, F.; Sefati, S.; Lorre, P.; Poiffaut, A.; Kadoury, S.; Armand, M.; Iordachita, I.; Kashyap, R. High-Resolution Optical Fiber Shape Sensing of Continuum Robots: A Comparative Study. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar] [CrossRef]
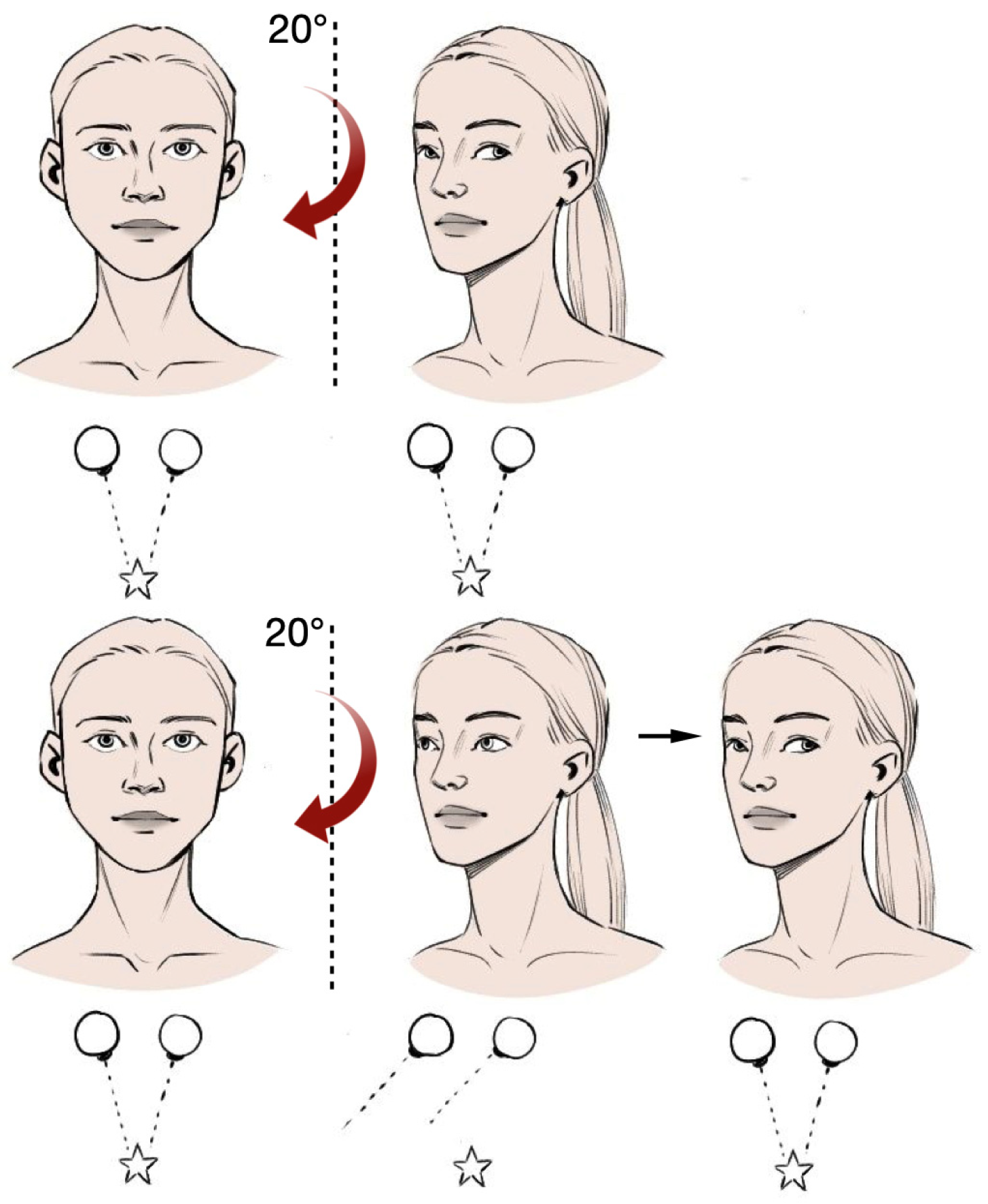



| Cosine KNN | Cubic KNN | Weighted KNN | Linear SVM | Quadratic SVM | Cubic SVM | SVM with Gaussian Kernel | Naive Bayes Classifier | Gaussian Naive Bayes Classifier | |
|---|---|---|---|---|---|---|---|---|---|
| Average accuracy | 89.6% | 89.5% | 91.1% | 92.2% | 91.5% | 90.5% | 91.7% | 90.1% | 90.5% |
| Signal Source | Technical/ Algorithmic Solution | Best Result of Head Pose Estimation | Time Characteristics of Algorithm Execution | Suitability of the Algorithm |
|---|---|---|---|---|
| Impedance sensor | Classical machine learning | The system can operate in “almost” real-time [12]. | Unsuitable | |
| Camera | Deep learning, neural networks | MAE of position angle detection reaches 1.96 degrees [20]. | The algorithm can process more than 30 frames per second [22]. | Suitable |
| Attention networks | MAE of position angle detection ranges from 5.02 to 15.77 degrees [24]. | The execution speed of the algorithm depends on the execution of the system. | Unsuitable | |
| Geometric transformations | Average MAE across angles ranged from 3.38 to 7.45 degrees considering the results on all public data [27]. | The algorithm is capable of processing up to 15 frames per second [25]. | Unsuitable | |
| Decision trees | The error in estimating the 3 position angles ranges from 7.9 to 9.2 degrees with an error of ±8.3 to ±13.7 degrees, respectively [28]. | The algorithm can process one 3D frame in 25 ms [28]. | Unsuitable | |
| Search by template matching | The head pose estimation error is 1.4 degrees [31]. | The algorithm supports real-time computation [30]. | Suitable | |
| Viola–Jones algorithm | The head pose estimation error ranges from 3.9 to 4.9 degrees, considering tests on 2 databases [33]. | The average execution time of the algorithm on smartphones varies from 68 to 316 ms, depending on the smartphone model [34]. | Unsuitable | |
| IMU sensors | LSTM network | The mean error in estimating head position angles is 0.8685 with an RMS (route mean square) of 0.9871 [36]. | The algorithms can operate in real-time [35,36]. | Suitable |
| EMG sensor | Linear regression | The average R-squared values between predicted and actual head position angles were 0.87 ± 0.06 [average ± STD], 0.86 ± 0.08, and 0.86 ± 0.06 for the three datasets [38]. | The system can operate in real-time [38]. | Suitable |
| Optical fiber | Single-point optical fibers based on FBG | The roll angle measurement error is within the range of ±2° [45]. | The wing stresses were evaluated at a frequency of 100 Hz [44]. | Suitable |
| Distributed fiber optic sensors | The measurement error of the spool diameter was 0.3 mm [48]. | The execution speed of the algorithm depends on the execution of the system. | Suitable |
| Signal Source | Technical/ Algorithmic Solution | Best Result of Head Pose Estimation | Highest Speed of Algorithm Execution | Suitability of the Algorithm |
|---|---|---|---|---|
| Camera | Deep learning, neural networks | The frame rate ranges from 30 to 60 Hz [54]. | Suitable | |
| SVM algorithm | The recall metric for pupil detection ranges from 87.68 to 99.72, depending on the dataset [65]. | The computation time of one frame (image) is 20.4 ms [65]. | Unsuitable | |
| Classical machine learning | More than 87% of the data have pupil position errors of less than 5 pixels [96]. | The developed system can be used to execute up to 25 commands per second [97]. | Unsuitable | |
| Color histograms, template matching | When the normalized error (between predicted pupil position and real pupil position) is less than 0.05, the proportion of data with correctly detected pupil position is 82.5% [80]. | The system can operate at a frame rate of 30 Hz [68]. | Unsuitable | |
| Geometric transformations | When the distance from the user to the screen is 60 and 80 cm, the pupil position detection accuracy can reach 1.5–2.2° [85]. | The algorithm can process more than 8 frames per second [86]. | Suitable | |
| Decision trees |
| Processing speeds can reach 30–50 frames per second on most devices [91]. | Suitable | |
| Viola–Jones algorithm | The eye blink detection accuracy is 87% and the accuracy of simple pupil detection is 97% [94]. | The method can achieve real-time mode [92]. | Unsuitable | |
| CHT | No numerical values were provided | The execution speed of the algorithm depends on the execution of the system. | - | |
| RASNAC | 99% of the inner boundary and 98% of the outer boundary of the iris are localized correctly [99]. | The execution speed of the algorithm depends on the execution of the system. | Suitable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mamykin, G.D.; Kulesh, A.A.; Barkov, F.L.; Konstantinov, Y.A.; Sokol’chik, D.P.; Pervadchuk, V. Methods for Detecting the Patient’s Pupils’ Coordinates and Head Rotation Angle for the Video Head Impulse Test (vHIT), Applicable for the Diagnosis of Vestibular Neuritis and Pre-Stroke Conditions. Computation 2024, 12, 167. https://doi.org/10.3390/computation12080167
Mamykin GD, Kulesh AA, Barkov FL, Konstantinov YA, Sokol’chik DP, Pervadchuk V. Methods for Detecting the Patient’s Pupils’ Coordinates and Head Rotation Angle for the Video Head Impulse Test (vHIT), Applicable for the Diagnosis of Vestibular Neuritis and Pre-Stroke Conditions. Computation. 2024; 12(8):167. https://doi.org/10.3390/computation12080167
Chicago/Turabian StyleMamykin, G. D., A. A. Kulesh, Fedor L. Barkov, Y. A. Konstantinov, D. P. Sokol’chik, and Vladimir Pervadchuk. 2024. "Methods for Detecting the Patient’s Pupils’ Coordinates and Head Rotation Angle for the Video Head Impulse Test (vHIT), Applicable for the Diagnosis of Vestibular Neuritis and Pre-Stroke Conditions" Computation 12, no. 8: 167. https://doi.org/10.3390/computation12080167
APA StyleMamykin, G. D., Kulesh, A. A., Barkov, F. L., Konstantinov, Y. A., Sokol’chik, D. P., & Pervadchuk, V. (2024). Methods for Detecting the Patient’s Pupils’ Coordinates and Head Rotation Angle for the Video Head Impulse Test (vHIT), Applicable for the Diagnosis of Vestibular Neuritis and Pre-Stroke Conditions. Computation, 12(8), 167. https://doi.org/10.3390/computation12080167








