Abstract
In Chile and worldwide, life expectancy has consistently increased over the past six decades. Thus, the purpose of this study was to identify, measure, and estimate the population mortality ratios in Chile, mortality estimates are used to calculate life expectancy when constructing life tables. The Bayesian approach, specifically through Approximate Bayesian Computation (ABC) is employed to optimize parameter selection for these calculations. ABC corresponds to a class of computational methods rooted in Bayesian statistics that could be used to estimate the posterior distributions of the model parameters. For this research, ABC was applied to estimate the mortality ratios in Chile, using information available from 2004 to 2021. The results showed heterogeneity in the results when selecting the best model. Additionally, it was possible to generate projections for the next 10 years for the series analysed in the research. Finally, the main contribution of this research is that we measured and estimated the population mortality rates in Chile, defining the optimal selection of parameters, in order to contribute to creating a link between social and technical sciences for the advancement and implementation of current knowledge in the field of social structures.
1. Introduction
Health is increasingly seen as a critical aspect of economic growth, and tracking healthy life expectancy is essential for assessing the financial sustainability of health and social care systems [1]. The authors of [2] found that life expectancy was more frequently incorporated into screening and treatment guidelines as evidence to facilitate clinical decision making related to the patient, and that life expectancy incorporating health status differed substantially from the life tables and health status for standard United States cases.
According to [3], the increase in life expectancy in high-income countries in Asia-Pacific is largely due to a shift in mortality from noncommunicable diseases to old age, which has led to rapid population aging and calls for policies that focus on healthy years in old age. On the other hand, projections of life expectancy in Western countries indicate that life expectancy will indeed continue to increase in most Western countries, but an important open question is whether longer life expectancy will be associated with more or fewer years of ill health. It is, therefore, useful to supplement projections of life expectancy with projections of health expectancy. The authors of [4] point out that when choosing a policy, analytical and applied factors should be considered, as well as their methods of calculation for life expectancy and mortality tables, focusing on needs, audience and communication strategy; community values and norms to explicitly address inequalities; and analytical capacity.
Demographic change, with the aging of societies, and epidemiological change, with an increase in chronic diseases, is unquestionable globally. Among the consequences of these changes is the increase in multimorbidity, fragility, and, on the other hand, the increase in life expectancy—which means an increase in demand for health and social services. This scenario involves complexity in the management and organization of care, which require a structural and functional adaptation of the available health resources if we want to conserve them and make them sustainable. However, the effects of decision making in the medium- and long-term in health systems pose a great challenge without the help of technology, that is, without the use of computational tools and mathematical models. This is not a new challenge—scientists from different areas of knowledge have questioned the feasibility and sustainability of health systems for several decades. In this context, it is important to highlight the link between social and technical sciences for the advancement and implementation of current knowledge in this field.
Monitoring life expectancy in small areas is important for health policy, but poses difficulties for conventional life table analysis [5]. Moreover, the implicit model underlying conventional life table analysis involves a parameterised fixed-effects approach. According to the social class ranking, there is a clear relationship between educational attainment and life expectancy. The social class rank is even higher for health expectancy than for life expectancy.
To point out that there is a gap in the demographic literature associated with the interpretation of periodic trends in life expectancy, the tempo [6] effects are presented; this is the case when a large number of deaths are suddenly postponed. Under the above conditions, the life table increases the longevity of the population by weighting deferred deaths with the remaining life expectancy. The study by [7] shows that life expectancy at age 50 differs by 8.6 years for men and 5.5 years for women between the highest and lowest income quintiles. The difference in disability-free life expectancy is 12.8 and 11.0 years for men and women, respectively. The mortality effect contributes equally to the difference in disability-free life expectancy for men and slightly more for women.
The research by [8] shows that women live longer, but spend more years in poor health than men. The same authors emphasize the need to consider gender differences in the demand for health care. It is also important to consider the need for policies that increase the number of years that older people can live in good health. The results of [9] expose the existence of ethno-racial inequalities in life expectancy in Chile, and show that Mapuche indigenous peoples are more disadvantaged in terms of survival than other indigenous and non-indigenous groups, with implications for decision making on ethnic policies.
In the case of life expectancy, current health policies need to take into account the growing number of beneficiaries with multiple chronic diseases when determining population projections and funding solvency [10]. According to [11], life expectancy is a measure used to compare differences in health between populations. The use of combined flexible parametric methods to estimate life expectancy in small samples has yielded promising results, allowing for the modelling of life expectancy by exact age, with a higher statistical precision and lower bias, and a prediction of different patterns of covariates without stratification.
In terms of life risk measurement, [12] indicates that each individual has one life and that this life has an age-specific mortality risk. If one adjusts this mortality risk of an individual with their age-specific probability of living, the life expectancy would change.
Research by [13] shows that the life expectancy curves of homogeneous and inhomogeneous populations intersect at the average age at which the frailest would have died and at the maximum age lived in the population (when the last members of the cohort would have died).
An analysis of the life tables suggests that some immigrant groups have different life expectancies because the standardized mortality ratio is sensitive to demographic differences between the groups being compared [11]. For [14], the methods associated with life tables do not usually involve an explicit statistical model, but the underlying statistical densities are applied when estimates of standard errors are required. The authors propose a Bayesian random-effects method [15,16,17,18] that aggregates the force into areas, ages, and groups using random-effects methods that do the following: (a) identify correlations between neighboring areas and ages and (b) detect similarities in spatial and age effects between stratified demographic groups (e.g., gender).
One of the first attempts to model human mortality was that of the English actuary Benjamin Gompertz, who argued that, above a certain age, the logarithm of the mortality force is a linear function of age. This hypothesis, later called Gompertz’s law, has been widely used in demographic and actuarial projections of mortality over the last two centuries [19]. The authors of [20] applied the Gompertz–Makeham mortality model framework relationship commonly used in human and wildlife studies, assuming that the Gompertz rate parameter is affected by individual heterogeneity, and show that in the results of a simulation study, the model adequately recovers the parameters used for the simulation.
According to [21], mortality models can be divided into static (functions of age only) versus dynamic (functions of age and current year), and deterministic versus stochastic models. The authors considered the Gompertz and Makeham models, which are deterministic and static, and the Lee–Carter method, which predicts mortality stochastically as a random walk with drift. In addition, the authors pointed out that models based on Gompertz and Makeham are widely used for educational, forecasting and risk assessment purposes, and the most significant recent advances in mortality modeling and forecasting: the Lee–Carter method.
Mortality estimates are used to construct life expectancies in the construction of life tables. When comparing different estimates of life expectancy, the results of [22] show that the Lee–Carter model without the long-memory component can provide underestimates of life expectancy, while extensions to the structure of the long-memory model reduce this effect. However, the empirical results show that the estimation using the Gompertz–Makeham methodology as opposed to the Lee–Carter methodology is similar [21]; for this reason, the widely known Gompertz–Makeham methodology is used in this research.
According to [23], mortality improvement is a challenge for public pension planning and for the private annuity business. Anticipating future mortality is important for public policy as well as for the management of financial institutions. As population mortality declines, national social security systems and insurance companies in most developed countries are reassessing their mortality tables to reflect longevity risk [24].
Taking into account life expectancy and its impact on government policies, as well as the existing life table, this research aims to estimate the mortality curves of the male and female population, based on projections of the parameters that determine the mortality of each cohort, using the ABC (Approximate Bayesian Computation) method. The ABC approach provides us with a flexible methodology that can be adapted to highly complex estimation problems [6,25,26,27,28,29], such as estimating the mortality law of a population. In this regard, we can test different models of population mortality behavior without significantly altering the structure of the methodology that will be proposed in this research work.
This manuscript is divided into four main sections, which include the Materials and Methods, the Results, the Discussion and, finally, the Conclusions.
2. Materials and Methods
In this research, we used official data from the Chilean government on vital statistics obtained from https://www.ine.gob.cl/estadisticas/sociales/demografia-y-vitales/nacimientos-matrimonios-y-defunciones (accessed on 29 April 2024). Specifically, we utilized statistics on the number of deaths for each cohort, with information available from 2004 to 2021, which considered the consolidated official data for the estimates and projections to be made.
Figure 1 shows the evolution of life expectancy over time for the Chilean population. We can observe that life expectancy has consistently increased over the past six decades. This growth in life expectancy is not exclusive to Chile, it is a trend observed worldwide. The reasons for the improvement in life expectancy are centered around sustained improvements in quality of life and increased spending on healthcare, among other social variables that have been extensively studied in the literature [30,31].
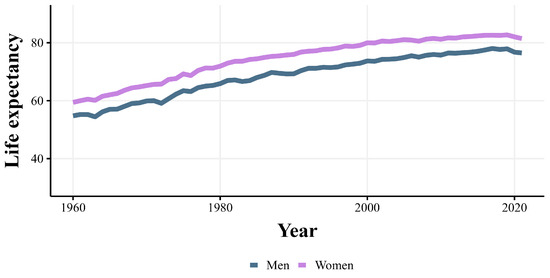
Figure 1.
Evolution of life expectancy in Chile.
Focusing on life expectancy raises the need to model survival for each specific cohort and thus generate various public policies oriented towards demographic aspects. However, if we extend the static analysis to a temporal analysis, this prompts questions about the stability of the parameters that define population mortality and creates an opportunity to develop methodological improvements for projecting population life expectancy and its evolution over time.
2.1. Gompertz–Makeham Law
One of the most well-known and widely used models for estimating population mortality rates corresponds to those originally developed by Gompertz [32] and Makeham [33], and is constructed by using the instantaneous force of mortality , where i corresponds to the age of the specific cohort. Estimating the Gompertz law requires the estimation of two parameters that can be estimated using standard statistical techniques related to the evolution of the age of the population. However, Makeham’s development adds a third parameter in the estimation process, which requires numerical approximation techniques but yields a better fit to population data by considering an extrinsic mortality effect [34,35]. In this research, we use a version of the model of Gompertz–Makeham, which we describe as
where parameter C corresponds to the extrinsic effect of mortality, b corresponds to a exponential adjustment constant, and m corresponds to a factor what we can interpret as a population decay law over time and that is related to the life expectancy of the population. For further references on modeling the Gompertz–Makeham law, see [36,37].
For the calculation of the probability of death in the following period , where , we use the following definition of the survival function
Proposition 1.
Under Gompertz–Makeham’s mortality law (Equation (1)), with , the survival probability to period t is
Proof.
Solving the definite integral for the above equation, we have
Now, assuming , the survival probability is
□
Figure 2 shows the evolution of the population decay under different parameterizations, starting with an initial age of 50 years. This figure illustrates how the population declines as age increases and it enables the projection of the population’s age composition, facilitating the establishment of specific demographic policies tailored to the social reality.
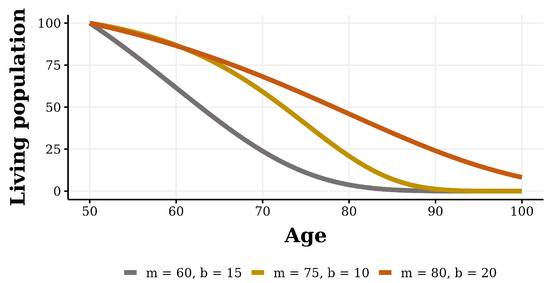
Figure 2.
Different survival curves with synthetic data.
Within the essential elements for estimating the parameters that define the Gompertz–Makeham law, it is necessary to understand the mortality dynamics of different population cohorts. With mortality data from various cohorts, we generate adjustments and estimates of the parameter values for the Equation (3).
2.2. Mortality Death Rates
The mortality death rate tables are used in various applications such as the estimation of life expectancy and calculation of life pension amounts, among many other applications. The mortality death rate tables correspond to a matrix of values belonging to a specific cohort i at a specific time t, which allows us to understand the temporal evolution of death rates. We define as a vector that represents the proportion of survivors in the following year for the number of people in the specific cohort i at a moment in time t. The probability density of each element of vector is defined as follows:
where corresponds to the set of parameters of cohort i in period t that define the stochastic behavior of the elements of vector . We describe the evolution of the parameter values that define the density function as
where corresponds to a specific function of parameter j that depends on cohort i in period t; corresponds to an error term with a normal distribution of variance . This description allows us to understand the evolution of the parameter values that define the survival behavior of members of a specific cohort as a random phenomenon. As examples of functions that model the stochastic temporal evolution of parameters, we can mention [38,39], among other authors.
For this research, we assume that the function describing the survival of an individual from cohort i for the following year corresponds to a random variable that is Bernoulli distributed with parameter , where parameter can be interpreted as the approximate proportion of inviduals in cohort i who will die in the next period, which we describe as
On the other hand, we propose that parameter evolves over time according to an autoregressive integrated moving average model (ARIMA) with respect to the same cohort. In this sense, the autoregressive factor of the same cohort corresponds to the natural survival factor at a certain age and the moving average is related to the behaviour of the error term. We describe the ARIMA(S, 0, Z) model and the ARIMA(S, 1, Z) model in the following equations
This formulation allows us to understand the evolution of parameters over time and helps us comprehend their stability as a random phenomenon. Another important aspect is that it provides us with an interesting tool for projecting individual survival and, consequently, the age composition of society. One element to consider corresponds to the limitations of time series techniques in forecasting, especially when extending over a very large time span.
2.3. Estimation of Parameters Using ABC Techniques
In this section, we define the parameter estimation procedure for the Gompertz law using techniques based on Bayesian inference. In Bayesian analysis, the unknown parameter that defines the mortality behavior of the population is represented as a random variable with a probability distribution , known as the prior distribution. The prior distribution encapsulates the initial beliefs about the parameter values held by the researcher, which must be updated based on the evidence revealed by the observed data.
Given a set of parameters , the observed data follows a density function that defines a parametric model with the parameters value , which determines the behavior of the random variable. With this in mind, we can define the joint distribution as
and the marginal density of X is defined as follows:
The conditional density of given the observed values of X corresponds to and is known as the posterior distribution. The posterior distribution is defined as
Within modern techniques for estimating the posterior distributions of parameters that define random phenomena, we can name methods like Approximate Bayesian Computation (ABC). In the literature, notable mentions include [6,25,26,27,28,29]. ABC techniques comprise a series of acceptance–rejection algorithms that utilize summary statistics from a random sample clustered around a target value for the estimation of the posterior distribution of parameters. These techniques have demonstrated significant flexibility due to the ease of generating independent random samples and allow for approximations of the true parameter distributions when analytical estimation is complex or not feasible.
Algorithm 1 shows how to apply ABC techniques for estimating population decay, using Equation (3) as a basis. The algorithm takes the following requirements to start: Nm which corresponds to the number of samples needed to calculate a probability density of the parameters; , which corresponds to the a priori density of parameter m; , which corresponds to the a priori density of parameter b; , which corresponds to the initial age at which the population decline is to be estimated; , which corresponds to the terminal age for the assessment of population decline; , which corresponds to the annual mortality on which the estimate will be made, which can be obtained from the observed mortality data of a population or its projection; and , which corresponds to the error value that we are willing to accept for the generation of the probability density of the parameters.
| Algorithm 1 Modelling of population decay. |
|
One of the most important steps in Bayesian methodologies is the selection of the prior m and b parameters. An appropriate selection of the prior improves the estimation results of the posterior distribution [40] and accelerates computational calculations, making the use of these methodologies feasible in many cases. However, often, there is no information regarding the best prior to be used, and a non-informative distribution such as a uniform distribution must be used, assuming the possibility of biases in the results that must be corrected for by proper selection of the prior distribution. In our procedure, we suggest using a uniform distribution for the characterization of the prior, as we do not have information on the behavior of all mortality parameters as a whole.
In the following step, it is necessary to randomly select values for m and b, using the priors determined for the parameters. Subsequently, the decay of real mortality and that estimated based on the selected parameters is calculated. Once the decays, both real and based on the selected parameters, are obtained, the difference is measured. If the difference is below the value, it is accepted and incorporated into the M and B vectors. Finally, we can calculate the posterior density using the M and B vectors.
Figure 3 shows a summary of the methodology used for estimating the survival curves. First, it is necessary to obtain historical mortality data of the population. This allows us to estimate the value of the mortality parameters for each cohort for each year, thus obtaining the time series of the estimated parameter values. Second, we proceed to project the parameter values for a certain number of years, based on the methodology described in Equations (7) and (8). Third, we use the projections of each cohort as inputs for Algorithm 1, thereby obtaining the parameter densities used to calibrate the mortality curve described in Equation (3). Finally, we proceed to obtain random values for the parameters in Equation (3) using the calculated densities, in order to obtain the survival projection of the population. This provides a survival density for each of the projected ages, which can be used for some social application in the context of population projection.
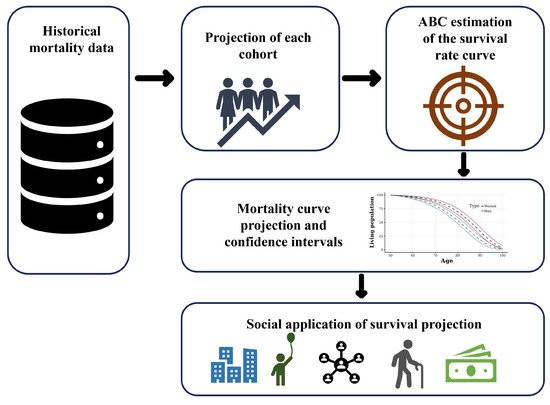
Figure 3.
Summary of the methodology used in the research.
3. Results
In this section, we proceed to present the results of the methodology proposed in the previous sections. Firstly, we display the results in Table 1 for some of the regressions performed when estimating the projections of the parameter evolution over time, based on the general expression of Equations (7) and (8) for 2030. In this case, we selected the ARIMA model with the lowest AIC criteria, which allows for combining a model with low variance and a limited number of parameters to be estimated, a fundamental element due to the limited number of observations for each cohort. Columns AR, I, and MA correspond to the number of autoregressive, integrated, and moving average parameters in the model. We also incorporate the information of the AIC and BIC values for the selected models.

Table 1.
Parameter estimation for a selected sample of cohorts.
The results show heterogeneity of the results for the selection of the best model. In some cases, eliminating the trend using differencing is sufficient to obtain a stationary process, while in others it is necessary to consider the autoregressive and moving average components to obtain a stationary process.
Based on the selected models, we then generate projections for the next 10 years, which gives us the possible results for the parameter that defines the mortality of each cohort value with 95% confidence. This projection is shown in Figure 4, which considers projections for men and women aged 50, 70, and 90. In general, we can observe that for all projections, the mortality rate for men is higher than for women, indicating a significant difference in the age composition of the elderly population. With these projections, we can generate the survival curve described in Equation (3), using the methodology of parameter estimation using the ABC techniques described in Algorithm 1, which is a necessary element for the generation of social applications requiring the use of population projection.
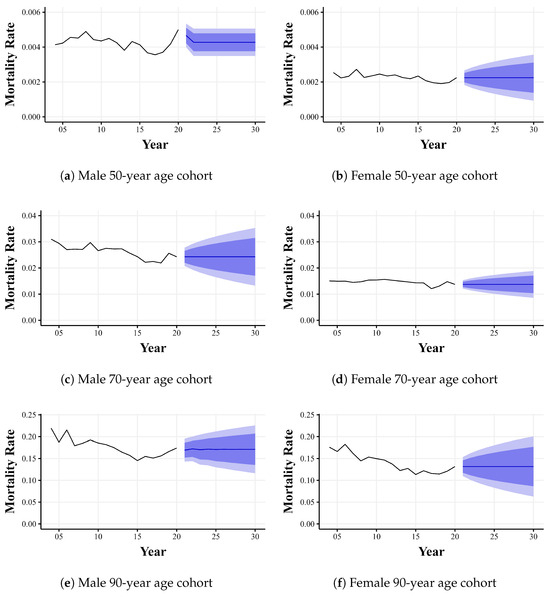
Figure 4.
Projection of the parameter for different ages and different sexes.
Table 2 shows the estimation of the parameters for Equation (2) describing the behavior of population decay for men and women, obtained as the main results of Algorithm 1. The estimation uses the expected value of the projection of the parameters that determine the mortality rate for each cohort; the 5th percentile case corresponds to the best case scenario for each of the cohorts as it marks the lowest mortality scenario to which the population could be subjected and the 95th percentile case corresponds to the worst case mortality rate for each cohort. The columns identify the average value and standard deviation for parameters m and b for each of the cases. We can observe that the scenarios for parameter m for men range between and , while for parameter b it ranges between and ; for women, parameter m ranges between and and parameter b between and .

Table 2.
Estimation of population decay parameters for men and women.
Figure 5 shows the displacement of the survival curve for males and females, using the mean value of the parameters shown in Table 2 and compared with the estimated mortality curve for 2000 as a baseline. It is observed that for both cases, there is an improvement in life expectancy, which impacts the age composition of the elderly population and will have an important impact on other related elements, such as the estimation of pensions and health services, to name a few.
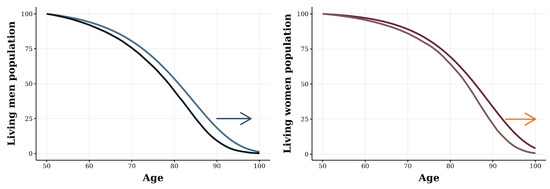
Figure 5.
Evolution of the projection for the expected value of population decay. The shift to the right implies improvements in the life expectancy of the population.
Finally, ww generate confidence bands for the population decay estimate using the values associated with the 5th percentile and 95th percentile of the projections of the parameters defined above, and we use Algorithm 1 for the estimation of their parameters. Figure 6 shows the population decay projection for males and females, with the respective confidence bands. It is worth mentioning that this procedure generates confidence bands, considering the “best” and “worst” case in terms of the estimation of the mortality rate parameters, which makes these confidence bands conservative scenarios in terms of the estimation of the population decay projection. For the generation of confidence bands considering specific percentiles, independent simulations must be performed for each of the cohorts. Then, the parameter estimation procedure defined in Algorithm 1 must be performed on a sufficiently large number of each of the cohorts to obtain the density of the decay projection.
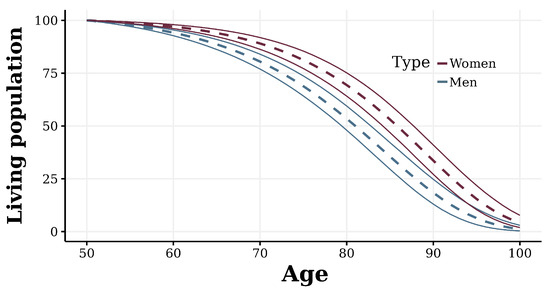
Figure 6.
Estimation of population projections until 2030. The dotted lines correspond to the mean value of the projections.
Determination of Life Annuity
To understand how the proposed methodology significantly impacts various applications, we proceed with a simple example of determining a citizen’s life annuity. In this context, we consider a man who retires at the age of 65 with an accumulated amount of USD 100,000. Additionally, we use the 2010 mortality data as the baseline and contrast it with the 2030 population density projections generated and shown in the results. The life annuity of the citizen s is calculated as
where corresponds to the level of wealth that individual s has at the time of retirement; corresponds to the commission of the insurance companies when offering the annuity, which for this example we will take as zero; corresponds the actuarial annuity factor (see [41]) at age i, which can be calculated as
where corresponds to the function defined in Equation (3) that defines the probability of survival in retirement age i at t years in the future, and r represents the effective annual valuation rate used to discount the cash flows, which for this example we consider a value of 3%.
Table 3 shows the estimated values for the calculation of the life annuity for a man retiring at age 65. The first and fifth columns correspond to the age of the individual; the second and sixth correspond to the discount factor used (3% per year); the third and seventh columns correspond to the estimated survival of the individual to survive to the age of the corresponding row, considering the mortalities of 2010; and, finally, the fourth and eighth columns are equivalent to the third and seventh, but for the projection of 2030.

Table 3.
Values for life annuity estimation.
Finally, Table 4 shows the results of the calculation of the life annuity for the 65-year-old pensioner. The first column corresponds to the estimation of the actuarial annuity factor, considering the 2010 mortalities; the second column corresponds to the estimation of the actuarial annuity factor, but now considering the 2030 projection; the third and fourth columns correspond to the calculated annuity; and the fifth column shows the percentage variation between annuities. It is observed that as life expectancy improves, based on the proposed methodology, annuities decrease as people live longer. The amount must be distributed over a longer expected life span.

Table 4.
Results of the impact of the evolution of mortality.
4. Discussion
The debate on health and its various implications for the population has been an aspect of recurring and significant importance in citizen, political, and economic emergencies in different countries around the world.
The literature shows a growing need for the adequate estimation of life expectancy to try to project population dynamics and make decisions on public policy [42,43]. However, the implementation of new estimation methodologies provides a new framework on which to make these projections.
In this sense, the three stages of the methodology proposed in this research, (1) estimation of the population survival curve, (2) projection of the parameters that define the mortality of each cohort, and (3) estimation of the parameters using a Bayesian methodology, allow us to understand the projections of the survival curves as a random phenomenon, unlike most of the approximations that are made in the literature [36,37,44].
The appropriate estimation of survival curves presents an intrinsic problem due to the heterogeneity of the population. High-income countries have a longer life expectancy due to the treatment of diseases [3] and the case of rural populations versus urban populations [45], among other sources of variation, which makes it complex to have a single function that describes the evolution of the population as it becomes older.
The proposed methodology allows us to generate a variety of possible results for the population projection by means of the Bayesian methodology presented in this research and, therefore, absorbs technological changes that can cause drastic improvements in life expectancy, as well as catastrophic events that can induce a rise in mortality.
The results shown in the research show a difference in the estimation of the parameters that define the survival curve of men and women, showing a differentiated behavior that implies a new projection for the population pyramid, which are essential elements for the generation of gender public policies focused on the elderly. These general results imply a significant proportion of elderly women who will require specialized social services in the near future.
On the other hand, an intermediate result that we can observe is the estimation of models that define the time evolution of the mortality parameters of each cohort of the population. In general, we can observe that in a significant proportion of cohorts, the best model defining the time series process of the parameters is based on a simple differencing; however, other cohorts establish more complex models for the dynamics.
In general, we can mention that the methodology allows for flexibility within different populations and other applications that require establishing the survival dynamics of a population.
Our approach differs from other significant methodologies such as the estimation of mortality curves [19,46,47,48]. In our case, we consider the projection of the parameters that define mortality as the fundamental input for estimating mortality curves. Furthermore, the proposed methodology, conceived as modular components—with the use of Gompertz–Makeham’s law being one of those modules—allows us the possibility to employ other estimation approaches for mortality curves that can serve as model contrasts.
An important element to consider is the selection of the prior distribution implemented in the algorithm. In our case, a non-informative distribution (uniform distribution) is used for the methodology, assuming computational costs and potential biases due to the inadequate selection of the distribution [40]. This point should be considered in future research with a larger amount of data available for estimations because small fluctuations in the estimates can have a significant impact on the projections.
5. Conclusions
In the present research we used official data from the Government of Chile on vital mortality statistics. Specifically, statistics were used on the number of deaths for each cohort, with information available from 2004 to 2021, considering the consolidated official data for the estimates and projections to be made.
It can be observed that life expectancy has increased steadily over the last six decades. This growth in life expectancy is not unique to Chile; it is a global phenomenon. The reasons for the improvement in life expectancy are centred on the sustained increase in the quality of life and the increase in spending on medical services, among other social variables, which have been widely studied in the literature.
We have developed a methodology for estimating the curves that determine life expectancy, based on the temporal evolution of the parameters that determine the mortality of the population, using an ARIMA model. This methodology is based on the projection of the parameters to subsequently estimate the Gompertz–Makeham curve, using a Bayesian approach known as Approximate Bayesian Computation (ABC).
In fact, research such as that presented here can help to define priorities for work, monitoring, and the implementation of measures to improve the weaknesses observed in public systems that use the life expectancy of the population to define their services, which have a significant impact on the economy and that, today, represent a high level of public attention and scrutiny for the politicians and employers responsible for these services in relation to pensions and health systems.
The methodology presented makes it possible to establish the mean value of the shift of the survival curve for the population over the age of 50 and the projections of the best and worst scenarios, which can be interpreted as confidence bands in the prognosis of the survival of the population.
According to the literature, the relevance of the health area for economic growth could be a path of work and planning for the parties involved, with the purpose of focusing on one of their priority problems, such as economic reactivation, with the aim of achieving growth rates, being a reason it is an area of interest in the international arena, drastically reducing poverty and raising per capita income.
Regarding limitations and future directions, we plan to address extreme conditions such as financial crises or pandemic conditions, utilising alternative entropy estimation methods, such as the histogram-based method, to evaluate the predictability of the survival curves in Chile through the maximum entropy method, incorporating extreme volatility data influenced by social contexts. Additionally, as a comparative projection, this study could analyze the strategic weight that a series of variables that have been in the focus of public and private discussions, such as education, sustainability, environmental balance, mental health, gender equality, the modernization of the State, and the democratization of digital technologies.
Author Contributions
Data curation, H.d.l.F.-M., K.C.-J., C.E.-G. and R.R.-T.; formal analysis H.d.l.F.-M., K.C.-J. and R.R.-T.; investigation, H.d.l.F.-M., K.C.-J., C.E.-G. and R.R.-T.; methodology, H.d.l.F.-M., K.C.-J., C.E.-G. and R.R.-T.; writing—original draft, H.d.l.F.-M., K.C.-J., C.E.-G. and R.R.-T.; writing—review and editing, H.d.l.F.-M., K.C.-J., C.E.-G. and R.R.-T. All authors have read and agreed to the published version of the manuscript.
Funding
The research work of H. de la Fuente-Mella was partially supported by Proyecto FONDECYT Regular. Código del Proyecto: 1230881. Agencia Nacional de Investigación y Desarrollo de Chile (ANID).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alaimo, L.S.; Levantesi, S.; Nigri, A. Fuzzy clustering of the healthy life expectancy decomposition: A multi-population analysis. Socio-Econ. Plan. Sci. 2024, 92, 101805. [Google Scholar] [CrossRef]
- Cho, H.; Wang, Z.; Yabroff, K.R.; Liu, B.; McNeel, T.; Feuer, E.J.; Mariotto, A.B. Estimating life expectancy adjusted by self-rated health status in the United States: National health interview survey linked to the mortality. BMC Public Health 2022, 22, 141. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.; Ko, W.; Muhwava, W.; Choi, Y.; Kim, H.; Park, Y.S.; Jambere, G.B.; Cho, Y. Mind the gaps: Age and cause specific mortality and life expectancy in the older population of South Korea and Japan. BMC Public Health 2020, 20, 819. [Google Scholar] [CrossRef] [PubMed]
- Roubal, A.M.; Pollock, E.A.; Gennuso, K.P.; Blomme, C.K.; Givens, M.L. Comparative methodologic and practical considerations for life expectancy as a public health mortality measure. Public Health Rep. 2022, 137, 255–262. [Google Scholar] [CrossRef] [PubMed]
- Congdon, P. Life expectancies for small areas: A Bayesian random effects methodology. Int. Stat. Rev. 2009, 77, 222–240. [Google Scholar] [CrossRef]
- Peters, G.W.; Fan, Y.; Sisson, S.A. On sequential Monte Carlo, partial rejection control and approximate Bayesian computation. Stat. Comput. 2012, 22, 1209–1222. [Google Scholar] [CrossRef]
- Brønnum-Hansen, H.; Foverskov, E.; Andersen, I. Income inequality in life expectancy and disability-free life expectancy in Denmark. J. Epidemiol. Community Health 2021, 75, 145–150. [Google Scholar] [CrossRef]
- Camargos, M.C.S.; do Nascimento Rodrigues, R.; Machado, C.J. Healthy life expectancy to Brazilian elders, 2003. Ciência Saúde Coletiva 2009, 14, 1903. [Google Scholar] [CrossRef]
- Sandoval, M.H.; Alvear Portaccio, M.E.; Albala, C. Life expectancy by ethnic origin in Chile. Front. Public Health 2023, 11, 1147542. [Google Scholar] [CrossRef]
- DuGoff, E.H.; Canudas-Romo, V.; Buttorff, C.; Leff, B.; Anderson, G.F. Multiple chronic conditions and life expectancy: A life table analysis. Med. Care 2014, 52, 688–694. [Google Scholar] [CrossRef]
- Tyrer, F.; Chudasama, Y.V.; Lambert, P.C.; Rutherford, M.J. Flexible parametric methods for calculating life expectancy in small populations. Popul. Health Metrics 2023, 21, 13. [Google Scholar] [CrossRef] [PubMed]
- Kamerud, D.B. Mortality risk and life expectancy. J. Oper. Res. Soc. 1989, 40, 199–200. [Google Scholar] [CrossRef]
- Wajiga, G.; Adekola, O.A. Life-expectancy in a nonhomogeneous population. J. Oper. Res. Soc. 1998, 49, 1011–1012. [Google Scholar] [CrossRef]
- Ho Dang, P.; Nguyen, T.N. New methods of life expectancy estimation. Environ. Ecol. Stat. 2022, 29, 587–606. [Google Scholar] [CrossRef]
- Cairns, A.J.; Blake, D.; Dowd, K.; Coughlan, G.D.; Khalaf-Allah, M. Bayesian stochastic mortality modelling for two populations. ASTIN Bull. J. IAA 2011, 41, 29–59. [Google Scholar]
- Pham, H.; Pham, H.T. A Bayesian approach for multi-stage models with linear time-dependent hazard rate. Monte Carlo Methods Appl. 2019, 25, 307–316. [Google Scholar] [CrossRef]
- Kim, Y.; Kang, S.B.; Berliner, L.M. Bayesian diffusion process models with time-varying parameters. J. Korean Stat. Soc. 2012, 41, 137–144. [Google Scholar] [CrossRef]
- Poon, A.; Zhu, D. A new Bayesian model for contagion and interdependence. Econom. Rev. 2022, 41, 806–826. [Google Scholar] [CrossRef]
- Li, H.; Tan, K.S.; Tuljapurkar, S.; Zhu, W. Gompertz law revisited: Forecasting mortality with a multi-factor exponential model. Insur. Math. Econ. 2021, 99, 268–281. [Google Scholar] [CrossRef]
- Colchero, F.; Kiyakoglu, B.Y. Beyond the proportional frailty model: Bayesian estimation of individual heterogeneity on mortality parameters. Biom. J. 2020, 62, 124–135. [Google Scholar] [CrossRef]
- Melnikov, A.; Romaniuk, Y. Evaluating the performance of Gompertz, Makeham and Lee–Carter mortality models for risk management with unit-linked contracts. Insur. Math. Econ. 2006, 39, 310–329. [Google Scholar] [CrossRef]
- Yan, H.; Peters, G.W.; Chan, J. Mortality models incorporating long memory for life table estimation: A comprehensive analysis. Ann. Actuar. Sci. 2021, 15, 567–604. [Google Scholar] [CrossRef]
- Delwarde, A.; Denuit, M.; Eilers, P. Smoothing the Lee–Carter and Poisson log-bilinear models for mortality forecasting: A penalized log-likelihood approach. Stat. Model. 2007, 7, 29–48. [Google Scholar] [CrossRef]
- Giacometti, R.; Bertocchi, M.; Rachev, S.T.; Fabozzi, F.J. A comparison of the Lee–Carter model and AR–ARCH model for forecasting mortality rates. Insur. Math. Econ. 2012, 50, 85–93. [Google Scholar] [CrossRef]
- Beaumont, M.A.; Cornuet, J.M.; Marin, J.M.; Robert, C.P. Adaptive approximate Bayesian computation. Biometrika 2009, 96, 983–990. [Google Scholar] [CrossRef]
- Toni, T.; Welch, D.; Strelkowa, N.; Ipsen, A.; Stumpf, M.P. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface 2008, 6, 187–202. [Google Scholar] [CrossRef] [PubMed]
- Sisson, S.A.; Fan, Y.; Tanaka, M.M. Sequential monte carlo without likelihoods. Proc. Natl. Acad. Sci. USA 2007, 104, 1760–1765. [Google Scholar] [CrossRef] [PubMed]
- Marjoram, P.; Molitor, J.; Plagnol, V.; Tavaré, S. Markov chain Monte Carlo without likelihoods. Proc. Natl. Acad. Sci. USA 2003, 100, 15324–15328. [Google Scholar] [CrossRef]
- Rubilar-Torrealba, R.; Chahuán-Jiménez, K.; de la Fuente-Mella, H. A Stochastic Analysis of the Effect of Trading Parameters on the Stability of the Financial Markets Using a Bayesian Approach. Mathematics 2023, 11, 2527. [Google Scholar] [CrossRef]
- Roffia, P.; Bucciol, A.; Hashlamoun, S. Determinants of life expectancy at birth: A longitudinal study on OECD countries. Int. J. Health Econ. Manag. 2023, 23, 189–212. [Google Scholar] [CrossRef]
- Kabir, M. Determinants of life expectancy in developing countries. J. Dev. Areas 2008, 41, 185–204. [Google Scholar] [CrossRef]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. In a letter to Francis Baily, Esq. FRS &c. By Benjamin Gompertz, Esq. FR S. Philos. Trans. R. Soc. Lond. 1825, 115, 252–253. [Google Scholar]
- Makeham, W.M. On the law of mortality and the construction of annuity tables. J. Inst. Actuar. 1860, 8, 301–310. [Google Scholar] [CrossRef]
- Hallén, A. Makeham’s addition to the Gompertz law re-evaluated. Biogerontology 2009, 10, 517–522. [Google Scholar] [CrossRef] [PubMed]
- Golubev, A. How could the Gompertz–Makeham law evolve. J. Theor. Biol. 2009, 258, 1–17. [Google Scholar] [CrossRef]
- Missov, T.I. Gamma-Gompertz life expectancy at birth. Demogr. Res. 2013, 28, 259–270. [Google Scholar] [CrossRef]
- Missov, T.I.; Lenart, A. Gompertz–Makeham life expectancies: Expressions and applications. Theor. Popul. Biol. 2013, 90, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Stock, J.H.; Watson, M.W. Median unbiased estimation of coefficient variance in a time-varying parameter model. J. Am. Stat. Assoc. 1998, 93, 349–358. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, L. Additive hazards regression with missing censoring information. Stat. Sin. 2003, 1237–1257. [Google Scholar]
- van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J.; et al. Bayesian statistics and modelling. Nat. Rev. Methods Prim. 2021, 1, 1. [Google Scholar] [CrossRef]
- Winklevoss, H.E. Pension Mathematics with Numerical Illustrations; University of Pennsylvania Press: Philadelphia, PA, USA, 1993. [Google Scholar]
- Rostan, P.; Belhachemi, R.; Rostan, A. Appraising the financial sustainability of a pension system with signal processing. Stud. Appl. Econ. 2015, 33, 801–816. [Google Scholar] [CrossRef]
- Queiroz, B.L.; Ferreira, M.L.A. The evolution of labor force participation and the expected length of retirement in Brazil. J. Econ. Ageing 2021, 18, 100304. [Google Scholar] [CrossRef]
- Salinari, G.; De Santis, G. One or more rates of ageing? The extended gamma-Gompertz model (EGG). Stat. Methods Appl. 2020, 29, 211–236. [Google Scholar] [CrossRef]
- Baeten, S.; Van Ourti, T.; Van Doorslaer, E. Rising inequalities in income and health in China: Who is left behind? J. Health Econ. 2013, 32, 1214–1229. [Google Scholar] [CrossRef]
- Carter, L.R.; Lee, R.D. Modeling and forecasting US sex differentials in mortality. Int. J. Forecast. 1992, 8, 393–411. [Google Scholar] [CrossRef]
- Conde-Gutiérrez, R.; Colorado, D.; Hernández-Bautista, S. Comparison of an artificial neural network and Gompertz model for predicting the dynamics of deaths from COVID-19 in México. Nonlinear Dyn. 2021, 104, 4655–4669. [Google Scholar] [CrossRef]
- Mohamed, H.S.; Ali, M.M.; Yousof, H.M. The Lindley Gompertz Model for Estimating the Survival Rates: Properties and Applications in Insurance. Ann. Data Sci. 2023, 10, 1199–1216. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).