Abstract
This study investigates dynamic behaviors within a competition Cournot duopoly framework incorporating consumer surplus, and social welfare through the bounded rationality method. The distinctive aspect of the competition game is the incorporation of discrete difference equations into the players’ optimization problems. Both rivals seek to achieve optimal quantity outcomes by maximizing their respective objective functions. The first firm seeks to enhance the average between consumer surplus and its profit, while the second firm focuses on its profit optimization with a social welfare component. The game map features four fixed points, with one being the Nash equilibrium point at the intersection of marginal objective functions. Our analysis explores equilibrium stability, dynamic complexities, basins of attraction, and the emergence of chaos through double routes via flip bifurcation and Neimark-Sacker bifurcations. We observe that increased adjustment speeds can destabilize the system, leading to a richness of dynamic complexity.
1. Introduction
When a business is operating, its managers frequently only consider their own earnings and disregard corporate societal responsibilities (CSR). They believe that participating in CSR will raise product prices, which will have an impact on company profits. CSR and corporate earnings appear to be at odds with one another. However in reality, CSR will undoubtedly boost businesses’ profits. More precisely, integrating CSR impact means that businesses should consider the community, the environment, and customers when generating earnings for their stockholders and staff. Additionally, CSR mandates that companies focus on elements of human value in the manufacturing process, the ecosystem, and consumer behavior rather than profit as their only objective. As a result, the company will forge a regarded reputation among clients and the general public. Customers will consequently implicitly believe that the company’s goods are higher caliber and more dependable. Customers are likely to make purchases, and the business will make more money. Given the context mentioned above, many businesses now seek CSR initiatives as opposed to their original goal of profit growth. Several scholars have examined and analyzed how static games incorporate CSR in their research [1,2,3,4,5,6,7,8,9]. According to Zhou et al. research [10], the duopoly game created by taking into account consumer surplus and bounded reasoning are more practical than the standard duopoly game, which is limited to focusing on maximizing profits. An incorporated oligopoly with a publicly traded firm competing against two private companies that may adopt CSR is analyzed in [11]. The study identifies optimal privatization regulations based on CSR levels and price differences, highlighting nationalization or full privatization as possible outcomes.The balance occurs in a dual-monopoly industry where companies engage in CSR activities with management oversight. The financial prosperity of the companies (as opposed to the well-being of customers and community) is benefited (as opposed to damaged) by the CSR decisions, as shown in the subgame perfect Nash equilibrium aspect of the competition [12]. Companies social responsibility’s impacts For the CSR company, CSR on the nutritional content of the food business increases both the level of quality and amount of the food, while it decreases those for optimizing revenues company. Furthermore, CSR encourages both the overall business quality and amount. Additionally, CSR lowers the revenue of the MP company but [13] focused on the inverted U-formations connection that exists between CSR and the revenues of the CSR company. Both rival Companies aim to optimize two distinct objective functions; the first a company wants to do this by optimizing the standard of societal welfare and revenue while the second a company only wants to do this by optimizing relative revenue as indicated in [14]. The forms of the quasi that describe the stages plane of a couple of companies whose generates are a lot where the initial company thinks about optimizing its revenue whereas the next company thinks about optimizing its social welfare discover that the model’s route is noninvertible of form have been examined in [15]. A combining triopoly with product distinction and customer perception was proposed by Wen et al. [16] in which quantities rivalry is carried out by a public firm that seeks to maximize welfare and private companies that are interested in CSR. Liu and Matsumura [17] analytically examine how shared ownership influences the total volume of foreign trade in an oligopoly market and its effects on global welfare.
In [18], the bounded rationality method was used to study oligopoly market patterns with customer excess, focusing on global dynamics, stability, and synchronization in a duopoly. Critical curves were introduced to analyze global bifurcation, and a Cournot game with customer excess and limited reasoning was described. Because there are numerous complicated attractors present, multi-stability is seen to address the possibility of varying attractors coexisting, an examination of the regions of attraction are given and the complaints of each company are a mixture of their revenue and the consumer surplus, then a nonlinear duopoly bounded rational companies do not only seek to optimize revenues but also take consumer surplus through consideration in [19].
The dynamic Cournot duopoly model depicts rival companies operating without complete knowledge of the demand function. Due to this informational gap, they adopt a local benefit optimization approach, making adjustments based on marginal revenue approximations within their respective regions. When the marginal prices set by both firms are not excessively high, a non-cooperative Nash equilibrium can be established. When companies exhibit relatively slow adjustment speeds, this equilibrium solution is locally asymptotically stable. This implies that the local adjustment process converges towards the unique Nash equilibrium, provided that the duopoly game begins with an initial output strategy within a well-defined restricted region around the Nash equilibrium, as explored in [20]. The study delves into synchronized dynamics involving a dual non-invertible map with an invariant one-dimensional submanifold, as discussed in [21]. Through investigations into synchronization, intermittency, and the complex organization of attraction collections within discrete-time systems featuring nonlinear demand and price functions, the system reveals intriguing stability and multi-stability issues. Significantly, the study reveals V-shaped stable configurations known as aperiodic stable structures and variously shaped attraction basins that incorporate the convergence of attractors, as outlined in [22]. Additionally, an examination is conducted on the dynamic interactions within a duopoly system consisting of closely matching or nearly identical suppliers to evaluate the impact of minor differences among players. The behavior of these systems transitions towards uneven patterns in the presence of similar entities, hinting at the possibility of achieving synchronized dynamics, as explained in [23,24].
In a dynamic duopoly Cournot model, Y. Cao et al. [25] illustrate that the presence of multiple attractors results in scattered locations within two-dimensional bifurcation diagrams, highlighting the discovery of Milnor attractors and various other attractors. Within the framework of a mixed duopoly dynamic model characterized by bounded rationality, which involves a collaboration between a public-private joint venture and a private firm producing homogeneous goods and operating within a shared market, the investigation detailed in [26] explores the system’s stability and multi-stability. Furthermore, the map representing market heterogeneity with isoelastic demand functions is both nonlinear and noninvertible, necessitating an analysis of stable attractors, as explored in [27,28,29]. The objective presented in [30] is to investigate these dynamics within a banking duopoly model characterized by varying requirements. In this model, small and large financial institutions follow distinct forecasting rules, enabling an assessment of how regulations affect them differently. Notably, the model incorporates an asymmetry in cost structures: small financial institutions adhere to a linear cost function, whereas large financial institutions operate under a quadratic cost function.
According to [3], an oligopoly occurs when a small number of companies that produce unique goods control the market. One usually aims to maximize earnings in oligopoly models. Since one frequently has multiple objectives, this is not realistic. Weights are used to model a multiobjective oligopoly in [1], where both profit and sales maximization are considered. Then, profit maximization is combined with risk minimization. Numerous state-owned public companies compete with private companies in product markets in numerous nations. Government strategy in many developing nations has recently included the partial privatization of public companies. The research that examines the impact of partial privatization on public firms on the choice of R&D risk in a mixed duopoly market is strongly linked to [6]. There has been a recent emergence of literature on “mixed markets,” which include both public and private businesses. Indeed, in many nations, a large number of public companies compete with private companies in the private products market. A mixed oligopoly in which public firms compete with private firms that may adopt corporate social responsibility (CSR) is described by [11,15,31]. Many existing works assume that the public firm maximizes social welfare while the private firm maximizes its own profits. The best privatization strategy is then determined based on the degree of corporate social responsibility and the cost variations across companies; either full privatization or nationalization may be the best option.
This paper aims to explore a game model that incorporates a linear inverse demand function and linear marginal costs. Using a bounded rationality approach, the model is developed by optimizing objectives that balance profit, a share of consumer surplus and weighted social welfare. In our game, the first firm is privately owned and adopts a strategy where its owners maximize the sum of its profit and a share of consumer surplus. The second firm is publicly owned and implements a strategy focused on maximizing a combination of profit and social welfare. The study delves into the analysis of the game model through local stability, examining aspects such as the bifurcations and chaos. The following sections outline the structure of this paper. Section 2 introduces the nonlinear map depicting the current game. Moving on to Section 3, we determine the fixed points of the map and explore its stability criteria. Section 4 conducts a comprehensive analysis of the map’s complex dynamic properties, including bifurcations, periodic cycles, and chaotic attractors. Lastly, Section 5 presents the conclusions drawn from the research.
2. Cournot Model Structure
Throughout this section, the game involves two firms, identified as i, which adopt a strategy based on quantities and offer goods with differentiations. The output levels produced by these firms are represented as . To derive the firms’ demand functions, we must consider the following utility function:
where the parameter denotes the magnitude of the market demand, while indicates the extent of horizontal product differentiation. Assuming the consumer’s budget constraint is:
In this context, M symbolizes the budget allocated by consumers for the product, while denotes the prices of the goods. This setup leads us to the subsequent maximization problem:
Building on [32], one can derive the demand system resulting from this type of product differentiation by starting with a budget constraint. Using the Lagrange method, we formulate the optimization problem (1) to (3), where products are differentiated. The normalized linear (inverse) demand functions, based on quadratic preferences, are presented below. By solving this optimization problem and setting the partial derivative with respect to with respect to to zero, we obtain the inverse demand functions for firms i, in the following manner:
With the cost function of firm i taking the form , where denotes the marginal cost for the firm, we can deduce that
In the business world, many organizations prioritize corporate social responsibility alongside their financial prosperity. Numerous empirical studies have illustrated how the integration of corporate social responsibility impacts business performance, where it is defined in terms of either consumer surplus or social welfare . In this examination, we focus on two firms with distinct objectives due to their differing natures. firm 1 not only aims to maximize its profits but also considers , while firm 2 strives for profit maximization while also factoring in corporate social responsibility considerations. , often termed as consumer surplus, represents the disparity between the total amount consumers were willing to pay for a specific quantity of goods and the actual price paid. Given the context provided, [10,11] can be mathematically expressed as:
We regarded social welfare is used to represent corporate social responsibility (CSR). Consumer surplus (CS) and the income of two firms are combined to form the ,
Kople [5] examines the endogenous selection of a quantity or price contract in a mixed duopoly with a socially conscious company that optimizes both consumer welfare and profit. Price-quantity contracts may coexist in equilibrium, welfare may be lower in price competition than in quantity competition and the businesses’ profit ranking may differ from that of a private duopoly or a mixed duopoly with a public enterprise. Therefore, the degree of social concern and market competition play a critical role in determining the best market strategy for a company that employs a social strategy. Lihua Han [7] notes that in order to investigate the impact of companies’ corporate social responsibility (CSR) initiatives on the privatization of a public company, CSR is incorporated into a conventional mixed oligopoly. Profits and consumer surplus are taken into account by private CSR companies. It has been demonstrated that as the proportion of consumer surplus that CSR enterprises consider rises, the ideal level of nationalization or privatization falls. Put another way, when the private companies are CSR rather than just profit-maximizing, the government need to own a larger portion of the partially privatized company. Additionally, we discover that it is socially desirable for CSR companies to somewhat (but not entirely) take into account the advantages of their customers.
Building on [5,7] we assume the first firm, as a private company (Private CSR firm), seeks to maximize the combined value of its profit and a share of the consumer surplus, embodying its socially responsible approach. In accordance with the aforementioned hypotheses above, the objective function of firm 1 may be expressed as follows:
Here, represents firm 1’s profit, while belongs to the interval , indicates the exogenously determined level of social concern. is the proportion of consumer surplus (shows how important social responsibility is to each private company’s intended purpose). Stakeholders of firm1 will have if the entire amount is captured, and if none is. This parameter indicates the extent to which the first firm prioritizes consumer surplus in its decision-making. The incentive scheme outlined in (8) incorporates a weighting of consumer surplus, emphasizing the strategic role of social responsibility (as discussed in [2,4,9]). The parameter represents the weight the owner (the first player) assigns to consumer surplus, reflecting the private firm’s level of social responsibility.
However, the objective function of firm 2 can be formulated differently. The second firm, as a public company, strives to maximize its objective function by combining profit and social welfare. Since this study considers a public firm, its goal is not only to maximize its own profit but also to take social welfare into account. Therefore, the objective function of this firm can be expressed as follows:
where represents the degree of public ownership of the second firm. If means that firm 2 is a complete public firm and it maximizes the social welfare while means that firm 2 is a complete private firm. In this contract, as stated in [9], the manager’s compensation is determined by a convex linear combination of profits and social welfare. Consequently, the weight assigned to social welfare can be greater than, less than, or equal to the weight assigned to profits. When this parameter is set below one, it encourages the manager to adopt a more aggressive market approach by operating with a lower marginal cost.
Establishing the information sets of both firms in relation to the objective function is essential for understanding how firm behavior evolves over time. The concept of bounded rationality offers a different perspective, acknowledging that players may not always fully comprehend each other’s actions or make perfectly rational decisions. As a result, firms determine their output based on expected marginal payoffs. In a dynamic competitive environment, players with bounded rationality may not be able to make optimal decisions instantly. Instead, they gradually refine their strategies based on marginal profits. For instance, if a firm experiences a positive marginal profit in the current period, it is likely to assume that increasing its investment in the next period will enhance profitability. Conversely, if it incurs a negative marginal profit, it will likely scale back its investment in the following period to mitigate losses. This adaptive decision-making process closely reflects real-world business behavior in complex and uncertain environments. Many researchers [18,19,20,21,22,23,24,25,26,27,28] refer to this specific mechanism as the dynamic gradient adjustment mechanism.
In this model, we consider that two firms with restricted rationality make choices concurrently in a discrete-time dynamic environment. That is, all firms have little knowledge about the choices made by their rivals and the needs of the market. To determine the output at period , they can only utilize the local estimation of the objective function’s sharpest slope at period t. The quantity adjustment method for company i concerning time may be determined by applying F. Wu et al. [33] and is given as follows:
where represents the net profits of the firm at time t, while captures the rate at which the quantity adjustment for firm i responds to a marginal change in profits denoted by . If , the firm will increase its output in period ; conversely, if , the firm will decrease its output in period . By combining Equations (10) and (11), we derive the two-dimensional nonlinear map that illustrates the dynamics of the game:
The adjustment speed reflects how rapidly firms react to changes in their marginal profit signals. By analyzing model (12), we can identify the benefits firms gain, the achievement of their objectives, and the overall market stability when two firms choose different parameters. Furthermore, this study enables us to predict firms’ development status and trends under specific fixed parameter combinations. These insights provide theoretical guidance for managers and business owners, helping them navigate the market more effectively and ensure stable growth.
3. Dynamic Behavior of the Equilibrium Points
This section is dedicated to analyzing the stability criteria of equilibrium points within the given model under different parameter settings. To simplify computation, we introduce specific quantities such that , , , and , thus simplifying model (12) to:
The Nash equilibrium is considered a set of strategies where a modification in the strategy of any participant does not lead to an enhancement in the profits of all involved parties. As a result, to optimize their gains, each participant persists with their current strategy. Table 1 summarizes the stability of the Nash equilibrium solution within model (13).

Table 1.
Stability of the model’s Nash equilibrium solution.
So, we can get four points of equilibrium for model (13) through calculation as follows:
We refer to the equilibrium points , , and as border equilibrium points since they are all on the coordinate axis, whereas is also known as a Nash equilibrium point or an internal equilibrium point. The positivity of equilibrium point is guaranteed since can never be negative, and for equilibrium point to be non-negative, it is essential that . In cases where the selected parameters align with economic significance, the condition of non-negativity is consistently met. Therefore, the aforementioned parameters must fulfill at least one of the following criteria for equilibrium point to remain non-negative:
or
3.1. Stability of the Border Equilibrium
We investigate the four equilibria mentioned above for stability. Let’s start by calculating the Jacobian matrix for model (13) at any position, as shown below.
Four equilibrium points are individually substituted into matrix (17) to produce the Jacobian matrices of each equilibrium point. The eigenvalues of each equilibrium point’s Jacobian matrix are then calculated to ascertain the kind and stability of the point.
Proposition 1.
The trivial equilibrium is unstable source node.
Proof.
It is evident that the Jacobian matrix at has the following structure:
It is evident that forms a diagonal matrix. Consequently, the eigenvalues can be expressed as where The parameters and A being non-negative allows us to determine that both the moduli of and are greater than 1. As a result of both eigenvalues being beyond the unit circle, then node is unstable. □
Proposition 2.
Borderline equilibrium point has at least four distinct topological types for every value of the parameters:
- 1.
- is a sink stable point if and
- 2.
- is unstable source node if and
- 3.
- is a saddle point for the other values of parameters except the values in (1) and (2),
- 4.
- is a non-hyperbolic point if and .
Proof.
Through computation, we can find the Jacobian matrix at the equilibrium point , which is depicted as:
which has two eigenvalues,
Since for values , (1): If and then hence if, This leads to is a sink stable point. (2): If and then hence if In this case, is an unstable source node. (3): For the other values of parameters except the values in (1) and (2) is a saddle point, (i.e.) if and and if then (4): It is clear that one of these eigenvalues of equals 1, while the other is neither 1 nor −1. Then, each parameter is found in the following area:
Consequently, may undergo a flip bifurcation as the parameters vary within a small vicinity of □
Proposition 3.
Borderline equilibrium point has at least four distinct topological types for every value of the parameters:
- 1.
- is a sink stable point if and
- 2.
- is unstable source node if and
- 3.
- is a saddle point if and
- 4.
- is a non-hyperbolic point if and
Proof.
Substitute into , then the Jacobian matrix of model (13) at point takes the form:
we derive two related eigenvalues of such as form:
Since for values , (1): If and then hence if, This leads to is a sink stable point. (2): If and then hence if In this case, is an unstable source node. (3): For and then and if, at this moment is a saddle point. (4): is an unstable node in all other respects. The possibility of a flip bifurcation should be noted at the following region:
□
3.2. Nash Equilibrium Stability
In the field of economics, the boundary equilibrium point signals the failure of two firms, whereas and exemplify a situation where one firm dominates the market, resulting in a monopoly. Generally, a stable Nash equilibrium point in the economic market signifies that both firms ensure the market’s steady growth while securing their own profits. Following this, we will assess the local stability of . Determining the eigenvalues linked with matrix (17) directly at the Nash equilibrium point is intricate due to the complex structure of the matrix in that specific context. However, by using merely the Jury criteria [34], we may investigate the local stability of . The following form can be used to represent the matrix of the system (13) at :
Then the trace and determinant of the matrix can be obtained as:
By utilizing the Jury criteria, we can assess the local stability of . Meeting all the conditions outlined in the Jury requirement allows us to establish the asymptotic stability of the Nash equilibrium . The specific expression of the Jury criteria is as follows:
The above set of inequalities may be calculated using a complicated formula if we replace the particular mathematical expressions of and into the aforementioned equations:
As a result, Equation (24) illustrates the stable domain of . Failure to satisfy the first criterion may lead to a fold bifurcation, a transcritical bifurcation, or a pitchfork bifurcation. If the second criterion is not fulfilled, a flip bifurcation could occur. Additionally, the Neimark-Sacker bifurcation might occur if the third criterion is not satisfied.
Proposition 4.
The unique Nash equilibrium is stable if and only if condition (24) holds.
The stability criteria of four equilibria are given by the aforementioned assertions. Decision-makers can influence a company’s behavior in the real economic market by ensuring that certain requirements are satisfied, such as stability, and by selecting parameters that fall within the range of stability. This will allow the firm to grow steadily or arrive at the desired state. We provide a demonstration with several examples to validate the accuracy of our results and to elaborate on how parameters influence the stable region. This discussion explores the system’s behavior, showing how it transitions between chaos and stability for certain parameter values. It also examines how changes in parameters affect the stability of the Nash equilibrium, illustrated with a clear bifurcation diagram. This helps validate the results and provides a better understanding of the system’s dynamics.
4. Numerical Simulation
In this section, we will delve into an in-depth examination of the complex dynamical patterns exhibited by model (13). We will employ numerical simulation methods to thoroughly explore the system’s behaviors and characteristics. This section studies the game’s dynamics. It focuses on how differences in objectives affect behavior under the gradient rule. It examines how the stability threshold changes with each firm’s level of CSR. The analysis explores whether CSR and social welfare stabilize or destabilize market equilibrium. It aims to understand the impact of CSR on market robustness. We will conduct a thorough investigation into the appearance of a flip bifurcation and a Neimark-Sacker bifurcation through comprehensive numerical simulations. These simulations will involve the use of bifurcation transition diagrams, computations of the maximum Lyapunov exponent (MLE) for assessing chaos, phase plane diagrams to visualize system trajectories, and an array of related techniques. By employing these tools, we aim to gain a detailed understanding of the system’s behavior at critical points and transitions [35].
Considering a specific set of constant parameters, namely and , Figure 1 depicts the alteration in the stable region within the parameter planes of and . Figure 1a, demonstrates the system’s stable area and bifurcation curves when , curves are shown by the curves, the flip bifurcation curve by the black arc, and the green curve shows Neimark-Sacker bifurcation and the stable zone of the system is defined as the region enclosed by the blue and green bifurcation curves. In the detailed analysis presented in Figure 1b, focusing on an alternate parameter configuration denoted by , a comprehensive exploration of the system’s behavior unfolds. As the system evolves, the pivotal moment arises when either or traverses the green curve within the stability domain. At this juncture, the stable Nash equilibrium point experiences a critical loss of stability, marking the onset of a Neimark-Sacker bifurcation. Subsequently, the system undergoes a transformative phase as the value of or surpasses the blue curve within the stability domain, initiating a flip bifurcation. This bifurcation event propels the system into a regime where it oscillates between periods 1 and 2, periods 4 and 8, and further periodic intervals. This progressive transition towards chaos signifies a significant shift in the system’s dynamics, eventually leading to a state of intricate and unpredictable behavior. Figure 1c displays the system’s stable zone and bifurcation curves with an emphasis on parameters , ranging in . The system will traverse the flip bifurcation curves, as indicated by the black curve. A flip bifurcation will cause to lose its stability, for example, if we choose parameters like . Following this type of bifurcation, a pair of stable fixed points and stable period-4 fixed points will emerge one after the other.
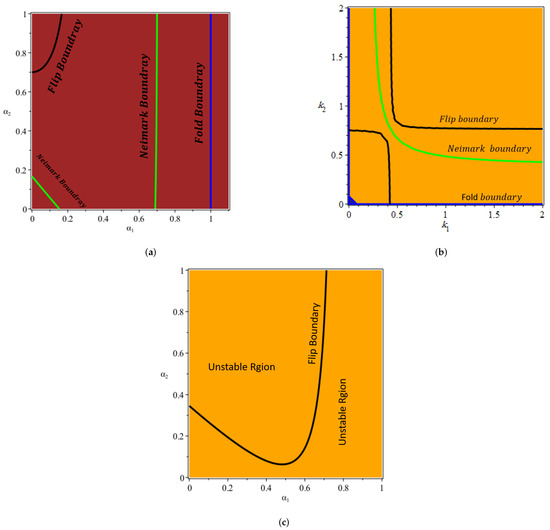
Figure 1.
The stable region in the parameters plane for model (13). (a) The stability region for . (b) The stability region for . (c) The stability region for .
The red curve in Figure 2 represents the outputs of firm 1, whereas the blue curve represents the outputs of firm 2. The bifurcation parameters are and with initial condition , and we fix the parameter values, and . The rate of quantity adjustment for enterprise 2 is determined by as the bifurcating parameter first in Figure 2a when enterprise 1 is a fully private enterprise and , According to these bifurcation diagrams, both firms’ outputs are stable throughout the interval , as is the distinct positive Cournot-Nash equilibrium point . However, during flip bifurcation, the system enters chaos when reaches the critical value A 2D bifurcation diagram for the rate of quantity adjustment for firm 1, , with parameters , . This is shown in Figure 2b. For instance, the output systems of both businesses are stable and disturbed when as The system’s dynamical behavior is extremely complex between . A period-doubling bifurcation, sometimes called a period-halving bifurcation, is caused by an increase in When , four multiperiodic windows may be observed, and the system thereafter descends into chaos. We look at how the differentiation index affects system stability in Figure 2c. For parameters , , indicating that firm 2 is completely private and solely wants to maximize its own profit. When the degree of public ownership of firm 1 satisfies , system (13) is in a period-1 stable state, indicating that the market has stabilized and that the stakeholders of firm 1 will have a partial amount of social responsibility. This indicates that has a significant impact on the stability of the system. Moreover, flip bifurcation is seen to occur as the parameters continue to change (i.e., as lowers ), it indicates that the market would be unstable when firm 1 gets completely private. To analyze the impact of fully privatizing firm1 on the market, we show the parameters in Figure 2d We find that firm 2’s output stabilizes when and that the sum of the producer and consumer surpluses is greatest at the ideal level of nationalization.
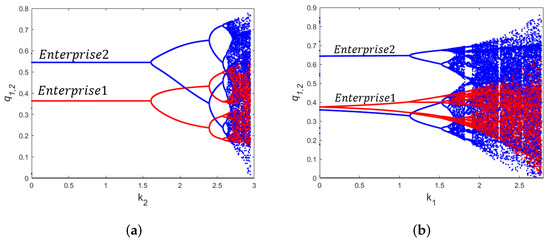
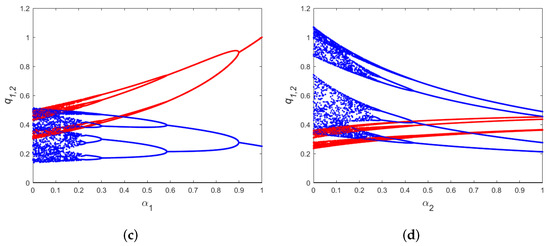
Figure 2.
The 1-D bifurcation diagrams for for model (13) with varying values of parameters. (a) The 1-D bifurcation diagrams for for model (13) with respect to when (b) The 1-D bifurcation diagrams for for model (13) with respect to when (c) The 1-D bifurcation diagrams for for model (13) with respect to when (d) The 1-D bifurcation diagrams for for model (13) with respect to when
An evident chaotic perturbation emerges, as depicted by the Lyapunov exponent breaching zero during the tangential bifurcation phase for the fixed parameters , as illustrated in Figure 3. By analyzing the Lyapunov exponent diagram in Figure 3a with specific values , distinctions among stable, quasi-periodic, chaotic, and divergent states become discernible. When the maximum Lyapunov exponent remains below 1 concerning , the dynamical system corresponds to either a periodic or stable state. For a varied range of values with , an examination of the average Lyapunov exponent reveals the periodic nature of the system’s orbit when the value is negative. This observation is highlighted in Figure 3b, distinguishing the system’s behavior under different conditions. Figure 3c, where is taken as the variable parameter, for fixed parameters and Figure 3d, where is taken as the variable parameter, for fixed parameters are provide the transverse Lyapunov exponent.
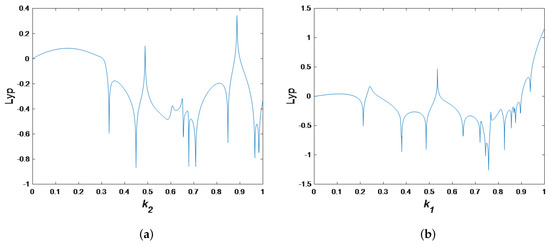
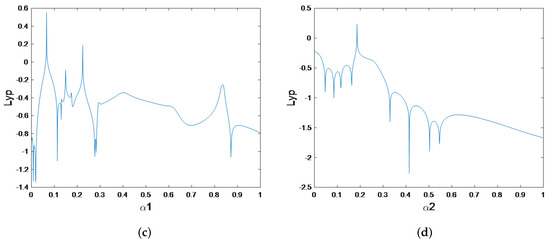
Figure 3.
Largest Lyapunov exponents diagrams for model (13) with varying values of parameters. (a) Largest Lyapunov exponents diagrams for model (13) with respect to associated with Figure 2a. (b) Largest Lyapunov exponents diagrams for model (13) with respect to associated with Figure 2b. (c) Largest Lyapunov exponents diagrams for model (13) with respect with respect to associated with Figure 2c. (d) Largest Lyapunov exponents diagrams for model (13) with respect to associated with Figure 2d.
The attractor is a period-1 takes place when the parameters which can be seen in Figure 4a. Fixed the parameters as the numerical simulation can provide the attractor under various weights of Figure 4b describes 2-cycle of model (13) for While when the parameters varied as we can see the portrait starts to create new phenomena due to breakdown of the invariant closed curve, in Figure 4c. As seen in Figure 4d, the broken attractor keeps spreading and merging to generate two invariant closed curve as . Figure 4e,f show the dynamic behaviors that two previously stated chaotic attractors exhibit as they expand and combine to produce a single chaotic attractor component.
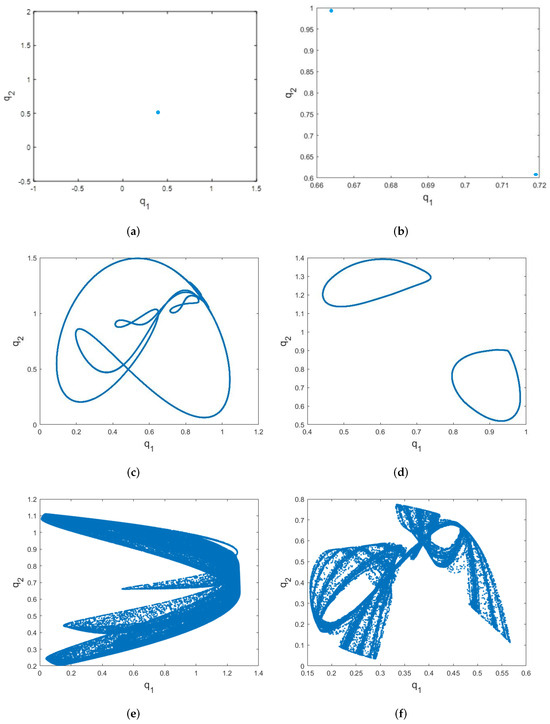
Figure 4.
Visualization of phase portraits for model (13) with varying values of parameters (a) The phase portrait for model (13) when (b) The phase portrait for model (13) when (c) The phase portrait for model (13) when (d) The phase portrait for model (13) when (e) The phase portrait for model (13) when (f) The phase portrait for model (13) when
Figure 5 shows the chart of dynamic modes for fixed parameters It is commonly known that the dynamic modes chart can show the market strategy area of these two firms. Various periodic modes are denoted by various colors in Figure 5. The Color bar is located on the right side of the dynamic modes chart and provides readers with further information about each color’s specific meaning. A quasiperiodic state or a chaotic state with a period longer than 30 is represented by the red zone in the diagram of dynamic modes. In Figure 5a, the dynamic modes are portrayed within the parameter plane of with and . Transitioning to Figure 5b, which represents the chart of dynamic modes in the parameter plane with and , the system exhibits a bifurcation sequence as increases. This progression is characterized by a shift from period-1 to period-2, then from period-2 to period-4, and so forth, eventually culminating in a chaotic state. Moving on to Figure 5c with while considering as variable parameters, the system cyclically transitions through periods 1, 2, 4, and beyond. Through a flip bifurcation, the stable Nash equilibrium point loses stability, transforming into a stable period-2 cycle. Subsequently, a Neimark-Sacker bifurcation induces the stable period-2 cycle to lose stability, leading to the emergence of a quasiperiodic state, as elucidated in Figure 5d. Finally, Figure 5e illustrates the system progressing through period-4, period-8, period-16, and onward, ultimately transitioning into a chaotic state. This comprehensive visual depiction encapsulates the system’s evolution through various dynamic states as influenced by the interplay of parameters and bifurcation phenomena.
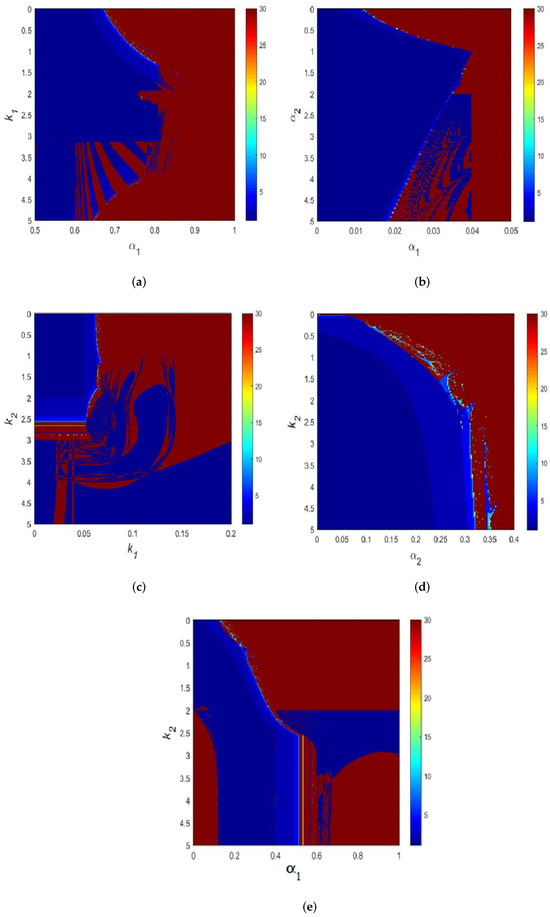
Figure 5.
The dynamic modes of model (13) with varying values of parameters. (a) The dynamic modes of model (13) in plane , when (b) The dynamic modes of model (13) in plane , when (c) The dynamic modes of model (13) in plane , when (d) The dynamic modes of model (13) in plane , when (e) The dynamic modes of model (13) in plane , when
5. Conclusions
This study introduces a Cournot model using heterogeneous products as its foundation. Building upon the interplay between corporate social responsibility and business strategies within oligopolistic competition, a dynamic Cournot duopoly model is formulated with considerations for bounded rationality. Given the distinct objectives of both firms involved, firm 1 aims to maximize its profits while factoring in consumer surplus (CS), whereas firm 2 seeks profit maximization while also prioritizing social welfare (W). To delve deeper, a combination of analytical methods and numerical simulations is employed to explore the local stability and intricate dynamical behaviors exhibited by the system. Through our analysis, we uncover instances of the Neimark-Sacker bifurcation within the model, impacting the local stability of each equilibrium point and leading to system-wide fluctuations and instability. The analysis examined how the dynamics of the game map are influenced by the degree of social responsibility, which was considered a crucial parameter. The research explored the effect of the degree substitutability on the overall stability of the market. It was observed that as the degree of substitutability goods (or complementarity) between products increases, the market loses stability through the period-doubling bifurcation, followed by a repeating flip cascade, leading to chaotic behavior. It has been observed that the onset of chaotic dynamics results in a reduction in the level of the degree of social responsibility. Moreover, our investigation reveals that key parameters such as , , and d play a pivotal role in determining the stability region of the Nash equilibrium point. Numerical simulations are then utilized to analyze the dynamic behaviors of the model, employing various techniques such as bifurcation diagrams, maximum Lyapunov exponents and basins of attraction to illustrate the intricate dynamics of the system (13).
From Figure 1 and Figure 2, our dynamic analysis reveals that under the gradient rule, instability arises in the game. Specifically, there exists a threshold for the adjustment speed beyond which the Nash equilibrium becomes unstable. Surpassing this threshold triggers a cascade of flip bifurcations, leading to increasingly complex attractors. This finding aligns with existing research on nonlinear oligopoly dynamics. Moreover, a higher specific weight of consumer surplus in the objective function of the socially responsible firm expands the range of adjustment speed values that ensure Nash equilibrium stability. In particular, when the weight assigned to corporate social responsibility (CSR) is relatively low and the first firm is reluctant to adjust its quantity, greater social welfare from the public firm enhances market stability.
Furthermore, a detailed examination of the system’s complex dynamical behaviors is conducted through the presentation of dynamic modes with diverse parameter combinations. The study also investigates the intricate structures of attraction basins within the proposed game’s two-dimensional non-invertible map. In conclusion, our research underscores the potential negative impact of chaos on oligopoly games with societal welfare, highlighting the importance of understanding and managing complex dynamical systems in economic contexts.
Author Contributions
Conceptualization, A.A.E., A.M.A. (A. M. Awad) and A.M.A. (Abdullah M. Adawi); methodology, A.A.E., A.M.A. (A. M. Awad) and A.M.A. (Abdullah M. Adawi); software, A.M.A. (A. M. Awad) and A.M.A. (Abdullah M. Adawi); validation, A.A.E., A.M.A. (A. M. Awad) and A.M.A. (Abdullah M. Adawi); supervision: A.A.E.; simulations: A.A.E., A.M.A. (A. M. Awad) and A.M.A. (Abdullah M. Adawi); writing and editing: A.A.E., A.M.A. (A. M. Awad) and A.M.A. (Abdullah M. Adawi). All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2024/01/31914).
Institutional Review Board Statement
This article does not contain any studies with human participants or animals performed by any of the authors.
Data Availability Statement
All data included in this manuscript are available upon request by contacting with the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ahmed, E.; Hegazi, A.S.; Abd El-Hafez, A.T. On Multiobjective Oligopoly. Nonlinear Dyn. Psychol. Life Sci. 2003, 7, 205–219. [Google Scholar] [CrossRef] [PubMed]
- Fanti, L.; Buccella, D. Corporate social responsibility in a game-theoretic context. Econ. Politica Ind. 2017, 44, 371–390. [Google Scholar] [CrossRef]
- Fanti, L.; Gori, L. The Dynamics of a Bertrand Duopoly with Differentiated Products and Bounded Rational Firms Revisited. MPRA Paper No. 33268, Posted 9 September 2011 14:51 UTC. Available online: https://mpra.ub.uni-muenchen.de/33268/ (accessed on 10 May 2025).
- Kopel, M.; Brand, B. Socially responsible firms and endogenous choice of strategic incentives. Econ. Model. 2012, 29, 982–989. [Google Scholar] [CrossRef]
- Kopel, M. Price and Quantity Contracts in a Mixed Duopoly with a Socially Concerned Firm. Manage. Decis. Econ. 2015, 36, 559–566. [Google Scholar] [CrossRef]
- Xing, M. Partial Privatization Policy and the R&D Risk Choice in a Mixed Duopoly Market. Manch. Sch. 2019, 87, 60–80. [Google Scholar]
- Han, L. Partial ownership for a public firm and corporate social responsibility. Theor. Econ. Lett. 2019, 9, 2447. [Google Scholar] [CrossRef][Green Version]
- Bárcena-Ruiz, J.C.; Garzón, M.B.; Sagasta, A. Partial privatization and the degree of corporate social responsibility of private investors. Econ. Model. 2024, 141, 106892. [Google Scholar] [CrossRef]
- Andaluz, J.; Jarne, G. Static and dynamic approaches to corporate social responsibility as a strategic tool. J. Dyn. Games 2025. [Google Scholar] [CrossRef]
- Zhou, W.; Cao, Y.; Elsonbaty, A.; Elsadany, A.A.; Chu, T. Bifurcation Analysis of a Bounded Rational Duopoly Game with Consumer Surplus. Int. J. Bifurc. Chaos 2021, 31, 2150097. [Google Scholar] [CrossRef]
- Kim, S.-L.; Lee, S.-H.; Matsumura, T. Corporate Social Responsibility and Privatization Policy in a Mixed Oligopoly. J. Econ. 2019, 128, 67–89. [Google Scholar] [CrossRef]
- Fanti, L.; Buccella, D. Corporate Social Responsibility, Profits and Welfare with Managerial Firms. Int. Rev. Econ. 2017, 64, 341–356. [Google Scholar] [CrossRef]
- Chen, Y.; Nie, P.-Y. Duopoly Competition in Food Industry Considering Corporate Social Responsibility. Qual. Assur. Saf. Crops Foods 2016, 8, 33–40. [Google Scholar] [CrossRef]
- Askar, S.; Foul, A.; Mahrous, T.; Djemele, S.; Ibrahim, E. Global and Local Analysis for a Cournot Duopoly Game with Two Different Objective Functions. Mathematics 2021, 9, 3119. [Google Scholar] [CrossRef]
- Askar, S.S.; Elsadany, A.A. Nonlinear Dynamics of Cournot Duopoly Game: When One Firm Considers Social Welfare. Discret. Dyn. Nat. Soc. 2021, 6697341. [Google Scholar] [CrossRef]
- Wen, J.; Diao, Y.; Wang, L.F.S.; Sun, J. Privatization, Entry and Corporate Social Responsibility with Consumer Cognition. MPRA Paper No. 115169, Posted 26 October 2022 15:04 UTC. Available online: https://mpra.ub.uni-muenchen.de/115169/ (accessed on 10 May 2025).
- Liu, Y.; Matsumura, T. Welfare Effects of Common Ownership in an International Duopoly. MPRA Paper No. 115177, Posted 27 October 2022 07:57 UTC. Available online: https://mpra.ub.uni-muenchen.de/115177/ (accessed on 10 May 2025).
- Li, W.-N.; Elsadany, A.A.; Zhou, W.; Zhu, Y.-L. Global Analysis, Multi-stability and Synchronization in a Competition Model of Public Enterprises with Consumer Surplus. Chaos Solitons Fractals 2021, 143, 110604. [Google Scholar] [CrossRef]
- Zhou, W.; Chu, T. Complex Dynamical Behavior of a Bounded Rational Duopoly Game with Consumer Surplus. In Research Advances in Chaos Theory; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Bischi, G.I.; Naimzada, A. Global Analysis of a Dynamic Duopoly Game with Bounded Rationality. In Advances in Dynamic Games and Applications; © Birkhāuser Boston: Boston, MA, USA, 2000. [Google Scholar]
- Bischi, G.-I.; Stefanini, L.; Gardini, L. Synchronization, Intermittency and Critical Curves in a Duopoly Game. Math. Comput. Simul. 1998, 44, 559–585. [Google Scholar] [CrossRef]
- Li, H.; Zhou, W.; Chu, T. Stability, Multistability, and Complexity Analysis in a Dynamic Duopoly Game with Exponential Demand Function. Complexity 2021, 2021, 9978320. [Google Scholar] [CrossRef]
- Bischi, G.-I.; Gallegati, M.; Naimzada, A. Symmetry-Breaking Bifurcations and Representative Firm in Dynamic Duopoly Games. Ann. Oper. Res. 1999, 89, 253–272. [Google Scholar] [CrossRef]
- Chu, T.; Yu, Y.; Wang, X. Complex Dynamical Behaviors of a Mixed Duopoly Game Based on Intellectual Property Rights Protection. Complexity 2020, 2020, 4601510. [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, W.; Chu, T.; Chang, Y. Global Dynamics and Synchronization in a Duopoly Game with Bounded Rationality and Consumer Surplus. Int. J. Bifurc. Chaos 2019, 29, 1930031. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, N.; Chu, T.; Chang, Y.-X. Stability and Multistability of a Bounded Rational Mixed Duopoly Model with Homogeneous Product. Complexity 2020, 2020, 4580415. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, J.; Chu, T.; Li, H. A Dynamic Duopoly Cournot Model with R&D Efforts and Its Dynamic Behavior Analysis. Complexity 2020, 2020, 9634878. [Google Scholar] [CrossRef]
- Lia, H.; He, R.; Zhou, W. Dynamic Behaviors in a Cournot Duopoly Model with Knowledge Spillover Effect Based on Constant Conjectural Variation. Math. Comput. Simul. 2022, 201, 305–323. [Google Scholar] [CrossRef]
- Askar, S.S. A Dynamic Duopoly Model: When a Firm Shares the Market with Certain Profit. Mathematics 2020, 8, 1826. [Google Scholar] [CrossRef]
- Brianzoni, S.; Campisi, G. Dynamical Analysis of a Banking Duopoly Model with Capital Regulation and Asymmetric Costs. Discret. Contin. Dyn. Syst.-B 2021, 26, 5807–5825. [Google Scholar] [CrossRef]
- Matsumura, T. Partial privatization in mixed duopoly. J. Public Econ. 1998, 70, 473–483. [Google Scholar] [CrossRef]
- Singh, N.; Vives, X. Price and quantity competition in a differentiated duopoly. Rand J. Econ. 1984, 15, 546–554. [Google Scholar] [CrossRef]
- Wu, F.; Liu, B.; Fu, N. The Complex Evolution of Information Quality Improvement in Competitive Market. RAIRO Oper. Res. 2023, 57, 351–369. [Google Scholar] [CrossRef]
- Andaluz, J.; Jarne, G. Stability of vertically differentiated Cournot and Bertrand-type models when firms are boundedly rational. Ann. Oper. Res. 2016, 238, 1–25. [Google Scholar] [CrossRef]
- Bischi, G.I.; Lamantia, F. Coexisting Attractors and Complex Basins in Discrete-time Economic Models. In Nonlinear Dynamical Systems in Economics; Lines, M., Ed.; Springer: Vienna, Austria, 2005; pp. 187–231. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).