Abstract
In virtual reality (VR) systems, a problem is the accurate reproduction of the user’s body in a virtual environment using inverse kinematics because existing motion capture systems have a number of drawbacks, and minimizing the number of key tracking points (KTPs) leads to a large error. To solve this problem, it is proposed to use the concept of a digital shadow and machine learning technologies to optimize the number of KTPs. A technique for movement process data collecting from a virtual avatar is implemented, modeling of nonlinear dynamic processes of human movement based on a digital shadow is carried out, the problem of optimizing the number of KTP is formulated, and an overview of the applied machine learning algorithms and metrics for their evaluation is given. An experiment on a dataset formed from virtual avatar movements shows the following results: three KTPs do not provide sufficient reconstruction accuracy, the choice of five or seven KTPs is optimal; among the algorithms, the most efficient in descending order are AdaBoostRegressor, LinearRegression, and SGDRegressor. During the reconstruction using AdaBoostRegressor, the maximum deviation is not more than 0.25 m, and the average is not more than 0.10 m.
1. Introduction
Virtual reality (VR) systems are actively used to solve various problems, ranging from professional training to psychological rehabilitation and ending with the entertainment industry. At the current stage of VR development, one of the urgent problems is the accurate reproduction of the user’s body in a virtual environment because reliable visualization of the body directly affects the immersion effect [1]. The solution to this problem is inextricably linked with the exact positioning of a person in real space. The basic delivery package of most VR systems includes a head-mounted display (HMD, also called VR-headset) and two controllers for moving and interacting with objects. Actions can be tracked using headset-mounted cameras, using external sensors and base stations (Lighthouse technology) and, finally, using motion capture suits [2].
In the first case, it is possible to use computer vision technologies, but they provide high-quality reproduction only for hands, in particular, palms and fingers; the recognition of the rest of the body is difficult due to the specific camera’s location [3].
On the other hand, the use of Lighthouse allows you to accurately position the headset, controllers, and additional sensors (trackers). The disadvantage of this approach is the inconvenience of the simultaneous use of multiple sensors for positioning all the key points of a person [4].
The third approach is based on the use of expensive—and often sensitive to external electromagnetic interference—suits with many inertial sensors, which significantly limits their use in mass solutions [5]. In addition to complex motion capture suits, inertial measuring units can be used to track movement, but their accuracy due to the continuous accumulation of errors may be insufficient for a number of situations [6].
Thus, there is a significant problem that consists of the imperfection of existing technical means, which do not allow for building an inexpensive, efficient, and accurate system for capturing human movements for subsequent visualization in a virtual space. Within the framework of this study, the problem of modeling nonlinear dynamic processes of human movement in virtual reality based on a digital shadow is considered, taking into account the need to maximally simplify the motion capture system, that is, reduce the number of tracked points.
This article has the following structure: The first section discusses the subject area, the main scientific and technical problems, analyzes the existing works, studies the process of human movement and tracking, reviews possible solutions to the inverse kinematics problem using machine learning algorithms and metrics to evaluate their effectiveness, and formulates the purpose of this study. The second section presents the theoretical basis of the study, including an analysis of the data collection process on human movement in virtual reality, modeling nonlinear dynamic processes of human movement based on a digital shadow, formulating the problem of the tracking points number optimization, reviewing the algorithms used for machine learning and metrics to evaluate them. The “Results” section presents the characteristics of the generated dataset of user movements obtained from virtual avatars, a comparison of various machine learning models by objective and subjective metrics. The study ends with a discussion of the results obtained and conclusions.
1.1. Study of the Processes of Human Body Movement and Tracking
VR software developers solve this problem using two main methods [7]: direct and inverse kinematics using various motion capture and tracking systems. Let us consider the differences between these approaches, and also compare the technical means for obtaining initial data on human body kinematics when interacting with virtual reality.
1.1.1. Direct Kinematics
In the case of direct kinematics, a sufficient amount of information about all key tracking points (KTPs) of the user’s body is required because the movement of the skeleton is modeled hierarchically top-down, starting, for example, from the shoulder, further to the elbow, and ending with the hand, that is, the child segments move relative to the parent segments without affecting them. By KTP, we mean such a point in a three-dimensional space that uniquely defines a segment or node of the human body and is necessary for the avatar reconstruction in virtual space. This approach is used in motion capture suits; therefore, it is expensive and requires the collection of a large amount of data on the position of all parts of the human body.
1.1.2. Inverse Kinematics
In contrast to direct kinematics, inverse kinematics is based on the processing of a limited amount of data about KTP. In inverse kinematics, on the contrary, the movement of child segments leads to a change in the position of the parent segments, that is, the algorithm calculates the position and orientation of the shoulder and elbow based on the position and orientation of the hand. The first approach is used in motion capture suits; the second is in conditions of limited information about the KTP, for example, when the developer has access only to the position of the user’s hands, according to which they restore the coordinates of the points of the entire arm and even the torso or legs (taking into account the height of the HMD and the position of the hands) [8]. Since the process of human movement is nonlinear and dynamic [9], individual parts of the body move independently of each other, which makes the task of modeling inverse kinematics non-trivial.
1.1.3. Comparison of Approaches to Human Movements Tracking
Direct or inverse kinematics is based on obtaining information about the human body or its individual parts’ position. Analyzing various approaches to collecting data on human movement, the following areas can be distinguished:
- -
- Tracking the trajectories of human movements using a motion capture suit (for example, Perception Neuron—a system based on inertial sensors [10]), which allows for tracking a change in the position of 59 segments of the human body relative to the base (reference) point. The disadvantage of this approach is the lack of information about the absolute person’s position value in a three-dimensional space and the high probability of data distortion when located close to a source of electromagnetic interference;
- -
- High-precision tracking of a person’s key points using trackers and virtual reality controllers with low measurement error in the visibility zone of base stations (up to 9 × 9 m) [11]. In the case of leaving the visibility zone of base stations or their overlapping, signal loss from sensors is possible, which leads to incorrect data; the size and weight of trackers limit the possible number of sensors attached to a person;
- -
- The application of computer vision technologies based on a single camera, stereo cameras, or a system of several synchronized cameras to obtain corrected and more accurate data about a person’s position in a three-dimensional space by recognizing key points of the human body, including fingers and face [12]. When using this technology, there are problems with recognizing key fragments of a person’s silhouette when the object is moving quickly or in low-light conditions.
Thus, each of the considered approaches has a number of disadvantages caused by technical limitations. The solution may be a combination of the above approaches within a unified motion capture system, but this will inevitably lead to increasing its cost and the problem of using it for a wide audience [13]. Therefore, it is especially important to implement an approach that will allow for fast, cheap, and high-precision data collection on human movement processes in various scenarios. Without a sufficient amount of information with a high degree of reliability (the data do not contain interference, noise, and distortion), it is impossible to form a digital shadow. The use of high-precision motion capture suits makes it possible to form a digital representation of a person in virtual space; however, this approach is time-consuming and requires the involvement of a large number of participants with different physical parameters. The main disadvantage is the inability to simulate, in the real world, a number of hard-to-reach movement scenarios and unsafe movements.
The solution to this problem is to combine data from two fundamentally different sources: motion capture systems and a virtual avatar from the game scene [14]. Because the procedure for constructing a digital representation of the human body in virtual space is based on a set of points in the metric coordinate system, then for the final implementation of the virtual avatar, the data source will not have a fundamental difference. The proposed approach will significantly speed up the data collection process (by speeding up animation and parallelization in a virtual scene).
Given the above, to collect the training dataset, you can use data only from the virtual model. A necessary condition for using the data obtained in this way is the reliable values of all the KTP coordinates in the metric coordinate system. Since KTPs collected in this way will allow a complete reconstruction of a virtual avatar, this approach can completely replace data collection using a large number of trackers, as well as computer vision technology. Knowing all the coordinates of the person’s points, it is possible to determine the angles between the segments, which makes it possible to replace the motion capture suit with the proposed approach. The correctness of data from a virtual avatar is ensured by the fact that they are a combination or modification of information from existing high-precision motion capture systems. A comparison of approaches to data collection is presented in Table 1, which allows us to conclude that KTP sets obtained from a virtual avatar can be used as initial data on a person’s position in space. Such data are abstracted from the source, which will make it possible to implement more universal models and information processing tools on their basis. In addition, this method is more productive, has no restrictions on the number and location of KTP, and is also the most accurate. Because the KTP coordinates are read from a digital object, the accuracy depends on the resolution of the digital representation used (float or double data type). By default, virtual reality game development environments such as Unity3D use a vector of three float variables, the values of which are measured in meters, to store point coordinates. In the C# programming language, the float type provides accuracy up to 9 digits after the decimal point (this provides an error of up to 10−6 mm), when using the double type up to 17 digits after the decimal point (an error of up to 10−13 mm).

Table 1.
Comparison of different approaches to collecting human movement data.
1.2. Approaches to Solving the Problem of Inverse Kinematics
Consider the existing research in the field of solving the problem of inverse kinematics using various human body motion capture systems.
In [15], five additional trackers fixed on the back, heels, and elbows of a person were used, which, together with two controllers and an HMD, make up eight key points, and based on their position, the developers solved the problem of inverse kinematics. The resulting system had a fairly low latency and high accuracy according to the subjective assessment of the participants in the control group.
The study in [16] is based on the analysis of human gait and the comparison of head movements in a VR-headset with the phases of the step, which made it possible to use only one point to restore leg movements using various approaches (Threshold, Pearson correlation method, SVM, and BLSTM). The BLSTM neural network provides the smallest error but cannot be used in real time, so the authors chose a method based on the Pearson correlation calculation between the acceleration of the head and legs. This approach is not universal and is limited to restoring points only with uniform walking.
A number of studies are focusing on a more accurate reconstruction of only certain parts of the body, such as the hands and fingers. For this, combinations of virtual reality gloves and additional inertial sensors for each finger [17] or a combination of cameras with a depth sensor and neural networks can be used to more accurately restore three-dimensional coordinates [18]. Neural networks are used to successfully reconstruct a three-dimensional model of the human body from a two-dimensional image, in which the main points of the skeleton are first recognized, and then, they are converted into a three-dimensional representation with the correction of the rotation angles of the segments [18].
Attempts to implement inverse kinematics using machine learning technologies have been carried out for a long time. Early works [19], rather pessimistically, assessed the possibility of solving this problem due to the insufficient performance and accuracy of neural networks at that time. However, in the future, significant progress can be observed in this direction; combinations of various neural networks are used to implement the inverse kinematics of robots [20], predicting body positions taking into account the environment based on a virtual skeleton [21] or a set of sensors [22]. The study in [23] considers the use of neural networks to restore the key points of a person’s silhouette when deleting from 10 to 40% of the data.
The analysis shows that for the approximation of the human movement process and the subsequent solution of the problem of inverse kinematics, one of the promising areas is the use of machine learning methods. This allows the use of a limited number of sensors or simplified motion capture systems, but requires the implementation of virtual avatar reconstruction algorithms. Finding the minimum number of KTPs will reduce the amount of information transmitted, the computational load, and the cost of motion-tracking system implementation. Thus, it is necessary to determine possible ways to solve this problem. The following are identified as the main directions for solving the problem of approximating the human movement process: a digital model, a digital twin, and a digital shadow [24]. Let us consider each of these options.
1.2.1. Digital Model
The most accurate and correct approach is to build a digital model that includes dependencies between all points of the human body, as well as kinematic and dynamic parameters in the body movement process. Thus, a digital model is a mathematical or digital representation of a physical object that functions independently of it but reliably reflects its characteristics and all processes occurring in it.
The development of such a mathematical model that fully describes all the patterns of human limb movement is a non-trivial task. In conditions when not all points of the body can be tracked or in the absence of a number of key points in the process of using inverse kinematics, this task may be unsolvable due to its high complexity. Therefore, the actual direction will be the implementation of numerical methods that provide acceptable accuracy in the reconstruction of the human body, considering a number of assumptions.
1.2.2. Digital Twin
A digital twin of an object is understood as a system consisting of a digital model (a system of mathematical and computer models that describes the structure and functionality of a real object) and bidirectional information links with the object. The founder of the concept of “digital twin”, M. Grieves, defines it as a “set of virtual information constructs that fully describes a potential or actual physical manufactured product from the micro atomic level to the macro geometrical level” [25].
A comprehensive database is needed to form a digital twin. In addition, for a number of areas, including objects with undetermined behavior, the creation of a digital twin is a task of high complexity and laboriousness with the need to verify, validate, and check the completeness and adequacy of the resulting model. For example, creating a digital twin of a person or even an animal remains a difficult task at the current level of technology. When solving the problem of precise positioning and reconstruction of the human body movements, the “digital twin” approach is also difficult to implement and redundant.
1.2.3. Digital Shadow
The concept of digital shadows was proposed as part of Industry 4.0 [26] as a kind of platform that combines information from various sources to enable real-time analysis of an object for decision making. A digital shadow is a mathematical or digital representation of an object with an automated data transfer channel from physical objects that influence the digital object.
Unlike the digital twin, the formation of a digital shadow does not require a comprehensive database, but one limited by the needs of a specific task. The digital shadow, built on the generalization and processing of large amounts of data on the nonlinear dynamic process of human movement, can be used to solve problems of direct and inverse kinematics and restore damaged or missing data. The concept of digital shadows corresponds to the principles of machine learning algorithms operation, which is also based on the collection and generalization of large amounts of information.
The considered digital shadow of the human movement processes should provide a connection between the initial data on the position of the person’s physical body and its reconstructed digital representation. Thus, the digital shadow realizes the complete restoration of the human body in the digital space, without using complex analytical calculations, due to the processing and generalization of data on a set of KTP.
Since for the successful implementation of the digital shadow, it is required to generalize the initial data on the position of the human physical body for subsequent reconstruction, this task is reduced to finding some regression dependence and, therefore, can be approximated using various machine learning algorithms.
1.3. Machine Learning Technologies for Solving the Task
In accordance with the previous analysis, it was found that the task of reconstructing the human body movements under the conditions of a limited number of KTPs can be successfully solved using machine learning methods. Consider the key approaches in this area, as well as the metrics, to assess the quality of their work.
1.3.1. Overview of Machine Learning Algorithms
Regression dependencies can be approximated using various machine learning algorithms that differ in their architecture, scope, and efficiency. Within the framework of this study, based on the analysis of existing works [27,28,29,30], the following algorithms were selected and implemented in common libraries for machine learning and big data processing:
LinearRegression—a linear model that optimizes the coefficients of the regression equation using the least squares method. The number of coefficients depends on the dimension of the input and output variables. It is distinguished by simple implementation and ease of interpretation of the results [31].
SGDRegressor—a linear regression model using stochastic gradient descent and various loss functions. The model shows high efficiency on large amounts of data [32].
Neural networks—nonlinear models with an arbitrary number of hidden layers, the ability to implement complex architectures (with multiple inputs and outputs), and use various nonlinear activation functions and loss functions. Due to the large number of parameters, they allow generalizing and identifying patterns with a sufficient volume of the training sample but require fine-tuning of the architecture and model parameters [33].
KNeighborsRegressor—k-nearest neighbor regression. The target is predicted by local interpolation of the targets associated with the nearest neighbors in the training set. The disadvantage of this method is that for its application, it is necessary to store the entire training set in memory, and performing regression can be computationally expensive because the algorithm analyzes all data points [32].
DecisionTreeRegressor—a model that predicts the value of a target variable by learning simple decision rules inferred from the data features. A tree can be seen as a piecewise constant approximation. The depth of the tree increases until a state of overfitting is observed [34]. A lack of depth will lead to the underfitting of the model.
RandomForestRegressor—a representative of averaging ensemble methods that allows you to combine the predictions of several basic models to improve the generalizing ability. A random forest is a meta estimator that fits a number of classifying decision trees on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting [35].
AdaBoostRegressor—one of the ensemble boosting methods, which begins by fitting a regressor on the original dataset and then fits additional copies of the regressor on the same dataset but where the weights of instances are adjusted according to the error of the current prediction. As such, subsequent regressors focus more on difficult cases [36].
It should be noted that for a number of algorithms (SGDRegressor and AdaBoostRegressor) that do not support multiple outputs, the use of the MultiOutputRegressor class is required, which allows for multi-purpose regression.
1.3.2. Overview of Metrics for Assessing the Quality of Human Movements Reconstruction
To assess the quality of reconstruction of human body movements after applying machine learning methods, both existing common metrics and those adapted to the specifics of the problem being solved were used [37]. The main metrics include the following:
Mean square error (MSE):
Calculation time, defined as the average time of calling the “predict” function of the machine learning algorithm for one instance of the sample, in milliseconds.
We also introduced two additional metrics aimed at estimating the Euclidean distance. This is the average Euclidean distance between the reference and predicted points:
The maximum Euclidean distance between the reference and predicted points within the entire avatar:
The total Euclidean distance between the reference and predicted points within the entire avatar:
The chosen metrics, thus, allow us to evaluate both the speed of the compared algorithms and their accuracy from different points of view. It should be noted that although such metrics as MSE and are common and generally accepted in solving problems of inverse kinematics, they do not consider the context and boundaries of body segments, which can lead to unrealistic solutions that do not correspond to human anatomy. makes it possible to give a pessimistic assessment of the methods, but does not reflect the quality of the reconstruction as a whole. Thus, these listed metrics can be used to analyze the solution quality, but do not provide an opportunity for an objective comparison of different approaches. The metric, on the contrary, reflects the total reconstruction error for all points of the human body, making it possible to identify both the general discrepancy and the deviation in individual KTP. Thus, will be used as the main criterion for evaluating machine learning algorithms. For its verification, an additional visual analysis of the results of solving the regression problem by a person is proposed.
1.4. Aim of This Study
The aim of this study is to model a nonlinear dynamic process of human movement in virtual reality under conditions of insufficient initial data on the position of key points of the body. The analysis of the subject area revealed that the achievement of the goal will be based on the following provisions:
- -
- To simplify the motion capture system, it is necessary to use an approach based on inverse kinematics;
- -
- The development of a mathematical model that fully describes all the patterns of human limb movement is a non-trivial task, as well as the implementation of a digital twin of the body movement process. In conditions when not all points of the body can be tracked or in the absence of a number of key points when using inverse kinematics, this task may be unsolvable due to its high complexity;
- -
- As the main method for solving the problem, the concept of digital shadows is proposed, which is based on the generalization of a large amount of data on various typical scenarios of human movements;
- -
- Machine learning algorithms will be used to approximate the regression dependency between a limited number of KTPs and a fully reconstructed human body model.
2. Materials and Methods
The research methodology includes the following steps:
- -
- Collecting data on KTP from one or more sources—motion capture systems (motion capture suits, VR trackers, IMU sensors, computer vision, and so on), as well as from a person’s virtual avatar;
- -
- Formalization of nonlinear dynamic motion processes in the form of a certain model adapted for subsequent software implementation of the digital shadow;
- -
- Optimization of the model to ensure effective operation in conditions of insufficient data on the person’s position;
- -
- Software implementation of a digital shadow, which allows modeling nonlinear dynamic motion processes in virtual reality under conditions of insufficient information, based on machine learning methods.
2.1. Modeling of Nonlinear Dynamic Processes of Human Movement Based on Digital Shadow
In the general case, the mathematical description of a digital shadow is a multidimensional vector of object/process characteristics at each moment of time. This vector includes both the values of input variables (internal and external environment parameters) and output parameters (internal and external). Then, in order to model nonlinear dynamic processes of human movement, at the first stage, we formalized the main components of the motion capture process and their characteristics.
Because, in the process of functioning, the digital shadow will interact with data from existing motion capture systems, it is necessary to analyze the specifics of their work. Three main directions for obtaining data on the movement process were identified above: a motion capture suit; virtual reality trackers; computer vision system.
When using a motion capture suit, a set is formed from one reference point and a number of segments (bones) located relative to it, the position of which is indicated using tilt angles along three axes. If necessary, the system allows recording, in addition to sensor rotation angle changes, its movement relative to the previous measurement [38]. We formalized the components of this process.
For a motion capture suit, the set of segments (bones) is defined as of size . For each segment , 3 or 6 values are given depending on the working mode:
where are the three-dimensional positions of the -th sensor, relative to previous measurement;
are the three-dimensional rotations of the -th sensor, relative to previous measurement;
Let us denote the reference point on the user’s back as . A set of segments, , is defined for each sample, so there is a correspondence between a set of discrete timestamps, , and a set of sensor values, . Because links are given between the segments, we define the order of their sequence and connection as , which is a partially ordered set.
Next, we consider the formalization of the components of a motion capture system based on virtual reality trackers. Let trackers , each of which is described by a tuple:
where are the absolute coordinates of -th tracker along the , , axes, as well as the angles of their rotation along these axes, respectively.
Let us assume that, by default, is placed on the user’s back, and are placed on the hands (or are controllers that the user holds in their hands), and are on the legs. Further location of trackers can be carried out on the basis of an expert approach in key nodes of the human body.
The formalization of a motion capture system based on computer vision, , includes a number of additional steps since the initial data for this approach are a frame (or a set of frames) on which it is necessary to recognize a person and their key points [39]. Therefore, at the first stage, it is necessary to carry out the following transformation of frame, , into a set of points, . Each point is represented as a tuple:
where are three-dimensional coordinates of point, , in the frame, .
The layout of points along the human body depends on the selected body recognition method, but always includes the reference points of the arms, legs, torso, and head. Most neural network models position points by two axes ( and ) due to the complexity of depth estimation when using a camera. A number of algorithms (for example, MediaPipe) emulate the determination of the coordinate relative to some reference point, but this value is not accurate and does not allow positioning the object in space. To accurately obtain the depth value, computer stereo vision or a system of several cameras can be used [40].
After formalizing the initial data from the considered motion capture systems, let us move on to modeling the digital shadow of the human movement process, based on data collection from a virtual avatar. This model is based on the processing of virtual KTPs (VKTPs), which correspond to coordinates along three axes. In the case of a sufficient number of VKTPs, their position allows restoring the position and rotation angles of the virtual avatar segments in a similar way to the motion capture systems discussed above.
Let a set of VKTPs be given, corresponding to the key areas of the human body and allowing its subsequent reconstruction in the virtual space. Let us denote the total number of VKTPs as .
Then, the total number of coordinate values can be specified through the vector:
The length of the vector is equal to . Then, the vector with the size of uniquely determines the digital representation of a person with the required accuracy (i.e., it allows modeling all the necessary parts of the virtual body and their connections). Let us introduce an additional designation of the -th element of the element of the , where .
Along with the virtual representation of a person (their digital shadow), denoted by the vector, there is a real position of the user’s body in space. Let us introduce the following notation:
The vector of user body coordinates values in the real world, :
where is the number of KTPs received from the real world (using any of the existing motion capture systems).
Length of the vector is .
Coordinate vector, , the dimensions of which correspond to the dimensions of , and the values of correspond to the real values of the user’s KTP. This vector is used as a reference for comparison with . Thus, the relationship defines the correspondence between KTP and VKTP.
Element of vector, , with -th index: , where Values of elements can be obtained from any motion capture system that supports coordinates, for example, from tracker position values according to Formula (2).
Thus, when comparing and vectors, one of three scenarios can occur:
- -
- The lengths are the same (when ), then if the condition of the KTP location relative to the VKTP placement scheme is met, all KTPs are used to build a virtual avatar;
- -
- If the number of real KTPs is less than the number of VKTPs (for ), including the situation when part of the KTP is discarded due to incorrect placement, there is a lack of initial data for constructing a virtual avatar, and it is required to implement algorithms for reconstructing the missing VKTPs based on incomplete input data;
- -
- If the number of real KTPs is greater than the number of VKTPs (when ), then the KTPs closest to the VKTPs are used to build a virtual avatar, the rest of the KTPs can be discarded.
In the three scenarios under consideration, when solving a specific problem, it is necessary to fix the location and number of KTPs (the set of KTPs is system-dependent and unchanged during operation). The accidental addition or removal of KTP during operation is not considered in this study, although it is a promising task from a practical point of view.
The second scenario is of greatest interest because the reconstruction of nonlinear dynamic processes of human movement based on insufficient data from real KTPs can reduce the complexity and cost of the motion capture system and increase the realism of displaying a user’s digital avatar in conditions of insufficient data. Consider the process of modeling nonlinear dynamic processes of human movement according to the second scenario using a digital shadow, which includes the following stages:
- Let there be some motion capture system that does not allow for a complete reconstruction of the person’s digital representation (insufficient number of sensors, interference, poor conditions for body recognition), that is, .
- The selected motion capture system transfers to the virtual environment a certain set of KTP values in the form of an vector.
- Each KTP is assigned the VKTP closest to it in position. Denote a subset of VKTPa as . Then, a relation is formed between two vectors: .
- The machine learning algorithm, , is selected, aimed at solving the regression problem of the following form:
Thus, a VKTP vector of length is input into a machine learning algorithm, and a reconstructed vector, , from all VKTP is expected at the output. If the selected algorithm can reconstruct with sufficient accuracy, then it can be used to model nonlinear dynamic processes of human movement in conditions of insufficient initial data.
- 5.
- After successful training of the algorithm, , the vector of real KTP is fed to its input, and the reconstruction of the virtual avatar is carried out: .
Then, the formalized research problem has the form: it is necessary to find the type and parameters of the machine learning algorithm, , for which the value of the total Euclidean distance between the predicted points ( vector) and real KTP ( vector) will be minimal:
where is the size of the control sample;
are coordinate values of the virtual and real points for the -th sample element.
An important component of solving problem (7) is minimizing the length of the vector of the initial KTP:
To successfully solve problems (12) and (13), it is necessary to form a training sample of sufficient size and train a set of machine learning algorithms, the input of which will be given various combinations of points.
2.2. Formation of Sets of Key Human Tracking Points
An important component in solving the tasks is to determine the minimum possible length KTP, as well as their placement. Obviously, there are some boundary conditions: for small , the algorithms may not work, and in the case of , the economic feasibility of problem-solving decreases.
The analysis of virtual human models showed that 18 VKTPs are enough to build them. This corresponds to many commercial solutions, for example, Perception Neuron based on 18 sensors [41]. Thus, when recording data, it is necessary to record values (3 coordinates per point). The location of these points should correspond to the connection nodes of the main segments of the human body: hand, elbow, shoulder, extreme points of the foot, knee, hip joint, extreme and central points of the back, head. The layout and numerical identifiers of each KTP are shown in Figure 1.
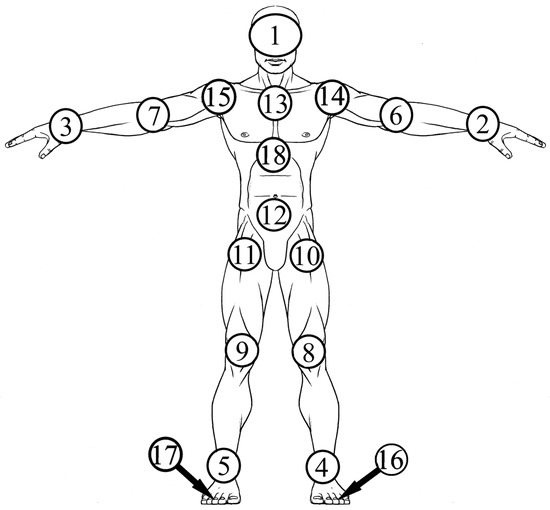
Figure 1.
Scheme and order of KTP placement, where 1–18—numerical identifiers of each KTP.
Note that the selected KTPs are system-dependent to one degree or another; this is due to the fact that the human body can change the position of individual parts only within certain limits, and the lengths of segments between points are constant. Individual KTPs can be quite independent of the other points (e.g., 2 from 3, 4, or 5) and move in space without affecting the position of the other KTPs, but such scenarios are specific. In the collected dataset, it is necessary to take into account the typical movements of the human body, which may include the specific scenarios indicated above (when halves or sides of the human body move independently of each other). The presence of a large amount of data on various typical movements will allow building regression between KTP from the input set and the full model of the human body through approximation and generalization. However, a number of exceptional scenarios may not be processed correctly enough, which will require expanding the dataset.
Further, in the process of experimental studies, it will be necessary to determine the location and number of KTPs sufficient for the effective reconstruction of the human body in virtual reality.
3. Results
In accordance with the above methodology for modeling nonlinear dynamic processes of human movement based on a digital shadow, it is necessary to conduct experimental studies, including collecting a dataset of various human movements from a virtual avatar, analyzing it, creating and comparing machine learning models, and generalizing the obtained experimental results.
3.1. Experiment Scheme
In the Unity 2022.2.1.f1 development environment, a scene is created that hosts a virtual avatar of a 173 cm tall person. Many animation assets are imported into the scene and applied sequentially to the virtual avatar. A total of 18 VKTPs are set on the avatar according to the scheme shown in Figure 1. Next, all animations are launched in the scene, and the points are recorded at a frequency of 600 Hz in the CSV format.
The collected data are processed in Python software using data analysis libraries (Pandas and SciPy). Further, various machine learning models are implemented; they are trained on a training dataset and evaluated on a control data set (using objective quantitative metrics and subjective visual analysis).
The software was launched and tested on the following hardware configuration: AMD Ryzen 5900X, 64 GB RAM, Nvidia RTX 3060 Ti, NVMe SSD, and operating system—Windows 10.
3.2. Description of the Dataset of Human Movements
To form a training dataset, data were collected from a virtual scene with 256 different types of animation (source—CMU Graphics Lab Motion Capture Database [42]) at a frequency of 30 times per second. In total, this allowed us to collect 1,088,174 records from 18 VKTPs (54 values per record). A total of 870,539 records were used as a training sample, 217,635 records were used as a test sample. A control set of 14,000 records with unique animation was also formed, which does not participate in either the training or test samples.
Further, an analysis of the collected data for all 18 key tracking points (Table 2) was carried out, during which the average values of the coordinates of the points along the three axes and their standard deviation, as well as the range of minimum and maximum values of each VKTP, were determined.

Table 2.
Statistical description of the dataset.
Checking the data for normality using the Shapiro test shows that the data are normally distributed with probability, . Similar results were shown by a normality test based on D’Agostino and Pearson’s criteria [43]. Thus, the use of parametric tests for data evaluation is inappropriate.
For the convenience of assessing the quality of machine learning algorithms, a software tool based on the Matplotlib library was implemented, which allows visualizing an arbitrary number of virtual avatars. Each avatar is built on the basis of 18 points, after which they are connected in the right order. Figure 2 shows examples from the collected dataset.
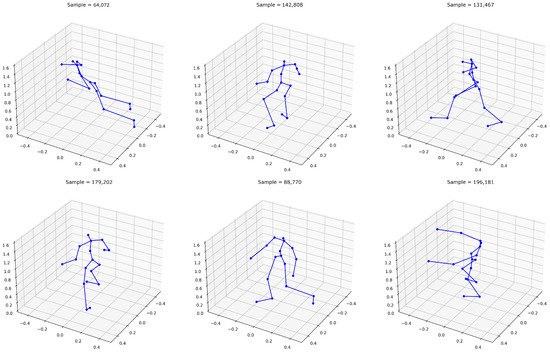
Figure 2.
Visualization of random samples from the dataset.
Thus, the collected data are very diverse, allowing us to conclude that the generated dataset is sufficient.
3.3. Determining the Optimal Layout of Tracking Points
To select the optimal location of KTPs and their combinations, a preliminary study was carried out, including the following steps:
A total of 131,089 variants from all possible combinations of KTP are formed, including 18 sets of 1 KTP and 131,071 sets from all possible combinations of KTP, given the limitation that they always use the KTP of the head (1). KTP (1) must be present in the sets due to the fact that a person is always wearing a helmet when using virtual reality. Thus, the indicated 131,071 sets were formed using a complete enumeration of all combinations of the remaining 17 KTPs.
Next, the LinearRegression algorithm was used for test reconstruction of the human body for all 131,089 KTP variants. For the training procedure, the previously designated training (more than 800,000 poses) and control (14,000 poses) datasets were used, which made it possible to cover most of the typical movements. The LinearRegression algorithm was chosen because of its high performance, ease of implementation, and repeatability of results.
For each from 1 to 18, the five best results were selected, as presented in Table 3, indicating the maximum deviation, , and its average deviation (SD) for the sample. Compact notation is used in the table if consecutive KTPs were used in the set. The results obtained allow us to determine the size limits of the KTP set. At , firstly, the maximum error is too high, and secondly, the absence of symmetrical points does not allow the correct process of all poses. At , an increase in the reconstruction error can be observed, since it is necessary to approximate individual small sets of KTPs with a fixed set of a large number of KTPs, which can be difficult in the case of the specific scenarios discussed earlier in Section 2.2 (in the case when the desired KTPs are sufficiently independent from the rest). When , all input data values are equal to the output data values, so there is no need to approximate such a dependence.

Table 3.
Comparison results of different KTP sets.
In addition to the size limits of the KTP sets, the conducted experiment makes it possible to form the priority of choosing the KTP in the process of expanding the sets from the smallest to the largest one. First, there is a clear superiority of certain points (2 and 3, 6 and 7, 16 and 17) due to their constant presence in almost all the best sets for various . Secondly, it is necessary to take into account the symmetry of pairs of some points (for example, 2 and 3, 6 and 7) when forming sets, because the use of only one point from a pair may reduce the reconstruction accuracy for one of the body halves. This leads to the need to use a two-point step when increasing the length of the KTP sets (i.e., = 3, 5, 7, and so on) so as not to break the symmetry. Finally, some KTPs, despite their frequent use in the best sets, are inconvenient for use in real life due to the difficulty of fixing sensors in these zones (for example, points 16 and 17) or can be replaced by the nearest points (for example, 18 by 13, 14 by 6, and 15 by 7).
Based on the assessment of the obtained preliminary results and the experience of experts (based on the greatest convenience of fixing trackers and their priority), the following order of adding points was formed: starting from the extreme points on the arms and legs and ending with intermediate positions (on the knees, elbows, back, and so on). As a result, 6 preferred sets were formulated, starting from the simplest with 3 KTPs and ending with the maximum with 13 KTPs:
- 3 KTPs: head (1) and left (2) and right (3) hand;
- 5 KTPs: 3 KTPs with the addition of the left (4) and right (5) foot (heel area);
- 7 KTPs: 5 KTPs with the addition of the left (6) and right (7) elbows;
- 9 KTPs: 7 KTPs with the addition of the left (8) and right (9) knee;
- 11 KTPs: 9 KTPs with the addition of the left (10) and right (11) hip joint;
- 13 KTPs: 11 KTPs with the addition of the lower (12) and upper (13) points of the back.
Thus, during the first stage of research, the optimal location and sets of KTPs were determined, on which it is further necessary to train various machine learning algorithms.
3.4. Description of Used Machine Learning Models
To select the optimal solution, several machine learning algorithms were analyzed, the main parameters of which are presented in Table 4. Model development was carried out in the PyCharm environment using Python 3.9 interpreter.

Table 4.
Parameters of selected machine learning algorithms.
At the preliminary stage, several architectures of multilayer neural networks were considered, some of which, due to an insufficient or excessive number of neurons and layers, did not achieve high accuracy values. As a result, two different architectures of neural networks were considered: the first, simpler one transforms the KTP vector (from 3 to 13) into a set of 18 VKTPs. The second one, which has multiple inputs, in addition to the current KTP data, uses, as the second input, a vector of 54 values from 18 VKTPs reconstructed in the previous step. On the one hand, this makes it possible to take into account previous body positions more correctly; on the other hand, it can lead to error accumulation. All neural networks were trained for 10 epochs, and the accuracy on the test set varied from 94 to 95 percent. The neural network models were implemented using the Keras framework based on Tensorflow.
Among the machine learning algorithms for solving the regression problem, the following were chosen: KNeighborsRegressor (KNN), DecisionTreeRegressor (DTR), LinearRegression (LR), RandomForestRegressor (RFR), SGDRegressor (SGDR), and AdaBoostRegressor (ADA). For their implementation, scikit-learn library (version 0.24.2) was used. The description and parameters of the models are presented in Table 4.
3.5. Analysis of Experimental Data
The selected machine learning algorithms were tested on 14,000 unique records not involved in the learning process. A comparison of algorithms by , , , and MSE metrics, as well as regression time, , for one set of input data is presented in Table 5. The algorithms are grouped depending on the number of initial VKTPs. The three best results in the group are selected in bold. The measurement of the calculation time of one reconstruction was performed on the CPU in one thread to achieve equivalent conditions.

Table 5.
Results of machine learning algorithm comparison.
Next, a visual comparison of the results obtained was carried out to determine the best algorithm because even high scores on the selected metrics may not provide a realistic reconstruction of the virtual avatar. To do this, every hundredth set of restored VKTPs was saved from the control group. Figure 3 and Figure 4 show comparisons of all algorithms for a random sample from the control group. The blue color denotes the reference position of the skeleton (vector ), and the red color indicates the reconstructed VKTP (vector ).
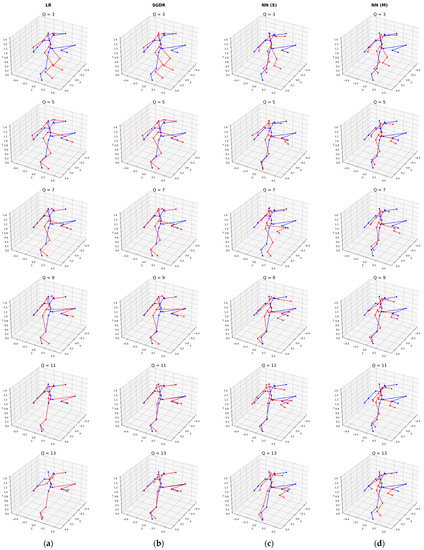
Figure 3.
Visual comparison of virtual avatar reconstruction quality using different machine learning algorithms: (a) LR; (b) SGDR; (c) NN (S); (d) NN (M).
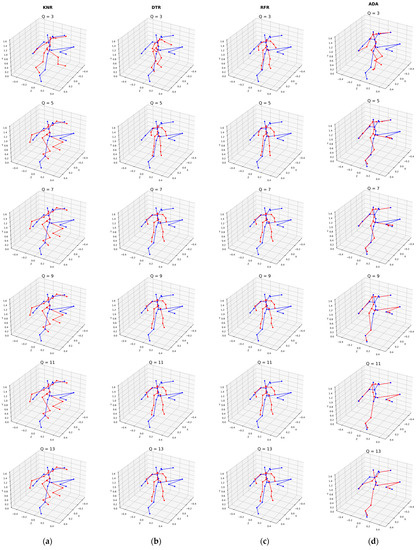
Figure 4.
Visual comparison of virtual avatar reconstruction quality using different machine learning algorithms: (a) KNR; (b) DTR; (c) RFR; (d) ADA.
As a result, there is a correlation between the visual realism of the reconstructed human body models and the metrics used: for lower values of , , and MSE, there is an improvement in the quality of the reconstruction relative to the high values. The main criterion——with the equality of other metrics, allows you to unambiguously determine the best solution, which, according to the observer, has an advantage from a visual point of view. Thus, this criterion is applicable for an objective assessment of the human body reconstruction quality.
4. Discussion
An analysis of the machine learning algorithm performances shows that the average reconstruction time does not exceed 2 milliseconds, which provides a sufficient calculation speed and will not affect the performance of virtual reality systems. The exception is the KNR algorithm, the VKTP calculation time for which is up to 37 milliseconds (at ), which makes it difficult to use it in real time.
Next, we analyze the minimum number of KTPs required for the reconstruction of a virtual avatar. The preliminary experiments show that the use of less than 3 and more than 13 KTPs is inappropriate; in addition, the need for symmetry of the used KTPs was revealed, which led to the formation of 6 sets. These sets are made up of KTP combinations that showed the best results in the preliminary tests to evaluate the number and location of KTPs (Section 3.3).
The conducted experimental studies and visual analysis show that the use of three points is not sufficient for all algorithms. The maximum deviation exceeds 0.4 m, and the average does not decrease below 0.15 m. These results are not acceptable. The reconstructions of virtual avatars shown in Figure 3 and Figure 4 have significant deviations in the region of the lower extremities; the position of the legs does not correspond to the real one. Thus, it is impossible to reliably reconstruct the legs of a virtual avatar, especially in complex poses, without having information about the KTP in the region of the lower extremities. With , machine learning algorithms are much better at positioning the lower extremities. The use of seven KTPs has a positive effect on difficult hand positions, especially in the elbow area. Using nine or more KTPs has a positive impact, but it is not significant or visually sensitive. Let us summarize the recommendations for choosing the number of KTPs:
- -
- : an option for simplified motion capture systems that do not require foot tracking and precise hand positioning;
- -
- : the optimal solution for most virtual reality systems due to the ability to accurately position all the user’s limbs;
- -
- : a solution for systems that require high accuracy in the positioning of the upper limbs, providing a reconstruction error comparable to more complex models.
Given the need to minimize the number of KTPs for a wide range of virtual reality systems, the optimal accuracy of virtual avatar reconstruction is achieved with five and seven input KTPs.
A comparison of various machine learning algorithms made it possible to evaluate them by objective and subjective metrics. The best results in quantitative metrics at were shown by LinearRegression (LR), SGDRegressor (SGDR), AdaBoostRegressor (ADA), and neural networks (with single and multiple inputs). Visual analysis shows that, in the most important range , these algorithms are generally comparable and show a corresponding quality similar to quantitative metrics. With an increase in the number of KTPs, neural networks begin to show worse results due to generalization because they introduce some deviations for all points. The remaining algorithms showed their inefficiency: DecisionTreeRegressor (DTR) and RandomForestRegressor (RFR) form an averaged universal body position that is too far from the real one, and KNeighborsRegressor (KNR) shows closer results but has the same drawback. Additionally, the KNR model has the largest size among all.
Taking into account the final accuracy by the criterion , model size and performance, the optimal machine learning algorithms for are (in descending order): AdaBoostRegressor, LinearRegression, and SGDRegressor. The other algorithms are not recommended for use.
The results obtained during the experiments are consistent in their accuracy with the studies carried out in [44], where, using six KTPs (HMD and five trackers), an average deviation of 0.02 m (for body segments, not specific KTPs) and a calculation time of 1.65 ms were obtained. In study [45], various algorithms produced a deviation from 0.07 to 0.11 m when using six KTPs.
Thus, the novelty of this study lies in the use of the digital shadow concept for modeling nonlinear dynamic processes of human movement in virtual reality and the development of algorithms for collecting and processing information to determine the minimum number of tracking points, as well as conducting experimental studies to find the optimal machine learning algorithm that allows for implementing reconstruction of the user’s virtual avatar under conditions of insufficient data.
Further research will be related to the integration of optimal machine learning algorithms into virtual reality systems. This will require the addition of new stages in the data processing pipeline in VR systems [46]. The functioning of such systems will not be based on the direct use of data from KTP (for example, virtual reality trackers), but on sending them to digital shadow software, receiving a restored VKTP set, forming a virtual avatar, and changing the final person’s model position in the scene. An avatar formed in this way will be as close as possible to the real position of the body, taking into account the minimum number of tracked points.
5. Conclusions
In this study, the problem of modeling nonlinear dynamic processes of human movement in virtual reality was considered to simplify motion capture systems and reduce the number of KTPs. To solve it, the concept of a digital shadow was proposed, including the formalization of the motion process based on the analysis of the functioning of various motion capture systems, the development of a procedure for generating a dataset from a virtual avatar, and the formulation and solution of the problem of minimizing the number of key points for tracking a person based on machine learning algorithms.
In the course of this study, the existing approaches to solving the problem of inverse kinematics in the conditions of a limited number of tracking points were analyzed using various machine learning algorithms. Further, a comparison of motion capture systems was carried out, and shortcomings of the data obtained from them were identified, which led to the development of a methodology for collecting information about human movements from a virtual avatar. This allows you to increase the speed of formation, size, and diversity of the dataset by simulating various scenarios in a virtual scene.
Next, the simulation of the human movement process in virtual reality was carried out, and the main components of the digital shadow were formalized, after which the task of optimizing the number of KTPs was formulated with the selection of the best machine learning algorithm.
A total of six main combinations of KTP were identified, for which various machine learning algorithms were compared for the reconstruction of the entire virtual avatar. It was found that the use of three KTPs is not sufficient for all algorithms, the maximum deviation is more than 0.4 m, and the average is more than 0.15 m; in addition, it is impossible to reliably reconstruct the legs of a virtual avatar, especially in complex poses. The use of five KTPs eliminates this problem, and seven KTPs allow complex hand positions to be reconstructed in the elbow area. The use of nine or more KTPs has a positive effect, but it is not significant and visually sensitive, so five to seven KTPs are recommended as the optimal number of points for various use cases. When comparing algorithms under these conditions for solving the regression problem, the best results were shown (in descending order): AdaBoostRegressor, LinearRegression/SGDRegressor, neural network (with multiple inputs), and neural network (with one input). When using AdaBoostRegressor, the maximum deviation is not more than 0.25 m, and the average is not more than 0.10 m.
The novelty of this study is the use of the digital shadow concept and the collection of data from a virtual avatar to simulate nonlinear dynamic processes of human movement in virtual reality. The proposed approaches make it possible to reduce the cost and complexity of motion capture systems, speed up the process of collecting information for training machine learning algorithms, and increase the amount of data by simulating various motion scenarios in virtual space.
Author Contributions
Conceptualization, A.O. and D.D.; methodology, A.O.; software, D.T.; validation, A.O. and A.V.; formal analysis, A.O. and A.V.; investigation, A.O., D.D. and A.V.; resources, D.T. and A.V.; data curation, D.T.; writing—original draft preparation, A.O.; writing—review and editing, A.O. and A.V.; visualization, D.T.; supervision, A.O. and D.D.; project administration, D.D.; funding acquisition, D.D. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by a grant of the Russian Science Foundation (grant number: 22-71-10057; https://rscf.ru/en/project/22-71-10057/ (accessed on 20 April 2023)).
Data Availability Statement
Data available in a publicly accessible repository that does not issue DOIs. Publicly available datasets were analyzed in this study. This data can be found here: mocap.cs.cmu.edu. The database was created with funding from NSF EIA-0196217.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Al-Jundi, H.A.; Tanbour, E.Y. A framework for fidelity evaluation of immersive virtual reality systems. Virtual Real. 2022, 26, 1103–1122. [Google Scholar] [CrossRef]
- Obukhov, A.D.; Volkov, A.A.; Vekhteva, N.A.; Teselkin, D.V.; Arkhipov, A.E. Human motion capture algorithm for creating digital shadows of the movement process. J. Phys. Conf. Ser. 2022, 2388, 012033. [Google Scholar] [CrossRef]
- Oudah, M.; Al-Naji, A.; Chahl, J. Hand Gesture Recognition Based on Computer Vision: A Review of Techniques. J. Imaging 2020, 6, 73. [Google Scholar] [CrossRef] [PubMed]
- Nie, J.Z.; Nie, J.W.; Hung, N.T.; Cotton, R.J.; Slutzky, M.W. Portable, open-source solutions for estimating wrist position during reaching in people with stroke. Sci. Rep. 2021, 11, 22491. [Google Scholar] [CrossRef] [PubMed]
- Hindle, B.R.; Keogh, J.W.L.; Lorimer, A.V. Inertial-Based Human Motion Capture: A Technical Summary of Current Processing Methodologies for Spatiotemporal and Kinematic Measures. Appl. Bionics Biomech. 2021, 2021, 6628320. [Google Scholar] [CrossRef]
- Filippeschi, A.; Schmitz, N.; Miezal, M.; Bleser, G.; Ruffaldi, E.; Stricker, D. Survey of Motion Tracking Methods Based on Inertial Sensors: A Focus on Upper Limb Human Motion. Sensors 2017, 17, 1257. [Google Scholar] [CrossRef]
- Gonzalez-Islas, J.-C.; Dominguez-Ramirez, O.-A.; Lopez-Ortega, O.; Peña-Ramirez, J.; Ordaz-Oliver, J.-P.; Marroquin-Gutierrez, F. Crouch Gait Analysis and Visualization Based on Gait Forward and Inverse Kinematics. Appl. Sci. 2022, 12, 10197. [Google Scholar] [CrossRef]
- Parger, M.; Mueller, J.H.; Schmalstieg, D.; Steinberger, M. Human upper-body inverse kinematics for increased embodiment in consumer-grade virtual reality. In Proceedings of the 24th ACM Symposium on Virtual Reality Software and Technology, Tokyo, Japan, 28 November 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Van Emmerik, R.E.; Rosenstein, M.T.; McDermott, W.J.; Hamill, J. A Nonlinear Dynamics Approach to Human Movement. J. Appl. Biomech. 2004, 20, 396–420. [Google Scholar] [CrossRef]
- Wu, Y.; Tao, K.; Chen, Q.; Tian, Y.; Sun, L. A Comprehensive Analysis of the Validity and Reliability of the Perception Neuron Studio for Upper-Body Motion Capture. Sensors 2022, 22, 6954. [Google Scholar] [CrossRef]
- Ikbal, M.S.; Ramadoss, V.; Zoppi, M. Dynamic Pose Tracking Performance Evaluation of HTC Vive Virtual Reality System. IEEE Access 2020, 9, 3798–3815. [Google Scholar] [CrossRef]
- Hellsten, T.; Karlsson, J.; Shamsuzzaman, M.; Pulkkis, G. The Potential of Computer Vision-Based Marker-Less Human Motion Analysis for Rehabilitation. Rehabil. Process Outcome 2021, 10, 11795727211022330. [Google Scholar] [CrossRef]
- Chen, W.; Yu, C.; Tu, C.; Lyu, Z.; Tang, J.; Ou, S.; Fu, Y.; Xue, Z. A Survey on Hand Pose Estimation with Wearable Sensors and Computer-Vision-Based Methods. Sensors 2020, 20, 1074. [Google Scholar] [CrossRef]
- Degen, R.; Tauber, A.; Nüßgen, A.; Irmer, M.; Klein, F.; Schyr, C.; Leijon, M.; Ruschitzka, M. Methodical Approach to Integrate Human Movement Diversity in Real-Time into a Virtual Test Field for Highly Automated Vehicle Systems. J. Transp. Technol. 2022, 12, 296–309. [Google Scholar] [CrossRef]
- Caserman, P.; Garcia-Agundez, A.; Konrad, R.; Göbel, S.; Steinmetz, R. Real-time body tracking in virtual reality using a Vive tracker. Virtual Real. 2019, 23, 155–168. [Google Scholar] [CrossRef]
- Feigl, T.; Gruner, L.; Mutschler, C.; Roth, D. Real-time gait reconstruction for virtual reality using a single sensor. In Proceedings of the 2020 IEEE International Symposium on Mixed and Augmented Reality Adjunct (ISMAR-Adjunct), Recife, Brazil, 9–13 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 84–89. [Google Scholar]
- Liu, H.; Zhang, Z.; Xie, X.; Zhu, Y.; Liu, Y.; Wang, Y.; Zhu, S.-C. High-Fidelity Grasping in Virtual Reality using a Glove-based System. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5180–5186. [Google Scholar]
- Li, J.; Xu, C.; Chen, Z.; Bian, S.; Yang, L.; Lu, C. HybrIK: A Hybrid Analytical-Neural Inverse Kinematics Solution for 3D Human Pose and Shape Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 3383–3393. [Google Scholar]
- Oyama, E.; Agah, A.; MacDorman, K.F.; Maeda, T.; Tachi, S. A modular neural network architecture for inverse kinematics model learning. Neurocomputing 2001, 38, 797–805. [Google Scholar] [CrossRef]
- Bai, Y.; Luo, M.; Pang, F. An Algorithm for Solving Robot Inverse Kinematics Based on FOA Optimized BP Neural Network. Appl. Sci. 2021, 11, 7129. [Google Scholar] [CrossRef]
- Kratzer, P.; Toussaint, M.; Mainprice, J. Prediction of Human Full-Body Movements with Motion Optimization and Recurrent Neural Networks. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1792–1798. [Google Scholar] [CrossRef]
- Bataineh, M.; Marler, T.; Abdel-Malek, K.; Arora, J. Neural network for dynamic human motion prediction. Expert Syst. Appl. 2016, 48, 26–34. [Google Scholar] [CrossRef]
- Cui, Q.; Sun, H.; Li, Y.; Kong, Y. Efficient human motion recovery using bidirectional attention network. Neural Comput. Appl. 2020, 32, 10127–10142. [Google Scholar] [CrossRef]
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in manufacturing: A categorical literature review and classification. IFAC-PapersOnLine 2018, 51, 1016–1022. [Google Scholar] [CrossRef]
- Grieves, M. Origins of the Digital Twin Concept. 2016. Available online: https://www.researchgate.net/publication/307509727 (accessed on 11 April 2023).
- Krüger, J.; Wang, L.; Verl, A.; Bauernhansl, T.; Carpanzano, E.; Makris, S.; Fleischer, J.; Reinhart, G.; Franke, J.; Pellegrinelli, S. Innovative control of assembly systems and lines. CIRP Ann. 2017, 66, 707–730. [Google Scholar] [CrossRef]
- Ribeiro, P.M.S.; Matos, A.C.; Santos, P.H.; Cardoso, J.S. Machine Learning Improvements to Human Motion Tracking with IMUs. Sensors 2020, 20, 6383. [Google Scholar] [CrossRef]
- Stančić, I.; Musić, J.; Grujić, T.; Vasić, M.K.; Bonković, M. Comparison and Evaluation of Machine Learning-Based Classification of Hand Gestures Captured by Inertial Sensors. Computation 2022, 10, 159. [Google Scholar] [CrossRef]
- Yacchirema, D.; de Puga, J.S.; Palau, C.; Esteve, M. Fall detection system for elderly people using IoT and ensemble machine learning algorithm. Pers. Ubiquitous Comput. 2019, 23, 801–817. [Google Scholar] [CrossRef]
- Halilaj, E.; Rajagopal, A.; Fiterau, M.; Hicks, J.L.; Hastie, T.J.; Delp, S.L. Machine learning in human movement biomechanics: Best practices, common pitfalls, and new opportunities. J. Biomech. 2018, 81, 1–11. [Google Scholar] [CrossRef]
- Bartol, K.; Bojanić, D.; Petković, T.; Peharec, S.; Pribanić, T. Linear regression vs. deep learning: A simple yet effective baseline for human body measurement. Sensors 2022, 22, 1885. [Google Scholar] [CrossRef] [PubMed]
- Turgeon, S.; Lanovaz, M.J. Tutorial: Applying Machine Learning in Behavioral Research. Perspect. Behav. Sci. 2020, 43, 697–723. [Google Scholar] [CrossRef]
- Pavllo, D.; Feichtenhofer, C.; Auli, M.; Grangier, D. Modeling Human Motion with Quaternion-Based Neural Networks. Int. J. Comput. Vis. 2020, 128, 855–872. [Google Scholar] [CrossRef]
- Almeida, R.O.; Munis, R.A.; Camargo, D.A.; da Silva, T.; Sasso Júnior, V.A.; Simões, D. Prediction of Road Transport of Wood in Uruguay: Approach with Machine Learning. Forests 2022, 13, 1737. [Google Scholar] [CrossRef]
- Li, B.; Bai, B.; Han, C. Upper body motion recognition based on key frame and random forest regression. Multimedia Tools Appl. 2020, 79, 5197–5212. [Google Scholar] [CrossRef]
- Sipper, M.; Moore, J.H. AddGBoost: A gradient boosting-style algorithm based on strong learners. Mach. Learn. Appl. 2022, 7, 100243. [Google Scholar] [CrossRef]
- Kanko, R.M.; Laende, E.K.; Davis, E.M.; Selbie, W.S.; Deluzio, K.J. Concurrent assessment of gait kinematics using marker-based and markerless motion capture. J. Biomech. 2021, 127, 110665. [Google Scholar] [CrossRef]
- Choo, C.Z.Y.; Chow, J.Y.; Komar, J. Validation of the Perception Neuron system for full-body motion capture. PLoS ONE 2022, 17, e0262730. [Google Scholar] [CrossRef]
- Al-Faris, M.; Chiverton, J.; Ndzi, D.; Ahmed, A.I. A Review on Computer Vision-Based Methods for Human Action Recognition. J. Imaging 2020, 6, 46. [Google Scholar] [CrossRef]
- Zheng, B.; Sun, G.; Meng, Z.; Nan, R. Vegetable Size Measurement Based on Stereo Camera and Keypoints Detection. Sensors 2022, 22, 1617. [Google Scholar] [CrossRef] [PubMed]
- Sers, R.; Forrester, S.; Moss, E.; Ward, S.; Ma, J.; Zecca, M. Validity of the Perception Neuron inertial motion capture system for upper body motion analysis. Meas. J. Int. Meas. Confed. 2020, 149, 107024. [Google Scholar] [CrossRef]
- The Daz-Friendly Bvh Release of Cmu Motion Capture Database. Available online: https://www.sites.google.com/a/cgspeed.com/cgspeed/motion-capture/the-daz-friendly-bvh-release-of-cmus-motion-capture-database (accessed on 22 March 2023).
- Demir, S. Comparison of Normality Tests in Terms of Sample Sizes under Different Skewness and Kurtosis Coefficients. Int. J. Assess. Tools Educ. 2022, 9, 397–409. [Google Scholar] [CrossRef]
- Zeng, Q.; Zheng, G.; Liu, Q. PE-DLS: A novel method for performing real-time full-body motion reconstruction in VR based on Vive trackers. Virtual Real. 2022, 26, 1391–1407. [Google Scholar] [CrossRef]
- Yi, X.; Zhou, Y.; Xu, F. Transpose: Real-time 3D human translation and pose estimation with six inertial sensors. ACM Trans. Graph. 2021, 40, 1–13. [Google Scholar] [CrossRef]
- Obukhov, A.; Volkov, A.A.; Nazarova, A.O. Microservice Architecture of Virtual Training Complexes. Inform. Autom. 2022, 21, 1265–1289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).