1. Introduction
Graphs are incredibly flexible data structures that can represent information through vertices and relations through edges, allowing them to model various phenomena with easily machine-readable structures. We can adopt graphs to represent the relationship between functions in programs, electronic logic devices in synthesis, connections between atoms, and molecules in biology, etc.
Understanding whether two graphs represent the very same object, that is, determining if the two graphs are isomorphic, belongs to the class of NP-complete problems. Scholars are still not sure whether it can be improved, but existing algorithms for solving this problem have exponential complexity [
1]. Given two graphs, i.e.,
and
, finding the largest graph simultaneously isomorphic to two subgraphs of the given graphs, i.e.,
, is even more challenging; it is usually known as the Maximum Common Subgraph (MCS) problem. Nevertheless, this problem is the key step in many applications, such as studying “small worlds” in social networks [
2,
3], searching the web [
4], analyzing biological data [
5], classifying large-scale chemical elements [
6], and discovering software malwares [
7]. Algorithms to find the MCS have been presented in the literature since the 70s [
8,
9]. Among the most significant approaches, we would like to mention the conversion to the Maximum Common Clique problem [
10], the use of constraint programming [
11,
12] and integer linear programming [
13], the extraction of subgraphs guided by a neural network model [
14,
15], the adoption of reinforcement learning [
16], and even multi-engines and GPU-based many-core implementations [
17].
This paper proposes a set of algorithms and related heuristics to assess the similarity of a set of graphs and determine how akin each of these graphs is to the whole group. More specifically, we approach the so-called Multi-MCS problem [
6,
18], i.e., we focus on finding the MCS or a quasi-MCS (one good approximation of the MCS) among
N (usually more than two) graphs. Notice that a possible solution to this problem consists of the iterated application of a standard MCS procedure to find the MCS between two graphs, i.e.,
, to a set of
N graphs
. Unfortunately, to apply this strategy, we need to fully parenthesize the set of graphs, and the number of possible parenthesizations is exponential in
N, i.e.,
[
19]. Moreover, as each computation
potentially has several equivalent solutions, not all parenthesizations deliver the same results. For example, given three graphs
, computing
may give optimal results, whereas computing
may even deliver an empty solution.
To analyze this problem, we examine the work by McCreesh et al. [
20]. This work introduces McSplit, i.e., an efficient branch-and-bound recursive procedure that, given two graphs,
and
, finds one of their MCSs, i.e.,
. The process is based on an intelligent invariant that, given a partial mapping between the vertices of the two graphs, considers a new vertex pair only if the vertices within the pair share the same
label. Labels are defined based on the interconnections between vertices. Two vertices only share the same label if they are connected in the same way to all previously mapped nodes. The algorithm also adopts an effective bound prediction that, given the current mapping and the labels of yet-to-map vertices, computes the best MCS size the current recursion path can achieve. In practice, the algorithm prunes all paths of the tree search that are not promising enough; thus, it drastically reduces the search space once a good-enough solution has been found. Unfortunately, even if the constraining effect may be fairly effective, pruning depends on the vertex selection order, which is statically computed at the beginning of the process and is one of the most impairing elements of McSplit. Indeed, the static node-degree heuristic may be sub-optimal, generate many ties on large graphs, and include no strategy to break those ties.
We extend this algorithm in different directions. We first generalize the original approach to handle N graphs simultaneously, i.e., , and find their MCS, i.e., . This algorithm finds maximal common subgraphs, is purely sequential, and extends the recursive process of the original function to generate (and couple) the simple permutations of sets of vertices. To maintain the original compactness and efficiency considering N graphs, we revisit the algorithmic invariant, the original bound computation, and the data structure used to store partial information. This algorithm also introduces a domain-sorting heuristic that speeds up the original McSplit procedure on a pair of graphs by more than a 2× factor and delivers even better improvements (up to 10×) when it is applied to more than two graphs.
This work is then extended to a parallel multi-core CPU-based procedure to improve its efficiency following the work by Quer et al. [
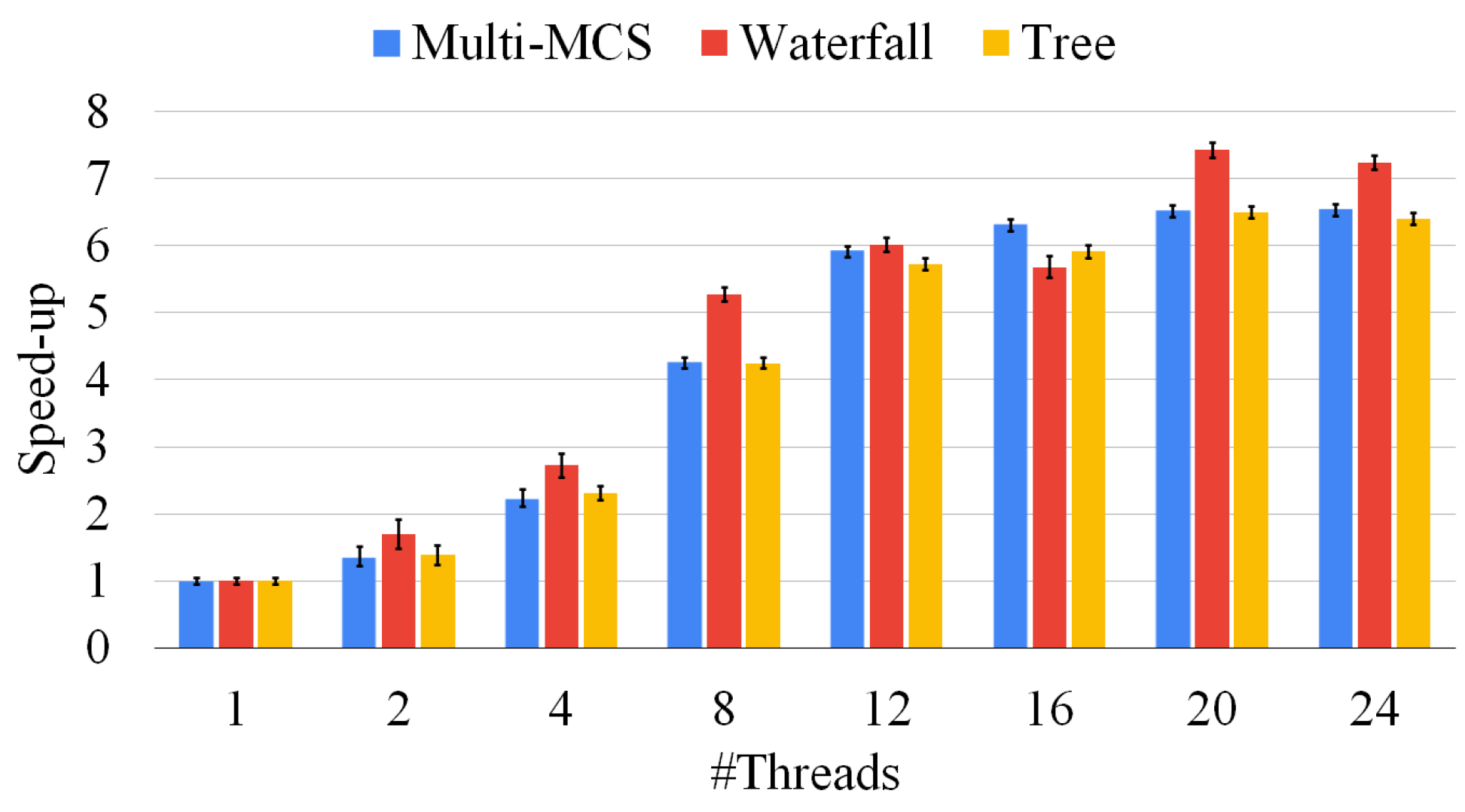
17]. We divide the work into independent tasks and assign these tasks to a thread pool, minimizing the contention among threads, and trying to balance the workload as much as possible, even though the problem remains an intrinsically unbalanced one. Although it is well known that the order in which nodes are processed greatly influences the execution time, we discovered that the order of the graphs also significantly impacts the speed of our procedure (up to over an order of magnitude) without any apparent drawback. As a consequence, we run experiments with different graph sorting heuristics, and we compare these heuristics in terms of computation time and memory used.
Unfortunately, even if the two previous strategies find maximal solutions and sorting heuristics can considerably improve running times, they can only manage a tiny number of medium-size graphs when faced with a timeout of 1000 s. As computation time is the main constraining factor as memory usage is usually not critical in this computation, several applications that produce non-exact solutions requiring only a fraction of the computation time can benefit from algorithms. By trading off computational costs and accuracy, we propose three heuristics to find the closest-possible maximal solution (a quasi-MCS). Moreover, we compare them in complexity, efficiency, and result size. The first strategy, which we call the “waterfall approach”, manipulates the N graphs linearly, such that the MCS of any two graphs, e.g., , is compared with the following graph in the list, e.g., . The second strategy, which we call the “tree approach”, manipulates the N graphs pair-by-pair in a tree-like fashion, e.g., . It is potentially far more parallelizable than the waterfall scheme and can be managed by a distributed approach in case of a high enough number of graphs. At the same time, the quality of its solutions is often limited by the choices performed in the higher nodes of the tree.
Finally, to show the scalability of the tree approach, we call a GPU unit and distribute the branches of the tree-like approach between the two devices leveraging a multi-threading CPU and a many-threading GPU unit. Although the GPU implementation cannot outperform the CPU version in speed, since the implementation deals with an inherently unbalanced problem, the presence of a second device allows us to reduce the execution time when applied to the tree approach.
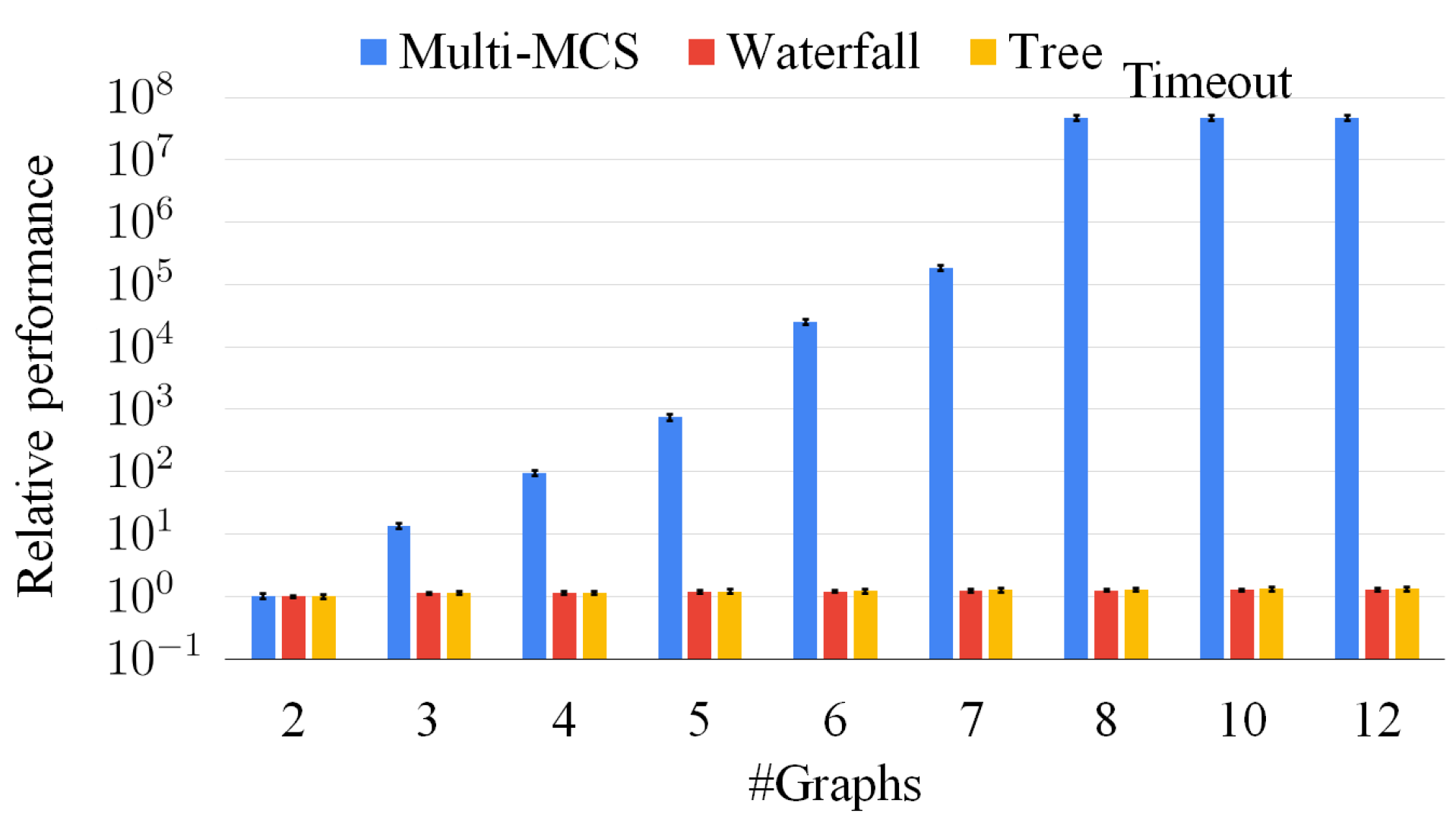
Our experimental results show the advantages and disadvantages of our procedures and heuristics. We take into consideration the asymptotic complexity and the elapsed time of our tools, and, as some of our strategies sacrifice optimality in favor of applicability, we also consider the result size as an essential metric to compare them. We prove that the heuristic approaches are orders of magnitude faster than the exact original implementations. Even if they cannot guarantee the maximality of their solution, we prove that their precision loss is shallow once the proper countermeasures are implemented.
To sum up, this paper presents the following contributions:
An extension of a state-of-the-art MCS algorithm to solve the Multi-MCS problem adopting both a sequential and a parallel multi-threaded approach. These solutions manipulate the N-graphs within a single branch-and-bound procedure.
A revisitation of the previous multi-threaded approach to solving the Multi-quasi-MCS problem, trading-off computation time and accuracy. In these cases, our solutions deal with the N-graphs on a graph-pair basis with different logic schemes.
A mixed parallel multi-core (CPU-based) and many-core (GPU-based) extension of the previous algorithms for a non-exhaustive search to further reduce the computational time distributing the effort on different computational units.
An analysis of sorting heuristics applicable to vertex bidomains, graph pairs, and set of graphs able to significantly improve the solution time with a minimal increase in the algorithmic complexity.
As far as we know, this is the first work facing the Multi-MCS (and the Multi-quasi-MCS) problem consistently, presenting both exact (maximal) and approximated (quasi-maximal) algorithms to solve it.
The paper is organized as follows.
Section 2 reports some background on multi-graph isomorphism and introduces McSplit.
Section 3 describes our sequential and parallel multi-core McSplit extensions to handle the Multi-MCS problem.
Section 4 shows our implementations of the Multi-quasi-MCS problem tackled as a linear (sequential) or tree (parallel) series of MCS searches.
Section 5 introduces the proposed sorting heuristics.
Section 6 reports our findings in terms of result size, computation time, and memory used.
Section 7 draws some conclusions and provides some hints on possible further developments.
3. The Multi-MCS Approach
While the MCS problem has multiple applications in different scenarios, Multi-MCS has been mainly studied in molecular science and cyber-security due to its extremely high costs. Surely, more efficient algorithms would push forward its applicability in other research sectors. For this reason, in this section, we present two algorithms extending McSplit [
20] to directly consider a set of
N graphs
. The first version is purely sequential, whereas the second one is its multi-core CPU-based parallel variation. The efficiency of both versions strongly depends on the graph order. As a consequence, we dedicate the last subsection of this part to describing our sorting heuristics.
3.1. The Sequential Approach
Our first contribution is to rewrite the McSplit algorithm in a sequential form and in such a way that it can handle any number of graphs. A single call to our branch-and-bound procedure
Multi-MCS (
) computes the MCS of
N graphs
.
Figure 3 illustrates the inputs and outputs of the function, and Algorithm 1 reports its pseudo-code.
To obtain an efficient implementation, we modify a few core steps of the original algorithms, maintaining the main perks of the logic flow together with its overall memory and time efficiency.
| Algorithm 1 The sequential Multi-MCS function: A unique recursive branch-and-bound procedure that given N graphs and computes |
- 1:
Multi-MCS () - 2:
- 3:
level = 0 - 4:
domains = initial domains - 5:
selectFirstNode (, C, S, level, domains) - 6:
return S
|
- 7:
selectFirstNode (, C, S, level, domains) - 8:
if () then - 9:
- 10:
end if - 11:
while do - 12:
bound = computeBound (, C) - 13:
if (bound ≤) then - 14:
return - 15:
end if - 16:
domain = selectLabelClass (, domains) - 17:
v = selectVertex (domain) - 18:
- 19:
- 20:
selectNextNode (, C, S, level + 1, domains, domain) - 21:
- 22:
end while
|
- 23:
selectNextNode (, C, S, level, domains, domain) - 24:
- 25:
for all u ∈ domain[H] do - 26:
- 27:
- 28:
if ((level % N) == N − 1) then - 29:
new_domains = filterDomains (, C, domains) - 30:
// Select new domain on first graph - 31:
selectFirstNode (, C, S, level + 1, new_domains) - 32:
else - 33:
// Select node from another graph - 34:
selectNextNode (, C, S, level + 1, domains, domain) - 35:
end if - 36:
- 37:
- 38:
end for
|
The algorithm selects a node of the first graph and a node of the second graph so that each edge and non-edge toward nodes belonging to the current solution is preserved. After selecting each new node pair, the algorithm divides the “remaining” nodes into sub-sets. These sub-sets are called “domains” in the original formulation, are created by function filterDomains, and group nodes sharing the same set of adjacency and non-adjacency toward the nodes in the current solution. Two domains belonging to different graphs that share the same adjacency rules to nodes in their respective graphs are then paired in what is called a “bidomain”. The nodes within a bidomain are thus compatible and can be matched. For each bidomain, the size of the smallest domain is used by function computeBound to compute how many nodes can still be added to the solution along that specific path, pruning the search whenever possible.
In our implementation, to handle more than two graphs and maintain the original algorithmic efficiency, we revise both the logic and the data structure of the algorithm. Our Multi-MCS procedure begins by initializing its variables C (representing the current solution), S (the best solution found) with an empty solution, and the variable level (representing the number of nodes already selected) to zero. Finally, it assigns an initial value to the variable domains, which depends on the nature of the graph: when the graph has no label, all nodes in the graph belong to a single domain; otherwise, the initial number of domains is equal to the number of different labels. Then, the algorithm performs the selection of a node from the first and a node from the second graph in two steps. Function selectFirstNode, called in line 4, selects the multi-domain (a bidomain extended to multiple graphs) from which the nodes is chosen to be added to our solution, and it selects the node of the first graph. Function selectNextNode, called in line 20, works on the same multi-domain until it has selected a node from each of the other graphs.
The function
selectFirstNode first updates the current best solution (lines 8–10). Then, it computes the current bound using the function
computeBound (line 12). If the bound proves that we will not be able to improve the current best solution, we return (line 14) and try to select a different set of nodes in order to reach a better solution. If we can still improve the current best solution, we then choose the multi-domain from which to select the vertices. This step is performed by function
selectLabelClass (line 16). While different node sorting heuristics can improve the performance of the algorithm, we followed the same logic used in the McSplit algorithm, preferring a fail-first approach. This method entails that the function always selects the smallest multi-domain to quickly check all possible matchings, and therefore, it allows us to definitely remove them from the current branch of execution. From the selected multi-domain, we select the node with the highest number of neighboring nodes (another heuristic borrowed from McSplit), we add it to our current solution, and we remove it from the list of non-selected nodes. In line 20, we call
selectNextNode to proceed to the other graphs. When all possible matchings have been checked, we remove the selected node from the solution and try to improve on the current one by avoiding the selection of the node just discarded. The standard C-like implementation proceeds with dynamically allocated data structures for the domains and bidomains. Nevertheless, in some cases, dynamic allocation may drastically influence performance. As a consequence, in
Section 3.2, we also discuss the possibility of adopting pre-allocated (static) memory to reduce overheads, even if this solution somehow limits the flexibility of the algorithm.
The function, selectNextNode, is a much simpler function. It works on the already chosen multi-domain and selects a vertex from each of the remaining graphs (i.e., )—more specifically, from the domains belonging to the same multi-domain. In this function, we refer to the set of all graphs with G. Since, as we have already discussed, the vertices belonging to the same multi-domain can be paired without producing conflicts, this is a pretty straightforward task. Once again, the order of selection is unsophisticated, as we chose the vertices by sorting them by the number of respective adjacency. Once we have selected a node from each graph, we call the function filterDomains (line 29) to update the domains previously computed, and we recur on the next multi-domain (line 31).
To better describe our procedure, following
Figure 2 and
Table 1, we illustrate a possible sequence of node selection and node labeling with three graphs in
Figure 4 and
Table 2. For the sake of simplicity,
Table 2 does not represent the actual execution steps performed by the algorithm since a correct execution of the procedure finds multiple non-maximal solutions from which it has to backtrack before gathering the MCS. As a consequence, we select a sequence of three steps that lead to one of the admissible MCS, showing the node selection process and the evolution of the labels. The example starts by selecting the nodes 1,
a, and
A from graphs
,
, and
, respectively. Starting from this partial solution, the function separates the other nodes into two domains, depending on their adjacency with the selected nodes. During the second step, the procedure selects the nodes 3,
c, and
B from the adjacent domain, creating three new domains. Finally, during the third step, function
Multi-MCS selects the nodes 4,
d, and
C. None of the resulting domains appears in all three graphs; thus, the algorithm backtracks to look for a better solution.
Table 2.
Labels on the non-mapped vertices of , and .
Table 2.
Labels on the non-mapped vertices of , and .
| a M = {1,a,A} | | b M = {13,ac,AB} | | | | c M = {134,acd,ABC} |
| | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | |
| 2 | 0 | b | 1 | B | 1 | | 2 | 00 | b | 10 | C | 11 | | | | 2 | 000 | b | 100 | D | 001 |
| 3 | 1 | c | 1 | C | 1 | | 4 | 11 | d | 11 | D | 00 | | | | 5 | 100 | e | 100 | | |
| 4 | 1 | d | 1 | D | 0 | | 5 | 10 | e | 10 | | | | | | | | f | 00 | | |
| 5 | 1 | e | 1 | | | | | | f | 000 | | | | | | | | | | | |
| | | f | 0 | | | | | | | | | | | | | | | | | | |
3.2. The Parallel Approach
To improve the efficiency of Algorithm 1 and following Quer et al. [
17], we modified the previous procedure to handle tasks in parallel. Algorithm 2 reports the new pseudo-code. Functions
selectFirstNode and
selectNextNode are not reported as they are identical to the ones illustrated in Algorithm 1.
| Algorithm 2 The parallel many-core CPU-based Multi-MCS Function: A unique recursive function that, given N graphs , computes running several tasks |
- 1:
Multi-MCS (, C, S, level, domain) - 2:
if (level % N) == 0 then - 3:
if () then - 4:
= { , C, S, level } - 5:
enqueue (selectFirstNode, ) - 6:
else - 7:
selectFirstNode (, C, S, level) - 8:
end if - 9:
else - 10:
selectNextNode (, C, S, level, domain) - 11:
end if
|
The parallelization of the algorithm is achieved by dividing the workload among a pool of threads. Each thread waits on a synchronized queue which is filled with new tasks as represented in line 5 of the pseudo-code. Two objects are loaded into the queue: the pointer to the function to be executed, i.e., function selectFirstNode; and the data block needed for the execution, i.e., the variable . Once an item has been placed in the queue, the first available (free) thread will start working independently from the others, thus allowing a high level of parallelism. Since synchronization among threads often requires a significant amount of time, we only divide the work between various threads if the variable is less than a threshold () whose value can be selected experimentally. After this level, the rest of the execution takes place similarly to Algorithm 2, so that all threads are independent from each other.
The main problem of this function is due to the use of variable-sized arrays. A detailed code implementation showed that the compiler could not optimize the memory allocation of the new data structures, and this inefficiency resulted in a significant slowdown of the program when compared to the original implementation on graph pairs. To address this issue, we then implemented a second version of the algorithm where the main data structures were allocated statically of an oversize dimension. This second version showed significant speed ups compared to the original one both in the MCS (where it has achieved the performances of the original function) and in the multi-MCS problem.
3.3. Conclusions on Exact Multi-MCS Approaches
To understand the complexity of the Multi-MCS problem, we borrow some definitions from the world of combinatorics. When we consider two graphs,
and
, excluding any possible optimization, the number of possible matches between the nodes of
(with
nodes) and the nodes of
(with
nodes) equals the number of injective functions from the set of vertices
and the set of vertices
. If we call
i the number of elements of the smaller set that we will not pair with one of the second set, it is sufficient to compute the following to obtain the number of these functions:
To understand the previous equation, let us start by focusing separately on the two fractions. The first element of the equation represents the number of permutations of elements of the elements of the second set, whereas the second fraction represents the number of combinations of the elements of the elements of the first set. The permutations represent, given a set of elements of the first graph, all possible distinct pairings one can achieve using the elements of the second graph. The combinations represent all possible distinct sets of elements that we can select from the first graph. To conclude, we need to compute the summation that goes from zero (when we take all the elements of the first graph) to , when we do not take any elements. We consider only the empty set.
When we add a third graph, or a third set, the equation remains largely unchanged, even if we need to add a new factor:
Although the algorithm is extremely efficient, it cannot deal with the complexity of the Multi-MCS problem in a timely manner when comparing even small graphs in a large enough number. For this reason, in the following section, we discuss the Multi-quasi-MCS problem, introducing non-exact methodologies able to solve the problem by visiting only a fraction of the search tree. Since the MCS problem is difficult to approximate with algorithms with lower complexity than those able to compute an exact solution, our approach inevitably fails to find the MCS, but we discuss features added to the code to lower the probability of such a problem presenting itself.
4. The Multi-Quasi-MCS Approach
Due to the extremely long time required to solve the multi-MCS problem, we decided to trade off time and maximality.
Section 4.1 illustrates a first approach considering the sequence of all graphs in pairs.
Section 4.2 shows an attempt to improve the maximality of the previous approach without increasing the complexity of the algorithm too much.
Section 4.3 illustrates an alternative approach that allows a greater degree of parallelization.
4.1. The Waterfall Approach
Our first Multi-quasi-MCS approach follows the logic illustrated in
Figure 5, and Algorithm 3 reports its pseudo-code. Due to the order in which the graphs are considered, we refer to this method as the “waterfall” approach.
| Algorithm 3 The trivial multi-graph, i.e., Multi-quasi-MCS , branch-and-bound procedure |
- 1:
Multi-quasi-MCS () - 2:
sol = Solve (, ) - 3:
for all g in do - 4:
= Solve (, g) - 5:
end for - 6:
return
|
The waterfall approach consists of finding the MCS between two graphs through the original McSplit algorithm. Then, the computed subgraph is used as a new input to solve the MCS problem with the next graph.
In our implementation (Algorithm 3, lines 2 and 4), we adopt a parallel version of McSplit (for pairs of graphs) to implement the function
Solve. However, from a high-level point of view, the approach is structurally sequential as it manipulates a graph pair at each stage, and parallelism is restricted to every single call to the
Solve function. Indeed, we present an approach that increases the level of parallelism in
Section 4.3. As a final observation, please notice that it is possible to implement several minor variations of Algorithm 3 by changing the order in which the graphs are considered. For example, we can easily insert graphs in a priority queue (i.e., a maximum or minimum heap) using the size of the graphs as the priority. In this case, we can extract two graphs from the queue just before calling the function
Solve in line 4 and insert the result, sol, in the same queue after this call. The main difference with the original algorithm is the design of the data structure necessary to store intermediate solutions and the logic used to store in it all intermediate results.
Albeit being very simple, Hariharan et al. [
18] prove that a similar approach may not be able to guarantee the quality of the solution and could even return a zero-sized solution where better ones exist. Furthermore, the size of the final solution is strictly dependent on the order in which the graphs are considered, making some ordering strictly better than others. For example,
Figure 6 illustrates an example with three graphs on which, using the order
, the waterfall approach returns an empty solution. The algorithm correctly identifies the MCS between graph
and
, selecting the nodes
a,
d, and
e on both of them. Unfortunately, the MCS between this solution and
is an empty graph as all nodes of
have self-loops, while none of the nodes of the intermediate solution share this characteristic. On the contrary, the exact approach, by analyzing all the graphs simultaneously, can select the nodes
b and
c as a Multi-MCS of the graphs
.
As previously mentioned, considering the graphs in different orders would allow us to obtain different and possibly better solutions. If we solved the triplet of graphs in reverse order , the solution between and would return nodes b and c, which possess both the self-loop and a double edge. Then, calculating the MCS between this solution and , both nodes b and c would be preserved, leading us to the exact solution.
Despite the above problems, the complexity of this solution is orders of magnitude smaller than the one of
Section 3. Let us designate the number of nodes of
,
and
to be
,
and
, respectively; let us call
the size of the MCS of the first two graphs. Then, the complexity of solving three graphs can be evaluated as
Which amounts to a significant improvement over Equation (
3), where the two summations were multiplied by each other.
4.2. The Multi-Way Waterfall Approach
To improve the quality of the solutions delivered by the waterfall approach, we modified it using the logic illustrated in
Figure 7.
To reduce the impact of selecting an “unfortunate” MCS solution, which means that using it as input for future MCS searches would inevitably lead to a “small” final common subgraph, we have opted to store an arbitrary number of solutions at each intermediate step. To avoid an exponential tree-like explosion in the number of considered solutions, we heuristically set this number to a constant value
. As a consequence, in each phase of the search, we consider the
most promising solutions collected in the previous step, and we generate
new best solutions for the next stage. The process is repeated until no graphs are left, as illustrated in
Figure 7.
One of the problems with the multi-way waterfall approach is that several intermediate solutions are isomorphic, making the entire process somehow redundant. To rectify this problem, for each MCS call, we insert a post-processing step checking for each new solution whether the selected nodes differ with respect to the ones chosen for the previous solution. This process flow avoids the simplest case of isomorphism. Although verifying the node selection is a very unreliable and approximate way of checking whether two solutions are isomorphic, it is extremely fast, does not slow down the execution, and improves the final result’s size in many cases. Indeed, in
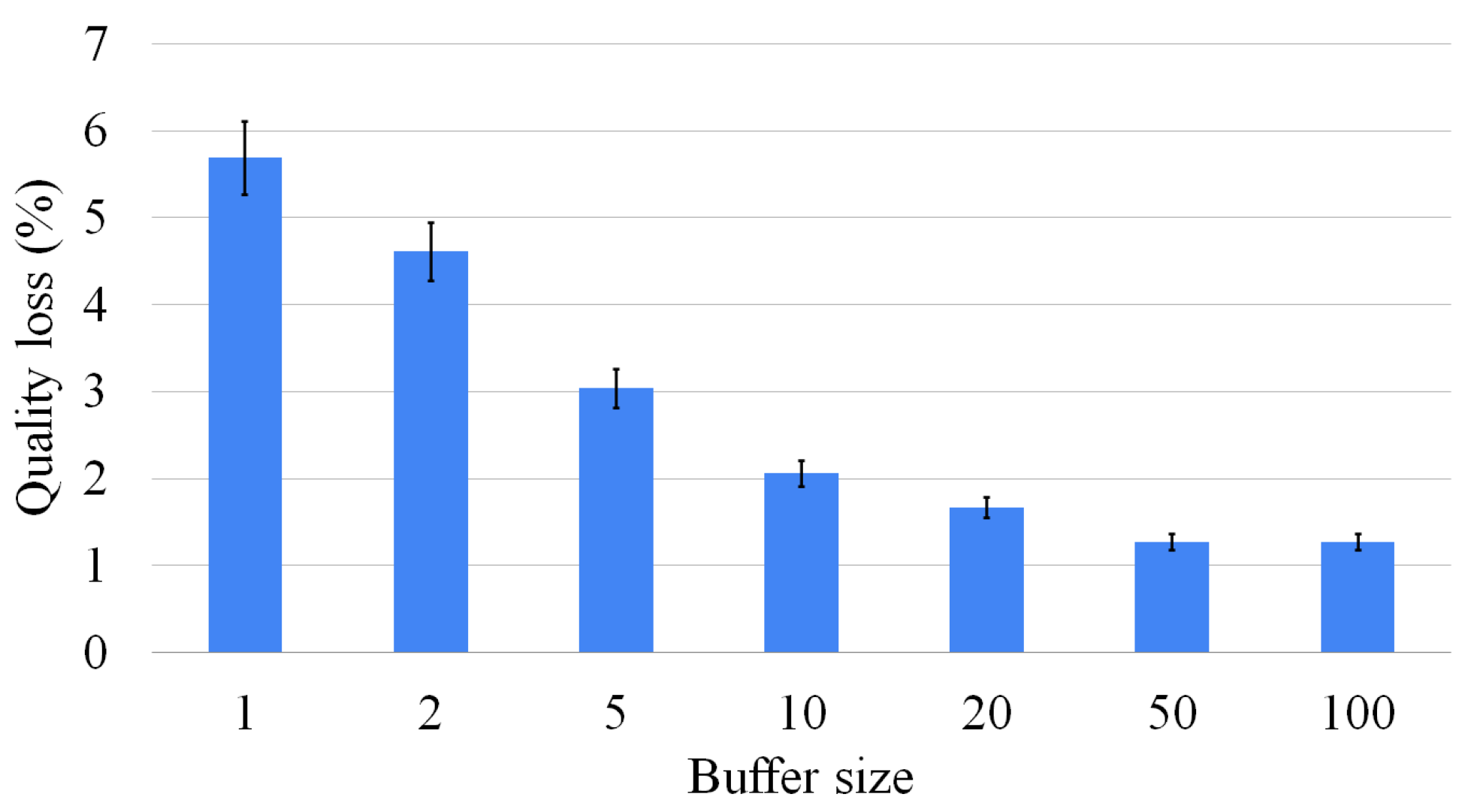
Section 6, we prove that over hundreds of executions, the size difference between the MCS and our solution is really small, usually consisting of only one vertex and occasionally two on MCS of the order of 10–25 vertices. Considering all experiments, the average error is under one vertex.
If we increase the number of intermediate solutions considered, the average error decreases, even if the reduction is limited if we consider more than five intermediate solutions. Overall, the multi-way waterfall approach is not only orders of magnitude faster than the exact approach, but the complexity of solving harder problems is slow-growing. For example, there are cases in which the exact approach cannot find a solution after 1000 s, and it returns only a partial solution, whereas this approach finds a larger solution within hundredths of a second.
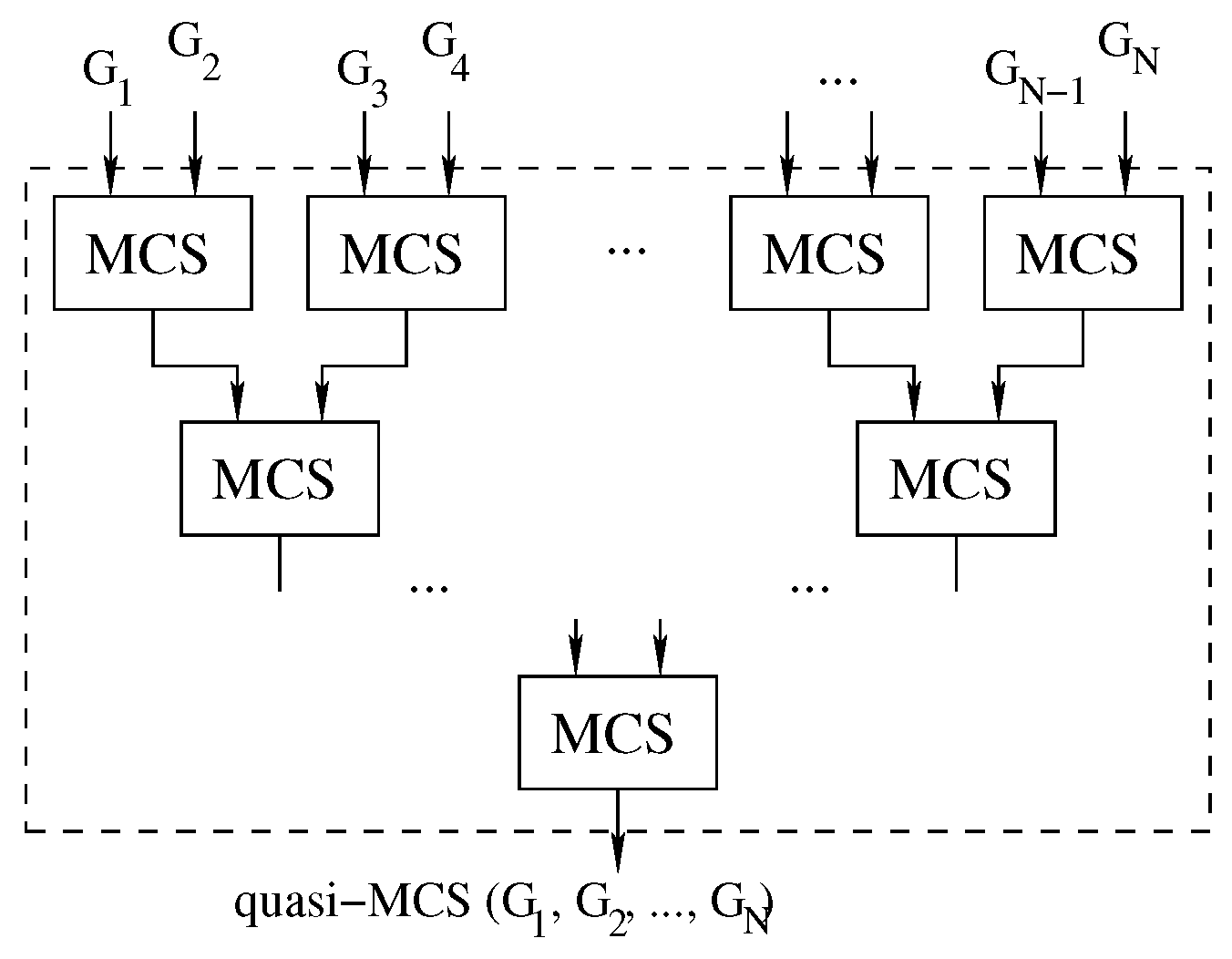
4.3. The Tree Approach
To further increase the parallelism of the approach, it is possible to consider pairs of graphs in a tree-like fashion until the final solution is discovered, as shown in
Figure 8.
Algorithm 4 shows a simple implementation of this approach. Due to the order in which the process is structured, we will refer to this implementation as the “tree” approach.
| Algorithm 4 The tree approach: increasing the parallelism of the waterfall strategy |
- 1:
Multi-quasi-MCS () - 2:
for to do - 3:
for to do - 4:
- 5:
- 6:
(Solve (, )) - 7:
end for - 8:
if then - 9:
() - 10:
end if - 11:
- 12:
- 13:
end for - 14:
return G
|
Algorithm 4 contains two main cycles. The loop in line 3 selects the pairs of graphs to be solved. Experimentally, we discovered that running the graphs by pairing the smallest and largest available graph at each iteration is more efficient. If the number of graphs present at a given loop is odd, the instruction at line 8 is meant to carry the graph over to the next iteration of the for cycle. Finally, the main loop (the one beginning at line 2) is in charge of repeating the main body of the function until only one graph remains.
Compared to the two waterfall strategies previously analyzed, the tree approach has the advantage of allowing separate computing units to work on different graph pairs. In the waterfall approach, due to the inherently unbalanced nature of the problem, doubling the number of threads does not always imply halving the solution time. On the contrary, solving graph pairs in parallel, as in the tree approach, reduces contention and provides better speed ups compared to the case in which the effort of all threads focuses on the same graph pair. In other words, instead of adding more computational power to a single pair of graphs as the waterfall approach, the tree strategy solves multiple graph pairs in parallel, improving the scalability of the method thanks to the presence of unrelated tasks. This also allows us to include a GPU (or multiple computers) in the computation without the necessity of introducing any sort of advanced synchronization. The disadvantage of the tree strategy is that we only consider one solution for each MCS problem, discarding a larger portion of the search space and potentially reducing the size of the final result. Furthermore, although the approach allows for better scaling, it does not guarantee that, given the same number of threads, it will outperform the previous method. We observed multiple times that the previous approach was both faster and produced a larger common subgraph. This behavior is caused by the fact that we wait for all graph pairs to be solved before generating the pairs from their solutions. This choice means that the time to be spent on a group of graphs is bound by the time spent to solve the pair of graphs that takes the longest. To mitigate this problem, we introduced a unified thread pool that allowed for any single threads to move from one pair of graphs to another; while this feature reduced the independence of the different MCSs, it allowed for a quicker run time on a single machine.
4.4. A Mixed CPU-GPU Tree Approach
To improve the performances of our algorithms, we ran some experiments adding a GPU to the standard power computation of the CPU. We explored two main approaches:
The first approach consists in dedicating a portion of the CPU computation power to produce partial problems to transfer to the GPU. The GPU, having at its disposal thousands of threads, can then solve each problem independently. While the GPU is busy with this work, the CPU can work on other instances following the original McSplit logic. Unfortunately, this approach does not bring relevant advantages to the overall computation time; on the fastest run, it usually marginally slows down the process. More specifically, this algorithm only shows significant speed ups when the workload is evenly distributed between threads, but cannot improve under a significant workload unbalance. Unfortunately, a medium-to-strong unbalanced workloads is present in the vast majority of the cases.
The second approach shows the ability of splitting the process among different computational units along the tree approach. Instead of letting the CPU solve all of the graph pairs, we move one pair to the GPU to reduce the workload on the CPU and improve the overall performance. However, the setup (and data loading phase) required to run the GPU take quite a long time, and as such, the process is unfit for the solution of small graph pairs. Nonetheless, this approach shows significant improvements in the more challenging instances, decreasing the solution time up to a factor of two.
The GPU version mentioned in this section is an extension of the one discussed by Quer et al. [
17]. The original version received two main extensions to improve its efficiency:
Since the original version had a tendency to take a significant amount of time to resolve stand-alone instances of graph pairs, we created a buffer of problems to pass to the GPU. In this way, the GPU kernel can process several high-complex sub-problems before needing new data or instructions from the CPU.
To increase the collaboration among GPU threads, we use the global memory to share some information, such as the size of the MCS found up to that moment. This value tends to change with a quite low frequency. It can therefore be easily maintained and updated in the device cache.