Abstract
In the field of cryptography, many algorithms rely on the computation of modular multiplicative inverses to ensure the security of their systems. In this study, we build upon our previous research by introducing a novel sequence, , that can calculate the modular inverse of a given pair of integers , i.e., . The computational complexity of this approach is , which is more efficient than the traditional Euler’s phi function method, . Furthermore, we investigate the properties of the sequence and demonstrate that all solutions of the problem belong to a specific set, , that only contains the minimum values of . This results in a reduction of the computational complexity of our method, especially when and it also opens new opportunities for discovering closed-form solutions for the modular inverse.
Keywords:
extended-Euclid algorithm; RSA algorithm; modular multiplicative inverse; public-key cryptography MSC:
11T71; 11Y16; 11Y05
1. Introduction
The modulo operation is a mathematical function that calculates the remainder of the division between two numbers, the dividend and the modulus. It is expressed as , where a and n are two positive numbers. This operation uses the Euclidean division method to find the remainder of dividing the dividend a by the divisor n.
The modular multiplicative inverse of an integer a is a number x such that is congruent to 1 modulo n, or in mathematical terms, . This means that the product of a and x gives a result that is equivalent to 1 when taken modulo n.
Modulo n forms an equivalence relation. The set of all integers equivalent to a modulo n, denoted by , is the set . This set is known as the congruence class or residue class of the integer a modulo n.
If an integer a has a modular multiplicative inverse modulo n, there are an infinite number of solutions that are equivalent to a with respect to the modulus n. Additionally, for any integer that is congruent to a modulo n, any element from the congruence class of x can serve as a modular multiplicative inverse. This can be represented as the multiplication of congruence classes modulo n, denoted by the symbol , where the modular multiplicative inverse of the congruence class is the congruence class such that .
The multiplication of congruence classes modulo n, represented by the symbol , is analogous to the concept of a multiplicative inverse in the set of real numbers. However, in this case, the numbers are replaced by congruence classes. This operation is used to solve linear congruences, such as Equation (1), where the goal is to find a solution for x that satisfies the equation and is equivalent to b modulo n:
In the field of public-key cryptography, solving Equation (1) is crucial in the RSA algorithm [1], which employs two large prime numbers that are modular multiplicative inverses with respect to a specific modulus to perform secure encryption and decryption operations. Many cryptographic algorithms, such as RSA, ElGamal, and NTRU, heavily rely on the use of modular multiplicative inverses in their calculations. Examples of this can be found in references such as Crandall [2], Rivest [3], Verkhovsky [4,5], ElGamal [6], Rabin [7], and Hoffstein [8]. Additionally, in recent times, Boolean functions have gained attention due to their useful properties in cryptography, specifically regarding “nonlinearity, propagation criterion, resiliency, and balance” [9].
In our previous study [10,11], we examined a particular sequence and its ability to determine the modular inverse for a given pair of integers , or . We found that the complexity of this search was , which is less than the classic Euler’s phi function method at . Additionally, we delved deeper into the properties of this sequence and discovered that all possible solutions of the problem belong to a set called , which only contains the minima of . This realization reduces the complexity of the algorithm, particularly when , and opens the possibility of finding a closed formula for the modular inverse.
In this paper, we present a particular sequence able to determine the modular inverse for a given pair of integers , i.e., . The complexity required for this search is , which is less than of the classic Euler’s phi function method. Moreover, we investigate more properties of such a sequence , concluding that all the possible solutions of the problem belong to a proper set, named , which contains only the minima of . This result reduces the complexity of our algorithm, especially when , and opens the way to the calculation of a possible closed formula for the modular inverse. Last but not least, we compare the complexity of our method with that of the post-quantum encryption (PQC) algorithm.
This research is structured as follows. Section 2 briefly reports the literature with a particular mention of post-quantum cryptography. In Section 3, the different methods for computing the modulus are discussed. Section 4 explores different expressions of that can help in comprehending the behavior of the sequence and in identifying the optimal approach for determining the critical index i. Section 5 discusses the results with particular attention to the sequence and its properties. It then provides a comparison between the complexity of our algorithm and that of the PQC method. Finally, Section 6 summarizes the research and hints at future developments.
2. Literature
When it was first introduced, RSA was considered to be a highly effective algorithm due to the lack of key exchange in the encryption and decryption process. However, the security of RSA relies heavily on the difficulty of factoring large numbers, a problem that is known to be NP-complete [12]. As technology progressed and computer speed increased, RSA keys began to be broken more frequently. To counteract this, developers have increased the length of the encryption key to ensure the continued security and privacy of systems protected by RSA. There have been other alternative solutions suggested to improve security in RSA cryptography. Some of these include the use of multiple public and private keys (Mezher et al. [13]), an enhanced version of RSA (ESRPKC) that incorporates the Chinese remainder theorem (Kumar et al. [14]), the use of random numbers and their modular multiplicative inverse (Islam et al. [15]), and an optimization algorithm (Cuckoo Search Optimization or CSA) to maintain data integrity in the cloud (Raja et al. [16]). A comprehensive overview of these methods can be found in the study by Mumtaz et al. [17]. In addition, the literature has proposed many solutions for specific needs such as lightweight algorithms suitable for use on resource-constrained nodes in sensitive applications (Bayat-Sarmadi et al. [18]).
Fault attacks are a type of attack on cryptographic algorithms that take advantage of malicious or unintentional errors introduced during their computation. The concept of Differential Cryptanalysis [19], combined with the pioneering work of Boneh, DeMillo, and Lipton [20,21], has given rise to the field of Differential Fault Attacks (DFA). DFA has revealed that many ciphers can be compromised if the errors can be manipulated in a specific manner. The DFA attack has shown that several ciphers can be compromised if the faults can be suitably controlled, and it is not limited to old ciphers but can be a powerful attack vector even for modern ciphers such as the Advanced Encryption Standard (AES). For a review, see Ali et al. [22]. Finally, on fault-detection methods capable of detecting random faults in the cipher implementation and, at the same time, against intelligent fault attacks, see Dofe et al. [23].
With the advent of post-quantum cryptography, post-quantum cryptography (PQC) will replace ECC/RSA so that every security application from smartphones to blockchains will be affected. However, there are still some issues to solve. For example, the SIKE protocol is a post-quantum candidate for cryptography that is considered to be the best alternative to curve-based cryptography. Nevertheless, its long latency is a drawback, since the serial large-degree isogeny computation, which is dominated by modular multiplications, can make it less competitive compared to other popular post-quantum candidates. A possible solution has been recently suggested by Tian et al. [24] who described an optimized SIKE algorithm, with a focus on achieving high speed and low latency. Furthermore, the rise of quantum computing has driven researchers to develop new security systems that can withstand future attacks. These post-quantum cryptographic approaches include hash-based, code-based, lattice-based, multivariate-quadratic-equations, and secret-key cryptography. They are all potential candidates because they are thought to be resistant to both classical and quantum computers, and applying Shor’s algorithm [25], the quantum-computer discrete-logarithm algorithm that can break classical schemes, is believed to be infeasible. Mozaffari-Kermani [26] proposed a method for constructing reliable and error-detection hash trees for stateless hash-based signatures. Such signatures are considered one of the leading post-quantum cryptographic schemes, as they offer security proofs that are based on plausible properties of the underlying hash function.
CRYSTALS-Kyber is a significant public-key encryption and key encapsulation mechanism, as it has been chosen by NIST for standardization and recommended for national security systems by the NSA. Therefore its implementations need to be evaluated for their resistance to side-channel attacks. Dubrova et al. [27] introduced a neural network recursive learning for training to attack -order masked implementations of CRYSTALS-Kyber in ARM Cortex-M4 CPU for message recovery. Last but not least, CRYSTALS-Dilithium has been selected by NIST as the new primary standard for quantum-safe digital signatures, and it has a constant-time implementation with consideration for side-channel resilience. For a profiling side-channel attack on the signature scheme CRYSTALS-Dilithium see Berzati et al. [28].
3. Preliminary Results
As is well known, there exists a unique (closed) formula in the literature for the computation of the modular inverse, which is related to Euler’s phi function
i.e.,
Equation (2) derives directly from Fermat’s little theorem, and its computation has complexity . This is because Euler’s phi function is related to the prime factorization with complexity . For a further comparison with other classic methods (and their complexities) about the modular inverse see ([10], Section 2) and Table 1.
| Algorithm1. Pseudocode of the algorithm for solving (10). |
| 1. Initialize , ; |
| 2. while |
| 3. set and ; |
| 4. end |
| 5. set and . |

Table 1.
Complexity comparison between the naive method (i.e., recursive multiplications), Euler’s phi function, extended Euclidean algorithm, and the suggested approach described by the pseudocode Algorithm 1.
We will begin by reviewing the important findings from a previous study by Bufalo et al. [10,11], as well as other relevant information that will be useful for our analysis. For the sake of notation, given , we denote by the floor integer part of x, and by the fractional one, i.e., . We will also be using a sequence called in our calculations for finding the modular inverse.
Definition 1.
Let be two integers with and . Define the sequence recursively by the equation
with
where M is the ceiling part of .
The explicit representation of can be found in the next proposition.
Proposition 1.
The solution of the difference Equation (3) is given by
Proof.
For the proof, see ([10], Proposition 1). □
Special care is deserved to the meaning and the mathematical form assumed by ’s, which allow giving other equivalent expressions of .
Proposition 2.
- (i)
- (ii)
Proof.
For the proof, see ([10], Proposition 2 and Corollary 1). □
The above results imply the next fundamental theorem.
Theorem 1.
Let be two integers with and . If is the sequence of Equation (3), define the "critical" index such that . Then the inverse of a modulo n is given by
Proof.
See ([10], Theorem 1). □
To illustrate the significance of Theorem 1, we will mention a related result.
Proposition 3.
The sequence is periodic of period a.
Proof.
See ([10], Proposition 3). □
It is immediately clear that the unique limitation of Theorem 1 is the determination of such critical index i, which can be found by solving the following equation
Although Equation (10) is nonlinear, one observes that , where (see [10], Proposition 4). The knowledge of jointly with the periodicity information provided by Proposition 3 suggests solving the modular problem (10) by the code detailed in Algorithm 1.
Observe that the complexity of the above algorithm is . Hence, this procedure is more convenient when (e.g., ). Notice that, even in the worst case (i.e., complexity ), the algorithm of Table 1 and the resolving formula (9) is still better compared to the Euler’s phi formula (2), which has complexity . Additionally, Section 5 delves further into the advantages of the algorithm when .
At this point, we present some new properties of which will be helpful in the next sections. In particular, we denote be the set .
Proposition 4.
Let be the sequence defined in Equation (3), then
- (i)
- for any , it holds .
- (ii)
- for any two different integers in , one has
Proof.
First of all, observe that Equation (8) may be rewritten as
- (i)
- By Definition 1 it is clear that and its (absolute) minimum is given by 0. Moreover, Equation (11) implies that is positive since .
- (ii)
- Without loss of generality, set (). Observe that if and only if , which is equivalent to say that (if ), or, equivalently , and this is true only if , which is absurd.
□
4. New Results about
In this section, we will study various equivalent formulations of to gain insight into the properties of the sequence and to determine the best way to calculate the critical index i.
Proposition 5.
The coefficient defined in Equation (4) is given by
Proof.
It is clear that
so, one has
which gives the assertion, being . □
Now, let us introduce the new quantity , as follows.
Definition 2.
Let be two positive integers . For any define
and
which denotes the amount of multipliers of a in .
Lemma 1.
Given two positive integers , it holds
Proposition 6.
For any , , the coefficients defined in Equation (4), may be rewritten as
where is defined by Equation (13).
Proof.
By virtue of Proposition 2, we have
In particular, it is easy to see that
where
due to Lemma 1, for any k. Therefore, with refer to Definition 2, we may write
that is . □
Proposition 7.
Consider two positive integers , with and let . Fixed , let be the quantity defined by Definition 2.
- (i)
- If and , thenIn particular, if there exists such that , then
- (ii)
- If and , thenIn particular, if there exists such that , then
Proof.
- (i)
- If , Propositions 5 and 6 yield that . Let us compute the smallest integer j such that . This is equivalent to solving the following equation:which may be rewritten asbeing . The latter equation holds iftherefore, the smallest integer j solving Equation (16) is given by . This prove Formula (14) for .Now, assume that Formula (14) holds for . Since , we want to compute the smallest integer j such that , that is equivalent to solveor, equivalently,Hence, the smallest integer j solving Equation (17) is given by .In particular, if there exists such that , then the smallest integer j solvingor, equivalently,is given by a (being ).
- (ii)
□
5. Empirical Findings and Discussion
Fixed , an interesting development inspired by Proposition 7 concerns the rule of the indices when , or when . In particular, as highlighted from Theorem 2, one has that
- •
- The sequence admits local minimum at if , or if .
- •
- The critical index i coincides with one of such indices.
This result is confirmed by computational experiments, as one can see from Figure 1. For a better understanding of the figure, as explained in ([10], Example 4), the blue line represents the series for , starting from and with a fixed (large) integer . The red line represents the periodic part of , which arises from the critical index and (highlighted by the red circles). In this example, , so all the minima are of type , which are 2, 4, 6, 9, 11, 13, 15, 18, 20, 22, 25, and obviously, 25 is one of them. We will refer to the previous set as . It is worth noting that the 11th index of corresponds to the critical index , such that . Figure 2 shows the set for .
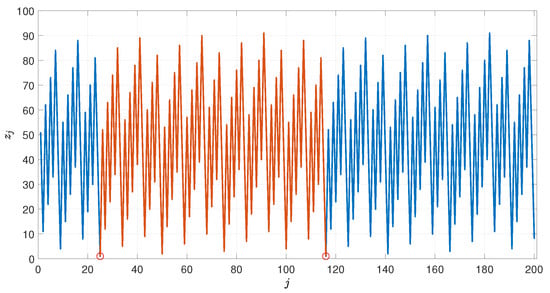
Figure 1.
The sequence for the case where and . The red line highlights the entire sequence between two consecutive unitary values of (represented by red circles).
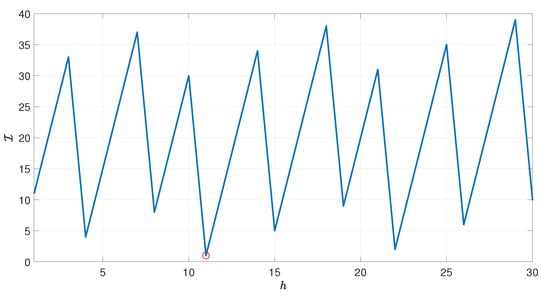
Figure 2.
Set representing the minima of when and .
Theorem 2.
The critical index i belongs to the set
Proof.
It is clear that the critical index i has to be a local minimum of the sequence that assumes only integer values and has 0 as an absolute minimum (see Proposition 4). Hence, it remains to prove that is the set of the local minimum of . Let us consider just the case for simplicity (the other one is analogous). It is easy to see, from Proposition 7, that
and
for any , and this concludes the proof. □
In light of the above results, Algorithm 2 can be rewritten as follows.
| Algorithm2. Pseudocode of the optimized algorithm solving (10). |
| 1. Initialize ; ; ; |
| 2. while |
| 3. if |
| 4. set ; |
| 5. else |
| 6. set ; |
| 7. end |
| 8. set and ; |
| 9. end |
| 10. set and . |
Moreover, what is observed from an empirical point of view is that:
- •
- The sequences of the minimum of oscillates till (see Figure 2);
- •
- The relative minimum defined in (19) belongs to the bundle of parallel straight lines (see Figure 3)
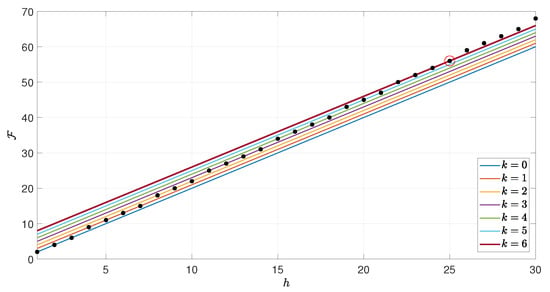 Figure 3. Set representing the bundle of parallel straight lines passing related to the minima of (when and ), for different values of k.In particular, each line contains or minima.
Figure 3. Set representing the bundle of parallel straight lines passing related to the minima of (when and ), for different values of k.In particular, each line contains or minima.
Remark 1.
We end with a note about the complexity of our algorithm. In the spirit of Theorem 2, if we restrict the searching of the critical index i to the set , also the complexity of the algorithm is reduced by a factor , i.e., from to . As explained in Section 3, the complexity is very good with respect to the literature, especially when . However, even when , the complexity sounds well. Indeed, in the extreme case , one has and approaches to 1 for large n. In other words, when a tends to n, one has that the complexity reduction tends to 100%, so that the resulting complexity is a constant, i.e., .
In the non-trivial case where , a complexity reduction of approximately 50% is observed. For example, if and , then and . In particular, in such case, the critical index i is just .
Therefore, we can conclude that our algorithm runs very well when or , while the worst case is the middle one, i.e., .
Post-Quantum Cryptography (PQC)
As is well known, the National Institute of Standards and Technology (NIST) has launched a program and competition to standardize one or more post-quantum cryptography (PQC) algorithms to fight against quantum attacks. In recent work, Huang [29] has conducted an early mathematical analysis of lattice-based and polynomial-based PQC. Such analysis can help businesses and organizations leverage NIST-selected PQC algorithms to safeguard their digital services from quantum attacks. In particular, the brute force failure probability for polynomial or multivariate PQC is calculated using Yitang Zhang’s Landau-Siegel zero bound according to [30].
In Figure 4 we compare the complexity of our optimized algorithm (see Algorithm 2) with those of coming from the post-quantum cryptography (PQC) architecture which was estimated by Huang [29] in Matlab. More specifically, Figure 4 represents the logarithm of complexity needed to encrypt/decrypt a message with a public/private key (modulus n). As shown, our proposed algorithm, in the best case, is better than the PCQ up to .
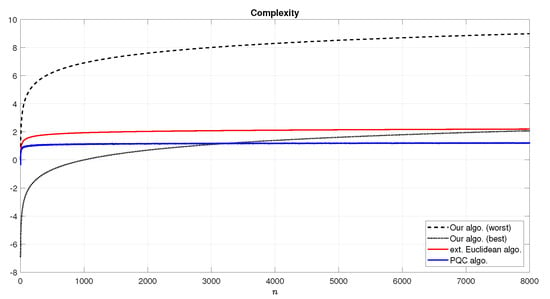
Figure 4.
Logarithm of complexity comparison between our algorithm in both a possible worst and better case (i.e., and , respectively–black dotted lines), the extended Euclidean algorithm (red line) and the post-quantum cryptography (PQC) algorithm (blue line).
6. Conclusions
This research builds upon previous work [10,11] where we introduced the concept of the modulo operation and discussed the standard methods for determining the inverse modulo n.
In the above-mentioned research, we determined that to find a closed-form solution for the equation in Equation (10), it was necessary to study the properties of the sequence . In this article, we expand on our previous aforementioned research by introducing a new sequence, , which can efficiently calculate the modular inverse of a given pair of integers , i.e., , particularly in the non-trivial case . This new method has a computational complexity of , which is more efficient than the traditional Euler’s phi function method, which has a computational complexity of . Additionally, we examine the properties of the sequence and demonstrate that all solutions to the problem belong to a specific set, , that only contains the minimum values of . This leads to a reduction in the computational complexity of our method, especially when , and also opens up new possibilities for finding closed-form solutions for the modular inverse.
Future studies will focus on the characteristics of the minimum sequences to understand the emergence of the critical index i, and to find a closed formula for the modular inverse.
Author Contributions
Conceptualization, M.B.; methodology, M.B. and D.B.; software, D.B.; validation, G.O., M.B. and D.B.; formal analysis, M.B. and D.B.; investigation, G.O., M.B. and D.B.; resources, M.B. and D.B.; data curation, M.B. and D.B.; writing—original draft preparation, M.B.; writing—review and editing, G.O. and M.B.; visualization, G.O. and M.B.; supervision, G.O. and M.B.; project administration, G.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available on request from the corresponding author.
Acknowledgments
G.O. and M.B. are members of GNAMPA and INdAM research groups.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rivest, R.L.; Shamir, A.; Adleman, L.M. Cryptographic Communications System and Method. US Patent 4,405,829, 20 September 1983. [Google Scholar]
- Crandall, R.; Pomerance, C.B. Prime Numbers: A Computational Perspective; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 182. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Verkhovsky, B. Overpass-Crossing Scheme for Digital Signature. In Proceedings of the International Conference on System Research, Informatics and Cybernetics, Baden-Baden, Germany, 22–25 July 2001; Volume 30. [Google Scholar]
- Verkhovsky, B. Enhanced Euclid Algorithm for Modular Multiplicative Inverse and Its Application in Cryptographic Protocols. IJCNS 2010, 3, 901–906. [Google Scholar] [CrossRef]
- ElGamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Rabin, M.O. Digitalized Signatures and Public-Key Functions as Intractable as Factorization; Technical Report; Massachusetts Institute of Technology Cambridge Lab for Computer Science: Cambridge, MA, USA, 1979. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H.; Silverman, J.H. An Introduction to Mathematical Cryptography; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1. [Google Scholar]
- Sosa-Gómez, G.; Paez-Osuna, O.; Rojas, O.; Madarro-Capó, E.J. A New Family of Boolean Functions with Good Cryptographic Properties. Axioms 2021, 10, 42. [Google Scholar] [CrossRef]
- Bufalo, M.; Bufalo, D.; Orlando, G. A Note on the Computation of the Modular Inverse for Cryptography. Axioms 2021, 10, 116. [Google Scholar] [CrossRef]
- Bufalo, D.; Bufalo, M.; Orlando, G.; Tetta, R. A new algorithm to find prime numbers with less memory requirements. J. Discret. Math. Sci. Cryptogr. 2023; in press. [Google Scholar] [CrossRef]
- Somani, U.; Lakhani, K.; Mundra, M. Implementing digital signature with RSA encryption algorithm to enhance the Data Security of cloud in Cloud Computing. In Proceedings of the 2010 First International Conference on Parallel, Distributed and Grid Computing (PDGC 2010), Solan, India, 28–30 October 2010; pp. 211–216. [Google Scholar]
- Mezher, A.E. Enhanced RSA cryptosystem based on multiplicity of public and private keys. Int. J. Electr. Comput. Eng. 2018, 8, 3949. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, R.; Pandey, S. An enhanced and secured RSA public key cryptosystem algorithm using Chinese remainder theorem. In Proceedings of the International Conference on Next Generation Computing Technologies, Dehradun, India, 30–31 October 2017; pp. 543–554. [Google Scholar]
- Islam, M.A.; Islam, M.A.; Islam, N.; Shabnam, B. A modified and secured RSA public key cryptosystem based on “n” prime numbers. J. Comput. Commun. 2018, 6, 78. [Google Scholar] [CrossRef]
- Raja shree, S.; Chilambu Chelvan, A.; Rajesh, M. An efficient RSA cryptosystem by applying cuckoo search optimization algorithm. Concurr. Comput. Pract. Exp. 2019, 31, e4845. [Google Scholar] [CrossRef]
- Mumtaz, M.; Ping, L. Forty years of attacks on the RSA cryptosystem: A brief survey. J. Discret. Math. Sci. Cryptogr. 2019, 22, 9–29. [Google Scholar] [CrossRef]
- Bayat-Sarmadi, S.; Kermani, M.M.; Azarderakhsh, R.; Lee, C.Y. Dual-Basis Superserial Multipliers for Secure Applications and Lightweight Cryptographic Architectures. IEEE Trans. Circuits Syst. II Express Briefs 2013, 61, 125–129. [Google Scholar] [CrossRef]
- Biham, E.; Shamir, A. Differential fault analysis of secret key cryptosystems. In Advances in Cryptology—CRYPTO ’97; Springer: Berlin, Germany, 2006; pp. 513–525. [Google Scholar] [CrossRef]
- Boneh, D.; DeMillo, R.A.; Lipton, R.J. On the Importance of Eliminating Errors in Cryptographic Computations. J. Cryptol. 2001, 14, 101–119. [Google Scholar] [CrossRef]
- Boneh, D.; DeMillo, R.A.; Lipton, R.J. On the Importance of Checking Cryptographic Protocols for Faults. In Advances in Cryptology—EUROCRYPT ’97; Springer: Berlin, Germany, 2001; pp. 37–51. [Google Scholar] [CrossRef]
- Ali, S.; Guo, X.; Karri, R.; Mukhopadhyay, D. Fault Attacks on AES and Their Countermeasures. In Secure System Design and Trustable Computing; Springer: Cham, Switzerland, 2016; pp. 163–208. [Google Scholar] [CrossRef]
- Dofe, J.; Frey, J.; Pahlevanzadeh, H.; Yu, Q. Strengthening SIMON Implementation Against Intelligent Fault Attacks. IEEE Embed. Syst. Lett. 2015, 7, 113–116. [Google Scholar] [CrossRef]
- Tian, J.; Wu, B.; Wang, Z. High-Speed FPGA Implementation of SIKE Based on an Ultra-Low-Latency Modular Multiplier. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3719–3731. [Google Scholar] [CrossRef]
- LaPierre, R. Shor Algorithm. In Introduction to Quantum Computing; Springer: Cham, Switzerland, 2021; pp. 177–192. [Google Scholar] [CrossRef]
- Mozaffari-Kermani, M.; Azarderakhsh, R. Reliable hash trees for post-quantum stateless cryptographic hash-based signatures. In Proceedings of the 2015 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFTS), Amherst, MA, USA, 12–14 October 2015; pp. 103–108. [Google Scholar] [CrossRef]
- Dubrova, E.; Ngo, K.; Gärtner, J. Breaking a Fifth-Order Masked Implementation of CRYSTALS-Kyber by Copy-Paste. Cryptology ePrint Archive. 2022. Available online: https://eprint.iacr.org/2022/1713 (accessed on 20 March 2023).
- Berzati, A.; Viera, A.C.; Chartouni, M.; Madec, S.; Vergnaud, D.; Vigilant, D. A Practical Template Attack on CRYSTALS-Dilithium. Cryptology ePrint Archive. 2023. Available online: https://eprint.iacr.org/2023/050 (accessed on 20 March 2023).
- Steed, H. Integer-Complexity-Bound-of-Post-Quantum-Cryptography. 2023. Available online: https://github.com/steedhuang/Integer-Complexity-Bound-of-Post-Quantum-Cryptography (accessed on 20 January 2023).
- Zhang, Y. Discrete mean estimates and the Landau-Siegel zero. arXiv 2022, arXiv:2211.02515. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).