Artificial Neural Network Model for Membrane Desalination: A Predictive and Optimization Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Artificial Neural Network Modeling
3. Results and Discussion
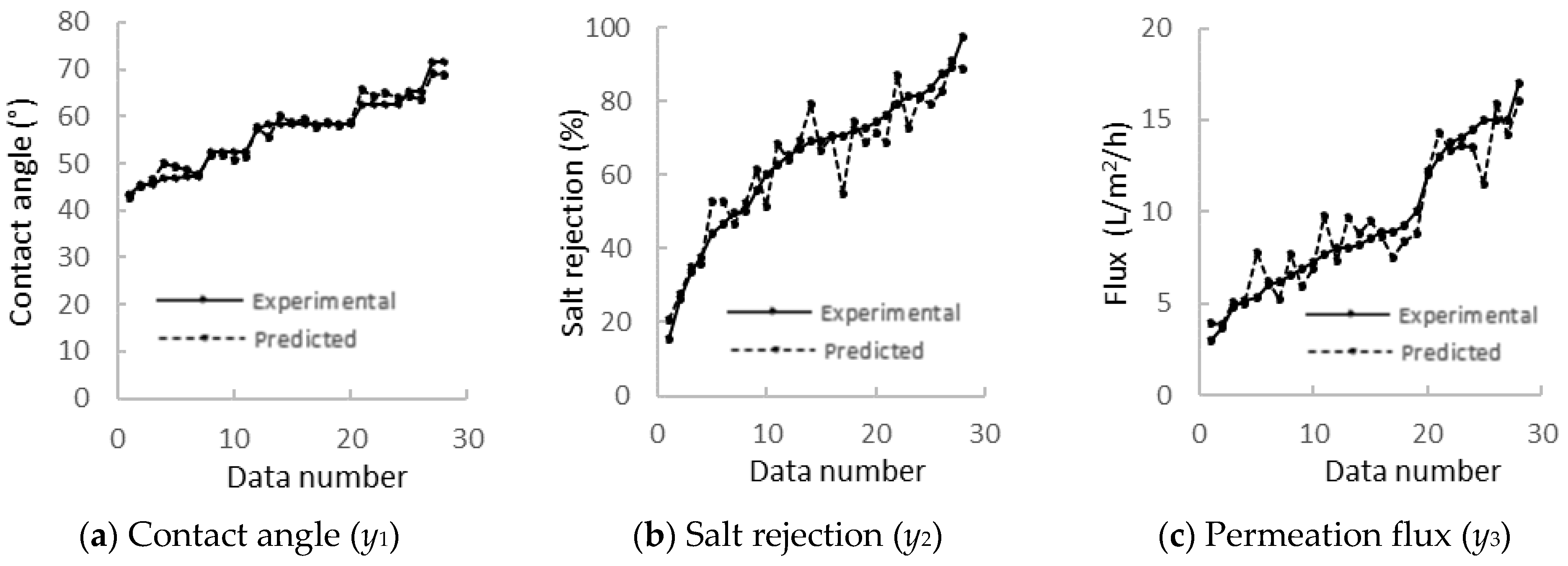
3.1. Regression Analysis and Performances
3.2. Mathematical Equation of a Trained ANN Model
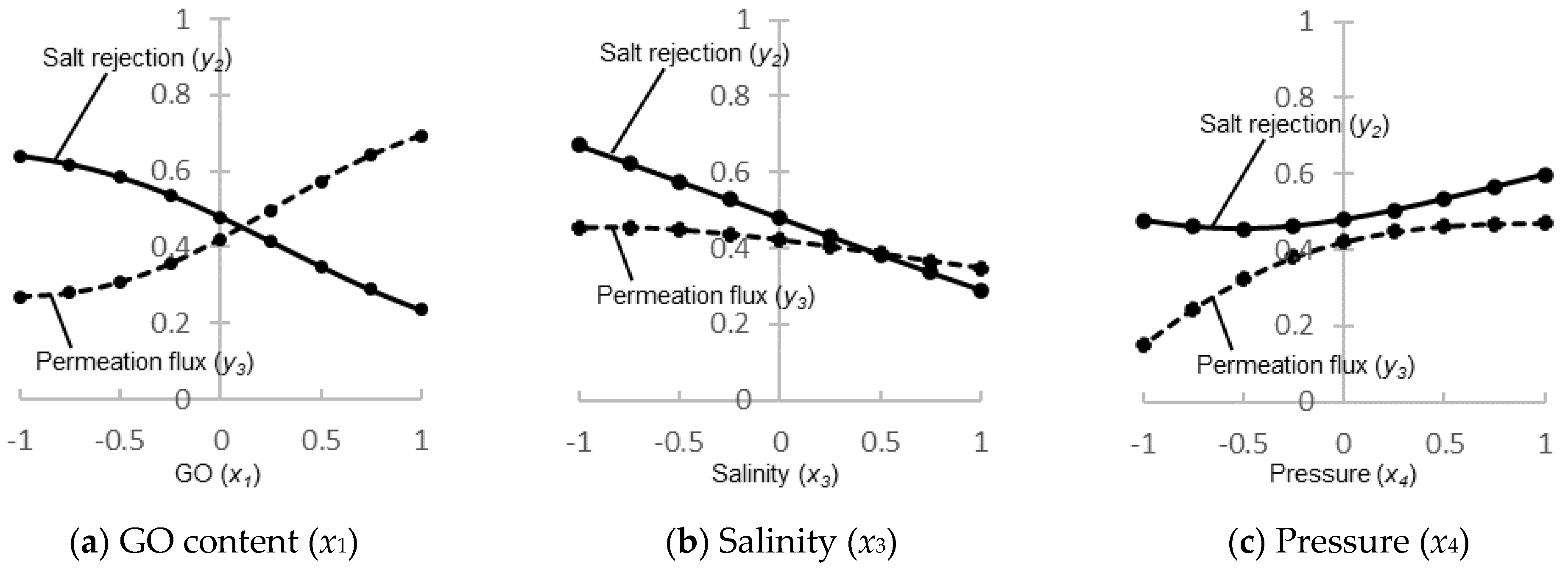
3.3. Three-Dimensional Response Patterns Simulated by the ANN Model
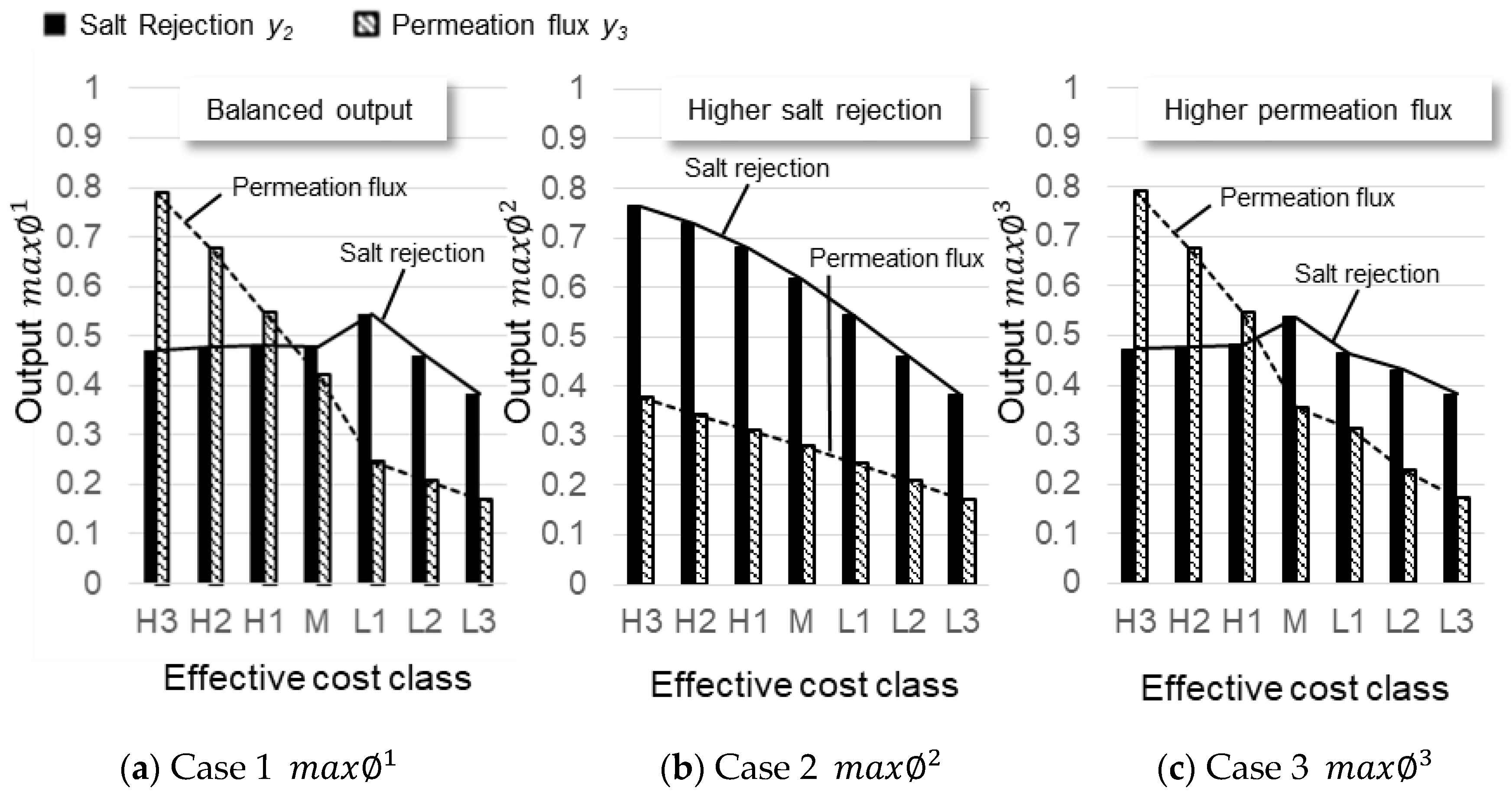
3.4. Optimizing Desalination Performance
3.5. Performance Criteria and Cost Constraints for Optimization
4. Limitations and Recommendations
5. Conclusions
- The ANN analysis from shallow to deep layer models showed acceptable ranges of fitting criteria with ≤ 0.90 (90%) and MSE ≤ 0.00199 (6% variance);
- Correlation R values were used to rank the significance level of input parameters against output responses. The rankings are sorted to show that GO content with R = −0.8647 and POSS content with R = −0.4228 have strong influences on contact angle, salinity (R = −0.6360 on the salt rejection), and operating pressure (R = −0.5410 on the permeation flux);
- Three objective functions and three-dimensional diagrams were applied to optimize effective cost conditions. It served as the database for the membranologists to decide the amount of GO to be used to fabricate membrane by considering the effects of operating conditions such as salinity and pressure to achieve the desired salt rejection, permeation flux, contact angle, and cost;
- The finding suggested that a membrane with 0.0063 wt% of GO, operated at 14.2 atm for a 5501 ppm salt solution, is the preferred optimal condition to achieve high salt rejection and permeation flux simultaneously.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qasim, M.; Badrelzaman, M.; Darwish, N.N.; Darwish, N.A.; Hilal, N. Reverse osmosis desalination: A state-of-the-art review. Desalination 2019, 459, 59–104. [Google Scholar] [CrossRef]
- Khulbe, K.; Matsuura, T. Recent progresses in preparation and characterization of RO membranes. J. Membr. Sci. Res. 2017, 3, 174–186. [Google Scholar]
- Bassyouni, M.; Abdel-Aziz, M.; Zoromba, M.S.; Abdel-Hamid, S.; Drioli, E. A review of polymeric nanocomposite membranes for water purification. J. Ind. Eng. Chem. 2019, 73, 19–46. [Google Scholar] [CrossRef]
- Ma, H.; Hsiao, B.S. Electrospun nanofibrous membranes for desalination. In Current Trends and Future Developments on (Bio-) Membranes; Elsevier: Amsterdam, The Netherlands, 2019; pp. 81–104. [Google Scholar]
- Tijing, L.D.; Woo, Y.C.; Choi, J.-S.; Lee, S.; Kim, S.-H.; Shon, H.K. Fouling and its control in membrane distillation—A review. J. Membr. Sci. 2015, 475, 215–244. [Google Scholar] [CrossRef]
- Kim, S.; Yoo, J.-B.; Yi, G.-R.; Lee, Y.; Choi, H.R.; Koo, J.C.; Oh, J.-S.; Nam, J.-D. An aggregation-mediated assembly of graphene oxide on amine-functionalized poly (glycidyl methacrylate) microspheres for core–shell structures with controlled electrical conductivity. J. Mater. Chem. C 2014, 2, 6462–6466. [Google Scholar] [CrossRef]
- Safarpour, M.; Safikhani, A.; Vatanpour, V. Polyvinyl chloride-based membranes: A review on fabrication techniques, applications and future perspectives. Sep. Purif. Technol. 2021, 279, 119678. [Google Scholar] [CrossRef]
- Kim, Y.; Noh, Y.; Lim, E.J.; Lee, S.; Choi, S.M.; Kim, W.B. Star-shaped Pd@ Pt core–shell catalysts supported on reduced graphene oxide with superior electrocatalytic performance. J. Mater. Chem. A 2014, 2, 6976–6986. [Google Scholar] [CrossRef]
- Ahmed, D.; Isawi, H.; Badway, N.; Elbayaa, A.; Shawky, H. Highly porous cellulosic nanocomposite membranes with enhanced performance for forward osmosis desalination. Iran. Polym. J. 2021, 30, 423–444. [Google Scholar]
- Shahlol, O.M.; Isawi, H.; El-Malky, M.G.; Al-Aassar, A.E.-H.M. Performance evaluation of the different nano-enhanced polysulfone membranes via membrane distillation for produced water desalination in Sert Basin-Libya. Arab. J. Chem. 2020, 13, 5118–5136. [Google Scholar]
- Rakhshan, N.; Pakizeh, M. The effect of functionalized SiO2 nanoparticles on the morphology and triazines separation properties of cellulose acetate membranes. J. Ind. Eng. Chem. 2016, 34, 51–60. [Google Scholar] [CrossRef]
- Habiba, U.; Afifi, A.M.; Salleh, A.; Ang, B.C. Chitosan/(polyvinyl alcohol)/zeolite electrospun composite nanofibrous membrane for adsorption of Cr6+, Fe3+ and Ni2+. J. Hazard. Mater. 2017, 322, 182–194. [Google Scholar] [CrossRef]
- Khan, S.B.; Alamry, K.A.; Bifari, E.N.; Asiri, A.M.; Yasir, M.; Gzara, L.; Ahmad, R.Z. Assessment of antibacterial cellulose nanocomposites for water permeability and salt rejection. J. Ind. Eng. Chem. 2015, 24, 266–275. [Google Scholar] [CrossRef]
- Ooi, C.S.; Chan, M.K. Nano Iron Oxide Impregnated Poly (Vinylidene Fluoride) Ultrafiltration Membrane for Palm Oil Mill Effluent Treatment. J. Eng. Technol. Adv. 2019, 2, 11–23. [Google Scholar]
- Chan, M.; Ooi, C. Reusability of Nano-Fe3O4/Polyvinylidene Difluoride Membrane for Palm Oil Mill Effluent Treatment. Trends Sci. 2022, 19, 4636. [Google Scholar] [CrossRef]
- Ma, D.; Peh, S.B.; Han, G.; Chen, S.B. Thin-film nanocomposite (TFN) membranes incorporated with super-hydrophilic metal–organic framework (MOF) UiO-66: Toward enhancement of water flux and salt rejection. ACS Appl. Mater. Interfaces 2017, 9, 7523–7534. [Google Scholar] [CrossRef] [PubMed]
- Isawi, H. Development of thin-film composite membranes via radical grafting with methacrylic acid/ZnO doped TiO2 nanocomposites. React. Funct. Polym. 2018, 131, 400–413. [Google Scholar]
- Wang, X.; Wang, X.; Xiao, P.; Li, J.; Tian, E.; Zhao, Y.; Ren, Y. High water permeable free-standing cellulose triacetate/graphene oxide membrane with enhanced antibiofouling and mechanical properties for forward osmosis. Colloids Surf. A Physicochem. Eng. Asp. 2016, 508, 327–335. [Google Scholar] [CrossRef]
- Shams, A.; Mirbagheria, S.A.; Jahanib, Y. Effect of graphene oxide on desalination performance of cellulose acetate mixed matrix membrane. Desalination Water Treat. 2019, 164, 62–74. [Google Scholar] [CrossRef]
- Liang, J.; Huang, Y.; Zhang, F.; Zhang, Y.; Li, N.; Chen, Y. The use of graphene oxide membranes for the softening of hard water. Sci. China Technol. Sci. 2014, 57, 284–287. [Google Scholar] [CrossRef]
- Shams, A.; Mirbagheri, S.A.; Jahani, Y. The synergistic effect of graphene oxide and POSS in mixed matrix membranes for desalination. Desalination 2019, 472, 114131. [Google Scholar] [CrossRef]
- Waqas, S.; Harun, N.Y.; Sambudi, N.S.; Archad, U.; Nordin, N.A.H.M.; Bilad, M.R.; Saeed, A.A.H.; Malik, A.A. SVM and ANN modelling approach for the optimization of membrane permeability of a membrane rotating biological contactor for wastewater treatment. Membranes 2022, 12, 821. [Google Scholar] [CrossRef]
- Behnam, P.; Shafieian, A.; Zargar, M.; Khiadani, M. Development of machine learning and stepwise mechanistic models for performance prediction of direct contact membrane distillation module—A comparative study. Chem. Eng. Process. Process Intensif. 2022, 173, 108857. [Google Scholar]
- Kovacs, D.J.; Li, Z.; Baetz, B.W.; Hong, Y.; Donnaz, S.; Zhao, X.; Zhou, P.; Ding, H.; Dong, Q. Membrane fouling prediction and uncertainty analysis using machine learning: A wastewater treatment plant case study. J. Membr. Sci. 2022, 660, 120817. [Google Scholar] [CrossRef]
- Jawad, J.; Hawari, A.H.; Zaidi, S.J. Artificial neural network modeling of wastewater treatment and desalination using membrane processes: A review. J. Chem. Eng. 2020, 419, 129540. [Google Scholar] [CrossRef]
- Tgarguifa, A.; Boundahmidi, T.; Fellaou, S. Optimal Design of the Distillation Process Using the Artificial Neural Networks Method. In Proceedings of the 2020 1st International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 19–20 March 2020; pp. 1–6. [Google Scholar]
- Mahadeva, R.; Kumar, M.; Patole, S.P.; Manik, G. Employing artificial neural network for accurate modeling, simulation and performance analysis of an RO-based desalination process. Sustain. Comput. Inform. Syst. 2022, 35, 100735. [Google Scholar] [CrossRef]
- Adda, A.; Hanini, S.; Bezari, S.; Laidi, M.; Abbas, M. Modeling and optimization of small-scale NF/RO seawater desalination using the artificial neural network (ANN). Environ. Eng. Res. 2022, 27, 200383. [Google Scholar] [CrossRef]
- Behnam, P.; Faegh, M.; Khiadani, M. A review on state-of-the-art applications of data-driven methods in desalination systems. Desalination 2022, 532, 115744. [Google Scholar] [CrossRef]
- Mohd Amiruddin, A.A.A.b.; Chan, M.K.; Ng, S. Development of Contact Angle Prediction for Cellulosic Membrane. In Proceedings of the International Conference on Intelligent Computing & Optimization, Hua Hin, Thailand, 30–31 December 2021; pp. 207–216. [Google Scholar]
- Chan, M.-K.; Ng, S.-C.; Zainuddin, S.N.M. 1 Statistical Analysis on the Relationship between Membrane Properties and Contact Angle. Appl. Stat. Methods Var. Discip. 2016, 5. Available online: https://www.uumpress.com.my/application-of-statistical-methods-in-various-disciplines (accessed on 15 March 2023).
- Chan, M.; Ng, S. Effect of membrane properties on contact angle. In Proceedings of the AIP Conference Proceedings, Penang, Malaysia, 10–12 April 2018; p. 020035. [Google Scholar]
- Mustafa, B.; Mehmood, T.; Wang, Z.; Chofreh, A.G.; Shen, A.; Yang, B.; Yuan, J.; Wu, C.; Liu, Y.; Lu, W.; et al. Next-generation graphene oxide additives composite membranes for emerging organic micropollutants removal: Separation, adsorption and degradation. Chemosphere 2022, 308, 136333. [Google Scholar] [CrossRef]
- Leaper, S.; Cáceres, E.O.A.; Luque-Alled, J.M.; Cartmell, S.H.; Gorgojo, P. POSS-Functionalized graphene oxide/PVDF electrospun membranes for complete arsenic removal using membrane distillation. ACS Appl. Polym. Mater. 2021, 3, 1854–1865. [Google Scholar]
- Chan, M.K.; Wang, C.C.; Arbai, A.A.B. Development of dynamic OBE model to quantify student performance. Comput. Appl. Eng. Educ. 2022, 35, 1293–1306. [Google Scholar] [CrossRef]
- Madaeni, S.S.; Shiri, M.; Kurdin, A.R. Modeling, optimization, and control of reverse osmosis water treatment in kazeroon power plant using neural network. Chem. Eng. Commun. 2015, 202, 6–14. [Google Scholar] [CrossRef]
- Jawad, J.; Hawari, A.H.; Zaidi, S.J. Modeling of forward osmosis process using artificial neural networks (ANN) to predict the permeate flux. Desalination 2020, 484, 114427. [Google Scholar] [CrossRef]
- Jawad, J.; Hawari, A.H.; Zaidi, S.J. Modeling and sensitivity analysis of the forward osmosis process to predict membrane flux using a novel combination of neural network and response surface methodology techniques. Membranes 2021, 11, 70. [Google Scholar] [CrossRef] [PubMed]
- Cottrell, M.; Olteanu, M.; Rossi, F.; Rynkiewicz, J.; Villa-Vialaneix, N.V. Neural networks for complex data. Künstliche Intelligenz. 2012, 26, 373–380. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Wang, Y.; Tian, S.; Han, N.; Li, W.; Wang, W.; Liu, H.; Yan, X.; Zhang, X. Fluffy-like amphiphilic graphene oxide (f-GO) and its effects on improving the antifouling of PAN-based composite membranes. Desalination 2022, 527, 115575. [Google Scholar] [CrossRef]
- Wang, L.; Cao, T.; Dykstra, J.E.; Porada, S.; Biesheuvel, P.; Elimelech, M. Salt and water transport in reverse osmosis membranes: Beyond the solution-diffusion model. Environ. Sci. Technol. 2021, 55, 16665–16675. [Google Scholar] [CrossRef]
- Golbaz, S.; Nabizadeh, R.; Rafiee, M.; Yousefi, M. Comparative study of RSM and ANN for multiple target optimisation in coagulation/precipitation process of contaminated waters: Mechanism and theory. J. Environ. Anal. Chem. 2020, 102, 8519–8537. [Google Scholar] [CrossRef]
- Zhu, B.; Kim, J.H.; Na, Y.-H.; Moon, I.-S.; Connor, G.; Maeda, S.; Morris, G.; Gray, S.; Duke, M. Temperature and pressure effects of desalination using a MFI-type zeolite membrane. Membranes 2013, 3, 155–168. [Google Scholar] [CrossRef]
- Liu, C.; Guo, Y.; Zhang, J.; Tian, B.; Lin, O.; Liu, Y.; Zhang, C. Tailor-made high-performance reverse osmosis membranes by surface fixation of hydrophilic macromolecules for wastewater treatment. RSC Adv. 2019, 9, 17766–17777. [Google Scholar] [CrossRef]
- Govardhan, B.; Fatima, S.; Madhumala, M.; Sridhar, S. Modification of used commercial reverse osmosis membranes to nanofiltration modules for the production of mineral-rich packaged drinking water. Appl. Water Sci. 2020, 10, 230. [Google Scholar] [CrossRef]
- Judd, S.J. Membrane technology costs and me. Water Res. 2017, 122, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Coutinho de Paula, E.; Amaral, M.C.S. Extending the life-cycle of reverse osmosis membranes: A review. Waste Manag. Res. 2017, 35, 456–470. [Google Scholar] [CrossRef] [PubMed]







| ANN Dataset | Number of Data | Source | Experimental Data |
|---|---|---|---|
| Training and Validation | 28 | [19,21] | DoE (BBD + CCD) |
| Input components (4) | x1 = GO (wt%), (max, min) = (0.0125, 0) x2 = POSS (wt%), (max, min) = (1.2, 0) x3 = Salinity (ppm), (max, min) = (9750, 1296) x4 = Pressure (atm), (max, min) = (21.68, 6.78) | |
| Output components (3) | y1 = Contact angle (° degree), (max, min) = (71.5, 43.3) y2 = Salt rejection (%), (max, min) = (97.4, 15.3) y3 = Permeation flux, (L/m2h), (max, min) = (17, 3) | |
| ANN models | Single hidden layer neural network Three hidden layers neural network | |
| Activation functions | TanH function at the hidden layer Linear/Sigmoid functions at the output layer | |
| Data scaling | Input x | Normalized between −1 and 1 Standardized to z-scores |
| Output y | Normalized between 0 and 1 | |
| Model No | Hidden Layer | Activation Functions | Data Scaling | R2 of y Response | MSE | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | Single: 8 neurons + 1 bias | Hidden: tanh Output: linear | Input: [−1, 1] Output: [0.1, 0.9] | T | 0.951 | 0.897 | 0.906 | 0.918 | 0.00186 |
| s | 0.02736 | 0.03640 | 0.04648 | - | - | ||||
| V | 0.943 | 0.908 | 0.849 | 0.900 | 0.00187 | ||||
| s | 0.02838 | 0.03635 | 0.05052 | - | - | ||||
| 2 | Three: 11:8:4 neurons +1 bias each | Hidden: tanh Output: sigmoid | Input: [−1, 1] Output: [0.1, 0.9] | T | 0.959 | 0.957 | 0.961 | 0.959 | 0.00098 |
| V | 0.949 | 0.960 | 0.953 | 0.954 | 0.00095 | ||||
| 3 | Three: 11:8:4 neurons +1 bias each | Hidden: tanh Output: sigmoid | Input: z-score Output: [0.1, 0.9] | T | 0.976 | 0.950 | 0.953 | 0.959 | 0.00097 |
| s | 0.02049 | 0.02359 | 0.01879 | - | - | ||||
| V | 0.970 | 0.951 | 0.937 | 0.952 | 0.00100 | ||||
| s | 0.02218 | 0.02328 | 0.01916 | - | - | ||||
| Correction R, Inputs | |||||
|---|---|---|---|---|---|
| GO (x1) | POSS (x2) | Salinity (x3) | Pressure (x4) | ||
| Output | Contact angle (y1) | −0.8647 | −0.4228 | 0.1621 | 0.0010 |
| Salt rejection (y2) | −0.3053 | 0.4149 | −0.6360 | 0.0004 | |
| Permeation flux (y3) | 0.2176 | 0.2698 | −0.2125 | 0.5410 | |
| Input | ||||||
|---|---|---|---|---|---|---|
| GO x1 (wt%) | POSS x2 (wt%) | Salinity (ppm) x3 (wt%) | Pressure (atm) x4 (wt%) | |||
| Output | CA y1 (°) | Max = 69.14 | 0.0125 | 0 | 9705 | 21.68 |
| Min = 46.38 | 0 | 0 | 1296 | 14.18 | ||
| SR y2 (%) | Max = 93.11 | 0.0016 | 0 | 1296 | 6.68 | |
| Min = 5.51 | 0.0125 | 0 | 9705 | 10.43 | ||
| PF y3 (L/m2h) | Max = 16.72 | 0.0125 | 0 | 1296 | 21.68 | |
| Min = 1.12 | 0.0031 | 0 | 1296 | 6.68 | ||
| Case | Criteria | |
|---|---|---|
| 1 | Balanced outputs | |
| 2 | Higher salt rejection output | |
| 3 | Higher permeation flux output |
| Effective Cost Lower ← Middle ← Higher | |||||||
|---|---|---|---|---|---|---|---|
| Input Bounds\Classes | L3 | L2 | L1 | M | H1 | H2 | H3 |
| GO | −0.75 | −0.5 | −0.25 | 0 | 0.25 | 0.5 | 0.75 |
| Salinity | 0.75 | 0.5 | 0.25 | 0 | −0.25 | −0.5 | −0.75 |
| Pressure | −0.75 | −0.5 | −0.25 | 0 | 0.25 | 0.5 | 0.75 |
| Case | Class | GO (wt%) | POSS (wt%) | SN (ppm) | PS (atm) | CA (°) | SR (%) | PF (L/m2h) |
|---|---|---|---|---|---|---|---|---|
| 1 | H3 | 0.75 (0.0109) | −1 (0) | −0.75 (2347) | 0.75 (19.8) | 0.29 (50.1) | 0.47 (53.5) | 0.75 (14.3) |
| H2 | 0.5 (0.0094) | −1 (0) | −0.5 (3398) | 0.5 (17.9) | 0.37 (52.8) | 0.48 (54) | 0.68 (13.1) | |
| H1 | 0.25 (0.0078) | −1 (0) | −0.25 (4449) | 0.25 (16.1) | 0.45 (55.7) | 0.48 (54.5) | 0.58 (11.4) | |
| M | 0 (0.0063) | -1 (0) | 0 (5501) | 0 (14.2) | 0.54 (58.8) | 0.48 (54.3) | 0.42 (8.6) | |
| L1 | -0.75 (0.0016) | -1 (0) | 0.25 (6552) | −0.25 (12.3) | 0.76 (66.6) | 0.54 (60.8) | 0.18 (4.4) | |
| L2 | −0.75 (0.0016) | −1 (0) | 0.5 (7603) | −0.5 (10.4) | 0.75 (66.4) | 0.46 (52.5) | 0.21 (4.9) | |
| L3 | −0.75 (0.0016) | −1 (0) | 0.75 (8654) | −0.75 (8.6) | 0.74 (66) | 0.38 (44.3) | 0.21 (4.9) | |
| 2 | H3 | −0.75 (0.0016) | −1 (0) | −0.75 (2347) | 0.75 (19.8) | 0.75 (66.2) | 0.76 (83.5) | 0.38 (7.9) |
| H2 | −0.75 (0.0016) | −1 (0) | −0.5 (3398) | 0.5 (17.9) | 0.76 (66.5) | 0.73 (79.8) | 0.34 (7.3) | |
| H1 | −0.75 (0.0016) | −1 (0) | −0.25 (4449) | 0.25 (16.1) | 0.76 (66.7) | 0.68 (74.8) | 0.31 (6.7) | |
| M | −0.75 (0.0016) | −1 (0) | 0 (5501) | 0 (14.2) | 0.76 (66.7) | 0.62 (68.4) | 0.28 (6.1) | |
| L1 | −0.75 (0.0016) | −1 (0) | 0.25 (6552) | −0.25 (12.3) | 0.76 (66.6) | 0.54 (60.8) | 0.25 (5.6) | |
| L2 | −0.75 (0.0016) | −1 (0) | 0.5 (7603) | −0.5 (10.4) | 0.75 (66.4) | 0.46 (52.5) | 0.21 (4.9) | |
| L3 | −0.75 (0.0016) | −1 (0) | 0.75 (8654) | −0.75 (8.6) | 0.74 (66) | 0.38 (44.3) | 0.17 (4.3) | |
| 3 | H3 | 0.75 (0.0109) | −1 (0) | −0.75 (2347) | 0.75 (19.8) | 0.29 (50.1) | 0.47 (53.5) | 0.79 (15.1) |
| H2 | 0.5 (0.0094) | −1 (0) | −0.5 (3398) | 0.5 (17.9) | 0.37 (52.8) | 0.48 (54) | 0.68 (13.1) | |
| H1 | 0.25 (0.0078) | −1 (0) | −0.25 (4449) | 0.25 (16.1) | 0.45 (55.7) | 0.48 (54.5) | 0.55 (10.9) | |
| M | −0.25 (0.0047) | −1 (0) | 0 (5501) | 0 (14.2) | 0.62 (61.7) | 0.54 (60.1) | 0.36 (7.5) | |
| L1 | −0.25 (0.0047) | −1 (0) | 0.25 (6552) | −0.25 (12.3) | 0.62 (61.7) | 0.46 (52.6) | 0.31 (6.7) | |
| L2 | −0.5 (0.0031) | −1 (0) | 0.5 (7603) | −0.5 (10.4) | 0.69 (64.1) | 0.43 (49.2) | 0.23 (5.2) | |
| L3 | −0.75 (0.0016) | −1 (0) | 0.75 (8654) | −0.75 (8.6) | 0.74 (66) | 0.38 (44.3) | 0.17 (4.3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, M.; Shams, A.; Wang, C.; Lee, P.; Jahani, Y.; Mirbagheri, S.A. Artificial Neural Network Model for Membrane Desalination: A Predictive and Optimization Study. Computation 2023, 11, 68. https://doi.org/10.3390/computation11030068
Chan M, Shams A, Wang C, Lee P, Jahani Y, Mirbagheri SA. Artificial Neural Network Model for Membrane Desalination: A Predictive and Optimization Study. Computation. 2023; 11(3):68. https://doi.org/10.3390/computation11030068
Chicago/Turabian StyleChan, MieowKee, Amin Shams, ChanChin Wang, PeiYi Lee, Yousef Jahani, and Seyyed Ahmad Mirbagheri. 2023. "Artificial Neural Network Model for Membrane Desalination: A Predictive and Optimization Study" Computation 11, no. 3: 68. https://doi.org/10.3390/computation11030068
APA StyleChan, M., Shams, A., Wang, C., Lee, P., Jahani, Y., & Mirbagheri, S. A. (2023). Artificial Neural Network Model for Membrane Desalination: A Predictive and Optimization Study. Computation, 11(3), 68. https://doi.org/10.3390/computation11030068









