Abstract
The significance of robot manipulators in engineering applications and scientific research has increased substantially in recent years. The utilization of robot manipulators to save labor and increase production accuracy is becoming a common practice in industry. Evolutionary computation (EC) techniques are optimization methods that have found their use in diverse engineering fields. This state-of-the-art review focuses on recent developments and progress in their applications for industrial robotics, especially for path planning problems that need to satisfy various constraints that are implied by both the geometry of the robot and its surroundings. We discuss the most-used EC method and the modifications that suit this particular purpose, as well as the different simulation environments that are used for their development. Lastly, we outline the possible research gaps and the expected directions future research in this area will entail.
1. Introduction
Recently, the field of robotics has attracted increased attention due to its prevalence in scientific and engineering applications, such as underwater and space exploration, welding, painting, assembly and medical applications, industrial and military uses, and many others [1]. Robot manipulators perform point-to-point motions under kinematic and dynamic constraints stemming from their geometry. Due to the coupling characteristics of multiple degrees-of-freedom (DOF), it is generally difficult to find a control for the robot manipulator that would precisely follow a desired trajectory [2]. This path planning problem, with its schematized depiction in Figure 1, is one of the most fundamental and challenging research topics in the field of industrial robotics, and it has received considerable interest from research institutions and industrial companies in recent decades. Traditionally, the two main formulations of the path planning problem for robotic manipulators use either the configuration space (C-space) representation or the kinematic model [3]. In the C-space representation, the path of the manipulator is reduced to the motion of a single point that moves in an n-dimensional space, where n is the number of links of the manipulator [4]. The approaches using the kinematic model of the manipulator combine path planning and redundancy resolution by solving the relationship between joint and task space motion [5].
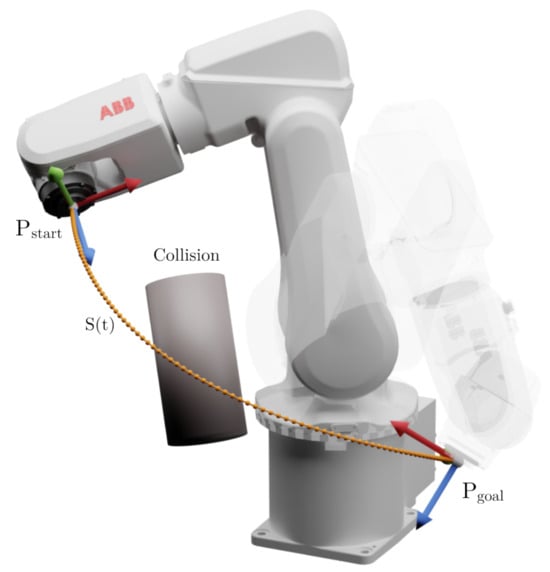
Figure 1.
The fundamental type of path planning task in industrial robotics involves finding a collision-free path from a starting point () to a goal point ().
Motion planning is a fundamental problem in industrial robotics because it involves generating a path or trajectory for various types of robotic structures to follow to accomplish a specific task while avoiding obstacles and complying with various constraints. The traditional task of planning trajectories for robots with high degrees-of-freedom, such as industrial robots (usually four to seven DOFs), has undergone a significant revolution in motion planning with the development of sampling-based algorithms [6,7,8]. Representative examples of these algorithms include Rapidly Exploring Random Trees (RRTs) and Probabilistic Roadmaps (PRMs). Deep neural network methods have also found applications in the motion planning problem, where a bi-directional rapidly-exploring random tree with long short-term memory is integrated for the task of multi-robot assembly operations [9], reinforcement learning for pick and place operations [10], as well as multi-objective reinforcement learning for various types of tasks in the relevant domain [11]. Recent reviews on the approaches for motion planning of industrial robots focused on neural networks [12], reinforcement learning techniques [13], and various forms of adaptive control [14,15].
Another possible solution to this type of problem is to use evolutionary algorithms to solve partial tasks in a given area. In recent years, evolutionary algorithms have been increasingly used in various areas of industrial robotics, including solving inverse kinematics problem [16,17], robot structure design [18,19,20], the utilization of digital twins [21,22,23], robot calibration [24], and, last but not least, path planning [25]. The generalization of evolutionary computation methods to different robotics settings, and the various open challenges, are currently a point of ongoing discussions [26,27,28].
The primary motivation of this paper lies in investigating recent advances and applications in the field of evolutionary algorithms focused on motion planning in industrial robotics, with the goal of expanding the research focus of the robotics lab Industry 4.0 Cell [29,30]. Although the utilization of evolutionary algorithms in the field of industrial robotics is growing in popularity, a text summarizing the state-of-the-art and recent developments was missing.
The remainder of this paper is structured as follows. Section 2 discusses the most common robotic structures used for experiments in path planning research. Section 3 presents the most widely used tools for implementing biologically inspired computational algorithms. Section 4, as the most important part of the paper, provides a thorough review of the use of evolutionary algorithms in industrial robotics for path planning. Finally, in Section 5, we summarize the lessons learned and recommend future research directions.
2. Industrial Robots
In the field of industrial robotics, one commonly encounters three basic types of robots [31]. Firstly, the parallel robot (also known as a delta robot) is a highly specialized robot widely used in various industries [32]. Its unique design typically consists of three arms connected to a fixed base in a triangular configuration. Delta robots are a popular choice in environments where hygiene and cleanliness are crucial due to their sealed design.
Secondly, Selective Compliance Assembly Robot Arm (SCARA) robots are known for their exceptional speed [33]. These robots have two rotary joints and one prismatic joint, with a fixed base. Their design allows for high-speed horizontal motion and precise vertical positioning, making them ideal for applications requiring both speed and accuracy. Both types of these robots excel in terms of speed, precision, and agility, making them perfect for tasks such as pick-and-place operations, packaging, and high-speed assembly.
Last but not least, a robotic arm is designed to mimic the functions and movements of a human arm [34]. This robotic system consists of multiple joints and links, enabling it to perform various tasks with precision and flexibility. Robots may come in different configurations, playing a crucial role in repetitive tasks such as welding, painting, pick-and-place operations, as well as more advanced applications such as surgical procedures or fruit picking. The mentioned types of robots are depicted in the Figure 2.

Figure 2.
The most common robotic structures used for experiments in motion planning research tasks. On the left side, there is a parallel robot with three to five degrees of freedom, a SCARA robot in the middle with four DOF, and an articulated robot on the right with six DOF.
3. Tools for Robotic Applications
One of the most commonly used tools for implementing biologically inspired (and also other standard) computational algorithms for path planning industrial robots is the MATLAB programming language, utilizing the Robotics System Toolbox (https://www.mathworks.com/products/robotics.html, accessed on 1 October 2023) and Global Optimization Toolbox (https://www.mathworks.com/products/global-optimization.html, accessed on 1 October 2023). It is proprietary software that provides all the essential functions and tools for addressing the given problem. The Robotics System Toolbox also offers the capability of direct integration with robotic platforms such as Kinova or Universal Robots.
Not to be overlooked is Robot Operating System (ROS) (http://wiki.ros.org/ROS/Introduction, accessed on 1 October 2023), which is primarily known for its openness and broad developer base. In the field of robotic trajectory planning based on evolutionary algorithms, ROS, along with its additional components, can be a valuable tool that allows for a wide range of possibilities for integration with real hardware. ROS is not limited to programming languages such as Python or C++; the core computation itself can be implemented in, for example, programming languages such as Julia, R, MATLAB, and others.
In the context of exploring the use of evolutionary algorithms to solve various types of optimization tasks, physics simulators such as PyBullet (https://pybullet.org/, accessed on 1 October 2023) and Multi-Joint dynamics with Contact (MuJoCo) (https://mujoco.org/, accessed on 1 October 2023) [35] can be employed. Within these programs, models of robotic arms and environments can be created for testing and optimizing robot behavior. Both of these simulators can be programmed using the Python programming language. An essential aspect of this is simulating the dynamics between bodies, collisions, and other factors [36].
In a limited representation within the field of developing robotic applications for trajectory planning using evolutionary algorithms, one also encounters commercial software such as RoboDK (https://robodk.com/, accessed on 1 October 2023). Specifically, RoboDK is offline programming software with a wide range of supported robots. Additionally, this software includes a post-processor for controlling real robots or can connect to a robot through TCP-IP communication, provided it is supported. The software also integrates capabilities for Matlab, Python, and C# APIs.
4. Evolutionary Algorithms
Over its long history, the field of evolutionary (or nature-inspired) computation produced a handful of pivotal evolutionary (metaheuristic) optimization algorithms, which were inspired by various natural processes [37]. Although there has been an explosion of “novel” evolutionary methods that draw on these principles [38,39,40], many of which were found to hide their lack of novelty behind a flawed experimental analysis [41,42,43,44] or a metaphor-rich jargon [45,46], these techniques are still among the most-utilized methods for diverse and complex applications, where the use of standard optimization methods is either found to be inadequate or overly computationally demanding [47,48]. Among these applications are for instance the design of mechanical components [49], quantum operators [50] or airfoil geometry [51], landslide displacement prediction [52], inverse kinematics control of a robot [53], or barrier option pricing in economics [54].
In this review, we focus on the application of evolutionary algorithms in industrial robotics. More specifically, we investigate the recent advances and progress in applying solid evolutionary computation techniques, such as Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Ant Colony Optimization (ACO), Differential Evolution (DE), and Artificial Bee Colony (ABC), on the path-planning related problems for industrial robots. These methods were selected for their prevalence, their competence in solving complex problems in diverse disciplines [55], and because they are still subjected to theoretical development. For each of the selected methods, we briefly describe its main mechanisms and then summarize the recent advances reported in the reviewed papers. Figure 3 and Figure 4 show the number of articles that focus on applying evolutionary computation techniques for industrial robotics problems in Web of Science, which serves as the main database of state-of-the-art research in evolutionary computation [56], and in this paper, respectively. We can observe an increasing trend, especially in the last three years. Table 1 summarizes the utilization of the reviewed evolutionary algorithms for the different robotic structures. Lastly, in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 we give a structured overview of the reviewed papers, with information about the utilized type of the robotic structure, type of studied problem, used software, and whether or not the given paper considered only a simulated environment (without a real-world implementation).
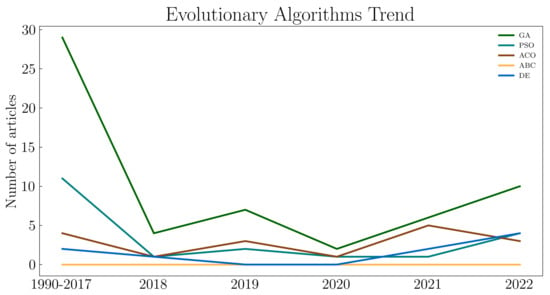
Figure 3.
The graph represents the number of publications through the years based on the Web of Science (WoS) server where the search query ‘industrial robotics path planning + presented evolutionary algorithm’ was entered. The selection also includes mobile robotics.
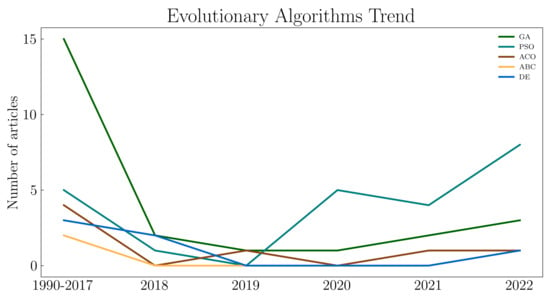
Figure 4.
An approximate trend in the utilization of the presented evolutionary algorithms is mentioned in this article. The trend indicates that the most commonly used evolutionary algorithms for robot trajectory planning are undoubtedly PSO and GA.

Table 1.
The use of robotic structures depending on the type of evolutionary algorithm used to solve the motion planning problem.
4.1. Particle Swarm Optimization
One of the oldest, but still extensively studied and used evolutionary computation techniques is PSO. This method was designed by simulating a simplified social model inspired by the foraging behavior of a bird flocking or fish schooling. In PSO, a population of particles iteratively searches for the optimal solution by adjusting their positions in a multi-dimensional search space based on their own experience and the collective knowledge of the swarm [57,58]. The main mechanisms of PSO are
where
- represents the current position of particle i at iteration t.
- is the velocity of particle i at iteration , which is determined based on the particle’s own best position () and the global best position found by any particle in the swarm ():
- w is the inertia weight;
- and are acceleration coefficients;
- and are random numbers sampled from the uniform distribution.
In Table 2 we list the reviewed papers that used PSO as the optimization method for path planning in industrial robotics applications. Time-optimal trajectory planning is one of the most extensively explored applications of the PSO algorithm in the context of solving motion planning problems for robotic arms. Several research publications aimed to enhance the PSO algorithm through various modifications [59,60,61,62,63]. One of the initial approaches introduced a modification where the entire trajectory was divided into segments, and optimization was performed at connection points called knot points. These knot points encompass parameters such as joint angles, joint angular velocities, and joint accelerations. The primary goal was to optimize these parameters at the knot points to achieve optimal time trajectory planning, representing an improved version of the PSO algorithm for this purpose [64].


Table 2.
Considered literature on the motion planning problem solved using PSO.
Table 2.
Considered literature on the motion planning problem solved using PSO.
| Ref. | Year | Type of Robotic Structure | Type of Problem | Software | Simulation Only |
|---|---|---|---|---|---|
| [64] | 2006 | 2-link (Redundant) | Point-to-point motion planning and trajectory tracking. | Unspecified | Yes |
| [59] | 2020 | Special | Point-to-point motion planning and trajectory tracking. | MATLAB | Yes |
| [60] | 2021 | Articulated (Industrial) | Point-to-point motion planning and trajectory tracking. | MATLAB | No |
| [61] | 2022 | Articulated (Industrial) | Collision-free path planning. | MATLAB | No |
| [62] | 2022 | 5-link (Redundant) | Point-to-point motion planning and trajectory tracking. | MATLAB | Yes |
| [63] | 2022 | Articulated | Point-to-point motion planning and trajectory tracking. | Unspecified | Yes |
| [65] | 2015 | Articulated (Industrial) | Point-to-point motion planning and trajectory tracking. | MATLAB | No |
| [66] | 2021 | Articulated (Industrial) | Collision-free path planning. | MATLAB | Yes |
| [67] | 2021 | Articulated (Industrial) | Optimal trajectory planning of complicated robotic timber joints. | Rhino & MATLAB | No |
| [68] | 2022 | Articulated | Point-to-point motion planning and trajectory tracking. | MATLAB | Yes |
| [69] | 2022 | Articulated (Collaborative) | Collision-free path planning. | MATLAB | Yes |
| [70] | 2023 | Articulated | Collision-free path planning. | Unspecified | No |
| [71] | 2020 | Paralell | Point-to-point motion planning and trajectory tracking. | MATLAB | Yes |
| [72] | 2020 | Articulated (Collaborative) | Collision-free path planning. | MATLAB & RoboDK | Yes |
| [73] | 2020 | Articulated (Collaborative) | Energy optimization for optimal motion planning. | CoppeliaSim | No |
| [74] | 2020 | Articulated (Industrial) | Energy optimization for optimal motion planning. | MATLAB | Yes |
| [75] | 2023 | Special | Collision-free path planning. | Unspecified | No |
| [76] | 2021 | Articulated (Industrial) | Collision-free path planning. | MATLAB | No |
| [77] | 2008 | 2-link (Redundant) | Point-to-point motion planning and trajectory tracking. | Unspecified | Yes |
| [78] | 2008 | Articulated | Point-to-point motion planning and trajectory tracking. | Unspecified | Yes |
| [79] | 2015 | Articulated | Point-to-point motion planning and trajectory tracking. | Unspecified | Yes |
| [80] | 2018 | 7-link dual-arm | Collision-free path planning. | Unspecified | Yes |
| [81] | 2022 | 4-link dual-arm | Collision-free path planning. | Unspecified | Yes |
| [82] | 2022 | Special | Collision-free path planning. | MATLAB | Yes |
Another explored area is the optimization of the trajectory itself. Enhanced versions of the PSO algorithm have inspired numerous research proposals [66,67,68,69,70]. One of the first modifications involved the utilization of the normalized step cost (NSC) for particle initialization. Building upon this change, a specialized method has been developed for reusing optimized parameters, storing them together with their respective NSC vectors. In cases of constraint violations, parameters resembling the query NSC vector were chosen to initialize particles, ultimately improving the PSO’s convergence in motion planning [65].
The PSO algorithm can be used not only with traditional robotic arms but also in solving trajectory planning problems for delta robots. In this area, a modified PSO was applied to optimize the spatial trajectory of a 4-3-3-4 degree polynomial interpolation. To obtain an optimal solution to the optimization process, particle parameters needed to be optimized to achieve the best solution for each particle, leading to an extension involving the addition of a dynamic change learning factor [71].
It is worth highlighting that the concept of Industry 4.0 takes collaborative robotics into account, which involves the idea of robots safely and efficiently collaborating with humans. The article [72] combined the methods of PSO and Charge Search System (CSS) for dynamic path planning with obstacle avoidance in the field of human–robot collaboration. The proposed method included the creation of a configuration space with obstacle regions, the formulation of motion planning with obstacle avoidance using the CSS method, and finally, the application of the PSO method to solve the path planning problem.
The PSO method, in conjunction with trajectory planning for robotic arms, has been enhanced and implemented in various fields, including space, agriculture, and energy consumption. In the context of energy consumption, the PSO method, along with a Bézier curve interpolator, was designed to increase energy efficiency [73]. The combination of the Bezier curve generator and PSO method generated smooth and energy-efficient trajectories for point-to-point movements. In this case, the method was tested on a collaborative robot UR3, with test results showing up to 40% savings, even in the worst-case scenario of 10%. However, a weakness of this approach still exists in conducting several hundred real-world experiments to find the optimal trajectory.
In the industrial sector, welding is an integral part of the process, and within Industry 4.0, repetitive welding tasks are being replaced by robots, specifically robotic arms. The authors of Ref. [74] addressed the optimization of trajectory planning for a collaborative welding robot working alongside other industrial manipulators. The goal was to minimize the energy consumption and running time of this robot while maintaining the smoothness of its motion, without unnecessary pauses. Trajectory planning is carried out by interpolating a cubic B-spline curve with time, which was optimized using PSO.
The field of agriculture presents an interesting challenge for trajectory planners based on the PSO method, specifically in the context of fruit or vegetable picking. The improved version PSO proposed in Ref. [75] can reduce collisions between the robotic arm and branches while increasing the overall collection success. This enhanced version of PSO is based on adaptively changing weights according to population density. Using the proposed improved PSO allowed for finding the optimal desired point in the manipulator’s workspace, minimizing the polynomial path length, and avoiding collisions with obstacles. A similar issue was also addressed based on the extended Multi-Objective Particle Swarm Optimization (MOPSO) method [76].
Robotic arms can be used not only on Earth but also in space. When solving problems in space, it is important to consider that prior states of individual arm joints are often needed when designing and implementing a trajectory planner. The metaheuristic solution, such as MOPSO or PSO, has been found for solving the free-floating space robot path planning problem [77,78,79,80,81] and it has also been extended to address obstacle avoidance. The method introduced in Ref. [82] offered an extension with three populations, where the first and second populations are optimized in the same way, while the third population depends on them. Another extension of PSO in this context could be the implementation of adaptive inertia weight [81].
4.2. Genetic Algorithm
GA is an optimization algorithm inspired by the process of natural selection and genetics [83]. It is a population-based search algorithm that utilizes the concept of the survival of the fittest. The new populations are produced through the iterative use of genetic operators on individuals present in the population. The key elements of GA include chromosome representation, selection, crossover, mutation, and fitness function computation.
GAs are highly versatile and can be applied to a wide range of problems, including the motion planning problem in the field of industrial robotics, where they are quite popular as is demonstrated by the list of reviewed papers shown in Table 3. The first article on this topic was published in 1991 [84]. The paper focused on a new GA-based obstacle avoidance method with a three-degree-of-freedom planar robotic manipulator. Another publication from the 1990s dealt with a similar topic, building on the previous article and improving the accuracy of finding the desired point [85]. The results of the papers show that there is great potential for the use of GAs in the field of robotics, as evidenced by the following published papers.
Since the 2000s, the number of articles published in this area has increased several-fold. One of the first publications presents a solution to the problem of determining the optimal trajectory for a two-link robot and two cooperating robots in 2D space using GAs and Adaptive Simulated Annealing (ASA) [86]. The GA and ASA techniques identify the optimal trajectory based on the minimum joint torque requirements, but the simulations show that although both methods converge to the global minimum, ASA converges to the solution faster than the GA. As in the previous case, the trajectory planning of the robotic manipulator is solved only in 2D space, with the difference being the use of a three-link arm [87]. Trajectory planning in joint space uses GAs to minimize vibration and/or execution time for point-to-point motion.

Table 3.
Considered literature on the motion planning problem solved using GA.
Table 3.
Considered literature on the motion planning problem solved using GA.
| Ref. | Year | Type of Robotic Structure | Type of Problem | Software | Simulation Only |
|---|---|---|---|---|---|
| [84] | 1991 | 3-link (redundant) | Path planning with obstacle avoidance. | Unspecified | Yes |
| [85] | 1995 | 3-link (redundant) | Collision-free path planning. | Unspecified | Yes |
| [86] | 2002 | 2-link (redundant) cooperating robots | Path planning and torque minimization. | Unspecified | Yes |
| [87] | 2002 | 3-link (redundant) | Point-to-point trajectory planning to minimize time and/or vibration. | Unspecified | Yes |
| [88] | 2004 | 2-link (redundant) | Minimization of rotation angles | Unspecified | Yes |
| [89] | 2004 | (2, 3)-link (redundant) | Collision-free path planning with multiple objectives. | Unspecified | Yes |
| [90] | 2008 | 3-link (redundant) | Collision-free point-to-point trajectory planning to minimize travel time and space. | Unspecified | Yes |
| [91] | 2008 | Articulated (Industrial) | Collision-free path planning for sand-blasting operation. | Unspecified | No |
| [92] | 2010 | 3-link (redundant) | Point-to-point trajectory planning to minimize time and energy. | Unspecified | Yes |
| [93] | 2011 | 2-link (redundant) and Articulated (Industrial) | Collision-free Cartesian path planning. | Unspecified | Yes |
| [94] | 2013 | 3-link (redundant) | Point-to-point motion planning in a complex geometric environment. | MATLAB | Yes |
| [95] | 2014 | Articulated (Collaborative) | Point-to-point motion planning and trajectory tracking. | MATLAB & Simulink | Yes |
| [96] | 2014 | Articulated (Industrial) | Minimization of the operating-time, energy consumption and rotations angles. | Unspecified | Yes |
| [97] | 2016 | 3-link (redundant) | Path planning to reach the position of an object obtained from EEG (electroencephalography) signals. | MATLAB | Yes |
| [98] | 2017 | Articulated (Collaborative) | Trajectory planning with obstacle avoidance. | MATLAB | No |
| [99] | 2018 | Articulated (Industrial) | Adaptive singularity-robust path planning. | ADAMS | Yes |
| [100] | 2019 | Articulated (Industrial) | Online time-optimal trajectory planning. | MATLAB | No |
| [101] | 2020 | Articulated (Industrial) cooperating robots | Path optimization to reduce joint torques. | Unspecified | No |
| [102] | 2021 | Articulated (Industrial) cooperating robots | Automatic calculation of paths of cooperating robots. | Helix Toolkit & BEPUphysics | No |
| [67] | 2021 | Articulated (Industrial) | Optimal trajectory planning of complicated robotic timber joints. | Rhino & MATLAB | No |
| [103] | 2022 | Special | Path planning method with obstacle avoidance for tomato picking. | MATLAB | No |
| [104] | 2022 | SCARA cooperating robots | Energy optimization for optimal motion planning. | Python & K-ROSET | No |
| [105] | 2022 | Articulated (Collaborative) | Minimization of the risk of collisions and travel time. | ABB RobotStudio | No |
The following several research works demonstrate the solution to the robot trajectory planning problem using the GA method for a two/three-link (redundant) robotic arm in two-dimensional (2D) space. The first paper presents an efficient optimization technique for a robotic arm with two DOF in an unstructured environment [88], and a similar paper, but for a robotic arm with three DOF [90], uses GAs to minimize travel time and space. The next paper discusses a robot arm with two and three degrees of freedom and its optimization using a multi-objective (Joint: , Cartesian: , Energy: ) GA approach based on kinematics to achieve the optimal solution [89]. The demonstration of the use of GAs in trajectory planning, using the example of a simple n-link (redundant) robotic arm in 2D space, is very popular because the results can be easily and quickly demonstrated. This statement is supported by the fact that several other papers have been published that utilize the mentioned robotic structure. Other research papers also focused on energy optimization using a GA for point-to-point trajectory planning for a three-link robotic arm [92]. In Ref. [94], the authors demonstrated point-to-point motion planning for a 3-DOF robotic arm with the extension, in which the path planning task was joined with the optimization objective of minimizing the joint angle traveling distance in an environment with complex geometric obstacles. Ref. [97] focused on using a GA for path planning to reach the object’s position with a 3-DOF robotic arm. The x and y coordinates of the object were obtained from EEG (electroencephalography) signals using a Brain–Computer Interface (BCI).
The solution to more complex industrial path planning problems with GAs, particularly in three-dimensional (3D) space, began in 2008 [91], when the GA was used to obtain an effective path with the minimum arm travel distances and magnitude of turns for the real-world problem of sand-blasting operation in steel bridge maintenance. Another problem focuses on a novel method called Continuous Genetic Algorithm (CGA) [93]. The method was tested to solve the problem of collision-free path planning while avoiding singularities for non-redundant manipulators such as the PUMA 560 and 2R (revolute joints manipulator). The proposed approach autonomously selected a collision-free path for the manipulators that minimized the deviation between the generated path and the desired Cartesian path, satisfied the joint limits of the manipulator, and maximized the minimum distance between the manipulator links and the obstacles.
As the number of publications increased, so did the complexity of the solved problems. This fact is confirmed by the selection of more complex robotic structures for the implementation of the path planning problem using GAs. The first publication that used a 7-DOF collaborative robotic manipulator, more precisely the KUKA LBR iiwa, implemented the hybrid algorithm based on PSO with real-coded GA to solve the problem of obtaining the set of seven joint angles for any point-to-point movement [95]. Another publication [96] used the robotic arm ABB IRB 6400 with 6-DOF to minimize various values such as operation time, joint rotation, energy consumption, as well as combined optimization, where the optimizer was designed based on a GA.
Since collaborative robots have been very popular in research, the next paper is realized with the UR10 robotic manipulator from Universal Robots [98]. A novel approach, based on a GA combined with a Modified Artificial Potential Field, was presented as a hybrid algorithm for trajectory planning with obstacle avoidance. Their approach was tested with both simulation and real-world application. Not only collaborative robots but also space robots have been used to solve path planning problems using GA. The problem of simulating an on-orbit detection platform, with the aim of improving tracking accuracy using a GA-based adaptive singularity-robust algorithm was studied in Ref. [99]. The proposed approach involved optimizing two adaptive parameters (maximum damping factor) and (parameter for evaluating the singularity of generalized Jacobian matrix) of the singular value decomposition. Compared to the standard damped least squares method, the accuracy of the end-effector tracking increased by 26.7%.
Recent research works show that path planning problems using evolutionary algorithms are tested not only on different types of robot structures but also on robots from various manufacturers. The first of the following papers addresses the problem of online time-optimal trajectory planning, comparing methods such as Adaptive Elite Genetic Algorithm with Singularity Avoidance, Adaptive Elite Genetic Algorithm, and Genetic Algorithm Combined with Singularity Avoidance for the 6-DOF robotic manipulator SIASUN SR10C [100]. Another article [101] dealt with the use of evolutionary algorithms for optimizing the paths of ABB IRB 120 robotic manipulators (single robot solution and multi-robotic collaboration) with the goal of decreasing the joint torques. The experiment compared the methods of evolutionary algorithms, including GAs, using random and average recombination, simulated annealing using linear and geometric cooling strategies, and differential evolution. The results show that the GA method provided the best results for the torque minimization problem. Next, similar to the previous case, an experiment is presented for industrial robots with 6-DOF in the single robot scenario and with 14-DOF in the cooperating robot scenario with an additional linear track. The main objective of their paper was to automatically calculate the paths of Kuka Quantec KR210 R3100 robotic manipulators using the GA method [102]. Ref. [67], using the KUKA-KR90 6-DOF robotic manipulator, focused on the real-world problem of cutting complex timber joints using a robotic chainsaw. PSO and Adaptive Genetic Algorithm (AGA) were applied to optimize the path distance and travel time interval, with both optimization methods achieving optimal objectives.
The number of recent works, specifically from 2022, on the problem of trajectory planning using GAs, shows that the area of evolutionary algorithms in industrial robotics still has great research potential (as we can see in Table 3). One of these recent articles [103] focused on the intelligent obstacle avoidance path planning method for the tomato-picking manipulator. A GA determined the parameters of the Artificial Potential Field (APF) method, and subsequent path planning was performed using the APF method in conjunction with reinforcement learning (RL). Another article deals with energy optimization for optimal motion planning for a dual-arm industrial robot [104], where achieving the optimal parameters involves fine-tuning using both GA and PSO. The GA was used to optimize PID gains, while PSO was applied to optimize both the robot configuration and motion simultaneously. Last but not least, the article [105] focused on trajectory optimization in collaborative robotics using the ABB YuMi dual arm. A GA randomly modified the parameters of the trajectory on a digital twin, and lexicographic optimization is used to evaluate the optimal robot trajectory online. The result was the minimization of the risk of collisions and travel time.
4.3. Ant Colony Optimization
ACO is a nature-inspired optimization algorithm commonly used to find approximate solutions to combinatorial optimization problems. It models the foraging behavior of ants to discover optimal paths or solutions. In ACO, artificial ants build solutions incrementally, laying pheromone trails to communicate their findings. Over time, these trails guide other ants toward better solutions [106,107].
The key components of ACO include:
- Ants: Artificial ants are used to explore and construct solutions. Each ant represents a potential solution to the problem;
- Pheromones: Ants deposit pheromones on the paths they traverse. Pheromone levels on a path represent the quality of that path;
- Decision Rule: Ants use a decision rule to probabilistically choose the next path to explore. Pheromone levels and heuristics guide their decisions;
- Pheromone Update: After all ants have completed their exploration, the pheromone levels are updated based on the quality of the solutions found. This guides future ant exploration.
The mathematical representation of the pheromone update in ACO is given by:
where:
- is the pheromone level on path .
- is the pheromone evaporation rate.
- is the pheromone increment for path .
The reviewed papers that utilize ACO are shown in Table 4. In the context of robotic arm trajectory planning, well-known methods such as RRT, EST, and PRM have been extensively used. In this regard, a method was proposed in Refs. [108,109] that employs a metaheuristic approach combining the PRM algorithm. The concept of this fusion is referred to as Ant Colony Robot Motion Planning (ACRMP). This combination leverages the characteristics of the ACO algorithm, where pheromones and collective ant behavior are utilized for robot navigation. Ants are divided into teams located at the nest and food sources, creating pheromone trails along the path between these points. This way, the optimal path through the traversable free space defined by PRM is sought.
Efficient collision-free path planning has also been investigated using the ACO algorithm in Ref. [110]. It has also been applied in Ref. [111] to dual-arm robots in three-dimensional configuration space (C space) using an enhanced version of the ACO metaheuristic. The improvements included strategic adjustments for joint movements, grid size optimization for space partitioning, improved local pheromone updates, and a strategy for ant return. These enhancements have resulted in increased performance and reduced collisions between robotic arms.
Collision-free trajectory planning has also been tested on a SCARA robot using the enhanced algorithm Dynamic Recursive Ant Colony Algorithm for Obstacle Avoidance Path Planning [112]. Key modifications involve the introduction of a sliding window and a forgetting factor. These adjustments alter correlation parameters and pheromone rules to better adapt to varying conditions, as fixed parameter values are insufficient for optimal performance throughout the calculation. Collaboration among ants is utilized to establish an optimal path for obstacle avoidance, and the proposed optimal path for manipulator motion is based on a dynamic recursive ant colony algorithm. Similar adjustments for the same type of manipulator have also been proposed, including a combination with the D* Algorithm [113].
Another explored area of research involves collision-free trajectory planning for high-precision assembly. An improvement proposed in this context introduces the Elite Smoothing Ant Colony Algorithm (ESACO) [114] for planning such collision-free paths with high precision. The enhanced ESACO algorithm improves the probabilistic transition formulation and pheromone update strategies to enhance algorithm reliability and flexibility. Additionally, a segmented B-spline curve is employed to eliminate inflection points and create a smooth path.


Table 4.
The considered literature on the motion planning problem solved using ACO.
Table 4.
The considered literature on the motion planning problem solved using ACO.
| Ref. | Year | Type of Robotic Structure | Type of Problem | Software | Simulation Only |
|---|---|---|---|---|---|
| [108] | 2005 | Articulated (Industrial) | Collision-free path planning. | Visual C++ | Yes |
| [109] | 2006 | Articulated (Industrial) | Collision-free path planning. | Visual C++ | Yes |
| [111] | 2009 | 3-link (redundant) dual-arm | Collision-free path planning. | Visual C++ | Yes |
| [110] | 2017 | 2-link (redundant) | Point-to-point motion planning and trajectory tracking. | MATLAB | Yes |
| [112] | 2019 | SCARA | Path planning with obstacle avoidance. | Unspecified | No |
| [113] | 2021 | 2-link (redundant) | Collision-free path planning. | Unspecified | Yes |
| [114] | 2022 | Articulated (Industrial) | Collision-free path planning. | ABB RobotStu-dio. | Yes |
4.4. Differential Evolution
DE is a type of evolutionary algorithm, which is based on mimicking the process of natural selection to gradually improve a group of potential solutions. In each iteration, DE generates new candidate solutions by combining information from three randomly chosen individuals from the current population. These new solutions are then compared to the current ones, and if they prove to be better based on a specific fitness measure, they replace the old solutions. DE is celebrated for its versatility as it employs mutation and crossover operations to effectively explore the solution space [115,116]. The whole process can be divided into three parts where the mathematical description corresponds to:
- Population Initialization:
- Mutation (differential variant):
- Crossover (exponential variant):
- Selection (elitism):where is the fitness function, , and are randomly selected indices from the population, and F is the mutation factor, represents random values for each element j of the vector, is the crossover constant, and is a randomly selected index.
In the context of industrial robotics problems, DE can be used to compute optimal trajectories for industrial robotic manipulators, aiming to minimize costs while adhering to constraints such as position, velocity, and torques. The reviewed papers utilizing DE for this purpose are shown in Table 5. An extension of the DE algorithm demonstrated good convergence and outperformed the state-of-the-art Non-dominated Sorting Genetic Algorithm (NSGA-II) in terms of results [117]. The comparison involved utilizing clamped cubic spline curves to optimize a cost function that includes transfer time, singularity avoidance, and acceleration. The extended version of Multi-Objective Differential Evolution also surpasses NSGA-II when planning optimal motions for industrial robotic manipulators in obstacle-filled spaces, considering both energy efficiency and obstacle avoidance [118].
DE can also find applications in determining optimal trajectories for robotic manipulators based on known joint paths [119]. Here, the objective was to minimize the end-effector position error and total joint displacements to achieve smooth motion close to the learned trajectory. The DE algorithm could effectively address these problems by working with candidate solution populations, even in situations involving singular points, without requiring Jacobian matrices.
Another critical area is energy-efficient path planning for industrial robotic arms in the presence of obstacles [120]. This problem is formulated as an optimization task to find the shortest and energy-optimal path for a robotic arm, avoiding obstacles while moving from the initial position to a predefined goal. Additionally, DE-based solutions can be applied in space robotics, specifically for free-floating space robots, where the algorithm considers forward kinematics and utilizes Bézier curves to plan joint trajectories, achieving orientation accuracy and effective base regulation [121].
The DE algorithm also found its application in the field of robotic grasping. The combination of the Fast Marching Square (FM) method and the DE optimization evolutionary filter creates an intriguing concept for computing robot trajectories [122]. In solving this problem, it was necessary to consider geometric constraints caused by the lengths of links in the kinematic chain comprising the robot arm and hand. During trajectory calculation, the potential field of the surroundings created using FM and the robot’s kinematic constraints are used as cost functions minimized by the DE-based evolutionary filter. Employing this optimization filter allowed for finding nearly optimal solutions that satisfy kinematic constraints while preserving the characteristics of trajectories computed with FM. The proposed method was tested on an advanced robot structure consisting of a mobile base with two arms.


Table 5.
Considered literature on the motion planning problem solved using DE.
Table 5.
Considered literature on the motion planning problem solved using DE.
| Ref. | Year | Type of Robotic Structure | Type of Problem | Software | Simulation Only |
|---|---|---|---|---|---|
| [117] | 2008 | Articulated | Optimal trajectory planning of dynamic free motion. | Visual C++ | Yes |
| [118] | 2010 | SCARA | Collision-free path planning. | Visual C++ | No |
| [119] | 2009 | Articulated (Industrial) | Point-to-point motion planning and trajectory tracking. | Unspecified | Yes |
| [120] | 2018 | 3-link (redundant) | Energy optimization for optimal motion planning. | MATLAB | Yes |
| [121] | 2018 | Articulated | Point-to-point motion planning and trajectory tracking. | Unspecified | Yes |
| [122] | 2022 | Special | Collision-free path planning. | MATLAB | No |
4.5. Artificial Bee Colony
The ABC algorithm is a population-based optimization algorithm inspired by the foraging behavior of honeybees. It was introduced in 2005 and has since been applied to a wide range of optimization problems. ABC simulates the process of honeybee colonies searching for the best food sources [123,124].
The ABC algorithm consists of the following main components:
- Population Initialization:
- Employed bees: In this phase, employed bees explore food sources and perform local searches around the food sources they are currently exploiting.
- Onlooker bees: Onlooker bees choose food sources to exploit based on the information provided by employed bees. The probability of selecting a food source is determined by its quality.
- Scout bees: Scout bees are responsible for discovering new food sources. If a food source has not been improved for a certain number of iterations, it is abandoned and replaced with a randomly generated solution.where N is the number of bees, represents the position of bee i at iteration t, is the initial position, is the position after exploration, is the fitness function, is a random number in the range , and is a randomly generated solution.
The best solution found by the employed and onlooker bees is updated if a better solution is discovered. Then the algorithm repeats the above phases for a specified number of iterations or until a termination condition is met. The reviewed papers utilizing ABC in the field of industrial robotics are shown in Table 6.
ABC is one of the newer algorithms designed to solve obstacle avoidance problems for free-flying space robots [125]. In the context of solving obstacle avoidance problems for free-flying space robots, it is significant from a trajectory planning perspective. An important feature is the ability to adjust the obstacle avoidance coefficient, allowing for trajectory optimization and increased adaptability of robots in various situations. The artificial bee colony algorithm also offers parallel execution, demonstrating strong robustness in solving these problems.
The significance of the ABC algorithm in research lies in its applications for planning and optimizing robotic manipulator trajectories. For example, it can be used for trajectory optimization, such as for a 3-DOF robotic manipulator [126] or planning the trajectory of a redundant dual-chain manipulator with a fixed base. The proposed use of the method involved the initial optimization of the configuration of the kinematic system of the dual-chain manipulator. Subsequently, the toolpath of the dual-chain manipulator was planned using the Rapidly-Exploring Random Tree Star algorithm. Finally, joint trajectories were generated using the Gradient Projection Method. One of the main objectives was to devise a suitable optimization method for the initial configurations of the dual-chain manipulator, enabling smooth motion planning for the dual-chain manipulator and optimizing the trajectory [127].
Another potential application of the ABC algorithm is palletizing planning using robotic arms in an industrial setting [128]. For instance, it can involve servicing three production lines, where considering cycle time and maximum allowable waiting time for each item is essential. To solve such problems, the ABC algorithm with Deb’s rules has been proposed. This results in increased production that meets specific requirements, such as minimizing the energy consumption per palletized item or ensuring equal container filling. The approach can be applied to various constraints, achieving optimal planning for robotic arms.


Table 6.
Considered literature on the motion planning problem solved using ABC.
Table 6.
Considered literature on the motion planning problem solved using ABC.
| Ref. | Year | Type of Robotic Structure | Type of Problem | Software | Simulation Only |
|---|---|---|---|---|---|
| [125] | 2012 | Special | Collision-free path planning. | MATLAB | Yes |
| [126] | 2013 | 3-link (redundant) | Point-to-point motion planning and trajectory tracking. | MATLAB | Yes |
| [127] | 2023 | Special | Collision-free path planning. | Unspecified | No |
| [128] | 2022 | Articulated (Collaborative) | Collision-free path planning. | MATLAB | No |
4.6. Other Methods
Apart from the already described methods, there are also other evolutionary computation techniques that were used in the field of industrial robotics. A brief overview of the reviewed papers regarding these methods is shown in Table 7.
The APF method, combined with the Simulated Annealing algorithm, can be employed for real-time motion planning of manipulators in a three-dimensional space [129]. The artificial potential field method is suitable due to its simple structure, but it faces the issue of local minima. To overcome the problem of local minima, the simulated annealing algorithm is utilized for optimization. This combination results in an extension of traditional manipulator motion planning, enabling obstacle avoidance and enhancing efficiency.
Among other algorithms that can be utilized for planning and optimizing trajectories for 6-DOF manipulators in an industrial setting, Cuckoo Search stands out. For instance, in the case of smooth motion planning with time optimization, the continuous quintic B-spline algorithm can be used for generating smooth trajectories, and the Adaptive Cuckoo Search algorithm can be employed to minimize motion time while adhering to dynamic constraints [130].
The Beetle Antennae Search algorithm can represent a motion planning method for redundant manipulators with variable joint velocity limits [131]. Unlike conventional approaches that require solving velocity kinematics equations and may overlook joint velocity constraints, the proposed method directly addresses the inverse kinematics equation to obtain the desired joint angles. Experiments conducted with a five-link planar manipulator and an industrial manipulator demonstrate the effectiveness and reliability of the proposed approach for motion planning in redundant manipulators.
The Grey Wolf Optimizer (GWO) metaheuristic also had its implementations for parallel robots concerning energy consumption during rapid object picking and placing [132]. Lamé curves were employed to round rectangular trajectories in the end-effector space of the robot. Additionally, a piecewise design method was used for trajectory planning considering position, velocity, and acceleration. The primary objective was to minimize the mechanical energy consumption of the delta robot, and the GWO algorithm was employed for trajectory optimization. Optimization of the Lamé curve parameters depends on specific conditions such as lifting height and the pick-and-place endpoints of the object. However, there are recent works about the negative theoretical [45] and empirical [41] properties of GWO.
Optimal trajectory planning in the field of grinding can have a positive impact on both processing quality and machining efficiency, especially when experimenting with and combining metaheuristics. One example is the enhanced Whale Optimization Algorithm, which combines Whale Optimization Algorithm (WOA) and DE [133]. This combination involves emulating the mutation and selection operations of DE during population initialization by WOA, followed by WOA’s search tasks. The optimization objective includes minimizing time and the rate of acceleration change to achieve smooth robot motion based on cubic spline interpolation. However, similar to GWO, the WOA method was also shown to contain substantial structural defects [44,134].
A comparison of 12 evolutionary computation techniques on the 6-DOF industrial robot trajectory planning problem was carried out in Ref. [135]. The authors compared both the standard techniques discussed above (such as DE, ABC, or ACO) and more recent techniques, which included some of the best-performing methods from recent IEEE Congress on Evolutionary Computation (CEC) Competitions on numerical optimization. The overall best methods that came from this analysis were the Covariance matrix adaptation evolution strategy (CMAES) [136], and the Success-history based adaptive differential evolution with linear population size reduction (LSHADE) [137]. Interestingly, in this setting, WOA was found to be between the worst methods.
In Ref. [138], the authors compared seven evolutionary computation techniques on a large set of optimization problems that were a combination of inverse kinematics and path planning in industrial robotics. The results of their investigation also show that the best-performing methods from the CEC competitions, in this case, LSHADE [137] and Adaptive Gaining-Sharing Knowledge (AGSK) [139], along with CMAES [136] are the overall best-suited methods for this application.


Table 7.
Considered literature on the motion planning problem solved using other evolutionary computation methods.
Table 7.
Considered literature on the motion planning problem solved using other evolutionary computation methods.
| Ref. | Year | Type of Robotic Structure | Type of Problem | Software | Simulation Only |
|---|---|---|---|---|---|
| [129] | 2019 | Articulated (Industrial) | Collision-free path planning. | Unspecified | Yes |
| [130] | 2021 | Articulated (Industrial) | Point-to-point motion planning and trajectory tracking. | MATLAB | No |
| [131] | 2020 | Articulated (Collaborative) | Point-to-point motion planning and trajectory tracking. | MATLAB | No |
| [132] | 2019 | Parallel | Point-to-point motion planning and trajectory tracking. | Unspecified | No |
| [133] | 2020 | Articulated (Industrial) | Point-to-point motion planning and trajectory tracking. | MATLAB & ABB RobotStudio | No |
| [135] | 2018 | Articulated (Industrial) | Point-to-point motion planning and trajectory tracking. | Unspecified | Yes |
| [138] | 2023 | Articulated (Industrial) | Optimal trajectory planning. | MATLAB | Yes |
4.7. Research Gaps and Directions
Although evolutionary algorithms are proving to be one of the potential and promising methods for industrial robotics path planning, there are still significant gaps in the application of these techniques. In the realm of utilizing and implementing evolutionary algorithms for these problems, the majority of the publications often present issues that are mostly related to simple point-to-point planning from the desired to the target position and collision-free path planning in a static environment. Moreover, these problems are frequently solved without testing the solutions on real-world implementations. New research in this area should address more complex real-world problems and also focus on multi-objective approaches [76,89]. Testing practical applications in the real world can highlight the applicability of the proposed solution (in terms of precision and computational complexity), as well as validate that the developed techniques operate using real industrial/collaborative robots rather than just simulations. Significant expansion could be achieved through research related to trajectory planning for painting and palletizing robots, which are widely used in the general industry.
A fundamental gap arises in benchmarking [140,141] individual methods for robotic trajectory planning, which would indicate the distinguishing features of various metaheuristics in comparison. This area is linked to the problem of recognizing and implementing state-of-the-art evolutionary computation techniques [138]. There should be more focus on the implementation of modern evolutionary algorithms, such as jSO [142], AGSK [139], LSHADE [137], and CMAES variants [136]. These methods were recently shown to have excellent performance on a range of various complex [43,143,144,145] and applied problems [146,147,148]. In addition, the development of a common framework/platform with a range of standardized industrial robotics path planning problems for benchmarking different methods (from the various possible approaches) would be immensely valuable. Such a platform should support multiple programming languages and various problem settings. The COCO platform (https://numbbo.github.io/coco/, accessed on 1 October 2023) for benchmarking black-box optimization methods could serve as a great source of inspiration [149].
It is important to emphasize that the low percentage of research applications in a given field translates into real-world applications, as we can see in the tables above, especially in terms of validation and testing on real industrial robots. It is quite common to develop the control in simulation, and then transfer it to real manipulators post-optimization to avoid the time and energy-consuming nature of performing all evaluations on the real hardware [28]. The central issue with this simulate-and-transfer approach is known as the reality gap [150]. Trajectories optimized in simulation can become ineffective once transferred to the physical manipulator because of their exploitation of features that are present only in the simulated world (and nonexistent in the real world). The differences between the real world and the simulation can vary—from simulation-only artifacts due to abstractions, simplifications, discreteness, and idealizations of physics implementations to inaccurate sensor modeling [28]. The reality gap is a frequent phenomenon and is still one of the main obstacles to progress in utilizing not only evolutionary computation [151] but other techniques as well [152].
An area where evolutionary algorithms can find justification is in solving path planning with a focus on energy consumption, which can be an important topic for practical use in production operations. Industrial robotic arms are electromechanical devices with a limited lifecycle. However, with a well-optimized trajectory that is more energy-efficient [73,74] and includes minimal robot stops, it would be possible to increase the lifetime of the robots themselves. Such research directions are becoming increasingly important, especially with respect to the issue of sustainability.
Another possible direction of further research could lie in the utilization of surrogate-assisted techniques [47,153,154], which are methods suited for problems where the computations of the objectives are prohibitively expensive. Such situations may arise in problems with complex, dynamic, or collaborative environments, or for problems with several objectives.
Lastly, one of the most significant shortcomings in the use of evolutionary algorithms in path planning is the limited availability of open-source code, especially in the field of industrial robotics, that could be used as a basis for real-world solutions. In addition, a description of the software used is essential, and many publications do not specify this information [155]. The majority of the publications use a proprietary multi-paradigm programming language MATLAB for their research. However, there is also a rationale for developing a solution in Python, a programming language that has grown in popularity among scientists in recent years. The Python programming language offers very similar features and tools to MATLAB, even for industrial robotics, such as Robotics Toolbox for Python (https://petercorke.github.io/robotics-toolbox-python/index.html, accessed on 1 October 2023) [156].
5. Conclusions
In this paper, we reviewed the recent trends and progress in the utilization of evolutionary computation techniques for the various path planning problems in industrial robotics. We have focused primarily on the well-studied evolutionary computation methods such as PSO, GA, DE, ACO, and ABC, as well as the best-performing methods from the CEC Competitions. The various enhancements of the standard techniques and the utilization of the state-of-the-art methods showed great potential for solving the studied industrial path planning problems.
In summary, great achievements of the evolutionary techniques in this area have been gained, especially in the last two decades. However, we have also identified an overabundance of recent studies that focus on the rather simple and already well-studied point-to-point planning and collision-free path planning problems in static environments. Finally, we have outlined several possible future research directions that would make the utilization of the evolutionary computation techniques in this field even more applicable.
Author Contributions
Conceptualization, M.J., R.P. and J.K.; methodology, J.K.; investigation, M.J. and R.P.; resources, M.J. and R.P.; data curation, M.J. and R.P.; writing—original draft preparation, M.J., R.P. and J.K.; writing—review and editing, M.J., R.P. and J.K.; visualization, M.J. and R.P.; supervision, J.K.; project administration, J.K.; funding acquisition, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the project IGA BUT No. FSI-S-23-8394 “Artificial intelligence methods in engineering tasks”.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Jin, L. Robot Manipulator Redundancy Resolution; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Billard, A.; Kragic, D. Trends and challenges in robot manipulation. Science 2019, 364, eaat8414. [Google Scholar] [CrossRef] [PubMed]
- Seereeram, S.; Wen, J.T. A global approach to path planning for redundant manipulators. IEEE Trans. Robot. Autom. 1995, 11, 152–160. [Google Scholar] [CrossRef]
- Kim, J.O.; Khosla, P.K. Real-time obstacle avoidance using harmonic potential functions. IEEE Trans. Robot. Autom. 1992, 8, 338–349. [Google Scholar] [CrossRef]
- Baillieul, J. Kinematic programming alternatives for redundant manipulators. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; IEEE: New York, NY, USA, 1985; Volume 2, pp. 722–728. [Google Scholar]
- Xanthidis, M.; Esposito, J.; Rekleitis, I.; O’Kane, J. Analysis of Motion Planning by Sampling in Subspaces of Progressively Increasing Dimension. J. Intell. Robot. Syst. 2020, 100, 777–789. [Google Scholar] [CrossRef]
- Liu, S.; Liu, P. Benchmarking and optimization of robot motion planning with motion planning pipeline. Int. J. Adv. Manuf. Technol. 2022, 118, 949–961. [Google Scholar] [CrossRef]
- Iversen, T.; Ellekilde, L.P. Benchmarking motion planning algorithms for bin-picking applications. Ind. Robot. Int. J. 2017, 44, 189–197. [Google Scholar] [CrossRef]
- Ying, K.C.; Pourhejazy, P.; Cheng, C.Y.; Cai, Z.Y. Deep learning-based optimization for motion planning of dual-arm assembly robots. Comput. Ind. Eng. 2021, 160, 107603. [Google Scholar] [CrossRef]
- Lobbezoo, A.; Qian, Y.; Kwon, H.J. Reinforcement Learning for Pick and Place Operations in Robotics: A Survey. Robotics 2021, 10, 105. [Google Scholar] [CrossRef]
- Plappert, M.; Andrychowicz, M.; Ray, A.; McGrew, B.; Baker, B.; Powell, G.; Schneider, J.; Tobin, J.; Chociej, M.; Welinder, P.; et al. Multi-Goal Reinforcement Learning: Challenging Robotics Environments and Request for Research. arXiv 2018, arXiv:1802.09464. [Google Scholar]
- Jin, L.; Li, S.; Yu, J.; He, J. Robot manipulator control using neural networks: A survey. Neurocomputing 2018, 285, 23–34. [Google Scholar] [CrossRef]
- Liu, R.; Nageotte, F.; Zanne, P.; de Mathelin, M.; Dresp-Langley, B. Deep reinforcement learning for the control of robotic manipulation: A focussed mini-review. Robotics 2021, 10, 22. [Google Scholar] [CrossRef]
- Ajwad, S.A.; Iqbal, J.; Ullah, M.I.; Mehmood, A. A systematic review of current and emergent manipulator control approaches. Front. Mech. Eng. 2015, 10, 198–210. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, B. A review on model reference adaptive control of robotic manipulators. Annu. Rev. Control 2017, 43, 188–198. [Google Scholar] [CrossRef]
- Starke, S.; Hendrich, N.; Magg, S.; Zhang, J. An efficient hybridization of Genetic Algorithms and Particle Swarm Optimization for inverse kinematics. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 1782–1789. [Google Scholar] [CrossRef]
- Ruppel, P.; Hendrich, N.; Starke, S.; Zhang, J. Cost Functions to Specify Full-Body Motion and Multi-Goal Manipulation Tasks. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 3152–3159. [Google Scholar] [CrossRef]
- Xiao, Y.; Fan, Z.; Li, W.; Chen, S.; Zhao, L.; Xie, H. A Manipulator Design Optimization Based on Constrained Multi-objective Evolutionary Algorithms. In Proceedings of the 2016 International Conference on Industrial Informatics—Computing Technology, Intelligent Technology, Industrial Information Integration (ICIICII), Wuhan, China, 3–4 December 2016; pp. 199–205. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, K.H. Computational Design of Modular Robots Based on Genetic Algorithm and Reinforcement Learning. Symmetry 2021, 13, 471. [Google Scholar] [CrossRef]
- Hsiao, J.C.; Shivam, K.; Chou, C.L.; Kam, T.Y. Shape Design Optimization of a Robot Arm Using a Surrogate-Based Evolutionary Approach. Appl. Sci. 2020, 10, 2223. [Google Scholar] [CrossRef]
- Xuan, D.T.; Huynh, T.V.; Hung, N.T.; Thang, V.T. Applying Digital Twin and Multi-Adaptive Genetic Algorithms in Human–Robot Cooperative Assembly Optimization. Appl. Sci. 2023, 13, 4229. [Google Scholar] [CrossRef]
- Eklund, M.; Sierla, S.; Niemistö, H.; Korvola, T.; Savolainen, J.; Karhela, T. Using a Digital Twin as the Objective Function for Evolutionary Algorithm Applications in Large Scale Industrial Processes. IEEE Access 2023, 11, 24185–24202. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Tao, B.; Jiang, G.; Sun, Y.; Kong, J.; Tong, X.; Zhao, G.; Chen, B. Genetic Algorithm-Based Trajectory Optimization for Digital Twin Robots. Front. Bioeng. Biotechnol. 2022, 9, 793782. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Q.; Sun, Y. Evolutionary Robot Calibration and Nonlinear Compensation Methodology Based on GA-DNN and an Extra Compliance Error Model. Math. Probl. Eng. 2020, 2020, 3981081. [Google Scholar] [CrossRef]
- Larsen, L.; Schuster, A.; Kim, J.; Kupke, M. Path Planning of Cooperating Industrial Robots Using Evolutionary Algorithms. Procedia Manuf. 2018, 17, 286–293. [Google Scholar] [CrossRef]
- Vargas, P.A.; Di Paolo, E.A.; Harvey, I.; Husbands, P. The Horizons of Evolutionary Robotics; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Doncieux, S.; Bredeche, N.; Mouret, J.B.; Eiben, A.E. Evolutionary robotics: What, why, and where to. Front. Robot. AI 2015, 2, 4. [Google Scholar] [CrossRef]
- Silva, F.; Duarte, M.; Correia, L.; Oliveira, S.M.; Christensen, A.L. Open issues in evolutionary robotics. Evol. Comput. 2016, 24, 205–236. [Google Scholar] [CrossRef] [PubMed]
- Parak, R.; Matousek, R. Comparison of multiple reinforcement learning and deep reinforcement learning methods for the task aimed at achieving the goal. MENDEL J. 2021, 27, 1–8. [Google Scholar] [CrossRef]
- Parak, R.; Juricek, M. Intelligent sampling of anterior human nasal swabs using a collaborative robotic arm. MENDEL J. 2022, 28, 32–40. [Google Scholar] [CrossRef]
- Nof, S.Y. Handbook of Industrial Robotics; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Bonev, I. Delta Parallel Robot-the Story of Success. Newsletter. 2001. Available online: http://www.parallelmic.org (accessed on 1 October 2023).
- Visioli, A.; Legnani, G. On the trajectory tracking control of industrial SCARA robot manipulators. IEEE Trans. Ind. Electron. 2002, 49, 224–232. [Google Scholar] [CrossRef]
- Moran, M.E. Evolution of robotic arms. J. Robot. Surg. 2007, 1, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar] [CrossRef]
- Collins, J.; Chand, S.; Vanderkop, A.; Howard, D. A Review of Physics Simulators for Robotic Applications. IEEE Access 2021, 9, 51416–51431. [Google Scholar] [CrossRef]
- Matousek, R.; Dobrovsky, L.; Kudela, J. How to start a heuristic? Utilizing lower bounds for solving the quadratic assignment problem. Int. J. Ind. Eng. Comput. 2022, 13, 151–164. [Google Scholar] [CrossRef]
- Campelo, F.; Aranha, C.d.C. Sharks, zombies and volleyball: Lessons from the evolutionary computation bestiary. In Proceedings of the CEUR Workshop Proceedings, Milan, Italy, 30 November 2021; Volume 3007, p. 6. [Google Scholar]
- Tzanetos, A.; Dounias, G. Nature inspired optimization algorithms or simply variations of metaheuristics? Artif. Intell. Rev. 2021, 54, 1841–1862. [Google Scholar] [CrossRef]
- Tzanetos, A.; Fister, I., Jr.; Dounias, G. A comprehensive database of Nature-Inspired Algorithms. Data Brief 2020, 31, 105792. [Google Scholar] [CrossRef]
- Niu, P.; Niu, S.; Chang, L. The defect of the Grey Wolf optimization algorithm and its verification method. Knowl.-Based Syst. 2019, 171, 37–43. [Google Scholar] [CrossRef]
- Kudela, J. Commentary on: “STOA: A bio-inspired based optimization algorithm for industrial engineering problems” [EAAI, 82 (2019), 148–174] and “Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization” [EAAI, 90 (2020), no. 103541]. Eng. Appl. Artif. Intell. 2022, 113, 104930. [Google Scholar]
- Kudela, J. A critical problem in benchmarking and analysis of evolutionary computation methods. Nat. Mach. Intell. 2022, 4, 1238–1245. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S. Deficiencies of the whale optimization algorithm and its validation method. Expert Syst. Appl. 2024, 237, 121544. [Google Scholar] [CrossRef]
- Camacho Villalón, C.L.; Stützle, T.; Dorigo, M. Grey wolf, firefly and bat algorithms: Three widespread algorithms that do not contain any novelty. In Proceedings of the International Conference on Swarm Intelligence, Belgrade, Serbia, 14–20 July 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 121–133. [Google Scholar]
- Aranha, C.; Camacho Villalón, C.L.; Campelo, F.; Dorigo, M.; Ruiz, R.; Sevaux, M.; Sörensen, K.; Stützle, T. Metaphor-based metaheuristics, a call for action: The elephant in the room. Swarm Intell. 2022, 16, 1–6. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. Recent advances and applications of surrogate models for finite element method computations: A review. Soft Comput. 2022, 26, 13709–13733. [Google Scholar] [CrossRef]
- Tzanetos, A.; Dounias, G. A comprehensive survey on the applications of swarm intelligence and bio-inspired evolutionary strategies. In Machine Learning Paradigms: Advances in Deep Learning-Based Technological Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 337–378. [Google Scholar]
- Tzanetos, A.; Blondin, M. A qualitative systematic review of metaheuristics applied to tension/compression spring design problem: Current situation, recommendations, and research direction. Eng. Appl. Artif. Intell. 2023, 118, 105521. [Google Scholar] [CrossRef]
- Žufan, P.; Bidlo, M. Advances in evolutionary optimization of quantum operators. MENDEL J. 2021, 27, 12–22. [Google Scholar] [CrossRef]
- Muller, J. Improving initial aerofoil geometry using aerofoil particle swarm optimisation. MENDEL J. 2022, 28, 63–67. [Google Scholar] [CrossRef]
- Ma, J.; Xia, D.; Wang, Y.; Niu, X.; Jiang, S.; Liu, Z.; Guo, H. A comprehensive comparison among metaheuristics (MHs) for geohazard modeling using machine learning: Insights from a case study of landslide displacement prediction. Eng. Appl. Artif. Intell. 2022, 114, 105150. [Google Scholar] [CrossRef]
- Kanagaraj, G.; Masthan, S.S.; Vincent, F.Y. Meta-heuristics based inverse kinematics of robot manipulator’s path tracking capability under joint limits. MENDEL J. 2022, 28, 41–54. [Google Scholar] [CrossRef]
- Febrianti, W.; Sidarto, K.A.; Sumarti, N. Approximate Solution for Barrier Option Pricing Using Adaptive Differential Evolution With Learning Parameter. MENDEL J. 2022, 28, 76–82. [Google Scholar] [CrossRef]
- Gogna, A.; Tayal, A. Metaheuristics: Review and application. J. Exp. Theor. Artif. Intell. 2013, 25, 503–526. [Google Scholar] [CrossRef]
- Darwish, A.; Hassanien, A.E.; Das, S. A survey of swarm and evolutionary computing approaches for deep learning. Artif. Intell. Rev. 2020, 53, 1767–1812. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Zhang, W.; Fu, S. Time-optimal Trajectory Planning of Dulcimer Music Robot Based on PSO Algorithm. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 4769–4774. [Google Scholar] [CrossRef]
- Shi, B.; Zeng, H. Time-Optimal Trajectory Planning for Industrial Robot based on Improved Hybrid-PSO. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 3888–3893. [Google Scholar] [CrossRef]
- Du, Y.; Chen, Y. Time Optimal Trajectory Planning Algorithm for Robotic Manipulator Based on Locally Chaotic Particle Swarm Optimization. Chin. J. Electron. 2022, 31, 906–914. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, Q. Time optimal trajectory planning of five degrees of freedom manipulator based on PSO algorithm. In Proceedings of the 2022 4th International Conference on Intelligent Control, Measurement and Signal Processing (ICMSP), Hangzhou, China, 8–10 July 2022; pp. 1059–1062. [Google Scholar] [CrossRef]
- Miao, X.; Fu, H.; Song, X. Research on motion trajectory planning of the robotic arm of a robot. Artif. Life Robot. 2022, 27, 561–567. [Google Scholar] [CrossRef]
- Huang, P.; Xu, Y. PSO-Based Time-Optimal Trajectory Planning for Space Robot with Dynamic Constraints. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 1402–1407. [Google Scholar] [CrossRef]
- Kim, J.J.; Lee, J.J. Trajectory Optimization with Particle Swarm Optimization for Manipulator Motion Planning. IEEE Trans. Ind. Inform. 2015, 11, 620–631. [Google Scholar] [CrossRef]
- Han, S.; Shan, X.; Fu, J.; Xu, W.; Mi, H. Industrial robot trajectory planning based on improved pso algorithm. J. Physics Conf. Ser. 2021, 1820, 012185. [Google Scholar] [CrossRef]
- Meng, Y.; Sun, Y.; Chang, W.-S. Optimal trajectory planning of complicated robotic timber joints based on particle swarm optimization and an adaptive genetic algorithm. Constr. Robot. 2021, 5, 131–146. [Google Scholar] [CrossRef]
- Zhou, W.; Fan, C.; Wang, L.; Xie, C.; Tang, T.; Liu, R. Path planning of manipulator based on improved particle swarm optimization. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 4283–4288. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, X.; Song, T. Serial Manipulator Time-Jerk Optimal Trajectory Planning Based on Hybrid IWOA-PSO Algorithm. IEEE Access 2022, 10, 6592–6604. [Google Scholar] [CrossRef]
- Ekrem, Ö.; Aksoy, B. Trajectory planning for a 6-axis robotic arm with particle swarm optimization algorithm. Eng. Appl. Artif. Intell. 2023, 122, 106099. [Google Scholar] [CrossRef]
- Liu, C.; Cao, G.H.; Qu, Y.Y.; Cheng, Y.M. An improved PSO algorithm for time-optimal trajectory planning of Delta robot in intelligent packaging. Int. J. Adv. Manuf. Technol. 2020, 107, 1091–1099. [Google Scholar] [CrossRef]
- Lin, C.J.; Li, M.Y. Motion planning with obstacle avoidance of an UR3 robot using charge system search. In Proceedings of the 2018 18th International Conference on Control, Automation and Systems (ICCAS), PyeongChang, Republic of Korea, 17–20 October 2018; pp. 746–750. [Google Scholar]
- Vysocký, A.; Papřok, R.; Šafařík, J.; Kot, T.; Bobovský, Z.; Novák, P.; Snášel, V. Reduction in Robotic Arm Energy Consumption by Particle Swarm Optimization. Appl. Sci. 2020, 10, 8241. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, C.; Zeng, Q.; Li, A.; Xie, N. Time-energy Optimal Trajectory Planning for Collaborative Welding Robot with Multiple Manipulators. Procedia Manuf. 2020, 43, 527–534. [Google Scholar] [CrossRef]
- Gao, R.; Zhou, Q.; Cao, S.; Jiang, Q. Apple-Picking Robot Picking Path Planning Algorithm Based on Improved PSO. Electronics 2023, 12, 1832. [Google Scholar] [CrossRef]
- Cao, X.; Yan, H.; Huang, Z.; Ai, S.; Xu, Y.; Fu, R.; Zou, X. A Multi-Objective Particle Swarm Optimization for Trajectory Planning of Fruit Picking Manipulator. Agronomy 2021, 11, 2286. [Google Scholar] [CrossRef]
- Huang, P.; Liu, G.; Yuan, J.; Xu, Y. Multi-Objective Optimal Trajectory Planning of Space Robot Using Particle Swarm Optimization. In Proceedings of the Advances in Neural Networks—ISNN 2008, Beijing, China, 24–28 September 2008; Sun, F., Zhang, J., Tan, Y., Cao, J., Yu, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 171–179. [Google Scholar]
- Xu, W.; Li, C.; Liang, B.; Liu, Y.; Xu, Y. The Cartesian Path Planning of Free-Floating Space Robot using Particle Swarm Optimization. Int. J. Adv. Robot. Syst. 2008, 5, 27. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J.; Walter, U. Trajectory planning of free-floating space robot using Particle Swarm Optimization (PSO). Acta Astronaut. 2015, 112, 77–88. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J.; Yuan, J.; Walter, U. Coordinated trajectory planning of dual-arm space robot using constrained particle swarm optimization. Acta Astronaut. 2018, 146, 259–272. [Google Scholar] [CrossRef]
- Ni, S.; Chen, W.; Ju, H.; Chen, T. Coordinated trajectory planning of a dual-arm space robot with multiple avoidance constraints. Acta Astronaut. 2022, 195, 379–391. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Zhang, Q.; Wei, X. Obstacle Avoidance Path Planning of Space Robot Based on Improved Particle Swarm Optimization. Symmetry 2022, 14, 938. [Google Scholar] [CrossRef]
- Grefenstette, J.J. Genetic algorithms and machine learning. In Proceedings of the Sixth Annual Conference on Computational Learning Theory, Santa Cruz, CA, USA, 26–28 July 1993; pp. 3–4. [Google Scholar]
- Khoogar, A.; Parker, J. Obstacle avoidance of redundant manipulators using genetic algorithms. In Proceedings of the IEEE Proceedings of the SOUTHEASTCON ’91, Williamsburg, VA, USA, 7–10 April 1991; Volume 1, pp. 317–320. [Google Scholar] [CrossRef]
- Toogood, R.; Hao, H.; Wong, C. Robot path planning using genetic algorithms. In Proceedings of the 1995 IEEE International Conference on Systems, Man and Cybernetics, Intelligent Systems for the 21st Century, Vancouver, BC, Canada, 22–25 October 1995; Volume 1, pp. 489–494. [Google Scholar] [CrossRef]
- Garg, D.P.; Kumar, M. Optimization techniques applied to multiple manipulators for path planning and torque minimization. Eng. Appl. Artif. Intell. 2002, 15, 241–252. [Google Scholar] [CrossRef]
- Yue, S.; Henrich, D.; Xu, P.; Tso, S. Point-to-Point trajectory planning of flexible redundant robot manipulators using genetic algorithms. Robotica 2002, 20, 269–280. [Google Scholar] [CrossRef]
- Tian, L.; Collins, C. An effective robot trajectory planning method using a genetic algorithm. Mechatronics 2004, 14, 455–470. [Google Scholar] [CrossRef]
- Pires, E.; Tenreiro Machado, J.; Moura Oliveira, P. Robot Trajectory Planning Using Multi-objective Genetic Algorithm Optimization. In Proceedings of the Genetic and Evolutionary Computation—GECCO 2004, Seattle, WA, USA, 26–30 June 2004; Volume 3102, pp. 615–626. [Google Scholar] [CrossRef]
- Kazem, B.I.; Mahdi, A.I.; Oudah, A.T. Motion Planning for a Robot Arm by Using Genetic Algorithm. 2008. Available online: https://api.semanticscholar.org/CorpusID:957663 (accessed on 1 October 2023).
- Ren, T.R.; Kwok, N.M.; Liu, D.K.; Huang, S.D. Path planning for a robotic arm sand-blasting system. In Proceedings of the 2008 International Conference on Information and Automation, Changsha, China, 20–23 June 2008; pp. 1067–1072. [Google Scholar] [CrossRef]
- Sharma, G.S.; Singh, M.; Singh, T. Optimization of energy in robotic arm using genetic algorithm. Int. J. Comput. Sci. Technol. 2011, 2, 315–317. [Google Scholar]
- Abo-Hammour, Z.; Alsmadi, P.O.; Bataineh, S.; Alomari, M.; Affach, N. Continuous Genetic Algorithms for Collision-Free Cartesian Path Planning of Robot Manipulators. Int. J. Adv. Robot. Syst. 2011, 8, 50902. [Google Scholar] [CrossRef]
- Machmudah, A.; Parman, S.; Zainuddin, A.; Chacko, S. Polynomial joint angle arm robot motion planning in complex geometrical obstacles. Appl. Soft Comput. 2013, 13, 1099–1109. [Google Scholar] [CrossRef]
- Tsai, C.C.; Hung, C.C.; Chang, C.F. Trajectory planning and control of a 7-DOF robotic manipulator. In Proceedings of the 2014 International Conference on Advanced Robotics and Intelligent Systems (ARIS), Taipei, Taiwan, 6–8 June 2014; pp. 78–84. [Google Scholar] [CrossRef]
- Števo, S.; Sekaj, I.; Dekan, M. Optimization of Robotic Arm Trajectory Using Genetic Algorithm. In Proceedings of the IFAC World Congress 2014, Cape Town, South Africa, 24–29 August 2014. [Google Scholar] [CrossRef]
- Roy, R.; Mahadevappa, M.; Kumar, C. Trajectory Path Planning of EEG Controlled Robotic Arm Using GA. Procedia Comput. Sci. 2016, 84, 147–151. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Sun, J. Research on Trajectory Planning of Manipulator Based on GA—APF Algorithm. In Proceedings of the 2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Honolulu, HI, USA, 31 July–4 August 2017; pp. 210–215. [Google Scholar] [CrossRef]
- Wu, J.; Bin, D.; Feng, X.; Wen, Z.; Zhang, Y. GA Based Adaptive Singularity-Robust Path Planning of Space Robot for On-Orbit Detection. Complexity 2018, 2018, 3702916. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, C.; Weng, Y. Online Time-Optimal Trajectory Planning for Robotic Manipulators Using Adaptive Elite Genetic Algorithm With Singularity Avoidance. IEEE Access 2019, 7, 146301–146308. [Google Scholar] [CrossRef]
- Baressi Šegota, S.; Anđelić, N.; Lorencin, I.; Saga, M.; Car, Z. Path planning optimization of six-degree-of-freedom robotic manipulators using evolutionary algorithms. Int. J. Adv. Robot. Syst. 2020, 17, 1–16. [Google Scholar] [CrossRef]
- Larsen, L.; Kim, J. Path planning of cooperating industrial robots using evolutionary algorithms. Robot. Comput.-Integr. Manuf. 2021, 67, 102053. [Google Scholar] [CrossRef]
- Fang, Z.; Liang, X. Intelligent obstacle avoidance path planning method for picking manipulator combined with artificial potential field method. Ind. Robot. Int. J. Robot. Res. Appl. 2022, 49, 835–850. [Google Scholar] [CrossRef]
- Nonoyama, K.; Liu, Z.; Fujiwara, T.; Alam, M.M.; Nishi, T. Energy-Efficient Robot Configuration and Motion Planning Using Genetic Algorithm and Particle Swarm Optimization. Energies 2022, 15, 2074. [Google Scholar] [CrossRef]
- Zanchettin, A.M.; Messeri, C.; Cristantielli, D.; Rocco, P. Trajectory optimisation in collaborative robotics based on simulations and genetic algorithms. Int. J. Intell. Robot. Appl. 2022, 6, 707–723. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant Colony Optimization: Overview and Recent Advances. In Handbook of Metaheuristics; Gendreau, M., Potvin, J.Y., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 311–351. [Google Scholar] [CrossRef]
- Mohamad, M.; Dunnigan, M.; Taylor, N. Ant Colony Robot Motion Planning. In Proceedings of the EUROCON 2005—The International Conference on “Computer as a Tool”, Belgrade, Serbia, 21–24 November 2005; Volume 1, pp. 213–216. [Google Scholar] [CrossRef]
- Mohamad, M.; Taylor, N.; Dunnigan, M. Articulated Robot Motion Planning Using Ant Colony Optimisation. In Proceedings of the 2006 3rd International IEEE Conference Intelligent Systems, London, UK, 4–6 September 2006; pp. 690–695. [Google Scholar] [CrossRef]
- Baghli, F.Z.; bakkali, L.E.; Lakhal, Y. Optimization of Arm Manipulator Trajectory Planning in the Presence of Obstacles by Ant Colony Algorithm. Procedia Eng. 2017, 181, 560–567. [Google Scholar] [CrossRef]
- Wang, J.; Guo, M.; Li, L.; Sun, S.; Gu, S. Collision-free path planning of Dual-arm robots based on improved ant colony algorithm. In Proceedings of the 2009 Chinese Control and Decision Conference, Guilin, China, 17–19 June 2009; pp. 1438–1442. [Google Scholar] [CrossRef]
- Huadong, Z.; Chaofan, L.; Nan, J. A Path Planning Method of Robot Arm Obstacle Avoidance Based on Dynamic Recursive Ant Colony Algorithm. In Proceedings of the 2019 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 12–14 July 2019; pp. 549–552. [Google Scholar] [CrossRef]
- Sadiq, A.; Raheem, F.; Abbas, N.F. Ant Colony Algorithm Improvement for Robot Arm Path Planning Optimization Based on D* Strategy. Int. J. Mech. Mechatronics Eng. 2021, 21, 96–111. [Google Scholar]
- Meng, X.; Zhu, X. Autonomous Obstacle Avoidance Path Planning for Grasping Manipulator Based on Elite Smoothing Ant Colony Algorithm. Symmetry 2022, 14, 1843. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Price, K. Differential evolution: A fast and simple numerical optimizer. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19–22 June 1996; pp. 524–527. [Google Scholar] [CrossRef]
- Saravanan, R.; Ramabalan, S. Evolutionary Minimum Cost Trajectory Planning for Industrial Robots. J. Intell. Robot. Syst. 2008, 52, 45–77. [Google Scholar] [CrossRef]
- Saravanan, R.; Ramabalan, S.; Balamurugan, C.; Subash, A. Evolutionary trajectory planning for an industrial robot. Int. J. Autom. Comput. 2010, 7, 190–198. [Google Scholar] [CrossRef]
- Gonzalez, C.; Blanco, D.; Moreno, L. Optimum robot manipulator path generation using Differential Evolution. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 3322–3329. [Google Scholar] [CrossRef]
- Das, S.D.; Bain, V.; Rakshit, P. Energy Optimized Robot Arm Path Planning Using Differential Evolution in Dynamic Environment. In Proceedings of the 2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 14–15 June 2018; pp. 1267–1272. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J.; Fang, J.; Yuan, J. Optimal trajectory planning of free-floating space manipulator using differential evolution algorithm. Adv. Space Res. 2018, 61, 1525–1536. [Google Scholar] [CrossRef]
- Muñoz, J.; López, B.; Quevedo, F.; Barber, R.; Garrido, S.; Moreno, L. Geometrically constrained path planning for robotic grasping with Differential Evolution and Fast Marching Square. Robotica 2023, 41, 414–432. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report, Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Jin, F.; Shu, G. Path planning of free-flying space robot based on artificial bee colony algorithm. In Proceedings of the 2012 2nd International Conference on Computer Science and Network Technology, Changchun, China, 29–31 December 2012; pp. 505–508. [Google Scholar] [CrossRef]
- Savsani, P.; Jhala, R.; Savsani, V. Optimized trajectory planning of a robotic arm using teaching learning based optimization (TLBO) and artificial bee colony (ABC) optimization techniques. In Proceedings of the 2013 IEEE International Systems Conference (SysCon), Orlando, FL, USA, 15–18 April 2013; pp. 381–386. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, J.; Zhang, Z.; Li, X. Motion Planning of Dual-Chain Manipulator Based on Artificial Bee Colony Algorithm. In Proceedings of the 2023 9th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 21–23 April 2023; pp. 55–60. [Google Scholar] [CrossRef]
- Szczepanski, R.; Erwinski, K.; Tejer, M.; Bereit, A.; Tarczewski, T. Optimal scheduling for palletizing task using robotic arm and artificial bee colony algorithm. Eng. Appl. Artif. Intell. 2022, 113, 104976. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, L.; Shao, Z. Path Planning for Obstacle Avoidance of Manipulators Based on Improved Artificial Potential Field. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zhao, X.; Zhao, P.; He, L. Time-optimal trajectory planning of serial manipulator based on adaptive cuckoo search algorithm. J. Mech. Sci. Technol. 2021, 35, 3171–3181. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, C.; Li, S.; Li, Z. Motion Planning of Redundant Manipulator With Variable Joint Velocity Limit Based on Beetle Antennae Search Algorithm. IEEE Access 2020, 8, 138788–138799. [Google Scholar] [CrossRef]
- Zhang, X.; Ming, Z. Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption. Appl. Sci. 2019, 9, 2770. [Google Scholar] [CrossRef]
- Wang, T.; Xin, Z.; Miao, H.; Zhang, H.; Chen, Z.; Du, Y. Optimal Trajectory Planning of Grinding Robot Based on Improved Whale Optimization Algorithm. Math. Probl. Eng. 2020, 2020, 3424313. [Google Scholar] [CrossRef]
- Camacho-Villalón, C.L.; Dorigo, M.; Stützle, T. Exposing the grey wolf, moth-flame, whale, firefly, bat, and antlion algorithms: Six misleading optimization techniques inspired by bestial metaphors. Int. Trans. Oper. Res. 2023, 30, 2945–2971. [Google Scholar] [CrossRef]
- Wichapong, K.; Pholdee, N.; Bureerat, S.; Radpukdee, T. Trajectory planning of a 6D robot based on Meta Heuristic algorithms. In Proceedings of the MATEC Web of Conferences, EDP Sciences, Moscow, Russia, 21–23 June 2018; Volume 220, p. 06004. [Google Scholar]
- Hansen, N. The CMA Evolution Strategy: A Tutorial. arXiv 2016, arXiv:1604.00772. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; IEEE: New York, NY, USA, 2014; pp. 1658–1665. [Google Scholar]
- Kůdela, J.; Juříček, M.; Parák, R. A Collection of Robotics Problems for Benchmarking Evolutionary Computation Methods. In Proceedings of the International Conference on the Applications of Evolutionary Computation (Part of EvoStar), Brno, Czech Republic, 12–14 April 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 364–379. [Google Scholar]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K.; Awad, N.H. Evaluating the performance of adaptive gainingsharing knowledge based algorithm on cec 2020 benchmark problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; IEEE: New York, NY, USA, 2020; pp. 1–8. [Google Scholar]
- Hellwig, M.; Beyer, H.G. Benchmarking evolutionary algorithms for single objective real-valued constrained optimization–a critical review. Swarm Evol. Comput. 2019, 44, 927–944. [Google Scholar] [CrossRef]
- Kudela, J.; Juricek, M. Computational and Exploratory Landscape Analysis of the GKLS Generator. In Proceedings of the GECCO ’23 Companion: Proceedings of the Companion Conference on Genetic and Evolutionary Computation, Lisbon, Portugal, 15–19 July 2023; pp. 443–446. [Google Scholar]
- Brest, J.; Maučec, M.S.; Bošković, B. Single objective real-parameter optimization: Algorithm jSO. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 1311–1318. [Google Scholar] [CrossRef]
- Bujok, P.; Tvrdík, J.; Poláková, R. Comparison of nature-inspired population-based algorithms on continuous optimisation problems. Swarm Evol. Comput. 2019, 50, 100490. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. New benchmark functions for single-objective optimization based on a zigzag pattern. IEEE Access 2022, 10, 8262–8278. [Google Scholar] [CrossRef]
- Del Ser, J.; Osaba, E.; Martinez, A.D.; Bilbao, M.N.; Poyatos, J.; Molina, D.; Herrera, F. More is not always better: Insights from a massive comparison of meta-heuristic algorithms over real-parameter optimization problems. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence (SSCI), Virtual, 5–7 December 2021; IEEE: New York, NY, USA, 2021; pp. 1–7. [Google Scholar]
- Kudela, J.; Zalesak, M.; Charvat, P.; Klimes, L.; Mauder, T. Assessment of the performance of metaheuristic methods used for the inverse identification of effective heat capacity of phase change materials. Expert Syst. Appl. 2023, 238, 122373. [Google Scholar] [CrossRef]
- Kudela, J. Chance-Constrained Optimization Formulation for Ship Conceptual Design: A Comparison of Metaheuristic Algorithms. Computers 2023, 12, 225. [Google Scholar] [CrossRef]
- Bujok, P.; Lacko, M.; Kolenovskỳ, P. Differential Evolution and Engineering Problems. MENDEL J. 2023, 29, 45–54. [Google Scholar] [CrossRef]
- Hansen, N.; Auger, A.; Ros, R.; Mersmann, O.; Tušar, T.; Brockhoff, D. COCO: A Platform for Comparing Continuous Optimizers in a Black-Box Setting. Optim. Methods Softw. 2021, 36, 114–144. [Google Scholar] [CrossRef]
- Jakobi, N. Evolutionary robotics and the radical envelope-of-noise hypothesis. Adapt. Behav. 1997, 6, 325–368. [Google Scholar] [CrossRef]
- Koos, S.; Mouret, J.B.; Doncieux, S. The transferability approach: Crossing the reality gap in evolutionary robotics. IEEE Trans. Evol. Comput. 2012, 17, 122–145. [Google Scholar] [CrossRef]
- Salvato, E.; Fenu, G.; Medvet, E.; Pellegrino, F.A. Crossing the reality gap: A survey on sim-to-real transferability of robot controllers in reinforcement learning. IEEE Access 2021, 9, 153171–153187. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, H.; Chugh, T.; Guo, D.; Miettinen, K. Data-driven evolutionary optimization: An overview and case studies. IEEE Trans. Evol. Comput. 2018, 23, 442–458. [Google Scholar] [CrossRef]
- Kudela, J.; Matoušek, R. Combining Lipschitz and RBF surrogate models for high-dimensional computationally expensive problems. Inf. Sci. 2023, 619, 457–477. [Google Scholar] [CrossRef]
- Kononova, A.V.; Vermetten, D.; Caraffini, F.; Mitran, M.A.; Zaharie, D. The Importance of Being Constrained: Dealing with Infeasible Solutions in Differential Evolution and Beyond. Evol. Comput. 2023, 1–46. [Google Scholar] [CrossRef] [PubMed]
- Corke, P.; Haviland, J. Not your grandmother’s toolbox–the Robotics Toolbox reinvented for Python. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May– 5 June 2021; IEEE: New York, NY, USA, 2021; pp. 11357–11363. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).