Abstract
The problem of finding the global minimum of a function is applicable to a multitude of real-world problems and, hence, a variety of computational techniques have been developed to efficiently locate it. Among these techniques, evolutionary techniques, which seek, through the imitation of natural processes, to efficiently obtain the global minimum of multidimensional functions, play a central role. An evolutionary technique that has recently been introduced is the Optimal Foraging Algorithm, which is a swarm-based algorithm, and it is notable for its reliability in locating the global minimum. In this work, a series of modifications are proposed that aim to improve the reliability and speed of the above technique, such as a termination technique based on stochastic observations, an innovative sampling method and a technique to improve the generation of offspring. The new method was tested on a series of problems from the relevant literature and a comparative study was conducted against other global optimization techniques with promising results.
1. Introduction
The basic goal of global optimization is to find the global minimum by searching for the appropriate scope of each problem. Primarily, a global optimization method aims to discover the global minimum of a continuous function, and it is defined as
with S defined as
Global optimization is a core part of applied mathematics [1] and computer science [2]. Additionally, it finds application in various fields such as physics [3,4,5], chemistry [6,7,8], economics [9,10], medicine [11,12], etc. Optimization methods are divided into deterministic and stochastic [13]. Deterministic methods guarantee finding the global optimal solution and are usually applied to small problems [14]. The most commonly used techniques in the first category are the so-called interval techniques [15,16], which divide the initial domain of the function until they discover a promising subset that may contain the global minimum. On the other hand, stochastic methods do not guarantee finding the global minimum and are mainly applied to large problems, but they are inefficient when nonlinear equality constraints are involved. Stochastic methods include a variety of techniques, such as Controlled Random Search methods [17,18,19], Simulated Annealing methods [20,21,22], methods based on the Multistart technique [23,24], etc. Furthermore, in the recent literature, a variety of hybrid methods have appeared that combine different optimization techniques [25,26]. Furthermore, due to the widespread usage of parallel programming architectures, a variety of methods have been proposed that take advantage of such systems [27,28,29,30].
The above techniques present various problems that have had to be addressed by researchers, such as, for example, the initialization of the possible solutions, the termination rules, etc. A number of researchers have dealt with the topic of the initialization of candidate solutions and have proposed techniques such as the repulsion method [31], an adaptive sampling method using the Kriging model [32], Monte Carlo-based sampling methods [33], a method which utilizes an Radial Basis Function (RBF) network [34] to obtain samples [35] etc. Additionally, in the direction of termination methods, a series of techniques have been proposed, such as sequential stopping rules [36], a stopping rule based on asymptotic considerations [37], a stopping rule that utilizes the likelihood of obtaining the specific set of solutions [38], etc.
An important group of stochastic techniques that has attracted the interest of many researchers is the group of evolutionary techniques. The branch of evolutionary computing includes the study of the foundations and applications of computational techniques based on the principles of natural evolution. Evolution in nature is responsible for the “design” of all living things on earth and the strategies they use to interact with each other. This branch of methods includes Differential Evolution methods [39,40], Particle Swarm Optimization (PSO) methods [41,42,43], Ant Colony optimization methods [44,45], genetic algorithms [46,47], etc. Zhu and Zhang proposed a novel method in this area that tackles optimization problems with a strategy based on animal foraging behavior [48]. This Optimal Foraging Algorithm (OFA) is a swarm-based algorithm motivated by animal behavioral ecology. Furthermore, Fu et al. proposed a variation of the OFA algorithm with the incorporation of the Differential Evolution technique [49]. Additionally, Jian and Zhu proposed a modification of the OFA algorithm with direction prediction [50] in order to enhance the performance of the original algorithm. Recently, Chen Ding and Guang Yu Zhu introduced an improved quasi-adversarial optimal social behavior search algorithm (QOS-OFA) to handle optimization problems [51].
The current work introduces a series of modifications to the OFA algorithm in order to speed up the process and to increase the effectiveness of the algorithm. These modifications include the following:
- The incorporation of a sampling technique that utilizes the K-means method [52]. The points that are sampled will more accurately and quickly lead to the global minimum of the function and additional points that might have been close enough using another sampling technique are discarded.
- The use of a termination technique based on stochastic observations. At each iteration of the algorithm, the smallest functional value is recorded. If this remains constant for a predetermined number of iterations, then the method terminates. This way, the method will terminate in time without needlessly wasting computing time on iterations that will simply produce the same result.
- The improvement of the offspring produced by the method using a few steps of a local minimization method. In the current work, a BFGS variant [53] was used as a local search procedure.
2. The Proposed Method
The OFA algorithm uses nature as a source of inspiration. The OFA algorithm has as its main purpose the evolution of the population using some iterative steps which will be presented in more detail below. The quality of the initial population can be improved, allowing the search space to be explored more efficiently. The first major modification introduced to the above technique is the use of a sophisticated technique of sampling points from the objective function. This sampling is based on the K-means technique and is presented in detail in Section 2.2. The second modification is to apply a few steps of a local search procedure in offspring creation if an offspring is not consistent with the bounds of the objective function . With this modification, it is ensured that a new point will be within the field definition of the function on the one hand, and on the other hand, it will have a slightly lower value than its predecessor. The third modification is to use an efficient termination rule to terminate the global optimization method effectively. This termination rule is outlined in Section 2.3.
2.1. The Main Steps of the Algorithm
The main steps of the used global optimization method are the following:
- Initialization step.
- (a)
- Define as the number of elements in the population.
- (b)
- Define as the maximum number of allowed iterations.
- (c)
- Initialize randomly the members of the population in set S. This forms the initial population denoted as P. The sampling is performed using the procedure in Section 2.2.
- (d)
- Create the QOP population, which stands for the quasi-opposite population of P, by calculating the quasi-opposite positions of P.
- (e)
- Set , the iteration number.
- (f)
- Select the fittest solutions from the population set using the QOBL method proposed in [51].
- Calculation step.
- (a)
- Produce the new offspring solutions based on the ranking order using the following equation:where are random numbers in and is a randomly selected solution from the population. The function is defined as
- (b)
- For , do
- i.
- If then . This step applies a limited number of steps of a local search procedure LS(x) to the current point. The parameter denotes the number of steps for the local search procedure. In the current work, the BFGS local optimization procedure is used, but other local search methods could be employed such as Gradient Descent [54], Steepest Descent [55], etc.
- ii.
- if then select for the next population else select . The values are uniformly distributed random numbers in .
- (c)
- End For.
- (d)
- Sort all solutions in the current population from the best to worst according to the function value.
- Termination check step.
- (a)
- Set .
- (b)
- Calculate to stopping rule in the work of Charilogis [56]. This termination method is described in Section 2.3.
- (c)
- If the termination criteria are not met then go to Calculation step, else terminate.
The steps of the proposed method are also graphically shown in Figure 1.
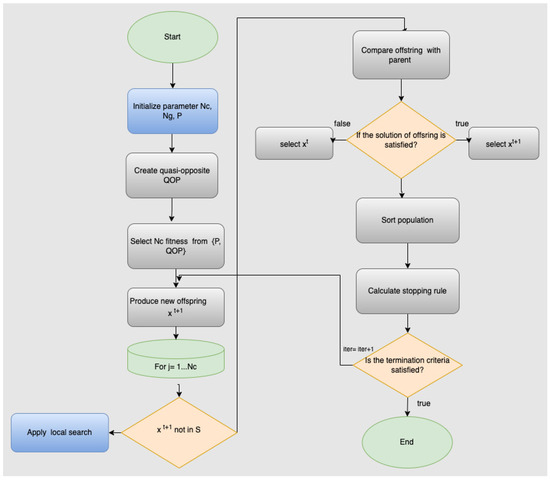
Figure 1.
The steps of the proposed method.
2.2. The Proposed Sampling Procedure
The proposed sampling technique initially produces a series of samples from the objective function and, subsequently, through the application of the K-means technique, only the located centers are considered as the final samples. The method was introduced by James MacQueen [57] and it is a clustering algorithm that has been used in data analysis and machine learning in a variety of research papers [58,59]. The algorithm seeks to estimate the centers of possible teams in a set of samples and its main steps are listed as follows:
- Define as k the number of clusters.
- Draw randomly initial points from the objective function.
- Assign randomly each point in a cluster .
- For every cluster do
- (a)
- Set as the number of points in .
- (b)
- Compute the center of the cluster as
- EndFor.
- Repeat
- (a)
- Set .
- (b)
- For each point do
- i.
- Set . The function is the Euclidean distance of points .
- ii.
- Set .
- (c)
- EndFor.
- (d)
- For each center do
- i.
- Update the center as
- (e)
- EndFor.
- If there is no significant change in centers terminate the algorithm and return the k centers as the final set of samples.
2.3. The Termination Rule Used
At every iteration t, the difference between the current best value and the previous best value is computed:
The algorithm terminates when for a series of predefined consecutive iterations , where is a small positive number, for example .
3. Results
This section will begin with a detailed description of the functions that will be used in the experiments, followed by an analysis of the experiments performed and comparisons with other global optimization techniques.
3.1. Test Functions
The functions used in the experiments have been proposed in a series of relative works [60,61] and they cover various scientific fields, such as medicine, physics, engineering, etc. Furthermore, these objective functions have been used by many researchers in a variety of publications [62,63,64,65,66]. The definitions of these functions are given below:
- Ackley function:where a = 20.0.
- Bf1 (Bohachevsky 1) function:
- Bf2 (Bohachevsky 2) function:
- Bf3 (Bohachevsky 3) function:
- Branin function: with .
- Camel function:
- Easom function:with
- Exponential function, defined asIn the conducted experiments, the values were used.
- ExtendedF10 function:
- F12 function:whereand
- F14 function:
- F15 function:
- F17 function:
- Griewank2 function:
- Griewank10 function: the function is given by the equationwith .
- Gkls function: is a constructed function with w local minima presented in [67], with . For the conducted experiments, the values and were utilized.
- Goldstein and Price function:with .
- Hansen function: , .
- Hartman 3 function:with and and
- Hartman 6 function:with and and
- Potential function: This function stands for the energy of a molecular conformation of N atoms that interacts via the Lennard-Jones potential [68]. The function is defined asFor the conducted experiments, the values were used.
- Rastrigin function:
- Rosenbrock function:The values were used in the conducted experiments.
- Shekel 5 function:
- Shekel 7 function:
- Shekel 10 function:
- Sinusoidal function, defined asThe values were used in the conducted experiments.
- Sphere function:
- Schwefel function:
- Schwefel 2.21 function:
- Schwefel 2.22 function:
- Test2N function:For the conducted experiments, the values were used.
- Test30N function:The values were used in the conducted experiments.
3.2. Experimental Results
A series of experiments was performed using the test functions presented previously. Every experiment was conducted 30 times using different seeds for the random generator each time. The averages of function calls were measured and are presented in the following tables. The software was coded in ANSI C++ with the assistance of the OPTIMUS optimization package, which is freely available from https://github.com/itsoulos/OPTIMUS (accessed on 2 July 2024). The values for the experimental parameters are shown in Table 1. Generally, the region of attraction of a local minimum is defined as
where is a local search procedure, such as BFGS. Global optimization methods usually find points which are in the region of attraction of a local minimum but not necessarily the local minimum itself. For this reason, at the end of their execution, a local minimization method is applied in order to ensure the exact finding of a local minimum. Of course, this does not imply that the minimum that will be located will be the total minimum of the function, since a function can contain tens or even hundreds of local minima.

Table 1.
Experimental settings. The numbers in cells denote the values used in the experiments for all parameters.
The following applies to Table 2:

Table 2.
Experimental results using different optimization methods. Numbers in cells represent average function calls.
- The column FUNCTION denotes the name of the objective problem.
- The column GENETIC denotes the application of a genetic algorithm to the objective problem. The genetic algorithm has chromosomes and the maximum number of allowed generations was set to .
- The column PSO stands for the application of Particle Swarm Optimizer to every objective problem. The number of particles was set to and the maximum number of allowed iterations was set to .
- The column EOFA represents the application of the proposed method using the values for the parameters shown in Table 1.
- The row SUM represents the sum of function calls for all test functions.
A statistical comparison of these results is also outlined in Figure 2.
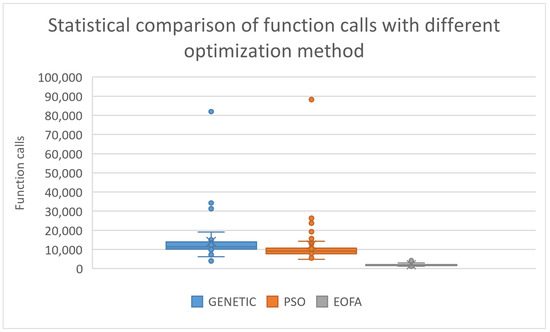
Figure 2.
Statistical representation of the function calls for different optimization methods.
As can be seen, the present method drastically reduces the required number of function calls to almost all objective functions. This, of course, also results in a significant reduction in the required computing time to find the global minimum. Furthermore, a scatter plot for the used optimization methods is shown in Figure 3, which also depicts the superiority of the current method.
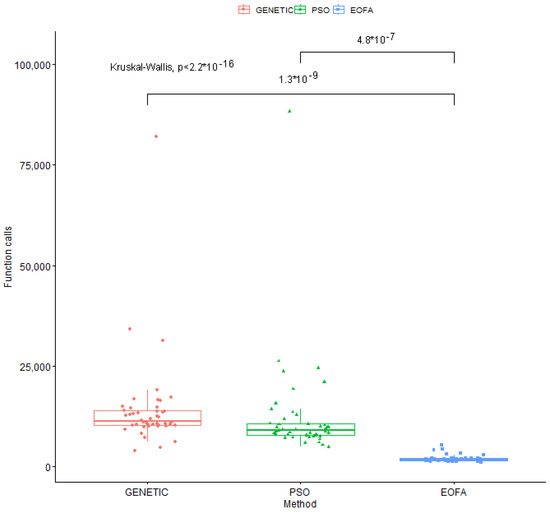
Figure 3.
Scatter plot representation of optimization methods with Kruskal–Wallis Ranking.
Furthermore, an additional experiment was conducted in order to measure the importance of the K-means sampling in the proposed method. In this test, three different sampling methods were used in the proposed method:
- The column UNIFORM stands for the application of uniform sampling in the proposed method.
- The column TRIANGULAR represents the application of the triangular distribution [69] to sample the initial points of the proposed method.
- The column KMEANS represents the sampling method presented in the current work.
The experimental results for this test are shown in Table 3.

Table 3.
Experiments using different sampling techniques for the proposed method.
The statistical comparison for the previous experiment is graphically outlined in Figure 4. The proposed sampling method significantly outperforms the remaining sampling techniques in almost all problems. Furthermore, the proposed global optimization technique outperforms the rest of the compared techniques, even if a different sampling technique is used.
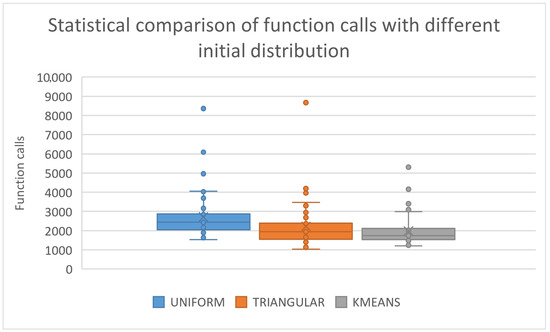
Figure 4.
Statistical representation for different sampling methods.
Moreover, a scatter plot representation of the used distributions with Kruskal–Wallis Ranking is depicted in Figure 5.
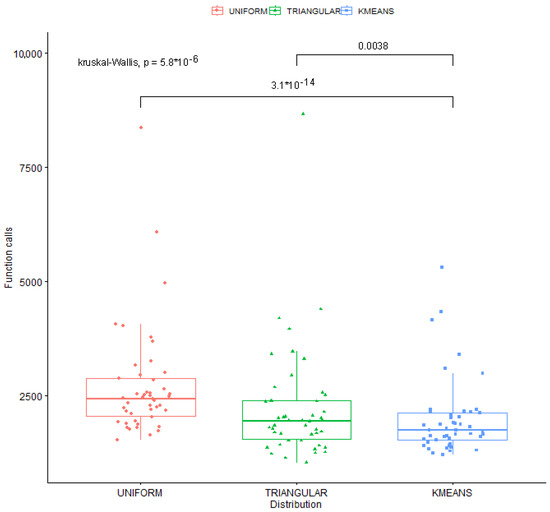
Figure 5.
Scatter plot representation of the used distributions with Kruskal–Wallis Ranking.
In this test, the p-value remains very low at any level of significance. Consequently, the null hypothesis is rejected, indicating that the experimental tests are statistically significant.
Furthermore, an additional test was carried out, where the function ELP was used to measure the effectiveness of the proposed method as the dimension increased. This function is defined as
where the parameter n defines the dimension of the function. A comparison between the genetic algorithm and the proposed method as n increases is shown in Figure 6.
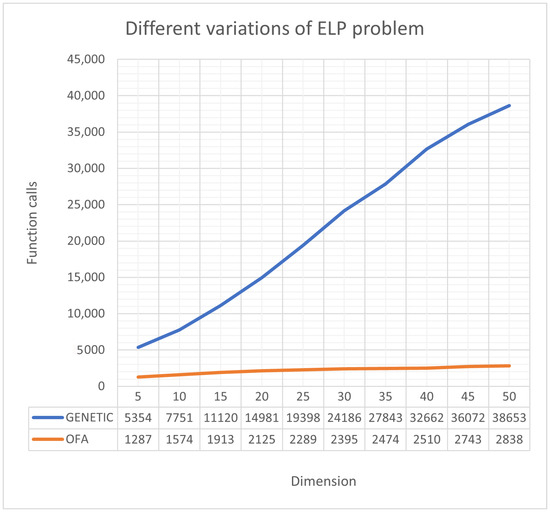
Figure 6.
Different variations of the ELP problem.
The required number of calls for the current method increases at a much lower rate than in the case of the genetic algorithm. This means that the method can cope with large-scale problems without significantly increasing the required computing time.
4. Conclusions
Three modifications were proposed to the EOFA optimization method in this article. The modifications were primarily aimed at improving the efficiency and speed of the global optimization algorithm. The first modification proposed the application of a sampling technique which incorporates the K-means method [52]. With the proposed modification, the points where the sampling was achieved helped to find the global minimum with the greatest accuracy and in the least possible time. The second amendment concerned termination rules. Termination rules help terminate functions immediately without unnecessarily wasting computational time on iterations. The third modification concerned the refinement of the offspring produced using the BFGS method [53] as a local search procedure. In the experiments conducted, different sampling techniques were used for the proposed method. More specifically, the following techniques were used: Uniform, Triangular and K-means. It was found that the K-means sampling technique yields much better results than the other two techniques and the total number of calls is extremely lower.
Experiments were also performed using different optimization methods. More specifically, the following were used: genetic, PSO and EOFA. It was observed that the average number of EOFA calls is very limited compared to the other two.
Since the experimental results have been shown to be extremely promising, further efforts can be made to develop the technique in various areas. Among the future extensions of the application may be the use of parallel computing techniques to speed up the optimization process, such as the integration of MPI [70] or the OpenMP library [71].
Author Contributions
G.K., V.C. and I.G.T. conceived of the idea and the methodology, and G.K. and V.C. implemented the corresponding software. G.K. conducted the experiments, employing objective functions as test cases, and provided the comparative experiments. I.G.T. performed the necessary statistical tests. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
This research was financed by the European Union: Next Generation EU through the Program Greece 2.0 National Recovery and Resilience Plan, under the call RESEARCH–CREATE–INNOVATE, project name “iCREW: Intelligent small craft simulator for advanced crew training using Virtual Reality techniques” (project code: TAEDK-06195).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Intriligator, M.D. Mathematical Optimization and Economic Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Törn, A.; Ali, M.M.; Viitanen, S. Stochastic global optimization: Problem classes and solution techniques. J. Glob. Optim. 1999, 14, 437–447. [Google Scholar] [CrossRef]
- Yang, L.; Robin, D.; Sannibale, F.; Steier, C.; Wan, W. Global optimization of an accelerator lattice using multiobjective genetic algorithms. Nucl. Instrum. Methods Phys. Res. Accel. Spectrometers Detect. Assoc. Equip. 2009, 609, 50–57. [Google Scholar] [CrossRef]
- Iuliano, E. Global optimization of benchmark aerodynamic cases using physics-based surrogate models. Aerosp. Sci. Technol. 2017, 67, 273–286. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Heiles, S.; Johnston, R.L. Global optimization of clusters using electronic structure methods. Int. J. Quantum Chem. 2013, 113, 2091–2109. [Google Scholar] [CrossRef]
- Shin, W.H.; Kim, J.K.; Kim, D.S.; Seok, C. GalaxyDock2: Protein–ligand docking using beta-complex and global optimization. J. Comput. Chem. 2013, 34, 2647–2656. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Lee, J.; Ripoll, D.R.; Pillardy, J.; Scheraga, H.A. Protein structure prediction by global optimization of a potential energy function. Biophysics 1999, 96, 5482–5485. [Google Scholar] [CrossRef] [PubMed]
- Gaing, Z.-L. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Maranas, C.D.; Androulakis, I.P.; Floudas, C.A.; Berger, A.J.; Mulvey, J.M. Solving long-term financial planning problems via global optimization. J. Econ. Dyn. Control 1997, 21, 1405–1425. [Google Scholar] [CrossRef]
- Lee, E.K. Large-Scale Optimization-Based Classification Models in Medicine and Biology. Ann. Biomed. Eng. 2007, 35, 1095–1109. [Google Scholar] [CrossRef]
- Cherruault, Y. Global optimization in biology and medicine. Math. Comput. Model. 1994, 20, 119–132. [Google Scholar] [CrossRef]
- Liberti, L.; Kucherenko, S. Comparison of deterministic and stochastic approaches to global optimization. Int. Trans. Oper. Res. 2005, 12, 263–285. [Google Scholar] [CrossRef]
- Choi, S.H.; Manousiouthakis, V. Global optimization methods for chemical process design: Deterministic and stochastic approaches. Korean J. Chem. Eng. 2002, 19, 227–232. [Google Scholar] [CrossRef]
- Wolfe, M.A. Interval methods for global optimization. Appl. Math. Comput. 1996, 75, 179–206. [Google Scholar]
- Csendes, T.; Ratz, D. Subdivision Direction Selection in Interval Methods for Global Optimization. SIAM J. Numer. Anal. 1997, 34, 922–938. [Google Scholar] [CrossRef]
- Price, W.L. Global optimization by controlled random search. J. Optim. Theory Appl. 1983, 40, 333–348. [Google Scholar] [CrossRef]
- Krivy, I.; Tvrdik, J. The controlled random search algorithm in optimizing regression models. Comput. Stat. Data Anal. 1995, 20, 229–234. [Google Scholar] [CrossRef]
- Ali, M.M.; Torn, A.; Viitanen, S. A Numerical Comparison of Some Modified Controlled Random Search Algorithms. J. Glob. Optim. 1997, 11, 377–385. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
- Eglese, R.W. Simulated annealing: A tool for operational research. Simulated Annealing Tool Oper. Res. 1990, 46, 271–281. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Lagaris, I.E. MinFinder: Locating all the local minima of a function. Comput. Phys. Commun. 2006, 174, 166–179. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, P. A multi-start central force optimization for global optimization. Appl. Soft Comput. 2015, 27, 92–98. [Google Scholar] [CrossRef]
- Perez, M.; Almeida, F.; Moreno-Vega, J.M. Genetic algorithm with multistart search for the p-Hub median problem. In Proceedings of the 24th EUROMICRO Conference (Cat. No. 98EX204), Vasteras, Sweden, 27 August 1998; Volume 2, pp. 702–707. [Google Scholar]
- Oliveira, H.C.B.d.; Vasconcelos, G.C.; Alvarenga, G. A Multi-Start Simulated Annealing Algorithm for the Vehicle Routing Problem with Time Windows. In Proceedings of the 2006 Ninth Brazilian Symposium on Neural Networks (SBRN’06), Ribeirao Preto, Brazil, 23–27 October 2006; pp. 137–142. [Google Scholar]
- Larson, J.; Wild, S.M. Asynchronously parallel optimization solver for finding multiple minima. Math. Program. Comput. 2018, 10, 303–332. [Google Scholar] [CrossRef]
- Bolton, H.P.J.; Schutte, J.F.; Groenwold, A.A. Multiple Parallel Local Searches in Global Optimization. In Recent Advances in Parallel Virtual Machine and Message Passing Interface; EuroPVM/MPI 2000. Lecture Notes in Computer Science; Dongarra, J., Kacsuk, P., Podhorszki, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1908. [Google Scholar]
- Kamil, R.; Reiji, S. An Efficient GPU Implementation of a Multi-Start TSP Solver for Large Problem Instances. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; pp. 1441–1442. [Google Scholar]
- Van Luong, T.; Melab, N.; Talbi, E.G. GPU-Based Multi-start Local Search Algorithms. In Learning and Intelligent Optimization. LION 2011; Lecture Notes in Computer Science; Coello, C.A.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6683. [Google Scholar]
- Sepulveda, A.E.; Epstein, L. The repulsion algorithm, a new multistart method for global optimization. Struct. Optim. 1996, 11, 145–152. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, H.; Gao, L.; Li, X.; Li, P. A local adaptive sampling method for reliability-based design optimization using Kriging model. Struct. Multidisc. Optim. 2014, 49, 401–416. [Google Scholar] [CrossRef]
- Homem-de-Mello, T.; Bayraksan, G. Monte Carlo sampling-based methods for stochastic optimization. Surv. Oper. Res. Manag. Sci. 2014, 19, 56–85. [Google Scholar] [CrossRef]
- Park, J.; Sandberg, I.W. Universal Approximation Using Radial-Basis-Function Networks. Neural Comput. 1991, 3, 246–257. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Tzallas, A.; Tsalikakis, D. Use RBF as a Sampling Method in Multistart Global Optimization Method. Signals 2022, 3, 857–874. [Google Scholar] [CrossRef]
- Hart, W.E. Sequential stopping rules for random optimization methods with applications to multistart local search. SIAM J. Optim. 1998, 9, 270–290. [Google Scholar] [CrossRef]
- Tsoulos, I.G. Modifications of real code genetic algorithm for global optimization. Appl. Math. Comput. 2008, 203, 598–607. [Google Scholar] [CrossRef]
- Ohsaki, M.; Yamakawa, M. Stopping rule of multi-start local search for structural optimization. Struct. Multidisc. Optim. 2018, 57, 595–603. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liu, J.; Lampinen, J. A Fuzzy Adaptive Differential Evolution Algorithm. Soft Comput. 2005, 9, 448–462. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization An Overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Company: Reading, MA, USA, 1989. [Google Scholar]
- Michaelewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Zhu, G.Y.; Zhang, W.B. Optimal foraging algorithm for global optimization. Appl. Soft Comput. 2017, 51, 294–313. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, W.; Qu, C.; Huang, B. Optimal Foraging Algorithm Based on Differential Evolution. IEEE Access 2020, 8, 19657–19678. [Google Scholar] [CrossRef]
- Jian, Z.; Zhu, G. Optimal foraging algorithm with direction prediction. Appl. Soft Comput. 2021, 111, 107660. [Google Scholar] [CrossRef]
- Ding, C.; Zhu, G. Improved optimal foraging algorithm for global optimization. Computing 2024, 106, 2293–2319. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means algorithm: A comprehensive survey and performance evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Amari, S.I. Backpropagation and stochastic gradient descent method. Neurocomputing 1993, 5, 185–196. [Google Scholar] [CrossRef]
- Meza, J.C. Steepest descent. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 719–722. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.G. Toward an Ideal Particle Swarm Optimizer for Multidimensional Functions. Information 2022, 13, 217. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some Methods for classification and Analysis of Multivariate Observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June–18 July 1967; pp. 281–297. [Google Scholar]
- Li, Y.; Wu, H. A clustering method based on K-means algorithm. Phys. Procedia 2012, 25, 1104–1109. [Google Scholar] [CrossRef]
- Arora, P.; Varshney, S. Analysis of k-means and k-medoids algorithm for big data. Procedia Comput. Sci. 2016, 78, 507–512. [Google Scholar] [CrossRef]
- Montaz Ali, M. Charoenchai Khompatraporn, Zelda B. Zabinsky, A Numerical Evaluation of Several Stochastic Algorithms on Selected Continuous Global Optimization Test Problems. J. Glob. Optim. 2005, 31, 635–672. [Google Scholar]
- Floudas, C.A.; Pardalos, P.M.; Adjiman, C.; Esposoto, W.; Gümüs, Z.; Harding, S.; Klepeis, J.; Meyer, C.; Schweiger, C. Handbook of Test Problems in Local and Global Optimization; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Ali, M.M.; Kaelo, P. Improved particle swarm algorithms for global optimization. Appl. Math. Comput. 2008, 196, 578–593. [Google Scholar] [CrossRef]
- Koyuncu, H.; Ceylan, R. A PSO based approach: Scout particle swarm algorithm for continuous global optimization problems. J. Comput. Des. Eng. 2019, 6, 129–142. [Google Scholar] [CrossRef]
- Siarry, P.; Berthiau, G.; Durdin, F.; Haussy, J. Enhanced simulated annealing for globally minimizing functions of many-continuous variables. ACM Trans. Math. Softw. 1997, 23, 209–228. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Lagaris, I.E. GenMin: An enhanced genetic algorithm for global optimization. Comput. Phys. Commun. 2008, 178, 843–851. [Google Scholar] [CrossRef]
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Del Ser, J.; Herrera, F. A prescription of methodological guidelines for comparing bio-inspired optimization algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Gaviano, M.; Ksasov, D.E.; Lera, D.; Sergeyev, Y.D. Software for generation of classes of test functions with known local and global minima for global optimization. ACM Trans. Math. Softw. 2003, 29, 469–480. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the Determination of Molecular Fields. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar]
- Stein, W.E.; Keblis, M.F. A new method to simulate the triangular distribution. Math. Comput. Model. Vol. 2009, 49, 1143–1147. [Google Scholar] [CrossRef]
- Gropp, W.; Lusk, E.; Doss, N.; Skjellum, A. A high-performance, portable implementation of the MPI message passing interface standard. Parallel Comput. 1996, 22, 789–828. [Google Scholar] [CrossRef]
- Chandra, R. Parallel Programming in OpenMP; Morgan Kaufmann: Cambridge, MA, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).