Enhancing Algorithm Selection through Comprehensive Performance Evaluation: Statistical Analysis of Stochastic Algorithms
Abstract
:1. Introduction
- The p-value tests reveal significant performance disparities between algorithm pairs, highlighting statistical significance in the comparisons. The algorithms being compared also display statistical significance in terms of the values of their achieved solutions and their distribution. Thus, this study compares algorithms that exhibit similar abilities in both exploration and exploitation;
- Analyzing algorithm performance across a range of test functions, including classical benchmarks and CEC-C06 2019 conference functions, reveals varying effectiveness, with certain algorithms demonstrating superiority in specific contexts;
- The study assesses algorithms across various test functions to understand their suitability for different optimization challenges and seeks to identify algorithm pairs with favorable statistical distributions;
- The study investigates multiple nonparametric statistical hypothesis models, such as the Wilcoxon rank-sum test, single-factor, and two-factor analyses, to gain insights into algorithm performance across diverse evaluation criteria, improving our overall understanding of their capabilities;
- Identifying inaccuracies in previous statistical test results during algorithm comparisons, thoroughly investigating these discrepancies, and integrating the rectification process;
- The results offer valuable guidance in choosing appropriate algorithms, highlighting their proven performance in various scenarios. This supports professionals in making informed decisions when statistically evaluating algorithm pairs.
2. Related Works
3. Evaluating Performance for the Selection of the Reference Algorithm
- ▪
- The primary algorithm, DA, is often gradient descent, a common first-order optimization approach. DA employs particle-based exploration, like PSO, by initializing dragonfly positions and step vectors within variable-defined ranges using random values. It combines simplicity with elements of the stochastic gradient descent, adaptive learning rate, and conjugate gradient methods. However, DA can be sensitive to randomness and may not always converge [41];
- ▪
- WOA utilizes a multistrategy approach, combining mathematical formulations and loop structures, as demonstrated in a specific case study which was influenced by the hunting behaviors of humpback whales. Its advantages include effective strategies like prey search, prey encirclement, and spiral bubble-net movements. However, it may be computationally expensive and lacks a guarantee of reaching the global optimum [42];
- ▪
- SSA, the other algorithm of choice, exhibits resemblances to other swarm-based optimization methods, like PSO and ACO, particularly in terms of collective intelligence and exploration–exploitation mechanisms with mathematical looping. SSA is beneficial for locating optimal points, demonstrating versatility, and enhancing global exploration capability and convergence speed. However, it is prone to issues such as vulnerability to schedules, occasional entrapment in local optima, and sensitivity to mutation and crossover strategies [34];
- ▪
- FDO improves individual positions by adding velocity to their current locations, drawing from PSO principles and also influenced by bees’ swarming behavior and collaborative decision-making. However, FDO’s drawback lies in limited exploration, slow convergence, and sensitivity to proposal distribution [43];
- ▪
- LPB enhances computational complexity for high school graduates’ university transition and study behaviors using genetic algorithm operators. It is versatile and adaptable to different optimization tasks and problem domains, making it a versatile choice. However, LPB has limited exploration, slow convergence, and sensitivity to proposal distribution [44];
- ▪
- ▪
- The FOX algorithm is inspired by the hunting strategies of real foxes, employing distance measurement techniques for efficient prey pursuit. It is ideal for optimizing costly to evaluate functions with simplicity and efficiency. However, it can become computationally expensive and necessitates a careful choice of priors [33].
4. Methodological Framework for Extended Statistical Comparisons
- ▪
- Initiating the quest by delving into the article, unraveling solutions to the problem;
- ▪
- Choosing from the array of contemporary and renowned stochastic optimization algorithms;
- ▪
- Subjecting each algorithm to a rigorous evaluation, involving 30 times for each test function, to unearth the ultimate optimal solution;
- ▪
- Unveiling the statistical gems within, such as the illustrious mean, the steadfast median, and more, as they illuminate the path to standard solutions;
- ▪
- To determine the sample size for each pair of samples with respect to the chosen test function and pair of algorithms, the following should be showcased:
- ˗
- When dealing with a sample that does not conform to CLT and lacks balanced data, it is advisable to subject it to the influential Wilkson rank-sum test. If it does not pass, a reconsideration of the evaluation will be necessary;
- ˗
- For a sample that exhibits normal distributions, it should be scrutinized with the influential ANOVA F test, involving a thorough examination of variances.
- ▪
- Concluding the computation, the influence of p-values will be instrumental in appraising all test functions in alignment with the pair of algorithms. This will determine the algorithms’ performance and suitability for the task at hand.
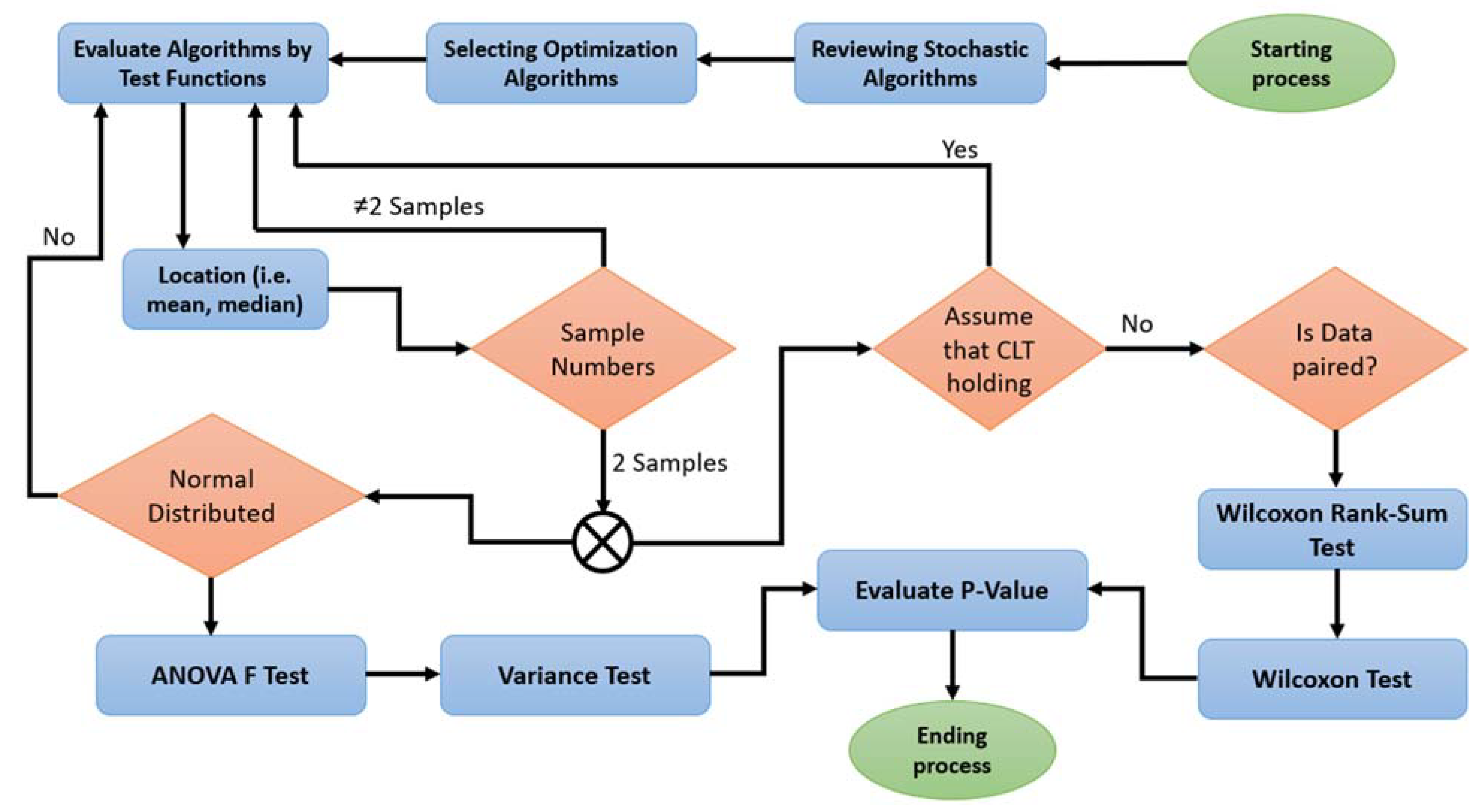
4.1. Wilkson Rank-Sum Test
- Hypothesis formulation: The hypotheses encompass the null hypothesis (), indicating that the two samples originate from populations with the same distribution, and the alternative hypothesis (), implying that the two samples arise from populations with distinct distributions.
- Combining and ranking data: Begin by consolidating the two samples into a unified dataset. Proceed to assign ranks to the combined data, arranging them in ascending order, irrespective of their source sample. In the case of tied values, allocate the average rank to these tied values.
- Calculating rank sums: Compute the sum of ranks for each sample. Denote the sum of ranks for sample one as and for sample two as .
- Calculating the test statistic (U): In this pivotal stage, our attention is captivated by the intricate calculation of the test statistic (U). This calculation takes into account the smaller rank sum and the sample sizes associated with it. However, it is important to note that this process is subject to specific conditions and limitations. The calculation U depends on the comparison of two rank sums, and , which correspond to the two groups being compared using the rank-sum ( or ) method, as we have assessed two algorithms in this study. The computation of U is illustrated by Equation (1) and as follows:where represent the number of data points in each respective sample; in our study, each sample consists of 30 data-observation points.Then:If is the smaller rank sum, then U is equal to .If is the smaller rank sum, then U is equal to .
- Calculating the expected value and variance of U: During this stage, you should compute the expected value and variance of the test statistic by employing the formula specific to the Wilcoxon rank-sum test.
- Calculating the : Determine the Z-score utilizing Formula (2). Subsequently, compute the expected value using Equation (3), and find the variance by using Equation (4).where
- Calculating the p-value and making a decision: For a two-tailed test, which involves comparing distributions for differences in both directions, calculate the p-value using the standard normal distribution linked to the absolute value of the calculated (where represents the ). Furthermore, in the context of a one-tailed test, where the aim is to compare distributions for differences in a specific direction, compute the p-value by referring to the relevant tail of the standard normal distribution as assessed through Formula (5).
4.2. Single-Factor ANOVA Table
- Determining the degrees of freedom: First, one crucial step involves determining the degrees of freedom for both the numerator, which signifies the between-group variability, and the denominator, which signifies the within-group variability, of the F-statistic. This process is elaborated upon in Figure 2.
- Employing the observed F-statistic: Next, utilize the observed F-statistic alongside the degrees-of-freedom values. You can then either consult an F-distribution table or employ statistical software to precisely calculate the p-value.
- Comparison with the significance level: Finally, compare the calculated p-value with a selected significance level (alpha), often set at α = 0.05. This comparison determines if the obtained outcome holds statistical significance. Should the p-value be lower than the significance level, the null hypothesis is rejected.
4.3. Two-Factor ANOVA Table
5. Result and Statistical Analysis
5.1. Statistical Assessment of Classical Benchmark Test Functions
5.1.1. Unimodal Benchmark Test Functions
5.1.2. Multimodal Benchmark Test Functions
5.1.3. Composite Benchmark Test Functions
5.2. Statistical Assessment of CEC-C06 2019 Benchmark Test Functions
5.3. Algorithmic Time-Complexity Analysis
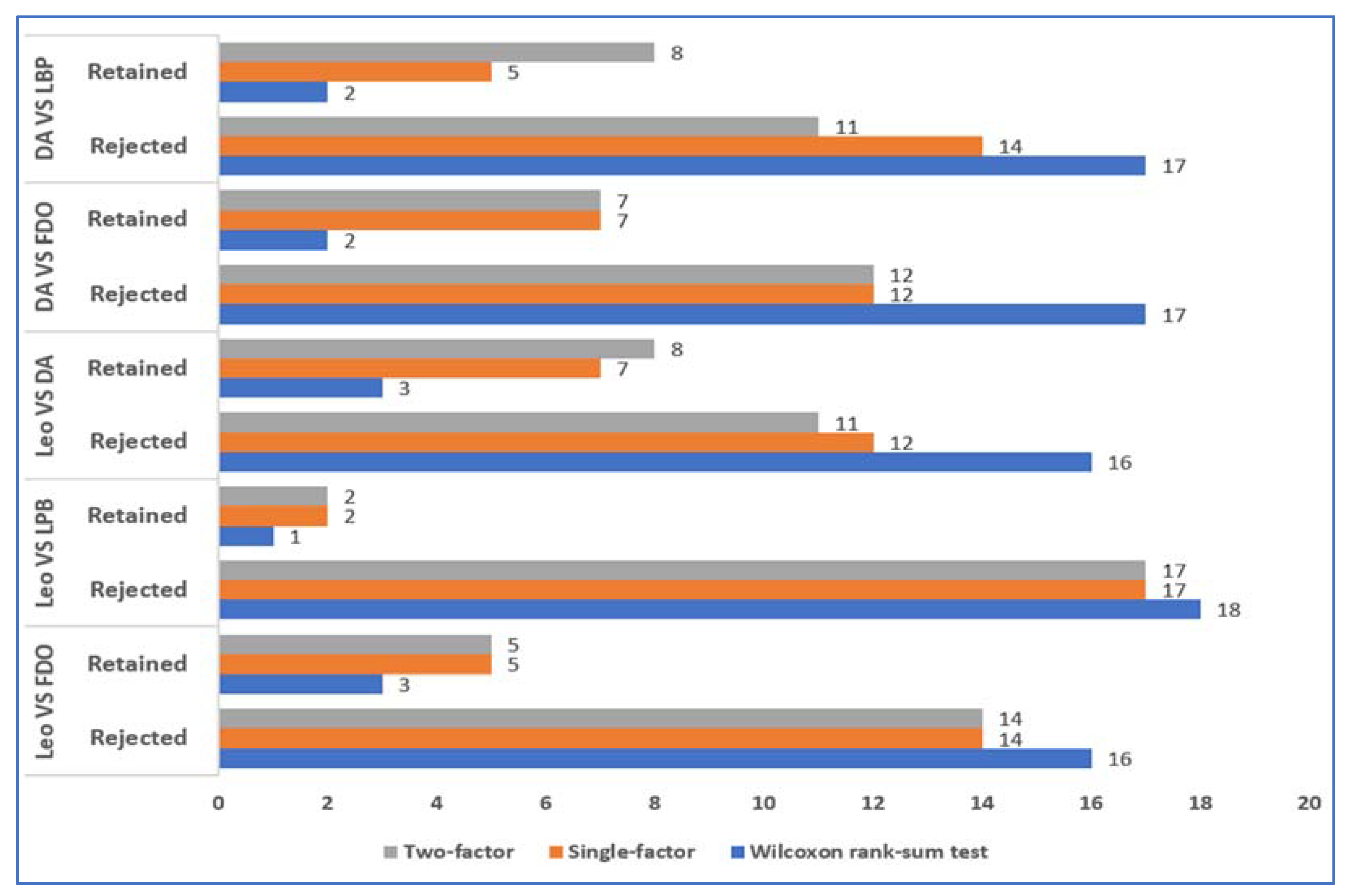
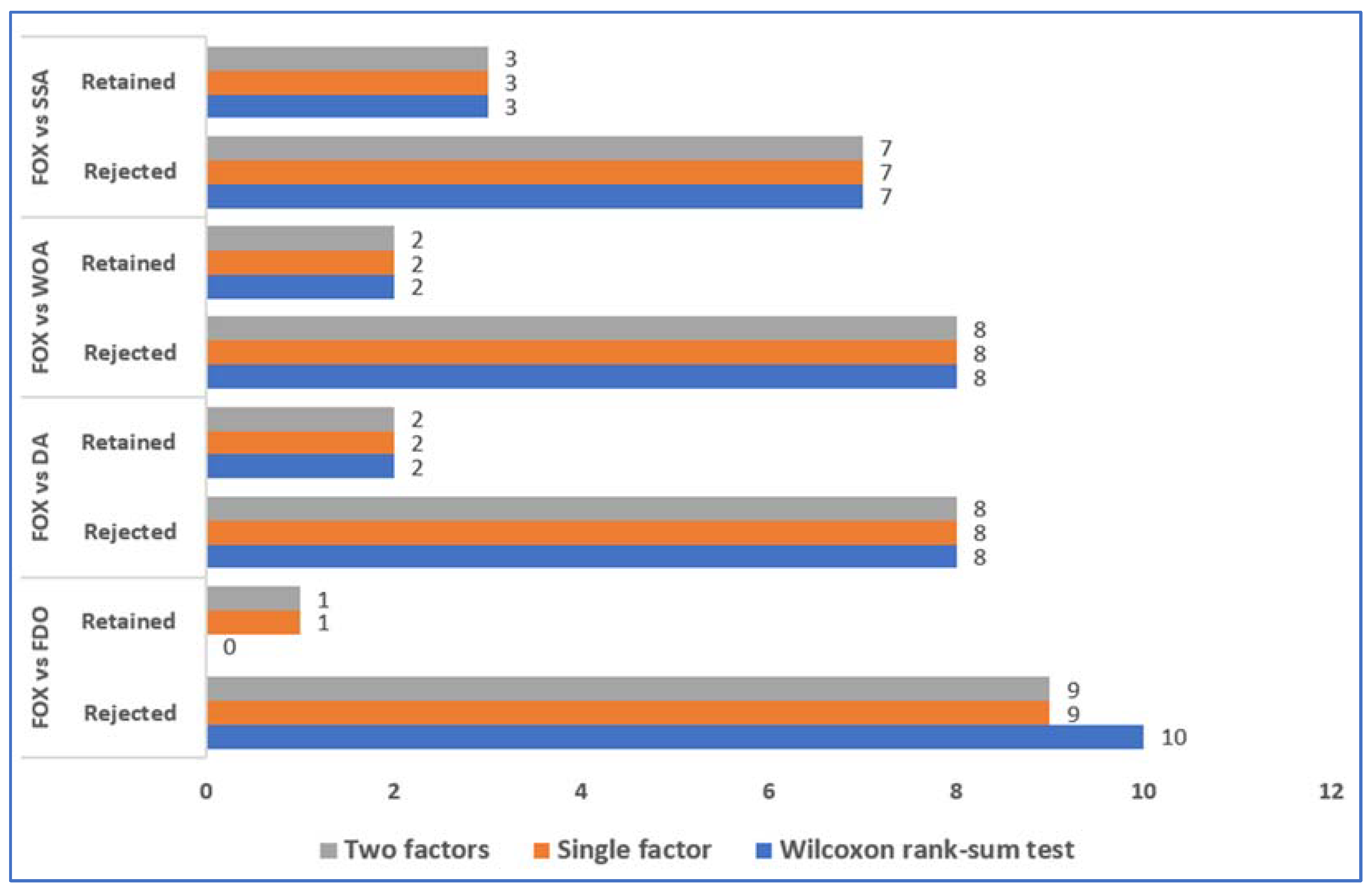
6. Evaluation and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clark, A. Whatever next? Predictive Brains, Situated Agents, and the Future of Cognitive Science. Behav. Brain Sci. 2013, 36, 181–204. [Google Scholar] [CrossRef] [PubMed]
- Kapur, R. Research Methodology: Methods and Strategies; Department of Adult Education and Continuing Extension, University of Delhi: New Delhi, India, 2018. [Google Scholar]
- Horn, R.V. Statistical Indicators: For the Economic and Social Sciences; Cambridge University Press: Cambridge, UK, 1993; ISBN 0521423996. [Google Scholar]
- Li, B.; Su, P.; Chabbi, M.; Jiao, S.; Liu, X. DJXPerf: Identifying Memory Inefficiencies via Object-Centric Profiling for Java. In Proceedings of the 21st ACM/IEEE International Symposium on Code Generation and Optimization, Montréal, QC, Canada, 25 February–1 March 2023; pp. 81–94. [Google Scholar]
- Li, B.; Xu, H.; Zhao, Q.; Su, P.; Chabbi, M.; Jiao, S.; Liu, X. OJXPerf: Featherlight Object Replica Detection for Java Programs. In Proceedings of the 44th International Conference on Software Engineering, Pittsburgh, PA, USA, 21–29 May 2022; pp. 1558–1570. [Google Scholar]
- Eftimov, T.; Korošec, P.; Seljak, B.K. A Novel Approach to Statistical Comparison of Meta-Heuristic Stochastic Optimization Algorithms Using Deep Statistics. Inf. Sci. 2017, 417, 186–215. [Google Scholar] [CrossRef]
- Jiang, M.; Rocktäschel, T.; Grefenstette, E. General Intelligence Requires Rethinking Exploration. R. Soc. Open Sci. 2023, 10, 230539. [Google Scholar] [CrossRef] [PubMed]
- Vikhar, P.A. Evolutionary Algorithms: A Critical Review and Its Future Prospects. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 261–265. [Google Scholar]
- Abdullah, J.M.; Ahmed, T. Fitness Dependent Optimizer: Inspired by the Bee Swarming Reproductive Process. IEEE Access 2019, 7, 43473–43486. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly Algorithm: A New Meta-Heuristic Optimization Technique for Solving Single-Objective, Discrete, and Multi-Objective Problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Aladdin, A.M.; Rashid, T.A. Leo: Lagrange Elementary Optimization. arXiv 2023, arXiv:2304.05346. [Google Scholar]
- Tan, J.; Jiao, S.; Chabbi, M.; Liu, X. What Every Scientific Programmer Should Know about Compiler Optimizations? In Proceedings of the 34th ACM International Conference on Supercomputing, Barcelona, Spain, 29 June–2 July 2020; pp. 1–12. [Google Scholar]
- Hussain, K.; Najib, M.; Salleh, M.; Cheng, S.; Naseem, R. Common Benchmark Functions for Metaheuristic Evaluation: A Review. JOIV Int. J. Inform. Vis. 2017, 1, 218–223. [Google Scholar] [CrossRef]
- Bujok, P.; Zamuda, A. Cooperative Model of Evolutionary Algorithms Applied to CEC 2019 Single Objective Numerical Optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 366–371. [Google Scholar]
- Swain, M. The Output Hypothesis: Theory and Research. In Handbook of Research in Second Language Teaching and Learning; Routledge: Abingdon, UK, 2005; pp. 471–483. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A Practical Tutorial on the Use of Nonparametric Statistical Tests as a Methodology for Comparing Evolutionary and Swarm Intelligence Algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A Study on the Use of Non-Parametric Tests for Analyzing the Evolutionary Algorithms’ Behaviour: A Case Study on the CEC’2005 Special Session on Real Parameter Optimization. J. Heuristics 2009, 15, 617–644. [Google Scholar] [CrossRef]
- Hajiakbari Fini, M.; Yousefi, G.R.; Haes Alhelou, H. Comparative Study on the Performance of Many-objective and Single-objective Optimisation Algorithms in Tuning Load Frequency Controllers of Multi-area Power Systems. IET Gener. Transm. Distrib. 2016, 10, 2915–2923. [Google Scholar] [CrossRef]
- Good, P.I.; Hardin, J.W. Common Errors in Statistics (and How to Avoid Them); John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 1118360117. [Google Scholar]
- Opara, K.; Arabas, J. Benchmarking Procedures for Continuous Optimization Algorithms. J. Telecommun. Inf. Technol. 2011, 4, 73–80. [Google Scholar]
- Sivanandam, S.N.; Deepa, S.N.; Sivanandam, S.N.; Deepa, S.N. Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 354073189X. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Wong, K.P.; Dong, Z.Y. Differential Evolution, an Alternative Approach to Evolutionary Algorithm. In Proceedings of the 13th International Conference on Intelligent Systems Application to Power Systems, Arlington, VA, USA, 6–10 November 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 73–83. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime Mould Algorithm: A New Method for Stochastic Optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Shabani, F.; Kumar, L.; Ahmadi, M. A Comparison of Absolute Performance of Different Correlative and Mechanistic Species Distribution Models in an Independent Area. Ecol. Evol. 2016, 6, 5973–5986. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, J.M.; Rashid, T.A.; Maaroof, B.B.; Mirjalili, S. Multi-Objective Fitness-Dependent Optimizer Algorithm. Neural Comput. Appl. 2023, 35, 11969–11987. [Google Scholar] [CrossRef]
- Venugopal, P.; Maddikunta, P.K.R.; Gadekallu, T.R.; Al-Rasheed, A.; Abbas, M.; Soufiene, B.O. An Adaptive DeepLabv3+ for Semantic Segmentation of Aerial Images Using Improved Golden Eagle Optimization Algorithm. IEEE Access 2023, 11, 106688–106705. [Google Scholar]
- Mohammadi-Balani, A.; Nayeri, M.D.; Azar, A.; Taghizadeh-Yazdi, M. Golden Eagle Optimizer: A Nature-Inspired Metaheuristic Algorithm. Comput. Ind. Eng. 2021, 152, 107050. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-Flame Optimization Algorithm: A Novel Nature-Inspired Heuristic Paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Gadekallu, T.R.; Kumar, N.; Baker, T.; Natarajan, D.; Boopathy, P.; Maddikunta, P.K.R. Moth Flame Optimization Based Ensemble Classification for Intrusion Detection in Intelligent Transport System for Smart Cities. Microprocess. Microsyst. 2023, 103, 104935. [Google Scholar] [CrossRef]
- Rahman, C.M.; Rashid, T.A. A New Evolutionary Algorithm: Learner Performance Based Behavior Algorithm. Egypt. Inform. J. 2021, 22, 213–223. [Google Scholar] [CrossRef]
- Mohammed, H.; Rashid, T. FOX: A FOX-Inspired Optimization Algorithm. Appl. Intell. 2023, 53, 1030–1050. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Wang, S.; Yang, R.; Li, Y.; Xu, B.; Lu, B. Single-Factor Analysis and Interaction Terms on the Mechanical and Microscopic Properties of Cemented Aeolian Sand Backfill. Int. J. Miner. Metall. Mater. 2023, 30, 1584–1595. [Google Scholar] [CrossRef]
- Woolson, R.F. Wilcoxon Signed-rank Test. In Wiley Encyclopedia of Clinical Trials; Wiley: Hoboken, NJ, USA, 2007; pp. 1–3. [Google Scholar]
- Liu, Q.; Gehrlein, W.V.; Wang, L.; Yan, Y.; Cao, Y.; Chen, W.; Li, Y. Paradoxes in Numerical Comparison of Optimization Algorithms. IEEE Trans. Evol. Comput. 2019, 24, 777–791. [Google Scholar] [CrossRef]
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Del Ser, J.; Herrera, F. A Prescription of Methodological Guidelines for Comparing Bio-Inspired Optimization Algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Osaba, E.; Villar-Rodriguez, E.; Del Ser, J.; Nebro, A.J.; Molina, D.; LaTorre, A.; Suganthan, P.N.; Coello, C.A.C.; Herrera, F. A Tutorial on the Design, Experimentation and Application of Metaheuristic Algorithms to Real-World Optimization Problems. Swarm Evol. Comput. 2021, 64, 100888. [Google Scholar] [CrossRef]
- Molina, D.; LaTorre, A.; Herrera, F. An Insight into Bio-Inspired and Evolutionary Algorithms for Global Optimization: Review, Analysis, and Lessons Learnt over a Decade of Competitions. Cogn. Comput. 2018, 10, 517–544. [Google Scholar] [CrossRef]
- Emambocus, B.A.S.; Jasser, M.B.; Amphawan, A.; Mohamed, A.W. An Optimized Discrete Dragonfly Algorithm Tackling the Low Exploitation Problem for Solving TSP. Mathematics 2022, 10, 3647. [Google Scholar] [CrossRef]
- ben oualid Medani, K.; Sayah, S.; Bekrar, A. Whale Optimization Algorithm Based Optimal Reactive Power Dispatch: A Case Study of the Algerian Power System. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Aladdin, A.M.; Abdullah, J.M.; Salih, K.O.M.; Rashid, T.A.; Sagban, R.; Alsaddon, A.; Bacanin, N.; Chhabra, A.; Vimal, S.; Banerjee, I. Fitness-Dependent Optimizer for IoT Healthcare Using Adapted Parameters: A Case Study Implementation. In Practical Artificial Intelligence for Internet of Medical Things; CRC Press: Boca Raton, FL, USA, 2023; pp. 45–61. [Google Scholar]
- Vijaya Bhaskar, K.; Ramesh, S.; Chandrasekar, P. Evolutionary Based Optimal Power Flow Solution For Load Congestion Using PRNG. Int. J. Eng. Trends Technol. 2021, 69, 225–236. [Google Scholar]
- Tuan, H.D.; Apkarian, P.; Nakashima, Y. A New Lagrangian Dual Global Optimization Algorithm for Solving Bilinear Matrix Inequalities. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2000, 10, 561–578. [Google Scholar] [CrossRef]
- Wiuf, C.; Schaumburg-Müller Pallesen, J.; Foldager, L.; Grove, J. LandScape: A Simple Method to Aggregate p-Values and Other Stochastic Variables without a Priori Grouping. Stat. Appl. Genet. Mol. Biol. 2016, 15, 349–361. [Google Scholar] [CrossRef]
- Aladdin, A.M.; Rashid, T.A. A New Lagrangian Problem Crossover—A Systematic Review and Meta-Analysis of Crossover Standards. Systems 2023, 11, 144. [Google Scholar] [CrossRef]
- Potvin, P.J.; Schutz, R.W. Statistical Power for the Two-Factor Repeated Measures ANOVA. Behav. Res. Methods Instrum. Comput. 2000, 32, 347–356. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R. Sample Size and Its Role in Central Limit Theorem (CLT). Comput. Appl. Math. J. 2018, 4, 1–7. [Google Scholar]
- Derrick, B.; White, P. Comparing Two Samples from an Individual Likert Question. Int. J. Math. Stat. 2017, 18, 1–13. [Google Scholar]
- Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Berry, K.J.; Mielke, P.W., Jr.; Johnston, J.E. The Two-Sample Rank-Sum Test: Early Development. Electron. J. Hist. Probab. Stat. 2012, 8, 1–26. [Google Scholar]
- Hasan, D.O.; Aladdin, A.M.; Amin, A.A.H.; Rashid, T.A.; Ali, Y.H.; Al-Bahri, M.; Majidpour, J.; Batrancea, I.; Masca, E.S. Perspectives on the Impact of E-Learning Pre- and Post-COVID-19 Pandemic—The Case of the Kurdistan Region of Iraq. Sustainability 2023, 15, 4400. [Google Scholar] [CrossRef]
- Oyeka, I.C.A.; Umeh, E.U. Statistical Analysis of Paired Sample Data by Ranks. Sci. J. Math. Stat. 2012, 2012, sjms-102. [Google Scholar]
- Task, C.; Clifton, C. Differentially Private Significance Testing on Paired-Sample Data. In Proceedings of the 2016 SIAM International Conference on Data Mining, Miami, FL, USA, 5–7 May 2016; SIAM: Philadelphia, PA, USA, 2016; pp. 153–161. [Google Scholar]
- Bewick, V.; Cheek, L.; Ball, J. Statistics Review 9: One-Way Analysis of Variance. Crit. Care 2004, 8, 130. [Google Scholar] [CrossRef] [PubMed]
- Olive, D.J.; Olive, D.J. One Way Anova. In Linear Regression; Springer: Cham, Switzerland, 2017; pp. 175–211. [Google Scholar]
- Protassov, R.S. An Application of Missing Data Methods: Testing for the Presence of a Spectral Line in Astronomy and Parameter Estimation of the Generalized Hyperbolic Distributions; Harvard University: Cambridge, MA, USA, 2002; ISBN 0493868720. [Google Scholar]
- Huang, C.; Li, Y.; Yao, X. A Survey of Automatic Parameter Tuning Methods for Metaheuristics. IEEE Trans. Evol. Comput. 2019, 24, 201–216. [Google Scholar] [CrossRef]
- Vafaee, F.; Turán, G.; Nelson, P.C.; Berger-Wolf, T.Y. Balancing the Exploration and Exploitation in an Adaptive Diversity Guided Genetic Algorithm. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 22 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2570–2577. [Google Scholar]
- Dyer, M.; Stougie, L. Computational Complexity of Stochastic Programming Problems. Math. Program. 2006, 106, 423–432. [Google Scholar] [CrossRef]
- Shahbazi, N.; Lin, Y.; Asudeh, A.; Jagadish, H. V Representation Bias in Data: A Survey on Identification and Resolution Techniques. ACM Comput. Surv. 2023, 55, 293. [Google Scholar] [CrossRef]
- Derrac, J.; Garcia, S.; Sanchez, L.; Herrera, F. Keel Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J. Mult.-Valued Log. Soft Comput. 2015, 17, 255–287. [Google Scholar]




| Algorithm | Litreature Year | Problem Types | Statistical Model | Referncing |
|---|---|---|---|---|
| Differential Evolution | 2005 | Single | Statistical standards | [23] |
| Whale Optimization | 2016 | Both | Wilcoxon sum-rank | [24] |
| Slime Mould | 2020 | Single | Wilcoxon sum-rank | [25] |
| Fitness-Dependent Optimizer | 2019 | Both | ANOVA single-factor and Friedman test | [9,27] |
| Golden Eagle Optimization | 2021 | Single | Wilcoxon sum-rank and statistical standards | [28,29] |
| Moth–flame Optimization | 2015 | Both | Wilcoxon sum rank | [30,31] |
| Learner-Performance-based Behavior | 2021 | Single | ANOVA single-factor | [32] |
| Leo | 2023 | Single | Wilcoxon sum-rank | [11] |
| FOX | 2023 | Single | ANOVA single-factor | [33] |
| Salp Swarm Algorithm | 2017 | Both | Wilcoxon sum-rank | [34] |
| Source of Variation | The Sum of Squares (SS) | Degree of Freedom (DF) | Mean Square (MS) | |
|---|---|---|---|---|
| Factor (F) (Treatments) | ||||
| Residual (E) (Error) | ||||
| Corr. Total |
| TFs | p-Value Tests | Leo vs. FDO | Leo vs. LPB | Leo vs. DA |
|---|---|---|---|---|
| TF1 | Wilcoxon rank-sum test | 0.000002 | 0.000031 | 0.000031 |
| Single-factor | 5.78 × 10−2 | 7.72 × 10−6 | 5.78 × 10−2 | |
| Two-factor | 6.27 × 10−2 | 3.24 × 10−5 | 6.27 × 10−2 | |
| TF2 | Wilcoxon rank-sum test | 0.047162 | 0.000002 | 0.000002 |
| Single-factor | 6.48 × 10−2 | 1.09581 × 10−10 | 3.08665 × 10−6 | |
| Two-factor | 1.16 × 10−1 | 1.16757 × 10−8 | 1.60543 × 10−5 | |
| TF3 | Wilcoxon rank-sum test | 0.002585 | 0.000002 | 0.000002 |
| Single-factor | 1.02 × 10−1 | 5.52049 × 10−9 | 1.67 × 10−1 | |
| Two-factor | 1.00 × 10−1 | 1.65436 × 10−7 | 1.72 × 10−1 | |
| TF4 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000031 |
| Single-factor | 9.49 × 10−8 | 8.74288 × 10−23 | 3.22 × 10−1 | |
| Two-factor | 1.20 × 10−6 | 7.61671 × 10−16 | 3.26 × 10−1 | |
| TF5 | Wilcoxon rank-sum test | 0.557743 | 0.781264 | 0.000148 |
| Single-factor | 5.18 × 10−2 | 2.03 × 10−1 | 4.50 × 10−2 | |
| Two-factor | 6.28 × 10−2 | 2.30 × 10−1 | 5.14 × 10−2 | |
| TF6 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.057096 |
| Single-factor | 7.00 × 10−5 | 1.83 × 10−4 | 3.16 × 10−1 | |
| Two-factor | 1.84 × 10−4 | 4.02 × 10−4 | 3.21 × 10−1 | |
| TF7 | Wilcoxon rank-sum test | 0.000002 | 0.000097 | 0.000002 |
| Single-factor | 3.48738 × 10−14 | 1.06251 × 10−5 | 5.30 × 10−3 | |
| Two-factor | 7.24577 × 10−11 | 5.96148 × 10−5 | 6.98 × 10−3 |
| TFs | p-Value Tests | DA vs. FDO | DA vs. LBP |
|---|---|---|---|
| TF1 | Wilcoxon rank-sum test | 4.32 × 10−8 | 0.000002 |
| Single-factor | 3.10 × 10−1 | 7.72 × 10−6 | |
| Two-factor | 3.14 × 10−1 | 3.23997 × 10−5 | |
| TF2 | Wilcoxon rank-sum test | 0.000002 | 0.000002 |
| Single-factor | 6.47 × 10−2 | 1.07 × 10−10 | |
| Two-factor | 6.98 × 10−2 | 1.16 × 10−8 | |
| TF3 | Wilcoxon rank-sum test | 0.000002 | 0.000002 |
| Single-factor | 8.72 × 10−2 | 5.52 × 10−9 | |
| Two-factor | 9.25 × 10−2 | 1.65 × 10−7 | |
| TF4 | Wilcoxon rank-sum test | 0.000031 | 0.000031 |
| Single-factor | 3.21 × 10−1 | 3.42 × 10−6 | |
| Two-factor | 3.26 × 10−1 | 4.25684 × 10−5 | |
| TF5 | Wilcoxon rank-sum test | 0.005667 | 0.002765 |
| Single-factor | 4.04 × 10−3 | 6.74 × 10−3 | |
| Two-factor | 5.94 × 10−3 | 1.05 × 10−2 | |
| TF6 | Wilcoxon rank-sum test | 0.323358 | 0.000031 |
| Single-factor | 3.16 × 10−1 | 7.53 × 10−1 | |
| Two-factor | 3.21 × 10−1 | 7.63 × 10−1 | |
| TF7 | Wilcoxon rank-sum test | 0.000002 | 0.000002 |
| Single-factor | 3.17 × 10−14 | 7.77 × 10−13 | |
| Two-factor | 6.69 × 10−11 | 5.47 × 10−10 |
| TFs | p-Value Tests | Leo vs. FDO | Leo vs. LPB | Leo vs. DA |
|---|---|---|---|---|
| TF8 | Wilcoxon rank-sum test | 0.000016 | 0.000002 | 0.031603 |
| Single-factor | 7.18 × 10−5 | 1.30915 × 10−21 | 2.20 × 10−2 | |
| Two-factor | 1.97 × 10−4 | 2.73227 × 10−15 | 2.56 × 10−2 | |
| TF9 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 5.98981 × 10−16 | 1.25973 × 10−23 | 1.25717 × 10−23 | |
| Two-factor | 1.45999 × 10−11 | 2.62462 × 10−16 | 2.6251 × 10−16 | |
| TF10 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 6.72092 × 10−13 | 1.16363 × 10−9 | 5.59255 × 10−13 | |
| Two-factor | 3.55204 × 10−10 | 5.61266 × 10−8 | 3.95574 × 10−10 | |
| TF11 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 1.0768 × 10−15 | 5.96269 × 10−17 | 8.59 × 10−3 | |
| Two-factor | 8.64413 × 10−12 | 1.55804 × 10−12 | 1.09 × 10−2 | |
| TF12 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.328571 |
| Single-factor | 3.67963 × 10−10 | 1.97 × 10−4 | 1.38 × 10−1 | |
| Two-factor | 2.62616 × 10−8 | 4.28 × 10−4 | 1.43 × 10−1 | |
| TF13 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.517048 |
| Single-factor | 7.41491 × 10−7 | 1.65 × 10−3 | 1.67 × 10−1 | |
| Two-factor | 5.50366 × 10−6 | 2.56 × 10−3 | 1.72 × 10−1 |
| TFs | p-Value Tests | DA vs. FDO | DA vs. LBP |
|---|---|---|---|
| TF8 | Wilcoxon rank-sum test | 0.00002 | 0.000002 |
| Single-factor | 8.43646 × 10−5 | 4.23 × 10−27 | |
| Two-factor | 2.14 × 10−4 | 3.47 × 10−18 | |
| TF9 | Wilcoxon rank-sum test | 0.000002 | 0.000002 |
| Single-factor | 7.74 × 10−20 | 1.91 × 10−5 | |
| Two-factor | 3.38 × 10−14 | 6.56 × 10−5 | |
| TF10 | Wilcoxon rank-sum test | 0.0000001 | 0.000002 |
| Single-factor | 3.21 × 10−1 | 1.08 × 10−9 | |
| Two-factor | 3.26 × 10−1 | 5.41 × 10−8 | |
| TF11 | Wilcoxon rank-sum test | 0.000002 | 0.000002 |
| Single-factor | 1.08 × 10−15 | 5.96 × 10−17 | |
| Two-factor | 8.64 × 10−12 | 1.56 × 10−12 | |
| TF12 | Wilcoxon rank-sum test | 0.000002 | 0.158855 |
| Single-factor | 4.00 × 10−10 | 1.38 × 10−1 | |
| Two-factor | 2.61 × 10−8 | 1.43 × 10−1 | |
| TF13 | Wilcoxon rank-sum test | 0.000002 | 0.004682 |
| Single-factor | 7.73 × 10−7 | 1.85 × 10−1 | |
| Two-factor | 5.77 × 10−6 | 1.91 × 10−1 |
| TFs | p-Value Tests | Leo vs. FDO | Leo vs. LPB | Leo vs. DA |
|---|---|---|---|---|
| TF14 | Wilcoxon rank-sum test | 0.002929 | 0.000013 | 0.000013 |
| Single-factor | 5.91 × 10−4 | 5.4285 × 10−7 | 5.4285 × 10−7 | |
| Two-factor | 9.91 × 10−4 | 4.36958 × 10−6 | 4.36958 × 10−6 | |
| TF15 | Wilcoxon rank-sum test | 0.781264 | 0.012453 | 0.000359 |
| Single-factor | 4.85 × 10−1 | 4.70 × 10−1 | 1.74 × 10−1 | |
| Two-factor | 4.96 × 10−1 | 4.93 × 10−1 | 1.79 × 10−1 | |
| TF16 | Wilcoxon rank-sum test | 0.000115 | 0.000002 | 0.000001 |
| Single-factor | 5.05424 × 10−7 | 5.04706 × 10−7 | 5.0468 × 10−7 | |
| Two-factor | 4.14528 × 10−6 | 4.14087 × 10−6 | 4.14078 × 10−6 | |
| TF17 | Wilcoxon rank-sum test | 0.120288 | 0.000002 | 0.000001 |
| Single-factor | 6.19 × 10−3 | 1.21 × 10−3 | 1.21 × 10−3 | |
| Two-factor | 7.95 × 10−3 | 1.96 × 10−3 | 1.96 × 10−3 | |
| TF18 | Wilcoxon rank-sum test | 0.00015 | 0.000393 | 0.00015 |
| Single-factor | 2.84942 × 10−5 | 2.86032 × 10−5 | 2.84942 × 10−5 | |
| Two-factor | 8.98958 × 10−5 | 9.02907 × 10−5 | 8.98958 × 10−5 | |
| TF19 | Wilcoxon rank-sum test | 0.000004 | 0.000002 | 0.000002 |
| Single-factor | 9.00179 × 10−7 | 8.68172 × 10−7 | 8.6827 × 10−7 | |
| Two-factor | 6.30703 × 10−6 | 6.18774 × 10−6 | 6.18881 × 10−6 |
| TFs | p-Value Tests | DA vs. FDO | DA vs. LBP |
|---|---|---|---|
| TF14 | Wilcoxon rank-sum test | 0.000049 | 1.00 |
| Single-factor | 2.37 × 10−7 | 4.63 × 10−2 | |
| Two-factor | 2.38 × 10−6 | 5.10 × 10−2 | |
| TF15 | Wilcoxon rank-sum test | 0.047039 | 0.000082 |
| Single-factor | 7.39 × 10−2 | 2.54 × 10−2 | |
| Two-factor | 7.90 × 10−2 | 2.92 × 10−2 | |
| TF16 | Wilcoxon rank-sum test | 0.00000004 | 0.000292 |
| Single-factor | 0 × 100 | 3.38 × 10−2 | |
| Two-factor | 0 × 100 | 3.80 × 10−2 | |
| TF17 | Wilcoxon rank-sum test | 0.000001 | 0.001474 |
| Single-factor | 4.40 × 10−5 | 8.93 × 10−2 | |
| Two-factor | 1.27 × 10−4 | 9.46 × 10−2 | |
| TF18 | Wilcoxon rank-sum test | 0.000001 | 0.000132 |
| Single-factor | 3.55 × 10−48 | 7.90 × 10−3 | |
| Two-factor | 4.44 × 10−29 | 1.01 × 10−2 | |
| TF19 | Wilcoxon rank-sum test | 0.630701 | 0.000146 |
| Single-factor | 1.82 × 10−3 | 3.58 × 10−1 | |
| Two-factor | 2.81 × 10−3 | 3.62 × 10−1 |
| TF | p-Value Tests | Leo vs. FOX | Leo vs. FDO | Leo vs. WOA | Leo vs. SSA | Leo vs. DA |
|---|---|---|---|---|---|---|
| CEC01 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.038723 | 0.360039 | 0.000012 |
| Single-factor | 3.88 × 10−9 | 3.88 × 10−9 | 1.23 × 10−3 | 3.67 × 10−1 | 3.13 × 10−4 | |
| Two-factor | 1.30 × 10−7 | 1.30 × 10−7 | 2.12 × 10−3 | 4.11 × 10−1 | 5.78 × 10−4 | |
| CEC02 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 1.39 × 10−48 | 2.10 × 10−117 | 1.05 × 10−48 | 1.47 × 10−48 | 3.25 × 10−4 | |
| Two-factor | 2.72 × 10−29 | 8.99 × 10−64 | 2.47 × 10−29 | 2.86 × 10−29 | 6.48 × 10−4 | |
| CEC03 | Wilcoxon rank-sum test | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| Single-factor | 2.15 × 10−167 | 2.46 × 10−170 | 2.46 × 10−170 | 3.39 × 10−169 | 2.46 × 10−164 | |
| Two-factor | 2.45 × 10−88 | 3.08 × 10−90 | 3.08 × 10−90 | 3.72 × 10−89 | 1.36 × 10−86 | |
| CEC04 | Wilcoxon rank-sum test | 0.000002 | 0.000005 | 0.000002 | 0.000125 | 0.000012 |
| Single-factor | 3.34 × 10−15 | 4.03 × 10−9 | 1.81 × 10−9 | 1.42 × 10−5 | 6.11 × 10−4 | |
| Two-factor | 2.23 × 10−11 | 4.07 × 10−8 | 6.67 × 10−8 | 3.81 × 10−5 | 1.19 × 10−3 | |
| CEC05 | Wilcoxon rank-sum test | 0.000002 | 0.000004 | 0.688359 | 0.000026 | 0.033264 |
| Single-factor | 1.95 × 10−20 | 1.92 × 10−10 | 7.86 × 10−1 | 6.79 × 10−9 | 4.42 × 10−2 | |
| Two-factor | 4.08 × 10−14 | 5.52 × 10−9 | 7.92 × 10−1 | 6.07 × 10−7 | 3.42 × 10−2 | |
| CEC06 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 9.18 × 10−10 | 4.64515 × 10−50 | 3.21068 × 10−39 | 2.61977 × 10−14 | 1.25449 × 10−28 | |
| Two-factor | 1.98 × 10−8 | 1.85926 × 10−32 | 2.283 × 10−23 | 2.7012 × 10−12 | 2.08731 × 10−18 | |
| CEC07 | Wilcoxon rank-sum test | 0.000148 | 0.171376 | 0.000115 | 0.011079 | 0.000359 |
| Single-factor | 1.76 × 10−5 | 8.80 × 10−2 | 9.77315 × 10−7 | 2.65 × 10−3 | 2.93533 × 10−6 | |
| Two-factor | 4.54 × 10−5 | 9.17 × 10−2 | 4.74379 × 10−6 | 9.32 × 10−3 | 3.93668 × 10−5 | |
| CEC08 | Wilcoxon rank-sum test | 0.000082 | 0.000008 | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 1.28 × 10−5 | 3.56726 × 10−8 | 4.28708 × 10−23 | 1.22371 × 10−13 | 4.68724 × 10−21 | |
| Two-factor | 1.43 × 10−5 | 5.00 × 10−7 | 6.5426 × 10−15 | 1.75576 × 10−11 | 7.46623 × 10−16 | |
| CEC09 | Wilcoxon rank-sum test | 0.001593 | 0.000002 | 0.000002 | 0.002765 | 0.000003 |
| Single-factor | 7.31 × 10−4 | 4.58088 × 10−13 | 4.69055 × 10−11 | 5.76 × 10−3 | 3.33322 × 10−6 | |
| Two-factor | 2.34 × 10−3 | 3.49104 × 10−10 | 7.97908 × 10−9 | 1.07 × 10−2 | 8.5846 × 10−6 | |
| CEC10 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 6.40 × 10−82 | 8.8928 × 10−155 | 4.78917 × 10−54 | 6.32896 × 10−57 | 1.62182 × 10−43 | |
| Two-factor | 3.12 × 10−46 | 1.85107 × 10−82 | 1.84546 × 10−32 | 1.23696 × 10−32 | 6.88248 × 10−27 |
| TF | p-Value Tests | DA vs. FDO | WOA vs. FDO | SSA vs. FDO | FOX vs. FDO |
|---|---|---|---|---|---|
| CEC01 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.018519 |
| Single-factor | 4.03 × 10−5 | 1.08 × 10−4 | 3.18 × 10−9 | 4.12 × 10−4 | |
| Two-factor | 1.18 × 10−4 | 2.62 × 10−4 | 1.13 × 10−7 | 2.73 × 10−4 | |
| CEC02 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 1.81 × 10−5 | 1.10 × 10−196 | 3.17 × 10−252 | 4.01 × 10−250 | |
| Two-factor | 6.30 × 10−5 | 2.06 × 10−103 | 3.49 × 10−131 | 3.93 × 10−130 | |
| CEC03 | Wilcoxon rank-sum test | 0.040475 | 4.32 × 10−8 | 0.000003 | 0.000003 |
| Single-factor | 2.45 × 10−1 | 1.20 × 10−306 | 3.64 × 10−1 | 3.46 × 10−1 | |
| Two-factor | 2.50 × 10−1 | 2.15 × 10−158 | 3.67 × 10−1 | 3.50 × 10−1 | |
| CEC04 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.115608 | 0.000002 |
| Single-factor | 1.24 × 10−4 | 7.44 × 10−11 | 9.59 × 10−2 | 7.85 × 10−16 | |
| Two-factor | 2.82 × 10−4 | 7.17 × 10−9 | 1.18 × 10−1 | 7.00 × 10−12 | |
| CEC05 | Wilcoxon rank-sum test | 0.000007 | 0.000002 | 0.004992 | 0.000002 |
| Single-factor | 6.05 × 10−9 | 2.37 × 10−15 | 7.88 × 10−3 | 8.92 × 10−25 | |
| Two-factor | 4.16 × 10−7 | 2.78 × 10−12 | 5.48 × 10−3 | 5.28 × 10−17 | |
| CEC06 | Wilcoxon rank-sum test | 0.000006 | 0.000031 | 0.000002 | 0.000002 |
| Single-factor | 2.90 × 10−9 | 1.97 × 10−8 | 2.20 × 10−28 | 1.69 × 10−34 | |
| Two-factor | 4.67 × 10−8 | 9.96 × 10−7 | 1.63 × 10−19 | 2.30 × 10−22 | |
| CEC07 | Wilcoxon rank-sum test | 0.000004 | 0.000002 | 0.000011 | 0.000002 |
| Single-factor | 2.69 × 10−10 | 6.27 × 10−15 | 1.04 × 10−6 | 1.84 × 10−13 | |
| Two-factor | 2.48 × 10−8 | 2.12 × 10−11 | 8.20 × 10−6 | 1.26 × 10−10 | |
| CEC08 | Wilcoxon rank-sum test | 0.000332 | 0.000082 | 0.120445 | 0.03001 |
| Single-factor | 2.36 × 10−5 | 5.23 × 10−6 | 1.32 × 10−1 | 1.62 × 10−2 | |
| Two-factor | 1.11 × 10−4 | 9.87 × 10−6 | 1.27 × 10−1 | 2.47 × 10−2 | |
| CEC09 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 1.80 × 10−10 | 7.40 × 10−19 | 3.80 × 10−43 | 8.52 × 10−36 | |
| Two-factor | 1.63 × 10−8 | 1.22 × 10−13 | 1.59 × 10−26 | 9.36 × 10−23 | |
| CEC10 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000001 | 0.000002 |
| Single-factor | 2.22 × 10−111 | 2.46 × 10−122 | 6.40 × 10−131 | 8.61 × 10−198 | |
| Two-factor | 9.27 × 10−61 | 3.08 × 10−66 | 1.57 × 10−70 | 5.76 × 10−104 |
| TF | p-Value Tests | FOX vs. FDO | FOX vs. DA | FOX vs. WOA | FOX vs. SSA |
|---|---|---|---|---|---|
| CEC01 | Wilcoxon rank-sum test | 0.018519 | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 0.000412408 | 4.03456 × 10−5 | 0.000108313 | 3.18 × 10−9 | |
| Two-factor | 0.000273177 | 0.000118478 | 0.000262183 | 1.13 × 10−7 | |
| CEC02 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000003 | 0.000104 |
| Single-factor | 4.01 × 10−250 | 3.88 × 10−4 | 3.93 × 10−8 | 1.14 × 10−7 | |
| Two-factor | 3.93 × 10−130 | 7.50 × 10−4 | 5.41 × 10−7 | 1.20 × 10−5 | |
| CEC03 | Wilcoxon rank-sum test | 0.000003 | 0.243615 | 0.317311 | 0.654721 |
| Single-factor | 3.46 × 10−1 | 6.46 × 10−1 | 3.21 × 10−1 | 7.33 × 10−1 | |
| Two-factor | 3.50 × 10−1 | 6.54 × 10−1 | 3.26 × 10−1 | 7.38 × 10−1 | |
| CEC04 | Wilcoxon rank-sum test | 0.000002 | 0.000007 | 0.000015 | 0.000002 |
| Single-factor | 7.85 × 10−16 | 1.59 × 10−7 | 2.81 × 10−8 | 1.11 × 10−15 | |
| Two-factor | 7.00 × 10−12 | 2.36 × 10−7 | 2.00168 × 10−6 | 8.66 × 10−12 | |
| CEC05 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 8.92 × 10−25 | 5.39 × 10−22 | 3.91 × 10−21 | 2.13 × 10−24 | |
| Two-factor | 5.28 × 10−17 | 2.87 × 10−14 | 1.03 × 10−15 | 9.25 × 10−17 | |
| CEC06 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.001287 |
| Single-factor | 1.69 × 10−34 | 2.16 × 10−18 | 3.41 × 10−26 | 5.31 × 10−3 | |
| Two-factor | 2.30 × 10−22 | 2.22 × 10−12 | 1.88 × 10−19 | 1.22 × 10−3 | |
| CEC07 | Wilcoxon rank-sum test | 0.000002 | 0.14139 | 0.703564 | 0.205888 |
| Single-factor | 1.84 × 10−13 | 8.37 × 10−2 | 4.94 × 10−1 | 4.73 × 10−1 | |
| Two-factor | 1.26 × 10−10 | 1.12 × 10−1 | 4.62 × 10−1 | 4.74 × 10−1 | |
| CEC08 | Wilcoxon rank-sum test | 0.03001 | 0.000003 | 0.000002 | 0.000174 |
| Single-factor | 1.62 × 10−2 | 1.83 × 10−12 | 5.78 × 10−14 | 1.21 × 10−5 | |
| Two-factor | 2.47 × 10−2 | 6.76 × 10−10 | 4.11 × 10−11 | 2.47 × 10−5 | |
| CEC09 | Wilcoxon rank-sum test | 0.000002 | 0.000003 | 0.000002 | 0.062676 |
| Single-factor | 8.52 × 10−36 | 7.50917 × 10−5 | 3.83 × 10−9 | 1.06 × 10−1 | |
| Two-factor | 9.36 × 10−23 | 2.23 × 10−4 | 5.23 × 10−8 | 1.12 × 10−1 | |
| CEC10 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 | 0.000003 |
| Single-factor | 8.61 × 10−198 | 4.10 × 10−12 | 1.56 × 10−20 | 5.56 × 10−4 | |
| Two-factor | 5.76 × 10−104 | 1.20 × 10−9 | 1.42 × 10−14 | 9.75 × 10−4 |
| TF | p-Value Tests | DA vs. WOA | DA vs. SSA | WOA vs. SSA |
|---|---|---|---|---|
| CEC01 | Wilcoxon rank-sum test | 0.599936 | 0.000005 | 0.023038 |
| Single-factor | 4.04 × 10−1 | 2.22 × 10−4 | 8.21 × 10−4 | |
| Two-factor | 4.24 × 10−1 | 4.66 × 10−4 | 1.37 × 10−3 | |
| CEC02 | Wilcoxon rank-sum test | 0.000002 | 0.000002 | 0.000002 |
| Single-factor | 3.89 × 10−4 | 3.88 × 10−4 | 8.78 × 10−10 | |
| Two-factor | 7.51 × 10−4 | 7.50 × 10−4 | 4.43 × 10−8 | |
| CEC03 | Wilcoxon rank-sum test | 0.03936 | 0.243615 | 0.317311 |
| Single-factor | 2.32 × 10−1 | 4.52 × 10−1 | 3.21 × 10−1 | |
| Two-factor | 2.37 × 10−1 | 4.61 × 10−1 | 3.26 × 10−1 | |
| CEC04 | Wilcoxon rank-sum test | 0.051931 | 0.000002 | 0.000002 |
| Single-factor | 5.70 × 10−1 | 1.83 × 10−4 | 1.63 × 10−10 | |
| Two-factor | 5.80 × 10−1 | 4.15 × 10−4 | 1.68 × 10−8 | |
| CEC05 | Wilcoxon rank-sum test | 0.051924 | 0.000024 | 0.000002 |
| Single-factor | 3.02 × 10−2 | 6.31 × 10−7 | 4.70 × 10−13 | |
| Two-factor | 4.21 × 10−2 | 2.53 × 10−6 | 6.72 × 10−10 | |
| CEC06 | Wilcoxon rank-sum test | 0.013975 | 0.000002 | 0.000002 |
| Single-factor | 2.52 × 10−2 | 2.53 × 10−13 | 2.94 × 10−20 | |
| Two-factor | 1.26 × 10−2 | 3.21 × 10−10 | 7.77 × 10−13 | |
| CEC07 | Wilcoxon rank-sum test | 0.221022 | 0.015658 | 0.205888 |
| Single-factor | 2.11 × 10−1 | 3.99 × 10−2 | 2.13 × 10−1 | |
| Two-factor | 2.01 × 10−1 | 7.57 × 10−3 | 2.11 × 10−1 | |
| CEC08 | Wilcoxon rank-sum test | 0.926255 | 0.000261 | 0.004992 |
| Single-factor | 7.69 × 10−1 | 7.53 × 10−4 | 1.52 × 10−4 | |
| Two-factor | 7.91 × 10−1 | 7.57 × 10−4 | 1.48 × 10−3 | |
| CEC09 | Wilcoxon rank-sum test | 0.797098 | 0.000002 | 0.000002 |
| Single-factor | 8.57 × 10−1 | 3.11773 × 10−5 | 5.78 × 10−10 | |
| Two-factor | 8.68 × 10−1 | 9.97662 × 10−5 | 4.24 × 10−8 | |
| CEC10 | Wilcoxon rank-sum test | 0.829009 | 0.000002 | 0.000005 |
| Single-factor | 6.75 × 10−1 | 2.85 × 10−8 | 1.79 × 10−13 | |
| Two-factor | 7.03 × 10−1 | 7.21 × 10−8 | 2.27 × 10−9 |
| Sets | TFs Sample | Time-Complexity Average (Seconds) | |||
|---|---|---|---|---|---|
| DA | FDO | LPB | Leo | ||
| Unimodal | TF7 | 52.63769 | 23.7459 | 6.021400933 | 5.5880676 |
| Multimodal | TF13 | 42.98127 | 58.4801 | 4.7816489 | 4.692978 |
| Composite Modal | TF19 | 47.09351493 | 24.35697 | 5.313835 | 5.780502 |
| CEC-C06 2019 | CEC10 | 56.63626987 | 34.8759 | 4.966151 | 5.1998505 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, A.A.H.; Aladdin, A.M.; Hasan, D.O.; Mohammed-Taha, S.R.; Rashid, T.A. Enhancing Algorithm Selection through Comprehensive Performance Evaluation: Statistical Analysis of Stochastic Algorithms. Computation 2023, 11, 231. https://doi.org/10.3390/computation11110231
Amin AAH, Aladdin AM, Hasan DO, Mohammed-Taha SR, Rashid TA. Enhancing Algorithm Selection through Comprehensive Performance Evaluation: Statistical Analysis of Stochastic Algorithms. Computation. 2023; 11(11):231. https://doi.org/10.3390/computation11110231
Chicago/Turabian StyleAmin, Azad Arif Hama, Aso M. Aladdin, Dler O. Hasan, Soran R. Mohammed-Taha, and Tarik A. Rashid. 2023. "Enhancing Algorithm Selection through Comprehensive Performance Evaluation: Statistical Analysis of Stochastic Algorithms" Computation 11, no. 11: 231. https://doi.org/10.3390/computation11110231
APA StyleAmin, A. A. H., Aladdin, A. M., Hasan, D. O., Mohammed-Taha, S. R., & Rashid, T. A. (2023). Enhancing Algorithm Selection through Comprehensive Performance Evaluation: Statistical Analysis of Stochastic Algorithms. Computation, 11(11), 231. https://doi.org/10.3390/computation11110231









