Abstract
The dynamic behavior of solid Si targets irradiated by nanosecond laser pulses is computationally studied with transient, thermοmechanical three-dimensional finite element method simulations. The dynamic phase changes of the target and the generation and propagation of surface acoustic waves around the laser focal spot are provided by a finite element model of a very fine uniformly structured mesh, able to provide high-resolution results in short and long spatiotemporal scales. The dynamic changes in the Si material properties until the melting regime are considered, and the simulation results provide a detailed description of the irradiated area response, accompanied by the dynamics of the generation and propagation of ultrasonic waves. The new findings indicate that, due to the low thermal expansion coefficient and the high penetration depth of Si, the amplitude of the generated SAW is small, and the time and distance needed for the ultrasound to be generated is higher compared to dense metals. Additionally, in the melting regime, the development of high nonlinear thermal stresses leads to the generation and formation of an irregular ultrasound. Understanding the interaction between nanosecond lasers and Si is pivotal for advancing a wide range of technologies related to material processing and characterization.
1. Introduction
The high power of laser light and the ability of remote manipulation make pulsed laser irradiation a powerful tool for exploring the properties, the composition, and the structure of solid materials in relation to their dynamic behavior when excited. Irradiation with nanosecond laser pulses has many applications, such as welding, cutting, drilling, marking, machining, annealing, surface cleaning, melting, and ablation [1,2,3,4,5]. In addition, due to the high energy absorbed by the material, permanent deformations occur around the focal spot, making the method suitable for forming micro- or nanostructures at the surface of solid workpieces [6].
Computational simulations are valuable for studying the behavior of materials under laser irradiation. Numerical simulations can predict changes in the properties and the structure of the material by choosing the proper values for the initial properties of the material and the parameters of the laser systems. To understand the behavior of solids under nanosecond laser irradiation, in recent years, several studies have been conducted via numerical simulations. Lingyu et al. [7] developed a model to explore the dynamics of amorphous Fe alloy during nanosecond-pulsed laser processing and the effect of irradiation on the surface morphology. Gao et al. [8] developed a model for studying the temperature-dependent properties of Al alloy during nanosecond-pulsed laser irradiation. Kyota et al. [9] simulated the interaction of nanosecond laser pulses with monocrystalline Si for subsurface modifications. Acosta-Zepeda et al. [10] computationally described the topographies induced by nanosecond laser pulses on the Si surface. Zeng and Yao [11] simulated the creation of laser-generated ultrasonic waves to detect surface defects on a cylinder pipe. Orphanos et al. [12] performed numerical simulations and experimental interferometry measurements to study the laser-generated surface acoustic waves (SAWs) in multilayered materials. Marine et al. [13] studied the electronic mechanisms of the nanosecond laser ablation of Si, while Darif et al. [14] performed numerical simulations to study nanosecond laser annealing for crystalline Si.
The study of how nanosecond laser pulses interact with Si remains a consistently intriguing research problem due to its significant potential in various emerging applications. These applications span across diverse fields, including laser-based processing [1,2,3,4,5,6], metallization (deposition of thin metal films onto silicon substrates) [15], wafering [16], nanofabrication [17], and dewetting [18], as well as the creation of high-frequency ultrasounds for nondestructive material characterization [19]. Furthermore, this is of interest for a wide range of applications such as medicine [20], chemistry [21], biology [22], and microfluidics [23,24].
In our previous research works [25,26], finite element method (FEM) simulation studies, based on 3D multiphysics thermo-structural models, were performed to describe the spatiotemporal response of thin metal film surfaces excited by nanosecond laser pulses in the thermoelastic, plastic, melting, and ablation regimes and validated by laser whole-field interferometric technique experiments. In the current study, which focuses on the problem of the interaction between the nanosecond-pulsed laser and Si, for laser energies below the boiling point of Si, a 3D FEM thermo-structural transient model, discretized by a very fine uniform mesh, is developed to simulate the dynamic behavior of a solid Si target. A Gaussian pulsed laser source with a 6 ns pulse duration at 532 nm irradiates the Si target, and the model simulates the interactions with Si in the thermoelastic, plastic, and melting regimes. A Johnson–Cook material model which considers fracture and controls the phase changes is adopted, and temperature-dependent mechanical and thermal properties are considered. The developed model simulates the complex dynamics of the Si target during and after the interaction with the ns laser by computing at every timestep the temperatures, displacements, stresses, and strains. Representative simulation results indicate the SAW generation and propagation, within and beyond the area of the laser spot. The structured mesh uniformity along with the very fine discretization of the Si target allow for further modeling of unsymmetric features like cracks, inclusions, and surface roughness characteristics for multiscale studies [26,27]. The crucial areas where high gradients of temperatures and stresses are developed are identified here, and we indicate where and of which type; wisely, locally adaptive grids can be used for advanced sophisticated Si structured or unstructured FEM models [25]. This research sheds light on the dynamic thermomechanical response of the irradiated Si sample, a behavior greatly influenced by its low values of density, thermal expansion coefficient, and absorption coefficient, in contrast to the dense metals typically explored in the existing literature [25,26]. The new findings show that the amplitude of the generated SAW is small, the time and distance needed for the ultrasound to be generated is higher compared to dense metals, and in the melting regime, the development of high nonlinear thermal stresses leads to the generation and formation of an irregular ultrasound. Thus, the results are important for applications such as nondestructive material characterization, industrial applications for accurate material inspection, medical imaging, laser material processing, metallization, wafering, and dewetting. The developed high-resolution multiphysics simulation model of Si is ideal for material diagnostics and machining process evaluations, where the thermomechanical properties of Si change rapidly in time and space. To the authors’ knowledge, this is the first time a ns pulsed crystalline Si interaction study was performed to investigate the generation and propagation of SAWs via FEM simulations.
2. Numerical Modeling and Simulation
The acoustomechanical dynamic response of the Si solid target was studied with a FEM model simulated in LS-DYNA [28], capable of describing the interaction of the ns laser pulse with the target. The multiphysics coupled thermal–mechanical simulations were performed on the High-Performance Computer (HPC) Advanced Research Information System (ARIS) [29]. A typical run for a simulation time of 100 ns on the fat node island of ARIS was performed on 1 node with 512 GB of memory and 40 cores at 2.4 GHz (four sockets) each, for 8 h of wall-clock time. The ns laser beam is assumed to be of a Gaussian spatiotemporal profile, while the volumetric heat flux that is absorbed by the target is given by the following:
where t0 is the laser pulse duration at Full Width at Half Maximum (FWHM), r is the vector of location, and r0 is the FWHM beam radius; I0(t) is the initial laser intensity at the surface of the target; αb is the absorption coefficient of the material; R the reflectance of the material, and (1 − R)I0(t) is the portion of radiation that penetrates the surface and propagates inside the target. The last term expresses the attenuation of laser light at depth y from the irradiated top surface of the target [25]. The heat conduction equation governing the coupled thermomechanical problem and neglecting convective and radiated energy transport is described by the following:
where ρ is the mass density, T is the temperature, Cp is the specific heat at constant pressure, k is the thermal conductivity for a uniform and isotropic target, and Lm is the latent heat of melting. The volumetric heat flux Q(r, t) is the heat source term and represents the energy absorbed per unit time and unit volume.
The rapid local thermal expansion in the area of the focal spot results in the development of a stress field, and consequently, ultrasonic waves are generated and propagate the Si solid target. The wave propagation is given by [25]:
where is the displacement; λ and μ are the material-dependent Lame constants, and α is the thermoelastic expansion coefficient.
The mechanical behavior of the solid target [30] can be expressed by Equations (4) and (5):
where T0 is the ambient temperature and σij and εij are the stress and strain tensors at the ij plane.
The mathematical modeling of the hydrodynamic and the bulk behavior of the Si target due to the very high strain rates is performed by the Grüneisen equation of state (EOS) for compressed materials:
and for expanded materials, this results in the following:
where E is the internal energy per initial volume, C is the sound speed, μ is defined by the relation μ = (ρ/ρ0) − 1, and γ0, α1, s1, s2, and s3 are unitless constants. s1, s2, and s3 are the coefficients of the slope in the up-us curve (shock velocity us varies linearly, with respect to the particle velocity up), γ0 is the Grüneisen parameter, and α1 represents the first-order volume correction to γ0 [30].
The properties of crystalline Si are described by the empirical Johnson–Cook (J-C) [3,30] material model that provides the flow stress σ with Equation (8):
where A, B, C, n, and m are the experimental constants that depend on the material type, T is the temperature of the target, Tr is the room temperature, Tm is the melting point, and and are the plastic strain rate and reference strain rate, respectively. The material model includes a fracture model in case of high strain rates. It defines the equivalent plastic strain in case of damage and the damage parameter D, defined by Equations (9) and (10):
where D1–D5 are the failure parameters. D1 represents the initial failure strain, D2 the exponential, D3 the triaxility, D4 the strain rate, and D5 the temperature factors. The factor σVM is the Von Mises stress. When the damage parameter D becomes 1, the material fractures. The values of the mechanical and thermal properties and Johnson–Cook model parameters for crystalline Si which were used for the simulations were adopted from [31,32,33,34,35,36,37,38].
To develop a model capable of simulating the dynamic behavior of the irradiated area near the laser spot, where high temperature gradients are developed and high induced stresses/strains generate the SAWs, as well as to monitor the propagation of the SAWs far from the focal spot in the entire computational domain [25,26,27,30], simulation tests were performed regarding the mesh discretization and the domain dimensions. The mesh convergence analysis revealed that an element size of 1 μm × 0.3 μm × 1 μm (for X × Y × Z axes) is optimal to describe these thermomechanical dynamic features, in short and long spatiotemporal scales. Since non-reflective boundary conditions are set at the bottom of the target and the propagation depth of the SAWs is less than ~4 μm, the target was modeled as having a thickness of 9 μm. The domain dimensions which allow for the monitoring of the SAW generation and propagation were specified to be 450 μm × 9 μm × 450 μm, resulting in the generation of a uniform mesh of approximately 6 million elements. Moreover, the irradiation of the top plane of the sample was modeled by the Gaussian pulse given by Equation (1), applied at the center of the rectangular top surface, and non-reflective boundary conditions were enforced on all other surfaces. A hexahedral, eight-node, 3D solid finite element was also employed to conduct the transient analysis [30].
The pre-processing input data were stored and loaded once at the beginning of the coupled thermal–mechanical analysis described in Figure 1. The criteria (flags) used are strictly related to the resulting temperature fields, as shown in the decision rhombus boxes of the flow chart. At the end of a particular step, if the temperature of an element is higher than the melting temperature (Tm), phase change occurs, which is considered by including the latent heat of melting (Lm) in the model.
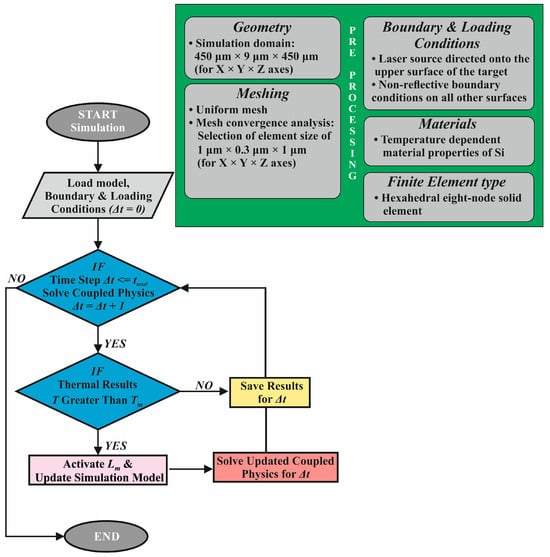
Figure 1.
Pre-processing and processing flow chart.
3. Results and Discussion
3.1. Thermomechanical Response
The knowledge of the matter’s change from elastic to plastic and to a melted regime is a consistently intriguing research problem due to its significant potential in various emerging applications, such as nondestructive material characterization. To study the dynamic response of the Si target in the thermoelastic, plastic, and melting regimes, the laser fluences of 0.45 J/cm2, 0.75 J/cm2, and 1.35 J/cm2, respectively, were considered by the FEM model and simulated. The selection of the input energy range was guided by temperature considerations, specifically tailored to facilitate the transition of the Si sample through distinct phases—from its solid state to a plastic state and ultimately to a molten phase. Thus, the stated values of laser fluence were selected after numerous runs. In the thermoelastic regime (laser fluence 0.45 J/cm2), the highest temperature achieved was 1125 °C, and as a result, only elastic deformations were observed. For the laser fluence of 0.75 J/cm2, the maximum temperature value was 1250 °C, observed at the center of the sample, and thus, plastic deformations in the area of the laser spot occurred. When laser fluence became 1.35 J/cm2, the energy absorbed by the Si target led to temperature values greater than the melting point (1412 °C) of Si, and a small volume within the region of the laser spot melted.
For all three regimes, a bulge was initially created at the center of the target due to the intense heating, and an ultrasonic wave was generated at the edge of the bulge’s ends and propagated in the solid target. The left column of Figure 2 shows a 150 × 150 μm2 rectangular area in the center of the model, where the SAW was clearly observable 22 ns after the laser irradiation, in every regime, within a distance ranging from 58 μm to 60 μm from the center of the laser spot. A lineout of the vertical displacements is enclosed in the lower right corner of each figure, with an inset of zoomed details around the SAW. The minimum value of the colormaps is set to −50 pm for the SAW to be clearly visible. Therefore, in the right column of Figure 2, a 40 × 40 μm2 square area around the focal spot depicts the zoomed center of the target, including the colormap in a full range, for a complete description of the target’s response. Specifically, in the case of the thermoelastic regime, the SAW at the 22nd ns had a width of 6.5 μm and an amplitude of 22 pm. At this time, the bulge formed at the center of the target had a diameter of 38 μm and an amplitude of 18 nm, and a maximum Von Mises stress value of 0.73 GPa was computed within the bulge volume where the temperature was approximately 1100 °C. It should be noted that in the thermoelastic regime, the maximum temperature and Von Mises stress values of 1125 °C and 0.80 GPa, respectively, were both achieved in the 17th ns. In the case of laser fluence 0.75 J/cm2, plastic deformations occurred. The SAW in the 22nd ns had a width of 5 μm and an amplitude of 35 pm. The bulge at the center of the target had a diameter of 40 μm and an amplitude of 30 nm. The maximum Von Mises stress had a value of 0.87 GPa, computed within the bulge volume where the temperature approximates 1245 °C. It is noticed that in the plastic regime, the maximum Von Mises stress had a value of 0.95 GPa, overcoming the yield stress of Si (890 MPa) in the 15th ns, when the temperature is 1230 °C, while the temperature reaches its maximum value of 1250 °C in the 18th ns. The formation of plastic strains began in the 15th ns, within the area of the laser spot. When laser fluence was increased to 1.35 J/cm2, the SAW in the 22nd ns had a width of 4 μm and an amplitude of 90 pm. The bulge in the center of the target had a diameter of 41 μm and an amplitude of 60 nm. At this time, the maximum Von Mises stress had a value of 0.92 GPa, computed within the bulge volume where the temperature was approximately 1815 °C. The maximum Von Mises stress had a value of 1.01 GPa at 15 ns when the temperature was 1730 °C, while the maximum temperature value of 1970 °C was reached in the 17th ns. The formation of plastic strains began in the 12th ns within the area of the laser spot, while in the 15th ns, melting started. In the inset of Figure 2c (right side), it is evident that for radial distances of 4 μm to 6 μm, nonlinearities occur due to the melting effect. The smooth transition becomes rough due to the high temperature gradients and the phase change from solid to melted.
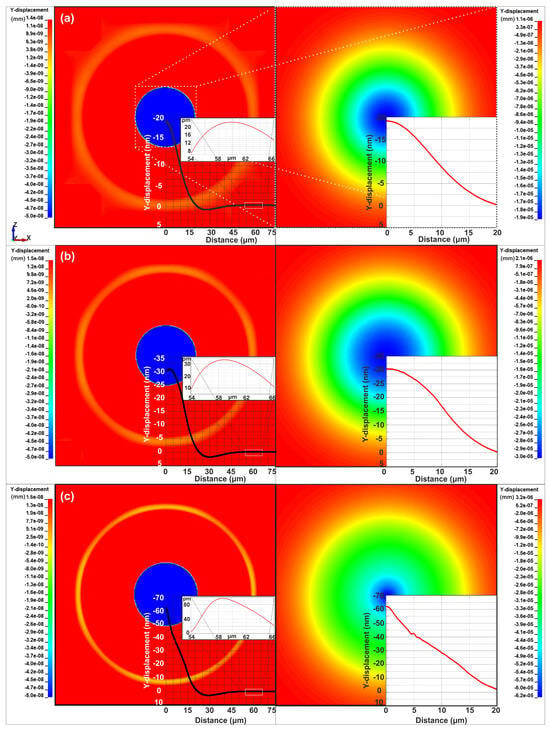
Figure 2.
Simulation results of the vertical Y displacement of the Si target surface at 22 ns for (a) the thermoelastic (laser fluence 0.45 J/cm2), (b) the plastic (laser fluence 0.75 J/cm2), and (c) the melting regime (laser fluence 1.35 J/cm2), within a 150 × 150 μm2 square area in the center of the model. The inset graphs show the displacement lineouts from the origin, in the center of the focal spot, along the radial X axis where zoomed graph details provide the SAW generation characteristics from 54 μm to 66 μm (left column). Zoomed details of the bulge within a 40 × 40 μm2 square area in the center of the model are also depicted (right column). Also, for the colorbar range of the contour plot 1.0e-06 is equivalent to 1 × 10−6.
Representative simulation results of the temperature, the vertical displacements, the Von Mises stresses, and the plastic strain distributions for the three fluences are demonstrated in Figure 3, at the crucial temporal time of the 17th ns after the laser irradiation, when the maximum temperature values of 1125 °C, 1250 °C, and 1970 °C were computed, respectively, for each regime.
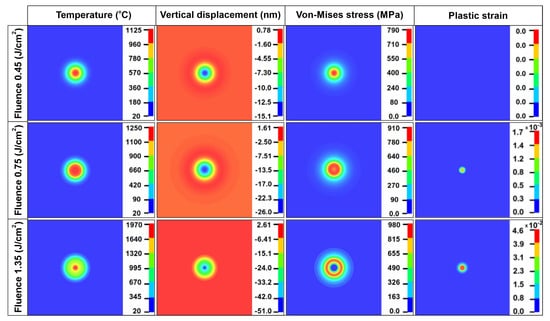
Figure 3.
Temperature distribution, vertical displacement, Von-Mises stress, and plastic strain distributions in the 17th ns after laser irradiation.
The vertical displacement results show that the bulge created in the area of the laser spot in the melting regime had an amplitude of 51 nm, three times greater compared to the thermoelastic and two times greater compared to the plastic regime amplitudes. The maximum Von Mises stress value in the thermoelastic regime was 790 MPa, lower than the yield stress of Si; thus, plastic strains did not exist. The maximum Von Mises stress value in the case of fluence 0.75 J/cm2 was 910 MPa, slightly greater than the yield stress (896 MPa [27]); thus, a small region in the center of the target entered the plastic regime. The plastic strain results indicate that permanent deformations within an area of a radius of 6 μm developed, since stresses overcome the yield stress of Si. The maximum Von Mises stress value in the melting regime, for the fluence of 1.35 J/cm2, was 1 GPa in the area of the laser spot in the center of the target where permanent deformations occur. In this regime, an area of a radius of 12 μm was permanently deformed.
Since heat conduction governs this coupled thermomechanical problem, four collinear nodes with (x,y,z) coordinates (in μm) x0 = (0,0,0), x1 = (4,0,0), x2 = (8,0,0), and x3 = (12,0,0) were selected to monitor the thermal and stress response of the target in the area of the bulge in relation to time, as shown in Figure 4. For all three regimes, a maximum temperature was computed at the peak of the Gaussian laser pulse at 17 ns. In the thermoelastic regime for both temperature and stress distributions, a similar behavior was observed, following linearly the Gaussian heat source term distribution. In the plastic regime, a nonlinear behavior was observed for both temperature and stress distributions for distances lower than 5 μm from the center of the laser spot, and in this region, temperature values above 1000 °C lasted for about 0.1 μs. Moreover, in this region, residual stresses developed. At 0.1 μs, the maximum temperature and the maximum Von Mises stress values were lower than the melting point and the yield strength, respectively. In the melting regime, within an area of a radius of less than 5 μm in the center of the target, a plateau in the temperature distribution was developed with varying duration that depended on the distance from the laser spot. Residual stresses with values greater than 890 MPa developed 600 ns after the laser initiation. The initial zero stress values are attributed to the phase change of the irradiated material. For distances greater than 5 μm from the focal spot, the thermomechanical dynamics follow the same behavior as described in the plastic regime.
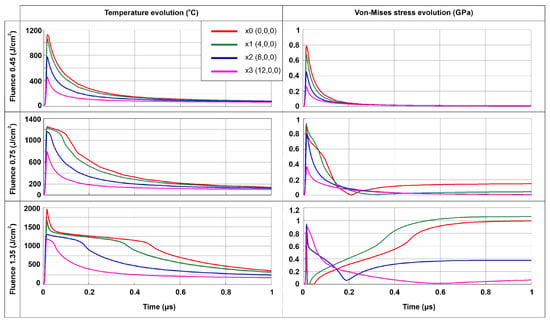
Figure 4.
The dynamic evolution of stresses and of temperature in relation to time for the thermoelastic, plastic, and melting regimes.
Figure 5 presents four characteristic temporal moments of temperature (left column) and vertical displacement (right column) in relation to distance from the center of the irradiation for the model in thermoelastic, plastic, and melting cases. At 9 ns for all three different cases, a smooth Gaussian distribution is evident for both temperature and displacement, since the temperature was below the melting point and only elastic phenomena occurred. From the 13th ns and later on, the temperature distribution became nonlinear for both plastic and melting cases and influenced the mechanical behavior of the Si sample. The radial extension of the temperature nonlinearity in space was less than 15 μm in the melting regime and less than 10 μm in the plastic regime. These radial distance values are in agreement with the developed plastic strain regions, as previously discussed regarding the results presented in Figure 3. Moreover, the displacement distribution for the melting case was affected by the temperature distribution, and this is evident from the 13th ns and later, where an irregular envelope bulge was created, characterized by geometrical nonlinearities extended at a distance of 10 μm in the 24th ns. At 17 ns, the highest temperatures developed for all three cases, while at 24 ns, a maximum amplitude for the generated SAW of about 30 pm, 40 pm, and 95 pm was observed for the elastic, plastic, and melting cases, respectively.
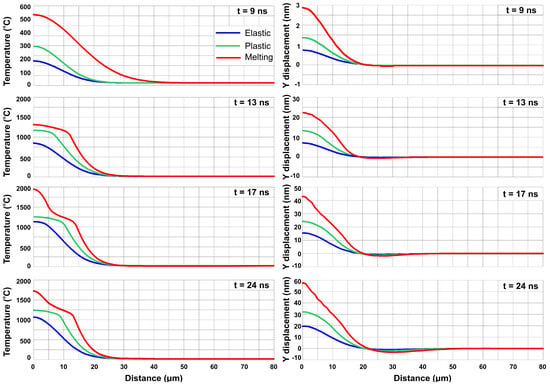
Figure 5.
Temperature (left column) and vertical displacement (right column) in relation to distance from the center of the irradiation for the model in thermoelastic, plastic, and melting cases.
3.2. Ultrasound Evolution
Figure 6 shows the spatial evolution of the vertical displacement for six different temporal moments (a)–(f) in the melting regime. For each of the graphs, a zoomed detail inset from 50 μm to 225 μm is provided to demonstrate the spatial characteristics and the dynamic evolution of the generation and propagation of the SAW. Observing the zoomed insets, it is evident that next to the deformed central bulge within the focal spot, a secondary bulge starts to form, having an initial amplitude of 0.1 nm and a width of 0.022 μm at 23 ns. This secondary bulge evolves in time with a mean velocity of 500 m/sec, and in the 51st ns, its amplitude approximates 0.2 nm with a width of 0.037 μm. At the same time, an ultrasound having an irregular envelope shape is generated. In the 23rd ns, the generation of two peaks on the top of the secondary bulge is observed, and the generation of the SAW is initiated. These peaks become three in the 27th and gradually in the 51st ns take the form of the SAW envelope presented in the inset of Figure 6f, consisting of seven peaks which propagate the surface of the Si target. This feature is only evident in the melting regime due to the high nonlinear thermal stresses developed within a circle area of 50 μm radius at 22 ns and the influence of thermal expansion. The computed mean envelope velocity of this SAW was computed as ~5000 m/s, while using the following analytical equations [39], the SAW velocity was found to be 5200 m/s.
where Cs is the shear velocity and CR is the SAW velocity. Due to the low thermal expansion coefficient of Si and its high penetration depth, the generated SAW has a small amplitude, and a long distance and time range is needed for the ultrasound to be generated, evolve, and propagate, in contradiction to our previous research works’ results [25,26], wherein the same laser source was used to irradiate Au, Al, and Cu. Compared to Si, the metallic film targets have a small penetration depth and greater thermal expansion coefficients, and thus, more than one SAW was generated. Moreover, the results of this study qualitatively agree with the results of Liu et al. [40], where molecular dynamic simulations showed that SAWs undergo nonlinear sharpening during propagation due to the elastic nonlinearity of single-crystal Si, which may lead to material fracture. To the authors’ knowledge, this the first time that these nonlinear phenomena were monitored via FEM simulations.
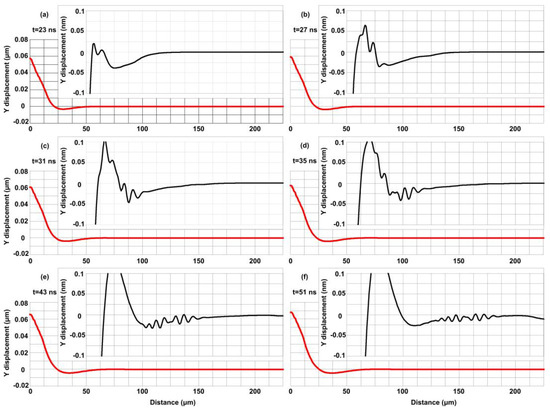
Figure 6.
Spatial evolution of the normal displacement for six different temporal moments (a–f) for the melting regime. Insets of zoomed details are also shown.
Moreover, Figure 7 shows the contour plots for the spatial evolution of the vertical displacement for the same temporal moments presented in Figure 6. The SAW generation and propagation in the form of concentric circles are in accordance with the line-out graphical results described in Figure 6 and correspond to the propagation of the SAW envelope, traveling with a mean velocity of 5000 m/s.
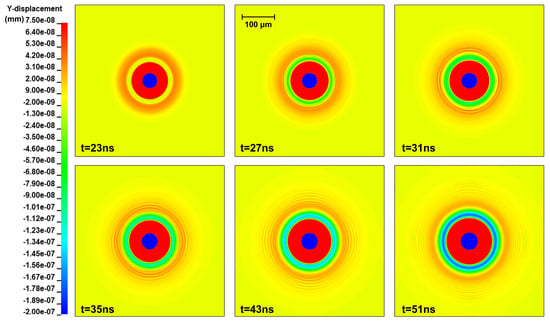
Figure 7.
Contour plots for the spatial evolution of the vertical displacement for six different temporal moments in the melting regime. Also, for the colorbar range of the contour plot 1.0e-08 is equivalent to 1 × 10−8.
4. Conclusions
The dynamic behavior of solid Si targets irradiated by nanosecond laser pulses is here studied with transient, thermοmechanical 3D FEM simulations. The dynamic phase changes of the irradiated target and the generation and propagation of a SAW are provided using a FEM model of a very fine uniformly structured mesh. The new findings indicate that: (a) due to the low thermal expansion coefficient and the high penetration depth of Si, the amplitude of the generated SAW is small, and the time and distance needed for the ultrasound to be generated is higher compared to metals such as Au, Cu, and Al and (b) in the melting regime, the development of high nonlinear thermal stresses leads to the generation of an irregular bulge and a secondary bulge of small amplitude, along with the generation and formation of an irregular and nonlinear ultrasound which propagates the solid Si target. The multiphysics simulation model presented herein allows for the determination of the spatiotemporal details of the SAW generation based on the thermomechanical properties of Si and simultaneously is used to monitor its propagation dynamics. The results are important for applications such as nondestructive material characterization, industrial applications for accurate material inspection, medical imaging, laser material processing, metallization, wafering, and dewetting.
More insights into the generation mechanism and the formation of the irregular SAW envelope may be provided by future simulations and experiments focusing on the influence of the laser fluence and spot characteristics on the SAW generation. The developed high-resolution multiphysics simulation model of Si allows for further modeling of unsymmetric features and multiscale studies since the crucial areas of high gradient temperatures and stresses are identified here. These findings are of crucial importance, especially for experimental diagnostics regarding the material properties and laser machining process evaluations of Si, in relation to the laser fluence used.
Author Contributions
Conceptualization, V.D. and E.K.; methodology, V.D. and E.K.; software, H.P.; validation, M.B., M.T. and N.A.P.; investigation, H.P.; data curation, H.P.; writing—original draft preparation, H.P.; writing—review and editing, V.D., E.K., M.B., M.T. and N.A.P.; supervision, V.D. and E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available within the article.
Acknowledgments
This work was supported by computational time granted by the Greek Research & Technology Network (GRNET) in the National HPC facility ARIS under project ID pr013024-LaMPIOS II.
Conflicts of Interest
The authors declare no conflict of interest.
References
- OPTEC. Laser Material Removal: Drilling Cutting and Marking; University of Central Florida: Orlando, FL, USA, 2008. [Google Scholar]
- Steen, W.M.; Mazumder, J. Laser Material Processing, 4th ed.; Springer: London, UK, 2010. [Google Scholar]
- Yang, J.; Sun, S.; Brandt, M.; Yan, W. Experimental investigation and 3D finite element prediction of the heat affected zone during laser assisted machining of Ti6Al4V alloy. J. Mater. Process. Technol. 2010, 210, 2215–2222. [Google Scholar] [CrossRef]
- Available online: https://www.worldoflasers.com/laserapplindustrial.htm (accessed on 26 September 2023).
- Pouli, P.; Papakonstantinou, E.; Frantzikinaki, K.; Panou, A.; Frantzi, G.; Vasiliadis, C.; Fotakis, C. The two-wavelength laser cleaning methodology; theoretical background and examples from its application on CH objects and monuments with emphasis to the Athens Acropolis sculptures. Herit. Sci. 2016, 4, 9. [Google Scholar] [CrossRef]
- Brown, M.S.; Arnold, C.B. Fundamentals of Laser-Material Interaction and Application to Multiscale Surface Modification. In Laser Precision Microfabrication; Springer: Berlin/Heidelberg, Germany, 2010; Available online: https://spikelab.mycpanel.princeton.edu/papers/book02.pdf (accessed on 26 September 2023).
- Guo, L.; Geng, S.; Gao, X.; Wang, W. Numerical simulation of heat transfer and fluid flow during nanosecond pulsed laser processing of Fe78Si9B13 amorphous alloys. Int. J. Heat Mass Transf. 2021, 170, 121003. [Google Scholar] [CrossRef]
- Gao, J.; Cao, Y.; Lu, L.; Hu, Z.; Wang, K.; Guo, F.; Yan, Y. Study on the interaction between nanosecond laser and 6061 aluminum alloy considering temperature dependence. J. Alloys Compd. 2022, 892, 162044. [Google Scholar] [CrossRef]
- Kyota, H.; Higashi, M.; Curosu, T.; Lida, M. Numerical simulation and validation of subsurface modification and crack formation induced by nanosecond-pulsed laser processing in monocrystalline silicon. J. Appl. Phys. 2021, 130, 239901. [Google Scholar] [CrossRef]
- Acosta-Zepeda, C.; Saavedra, P.; Bonse, J.; Haro-Poniatowski, E. Modeling of silicon surface topographies induced by single nanosecond laser pulse induced melt-flows. J. Appl. Phys. 2019, 125, 175101. [Google Scholar] [CrossRef]
- Zeng, W.; Yao, Y. Numerical simulation of laser-generated ultrasonic waves for detection surface defect on a cylinder pipe. Optik 2020, 212, 164650. [Google Scholar] [CrossRef]
- Orphanos, Y.; Dimitriou, V.; Kaselouris, E.; Bakarezos, E.; Vainos, N.; Tatarakis, M.; Papadogiannis, N.A. An integrated method for material properties characterization based on pulsed laser generated surface acoustic waves. Microelectron. Eng. 2013, 112, 249–254. [Google Scholar] [CrossRef]
- Marine, W.; Bulgakova, N.M.; Patrone, L.; Ozerov, I. Insight into electronic mechanisms of nanosecond-laser ablation of silicon. J. Appl. Phys. 2008, 103, 094902. [Google Scholar] [CrossRef]
- Darif, M.; Semmar, N. Numerical Simulation of Si Nanosecond Laser Annealing by COMSOL Multiphysics. In Proceedings of the COMSOL Conference, Hannover, Germany, 5 November 2008. [Google Scholar]
- Erdoğan, E.; Kundakçı, M.; Mantarcı, A. InGaN thin film deposition on Si(100) and glass substrates by termionic vacuum arc. J. Phys. Conf. Ser. 2016, 707, 012019. [Google Scholar] [CrossRef]
- Domke, M.; Egle, B.; Stroj, S.; Bodea, M.; Schwarz, E.; Fasching, G. Ultrafast-laser dicing of thin silicon wafers: Strategies to improve front- and backside breaking strength. Appl. Phys. A 2017, 123, 746. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Z.; Zhang, Z.; Yue, Y.; Li, D.; Maple, C. Direct modification of silicon surface by nanosecond laser interference lithography. Appl. Surf. Sci. 2013, 282, 67–72. [Google Scholar] [CrossRef]
- Ernst, O.C.; Uebel, D.; Kayser, S.; Lange, F.; Teubner, T.; Boeck, T. Revealing all states of dewetting of a thin gold layer on a silicon surface by nanosecond laser conditioning. Appl. Surf. Sci. Adv. 2021, 3, 100040. [Google Scholar] [CrossRef]
- Podymova, N.B.; Kalashnikov, I.E.; Bolotova, L.K.; Kobeleva, L.I. Laser-ultrasonic nondestructive evaluation of porosity in particulate reinforced metal-matrix composites. Ultrasonics 2019, 99, 105959. [Google Scholar] [CrossRef] [PubMed]
- Zhong, D.; Li, Z. Assessing the dynamic characteristics of a femtosecond laser micro plasma expansion process with an optical fiber sensing probe. In Frontier Research and Innovation in Optoelectronics Technology and Industry; CRC Press: Boca Raton, FL, USA, 2018; pp. 235–239. [Google Scholar]
- Kautek, W.; Rudolph, P.; Daminelli, G.; Krüger, J. Physico-chemical aspects of femtosecond-pulse-laser-induced surface nanostructures. Appl. Phys. A 2005, 81, 65–70. [Google Scholar] [CrossRef]
- Doukas, A.G.; Flotte, T.J. Physical characteristics and biological effects of laser-induced stress waves. Ultrasound Med. Biol. 1996, 22, 151–164. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Hong, M. Femtosecond Laser Precision Engineering: From Micron, Submicron, to Nanoscale. Ultrafast Sci. 2021, 2021, 9783514. [Google Scholar] [CrossRef]
- Lim, A.E.; Goh, S. Effect of Microchannel Diameter on Electroosmotic Flow Hysteresis. Energies 2023, 16, 2154. [Google Scholar] [CrossRef]
- Dimitriou, V.; Kaselouris, E.; Orphanos, Y.; Bakarezos, M.; Vainos, N.; Tatarakis, M.; Papadogiannis, N.A. Three-dimensional transient behavior of thin films surface under pulsed laser excitation. Appl. Phys. Lett. 2013, 103, 114104. [Google Scholar] [CrossRef]
- Kaselouris, E.; Nikolos, I.K.; Orphanos, Y.; Bakarezos, E.; Papadogiannis, N.A.; Tatarakis, M.; Dimitriou, V. Elastoplastic study of nanosecond-pulsed laser interaction with metallic films using 3D multiphysics fem modeling. Int. J. Damage Mech. 2016, 25, 42–55. [Google Scholar] [CrossRef]
- Kaselouris, E.; Skarvelakis, E.; Nikolos, I.K.; Stavroulakis, G.E.; Orphanos, Y.; Bakarezos, E.; Papadogiannis, N.A.; Tatarakis, M.; Dimitriou, V. Simulation of the transient behavior of matter with characteristic geometrical variations & defects irradiated by nanosecond laser pulses using FEA. Key Eng. Mater. 2016, 665, 157–160. [Google Scholar]
- Hallquist, J. LS-DYNA Theory Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006. [Google Scholar]
- Aris Documentation. Available online: http://doc.aris.grnet.gr/system/hardware/ (accessed on 26 September 2023).
- Orphanos, Y.; Kosma, K.; Kaselouris, E.; Vainos, N.; Dimitriou, V.; Bakarezos, M.; Tatarakis, M.; Papadogiannis, N.A. Integrated nanosecond laser full-field imaging for femtosecond laser-generated surface acoustic waves in metal film-glass substrate multilayer materials. Appl. Phys. A 2019, 125, 269. [Google Scholar] [CrossRef]
- Available online: https://www.azom.com/properties.aspx?ArticleID=599 (accessed on 26 September 2023).
- Available online: https://encyclopediaofmath.org/wiki/Lam%C3%A9_constants (accessed on 26 September 2023).
- Liu, B.; Li, S.; Li, R.; Chen, C.; Liang, L. Finite element simulation and experimental research on microcutting mechanism of single crystal silicon. Int. J. Adv. Manuf. Technol. 2020, 110, 909–918. [Google Scholar] [CrossRef]
- Available online: https://www.virginiasemi.com/?cont_uid=50 (accessed on 26 September 2023).
- Masolin, A.; Bouchard, P.O.; Martini, R.; Bernacki, M. Thermo-mechanical and fracture properties in single-crystal silicon. J. Mater. Sci. 2013, 48, 979–988. [Google Scholar] [CrossRef]
- Available online: http://www.ioffe.ru/SVA/NSM/Semicond/Si/thermal.html (accessed on 26 September 2023).
- Available online: https://www.nuclear-power.com/silicon-specific-heat-latent-heat-vaporization-fusion/ (accessed on 26 September 2023).
- Available online: https://studylib.net/doc/6931620/10.7-given-here-are-the-solidus-and-liquidus-temperatures (accessed on 26 September 2023).
- Zhan, Y.; Liu, C.; Zhang, F.; Qiu, Z. Experimental study and finite element analysis based on equivalent load method for laser ultrasonic measurement of elastic constants. Ultrasonics 2016, 69, 243–247. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Lin, B.; Liang, X.; Du, A.; Ma, X. Fracture of single crystal silicon caused by nonlinear evolution of surface acoustic waves. Eng. Fract. Mech. 2022, 269, 108505. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).