Effects of the Number of Classes and Pressure Map Resolution on Fine-Grained In-Bed Posture Classification
Abstract
:1. Introduction
- Analyze and validate the use of ML algorithms in the classification of a large number of bedridden people postures, which will help to identify the real position of the bedridden person with high accuracy. Although these algorithms have already been used for posture classification with good results, their application to as many as 28 postures had not yet been evaluated.
- Analyze the impact of pressure map resolution on the accuracy of ML algorithms in classifying bedridden people postures. There are different studies conducted using varying amounts of sensors, but comparing the results of the different algorithms on the same dataset will allow for a better understanding of how the accuracy is affected by the number of sensors and demonstrate that a solution considering fewer sensors, which is not only cheaper but also computationally lighter, is a viable solution.
- Use the PoPu dataset [6], one of the datasets that presents a greater number of different postures and a greater number of samples obtained from real people. To the best of our knowledge, this is the first time the dataset has been used in a posture classification study.
2. Related Work
3. Dataset Description
4. Methodology
4.1. Algorithms
4.2. Experiments and Results
- k-NN: k = 3;
- SVC: kernel = linear, C = 0.025;
- Decision tree: max_depth = 30;
- Random forest: max_depth = 30;
- Multilayer perceptron: alpha = 0.001, max_iterations = 1000
4.2.1. Initial Experiments
- Normalized (0–1) pressure values;
- Participant sex;
- Participant weight;
- Participant height.
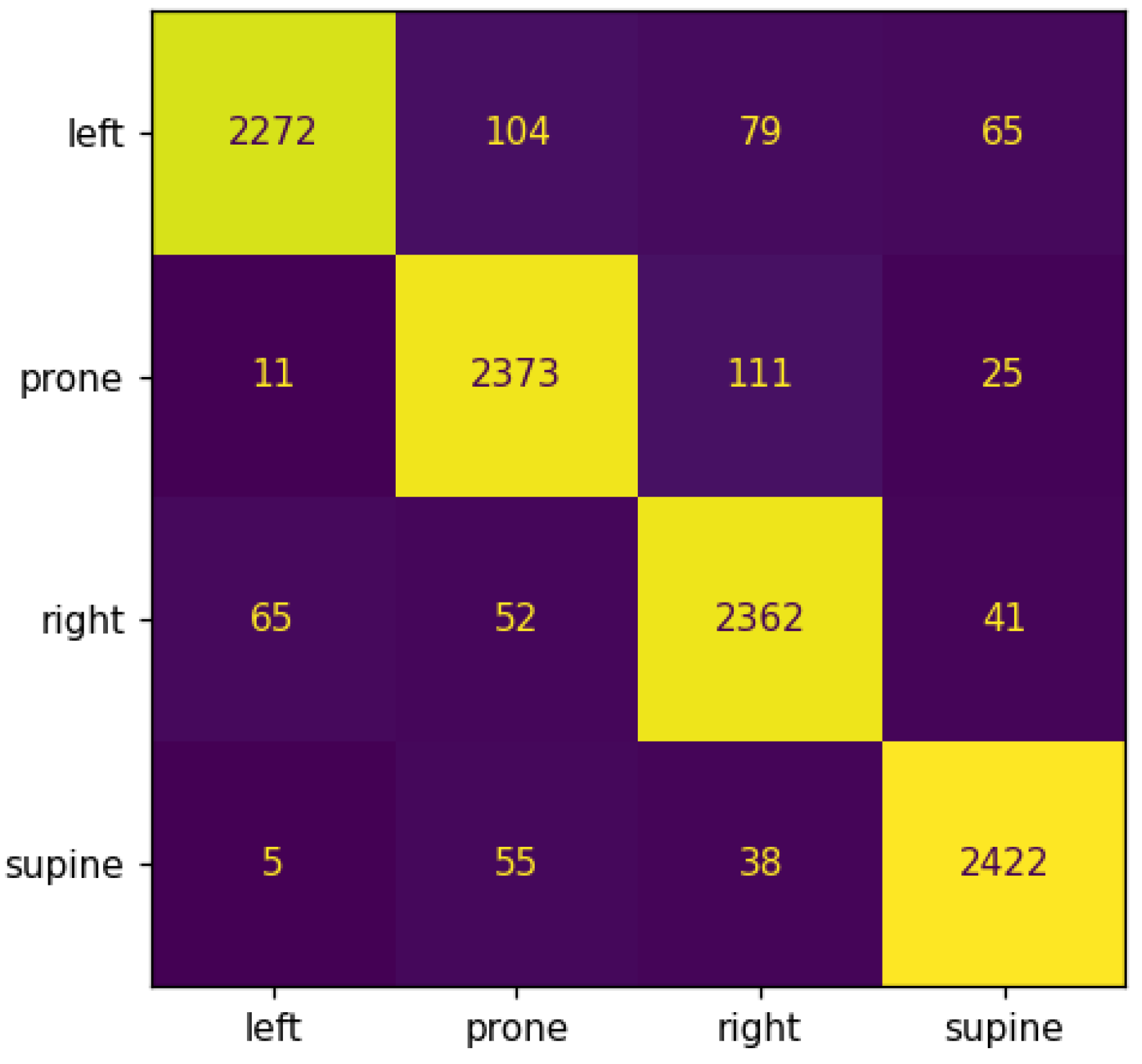
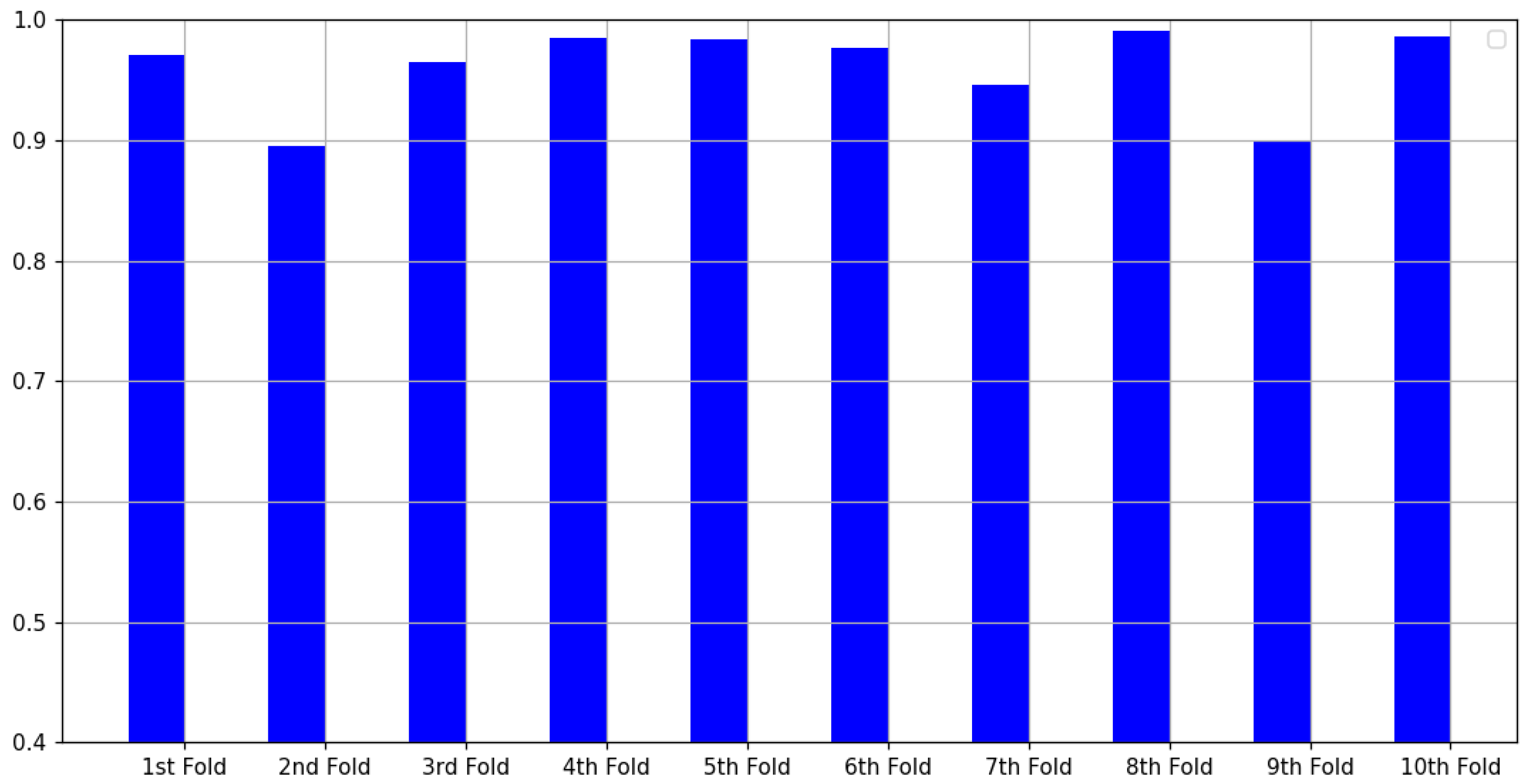
4.2.2. Further Validation
- Average accuracy (%): 95.96%
- Standard deviation: 0.0356
- Average precision: 0.9596
- Average recall: 0.9596
- Average F1-score: 0.9596
- Average accuracy (%): 96.25%
- Standard deviation: 0.0741
- Average precision: 0.9633
- Average recall: 0.9625
- Average F1-score: 0.9603
4.2.3. Pre-Calculated Main Posture Experiment
4.2.4. Pressure Only Experiment
4.2.5. Pressure Matrix Resolution Reduction Experiments
5. Discussion and Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nguyen, H.H.; Dang, B.L.; Dam, H.P.; Dang, Q.H.; Nguyen, D.M.; Vo, V.A. A novel implementation of sleeping posture classification using RANC ecosystem. In Proceedings of the 2022 International Conference on Advanced Technologies for Communications (ATC), Ha Noi, Vietnam, 20–22 October 2022; pp. 369–374. [Google Scholar] [CrossRef]
- Hudec, R.; Matúška, S.; Kamencay, P.; Benco, M. A Smart IoT System for Detecting the Position of a Lying Person Using a Novel Textile Pressure Sensor. Sensors 2021, 21, 206. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Santacruz, E.; Cruz-Santos, W.; Gamboa-Zúñiga, M. Design and Implementation of an Intelligent System for Controlling a Robotic Hospital Bed for Patient Care Assistance. Comput. Sist. 2015, 19, 467–474. [Google Scholar] [CrossRef]
- Stern, L.; Roshan Fekr, A. In-Bed Posture Classification Using Deep Neural Network. Sensors 2023, 23, 2430. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, L.; Ribeiro, F.; Metrôlho, J. Pressure-Based Posture Classification Methods and Algorithms: A Systematic Review. Computers 2023, 12, 104. [Google Scholar] [CrossRef]
- Fonseca, L.; Ribeiro, F.; Metrôlho, J.; Santos, A.; Dionisio, R.; Amini, M.M.; Silva, A.F.; Heravi, A.R.; Sheikholeslami, D.F.; Fidalgo, F.; et al. PoPu-Data: A Multilayered, Simultaneously Collected Lying Position Dataset. Data 2023, 8, 120. [Google Scholar] [CrossRef]
- Hu, Q.; Tang, X.; Tang, W. A Real-Time Patient-Specific Sleeping Posture Recognition System Using Pressure Sensitive Conductive Sheet and Transfer Learning. IEEE Sens. J. 2021, 21, 6869–6879. [Google Scholar] [CrossRef]
- Matar, G.; Lina, J.-M.; Kaddoum, G. Artificial Neural Network for in-Bed Posture Classification Using Bed-Sheet Pressure Sensors. IEEE J. Biomed. Health Inform. 2020, 24, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Elsharif, E.; Drawil, N.; Kanoun, S. Automatic Posture and Limb Detection for Pressure Ulcer Risk Assessment. In Proceedings of the 2021 IEEE 1st International Maghreb Meeting of the Conference on Sciences and Techniques of Automatic Control and Computer Engineering MI-STA, Tripoli, Libya, 25–27 May 2021; pp. 142–149. [Google Scholar] [CrossRef]
- Fonseca, L.; Ribeiro, F.; Metrôlho, J. Lying-People Pressure-Map Datasets: A Systematic Review. Data 2023, 8, 12. [Google Scholar] [CrossRef]
- Mihálik, O.; Sýkora, T.; Husák, M.; Fiedler, P. In-Bed Posture Classification Based on Sparse Representation in Redundant Dictionaries. IFAC-PapersOnLine 2022, 55, 374–379. [Google Scholar] [CrossRef]
- Kim, T.-H.; Hong, Y.-S. Prediction of Body Weight of a Person Lying on a Smart Mat in Nonrestraint and Unconsciousness Conditions. Sensors 2020, 20, 3485. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Liang, H.; Xiao, F.; Wang, G.; Hussain, R. Pressure Image Recognition of Lying Positions Based on Multi-feature value Regularized Extreme Learning Algorithm. Appl. Math. Nonlinear Sci. 2023, 8, 559–572. [Google Scholar] [CrossRef]
- Tam, A.Y.-C.; So, B.P.-H.; Chan, T.T.-C.; Cheung, A.K.-Y.; Wong, D.W.-C.; Cheung, J.C.-W. A Blanket Accommodative Sleep Posture Classification System Using an Infrared Depth Camera: A Deep Learning Approach with Synthetic Augmentation of Blanket Conditions. Sensors 2021, 21, 5553. [Google Scholar] [CrossRef]
- Pouyan, M.B.; Birjandtalab, J.; Heydarzadeh, M.; Nourani, M.; Ostadabbas, S. A pressure map dataset for posture and subject analytics. In Proceedings of the 2017 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Orlando, FL, USA, 16–19 February 2017; pp. 65–68. [Google Scholar] [CrossRef]
- Liu, S.; Huang, X.; Fu, N.; Li, C.; Su, Z.; Ostadabbas, S. Simultaneously-Collected Multimodal Lying Pose Dataset: Enabling In-Bed Human Pose Monitoring. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 1106–1118. [Google Scholar] [CrossRef]
- Clever, H.M.; Erickson, Z.; Kapusta, A.; Turk, G.; Liu, C.K.; Kemp, C.C. Bodies at Rest: 3D Human Pose and Shape Estimation from a Pressure Image using Synthetic Data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Ren, W.; Ma, O.; Ji, H.; Liu, X. Human Posture Recognition Using a Hybrid of Fuzzy Logic and Machine Learning Approaches. IEEE Access 2020, 8, 135628–135639. [Google Scholar] [CrossRef]
- Tactile Surface Sensor|Real-Time Surface Pressure Mapping Technology|Pressure Pad|Force Sensitive Resistor|Matrix Tactile Sensor|Pressure Mapping System FSR. Available online: https://tactilus.net/ (accessed on 1 June 2023).



| Posture Variations | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Supine |  |  |  |  |  |  |  |
| Prone |  |  |  |  |  |  |  |
| Facing left |  |  |  |  |  |  |  |
| Facing right |  |  |  |  |  |  |  |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 92.11% | 91.31% | 80.07% | 95.32% | 95.60% |
| Standard Deviation | 0.0071 | 0.0259 | 0.0331 | 0.0179 | 0.0196 |
| Average Precision | 0.9211 | 0.9131 | 0.8007 | 0.9532 | 0.9560 |
| Average Recall | 0.9211 | 0.9131 | 0.8007 | 0.9532 | 0.9560 |
| Average F1 score | 0.9211 | 0.9131 | 0.8007 | 0.9532 | 0.9560 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 43.87% | 58.40% | 35.66% | 63.58% | 59.50% |
| Standard Deviation | 0.0173 | 0.0245 | 0.0243 | 0.0240 | 0.0278 |
| Average Precision | 0.4387 | 0.5840 | 0.3566 | 0.6358 | 0.5950 |
| Average Recall | 0.4387 | 0.5840 | 0.3566 | 0.6358 | 0.5950 |
| Average F1-score | 0.4387 | 0.5840 | 0.3566 | 0.6358 | 0.5950 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 43.95% | 58.84% | 46.64% | 64.10% | 59.60% |
| Standard Deviation | 0.0174 | 0.0260 | 0.0265 | 0.0178 | 0.0266 |
| Average Precision | 0.4395 | 0.5884 | 0.4664 | 0.6410 | 0.5960 |
| Average Recall | 0.4395 | 0.5884 | 0.4664 | 0.6410 | 0.5960 |
| Average F1-score | 0.4395 | 0.5884 | 0.4664 | 0.6410 | 0.5960 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 92.07% | 91.25% | 80.05% | 95.37% | 95.24% |
| Standard Deviation | 0.0073 | 0.0258 | 0.0298 | 0.0156 | 0.0218 |
| Average Precision | 0.9207 | 0.9125 | 0.8005 | 0.9537 | 0.9524 |
| Average Recall | 0.9207 | 0.9125 | 0.8005 | 0.9537 | 0.9524 |
| Average F1-score | 0.9207 | 0.9125 | 0.8005 | 0.9537 | 0.9524 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 43.80% | 58.25% | 35.75% | 63.06% | 59.10% |
| Standard Deviation | 0.0175 | 0.0240 | 0.0314 | 0.0304 | 0.0244 |
| Average Precision | 0.4380 | 0.5825 | 0.3575 | 0.6306 | 0.5910 |
| Average Recall | 0.4380 | 0.5825 | 0.3575 | 0.6306 | 0.5910 |
| Average F1-score | 0.4380 | 0.5825 | 0.3575 | 0.6306 | 0.5910 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 91.34% | 91.16% | 79.07% | 95.29% | 95.31% |
| Standard Deviation | 0.0115 | 0.0252 | 0.0379 | 0.0130 | 0.0185 |
| Average Precision | 0.9134 | 0.9116 | 0.7907 | 0.9529 | 0.9531 |
| Average Recall | 0.9134 | 0.9116 | 0.7907 | 0.9529 | 0.9531 |
| Average F1-score | 0.9134 | 0.9116 | 0.7907 | 0.9529 | 0.9531 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 43.67% | 57.80% | 34.52% | 61.25% | 58.59% |
| Standard Deviation | 0.0169 | 0.0214 | 0.0250 | 0.0152 | 0.0281 |
| Average Precision | 0.4367 | 0.5780 | 0.3452 | 0.6125 | 0.5859 |
| Average Recall | 0.4367 | 0.5780 | 0.3452 | 0.6125 | 0.5859 |
| Average F1-score | 0.4367 | 0.5780 | 0.3452 | 0.6125 | 0.5859 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 87.90% | 88.91% | 75.94% | 94.23% | 94.59% |
| Standard Deviation | 0.0188 | 0.0168 | 0.0322 | 0.0124 | 0.0178 |
| Average Precision | 0.8790 | 0.8891 | 0.7594 | 0.9423 | 0.9459 |
| Average Recall | 0.8790 | 0.8891 | 0.7594 | 0.9423 | 0.9459 |
| Average F1-score | 0.8790 | 0.8891 | 0.7594 | 0.9423 | 0.9459 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 38.87% | 53.85% | 32.37% | 55.76% | 53.86% |
| Standard Deviation | 0.0336 | 0.0230 | 0.0135 | 0.0348 | 0.0238 |
| Average Precision | 0.3887 | 0.5385 | 0.3237 | 0.5576 | 0.5386 |
| Average Recall | 0.3887 | 0.5385 | 0.3237 | 0.5576 | 0.5386 |
| Average F1-score | 0.3887 | 0.5385 | 0.3237 | 0.5576 | 0.5386 |
| Algorithm | k-NN | Linear SVM | Decision Tree | Random Forest | MLP |
|---|---|---|---|---|---|
| Average Accuracy % | 68.93% | 77.97% | 66.44% | 83.03% | 81.62% |
| Standard Deviation | 0.0273 | 0.0132 | 0.0441 | 0.0148 | 0.218 |
| Average Precision | 0.6893 | 0.7797 | 0.6644 | 0.8303 | 0.8162 |
| Average Recall | 0.6893 | 0.7797 | 0.6644 | 0.8303 | 0.8162 |
| Average F1-score | 0.6893 | 0.7797 | 0.6644 | 0.8303 | 0.8162 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fonseca, L.; Ribeiro, F.; Metrôlho, J. Effects of the Number of Classes and Pressure Map Resolution on Fine-Grained In-Bed Posture Classification. Computation 2023, 11, 239. https://doi.org/10.3390/computation11120239
Fonseca L, Ribeiro F, Metrôlho J. Effects of the Number of Classes and Pressure Map Resolution on Fine-Grained In-Bed Posture Classification. Computation. 2023; 11(12):239. https://doi.org/10.3390/computation11120239
Chicago/Turabian StyleFonseca, Luís, Fernando Ribeiro, and José Metrôlho. 2023. "Effects of the Number of Classes and Pressure Map Resolution on Fine-Grained In-Bed Posture Classification" Computation 11, no. 12: 239. https://doi.org/10.3390/computation11120239
APA StyleFonseca, L., Ribeiro, F., & Metrôlho, J. (2023). Effects of the Number of Classes and Pressure Map Resolution on Fine-Grained In-Bed Posture Classification. Computation, 11(12), 239. https://doi.org/10.3390/computation11120239









