Evaluation of the Leak Detection Performance of Distributed Kalman Filter Algorithms in WSN-Based Water Pipeline Monitoring of Plastic Pipes

Abstract

Water is a basic necessity and one of the most valuable resources for human living. Sadly, large quantities of treated water get lost daily worldwide, especially in developing countries, through leaks in the water distribution network. Wireless sensor network-based water pipeline monitoring (WWPM) systems using low-cost micro-electro-mechanical systems (MEMS) accelerometers have become popular for real-time leak detection due to their low-cost and low power consumption, but they are plagued with high false alarm rates. Recently, the distributed Kalman filter (DKF) has been shown to improve the leak detection reliability of WWPM systems using low-cost MEMS accelerometers. However, the question of which DKF is optimal in terms of leak detection reliability and energy consumption is still unanswered. This study evaluates and compares the leak detection reliability of three DKF algorithms, selected from distributed data fusion strategies based on diffusion, gossip and consensus. In this study, we used a combined approach involving simulations and laboratory experiments. The performance metrics used for the comparison include sensitivity, specificity and accuracy. The laboratory results revealed that the event-triggered diffusion-based DKF is optimal, having a sensitivity value of 61%, a specificity value of 93%, and an accuracy of 90%. It also has a lower communication burden and is less affected by packet loss, making it more responsive to real-time leak detection.

1. Introduction

Water is an essential component of human survival, needed for drinking, washing, sanitation and other domestic and industrial processes. That is why one of the United Nations’ sustainable development goals (goal 6) is to ensure the availability and sustainable management of water and sanitation for all. Despite the importance of water, there are 2.2 billion people globally without safely managed drinking water, including 785 million without basic drinking water [1]. The situation is more alarming in sub-Saharan Africa, where 42% of people are without a basic water supply [2]. Regardless of the water scarcity, it is shocking that in developing countries, especially in sub-Saharan Africa, the rate of water loss and non-revenue water (NRW) is high [3]. High NRW is mostly caused by leakages in the water distribution network (WDN), which sometimes exceed more than 70% of the total NRW [4,5]. Leakages are frequent in the WDNs in these regions because the pipes transporting water to the user’s premises are usually installed by the users themselves. The installations rarely meet the standard requirements, especially the recommended depth for burying the pipes. This leads to a scenario where not all the pipes are buried. Some parts of the pipes are buried underground while other parts are exposed to the surface (especially the final connections to the user’s meters). The exposed pipes are more vulnerable to damages resulting from punctures due to human activities or cracks, which lead to leaks/bursts in the WDN. Figure 1 displays an example of a WDN transporting water to a user’s premise in Buea, a town in the southwest of Cameroon. Due to the scarcity of water sources and the increase in the demand of water in these regions, caused by an increase in population and urbanization, it is required that water losses be minimized as much as possible by implementing smart technologies that detect leaks in real-time, prompt rapid repair intervention and that require little human intervention. One such technology, which has been used for more than a decade now, is the wireless sensor network-based water pipeline monitoring (WWPM) system, which is the most suitable technique to detect and localize leakages in pipelines [6,7].

WWPM systems can be categorized as either invasive or non-invasive, depending on the type of sensors they use. Invasive WWPM systems use intrusive sensors, such as flow and pressure sensors that monitor internal pipeline parameters, such as flow rate and internal pressure. Unlike invasive WWPM systems, non-invasive WWPM systems use non-intrusive sensors, such as piezoelectric patches [8], force-sensitive resistors [9,10], accelerometers [11,12,13], and acoustic sensors [14], to externally detect changes in the pipeline caused by leaks. These non-invasive methods have become very popular for leak detection because of features, such as their low-cost, low power consumption, ease of installation, and maintenance. Non-intrusive sensors like accelerometer sensors have gained more popularity in recent years and have constantly been deployed in most WWPM systems, especially those installed on metallic pipes. However, there are a lot of challenges involved in using accelerometers for monitoring plastic pipelines, which make up most of the WDNs in developing countries, since in plastic pipes, the attenuation is higher and the propagation of leak signals (vibration) does not go far [15,16]. Reliable leak detection requires that the accelerometers be placed very close to each other in order to have a higher spatial resolution [17]. Using high accuracy accelerometers can reliably detect most, if not all, of the leaks that occur in the pipeline. However, the need for lower inter-sensor distances and the expensive nature of high accuracy accelerometers will increase the overall cost of the WWPM system, making them not cost-effective and unsuitable for deployment in developing countries, especially in sub-Saharan Africa. Thus, the active research areas of vibration-based WWPM that have and continue to attract much research in recent years include the improvement of leak detection performance, energy consumption reduction, an extension of the WWPM system lifespan, and cost reduction [13,18].

Recently, in order to reduce the cost of WWPM systems, the use of low-cost MEMS accelerometers has gained a lot of popularity [19]. Many recent studies have used low-cost MEMS accelerometers in their works to achieve both lower cost and lower power consumption [11,12,13,20]. However, most of these studies still suffer from low leak detection reliability. Earlier studies, which have used low-cost MEMS accelerometers, proposed future work in the use of data filtering [11] or multi-sensor data fusion [12] to improve leak detection reliability. In a recent study, Nkemeni et al. [21] proposed a fully distributed leak detection solution based on the distributed Kalman filter (DKF), that combines both Kalman filtering and redundant multi-sensor data fusion. The authors applied a DKF algorithm for leak detection in WWPM systems using low-cost MEMS accelerometers and analyzed the leak detection performance and energy consumption of the DKF-based solution and compared it with a local Kalman filter (LKF) solution and a centralized Kalman filter (CKF) solution. Their results revealed that the DKF solution works, and it is a better compromise between LKF and CKF in terms of leak detection reliability and energy consumption.

According to He et al. [22], different variants of DKF algorithms for low-cost sensor networks exist, which can be classified as either diffusion-, gossip-, or consensus-based, depending on their underlying distributed data fusion strategy. The DKF algorithm used in [21] was a diffusion-based DKF proposed by Battistelli et al. [23], and the reason they used the diffusion-based DKF was because of its lower communication requirement and fully distributed property which made it a good candidate for real-time leak detection in WWPM systems using nodes that are battery-powered. However, the question of which category of DKF is optimal in terms of responsiveness to real-time monitoring, leak detection reliability, and energy consumption remains unanswered. This paper evaluates and compares the leak detection performance of three DKF algorithms, including a consensus-based [24], a gossip-based [25], and a diffusion-based [23] algorithm, for leak detection in WWPM systems using low-cost MEMS accelerometers for monitoring plastic water pipes, and demonstrates why diffusion-based DKFs are optimal. This study is novel, and it is the first, to the best of our knowledge, to evaluate the performance of DKF algorithms in the context of WWPM systems.

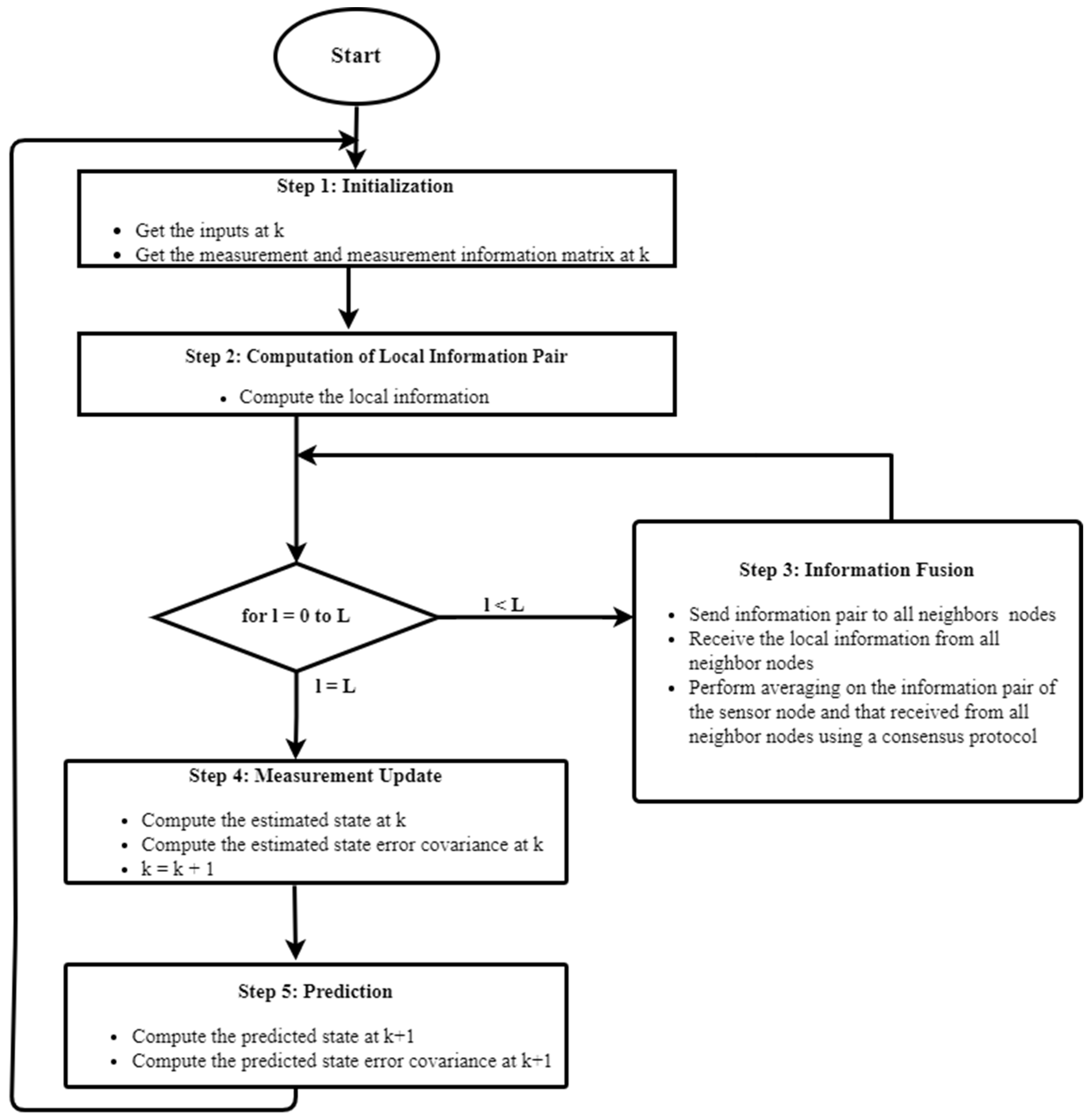
The first objective of this paper is to select three DKF algorithms from the study of [22], one from each DKF category, and implement them. The second is to compare their leak detection performance and determine which of the three DKF algorithms is optimal for leak detection in WWPM systems composed of a network of low-cost MEMS accelerometer sensors. The main contribution of this paper is the use of a combined approach that involves both simulations and laboratory experiments to compare the leak detection performance of the three selected DKF algorithms in the context of WWPM. WSN has been used in previous studies to monitor both above-the-ground (surface) pipes [9] and underground (buried) pipes [10]. The goal of using WSN in monitoring both above-the-ground and underground pipes is to ensure that leaks are detected in real-time as they occur and also to reduce human intervention [13]. Although leaks emanating from above-the-ground pipes can be visually observed, WSN-based methods are preferred for monitoring these pipes because manual inspection methods are more laborious as they will require regular inspection, they provide a slow response and most times, the leaks will be detected only after a considerable amount of water has been lost. This study focuses on above-the-ground pipes since they are the most likely to leak.

2. Materials and Methods

2.1. Description of Methodological Approach

Our method is a combined approach involving simulations and laboratory experiments. The reason for the combined approach is as follows: we used the simulation results to obtain a first-hand assessment of our proposed solution, then later used the experimental results to validate the simulation results. The simulations were performed on the CupCarbon 4.2 platform, which is a smart city and internet of things wireless sensor network (SCI-WSN) simulator that is used to design, visualize, debug and validate distributed algorithms for monitoring, e.g., the collection of environmental data [26]. It offers two simulation environments: one enables the design of scenarios with mobility and the generation of natural events, while the other enables the simulation of discrete events in WSNs. The physical experiments were carried out on a WDN laboratory testbed.

2.2. Selected Distributed Kalman Filter Algorithms

A distributed Kalman filter (DKF) is a Kalman filter implemented on a distributed architecture where each sensor node is a fusion center, with the capability of processing measurements from its sensors and also communicating only with its directly connected neighboring sensor nodes. Several DKF algorithms are available in the literature, as can be seen in reviews on DKF [22,27,28]. He et al. [22] recently reviewed DKF algorithms for low-cost sensor networks and broadly classified them as either sequential, consensus, gossip or diffusion, based on how local sensor nodes communicate with their neighbors to perform data fusion. The sequential-based DKFs involve communication between two sensors at any point in time, and the fusion is performed repeatedly and sequentially. Hence, this type of distributed data fusion is only possible in linear WSNs. Consensus-based DKFs require each sensor node to transmit its local information and also receive information from all its neighbors at every time step and consensus iteration. Each node implementing a gossip-based DKF transmits its local information and receives information from just a selected neighbor at every time step and gossip iteration, while each sensor node implementing a diffusion-based DKF transmits its local information and receives information from all its neighbors at every time step and with only one communication iteration involved. He et al. [22] also evaluated DKF algorithms in terms of criteria, such as global convergence (the ability to converge to the value of the Bayesian optimal CKF asymptotically or in a finite time), local consistency (the ability to maintain a consensus in the estimates of neighboring sensor nodes), and communication burden (the number of communication rounds involved during fusion).

In low-cost WSN applications such as WWPM, criteria such as global convergence and the local consistency of the DKF algorithm affect the accuracy of the WWPM system, while the communication requirement of the DKF algorithm affects the energy consumption and thus the lifetime of the WWPM system. The effect of global convergence and communication requirements are contradictory to each other. Thus, a comprise is needed in order to achieve acceptable accuracy while conserving the lifetime of the WWPM system. Given that communications in low-cost WSNs deplete a sensor node’s battery faster, the accuracy of a DKF algorithm is emphasized more on its ability to maintain local consistency than its ability to achieve global convergence [27]. Local consistency is of vital importance in a distributed solution because inconsistency in the fused state estimate and covariance—resulting from spurious measurements and the cross-correlations between the local estimates of neighboring sensor nodes—may cause the DKF to diverge [29]. Most DKFs implement the covariance intersection (CI) technique to handle the cross-correlation between local estimates of neighboring sensor nodes and thus maintain local consistency. For this reason, we selected only DKF algorithms that maintain local consistency and have low transmission requirements.

Based on the classification and evaluation of DKF algorithms by the study carried out by He et al. [22], the following algorithms (shown in

Table 1. Comparison of selected DKF algorithms.

DKF Algorithm	Underlying Fusion Strategy	Convergence to CKF	Local Consistency	Communication Requirement	Fully Distributed
ICF [24]	Consensus-based	Yes	Yes	High	No
SGG-ICF [25]	Gossip-based	Yes	Yes	Moderate	No
EDKF [23]	Diffusion-based	No	Yes	Low	Yes

) were selected for each distributed data fusion strategy. They include the information-weighted consensus filter (ICF) proposed by Kamal et al. [24], the sample greedy gossip information-weighted consensus filter (SGG-ICF) proposed by Shin et al. [25], and the event-triggered diffusion-based Kalman filter (EDKF) proposed by Battistelli et al. [23].

ICF [24] and SGG-ICF [25] both enjoy local consistency and global convergence. However, they are not fully distributed since they need to know the network size during the fusion process [22]. Unlike ICF and SGG-ICF, EDKF [23], is a diffusion-based DKF algorithm since it involves just a single exchange between neighboring sensor nodes at each time step, and the local state and covariance are calculated and then corrected by a convex combination of the estimates of the neighbors [30]. It enjoys local consistency, however, does not converge to the optimal CKF. In addition, it is fully distributed, since information on the network size is not required during the fusion process [22,23], making it more scalable.

In the following subsections, we will describe and present the implementation details of the ICF and SGG-ICF algorithms. The description and implementation of the EDKF algorithm were presented in [21] and the mathematical representation and proofs of the algorithm are found in [23] for the interested reader.

2.2.1. Information-Weighted Consensus Filter Algorithm

The information-weighted consensus filter proposed by Kamal et al. [24] consists of five main steps: initialization, computation of local information pair, information fusion, measurement update and prediction. Every sensor node implementing the algorithm goes through the iterative process shown in Figure 2 and the mathematical representation and proofs of the algorithm are found in [24] for the interested reader. At time step k, every local sensor node (i) starts by getting inputs, such as the predicted state (${\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}{}^{-}$), the predicted state error covariance (${\mathrm{P}}_{\mathrm{k}}^{\mathrm{i}}{}^{-}$), the observation matrix (${\mathrm{H}}_{\mathrm{k} }^{\mathrm{i}}$), the consensus speed factor (ε), the number of consensus iterations (L), the measurement (${\mathrm{y}}_{\mathrm{k}}^{\mathrm{i}}$), and the measurement information matrix (${({\mathrm{R}}_{\mathrm{k}}^{\mathrm{i}})}^{-1}$). This is followed by the computation of the local information pair (${\mathrm{u}}_{\mathrm{k}}^{\mathrm{i}}$ and ${\mathrm{U}}_{\mathrm{k}}^{\mathrm{i}}$) by using the inputs received in the initialization step. The next step involves the fusion of local information with those of neighboring sensor nodes by using a consensus protocol. During each consensus iteration, the sensor node sends its local information pair (${\mathrm{u}}_{\mathrm{k}}^{\mathrm{i}}$ and ${\mathrm{U}}_{\mathrm{k}}^{\mathrm{i}}$) to all its neighbors and also receives the local information pair (${\mathrm{u}}_{\mathrm{k}}^{\mathrm{j}}$ and ${\mathrm{U}}_{\mathrm{k}}^{\mathrm{j}}$) of all its neighbors. A consensus algorithm is then used to compute the average of each of the elements in the information pair during the information fusion step. At the end of L consensus iterations, the fused information pair is obtained (${\mathrm{u}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}$ and ${\mathrm{U}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}$). The fused information pair is then used in the measurement update step to compute the state estimate (${\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}$) and estimated state error covariance $({\mathrm{P}}_{\mathrm{k}}^{\mathrm{i}})$ at time step k. Lastly, the prediction step involves propagating the estimated state and estimated state error covariance in time by at time by computing the predicted state (${\widehat{\mathrm{x}}}_{\mathrm{k}+1}^{\mathrm{i}}{}^{-}$) and the predicted state error covariance (${\mathrm{P}}_{\mathrm{k}+1}^{\mathrm{i}}{}^{-}$) at time step k + 1.

After 𝐿 consensus iterations, the measurement update of the ICF algorithm is given by:

$${\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}={\left({\mathrm{U}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}\right)}^{-1}{\mathrm{u}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}$$

(1)

$${\left({\mathrm{P}}_{\mathrm{k}}^{\mathrm{i}}\right)}^{-1}={ \mathrm{NU}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}$$

(2)

where N is the number of sensor nodes in the network and the updated local information pair at node i after L iterations is given by:

$${\mathrm{u}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}={ \mathrm{u}}_{\mathrm{k}-1}^{\mathrm{i}}+ϵ{\displaystyle \sum }_{\mathrm{j} \in \mathrm{Ci}}({\mathrm{u}}_{\mathrm{k}-1}^{\mathrm{j}}-{ \mathrm{u}}_{\mathrm{k}-1}^{\mathrm{i}})$$

(3)

$${\mathrm{U}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}={ \mathrm{U}}_{\mathrm{k}-1}^{\mathrm{i}}+ϵ{\displaystyle \sum }_{\mathrm{j} \in \mathrm{Ci}}({\mathrm{U}}_{\mathrm{k}-1}^{\mathrm{j}}-{ \mathrm{U}}_{\mathrm{k}-1}^{\mathrm{i}})$$

(4)

where C_i is the set of connected neighbors of sensor node i. The local information pair of sensor node i to be fused with that of sensor node j is defined as:

$${\mathrm{u}}_{\mathrm{k}}^{\mathrm{i}}=\frac{1}{\mathrm{N}}{\left({\mathrm{P}}_{\mathrm{k}}^{\mathrm{i}}{}^{-}\right)}^{-1}{\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}{}^{-}+{ \mathrm{H}}_{\mathrm{k}}^{\mathrm{i}}{}^{\mathrm{T}}{({\mathrm{R}}_{\mathrm{k}}^{\mathrm{i}})}^{-1}{\mathrm{y}}_{\mathrm{k} }^{\mathrm{i}}$$

(5)

$${\mathrm{U}}_{\mathrm{k}}^{\mathrm{i}}=\frac{1}{\mathrm{N}}{\left({\mathrm{P}}_{\mathrm{k}}^{\mathrm{i}}{}^{-}\right)}^{-1}+{ \mathrm{H}}_{\mathrm{k}}^{\mathrm{i}}{}^{\mathrm{T}}{({\mathrm{R}}_{\mathrm{k}}^{\mathrm{i}})}^{-1}{\mathrm{H}}_{\mathrm{k} }^{\mathrm{i}}$$

(6)

2.2.2. Sample Greedy Gossip Information-Weighted Consensus Filter algorithm

The gossip-based DKF algorithm proposed by Shin et al. [25] consists of four main steps: prediction, computation of local information pair, information fusion and measurement update. Every sensor node implementing the algorithm goes through the iterative process shown in Figure 3 and the mathematical representation and proofs of the algorithm are found in [25] for the interested reader. At time instant 𝑘, every local sensor node (i) computes the predicted state (${\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}{}^{-}$) and predicted state error covariance (${\mathrm{P}}_{\mathrm{k}}^{\mathrm{i}}{}^{-}$) based on the previous state estimate (${\widehat{\mathrm{x}}}_{\mathrm{k}-1}^{\mathrm{i}}$) and estimated state error covariance (${\mathrm{P}}_{\mathrm{k}}^{\mathrm{i}})$ at k-1, respectively. The next step involves computing the local information pair (${\mathrm{u}}_{\mathrm{k}}^{\mathrm{i}}$ and ${\mathrm{U}}_{\mathrm{k}}^{\mathrm{i}}$) which is exchanged with a neighbor node during each gossip iteration. This is then followed by the information fusion step, which is repeated iteratively for a total of L gossip iterations. During each gossip iteration, each sensor node first determines a set of active neighbors by generating a probability (p) and comparing it with a sample (qi) generated from a uniform distribution and stored in each of its neighbors. If the value of the sample stored by the neighboring sensor node is greater than or equal to the probability generated by the sensor node, then the neighbor sensor is placed into the active set of the sensor node, otherwise, the neighbor node is considered as inactive. Once the active neighbor nodes have been determined, the next task performed by the algorithm is to determine for each sensor node the neighbor node with the largest information discrepancy with whom it is going to perform averaging with during the information fusion step. This neighbor node is actually determined via a greedy algorithm that computes the Mahalanobis distance (${\mathrm{d}}_{\mathrm{i},\mathrm{j}}$) between the information pair of the sensor node and those of its active neighbors. The neighbor node, j*, with the largest Mahalanobis distance (${\mathrm{d}}_{\mathrm{i},\mathrm{j}*}$) is selected. The information fusion continues iteratively till after a total of L iterations is reached. After L gossip iterations, the fused information pair (${\mathrm{u}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}$ and ${\mathrm{U}}_{\mathrm{k},\mathrm{L}}^{\mathrm{i}}$) is available and is used to compute the updated state estimate (${\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}$) and estimated state error covariance ${\mathrm{P}}_{\mathrm{k}}^{\mathrm{i}}$ at time step k, during measurement update.

After 𝐿 gossip iterations, the measurement update of the SGG-ICF algorithm is given by Equations (1) and (2) while the local information to be shared between two local sensor nodes is given by Equations (5) and (6). The similarity measure (Mahalanobis distance ${\mathrm{d}}_{\mathrm{i},\mathrm{j}}$) is defined as:

$${\mathrm{d}}_{\mathrm{i},\mathrm{j}}={({\mathrm{u}}_{\mathrm{k}}^{\mathrm{i}}-{ \mathrm{u}}_{\mathrm{k}}^{\mathrm{j}})}^{\mathrm{T}}{\left({\mathrm{U}}_{\mathrm{k}}^{\mathrm{i}}+{ \mathrm{U}}_{\mathrm{k}}^{\mathrm{j}}\right)}^{-1}\left({\mathrm{u}}_{\mathrm{k}}^{\mathrm{i}}-{ \mathrm{u}}_{\mathrm{k}}^{\mathrm{j}}\right)$$

(7)

2.2.3. Implementation of Selected DKF Algorithms

The simulation scripts were written using the Sense Script language in CupCarbon, while for the laboratory experiments, the firmware uploaded to the nodes was written in C/C++ and compiled using the Arduino IDE, version 1.8.9. The KF parameters A, H, Q and R were assigned the values 1, 1, 0.001, and 0.081, respectively.

Table 2. Values assigned to DKF parameters.

Parameter	Value	Concerned Algorithms
State transition matrix (A)	1	All
Measurement matrix (H)	1	All
Process noise covariance (Q)	0.001	All
Measurement noise covariance (R)	0.0081	All
Network size (N)	2	ICF and SGG-ICF
Number of consensus or gossip iterations (L)	5	ICF and SGG-ICF
Convergence speed (ϵ)	0.65	ICF
Sensor activation probability (p)	0.5	SGG-ICF
Information transmission rate (α, β and δ)	0.001, 40, 40, respectively	EDKF

provides a summary of the values of the parameters assigned to the various DKF algorithms.

For the ICF algorithm, the value of the network size N was set to 2 (since we are working on a two-node linear WSN), and the number of consensus iterations (L) was set to the value 5 for both the simulation and the laboratory experiments. The number of consensus iterations was chosen to be 5 based on the results of He et al. [22] which revealed that the ICF algorithm converges asymptotically to the CKF value and also achieves local consistency with the number of communication iterations, L, having the value of 5. The convergence speed parameter (ϵ) was assigned the value of 0.65 in both the simulation and laboratory implementations. For the laboratory experiments, the firmware uploaded to the nodes after compiling the ICF algorithm using the Arduino IDE occupied a storage space of 232 kB.

For the SGG-ICF algorithm, the value of the network size N was also set to 2, and the number of gossip iterations (L) was set to the value of 5 for both the simulations and the physical experiments. The sensor activation probability (p) was assigned the value of 0.5. The Arduino sketch implementing the SGG-ICF algorithm that was uploaded to the sensor nodes also occupied a storage space of 232 kB.

Now that we have described the implementation of the DKF algorithms, we will, in the next section, provide a detailed description of the simulation and experimental setups and the simulations and experiments conducted on the simulation platform and the laboratory testbed, respectively.

2.3. Simulation Setup

2.3.1. Description of Simulation Setup

The simulation setup shown in Figure 4 is composed of two sensor nodes (S1 and S2) and natural event generators (A4 and A5). The natural event generators emulated the physical accelerometer sensors and were loaded with acceleration data collected from the laboratory testbed. The sensor nodes (S1 and S2) were loaded with scripts that implement the selected DKF algorithms during the simulations.

2.3.2. Simulations

In [21], which is the foundation to this study, we provide the reasons why we used the CupCarbon platform for simulations, described how the simulations were performed using CupCarbon, and also provided results that supported the validity of the two-node approach in demonstrating distributed data fusion in WWPM. We conducted several simulations on the setup depicted in Figure 4 to assess the performance of each of the selected DKF algorithms. Firstly, we ran simulations to evaluate the estimation accuracy of each DKF algorithm by computing the root mean squared error (RMSE). Finally, we then performed simulations to evaluate the leak detection performance of each DKF algorithm by loading the sensor nodes with datasets that contained a known number of leak and no-leak events. The results of these simulations are presented and discussed in Section 4.

2.4. Experimental Setup

2.4.1. Description of Experimental Setup

The laboratory testbed used in this study was similar to that described in [21], which was composed of two plastic water storage tanks with a capacity of 1000 L (one tank for storage placed on a tower height of 9 m and one supply tank placed beneath the tower), with water being supplied to the WDN by means of gravity using the upper storage tank. However, high-pressure PVC pipes with an outer diameter of 25 mm were used for the laboratory WDN setup, rather than low-pressure PVC pipes with a diameter of 32 mm—which were used in the previous study. The reason for the change was that high-pressure pipes, though expensive, are commonly used in the WDN of Cameroon due to their low susceptibility to external damages and high resistance to bursting. Our aim of this study was to use pipe materials commonly used in real-life WDNs.

The laboratory WDN setup was made up of two 25 mm diameter pressure pipes, with each having a length of 6 m, joined together to produce an L-shaped structure. Two valves were installed on the pipeline, one at the end of the pipeline, which is intended to act as the service valve to emulate water consumption at the client’s premise, and one placed 8 m away from the inlet of the water into the distribution pipe that acted as the leak valve to emulate leaks in the WDN. Based on our assumption that there are no vibrations generated by the opening/closing of taps at the client’s premise, the service valve remained closed throughout these experiments. The only vibrations in the pipeline system were assumed to be vibrations caused by leaks emulated by opening the leak valve. Figure 5 illustrates the laboratory testbed setup.

The laboratory WWPM system was composed of two sensor nodes, S1 and S2, which were placed before and after the leak valve, respectively, in the direction of the water flow (left to right), as shown in Figure 6. The composition and interfacing of the sensor node components are the same as those used in [21]. The main core of the ESP32 MCU on each sensor node was configured to operate only at a speed of 80 MHz. The nRF24L01+ radio module was configured to transmit at −12 dBm output power and receive at a data rate of 1 Mbps. The sensing range of the LSM9DS1 accelerometer was configured to operate at ±2 g since this has the highest sensitivity, with its bandwidth and sampling frequency set to 400 Hz and 953 Hz, respectively. The accelerometers of both sensor nodes were glued onto the pipe surface using hot glue, and wires were used to connect them to the ESP32 MCU. Figure 5c shows the mechanical coupling of the accelerometer and the pipe surface. Hot glue was used because it provided good mechanical coupling between the accelerometer and the pipe. In addition, it made it easier to remove the sensor from the pipe surface without destroying the sensor.

2.4.2. Laboratory Experiments

Firstly, we conducted experiments to characterize the leak by varying the distance of the sensor from the leak position and also varying the size of the leak. The results and discussion of the leak characterization experiments are found in Section 3. Secondly, to measure the leak detection performance of the selected DKF algorithms, we emulated a leak on the pipeline by opening the leak valve at specific times and then recorded the number of times each DKF implementation triggered an alarm when the valve was opened (true positive), when it failed to trigger an alarm when the valve was opened (false negative), when it triggered an alarm when the valve was closed (false positive), and when it did not trigger an alarm when the valve was closed (true negative). The results and discussions of the conducted leak detection performance experiments are found in Section 4.

2.5. Evaluation Metrics

In this section, we present the different metrics that we used to measure the reliability (performance) of the different DKF algorithm implementations in WWPM of plastic pipes.

Chan et al. [31] surveyed the different metrics used by WWPM studies available in the literature for evaluating the performance of their proposed leak detection algorithms. The performance metrics range from sensitivity, specificity, false alarm rate, precision, accuracy, etc. They presented a confusion matrix (which is mostly used for statistical classification in machine learning), which we adapted to a leak detection system, as shown in

Table 3. Leak detection confusion matrix.

		Event
		Leak	No Leak
Alarm	ON	TP	FP
	OFF	FN	TN

.

Now, assuming that a ‘leak event’ is represented by a Boolean ‘1’, a ‘no-leak event’ by a Boolean ‘0’, ‘alarm ON’ by a Boolean ‘1’, and ‘alarm OFF’ by a Boolean ‘0’, we generated the leak detection truth table given in

Table 4. Leak detection truth table.

Leak Event	Alarm	Description
0	0	TN
0	1	FP
1	0	FN
1	1	TP

.

• TP: represents the cases where there is truly a leak on the WDN and the system triggers an alarm;
• TN: represents the cases where there is no leak, and the system does not trigger an alarm;
• FP: represents the cases of a false alarm, i.e., cases where the system triggers an alarm but there is actually no leak;
• FN: represents the cases where the detection of a leak was missed, i.e., a leak actually occurs, but the system does not trigger an alarm.

The different metrics that we used to evaluate the leak detection reliability using the confusion matrix in Table 3 include:

• Sensitivity

This is also referred to as the true positive rate (TPR) and represents the ability of the leak detection system to accurately detect all the actual leak events that occur on the WDN and is expressed as:

$$\mathrm{Sensitivity}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN} }$$

(8)

2.

Miss Detection Rate (MDR)

This is also referred to as the false negative rate (FNR) and represents the ability of the leak detection system to fail to trigger an alarm when a leak occurs on the WDN. It is expressed as:

$$\mathrm{MDR}=1-\mathrm{Sensitivity}=\frac{\mathrm{FN}}{\mathrm{TP}+\mathrm{FN} }$$

(9)

3.

Specificity

This is also referred to as the true negative rate (TNR) and represents the ability of the alarm of the leak detection system to stay off when there is actually no leak on the WDN. It is expressed as:

$$\mathrm{Specificity}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP} }$$

(10)

4.

False Alarm Rate (FAR)

This is also referred to as the false positive rate (FPR) and represents the ability of the leak detection system to detect outliers in measurement which do not actually represent the existence of a leak as a leak on the WDN. It is expressed as:

$$\mathrm{FAR}=1-\mathrm{Specificity}=\frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN} }$$

(11)

5.

Accuracy

This is the sum of the correctly identified leakage and no leakage scenarios over the total number of detected events. It is expressed as:

$$\mathrm{Accuracy}=\frac{\mathrm{TP} + \mathrm{TN}}{\mathrm{TP}+\mathrm{FP}+ \mathrm{FN}+\mathrm{TN} }$$

(12)

The presence or absence of a leak on the WDN is determined using the steady-state method [32], by comparing the estimated pipe state at time k (${\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}$) with a baseline value (${\mathrm{x}}_{\mathrm{k}}^{\mathrm{i}}$) of the pipe state when there is no leak on the WDN. If the difference is greater than a certain defined threshold (δ) then a leak alarm will be triggered, else no alarm will be triggered [33,34].

$$\begin{gathered} {\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}-{ \mathrm{x}}_{\mathrm{k}}^{\mathrm{i}}< \mathsf{\delta }, \mathrm{No} \mathrm{leak} \mathrm{scenario} \\ {\widehat{\mathrm{x}}}_{\mathrm{k}}^{\mathrm{i}}-{ \mathrm{x}}_{\mathrm{k}}^{\mathrm{i}}\ge \mathsf{\delta }, \mathrm{Leak} \mathrm{scenario} \end{gathered}$$

(13)

2.6. Summary

In this section, we selected three DKF algorithms for the implementation and evaluation of WWPM. The DKF algorithms selected include: a consensus-based DKF algorithm referred to as the information consensus filter (ICF) and is proposed by Kamal et al. [24], a sample greedy gossip information consensus filter (SGG-ICF) proposed by Shin et al. [25], and an event-triggered diffusion-based Kalman filter (EDKF) proposed by Battistelli et al. [23]. We then discussed the implementation of the DKF algorithms in the simulation platform (CupCarbon) and on the experimental platform (WDN testbed). This was followed by a description of both the simulation setup used for performing simulations and the laboratory setup used for validating the results obtained from the simulations. Finally, we selected sensitivity, specificity and accuracy as the metrics for evaluating and comparing the performance of the DKF algorithms in WWPM.

3. Leak Characterization

3.1. Introduction

In this section, we study the influence of the distance from the leak position and the size of the leak on the vibration data collected from the pipe surface using the LSM9DS1 accelerometer. The objective is to determine the maximum distance from which the accelerometer sensor should be placed from the leak position on the pipeline to effectively detect the presence or absence of a leak and the size of the leak that can be detected by the accelerometer. To study how the distance from the leak position affects leak detection, we varied the distance of the sensor from the leak position and collected vibration data at distances of 0.25 m, 0.5 m, 1 m, and 2 m from the leak position. For each distance from the leak position, we varied the leak size by tuning the size of the leak valve, measuring the flow rate, and then observing how it influenced the leak detection. When the leak valve was completely closed, the measured flow rate was 0 L/min, which corresponded to no leak in the pipeline. Opening the valve by quarter, half, and fully corresponded to leaks with flow rates of 7 L/min, 15 L/min, and 30 L/min, respectively, at a measured average pressure of 100 kPa.

As described in Section 2.4.1, the experimental setup is a closed-system. The leakage valve is the only point where water can get out of the pipe when it is open. When the valve is opened for a given leak size, it is left at that position for a period of time which implies that the leak is constant for that duration of time since the pressure is constant at 100 kPa. This means that in this experiment, the leakage is constant. This constant flow rate of a leak might, in most cases, correspond to short intervals in a real water pipeline system (where the pressure distribution is varying) because, even though a leak results from a hole or a crack in the pipe, which produces a constant leak size, the flow may vary depending on the pressure distribution of the water pipeline system. Our interest in this section rests with the investigation of the relationship between the leak flow rate and pipe surface acceleration and identifying leak flow rates that can produce sufficient vibration to be detected by the LSM9DS1 accelerometer. Despite the flow variation of a leak due to pressure variation, our proposed system will detect a leak once the flow rate is sufficient to generate a vibration that can be detected by the LSM9DS1 sensor, since it is designed to provide real-time monitoring.

3.2. Approach

To obtain the magnitude of the vibration in the X-, Y- and Z-axis, the measured acceleration in each of the 3D directions were subtracted from the offset value (the acceleration in that direction when there is no motion) and the result squared. They were summed up and the square root of the sum of the squares of the actual acceleration in each of the directions represented the resultant pipe surface acceleration. Assume that X_mea, Y_mea and Z_mea represent the acceleration measured in the X, Y and Z direction, respectively and X_0g, Y_0g and Z_0g represent the zero-g offset acceleration in the X, Y and Z direction, respectively. The actual acceleration in all three directions (X_act, Y_act and Z_act) were derived by subtracting the zero-g offset acceleration from the measured acceleration.

X_act = X_mea − X_0g

(14)

Y_act = Y_mea − Y_0g

(15)

Z_act = Z_mea − Z_0g

(16)

The magnitude of the resultant acceleration, A, caused by a leak is given by:

$$\mathrm{A}=\sqrt{{\mathrm{X}}_{\mathrm{act}}^2+{ \mathrm{Y}}_{\mathrm{act}}^2+{ \mathrm{Z}}_{\mathrm{act}}^2}$$

(17)

3.3. Results

Figure 7 represents the magnitude of the resultant acceleration of the vibration measured at different leak distances (0.25 m, 0.5 m, 1 m, and 2 m) from the leak position and leak sizes (7 L/min, 15 L/min, and 30 L/min). It is difficult to identify the data corresponding to no leak because the amplitude of the vibration is very close to zero. For each leak distance and leak size, 25,000 samples of vibration data were collected for a time duration of 27 s.

The results revealed that, as the distance from the leak position increases, there exists no significant difference between the leak data and the no-leak data. As shown in Figure 7, there was a significant difference between a leak scenario and a no-leak scenario for distances of 0.25 m, 0.5 m, and 1 m from the leak position. The results also revealed that the average amplitudes of the vibration at a distance of 0.25 m are much higher compared to the others. The amplitude decreases as the distance from the leak position increases. This is because the vibration signals are attenuated as they move away from the leak position, resulting in a decrease in their amplitude. At some distance far away from the leak position, the vibration signals can no longer be detected [13,15,16,35]. From the data collected, it shows that at a distance of 2 m from the leak position it becomes difficult to separate leak data from no-leak data when compared to the other leak distances. Additionally, the results revealed that for each of the leak distances, there is a significant difference in the magnitude of the measured acceleration for leak sizes of 15 L/min and 30 L/min when compared with no leak. However, there is no significant difference between the leak signatures (vibration data) of leaks with flow rates of 7 L/min when compared with vibration data collected from a no-leak scenario. This means that the accelerometer in our current setup can significantly differentiate a leak case from a no-leak case for leak sizes of 15 L/min, and it is unable to detect leaks of 7 L/min. This implies that, in our current setup, only fast leaks (i.e., high rates of the leaking flow or high-pressure leaks) can be detected by the accelerometer. This observation is in agreement with those reported by [36]. From the results presented above, we can confidently say that by placing the accelerometer sensor 1 m from the leak position, we can significantly detect most of the leaks having sizes ranging from 15 L/min to 30 L/min. These results are consistent with previous studies [12,13,15,37,38]. Nonetheless, comparing our result with those of [12], we see that there is a difference in the maximum distance that the accelerometer can be placed from the leak position to effectively detect leaks. According to Ismail et al. [12], the maximum distance for effective leak detection derived using the MPU6050 (which has similar characteristics to the LSM9DS1), was 0.5 m. However, our results revealed that we can effectively detect leaks at a distance of 1 m from the leak position using the LSM9DS1 accelerometer. The difference in the results can be explained by the fact, that in our study, we configured the accelerometer to the ±2 g sensing range which has more sensitivity (0.061 mg/LSB) whereas in [12], the authors configured the accelerometer to the ±16 g sensing range which has a lower sensitivity (0.732 mg/LSB). This means that to increase the sensor spacing and effectively detect a leak in plastic pipes, it is necessary to configure the MEMS accelerometers to the lowest sensing range since the magnitude of the vibrations on plastic pipes is low. It should be mentioned that in the case of underground (buried) pipes, which are most common in WDN, the detection distance will be lower than the 1 m which we obtained in our experiments since we used above-the-ground (surface) pipes. The reason is, there is a reduction in the vibration generated by the leak due to absorption by the surrounding soil [37]. The detection distance obtained from using surface pipes in this study gives us a first-hand idea of the maximum separation distance which can be expected in the case of buried pipes, which will be used in future experiments, since we will be dealing with a real WDN.

To obtain the baseline value, 86,400 samples of acceleration data were collected each day for a period of 3 days and an average was taken to obtain the baseline value when there was no leak in the pipeline. To deal with the noise when computing the baseline value, we applied a Kalman filter on the data before averaging the data collected for the 3 days period. Figure 8 represents the acceleration data collected for one day. By performing an average of the acceleration data collected for 3 days, we obtained the value of 1.00912 g. This led us to use the value of 1.01 g as the baseline value for leak detection. Thus, a leak alarm is triggered each time the difference between the estimated pipe surface acceleration and the baseline value exceeds the threshold value ($\mathsf{\delta }$) by 0.01 g.

3.4. Summary

In this section, we carried out leak characterization on the laboratory testbed and the results obtained revealed that leak sizes ranging from 15 L/min could be effectively detected at a distance of 1 m when the accelerometer was configured to the ±2 g sensing range. In the next section, we present the simulation and laboratory results of the performance evaluation of the selected DKF algorithms.

4. Performance Evaluation

The goal of this study was to compare the leak detection performance of the three DKF algorithms and determine which is optimal for leak detection in WWPM systems composed of a network of low-cost MEMS accelerometer sensors. We start this section by presenting the performance results obtained from the simulations and then end the section by presenting and discussing the results obtained from physical experiments for validation purposes. This will partially answer the question of which DKF algorithm is better and well suited for application in a fully distributed leak detection solution in WWPM systems using low-cost MEMS accelerometers.

4.1. Presentation and Discussion of Simulation Results

Figure 9 depicts the RMSE of the three selected DKF algorithms. For each DKF algorithm, the RMSE of both sensor nodes S1 and S2 are presented on the same plot.

From Figure 10, we see that there is no significant difference between RMSE of both sensor nodes S1 and S2 for all the DKF algorithms. The results in Figure 10 show that a difference in the RMSE value of both sensor nodes S1 and S2 only occurred for the cases of ICF and SGG-ICF at the beginning of the simulation. However, this difference becomes insignificant with time, as the RMSE values of both sensor nodes converge to the same value. This implies that all the three DKF algorithms compute consistent estimates and thus maintain local consistency in the estimates of neighboring sensor nodes. This agrees with the results published in [22], which showed that all three DKF algorithms achieved local consistency when applied in a low-cost sensor network target tracking application. The property of local consistency is especially very important for ensuring high reliability and reducing the FAR of a WWPM system implementing DKF, given that it will prevent contradictory outputs from neighboring sensor nodes as revealed in [21].

To compare the estimation accuracy of the three DKFs, Figure 10 depicts the RMSE of sensor node S1 for all three DKF algorithms. From Figure 10, we see that the RMSE of EDKF converges to 0.0667 while the RMSE value of SGG-ICF is slightly greater than that of ICF at the beginning, and they both converge to the value of 0.0397 with time. Moreover, it can be seen that ICF and SGG-ICF have lower RMSE values and can provide better estimation accuracy compared to EDKF. These results are also consistent with the results of He et al. [22]. Thus, we expect the leak detection performance of ICF and SGG-ICF to be higher than that of EDKF. To further evaluate the performance of the selected DKF algorithms, we carried out simulations on the two-node linear WSN presented in Section 2.3 using acceleration data collected from the field. The results of the performance of the selected DKF algorithms from simulations are depicted in Figure 11.

From Figure 11, it can be seen that ICF and SGG-ICF have leak sensitivities that are significantly higher compared to that of the EDKF. ICF has the highest sensitivity (100%), followed by SGG-ICF with a sensitivity of 95% and finally EDKF with a sensitivity of 65%. As shown in Figure 10, ICF had the lowest RMSE value, and this explains why it has the highest sensitivity in Figure 11. However, the overall accuracy of the DKF algorithms revealed that SGG-ICF has the highest accuracy (94%) followed by EDKF (93%), and lastly ICF (88%). This goes further to support the conclusions of [22], which stated that SGG-ICF is well suited for distributed state estimation in low-cost sensor networks as it provides more flexibility and strikes a balance between estimation accuracy and communication burden. However, based on the claim by Chan et al. [31], that accuracy may not be an optimal metric for evaluating the performance of a leak detection system, as it is dependent on class proportions, we cannot, at this point, state that SGG-ICF is better. We will need further experiments to conclude which DKF algorithm provides more reliable leak detection.

The presented simulation results imply that SGG-ICF and ICF are more sensitive to detecting leakages when compared to EDKF. This is because, in ICF and SGG-ICF, the sensor nodes exchange their local information multiple times between measurement updates whereas, in EDKF, the sensor nodes communicate with their neighbors at most, one time in between measurement updates. In addition, the event-triggered-commutation attribute of EDKF (which allows neighboring nodes to approximate the local information pairs of their neighbors and not to communicate when the difference between the predicted state and the last transmitted state is below a defined threshold) reduces its estimation accuracy. However, this attribute makes the EDKF have a lower communication requirement, unlike SGG-ICF and ICF, which have higher communication requirements, which will eventually lead to high power consumption. To validate these simulation results, we present in the next subsection the results of the performance of the three algorithms obtained from experiments conducted on the laboratory testbed.

4.2. Presentation and Discussion of Experimental Results

In this section, we present and discuss the results obtained from the laboratory experiment scenarios described in Section 2.4 in order to validate the simulation results presented in Section 4.1 above. The results of the performance of the selected DKF algorithms obtained from laboratory experiments are depicted in Figure 11.

From Figure 11, the leak sensitivities are 61%, 77%, and 75% for EDKF, ICF, and SGG-ICF, respectively. From the sensitivity results, it can be seen that ICF detected most of the leak events that occurred and missed detecting fewer leak events compared to SGG-ICF and EDKF. EDKF, with the lowest sensitivity of 61%, failed to detect 39% of the leak events that occurred in the pipeline, causing it to have the highest miss detection rate (MDR). This means that a high proportion of actual leaks will go unnoticed in the case of EDKF compared with the other algorithms. In terms of specificity, SGG-ICF is highest with 95% followed by EDKF with 93% and lastly, ICF with 80%. From the specificity results, it can be seen that SGG-ICF correctly detected most of the no-leak events and generated fewer false alarms compared to ICF and EDKF. ICF, with the lowest specificity of 80%, declared 20% of no-leak events as leak events, causing it to have the highest FAR. For a good leak detection system, it is better for the FAR to be higher than the MDR because the false alarms generated by the leak detection system can be ignored without it affecting the NRW. However, a higher MDR has an adverse effect on the NRW as it represents the true leaks that occur on the WDN and are undetected but lead to water losses and a high NRW. Thus, the sensitivity of a leak detection system has a powerful effect on the NRW, and we will focus more on this metric as a measure of the reliability of a leak detection system.

Knowing that sensitivity is a measure of how well the leak detection system detects true-leak events while specificity is a measure of how well the system recognizes no-leak events on the pipeline, this means that the DKF algorithm which has the highest sensitivity and specificity values is more reliable. This combined effect of sensitivity and specificity is captured by the accuracy metric. From Figure 11, SGG-ICF has the highest accuracy (92%), followed by EDKF with 90%, and lastly, ICF with 80%. This means that SGG-ICF is more reliable for leak detection compared to ICF and EDKF. This result is consistent with that obtained from simulations.

4.3. Comparison of Simulation and Experimental Results

In this subsection, we compare the results obtained from laboratory experiments with the simulation results and from there conclude which algorithm is optimal, based on the values of the performance metrics presented for both simulations and laboratory experiments.

Figure 12 presents the error between the simulation and laboratory results categorized by the DKF algorithm, while Figure 13 presents the error between the simulation and laboratory results categorized by performance metric. The laboratory results are taken as the reference to compute the error.

4.3.1. Comparison of the Sensitivity of Simulations and Laboratory Experiments

Comparing the results of the sensitivities obtained from simulations with those obtained from the laboratory experiments (Figure 11), we realize that there is a general decrease in the sensitivity obtained from the laboratory experiments when compared with those obtained from simulations. This decrease can be explained by the existence of packet loss during communication between neighboring sensor nodes in the physical experiments which are absent in the simulations. We see that there is no significant difference in the sensitivity of EDKF obtained from the laboratory experiments (61%) when compared to those obtained from simulations (65%). However, there are significant differences in the sensitivities of ICF and SGG-ICF obtained from simulations and laboratory experiments. For ICF and SGG-ICF, the sensitivities are 77% and 75%, respectively, from laboratory experiments as compared to 100% and 95%, respectively, recorded from simulations. This result implies that ICF and SGG-ICF are greatly affected by packet loss compared to EDKF. This can be attributed to the high communication requirement of ICF and SGG-ICF (which involves large amounts of exchanges between neighboring sensor nodes) and the highly unreliable wireless links in low-cost WSNs. For EDKF, its diffusion property alongside its event-triggered nature drastically reduces the number of exchanges between neighboring sensor nodes and thus, reduces the packet loss rate. We observed that in the physical experimentation of the EDKF, the packet loss rate was very low (<5%). This makes EDKF very appropriate for real-time application in systems where the dynamics of the system are changing fast. For ICF and SGG-ICF, which require multiple communications rounds between successive measurement updates to achieve excellent estimation accuracy, it is evident that their overall estimation accuracy depends on the packet loss rate. However, given that we are dealing with low-cost sensor networks where the communication links are unreliable, this increase in the number of data exchanges between neighboring sensor nodes will increase the likelihood of packets being lost. We observed in the physical experiments that out of five data exchanges that occurred between neighboring sensor nodes during the information fusion stage, only 60% of the transmitted packets were received successfully, meaning that only three out of five messages transmitted were successfully received. This explains the significant difference in the sensitivities of ICF and SGG-ICF obtained from simulations and laboratory experiments. The results in Figure 12 confirm that EDKF is the DKF algorithm least affected by packet loss due to its lower average error value when considering all three performance metrics. These results agree with the proposition of He et al. [22], which suggested the use of diffusion-based DKF algorithms in situations where communication resources are limited. Furthermore, it can be seen from Figure 13 that sensitivity is the performance metric most affected by packet loss. This can be explained by the fact that the occurrence of a leak in the pipeline leads to a sudden increase in the measured pipe surface acceleration, which results in an estimated acceleration that is significantly different from the previously estimated acceleration when there was no leakage in the pipeline. The DKF algorithm is required to react fast in order to capture this sudden change. As such, any delay resulting from packet loss and retransmission will minimize the chances of detecting this sudden increase in the pipe surface acceleration. However, the response time for ICF and SGG-ICF is slow since they have to involve numerous communication rounds between measurements. The loss of packets, due to the unreliable wireless links in low-cost WSNs, further worsens the estimation accuracy. Thus, to achieve high sensitivity, it is required that measurements be treated in a timely manner as they are obtained. This means that EDKF is more responsive to real-time leak detection and attractive for detecting fast leaks in WWPM systems compared with ICF and SGG-ICF.

4.3.2. Comparison of the Specificity of Simulations and Laboratory Experiments

The results in Figure 11 reveal that there is no significant difference between the specificity obtained from simulations and that obtained from physical experiments. From the results, we see that SGG-ICF has the highest specificity in the physical experiments as opposed to EDKF, which has the highest specificity from the simulation results. Generally, from the simulation and physical experiments results, we observed that the specificities of the DKF algorithms were high. This means that there is a low likelihood of an alarm being triggered when there is no real occurrence of a leak in the pipeline and this increases the reliability of the leak detection system.

4.3.3. Comparison of the Accuracy of Simulations and Laboratory Experiments

In terms of accuracy, SGG-ICF still has the highest accuracy (92%) which is slightly lower than that obtained from simulations (94%), followed by EDKF (90%), which is lower than the value derived from simulations (93%). In the same light, the accuracy of ICF obtained from laboratory experiments (80%) is significantly lower than that obtained from simulations (88%). We can deduce, that from the agreement of the trend of the accuracy values of both simulations and laboratory experiments, SGG-ICF has the highest leak detection performance. However, these results also confirm that accuracy is not a perfect metric for evaluating the performance of leak detection techniques due to its bias, based on its dependence on class proportions, as earlier stated in [31]. For example, in our case (which is also similar to what happens in real life), the number of no-leak events is greater than the number of leak events. Thus, the accuracy is affected more by its ability to correctly recognize the no-leak events than its ability to detect the leak events. This can be seen in Figure 11 when you compare the accuracy of ICF and EDKF. ICF has a higher sensitivity (which is a measure of the ability to detect leak events) compared to EDKF. However, its specificity (which is a measure of the ability to correctly recognize no-leak events) is lower than that of EDKF. The fact that EDKF has higher accuracy than ICF means that the accuracy, in this case, is affected more by its ability to correctly recognize the no-leak events than its ability to detect the leak events. The class imbalance does not affect the sensitivity and specificity metrics that we have also presented. Thus, by combining both sensitivity and specificity, we still see that SGG-ICF is the most performant algorithm, which agrees with the accuracy. Though the accuracy of SGG-ICF is slightly higher than that of EDKF, it has a high communication burden compared to EDKF. This high communication requirement will cause it to consume more battery power compared to EDKF. Thus, if we consider both the leak detection accuracy and power consumption, we realize that EDKF is the optimal algorithm among the three algorithms when dealing with battery-powered sensor nodes in WWPM applications.

4.4. Summary

In this section, we performed simulations and physical experiments to evaluate the leak detection performance of the selected DKF algorithms. The results from simulations and laboratory experiments revealed that ICF had the highest leak sensitivity, while SGG-ICF had the highest specificity and accuracy. The results of the leak detection performance for EDKF derived from simulations were close to that obtained from the laboratory experiments. However, there was a significant difference between the leak detection performance of ICF obtained from simulations and that derived from the laboratory experiments. The difference was explained by the fact that there was a loss of packets in the physical experiments during communications between sensor nodes that were not considered during simulations.

5. Conclusions

This paper presents the evaluation and comparison of the leak detection performance of three selected DKF algorithms implementing distributed data fusion strategies based on diffusion, gossip and consensus. For novelty, the study used a combined approach that involves simulations and laboratory experiments to compare the leak detection performance of the three selected DKF algorithms. A summary of the laboratory results is depicted in

Table 5. Summary comparison of laboratory results of the selected DKF algorithms.

DKF Algorithm	Underlying Fusion Strategy	Communication Requirement	Sensitivity	Specificity	Accuracy
ICF [24]	Consensus-based	High	77%	80%	80%
SGG-ICF [25]	Gossip-based	Moderate	75%	95%	92%
EDKF [23]	Diffusion-based	Low	61%	93%	90%

.

From the combination of both sensitivity and specificity in Table 5, it can be concluded that SGG-ICF is the most performant algorithm, which agrees with the accuracy. Though the accuracy of SGG-ICF is slightly higher than that of EDKF, it has a high communication burden compared to EDKF. This high communication requirement will cause it to consume more battery power compared to EDKF. Thus, if we consider both the leak detection accuracy and power consumption, we realize that EDKF is the optimal algorithm among the three algorithms when dealing with battery-powered sensor nodes in WWPM applications, as revealed by both the simulation and laboratory experiment performance results. The laboratory results reveal that the event-triggered diffusion-based DKF is optimal because it has a lower communication burden and is less affected by packet loss, which makes it more responsive to real-time leak detection.

Future work will involve the study of the power consumption of the three DKF implementations so that the combined effect of leak detection performance and energy efficiency can be used to determine which category of DKF is optimal for practical implementation in battery-powered sensor nodes. In addition, though results obtained from the laboratory testbed were satisfactory, extending the experiments to a field study that involves the deployment of a large-scale linear WSN on a real WDN with real-life conditions is also suggested for future work. This is important because the simplistic nature of the laboratory WDN does not capture all the complications in a real WDN. Another interesting point is that most WWPM studies are limited simulations and experiments on laboratory testbeds. Thus, extending experiments to real WDNs will contribute to the WWPM literature. In addition, we suggest, for future work, the implementation of machine learning techniques at the decision step of the leak detection algorithm. This implies that once the DKF has been used at the feature extraction phase to estimate the pipe surface vibration, the value can then be passed to a trained classifier at the decision phase to accurately determine the existence of a leak or no leak on the pipeline. Finally, the implementation of leak localization techniques, such as acoustic correlation analysis, will be investigated in future experiments.