Global Practical Output Tracking for a Class of Uncertain Inherently Time-Varying Delay Nonlinear Systems by Output Feedback

Abstract

This article addresses the problem of global practical output tracking by output feedback for a class of uncertain inherently time-varying delay nonlinear systems. Firstly, a homogeneous output-feedback controller is designed for the nominal uncertain inherently system by virtue of adding a power integrator technique. Then, with the help of an appropriate Lyapunov–Krasovskii functional and reduced-order observer, by using the homogeneous domination approach and adding a power integrator method, an output-feedback controller is successfully developed to guarantee all the states of the closed-loop system remain bounded and simultaneously making the tracking error arbitrarily small. The simulation results of an example verify the proposed approach.

1. Introduction

In this article, we consider a class of uncertain inherently time-varying delay nonlinear systems of the following form:

$$\begin{array}{l}{\dot{x}}_i(t)={\alpha }_i{x}_{i+1}{(t)}^{p_i}+{\phi }_i(t,\hspace{0.17em}x(t),\hspace{0.17em}{x}_1(t-d_1(t)),\dots ,x_n(t-d_n(t)),\hspace{0.17em}u(t)),\hspace{0.17em}\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n-1,\hspace{0.17em}\hspace{0.17em}\\ {\dot{x}}_n(t)={\alpha }_{n}u(t)\hspace{0.17em}+{\phi }_n(t,\hspace{0.17em}x(t),\hspace{0.17em}{x}_1(t-d_1(t)),\dots ,x_n(t-d_n(t)),\hspace{0.17em}u(t)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ y(t)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\alpha }_0{x}_1(t)-y_r(t),\end{array}$$

(1)

where $x(t)={(x_1(t),\dots ,x_n(t))}^T\in R^n$, $u(t)\in R$, and $y(t)\in R$ are the system state, control input, and output, respectively. $d_i(t)\ge 0,\hspace{0.17em}\hspace{0.17em}i=1,\dots ,\hspace{0.17em}n$ are time-varying delays satisfying $0\le d_i(t)\le d_i$ for constants $d_i,$ the system initial condition is $x(\theta )={\phi }_0(\theta ),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\theta \in [-d,\hspace{0.17em}0]\hspace{0.17em}$ with $d\ge {\max }_{1\le i\le n}\left\{d_i\right\}$. ${\phi }_i(\cdot ),\hspace{0.17em}i=1,\dots ,n$ are unknown continuous functions and ${\alpha }_i,\hspace{0.17em}i=0,1,\dots ,n$ are unknown constants. It assumes that the only measurable signal in system (1) to be the output y. $p_i\in R_{odd}^{\ge 1}$.

The issue of output tracking of nonlinear systems has attracted a great deal of attention over the past decades and a series of research results have been achieved ([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16], and references therein). Due to the lack of a common and effective approach to design a nonlinear observer, output-feedback tracking for uncertain inherently nonlinear systems is very complex and challenging compared to the state-feedback case. Therefore, the development of a theory for an output-feedback control design for this problem has been relatively slow. Many studies require a precise knowhow of the non-linear functions, ${\phi }_i(\cdot )$’s, that are necessary to construct the non-linear observers. When the non-linear terms, ${\phi }_i(\cdot )$’s, are not precisely known, the observers proposed in the works will no longer be implementable. To deal with the uncertain non-linear terms, ${\phi }_i(\cdot )$’s, one study [17] has developed a feedback domination method to achieve global output-feedback stabilization of System (1). It is showed that an observer and controller can be constructed without knowing the non-linearities and global stabilisation can be achieved under a linear growth condition. In articles [3,5,6,7,9,10,11], there are some results reported to help solve the problem of output-feedback tracking for inherently nonlinear systems, with the help of the homogeneous domination method proposed in [17]. The superiority of the feedback domination method compared with other methods is the controller and the observer are constructed only based on the nominal system of System (1). No precise information on the nonlinearities ${\phi }_i(\cdot )$ is needed. In other words, the same dynamic controller can be applied to different nonlinear systems as long as they satisfy Assumption 2. This property makes it possible to deal with nonlinear systems with unknown disturbances. Recently, the problem was extended to stochastic nonlinear systems and high-order switched nonlinear systems ([14,15,16], and references therein).

In various engineering and physical systems, etc., time delays are frequently encountered. Nevertheless, the above literature does not consider the effects of time delays. As everyone knows, a time-delay phenomenon will deteriorate the system’s performance and even make it adversely affect system stability or other performance aspects. Therefore, it is very important to investigate the stability or output-tracking issues of time-delay nonlinear systems. There have been quite a few reports on stabilization issues in recent years, but there are just a few references that are similar to the system considered in this study, such as [18,19,20,21,22,23,24,25,26,27]. There are not many reports of studies on the output-tracking control time-delay problem compared to the case of the stabilization problem. Recently, there have been a few interesting research results for the problems of output tracking via output feedback [28,29,30,31]. However, these works only investigated the partially linearizable case of System (1). Researchers [32,33] investigated and solved the problem by using state-feedback control. Recently, we have published research results on the issue of output-feedback control where the time delay is constant [34]. Naturally, an interesting question is whether it is possible to extend the results in [34] to non-deterministic, inherently time-varying delay nonlinear systems (1), which is the motivation behind this research.

This article addresses the problem of global practical output tracking by output feedback for a class of uncertain inherently time-varying delay nonlinear systems. With the help of an appropriate Lyapunov–Krasovskii functional and reduced-order observer, by using the homogeneous domination approach and adding a power integrator method, an output-feedback controller is successfully developed, to guarantee all the states of the closed-loop system remain bounded and simultaneously making the tracking error arbitrarily small.

The main contributions of this work can be highlighted as follows: (i) The considered nonlinear systems are uncertain inherently time-varying delays systems. Due to the appearance of uncertain inherently nonlinear terms and the time-varying delays, the observers in the existing results [28,29,30,34] and the Lyapunov–Krasovskii functionals are not applicable to System (1). Therefore, choosing an appropriate Lyapunov–Krasovskii functional and constructing an available observer are not easy work. In this work, we introduce a new Lyapunov–Krasovskii functional and by using a homogeneous domination approach, overcome a number of difficulties emerged in analysis and design, e.g., due to the non-linear terms, ${\phi }_i(\cdot )$, not being precisely known, or the Lyapunov–Krasovskii functionals and observers in the existing results no longer being applicable to System (1). Furthermore, many more complex nonlinear terms will be inevitably produced due to multiple time-varying delays. (ii) An output feedback controller with an observer is proposed for the considered system by utilizing a recursive design approach, and the output tracking of the corresponding closed-loop system is guaranteed. This work also extended the results in [8,34] to time-varying delay nonlinear systems.

The rest of this paper is organized as follows. Section 2 gives a useful definition and the lemmas. Section 3 gives the problem formulation and our main results. Section 4 gives a simulation example to verify the effectiveness of our proposed approach. The conclusions are included in Section 5.

Notations: $R^n$ denotes the real n-dimensional space and $R^{+}:=[0,\hspace{0.17em}\infty )$. For any vector $x:={(x_1,\dots ,x_n)}^T\in R^n$, $\left|\right|x\left|\right|$ denotes the Euclidean norm of $x$. A function $f:R^n\to R$ is said to be $C^k$ function if its partial derivatives exist and are continuous up to order $k,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1\le k<\infty .$ A $C^0$ function means it is continuous. A $C^{\infty }$ function means it is smooth; that is, it has continuous partial derivatives of any order. Besides, the arguments of functions (or functionals) are sometimes omitted or simplified, whenever no confusion can arise from the context. For instance, we sometimes denote a function $f(x(t))$ by $f(x)$,$f(\cdot )$, or $f$.

2. Useful Definition and Lemmas

In this section, we give a definition and several lemmas. These lemmas will play important roles in this paper.

Definition 1. [35]. 

For real numbers $r_i>0, i=1,\dots ,n$ and fixed coordinates

$$x=\left(x_1,\dots ,x_n\right)\in R^n, \forall \epsilon >0.$$

• The dilation${\Delta }_{\epsilon }^r(x)$ is defined by${\Delta }_s^r(x)=\left(s^{r_1}{x}_1,\cdots ,s^{r_n}{x}_n\right),\hspace{0.17em}$for$\forall \epsilon >0$, with $r_i$being called as the weights of the coordinate. For simplicity, we define dilation weight $\Delta =(r_1,\dots ,r_n)$.
• A function$V\in C(R^n,R)$ is said to be homogeneous of degree $m$ if there is a real number$m\ge 0$, such that

  $$\forall x\in R^n/\left\{0\right\},\hspace{0.17em}\hspace{0.17em}V({\Delta }_{\epsilon }^m(x))={\epsilon }^{m}V(x_1,\cdots ,x_n).$$
• A vector field$f={(f_1,\dots ,f_n)}^T\in C(R^n,R^n)$is said to be homogeneous of degree m if there is a real number$m\in R$, such that for$i=1,\dots ,n$

  $$\forall x\in R^n/\left\{0\right\},\hspace{0.17em}{f}_i({\epsilon }^{r_1}{x}_1,\cdots ,{\epsilon }^{r_n}{x}_n)={\epsilon }^{m+r_i}{f}_i(x_1,\cdots ,x_n).$$
• A homogeneous p-norm is defined as${\Vert x\Vert }_{\Delta ,p}={({{\displaystyle {\sum }_{i=1}^n\left|x_i\right|}}^{p/r_i})}^{1/p},\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}x\in R^n$for a constant$p\ge 1$. For simplicity, we choose$p=2$ and write${\Vert x\Vert }_{\Delta }$ for ${\Vert x\Vert }_{\Delta ,2}$.

Lemma  1. [35]. 

Given a dilation weight $\Delta$, suppose$V_1(x)$and$V_2(x)$are homogeneous functions of degree$m_1$and$m_2$, respectively. Then,$V_1(x)V_2(x)$is still a homogeneous function with respect to the same dilation weight$\Delta$. Moreover, the homogeneous degree of $V_1(x)V_2(x)$is$m_1+m_2$.

Lemma  2. [35]. 

Suppose$V:R^n\to R$is a homogeneous function of degree$m$with respect to the dilation weight$\Delta$. Then the following hold:

(i)

$\partial V/\partial x_i$ is homogeneous of degree$m-r_i$ with$r_i$ being the homogeneous weight of$x_i$.

(ii)

There is a constant$\overline{\sigma }>0$such that$V(x)\le \overline{\sigma }{\Vert x\Vert }_{\Delta }^m$. Moreover, if$V(x)$ is positive definite,$\underset{¯}{\sigma }{\Vert x\Vert }_{\Delta }^m\le V(x)$, for a constant$\underset{¯}{\sigma }>0$.

Lemma  3. [36].

For$x\in R,\hspace{0.17em}y\in R$and$p\ge 1$, the following holds:

$${\left|x+y\right|}^p\le 2^{p-1}\left|x^p+y^p\right|, {\left(\left|x\right|+\left|y\right|\right)}^{1/p}\le {\left|x\right|}^{1/p}+{\left|y\right|}^{1/p}\le 2^{\left(p-1\right)/p}{\left(\left|x\right|+\left|y\right|\right)}^{1/p}$$

If$p>0$is an odd integer, the following holds:

$${\left|x-y\right|}^p\le 2^{p-1}\left|x^p-y^p\right|, \left|x^{1/p}-y^{1/p}\right|\le 2^{\left(p-1\right)/p}{\left|x-y\right|}^{1/p}.$$

Lemma  4. [37]. 

For$x\in R,\hspace{0.17em}y\in R$and real number$p>0$, the following holds:

$$\left|x^p-y^p\right|\le p\left|x-y\right|\left|x^{p-1}+y^{p-1}\right|\hspace{0.17em}\le c\left|x-y\right|\left|{(x-y)}^{p-1}+y^{p-1}\right|$$

where$c=p$for$1<p\le 2$and$c=2^{p-1}p$for$p>2$.

Lemma  5. [38].

Let x, y be real variables. Then, for any positive real numbers $a,\hspace{0.17em}b,\hspace{0.17em}m$and$n$, the following holds:

$$a{\left|x\right|}^m{\left|y\right|}^n\le b{\left|x\right|}^{m+n}+\frac{n}{m+n}{\left(\frac{m+n}{n}\right)}^{-m/n}{a}^{(m+n)/n}{b}^{-m/n}{\left|y\right|}^{m+n}.$$

3. Problem Statement and Main Results

The purpose of this paper is to solve the problem of global practical output tracking by an observer-based output-feedback controller for System (1). The specific description will be formulated as follows.

The problem of global practical tracking via output feedback: For any given tolerance $\epsilon >0$ design, an output feedback controller is of the form

$$\begin{array}{l}\dot{\zeta }=\alpha (\zeta ,\hspace{0.17em}y),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\zeta \in R^m\\ u(t)=g(\zeta ,y),\end{array}$$

(2)

such that all states of the closed-loop Systems (1) and (2) are well defined and globally bounded on $[0,\infty )$, and for any initial condition $(x(0),\zeta (0))$, there exists a finite time $T(\epsilon ,\hspace{0.17em}x(0),\zeta (0))>0$, making the tracking error of Systems (1) and (2) satisfy

$$\left|y(t)\right|=\left|x_1(t)-y_r(t)\right|<\epsilon ,\hspace{1em}\forall t\ge T>0$$

(3)

To achieve the objective, it needs the following assumptions.

Assumption 1.

For $i=0,1,\dots ,n$there exist positive constants$\underset{¯}{\alpha }$and$\overline{\alpha }$such that

$$\underset{¯}{\alpha }\le \left|{\alpha }_i\right|\le \overline{\alpha }$$

Assumption 2.

There are constants $C_1>0,\hspace{0.17em}\hspace{0.17em}{C}_2>0$and$\tau \ge 0$such that

$$\left|{\phi }_i(t,\hspace{0.17em}x(t),\hspace{0.17em}{x}_1(t-d_1(t)),\dots ,x_n(t-d_n(t)),\hspace{0.17em}u(t))\right|\hspace{0.17em}\le C_1\left({\displaystyle \sum _{j=1}^i{\left|x_j(t)\right|}^{(r_i+\tau )/r_j}}+{\displaystyle \sum _{j=1}^i{\left|x_j(t-d_j(t))\right|}^{(r_i+\tau )/r_j}}\right)+C_2$$

(4)

where

$$r_1=1,\hspace{1em}{r}_{i+1}=(r_i+\tau )/p_i>0,\hspace{1em}i=1,\dots ,n$$

(5)

and$p_n=1$.

Assumption 3.

The time-delays $d_i(t)$are differentiable and satisfies

$$0\le d_i(t)\le d_i,{\dot{d}}_i(t)\le {\gamma }_i<1,$$

for constants$d_i$and ${\gamma }_i$, $\hspace{0.17em}i=1,\dots ,n$.

Assumption 4.

The reference signal $y_r\left(t\right)$ is continuously differentiable. Moreover, there is a constant$M>0$such that

$$\left|y_r(t)\right|\le M,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|{\dot{y}}_r(t)\right|\le M,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall t>-d.$$

Remark 1.

In the literature [3,4,5,6,7], although the control coefficients are all one, the output-feedback control design of System (1) is more complicated. Assumption 1 relaxes these control coefficients. Compared with [2,3,4,6,7], Assumption 2 is a milder condition; when $d_i(t)=0$, it becomes the assumptions in [3,4,5,6,7,8] that play an important role to solve the tracking problem. When time-delays are constants and $p_i=1,$ Assumption 2 becomes the assumptions in [28] and when $d_i\ne 0$ and $p_i>1$, it reduces the assumption in the existing results [32,34]. However, when $d_i(t)\ne 0$, the global output tracking of system (1) by output feedback is a relatively new problem because of a time-varying delay entering system states makes the control design more difficult because the existence of a time-varying delay effect makes the common assumption on the high-order system nonlinearities infeasible and which conditions should be placed to the nonlinearities remains unanswered. Assumption 4 represents the condition of the reference signal, which can already be called the standard condition for solving the tracking problem of nonlinear systems (see [3,4,5,6,7,8,28,32,33,34]).

Under Assumptions 1–4, the main purpose of this paper is designing the output-feedback control to solve the practical output-tracking problem for uncertain inherently time-varying delays nonlinear systems (1).

In order to achieve this goal, we make the following transformation:

$$z_1(t)={\alpha }_0{x}_1(t),\hspace{1em}{z}_i(t)={\tilde{\alpha }}_i{x}_i(t),\hspace{1em}i=2,\dots ,n$$

(6)

where ${\tilde{\alpha }}_{i-1}={\displaystyle {\prod }_{j=1}^{i-2}{\alpha }_j^{1/\left(p_{j-1}\cdots p_{i-2}\right)}},$ $p_0=1$. Using the new coordinates (6), System (1) can be rewritten as follows:

$$\begin{array}{l}{\dot{z}}_i(t)=z_{i+1}^{p_i}(t)+{\psi }_i(t,\hspace{0.17em}z(t),\hspace{0.17em}{z}_1(t-d_1(t)),\dots ,\hspace{0.17em}{z}_n(t-d_n(t)),u(t)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n-1,\\ {\dot{z}}_n\hspace{0.17em}(t)={\tilde{\alpha }}_{n}u(t)+{\psi }_n(t,\hspace{0.17em}z(t),\hspace{0.17em}{z}_1(t-d_1(t)),\dots ,\hspace{0.17em}{z}_n(t-d_n(t)),u(t)),\\ y(t)=z_1(t)-y_r(t)\end{array}$$

(7)

where

$$\begin{array}{l}{\psi }_i(t,\hspace{0.17em}z(t),\hspace{0.17em}{z}_1(t-d_1(t)),\dots ,\hspace{0.17em}{z}_n(t-d_n(t)),\hspace{0.17em}u(t))\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\tilde{\alpha }}_{i-1}{\phi }_i(t,\hspace{0.17em}z(t),\hspace{0.17em}{z}_1(t-d_1(t)),\dots ,\hspace{0.17em}{z}_n(t-d_n(t)),\hspace{0.17em}u(t)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n\end{array}$$

and ${\tilde{\alpha }}_n=\left({\displaystyle {\prod }_{j=1}^{n-1}{\alpha }_{j-1}^{1/\left(p_{j-1}\cdots p_{n-1}\right)}}\right){\alpha }_n$.

Using Assumption 1, it can be easily proved that Assumption 2 also holds for ${\psi }_i$,

$$\left|{\psi }_i(t,\hspace{0.17em}z(t),\hspace{0.17em}{z}_1(t-d_1(t)),\dots ,z_n(t-d_n(t)),\hspace{0.17em}u(t))\right|\hspace{0.17em}\le {\overline{C}}_1\left({\displaystyle \sum _{j=1}^i{\left|z_j(t)\right|}^{(r_i+\tau )/r_j}}+{\displaystyle \sum _{j=1}^i{\left|z_j(t-d_j(t))\right|}^{(r_i+\tau )/r_j}}\right)+{\overline{C}}_2$$

(8)

where ${\overline{C}}_i,\hspace{0.17em}i=1,2,$ are the new growth rates.

In what follows, we first design an output-feedback stabilizer for the system:

$${\dot{\eta }}_i(t)={\eta }_{i+1}^{p_i}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n-1,\hspace{0.17em}\hspace{0.17em}{\dot{\eta }}_n(t)={\tilde{\alpha }}_{n}u(t),\hspace{0.17em}\hspace{1em}y(t)={\eta }_1(t)$$

(9)

We adopt a similar the method as [8], which can construct a state-feedback stabilizer for the system (9), as described by Fact 1.

Fact 1. 

Suppose there exists a state-feedback stabilizer for System (9) of the form

$$u(\eta )=-{\beta }_n{\xi }_n^{(r_n+\tau )/\sigma }=-{\beta }_n{\left({\eta }_n^{\sigma /r_n}+{\beta }_{n-1}^{\sigma /r_n}\left({\eta }_{n-1}^{\sigma /r_{n-1}}+\cdots +{\beta }_2^{\sigma /r_3}\left({\eta }_2^{\sigma /r_2}+{\beta }_1^{\sigma /r_2}{\eta }_1^{\sigma }\right)\cdots \right)\right)}^{(r_n+\tau )/\sigma }$$

(10)

with a positive definite and proper Lyapunov function,

$$V_n={\displaystyle \sum _{i=1}^n{{\displaystyle {\int }_{{\eta }_i^{*}}^{{\eta }_i}\left(s^{\sigma /r_i}-{\eta }_i^{*\sigma /r_i}\right)}}^{\left(2\sigma -\tau -r_i\right)/\sigma }ds}$$

(11)

such that

$${\dot{V}}_n\le -{\displaystyle \sum _{j=1}^n{\xi }_j^2},$$

(12)

where${\xi }_i={\eta }_i^{\sigma /r_i}-{\eta }_i^{\ast \sigma /r_i}$,${\eta }_i^{\ast }=-{\beta }_{i-1}{\xi }_{i-1}^{r_i/\sigma }$, ${\eta }_1^{\ast }=0$,$\sigma \ge {\max }_{1\le i\le n}\left\{\tau +r_i\right\}$and${\beta }_i,\hspace{0.17em}\hspace{0.17em}i=1,\hspace{0.17em}\dots ,\hspace{0.17em}n$ are positive constants. Then, the closed-loop Systems (9) and (10) is globally asymptotically stable.

When states ${\eta }_2,\hspace{0.17em}\dots ,\hspace{0.17em}{\eta }_n$ are unmeasurable, it can replace ${\eta }_i$ with ${\widehat{\eta }}_i$ in (9) by the certainty equivalence principle and via using a similar approach as [8], which can construct an output-feedback stabilizer for System (9), as described by Fact 2.

Fact 2. 

Suppose there exists an observer-based output feedback stabilizer for System (9) of the form

$$\begin{array}{l}{\dot{\zeta }}_2=-l_1{\widehat{\eta }}_2^{p_1},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\eta }}_2^{p_1}={({\zeta }_2+l_1{\eta }_1)}^{r_2{p}_1/r_1}\hspace{0.17em}\\ {\dot{\zeta }}_i=-l_{i-1}{\widehat{\eta }}_i^{p_{i-1}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\eta }}_i^{p_{i-1}}={({\zeta }_i+l_{i-1}{\widehat{\eta }}_{i-1})}^{r_i{p}_{i-1}/r_{i-1}},\hspace{0.17em}\hspace{0.17em}i=3,\hspace{0.17em}\dots ,\hspace{0.17em}n\end{array}$$

(13)

$$u(\widehat{\eta })=-{\beta }_n{({\widehat{\eta }}_n^{\sigma /r_n}+{\beta }_{n-1}^{\sigma /r_n}({\widehat{\eta }}_{n-1}^{\sigma /r_{n-1}}+\cdots +{\beta }_2^{\sigma /r_3}({\widehat{\eta }}_2^{\sigma /r_2}+{\beta }_1^{\sigma /r_3}{\eta }_1^{\sigma })\cdots ))}^{(r_n+\tau )/\sigma }$$

(14)

with a positive definite, continuously differentiable and proper Lyapunov function,

$$Q=V_n+{\displaystyle \sum _{i=2}^n{U}_i}$$

(15)

$$V_n={\displaystyle \sum _{i=1}^n{{\displaystyle {\int }_{{\eta }_i^{*}}^{{\eta }_i}\left(s^{\sigma /r_i}-{\eta }_i^{*\sigma /r_i}\right)}}^{\left(2\sigma -\tau -r_i\right)/\sigma }ds}, U_i={\displaystyle {\int }_{{\left({\zeta }_i+l_{i-1}{\eta }_{i-1}\right)}^{\left(2\sigma -\tau -r_{i-1}\right)/r_{i-1}}}^{{\eta }_i^{\left(2\sigma -\tau -r_{i-1}\right)/r_i}}\left(s^{r_{i-1}/(2\sigma -\tau -r_{i-1})}-\left({\zeta }_i+l_{i-1}{\eta }_{i-1}\right)\right)ds}$$

such that

$$\dot{Q}\le -{\displaystyle \sum _{j=1}^n{\xi }_j^2}-{\displaystyle \sum _{j=2}^n{e}_j^2}$$

(16)

where ${\xi }_i={\eta }_i^{\sigma /r_i}-{\eta }_i^{\ast \sigma /r_i}$, ${\eta }_i^{\ast }=-{\beta }_{i-1}{\xi }_{i-1}^{r_i/\sigma }$,${\eta }_1^{\ast }=0$, $\sigma \ge {\max }_{1\le i\le n}\left\{\tau +r_i\right\}$,$e_i={\left({\eta }_i^{p_{i-1}}-{\widehat{\eta }}_i^{p_{i-1}}\right)}^{\sigma /(r_i{p}_{i-1})},$and $l_i$, ${\beta }_i$,$i=1,\hspace{0.17em}\dots ,\hspace{0.17em}n$ are positive constants. Then, the closed-loop Systems (9), (13), and (14) are globally asymptotically stable.

The proofs of Facts 1–2 are similar to ([8], Theorem 1), with some modifications, and the parameters $l_i$, $i=1,\hspace{0.17em}\dots ,\hspace{0.17em}n$, for the observer (13) also can be chosen by the technique proposed in [8]. Therefore, it is omitted here.

Note that from the construction of $Q$, it is not difficult to verify that $Q$ is positive, definite, and proper with respect to

$$H:={\left[{\eta }_1,\hspace{0.17em}\dots ,\hspace{0.17em}{\eta }_n,\hspace{0.17em}{\widehat{\eta }}_2,\hspace{0.17em}\dots ,\hspace{0.17em}{\widehat{\eta }}_n\right]}^T$$

(17)

The closed-loop Systems (9), (13), and (14) can be rewritten as

$$\dot{H}=F(H)={\left[{\eta }_2^{p_1},\hspace{0.17em}\dots ,\hspace{0.17em}{\eta }_n^{p_{n-1}},\hspace{0.17em}\tilde{\alpha }u\left({\eta }_1,\hspace{0.17em}{\widehat{\eta }}_2,\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}{\widehat{\eta }}_n\right),\hspace{0.17em}\hspace{0.17em}{f}_{n+1},\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}{f}_{2n-1}\right]}^T$$

(18)

where $f_{n+1}:={\dot{\zeta }}_2,f_{n+2}:={\dot{\zeta }}_3,\dots ,f_{2n-1}:={\dot{\zeta }}_n$.

Moreover, by introducing the dilation weight,

$$\Delta =\underset{\mathrm{for}\hspace{0.17em}{\eta }_1,\hspace{0.17em}\dots ,\hspace{0.17em}{\eta }_n\hspace{0.17em}}{\underbrace{[r_1,\hspace{0.17em}{r}_2,\hspace{0.17em}\dots ,\hspace{0.17em}{r}_n}},\hspace{0.17em}\underset{\mathrm{for}\hspace{0.17em}{\widehat{\eta }}_2,\dots ,{\widehat{\eta }}_n}{\underbrace{r_1,\hspace{0.17em}{r}_2,\hspace{0.17em}\dots ,\hspace{0.17em}{r}_{n-1}]}}$$

(19)

By Definition 1, it can be verified that $F(H)$ have a homogeneous degree $\tau$ and since System (18) is globally asymptotically stable by Fact 2, then there exists a Lyapunov function $Q(H)$ of homogeneous degree $2\sigma -\tau$ for dilation weight $\Delta$ and satisfies

$$\left|\dot{Q}(H)\right||{}_{(18)}=\left|\frac{\partial Q(H)}{\partial H}F(H)\right|\le -c_1{\Vert H\Vert }_{\Delta }^{2\sigma }$$

(20)

where $c_1>0$ is a constant and ${\Vert H\Vert }_{\Delta }={\left({\displaystyle {\sum }_{i=1}^{2n-1}{\left|H_i\right|}^{2/r_i}}\right)}^{1/2}$. Moreover, there is a constant $c_2>0$, such that the following holds:

$$\left|\frac{\partial Q(H)}{\partial H_i}\right|\le c_2{\Vert H\Vert }_{\Delta }^{2\sigma -\tau -r_i},\hspace{0.17em}\hspace{0.17em}{c}_2>0 \mathrm{for} i=1, \dots , n.$$

(21)

Next, an output-feedback controller to solve the problem of global practical output tracking will be constructed.

Theorem 1.

Under Assumptions 1–4, the problem of global practical output tracking for System (7) can be solved by an output-feedback control using Forms (13) and (14).

Proof. 

The observer-based output-feedback controller is constructed by introducing a scaling gain into the output feedback controller obtained in Fact 2. Before proceeding, we introduce the following a coordinates transformation:

$${\chi }_1(t):=y(t),\hspace{1em}{L}^{{\kappa }_i}{z}_i(t):={\chi }_i(t),\hspace{1em}i=2,\dots ,n,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{L}^{{\kappa }_n+1}v(t):=u(t)$$

(22)

where ${\kappa }_1=0,\hspace{0.17em}\hspace{0.17em}{\kappa }_i=({\kappa }_{i-1}+1)/p_{i-1}$, $i=2,\dots ,n$ and $L\ge 1$ is a constant to be determined. Under the coordinates (22), system (7) changed into

$$\begin{array}{l}{\dot{\chi }}_i(t)=L{\chi }_{i+1}^{p_i}(t)+{\psi }_i(\cdot )/L^{{\kappa }_i},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n-1,\\ {\dot{\chi }}_n(t)=L\tilde{\alpha }v(t)+{\psi }_n(\cdot )/L^{{\kappa }_n},\hspace{0.17em}\hspace{1em}\\ y(t)={\chi }_1(t)\end{array}$$

(23)

Using Lemma 3 and the fact $L\ge 1$, it is not difficult to prove that the following inequalities hold:

$$\begin{array}{l}\frac{1}{L^{{\kappa }_i}}\left|{\psi }_i(\cdot ))\right|\hspace{0.17em}\le \frac{C_1}{L^{{\kappa }_i}}({\left|{\chi }_1(t)+y_r(t)\right|}^{(r_i+\tau )/r_1}+{\displaystyle \sum _{j=2}^i{\left|L^{{\kappa }_j}{\chi }_j(t)\right|}^{(r_i+\tau )/r_j}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\left|{\chi }_1(t-d_1(t))+y_r(t-d_1(t))\right|}^{(r_i+\tau )/r_1}+{\displaystyle \sum _{j=2}^i{\left|L^{{\kappa }_j}{\chi }_j(t-d_j(t))\right|}^{(r_i+\tau )/r_j}})+\frac{C_2}{L^{{\kappa }_i}}\end{array}$$

(24)

Further, by Assumption 2, we can easily calculate

$$\frac{1}{L^{{\kappa }_i}}\left|{\psi }_i(\cdot )\right|\le {\overline{C}}_1{L}^{1-v}{\displaystyle \sum _{j=1}^i\left({\left|{\chi }_j(t)\right|}^{(r_i+\tau )/r_j}+{\left|{\chi }_j\left(t-d_j(t)\right)\right|}^{(r_i+\tau )/r_j}\right)}+\frac{{\overline{C}}_2}{L^{{\kappa }_i}},\hspace{1em}i=1,\hspace{0.17em}\dots ,\hspace{0.17em}n$$

(25)

where $\nu ={\min }_{2\le j\le i,\hspace{0.17em}\hspace{0.17em}1\le i\le n}\left\{1-{\kappa }_j(r_i+\tau )/r_j+{\kappa }_i\right\}>0$ and ${\overline{C}}_i>0,\hspace{0.17em}i=1,2$ only depending on $C_i,\hspace{0.17em}\tau \hspace{0.17em},\hspace{0.17em}{\kappa }_i\hspace{0.17em}\mathrm{and}\hspace{0.17em}M$.

Next, we construct an observer with the scaling gain L,

$$\begin{array}{l}{\dot{\zeta }}_2=-L{l}_1{\widehat{\chi }}_2^{p_1},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\chi }}_2^{p_1}={({\zeta }_2+l_1{\chi }_1)}^{r_2{p}_1/r_1}\hspace{0.17em}\\ {\dot{\zeta }}_i=-L{l}_{i-1}{\widehat{\chi }}_i^{p_{i-1}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\chi }}_i^{p_{i-1}}={({\zeta }_i+l_{i-1}{\widehat{\chi }}_{i-1})}^{r_i{p}_{i^1}/r_{i-1}},\hspace{0.17em}\hspace{0.17em}i=3,\hspace{0.17em}\dots ,\hspace{0.17em}n\end{array}$$

(26)

and the controller using the same construction of (14), i.e.,

$$u(t)=L^{{\kappa }_n+1}v(\widehat{\chi })=-L^{{\kappa }_n+1}{\beta }_n{({\widehat{\chi }}_n^{\sigma /r_n}+{\beta }_{n-1}^{\sigma /r_n}({\widehat{\chi }}_{n-1}^{\sigma /r_{n-1}}+\hspace{0.17em}\cdots +{\beta }_2^{\sigma /r_3}({\widehat{\chi }}_2^{\sigma /r_2}+{\beta }_1^{\sigma /r_3}{\chi }_1^{\sigma })\cdots ))}^{(r_n+\tau )/\sigma }.$$

(27)

Clearly, using the same notation (17), the system (23), (26) and (27) can be written as

$$\dot{X}=LF\left(X\right)+{\left[{\psi }_1(\cdot ),\hspace{0.17em}\frac{1}{L^{{\kappa }_2}}\hspace{0.17em}{\psi }_2(\cdot ),\hspace{0.17em}{\psi }_3(\cdot )\hspace{0.17em},\dots ,\frac{1}{L^{{\kappa }_n}}{\psi }_n(\cdot ),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0,\dots ,\hspace{0.17em}\hspace{0.17em}0\right]}^T$$

(28)

where $F(X)$ is same as defined in (18).

Therefore, adopting the Lyapunov function $Q(X)$, as in (15), its derivative along (28) satisfies

$$\begin{array}{l}\dot{Q}(X)=L\frac{\partial Q(X)}{\partial X}F(X)+\frac{\partial Q(X)}{\partial X}{\left[{\psi }_1(\cdot ),\hspace{0.17em}\frac{1}{L^{{\kappa }_2}}\hspace{0.17em}{\psi }_2(\cdot ),\hspace{0.17em}{\psi }_3(\cdot )\hspace{0.17em},\dots ,\frac{1}{L^{{\kappa }_n}}{\psi }_n(\cdot ),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0,\dots ,\hspace{0.17em}\hspace{0.17em}0\right]}^T\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le -L{c}_1{\Vert X\Vert }_{\Delta }^{2\sigma }+{\displaystyle \sum _{i=1}^n\frac{\partial Q(X)}{\partial X_i}}\frac{{\psi }_i(\cdot )}{L^{{\kappa }_i}}.\end{array}$$

(29)

Further, using (25), one obtains

$$\dot{Q}(X)\hspace{0.17em}\le -L{c}_1{\Vert X\Vert }_{\Delta }^{2\sigma }+{\overline{C}}_1{\displaystyle \sum _{i=1}^n{L}^{1-\nu }\left|\frac{\partial Q(X)}{\partial X_i}\right|({\displaystyle \sum _{j=1}^i{\left|{\chi }_j\right|}^{(r_i+\tau )/r_j}}}+{\displaystyle \sum _{j=1}^i{\left|{\chi }_j(t-d_j(t))\right|}^{(r_i+\tau )/r_j}})+{\overline{C}}_2{\displaystyle \sum _{i=1}^n\frac{1}{L^{{\kappa }_i}}\left|\frac{\partial Q(X)}{\partial X_i}\right|}.$$

(30)

Since, by Lemma 2 and [35], $\frac{\partial Q(X)}{\partial X_i}$ is homogeneous of degree $2\sigma -\tau -r_i$, the terms $\left|\frac{\partial Q(X)}{\partial X_i}\right|{\displaystyle \sum _{j=1}^i{\left|{\chi }_j\right|}^{(r_i+\tau )/r_j}}$ and $\left|\frac{\partial Q(X)}{\partial X_i}\right|{\displaystyle \sum _{j=1}^i{\left|{\chi }_j(t-d_j(t))\right|}^{(r_i+\tau )/r_j}}$ are homogeneous of degree $2\sigma$, and so it follows from Lemmas 1 and 2 that there exist positive constants ${\stackrel{⌢}{\omega }}_i\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{\stackrel{⌣}{\omega }}_i$ for $i=1,\dots ,n$, such that

$$\left|\frac{\partial Q(X)}{\partial X_i}\right|\left({\displaystyle \sum _{j=1}^i{\left|{\chi }_j\right|}^{(r_i+\tau )/r_j}}+{\displaystyle \sum _{j=1}^i{\left|{\chi }_j(t-d_j(t))\right|}^{(r_i+\tau )/r_j}}\right)\le {\stackrel{⌢}{\omega }}_i{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+{\stackrel{⌣}{\omega }}_i{\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\sigma }$$

Furthermore, it follows from Lemmas 2, 4, and 5 that there are positive constants $b_1,\hspace{0.17em}\hspace{0.17em}{\overline{b}}_2,\hspace{0.17em}\hspace{0.17em}{\tilde{b}}_2$ such that

$$\begin{array}{c}\left|\frac{\partial Q(X)}{\partial X_1}\right|\le b_1{\Vert X\Vert }_{\Delta }^{2\sigma -\tau -r_1}=b_1{\left(L^{1/2\sigma }{\Vert X\Vert }_{\Delta }\right)}^{2\sigma -\tau -r_1}{\left(L^{-\left(2\sigma -\tau -r_1\right)/\left(2\sigma (\tau +r_1)\right)}\right)}^{\tau +r_1}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le \frac{c_1}{2}L{\Vert X\Vert }_{\Delta }^{2\sigma }+{\overline{b}}_2{L}^{-\left(2\sigma -\tau -r_1\right)/(\tau +r_1)},\end{array}$$

$$\frac{1}{L^{{\kappa }_i}}\left|\frac{\partial Q(X)}{\partial X_i}\right|\le c_2{\Vert X\Vert }_{\Delta }^{2\sigma -\tau -r_i}{\left(L^{-{\kappa }_i/(\tau +r_i)}\right)}^{\tau +r_i}\le {\overline{c}}_2{\Vert X\Vert }_{\Delta }^{2\sigma }+{\tilde{b}}_2{L}^{-2\sigma {\kappa }_i/(\tau +r_i)},\hspace{1em}i=2,\dots ,n$$

(31)

Now, substituting (31) into (30) leads to

$$\begin{array}{l}\dot{Q}(X(t))\hspace{0.17em}\le -L{c}_1{\Vert X\Vert }_{\Delta }^{2\sigma }+{\overline{C}}_1{\displaystyle \sum _{i=1}^n{L}^{1-\nu }\left({\stackrel{⌢}{\omega }}_i{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+{\stackrel{⌣}{\omega }}_i{\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\sigma }\right)}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{c_1}{2}L{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+{\overline{b}}_2{L}^{-\left(2\sigma -\tau -r_1\right)/(\tau +r_1)}+{\displaystyle \sum _{i=2}^n\left({\overline{c}}_2{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+{\tilde{b}}_2{L}^{-2\sigma {\kappa }_i/(\tau +r_i)}\right)}\end{array}$$

$$\begin{array}{l}\le -L{c}_1{\Vert X\Vert }_{\Delta }^{2\sigma }+{\overline{C}}_1{\displaystyle \sum _{i=1}^n{L}^{1-\nu }\left({\stackrel{⌢}{\omega }}_i{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+{\stackrel{⌣}{\omega }}_i{\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\sigma }\right)}\\ \hspace{0.17em}\hspace{0.17em}+\frac{c_1}{2}L{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+{\overline{b}}_2{L}^{-\left(2\sigma -\tau -r_1\right)/(\tau +r_1)}+{\displaystyle \sum _{i=2}^n\left({\overline{c}}_2{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+{\tilde{b}}_2{L}^{-2\sigma {\kappa }_i/(\tau +r_i)}\right)}\\ \le -L[\left(\frac{c_1}{2}-(n-1){\overline{c}}_2{L}^{-1}-{\overline{C}}_1{L}^{-\nu }{\displaystyle \sum _{i=1}^n{\stackrel{⌢}{\omega }}_i}\right){\Vert X(t)\Vert }_{\Delta }^{2\sigma }-\left({\overline{C}}_1{L}^{-\nu }{\displaystyle \sum _{i=1}^n{\stackrel{⌣}{\omega }}_i}\right){\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\sigma }]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\overline{b}}_2{L}^{-1}+{\tilde{b}}_2{\displaystyle \sum _{i=2}^n{L}^{-2\sigma {\kappa }_i/(\tau +r_i)}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ \le -L[\left(\frac{c_1}{2}-(n-1){\overline{c}}_2{L}^{-1}-{\overline{C}}_1{L}^{-\nu }{\displaystyle \sum _{i=1}^n{\stackrel{⌢}{\omega }}_i}\right){\Vert X(t)\Vert }_{\Delta }^{2\sigma }-\left({\overline{C}}_1{L}^{-\nu }{\displaystyle \sum _{i=1}^n{\stackrel{⌣}{\omega }}_i}\right){\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\sigma }]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\overline{b}}_2{L}^{-1}+{\tilde{b}}_2(n-1)L^{-{\kappa }_{\min }}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

$$\begin{array}{l}\le -L\left(\frac{c_1}{2}-(n-1){\overline{c}}_2{L}^{-1}-L^{-\nu }{\overline{C}}_1{\displaystyle \sum _{i=1}^n{\stackrel{⌢}{\omega }}_i}\right){\Vert X(t)\Vert }_{\Delta }^{2\sigma }\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\left(L^{1-\nu }{\overline{C}}_1{\displaystyle \sum _{i=1}^n{\stackrel{⌣}{\omega }}_i}\right){\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\sigma }+{\overline{b}}_2{L}^{-1}+{\tilde{b}}_2(n-1)L^{-{\kappa }_{\min }}\end{array}$$

(32)

where ${\kappa }_{\min }=\min \left\{{\kappa }_i\right\}$

To eliminate the effect of time delays, we chose a Lyapunov–Krasovskii functional, as follows:

$$V(X)=Q(X)+S(X),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S(X)={\displaystyle \sum _{i=1}^n\frac{\lambda }{1-{\gamma }_i}{\displaystyle {\int }_{t-d_i(t)}^t{\Vert X(s)\Vert }_{\Delta }^{2\sigma }ds,}}$$

(33)

where $\lambda >0$ is a parameter to be determined later.

Since $Q(X)>0$ is continuously differentiable and proper, from Lemma 4.3 of Ref. [39], there exist two class $K_{\infty }$ functions, ${\pi }_1$ and ${\pi }_2$, such that

$${\pi }_1(\left|X\right|)\le Q(X)\le {\pi }_2(\left|X\right|)$$

(34)

According to the homogeneous theory, there are constants ${\delta }_i>0,\hspace{0.17em}i=1,2$, such that

$${\delta }_1{\Vert X\Vert }_{\Delta }^{2\sigma }\le W(X)\le {\delta }_2{\Vert X\Vert }_{\Delta }^{2\sigma }$$

(35)

where $W(X)>0$ is a function whose homogeneous degree is $2\sigma .$ Therefore, the following holds:

$${\overline{\pi }}_1(\left|X\right|)\le W(X)\le {\overline{\pi }}_2(\left|X\right|)$$

(36)

with two class $K_{\infty }$ functions ${\overline{\pi }}_1$ and ${\overline{\pi }}_2$.

With the help of $0\le d_i(t)\le d_i$ and ${\dot{d}}_i(t)\le {\gamma }_i<1$, it follows that

$$\begin{array}{l}{\displaystyle \sum _{i=1}^n\frac{\lambda }{1-{\gamma }_i}{\displaystyle {\int }_{t-d_i(t)}^t{\Vert X(s)\Vert }_{\Delta }^{2\sigma }ds\le }}\hspace{0.17em}{\overline{\delta }}_i{\displaystyle {\int }_{t-d_i}^t{\tilde{\pi }}_2(\left|X(s)\right|)ds\hspace{0.17em}}\le {\overline{\delta }}_i{\displaystyle {\int }_{-d_i}^0{\tilde{\pi }}_2(\left|X(\varsigma +t)\right|)d(\varsigma +t)}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le {\tilde{\delta }}_i\underset{-d_i\le \varsigma \le 0}{\sup }{\tilde{\pi }}_2(\left|X(\varsigma +t)\right|)\le {\stackrel{⌢}{\pi }}_2(X\left|z(\varsigma +t)\right|)\end{array}$$

(37)

where ${\overline{\delta }}_i>0$ and ${\tilde{\delta }}_i>0$ are constants and ${\tilde{\pi }}_2$ and ${\stackrel{⌢}{\pi }}_2$ are class $K_{\infty }$ functions, because

$$\left|X(t)\right|\le \underset{-d\le \varsigma \le 0}{\sup }\left|X(\varsigma +t)\right| \mathrm{and} \underset{-d_i\le \varsigma \le 0}{\sup }\left|z(\varsigma +t)\right|\le \underset{-d\le \varsigma \le 0}{\sup }\left|X(\varsigma +t)\right|.$$

Defining ${\pi }_2={\stackrel{⌣}{\pi }}_2+{\stackrel{⌢}{\pi }}_2$ from (33), (34), and (37), it follows that

$${\stackrel{⌣}{\pi }}_1(\left|X(t)\right|)\le S(X(t))\le {\pi }_2(\underset{-d\le \varsigma \le 0}{\sup }\left|X(\varsigma +t)\right|)$$

(38)

From, (20), (21), and (24), follows (32), (33), and (38), in that

$$\begin{array}{l}\dot{V}\hspace{0.17em}=\dot{Q}+{\displaystyle \sum _{i=1}^n\frac{\lambda }{1-{\gamma }_i}{\Vert X(t)\Vert }_{\Delta }^{2\sigma }-}{\displaystyle \sum _{i=1}^n\lambda {\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\sigma }}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le -L\left(\frac{c_1}{2}-(n-1){\overline{c}}_2{L}^{-1}-L^{-\nu }{\overline{C}}_1{\displaystyle \sum _{i=1}^n{\stackrel{⌢}{\omega }}_i}-{\displaystyle {\sum }_{i=1}^n\frac{\lambda }{1-{\gamma }_i}}\right){\Vert X(t)\Vert }_{\Delta }^{2\mu }-\left(\lambda -L^{1-\nu }{\overline{C}}_1{\displaystyle \sum _{i=1}^n{\stackrel{⌣}{\omega }}_i}\right){\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\mu }\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\overline{b}}_2{L}^{-1}+{\tilde{b}}_2(n-1)L^{-{\kappa }_{\min }}\\ \hspace{0.17em}\hspace{0.17em}=-L\left(\frac{c_1}{2}-(n-1){\overline{c}}_2{L}^{-1}-L^{-\nu }{m}_1-L^{-1}{\displaystyle {\sum }_{i=1}^n\frac{\lambda }{1-{\gamma }_i}}\right){\Vert X(t)\Vert }_{\Delta }^{2\mu }-\left(\lambda -L^{1-\nu }{m}_2\right){\Vert X(t-d_i(t))\Vert }_{\Delta }^{2\mu }\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\hat{b}}_2(L^{-1}+L^{-{\kappa }_{\min }})\end{array}$$

(39)

where $m_1={\overline{C}}_1{\displaystyle \sum _{i=1}^n{\stackrel{⌢}{\omega }}_i},\hspace{0.17em}\hspace{0.17em}{m}_2={\overline{C}}_1{\displaystyle \sum _{i=1}^n{\stackrel{⌣}{\omega }}_i}$ and ${\rho }_1={\overline{b}}_2{L}^{-1}+{\tilde{b}}_2(n-1)L^{-{\kappa }_{\min }}$

Therefore, by choosing $\lambda =m_2{L}^{1-\nu }$, and with a sufficiently large L, it satisfies

$$(n-1){\overline{c}}_2{L}^{-1}+L^{-\nu }\left(m_1+m_2{\displaystyle {\sum }_{i=1}^n\frac{1}{1-{\gamma }_i}}\right)\le \frac{c_1}{2}.$$

Then, the inequality (39) becomes

$$\dot{V}\hspace{0.17em}(X(t))\le -\frac{c_{1}L}{2}{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+\hspace{0.17em}{\rho }_1$$

(40)

In (33), $V_n(z)$ and $S(z)$ are homogeneous of degree $2\sigma -\tau$ and $2\sigma$ with respect to the dilation weight $\Delta$, respectively. Therefore, it follows from Lemma 2 that there exist constants ${\lambda }_i>0\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}{\varpi }_i>0\hspace{0.17em}\mathrm{for}\hspace{0.17em}i=1,2$ such that

$${\lambda }_1{\Vert X(t)\Vert }_{\Delta }^{2\sigma -\tau }\le Q(X(t))\le {\lambda }_2{\Vert X(t)\Vert }_{\Delta }^{2\sigma -\tau }$$

(41)

and

$${\varpi }_1{\Vert X(t)\Vert }_{\Delta }^{2\sigma }\le S(X(t))\le {\varpi }_2{\Vert X(t)\Vert }_{\Delta }^{2\sigma }.$$

(42)

Moreover, due to $2\sigma -\tau \le 2\sigma ,\hspace{0.17em}{L}^{\left(\tau -2\sigma \right)/\tau }<1,\hspace{0.17em}\tau -2\sigma <0,\hspace{0.17em}L>1$ and by Lemma 4, we have

$${\lambda }_2{\Vert X(t)\Vert }_{\Delta }^{2\sigma -\tau }=L{\left({\left({\lambda }_2/L\right)}^{1/\tau }\right)}^{\tau }{\Vert X(t)\Vert }_{\Delta }^{2\sigma -\tau }\le \frac{2\sigma -\tau }{2\sigma }L{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+\frac{\tau L^{\left(\tau -2\sigma \right)/\tau }}{2\sigma }{\lambda }_2^{2\sigma /\tau }$$

(43)

Then, we have

$$V(X(t))\le {\rho }_{2}L{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+\frac{\tau L^{\left(\tau -2\sigma \right)/\tau }}{2\sigma }{\lambda }_2^{2\sigma /\tau }$$

(44)

or

$$\frac{1}{{\rho }_2}V(X(t))\le L{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+\frac{\tau L^{\left(\tau -2\sigma \right)/\tau }}{2\sigma {\rho }_2}{\lambda }_2^{2\sigma /\tau },$$

(45)

where ${\rho }_2=:\left({\varpi }_2+(2\delta -\tau )/2\sigma \right)$.

Therefore, it follows from (33) and (44) that

$$\dot{V}\hspace{0.17em}(X(t))\hspace{0.17em}\le -\hspace{0.17em}\frac{c_1}{2}\left(L{\Vert X(t)\Vert }_{\Delta }^{2\sigma }+\frac{\tau L^{\left(\tau -2\sigma \right)/\tau }}{2\sigma {\rho }_2}{\lambda }_2^{2\sigma /\tau }\right)+\frac{\tau L^{\left(\tau -2\sigma \right)/\tau }}{2\sigma {\rho }_2}{\lambda }_2^{2\sigma /\tau }+\hspace{0.17em}{\rho }_1\le -\frac{c_1}{2{\rho }_2}V(X(t))+{\overline{\rho }}_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(46)

where $\hspace{0.17em}{\overline{\rho }}_1=\hspace{0.17em}\frac{c_1\tau L^{\left(\tau -2\sigma \right)/\tau }}{4\sigma {\rho }_2}{\lambda }_2^{2\sigma /\tau }+\hspace{0.17em}{\rho }_1=\frac{c_1\tau {\lambda }_2^{2\sigma /\tau }}{4\sigma {\rho }_2}{L}^{-\left(2\sigma -\tau \right)/\tau }+{\overline{b}}_2{L}^{-1}+{\tilde{b}}_2(n-1)L^{-{\kappa }_{\min }}.$

That is,

$$\frac{d}{dt}\left(e^{t{c}_1/(2{\rho }_2)}V(X(t))\right)\le e^{t{c}_1/(2{\rho }_2)}{\overline{\rho }}_1$$

(47)

taking integral on both sides,

$$e^{t{c}_1/(2{\rho }_2)}V(X(t))-V(X(0))\le \frac{2{\rho }_2}{c_1}{\overline{\rho }}_1\left(e^{t{c}_1/(2{\rho }_2)}-1\right).$$

(48)

Therefore, there exists a finite time $T>0,$

$$V(X(t))\le e^{-t{c}_1/{\rho }_2}V(X(0))+\frac{2{\rho }_2}{c_1}{\overline{\rho }}_1\left(1-e^{-t{c}_1/{\rho }_2}\right)\le \frac{6{\rho }_2}{c_1}{\overline{\rho }}_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{for}\hspace{0.17em}\hspace{0.17em}\mathrm{any}\hspace{0.17em}\hspace{0.17em}t>T$$

(49)

This leads to

$$\left|x_1(t)-y_r(t)\right|=\left|{\chi }_1(t)\right|\le \frac{3}{2\sigma L^{\left(2\sigma -\tau \right)/\tau }}{\lambda }_2^{2\sigma /\tau }+\frac{6{\overline{b}}_2{\rho }_2}{c_{1}L}+\frac{6(n-1){\tilde{b}}_2{\rho }_2}{c_1{L}^{{\kappa }_{\min }}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{for}\hspace{0.17em}\mathrm{any}\hspace{0.17em}\hspace{0.17em}t>T.$$

Thus, for any given tolerance $\epsilon >0$, there exists a sufficiently large $L$ such that

$$\left|x_1(t)-y_r(t)\right|\le \epsilon , \forall \hspace{0.17em}t>T>0.$$

This completes the proof of our main theorem. □

Remark 2.

In the observer and the controller design, the gain L needs to be assigned as a sufficiently large number to achieve the given tracking accuracy $\epsilon >0$. The value of L depends on the bounds of the reference signal$y_r(t)$and its first order derivative${\dot{y}}_r(t)$. In other words, once the bound of their and desired accuracy$\epsilon$are given, the gain L can be determined. Also note that, there are only three set of parameters L,$l_i$and${\beta }_i$need to be determined in our dynamic compensator. The choice of$l_i$and${\beta }_i$only depends on the nominal system (9). Therefore, they can be pre-fixed even for different nonlinear systems. This advantage greatly reduces the design complexity normally associated with the dynamic output feedback design.

At the end of this section, we show that the problem of global practical tracking via the output feedback of a system can be solved under the following mild assumption and the above Assumptions 1, 3, and 4 without the triangular increase condition in Assumption 2.

Assumption 5. 

There are constants ${\tilde{C}}_i>0,\hspace{0.17em}i=1,2,\hspace{0.17em}L>1,$$0<\nu \le 1$and $\tau \ge 0$ such that under the change of (22)

$$\frac{1}{L^{{\kappa }_i}}\left|{\psi }_i(\cdot )\right|\le {\tilde{C}}_1{L}^{1-v}[{\displaystyle \sum _{j=1}^n{\left|{\chi }_j(t)\right|}^{(r_i+\tau )/r_j}}+{\displaystyle \sum _{j=1}^n{\left|{\chi }_j\left(t-d_j(t)\right)\right|}^{(r_i+\tau )/r_j}}+v^{(r_i+\tau )/(r_n+\tau )}]+\frac{{\tilde{C}}_2}{L^{{\kappa }_i}},\hspace{1em}i=1,\hspace{0.17em}\dots ,\hspace{0.17em}n$$

(50)

where${\kappa }_1=0,\hspace{0.17em}{r}_1=1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{p}_i{\kappa }_{i+1}={\kappa }_i+1,$and$r_{i+1}=(r_i+\tau )/p_i>0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n$.

It is obvious that Assumption 5 is a special case of Assumption 2, and next, a more general result is given.

Theorem 2.

Under Assumptions 1 and 3–5, there exist an observer-based output-feedback control of the form (26)–(27) that solves the problem of global practical output tracking of System (23).

Proof. 

Similar to (25), Assumption 5 will directly lead to (32). The rest of the proof is similar to that of Theorem 1 and hence omitted here. □

4. Example and Simulations

Consider the following time-varying delay nonlinear system,

$$\begin{array}{l}{\dot{x}}_1(t)={\alpha }_1{x}_2^{7/5}(t)+x_1^{6/5}(t-d_1(t))\cos (x_2(t))\\ {\dot{x}}_2(t)={\alpha }_{2}u(t)+0.5\left(x_2^{3/5}(t-d_2(t))+1\right)x_1^{4/5}(t)\\ \hspace{0.17em}y(t)={\alpha }_0{x}_1(t)-y_r(t)\end{array}$$

(51)

where ${\alpha }_i\in [1,\hspace{0.17em}1.5],\hspace{0.17em}\hspace{0.17em}i=0,\hspace{0.17em}1,\hspace{0.17em}2$ are unknown constants and $d_1(t)=(0.3+{\sin }^2(t))/3$, $d_2(t)=0.2+{\sin }^2(t)/2(1+t^2)$ represent time-varying delays. Using only the measurement $y(t)$ to track the reference signal, $y_r(t)$ is our control purpose. Clearly, the system (51) is of Form (1). Subsequently, we chose the reference signal as $y_r(t)=0.2\sin 5t+{(\sin t)}^3$.

Then,

$$\left|y_r(t)\right|=\left|0.2\sin (5t)+{(\sin t)}^3\right|\le 1.2,\hspace{0.17em}\left|{\dot{y}}_r(t)\right|=\left|\cos (5t)+3{(\sin (t))}^2\cos (t)\right|\le 4.$$

(52)

By choosing $\tau =2/3$, together with $\hspace{0.17em}{r}_1=1$ and $p_1=7/5$, we obtained $\hspace{0.17em}{r}_2=1$ and $\sigma =7/5$.

Further, by Lemma 4, it can be verified that

$$\left|{\phi }_1(\cdot )\right|\le {\left|x_1(t-d(t))\right|}^{6/5}\le 2^{1/5}{\left|x_1(t-d(t))\right|}^{6/5}\le \frac{6}{7}{\left|x_1(t-d(t))\right|}^{7/5}+\frac{4}{7},$$

$$\begin{array}{l}\left|{\phi }_2(\cdot )\right|\le \frac{1}{2}{\left|x_1(t)\right|}^{4/5}{\left|x_2(t-d(t))\right|}^{3/5}+\frac{1}{2}{2}^{3/5}{\left|x_1(t)\right|}^{4/5}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le \frac{4}{2\times 7}{\left|x_1(t)\right|}^{7/5}+\frac{3}{2\times 7}{\left|x_2(t-d(t))\right|}^{3/5}+\frac{4}{2\times 7}{\left|x_1(t)\right|}^{7/5}+\frac{3}{2\times 7}{2}^{7/5}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le \frac{4}{7}\left({\left|x_1(t)\right|}^{7/5}+{\left|x_2(t)\right|}^{7/5}+{\left|x_2(t-d(t))\right|}^{7/5}\right)+\frac{6}{7}\end{array}$$

(53)

and

$$\begin{array}{l}0\le d_1(t)\le 13/30,\hspace{0.17em}\hspace{0.17em}{\dot{d}}_1(t)=\sin (2t)/3\le 1/3<1\\ 0\le d_2(t)\le 7/10,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\dot{d}}_2(t)=\sin (2t)/4(1+t^2)-t{\sin }^2(t)/2{(1+t^2)}^2\le 3/4<1\end{array}$$

(54)

Clearly, Assumptions 1–4 holds with $C_1\ge 6/7,\hspace{0.17em}$$C_2\ge 6/7$, and $M\ge 4$, and it is specifically assumed that ${\alpha }_0=1,\hspace{0.17em}{\alpha }_1=1.2,\hspace{0.17em}{\alpha }_2=1.4$.

Therefore, following the design procedure above, the output controller can be constructed as

$$\begin{array}{l}{\dot{\eta }}_2=-L^{5/7}{\left({\eta }_2+l_1\left(x_1-y_r\right)\right)}^{7/5}\\ u=-L^{9/7}{\beta }_2\left({\beta }_1{\left(x_1-y_r\right)}^{7/5}+{\left({\eta }_2+l_1\left(x_1-y_r\right)\right)}^{7/5}\right)\end{array}$$

(55)

choosing $l_1=4.1,\hspace{0.17em}{\beta }_1=1.1,\hspace{0.17em}{\beta }_2=4$ and $L=80$. To perform the simulation, we chose the reference signal $y_r(t)=0.2\sin 5t+{(\sin t)}^3$ and the initial states $\left(x_1(0),x_2(0),{\eta }_2(0)\right)=\left(2,\hspace{0.17em}-2,\hspace{0.17em}0.5\right)$. The simulation results are shown in Figure 1, Figure 2, Figure 3 and Figure 4. These figures verified the effectiveness of our design method.

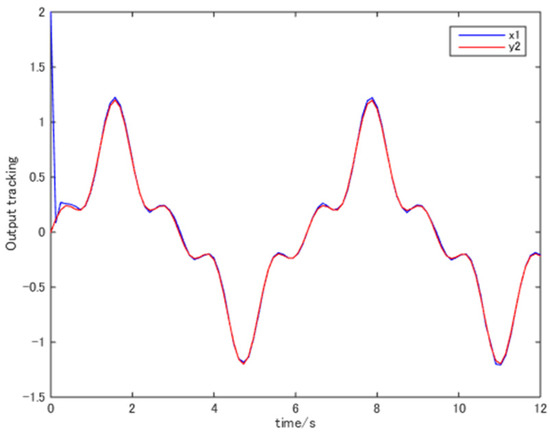
Figure 1. The trajectories of $x_1(t)$ and $y_r(t)$.

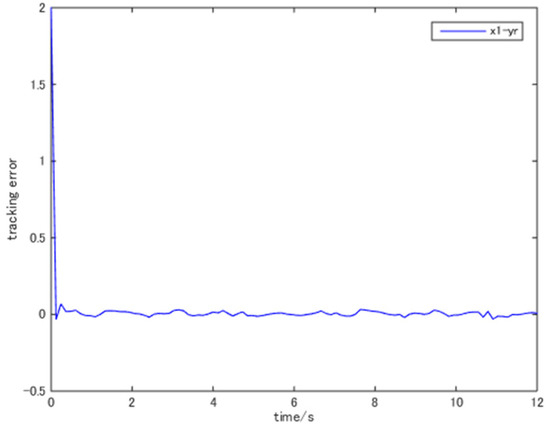
Figure 2. The trajectory of $x_1(t)-y_r(t)$.

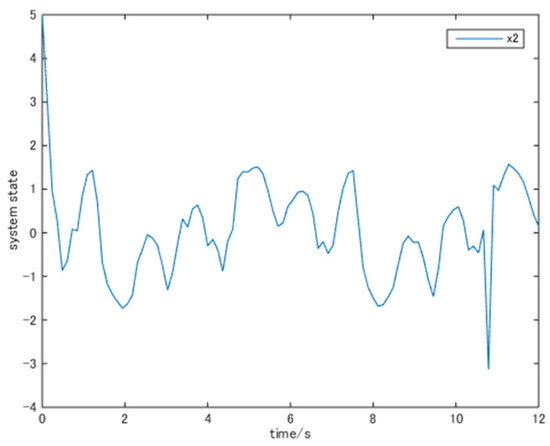
Figure 3. The trajectory of state $x_2(t)$.

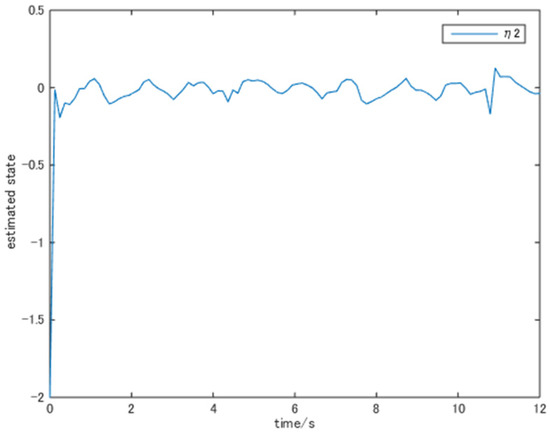
Figure 4. The trajectory of state ${\eta }_2(t)$.

It is worth pointing out that although System (51) is simple, it cannot solve the global practical tracking problem using the design methods presented in [1,3,4,5,6,7,8,10,11,34], because of the presence of time-varying delay terms $d_1(t)$ and $d_2(t)$. Reference [1] only considers state feedback for a certain class of p-normal form nonlinear systems, while Reference [3] only considers partially linear cases, etc. In [34], a special case where the time-delay is only constant was considered. This paper addresses the output-feedback-tracking problem of a class of high-order nonlinear time-varying delay systems. However, if some classes of a general nonlinear system can be transformed into the considered system in this article, then the method proposed in this article can also be used.

Next, we will verify that the same dynamic controller (55) can be applied to different nonlinear systems, achieving the tracking purpose. We changed the functions ${\phi }_i(\cdot )$ to

$$\begin{array}{l}{\phi }_1(\cdot )=x_1^{6/5}(t-d_1(t))+0.5\theta (t)\cos (x_2(t))\\ {\phi }_2(\cdot )=0.5\theta (t)\left(x_2^{3/5}(t-d_2(t))+1\right)x_1^{4/5}(t)+\theta (t)\end{array}$$

(56)

where $\left|\theta (t)\right|\le 1/2$ is a bounded disturbance. It is not difficult to prove that Function (56) also satisfies (53).

The observer and the controller remain the same as before. The numerical experiment demonstrates that the very same controller, without any change, achieves practical tracking for different functions (56). To perform the simulation, we chose the bounded disturbance as $\theta (t)=\cos t/2$ and the same reference signal $y_r(t)=0.2\sin 5t+{(\sin t)}^3$, with the initial states being $\left(x_1(0),x_2(0),{\eta }_2(0)\right)=\left(2,\hspace{0.17em}-2,\hspace{0.17em}0.5\right).$ The simulation results are shown in Figure 5, Figure 6, Figure 7 and Figure 8. These figures verified the effectiveness of our design method.

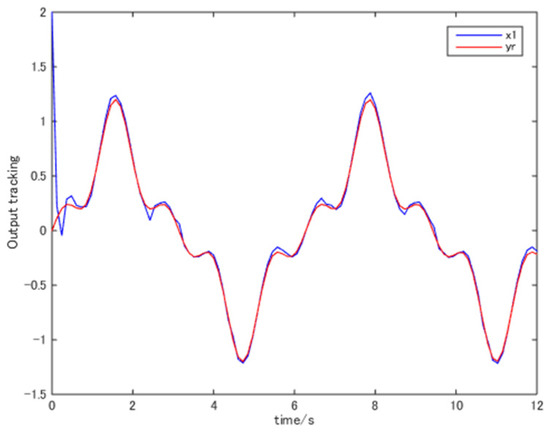
Figure 5. The trajectories of $x_1(t)$ and $y_r(t)$.

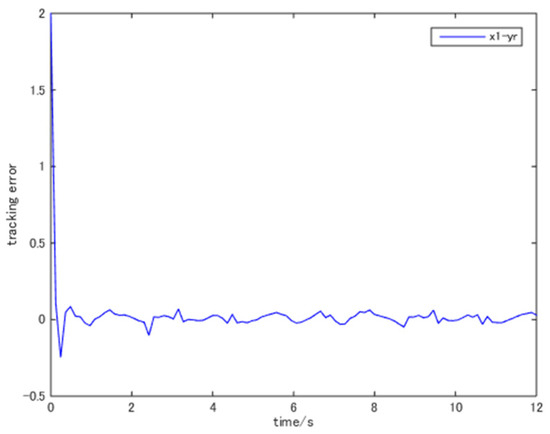
Figure 6. The trajectory of $x_1(t)-y_r(t)$.

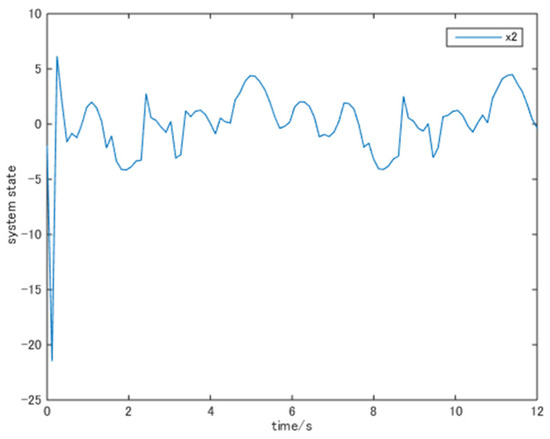
Figure 7. The trajectory of state $x_2(t)$.

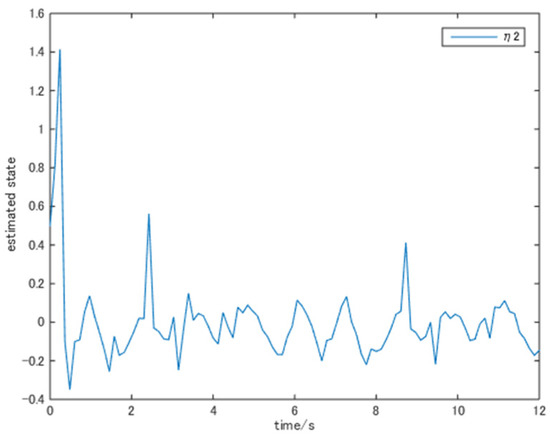
Figure 8. The trajectory of state ${\eta }_2(t)$.

5. Conclusions

This article has solved the problem of global output practical tracking for a class of uncertain inherently time-varying delays nonlinear systems via an observer-based output-feedback control. With the aid of the homogeneous domination method and the new Lyapunov–Krasovskii functional, a scaling gain is introduced into the proposed output-feedback controller to guarantee all states of the closed-loop system remain bounded and simultaneously making the tracking error arbitrarily small. The simulation results of the given example verified the effectiveness of our designed method. Some interesting problems still remained; for example, if the growth rate a in Assumption 2 is an unknown constant, how can we design an adaptive output-feedback controller for System (1)? Recently, a few results on switched or stochastic high-order time-delay nonlinear systems have been achieved (for example, [14,15,16]), but these papers only consider the systems with a high-order nonlinear growth. In addition, new research topics are also being extensively studied (for example, [40,41,42]). An important issue is whether these results can be extended to switched or stochastic nonlinear systems with low-order nonlinearities or the above topic systems.