Certain Concepts in Intuitionistic Neutrosophic Graph Structures

Abstract

A graph structure is a generalization of simple graphs. Graph structures are very useful tools for the study of different domains of computational intelligence and computer science. In this research paper, we introduce certain notions of intuitionistic neutrosophic graph structures. We illustrate these notions by several examples. We investigate some related properties of intuitionistic neutrosophic graph structures. We also present an application of intuitionistic neutrosophic graph structures.

1. Introduction

Fuzzy graph models are advantageous mathematical tools for dealing with combinatorial problems of various domains including operations research, optimization, social science, algebra, computer science, environmental science and topology. Fuzzy graphical models are obviously better than graphical models due to natural existence of vagueness and ambiguity. Initially, we needed fuzzy set theory to cope with many complex phenomenons having incomplete information. Fuzzy set theory [1] is a very strong mathematical tool for solving approximate reasoning related problems. These notions describe complex phenomenons very well, which are not properly described using classical mathematics. Atanassov [2] generalized the fuzzy set theory by introducing the notion of intuitionistic fuzzy sets. The intuitionistic fuzzy sets have more describing possibilities as compared to fuzzy sets. An intuitionistic fuzzy set is inventive and more useful due to the existence of non-membership degree. In many situations like information fusion, indeterminacy is explicitly quantified. Smarandache [3] introduced the concept of neutrosophic sets, and he combined the tricomponent logic, non-standard analysis, and philosophy. It is a branch of philosophy which studies the origin, nature and scope of neutralities as well as their interactions with different ideational spectra. Three independent components of neutrosophic set are: truth value, indeterminacy value and falsity value [3]. For convenient use of neutrosophic sets in real-life phenomena, Wang et al. [4] proposed single valued neutrosophic sets, which is a generalization of intuitionistic fuzzy sets [2] and has three independent components having values in a standard unit interval [0, 1]. Ye [5,6,7,8] proposed several multi criteria decision-making methods based on neutrosophic sets. Bhowmik and Pal [9,10] introduced the notion of intuitionistic neutrosophic sets.

Kauffman [11] introduced fuzzy graphs on the basis of Zadeh’s fuzzy relations [12]. Rosenfeld [13] discussed fuzzy analogue of many graph-theoretic notions. Later on, Bhattacharya [14] gave some remarks on fuzzy graphs. The complement of a fuzzy graph was defined by Sunitha and Vijayakumar [15]. Bhutani and Rosenfeld studied the notion of M-strong fuzzy graphs and their properties in [16]. Parvathi et al. defined operations on intuitionistic fuzzy graphs in [17]. Akram and Shahzadi [18] introduced neutrosophic soft graphs with applications. Dinesh and Ramakrishnan [19] introduced the notion of fuzzy graph structures and discussed some related properties. Akram and Akmal [20] introduced the concept of bipolar fuzzy graph structures. Recently, Akram and Sitara [21] introduced the concept of intuitionistic neutrosophic graph structures. Several notions’ graph structures have been studied by the same authors in [22,23,24,25,26,27]. In this research paper, we introduce certain notions of intuitionistic neutrosophic graph structures and illustrate these notions by examples. We also present an application of intuitionistic neutrosophic graph structures in decision-making. For other notations and applications, readers are referred to [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45] .

2. Intuitionistic Neutrosophic Graph Structures

Sampathkumar [46] introduced the graph structure, which is a generalization of an undirected graph and is quite useful in studying some structures like graphs, signed graphs, labeled graphs and edge colored graphs.

Definition 1.

[46] A graph structure $G=(V,R_1,\dots ,R_r)$ consists of a non-empty set V together with relations $R_1,R_2,\dots ,R_r$ on V, which are mutually disjoint such that each $R_h$, $1\le h\le r$ is symmetric and irreflexive.

One can represent a graph structure $G=(V,R_1,\dots ,R_r)$ in the plane, just like a graph where each edge is labeled as $R_h$, $1\le h\le r$.

Definition 2.

[3] An ordered triple $<T_N,I_N,F_N>$ in $]0^{-},1^{+}[$ in the universe of discourse V is called neutrosophic set, where $T_N$, $I_N$, $F_N$: V→$]0^{-},1^{+}[$, and their sum is without any restriction.

Definition 3.

[4] An ordered triple $<T_N,I_N,F_N>$ in $[0,1]$ in a universe of discourse V is called single-valued neutrosophic set, where $T_N$, $I_N$, $F_N$: V→$[0,1]$, and their sum is restricted between 0 and 3.

Definition 4.

[47] Let V be a fixed set. A generalized intuitionistic fuzzy set I of V is an object having the form I=$\left\{(u,{\mu }_I\left(u\right),{\nu }_I\left(u\right))\right|u\in V\}$, where the functions ${\mu }_I\left(u\right):\to [0,1]$ and ${\nu }_I\left(u\right):\to [0,1]$ define the degree of membership and degree of nonmembership of an element $u\in V$, respectively, such that

$$min\{{\mu }_I\left(u\right),{\nu }_I\left(u\right)\}\le 0.5, for all u\in V.$$

Definition 5.

[9,10] An intuitionistic neutrosophic set can be stated as a set having the form $I=\{T_I\left(u\right),I_I\left(u\right),F_I\left(u\right):u\in V\}$, where

$$\begin{gathered} min\{T_I\left(u\right),I_I\left(u\right)\}\le 0.5, \\ min\{F_I\left(u\right),I_I\left(u\right)\}\le 0.5, \\ min\{T_I\left(u\right),F_I\left(u\right)\}\le 0.5, \end{gathered}$$

and $0\le T_I\left(u\right)+I_I\left(u\right)+F_I\left(u\right)\le 2$.

Definition 6.

Let $\check{G}$ = $(P,P_1,P_2,\dots ,P_r)$ be a graph structure(GS), and then ${\check{G}}_i$ = $(O,O_1,O_2 and\dots ,O_r)$ is called an intuitionistic neutrosophic graph structure (INGS), if O = $<k,T\left(k\right),I\left(k\right),F\left(k\right)>$ and $O_h$ = $<(k,l),T_h(k,l),I_h(k,l),F_h(k,l)>$ are intuitionistic neutrosophic sets on P and $P_h$, respectively, such that

1.

$T_h(k,l)\le T\left(k\right)\wedge T\left(l\right)$, $I_h(k,l)\le I\left(k\right)\wedge I\left(l\right)$, $F_h(k,l)\le F\left(k\right)\vee F\left(l\right);$

2.

$T_h(k,l)\wedge I_h(k,l)\le 0.5,$ $T_h(k,l)\wedge F_h(k,l)\le 0.5,$ $I_h(k,l)\wedge F_h(k,l)\le 0.5;$

3.

$0\le T_h(k,l)+I_h(k,l)+F_h(k,l)\le 2$, $\forall (k,l)\in O_h$, $h=1,2,\dots ,r$,

where O is an underlying vertex set of ${\check{G}}_i$ and $O_h$ (h = 1, 2, …, r ) are underlying h-edge sets of ${\check{G}}_i$.

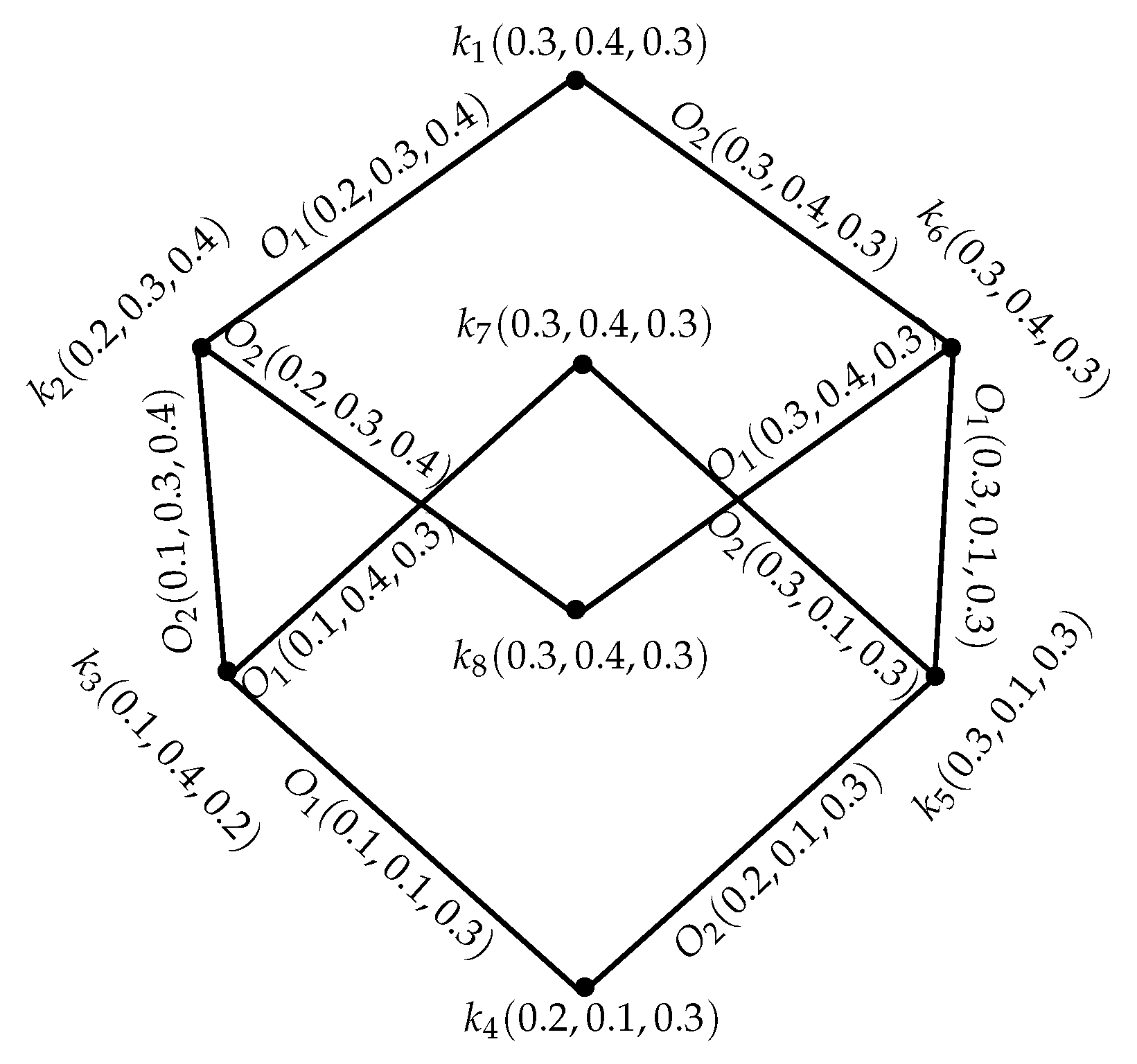
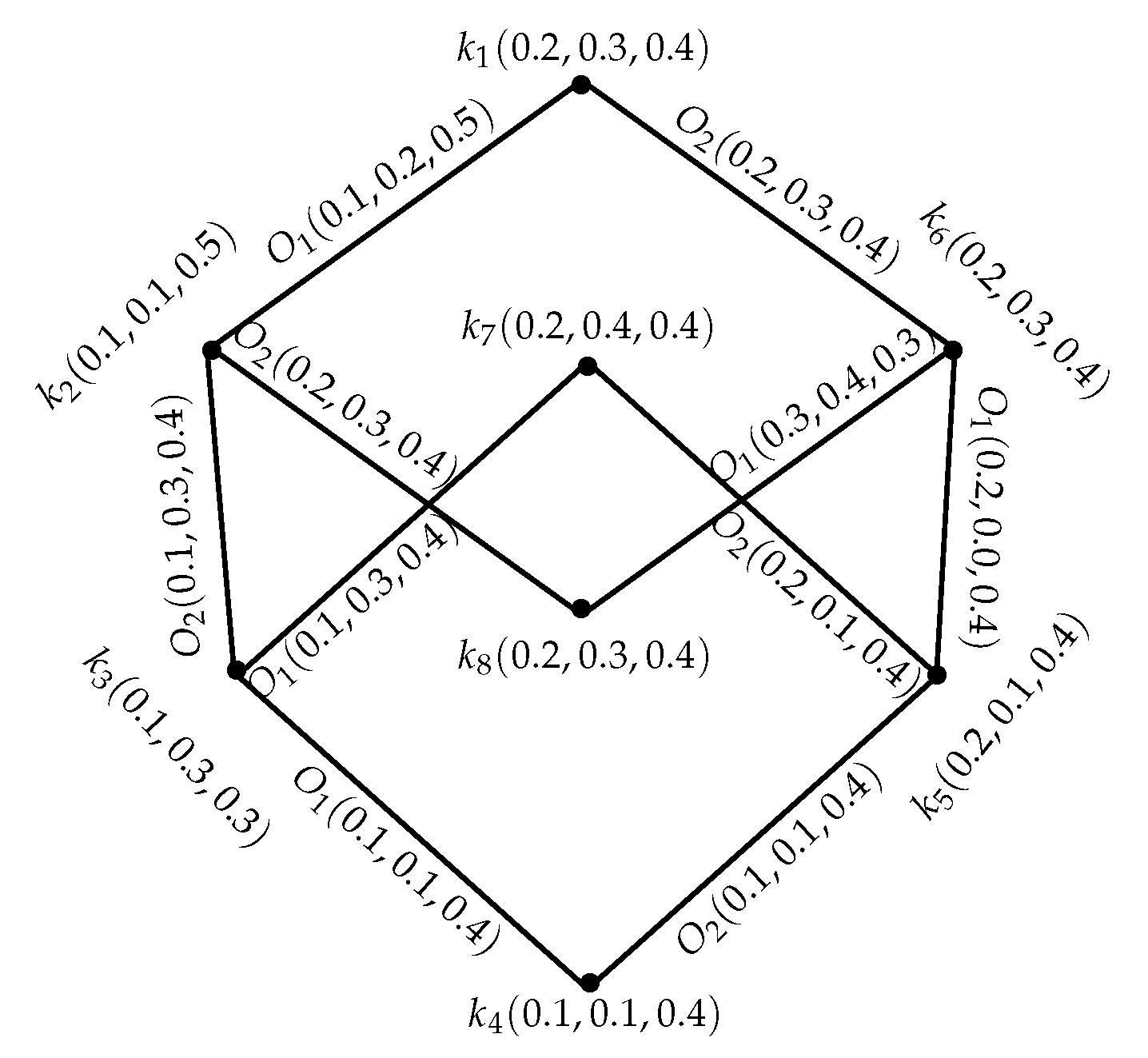
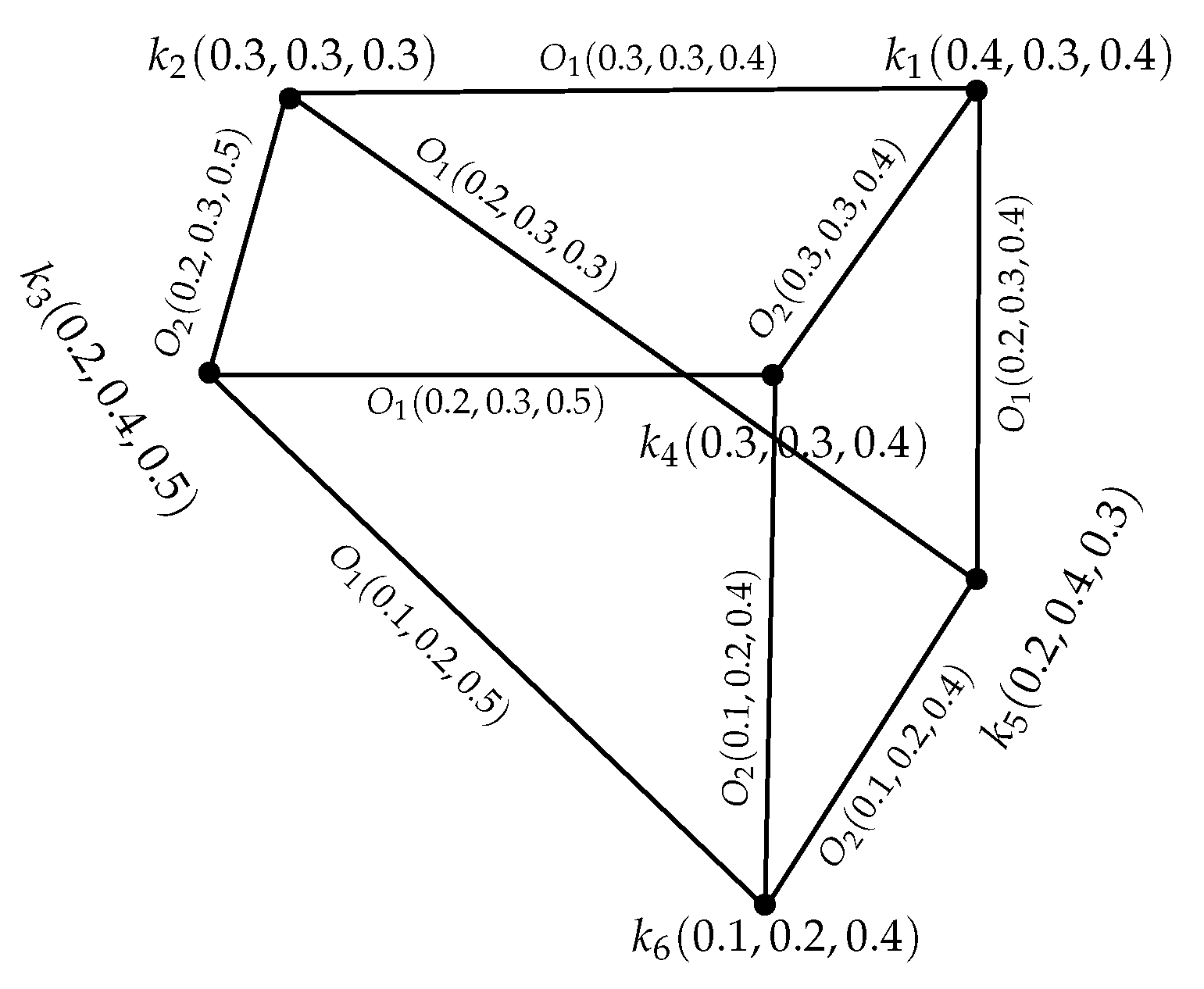
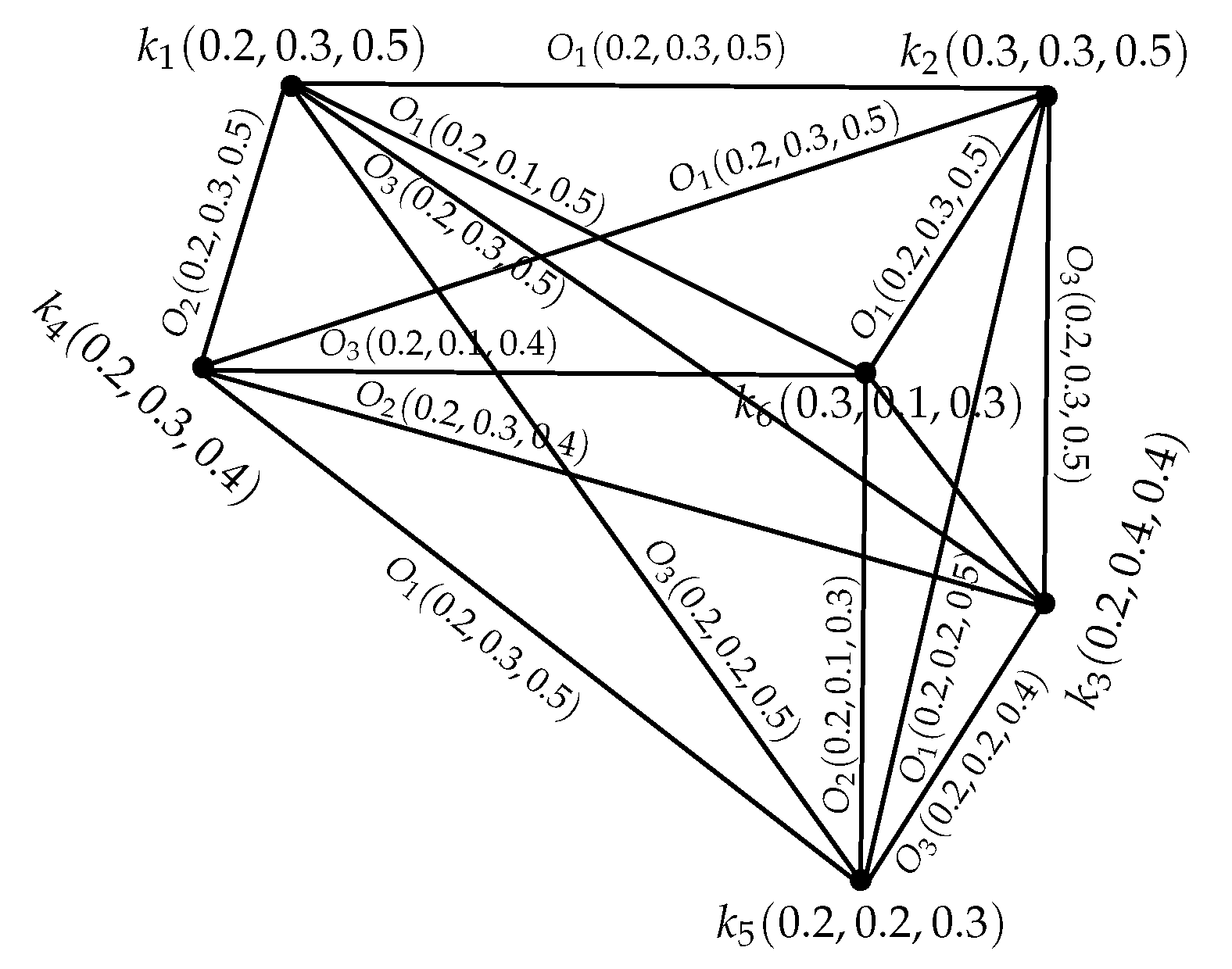
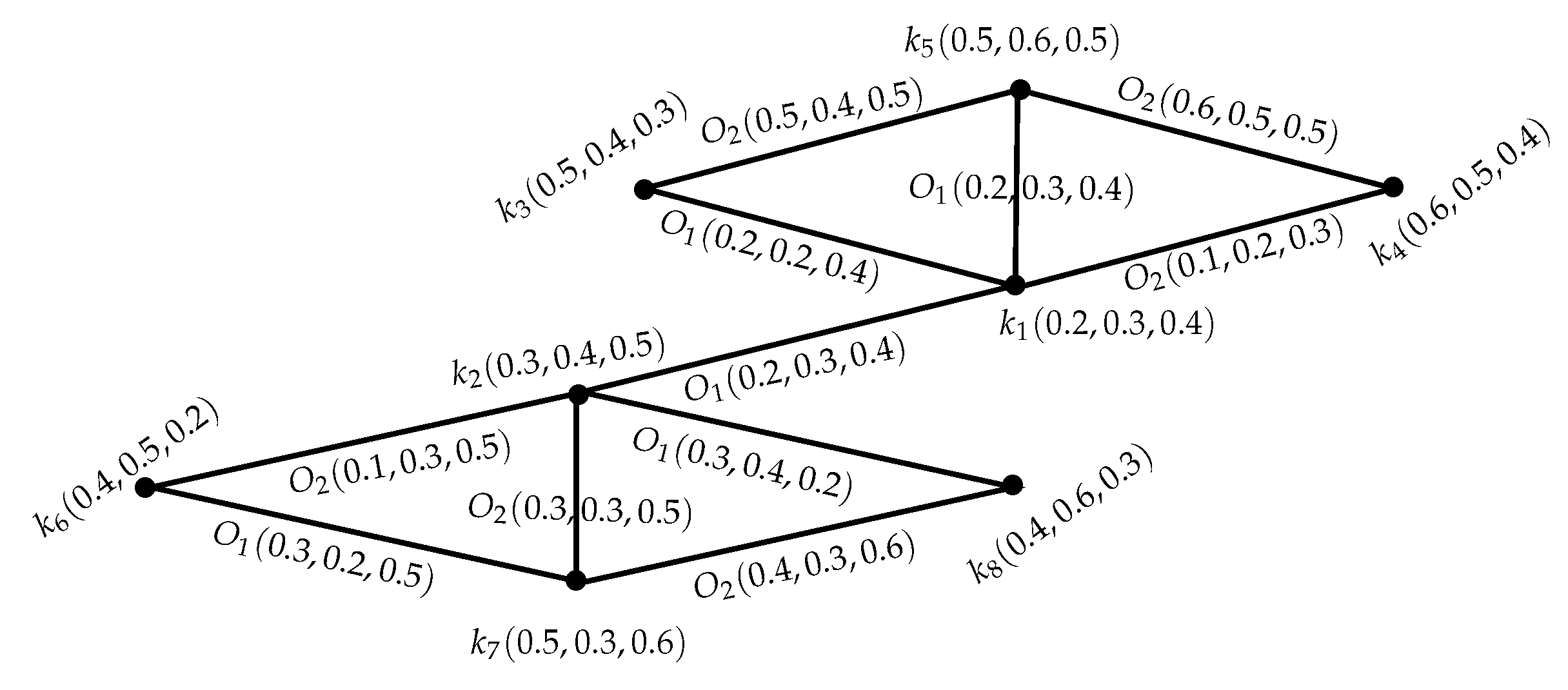
Example 1.

Consider a GS $\check{G}$ = $(P,P_1,P_2)$ such that O, $O_1$,$O_2$ are IN subsets of $P,P_1,P_2$, respectively, where

$$\begin{gathered} P=\{k_1,k_2,k_3,k_4,k_5,k_6,k_7,k_8\}, \\ {P}_1=\{k_1{k}_2,k_3{k}_4,k_5{k}_6,k_3{k}_7,k_6{k}_8\}, \\ {P}_2=\{k_2{k}_3,k_4{k}_5,k_1{k}_6,k_5{k}_7,k_2{k}_8\}. \end{gathered}$$

Through direct calculations, it is easy to show that ${\check{G}}_i$ = $(O,O_1,O_2)$ is an INGS of $\check{G}$ as represented in Figure 1.

Definition 7.

Let ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ be an INGS of $\check{G}$. If ${\check{H}}_i$ = $(O^{\prime },O_1^{\prime },O_2^{\prime },\dots ,O_r^{\prime })$ is an INGS of $\check{G}$ such that

$$\begin{gathered} T^{\prime }\left(k\right)\le T\left(k\right),I^{\prime }\left(k\right)\le I\left(k\right),F^{\prime }\left(k\right)\ge F\left(k\right)\forall k\in P, \\ {T}_h^{\prime }(k,l)\le T_h(k,l),I_h^{\prime }(k,l)\le I_h(k,l),F_h^{\prime }(k,l)\ge F_h(k,l),\forall (k,l)\in P_h,h=1,2,\dots ,r. \end{gathered}$$

Then, ${\check{H}}_i$ is said to be an intuitionistic neutrosophic (IN) subgraph structure of INGS ${\check{G}}_i$.

Example 2.

Consider an INGS ${\check{H}}_i$ = $(O^{\prime },O_1^{\prime },O_2^{\prime })$ of GS $\check{G}$ = $(P,P_1,P_2)$ as represented in Figure 2. Through routine calculations, it can be easily shown that ${\check{H}}_i$ is an IN subgraph structure of INGS ${\check{G}}_i$.

Definition 8.

An INGS ${\check{H}}_i$ = $(O^{\prime },O_1^{\prime },O_2^{\prime },\dots ,O_r^{\prime })$ is called an IN induced-subgraph structure of ${\check{G}}_i$ by Q ⊆ P if

$$\begin{gathered} T^{\prime }\left(k\right)=T\left(k\right),I^{\prime }\left(k\right)=I\left(k\right),F^{\prime }\left(k\right)=F\left(k\right),\forall k\in Q, \\ {T}_h^{\prime }(k,l)=T_h(k,l),I_h^{\prime }(k,l)=I_h(k,l),F_h^{\prime }(k,l)=F_h(k,l),\forall k,l\in Q,h=1,2,\dots ,r. \end{gathered}$$

Example 3.

The INGS in the given Figure 3 is an IN induced-subgraph structure of an INGS in Figure 1.

Definition 9.

An INGS ${\check{H}}_i$ = $(O^{\prime },O_1^{\prime },O_2^{\prime },\dots ,O_r^{\prime })$ is said to be a IN spanning-subgraph structure of ${\check{G}}_i$ if $O^{\prime }=O$ and

$$T_h^{\prime }(k,l)\le T_h(k,l),I_h^{\prime }(k,l)\le I_h(k,l),F_h^{\prime }(k,l)\ge F_h(k,l),h=1,2,\dots ,r.$$

Example 4.

An INGS shown in Figure 4 is an IN spanning-subgraph structure of an INGS in Figure 1.

Definition 10.

Let ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ be an INGS. Then, $kl\in P_h$ is named as a IN $O_h$-edge or shortly $O_h$-edge, if $T_h(k,l)>0$ or $I_h(k,l)>0$ or $F_h(k,l)>0$ or all these conditions are satisfied. As a result, support of $O_h$ is:

$$supp\left(O_h\right)=\{kl\in O_h:T_h(k,l)>0\}\cup \{kl\in O_h:I_h(k,l)>0\}\cup \{kl\in O_h:F_h(k,l)>0\},$$

$h=1,2,\dots ,r$.

Definition 11.

$O_h$-path in an INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is a sequence $k_1,k_2,\dots ,k_r$ of distinct vertices (except $k_r=k_1$) in P, such that $k_{h-1}{k}_h$ is an IN $O_h$-edge $\forall h=2,\dots ,r$.

Definition 12.

An INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is $O_h$-strong for any $h\in \{1,2,\dots ,r\}$ if

$$T_h(k,l)=min\{T\left(k\right),T\left(l\right)\},I_h(k,l)=min\{I\left(k\right),I\left(l\right)\},F_h(k,l)=max\{F\left(k\right),F\left(l\right)\},$$

$\forall kl\in supp\left(O_h\right)$. If ${\check{G}}_i$ is $O_h$-strong for all $h\in \{1,2,\dots ,r\}$, then ${\check{G}}_i$ is a strong INGS.

Example 5.

Consider an INGS ${\check{G}}_i$ = $(O,O_1,O_2)$ as represented in Figure 5. Then, ${\check{G}}_i$ is strong INGS, as it is $O_1-$ and $O_2-strong$.

Definition 13.

An INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is a complete INGS, if

1.

${\check{G}}_i$ is strong INGS.

2.

$supp\left(O_h\right)\ne \varnothing$, for all h = 1, 2, …, r.

3.

For all $k,l\in P$, $kl$ is a $O_h-edge$ for some h.

Example 6.

Let ${\check{G}}_i$ = $(O,O_1,O_2)$ be an INGS of GS $\check{G}$ = $(P,P_1,P_2)$, such that

$$\begin{gathered} P=\{k_1,k_2,k_3,k_4,k_5,k_6\}, \\ {P}_1=\{k_1{k}_6,k_1{k}_2,k_2{k}_4,k_2{k}_5,k_2{k}_6,k_1{k}_6\}, \\ {P}_2=\{k_2{k}_6,k_4{k}_3,k_5{k}_6,k_1{k}_4\}, \\ {P}_3=\{k_1{k}_5,k_5{k}_3,k_2{k}_3,k_1{k}_3,k_4{k}_6\}. \end{gathered}$$

By means of direct calculations, it is easy to show that ${\check{G}}_i$ is strong INGS.

Moreover, $supp\left(O_1\right)\ne \varnothing$, $supp\left(O_2\right)\ne \varnothing$, $supp\left(O_3\right)\ne \varnothing$, and every pair $k_h{k}_q$ of vertices of P, is $O_1$-edge or $O_2$-edge or an $O_3$-edge. Hence, ${\check{G}}_i$ is a complete INGS, that is, $O_1{O}_2{O}_3$-complete INGS.

Definition 14.

Let ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ be an INGS. The truth strength $T.P_{O_h}$, falsity strength $F.P_{O_H}$, and indeterminacy strength $I.P_{O_h}$ of an $O_h$-path, $P_{O_h}$ = $k_1,k_2,\dots ,k_n$ is defined as:

$$\begin{gathered} T.P_{O_h}=\underset{i=2}{\overset{n}{\bigwedge }}[T_{O_h}^P\left(k_{i-1}{k}_i\right)], \\ I.P_{O_h}=\underset{i=2}{\overset{n}{\bigwedge }}[I_{O_h}^P\left(k_{i-1}{k}_i\right)], \\ F.P_{O_h}=\underset{i=2}{\overset{n}{\bigvee }}[F_{O_h}^P\left(k_{i-1}{k}_i\right)]. \end{gathered}$$

Example 7.

Consider an INGS ${\check{G}}_i$ = $(O,O_1,O_2,O_3)$ as in Figure 6. We found an $O_1$-path $P_{O_1}$ = $k_2,k_1,k_6$. So, $T.P_{O_1}$= 0.2, $I.P_{O_1}$= 0.1 and $F.P_{O_2}$= 0.5.

Definition 15.

Let ${\check{G}}_i$ = $(O,O_1,O_2,\cdots ,O_r)$ be an INGS. Then,

• $O_h$-strength of connectedness of truth between k and l is defined as: $T_{O_h}^{\infty }\left(kl\right)$ = ${\displaystyle \underset{i\ge 1}{\bigvee }}\{T_{O_h}^i\left(kl\right)\}$, such that $T_{O_h}^i\left(kl\right)$ = $(T_{O_h}^{i-1}\circ T_{O_h}^1)\left(kl\right)$ for $i\ge 2$ and $T_{O_h}^2\left(kl\right)$ = $(T_{O_h}^1\circ T_{O_h}^1)\left(kl\right)$ = ${\displaystyle \underset{y}{\bigvee }}(T_{O_h}^1\left(ky\right)\wedge T_{O_h}^1)\left(yl\right)$.
• $O_h$-strength of connectedness of indeterminacy between k and l is defined as: $I_{O_h}^{\infty }\left(kl\right)$ = ${\displaystyle \underset{i\ge 1}{\bigvee }}\{I_{O_h}^i\left(kl\right)\}$, such that $I_{O_h}^i\left(kl\right)$ = $(I_{O_h}^{i-1}\circ I_{O_h}^1)\left(kl\right)$ for $i\ge 2$ and $I_{O_h}^2\left(kl\right)$ = $(I_{O_h}^1\circ I_{O_h}^1)\left(kl\right)$ = ${\displaystyle \underset{y}{\bigvee }}(I_{O_h}^1\left(ky\right)\wedge I_{O_i}^1)\left(yl\right)$.
• $O_h$-strength of connectedness of falsity between k and l is defined as: $F_{O_h}^{\infty }\left(kl\right)$ = ${\displaystyle \underset{i\ge 1}{\bigwedge }}\{F_{O_h}^i\left(kl\right)\}$, such that $F_{O_h}^i\left(kl\right)$ = $(F_{O_h}^{i-1}\circ F_{O_h}^1)\left(kl\right)$ for $i\ge 2$ and $F_{Q_h}^2\left(kl\right)$ = $(F_{O_h}^1\circ F_{O_h}^1)\left(kl\right)$ = ${\displaystyle \underset{y}{\bigwedge }}(F_{O_h}^1\left(ky\right)\vee F_{O_h}^1)\left(yl\right)$.

Definition 16.

An INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is called an $O_h$-cycle if $(supp\left(O\right),supp\left(O_1\right)$, $supp\left(O_2\right),\dots ,supp\left(O_r\right))$ is an $O_h-cycle$.

Definition 17.

An INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is an IN fuzzy $O_h$-cycle (for any h) if

1.

${\check{G}}_i$ is an $O_h$-cycle.

2.

There exists no unique $O_h$-edge $kl$ in ${\check{G}}_i$ such that

$T_{O_h}\left(kl\right)=min\{T_{O_h}\left(yz\right):yz\in P_h=supp\left(O_h\right)\}$ or $I_{O_h}\left(kl\right)=min\{I_{O_h}\left(yz\right):yz\in P_h=supp\left(O_h\right)\}$ or $F_{O_h}\left(kl\right)=max\{F_{O_h}\left(yz\right):yz\in P_h=supp\left(O_h\right)\}.$

Example 8.

Consider an INGS ${\check{G}}_i$ = $(O,O_1,O_2)$ as in Figure 6. Then, ${\check{G}}_i$ is an $O_1$-cycle and IN fuzzy $O_1-cycle$, since $(supp\left(O\right),supp\left(O_1\right),supp\left(O_2\right))$ is an $O_1$-cycle and no unique $O_1$-edge $kl$ satisfies the condition: $T_{O_h}\left(kl\right)=min\{T_{O_h}\left(yz\right):yz\in P_h=supp\left(O_h\right)\}$ or $I_{O_h}\left(kl\right)=min\{I_{O_h}\left(yz\right):yz\in P_h=supp\left(O_h\right)\}$ or $F_{O_h}\left(kl\right)=max\{F_{O_h}\left(yz\right):yz\in P_h=supp\left(O_h\right)\}.$

Definition 18.

Let ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ be an INGS and k a vertex in ${\check{G}}_i$. Let $(O^{\prime },O_1^{\prime },O_2^{\prime },\dots ,O_r^{\prime })$ be an IN subgraph structure of ${\check{G}}_i$ induced by $P\backslash \left\{k\right\}$ such that $\forall y\ne k,z\ne k.$

$T_{O^{\prime }}\left(k\right)=0=I_{O^{\prime }}\left(k\right)=F_{O^{\prime }}\left(k\right)$, $T_{O_h^{\prime }}\left(ky\right)$ = 0 = $I_{O_h^{\prime }}\left(ky\right)=F_{O_h^{\prime }}\left(ky\right)\forall$ edges $ky\in {\check{G}}_i$; $T_{O^{\prime }}\left(y\right)=T_O\left(y\right)$, $I_{O^{\prime }}\left(y\right)=I_O\left(y\right)$, $F_{O^{\prime }}\left(y\right)=F_O\left(y\right)$, $\forall y\ne k$; $T_{O_h^{\prime }}\left(yz\right)$ = $T_{O_h}\left(yz\right)$, $I_{O_h^{\prime }}\left(yz\right)$ = $I_{O_h}\left(yz\right)$, $F_{O_h^{\prime }}\left(yz\right)$ = $F_{O_h}\left(yz\right)$.

Then, k is IN fuzzy $O_h$ cut-vertex, for some h, if

$$T_{O_h}^{\infty }\left(yz\right)>T_{O_h^{\prime }}^{\infty }\left(yz\right),I_{O_h}^{\infty }\left(yz\right)>I_{O_h^{\prime }}^{\infty }\left(yz\right)$$

and

$$F_{O_h}^{\infty }\left(yz\right)>F_{O_h^{\prime }}^{\infty }\left(yz\right),for some y,z\in P\backslash \{k\}.$$

Note that k is an IN fuzzy $O_h-T$ cut-vertex, if $T_{O_h}^{\infty }\left(yz\right)>T_{O_h^{\prime }}^{\infty }\left(yz\right)$, IN fuzzy $O_h-I$ cut-vertex, if $I_{O_h}^{\infty }\left(yz\right)>I_{O_h^{\prime }}^{\infty }\left(yz\right)$ and IN fuzzy $O_h-F$ cut-vertex, if $F_{O_h}^{\infty }\left(yz\right)>F_{O_h^{\prime }}^{\infty }\left(yz\right)$.

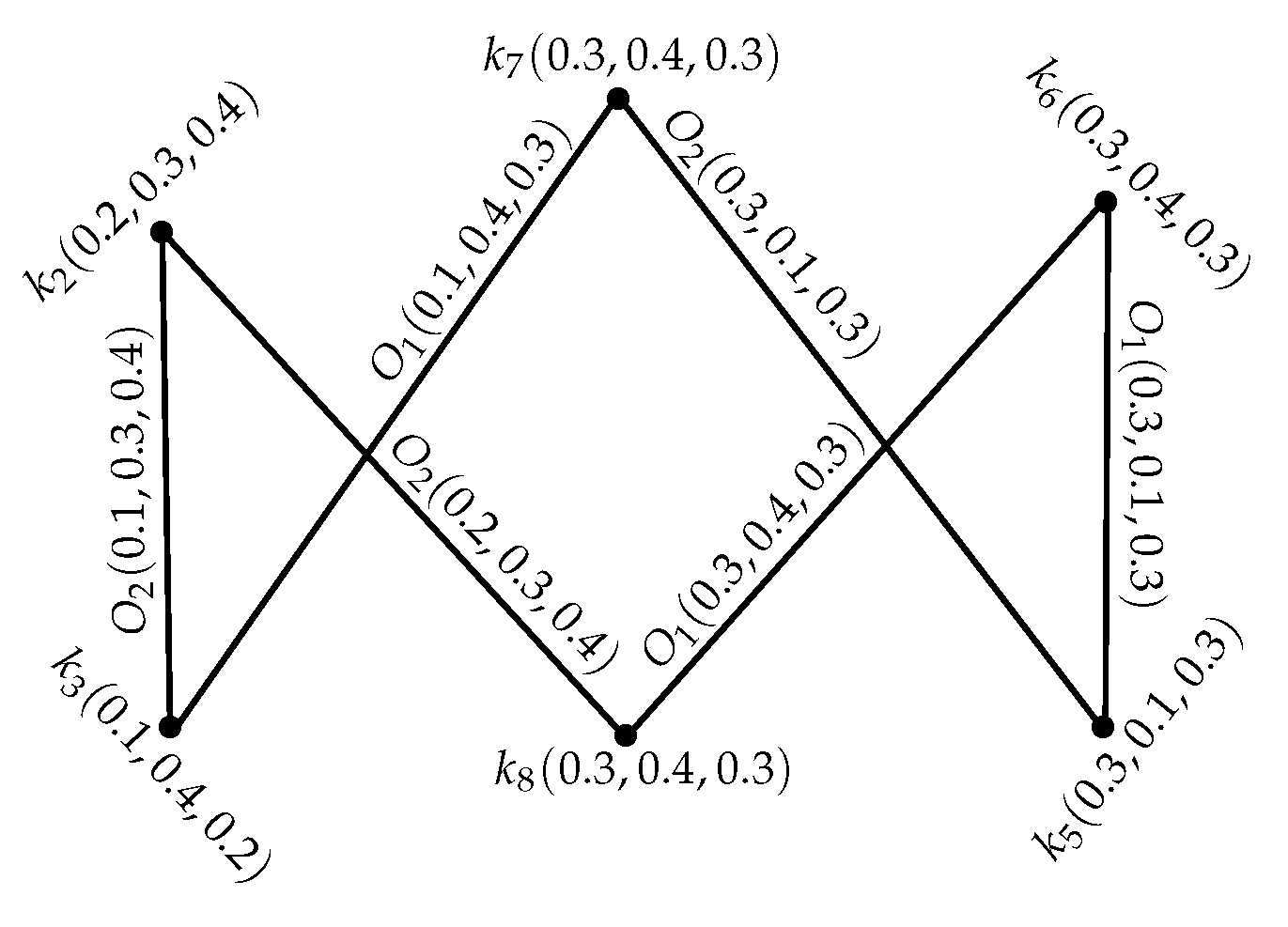
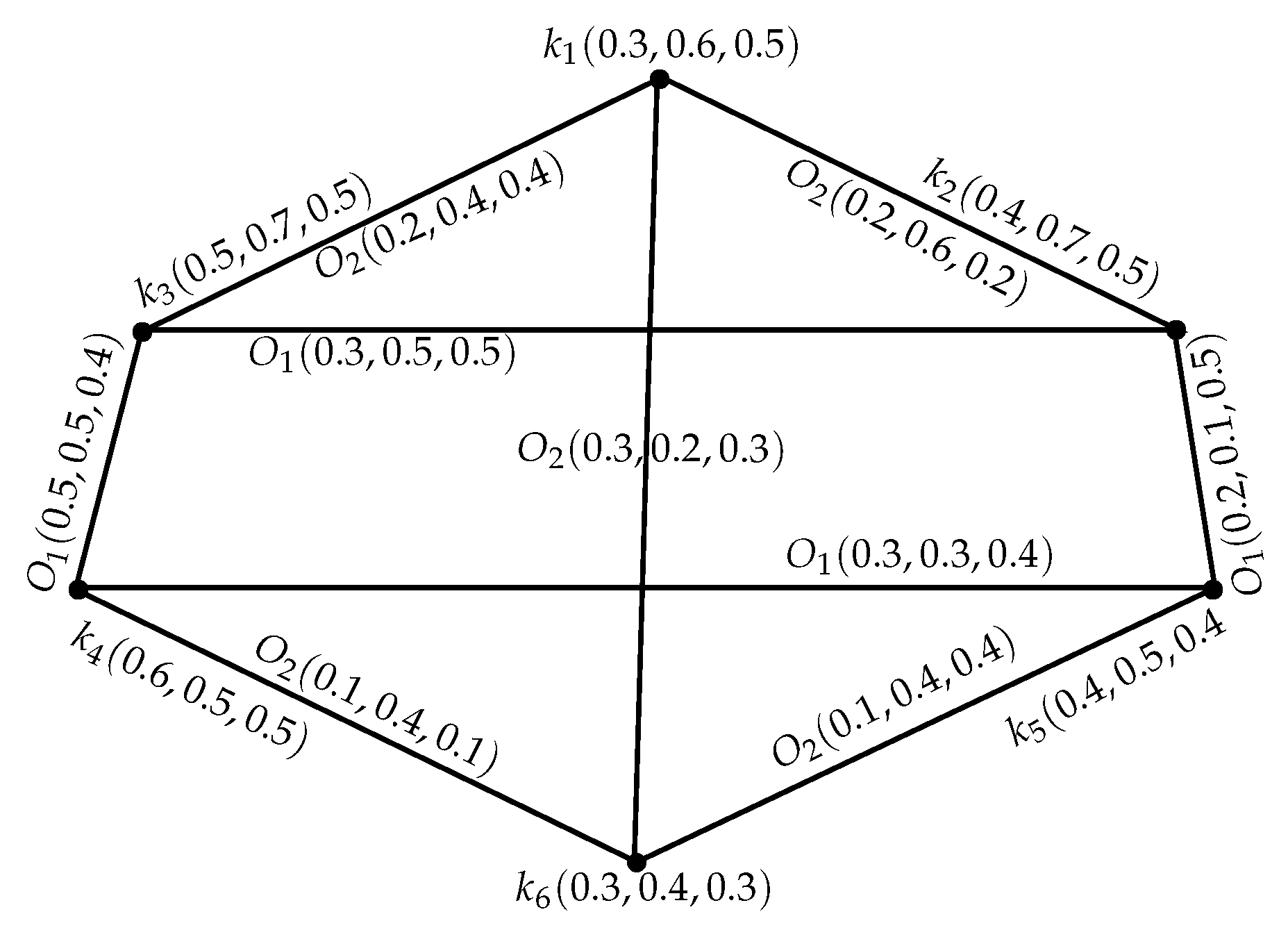
Example 9.

Consider an INGS ${\check{G}}_i$ = $(O,O_1,O_2)$ as represented in Figure 7 and ${\check{G}}_h^{\prime }$ = $(O^{\prime },O_1^{\prime },O_2^{\prime })$ is an IN subgraph structure of an INGS ${\check{G}}_i$, and we found it by deleting the vertex $k_2$. The vertex $k_2$ is an IN fuzzy $O_1$-I cut-vertex, since $I_{O_1^{\prime }}^{\infty }\left(k_2{k}_5\right)=0<0.5=I_{O_1}^{\infty }\left(k_2{k}_5\right)$, $I_{O_1^{\prime }}^{\infty }\left(k_4{k}_3\right)=0.7=I_{O_1}^{\infty }\left(k_4{k}_3\right)$ and $I_{O_1^{\prime }}^{\infty }\left(k_3{k}_5\right)=0.3<0.4=I_{O_1}^{\infty }\left(k_3{k}_5\right)$.

Definition 19.

Let ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ be an INGS and $kl$ an $O_h-edge$.

Let $(O^{\prime },O_1^{\prime },O_2^{\prime },\dots ,O_r^{\prime })$ be an IN fuzzy spanning-subgraph structure of ${\check{G}}_i$, such that

$T_{O_h^{\prime }}\left(kl\right)$ = 0 = $I_{O_h^{\prime }}\left(kl\right)$ = $F_{O_h^{\prime }}\left(kl\right)$, $T_{O_h^{\prime }}\left(qt\right)$ = $T_{O_h}\left(qt\right)$, $I_{O_h^{\prime }}\left(qt\right)$ = $I_{O_h}\left(qt\right)$, $F_{O_h^{\prime }}\left(qt\right)$ = $F_{O_h}\left(qt\right)$, ∀ edges $qt\ne kl$.

Then, $kl$ is an IN fuzzy $O_h$-bridge if

$T_{O_h}^{\infty }\left(yz\right)>T_{O_h^{\prime }}^{\infty }\left(yz\right)$, $I_{O_h}^{\infty }\left(yz\right)>I_{O_h^{\prime }}^{\infty }\left(yz\right)$ and $F_{O_h}^{\infty }\left(yz\right)>F_{O_h^{\prime }}^{\infty }\left(yz\right)$, for some $y,z\in P$.

Note that $kl$ is an IN fuzzy $O_h-T$ bridge if $T_{O_h}^{\infty }\left(yz\right)>T_{O_h^{\prime }}^{\infty }\left(yz\right)$, IN fuzzy $O_h-I$ bridge if $I_{O_h}^{\infty }\left(yz\right)>I_{O_h^{\prime }}^{\infty }\left(yz\right)$ and IN fuzzy $O_h-F$ bridge if $F_{O_h}^{\infty }\left(yz\right)>F_{O_h^{\prime }}^{\infty }\left(yz\right)$.

Example 10.

Consider an INGS ${\check{G}}_i$ = $(O,O_1,O_2)$ as shown in Figure 7 and ${\check{G}}_H^{\prime }$ = $(O^{″},O_1^{″},O_2^{″})$ is IN spanning-subgraph structure of an INGS ${\check{G}}_i$ found by the deletion of $O_1$-edge $\left(k_2{k}_5\right)$. Edge $\left(k_2{k}_5\right)$ is an IN fuzzy $O_1$-bridge. As $T_{O_1^{″}}^{\infty }\left(k_2{k}_5\right)$= $0.3<0.4$ = $T_{O_1}^{\infty }\left(k_2{k}_5\right)$, $I_{O_1^{″}}^{\infty }\left(k_2{k}_5\right)$= $0.3<0.4$= $I_{O_1}^{\infty }\left(k_2{k}_5\right)$, $F_{O_1^{″}}^{\infty }\left(k_2{k}_5\right)$= $0.4<0.5$ = $F_{O_1}^{\infty }\left(k_2{k}_5\right).$

Definition 20.

An INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is an $O_h$-tree, if $(supp\left(O\right),supp\left(O_1\right),supp\left(O_2\right),\dots ,supp\left(O_r\right))$ is an $O_h-tree$. Alternatively, ${\check{G}}_i$ is an $O_h$-tree, if there is a subgraph of ${\check{G}}_i$ induced by $supp\left(O_h\right)$, which forms a tree.

Definition 21.

An INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is an IN fuzzy $O_h$-tree if ${\check{G}}_i$ has an IN fuzzy spanning-subgraph structure ${\check{H}}_i$ = $(O^{″},O_1^{″},O_2^{″},\dots ,O_r^{″}),$ such that, for all $O_h$-edges $kl$ not in ${\check{H}}_i$,

${\check{H}}_i$ is an $O_h^{″}$-tree, and $T_{O_h}\left(kl\right)<T_{O_h^{″}}^{\infty }\left(kl\right)$, $I_{O_h}\left(kl\right)<I_{O_h^{″}}^{\infty }\left(kl\right)$, $F_{O_h}\left(kl\right)<F_{O_h^{″}}^{\infty }\left(kl\right)$.

In particular, ${\check{G}}_i$ is an IN fuzzy $O_h$-T tree if $T_{O_h}\left(kl\right)<T_{O_h^{″}}^{\infty }\left(kl\right)$, an IN fuzzy $O_h$-I tree if

$I_{O_h}\left(kl\right)<I_{O_h^{″}}^{\infty }\left(kl\right)$, and an IN fuzzy $O_h$-F tree if $F_{O_h}\left(kl\right)>F_{O_h^{″}}^{\infty }\left(kl\right)$.

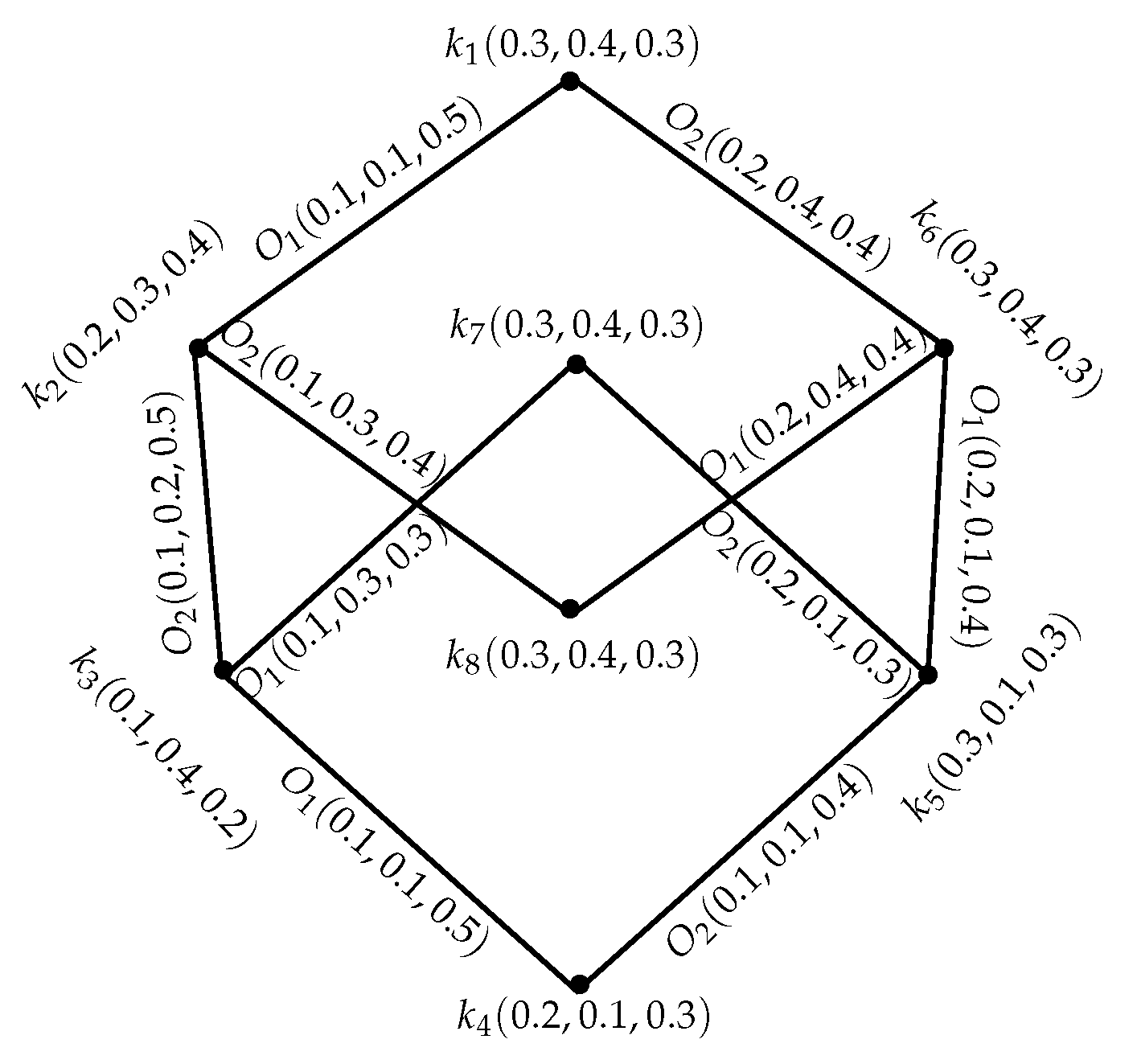
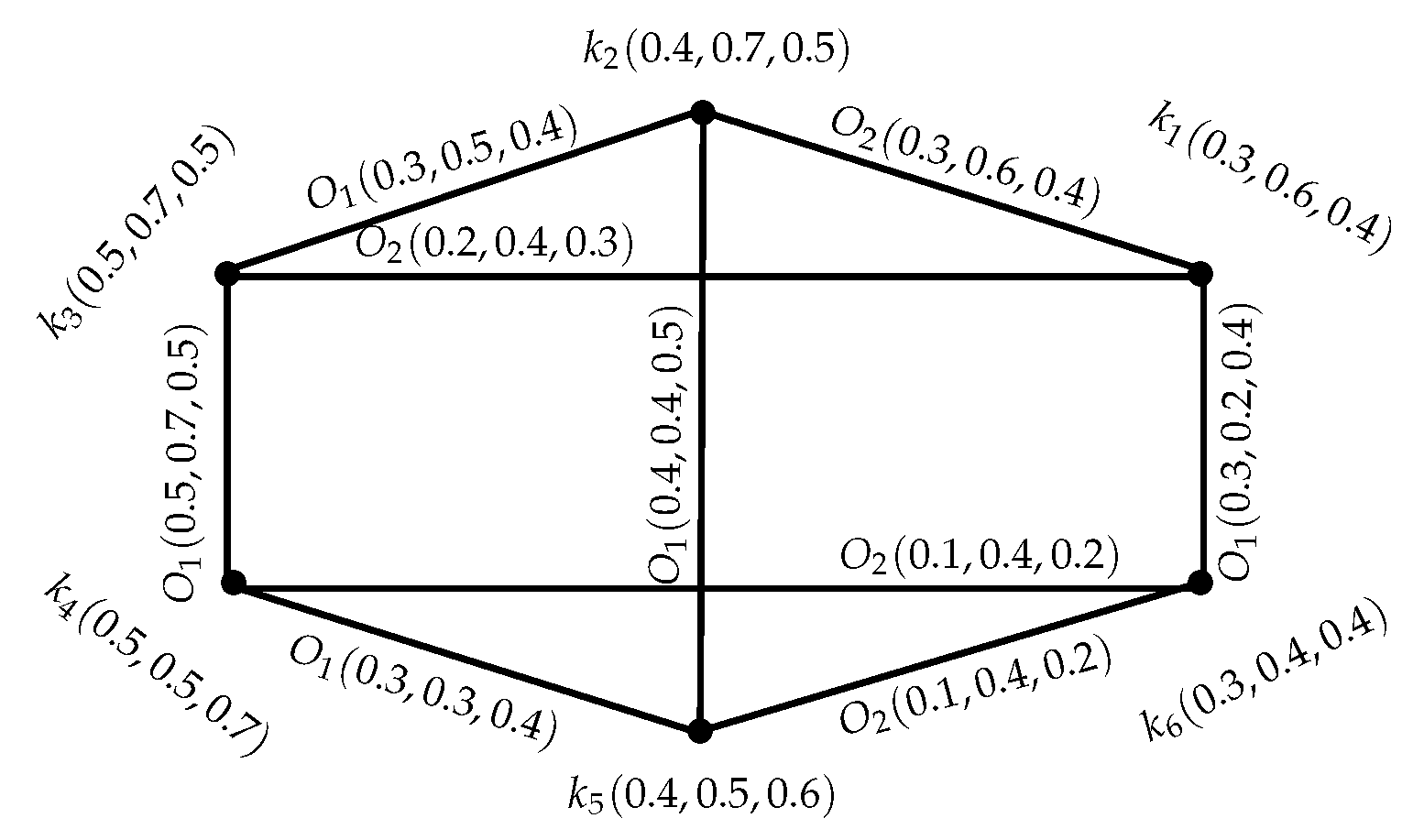
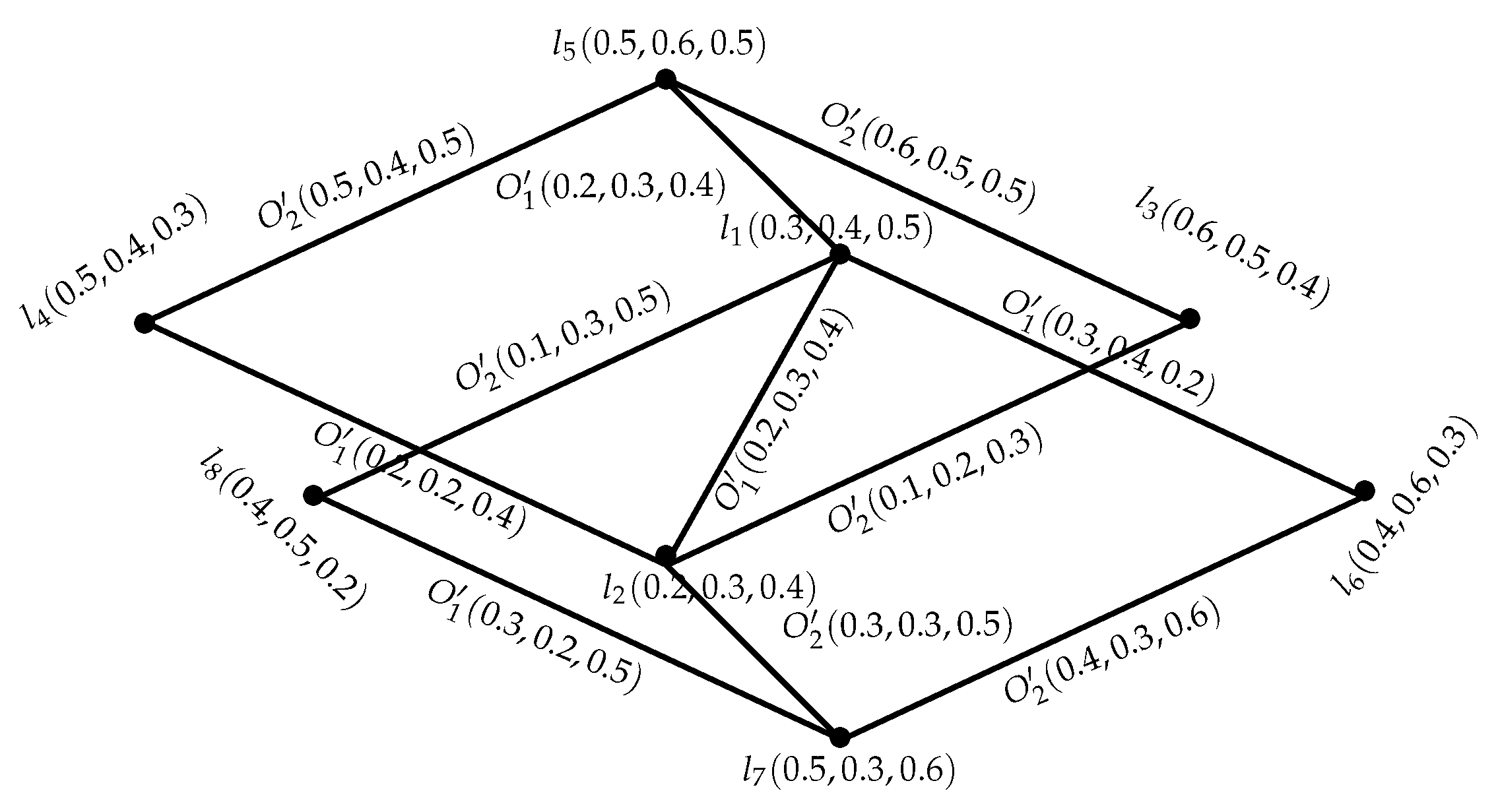
Example 11.

Consider an INGS ${\check{G}}_i$ = $(O,O_1,O_2)$ as shown in Figure 8. It is an $O_2$-tree, not an $O_1$-tree but it is IN fuzzy $O_1$-tree because it has an IN fuzzy-spanning subgraph $(O^{\prime },O_1^{\prime },O_2^{\prime })$ as an $O_1^{\prime }$-tree, which is found by the deletion of $O_1$-edge $k_2{k}_5$ from ${\check{G}}_i$. Moreover, $T_{O_1^{\prime }}^{\infty }\left(k_2{k}_5\right)=0.3>0.2=T_{O_1}\left(k_2{k}_5\right)$, $I_{O_1^{\prime }}^{\infty }\left(k_2{k}_5\right)=0.3>0.1=I_{O_1}\left(k_2{k}_5\right)$ and $F_{O_1^{\prime }}^{\infty }\left(k_2{k}_5\right)=0.4<0.5=F_{O_1}\left(k_2{k}_5\right).$

Definition 22.

An INGS ${\check{G}}_{i1}$ = $(O_1,O_{11},O_{12},\dots ,O_{1r})$ of graph structure $\check{G_1}$ = $(P_1,P_{11},P_{12},\dots ,P_{1r})$ is said to be isomorphic to an INGS ${\check{G}}_{i2}$ = $(O_2,O_{21},O_{22},\dots ,O_{2r})$ of the graph structure $\check{G_2}$ = $(P_2,P_{21},P_{22},\dots ,P_{2r})$, if there is a pair $(g,\psi )$, where $g:P_1\to P_2$ is a bijective mapping and ψ is any permutation on this set $\{1,2,\dots ,r\}$ such that;

$$\begin{gathered} T_{O_1}\left(k\right)=T_{O_2}\left(g\left(k\right)\right),I_{O_1}\left(k\right)=I_{O_2}\left(g\left(k\right)\right),F_{O_1}\left(k\right)=F_{O_2}\left(g\left(k\right)\right),\forall k\in P_1, \\ {T}_{O_{1h}}\left(kl\right)=T_{O_{2\varphi \left(h\right)}}\left(g\left(k\right)g\left(l\right)\right),I_{O_{1h}}\left(kl\right)=I_{O_{2\varphi \left(h\right)}}(g\left(k\right)g\left(l\right),F_{Q_{1h}}\left(kl\right)=F_{O_{2\varphi \left(h\right)}}\left(g\left(k\right)g\left(l\right)\right), \end{gathered}$$

$\forall kl\in P_{1h}$, h = 1,2,…,r.

Example 12.

Let ${\check{G}}_{i1}$ = $(O,O_1,O_2)$ and ${\check{G}}_{i2}$ = $(O^{\prime },O_1^{\prime },O_2^{\prime })$ be two INGSs as shown in the Figure 9.

${\check{G}}_{i1}$ and ${\check{G}}_{i2}$ are isomorphic under $(g,\psi )$, where $g:P\to P^{\prime }$ is a bijective mapping and ψ is the permutation on $\{1,2\}$, which is defined as $\psi \left(1\right)=2$, $\psi \left(2\right)=1$, and the following conditions hold:

$$\begin{gathered} T_O\left(k_h\right)=T_{O^{\prime }}\left(g\left(k_h\right)\right), \\ {I}_O\left(k_h\right)=I_{O^{\prime }}\left(g\left(k_h\right)\right), \\ {F}_O\left(k_h\right)=F_{O^{\prime }}\left(g\left(k_h\right)\right), \end{gathered}$$

$\forall k_h\in P$ and

$$\begin{gathered} T_{O_h}\left(k_h{k}_q\right)=T_{O_{\psi \left(h\right)}^{\prime }}\left(g\left(k_h\right)g\left(k_q\right)\right), \\ {I}_{O_h}\left(k_h{k}_q\right)=I_{O_{\psi \left(h\right)}^{\prime }}\left(g\left(k_h\right)g\left(k_q\right)\right), \\ {F}_{O_h}\left(k_h{k}_q\right)=F_{O_{\psi \left(h\right)}^{\prime }}\left(g\left(k_h\right)g\left(k_q\right)\right), \end{gathered}$$

$\forall k_h{k}_q\in P_h$, $h=1,2.$

Definition 23.

An INGS ${\check{G}}_{i1}$ = $(O_1,O_{11},O_{12},\dots ,O_{1r})$ of the graph structure $\check{G_1}$ = $(P_1,P_{11},P_{12},\dots ,P_{1r})$ is identical with an INGS ${\check{G}}_{i2}$ = $(O_2,O_{21},O_{22},\dots ,O_{2r})$ of the graph structure $\check{G_2}$ = $(P_2,P_{21},P_{22},\dots ,P_{2r})$ if $g:P_1\to P_2$ is a bijective mapping such that

$$\begin{gathered} T_{O_1}\left(k\right)=T_{O_2}\left(g\left(k\right)\right),I_{O_1}\left(k\right)=I_{O_2}\left(g\left(k\right)\right),F_{O_1}\left(k\right)=F_{O_2}\left(g\left(k\right)\right),\forall k\in P_1, \\ {T}_{O_{1h}}\left(kl\right)=T_{O_{2h}}\left(g\left(k\right)g\left(l\right)\right),I_{O_{1h}}\left(kl\right)=I_{O_{2h}}\left(g\left(k\right)g\left(l\right)\right),F_{O_{1h}}\left(kl\right)=F_{O_{2\left(h\right)}}\left(g\left(k\right)g\left(l\right)\right), \end{gathered}$$

$\forall kl\in P_{1h}$, $h=1,2,\dots ,r.$

Example 13.

Let ${\check{G}}_{i1}$ = $(O,O_1,O_2)$ and ${\check{G}}_{i2}$ = $(O^{\prime },O_1^{\prime },O_2^{\prime })$ be two INGSs of the GSs $\check{G_1}$ = $(P,P_1,P_2)$, $\check{G_2}$ = $(P^{\prime },P_1^{\prime },P_2^{\prime })$, respectively, as they are shown in Figure 10 and Figure 11.

SVINGSs ${\check{G}}_{i1}$ and ${\check{G}}_{i2}$ are identical under $g:P\to P^{\prime }$ is defined as :

$g\left(k_1\right)=l_2$, $g\left(k_2\right)=l_1$, $g\left(k_3\right)=l_4$, $g\left(k_4\right)=l_3$, $g\left(k_5\right)=l_5$, $g\left(k_6\right)=l_8$, $g\left(k_7\right)=l_7$, $g\left(k_8\right)=l_6$.

Moreover, $T_O\left(k_h\right)$ = $T_{O^{\prime }}\left(\left(k_h\right)\right)$, $I_O\left(k_h\right)$ = $I_{O^{\prime }}\left(g\left(k_h\right)\right)$, $F_O\left(k_h\right)$ = $F_{O^{\prime }}\left(g\left(k_h\right)\right)$, $\forall k_h\in P$ and $T_{O_h}\left(k_h{k}_q\right)$ = $T_{O_h^{\prime }}\left(g\left(k_h\right)g\left(k_q\right)\right)$, $I_{O_h}\left(k_h{k}_q\right)$ = $I_{O_h^{\prime }}\left(g\left(k_h\right)g\left(k_q\right)\right)$, $F_{O_h}\left(k_h{k}_q\right)$ = $F_{O_h^{\prime }}\left(g\left(k_h\right)g\left(k_q\right)\right)$, $\forall k_h{k}_q\in P_h$, $h=1,2$.

Definition 24.

Let ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ be an INGS and ψ is any permutation on $\{O_1,O_2,\dots ,O_r\}$ and on set $\{1,2,\dots ,r\}$, that is, $\psi \left(O_h\right)=O_q$ if and only if $\psi \left(h\right)=q$ $\forall h$. If $kl\in O_h$, for any h and

$T_{O_h^{\psi }}\left(kl\right)$ = $T_O\left(k\right)\wedge T_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigvee }}{T}_{\psi \left(O_q\right)}\left(kl\right)$, $I_{O_h^{\psi }}\left(kl\right)$ = $I_O\left(k\right)\wedge I_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigvee }}{I}_{\psi \left(O_q\right)}\left(kl\right)$,

$F_{O_h^{\psi }}\left(kl\right)$ = $F_O\left(k\right)\vee F_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigwedge }}{T}_{\psi \left(O_q\right)}\left(kl\right)$, $h=1,2,\dots ,r$, then, $kl\in O_t^{\psi }$, where t is chosen such that

$T_{O_t^{\psi }}\left(kl\right)\ge T_{O_h^{\psi }}\left(kl\right)$, $I_{O_t^{\psi }}\left(kl\right)\ge I_{O_h^{\psi }}\left(kl\right)$, $F_{O_t^{\psi }}\left(kl\right)\ge F_{O_h^{\psi }}\left(kl\right)$ $\forall h$. In addition, INGS $(O,O_1^{\psi },O_2^{\psi },\dots ,O_r^{\psi })$ is called a ψ-complement of an INGS ${\check{G}}_i$, and it is symbolized as ${\check{G}}_i^{\psi c}$.

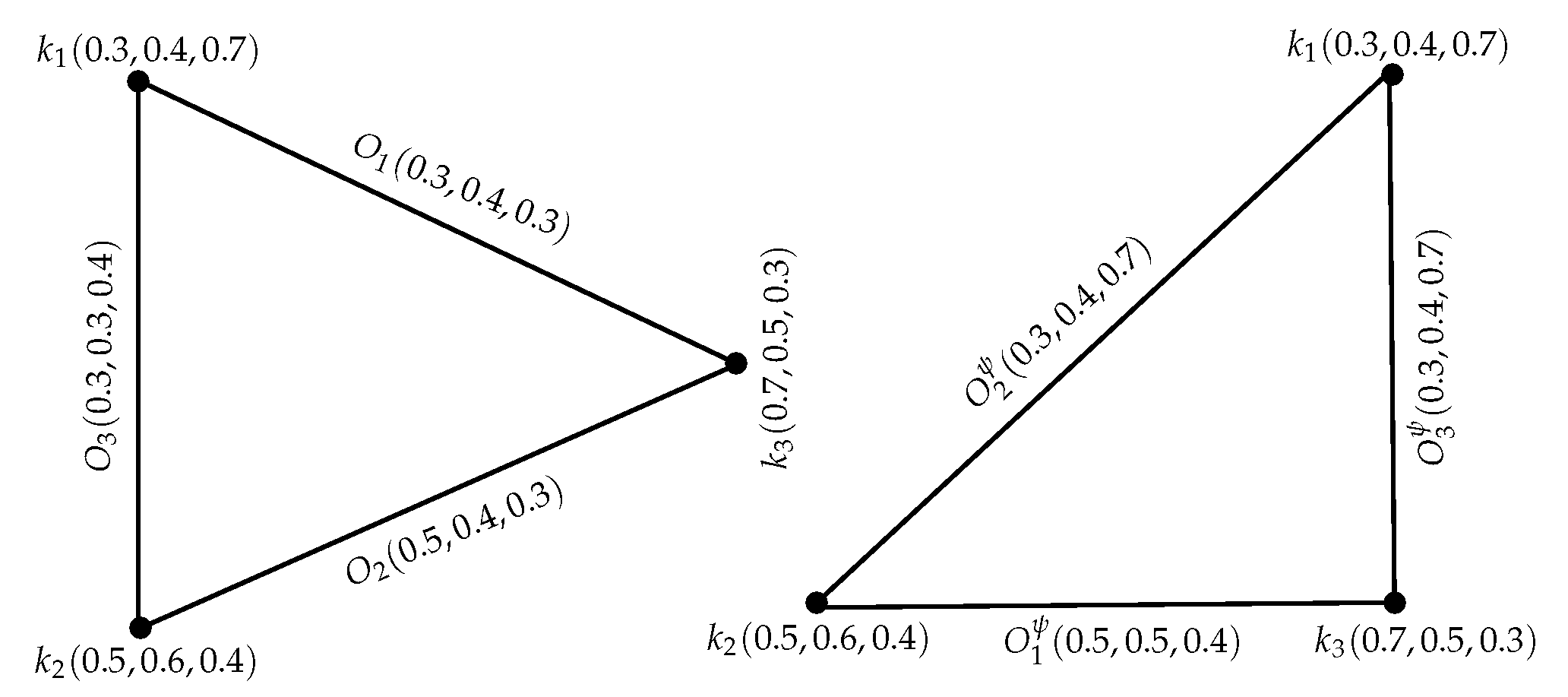
Example 14.

Let $O=\{(k_1,0.3,0.4,0.7),(k_2,0.5,0.6,0.4),(k_3,0.7,0.5,0.3)\}$, $O_1=\left\{(k_1{k}_3,0.3,0.4,0.3)\right\}$, $O_2=\left\{(k_2{k}_3,0.5,0.4,0.3)\right\}$, $O_3=\left\{(k_1{k}_2,0.3,0.3,0.4)\right\}$ be IN subsets of P, $P_1$, $P_2$, $P_3$, respectively.

Thus, ${\check{G}}_i$ = $(O,O_1,O_2,O_3)$ is an INGS of GS $\check{G}$ = $(P,P_1,P_2,P_3)$. Let $\psi \left(O_1\right)$ = $O_2$, $\psi \left(O_2\right)$ = $O_3$, $\psi \left(O_3\right)$ = $O_1$, where ψ is permutation on $\{O_1,O_2,O_3\}$. Now, for $k_1{k}_3,k_2{k}_3,k_1{k}_2$$\in O_1,O_2,O_3$, respectively:

$T_{O_1^{\psi }}\left(k_1{k}_3\right)=0$, $I_{O_1^{\psi }}\left(k_1{k}_3\right)=0$, $F_{O_1^{\psi }}\left(k_1{k}_3\right)=0.7$, $T_{O_2^{\psi }}\left(k_1{k}_3\right)=0$, $I_{O_2^{\psi }}\left(k_1{k}_3\right)=0$, $F_{O_2^{\psi }}\left(k_1{k}_3\right)=0.7$, $T_{O_3^{\psi }}\left(k_1{k}_3\right)=0.3$, $I_{O_3^{\psi }}\left(k_1{k}_3\right)=0.4$, $F_{O_3^{\psi }}\left(k_1{k}_3\right)=0.7$. So $k_1{k}_3\in O_3^{\psi }$,

$T_{O_1^{\psi }}\left(k_2{k}_3\right)=0.5$, $I_{O_1^{\psi }}\left(k_2{k}_3\right)=0.5$, $F_{O_1^{\psi }}\left(k_2{k}_3\right)=0.4$, $T_{O_2^{\psi }}\left(k_2{k}_3\right)=0$, $I_{O_2^{\psi }}\left(k_2{k}_3\right)=0.1$, $F_{O_2^{\psi }}\left(k_2{k}_3\right)=0.4$, $T_{O_3^{\psi }}\left(k_2{k}_3\right)=0$, $I_{O_3^{\psi }}\left(k_2{k}_3\right)=0.1$, $F_{O_3^{\psi }}\left(k_2{k}_3\right)=0.4$. So $k_2{k}_3\in O_1^{\psi }$,

$T_{O_1^{\psi }}\left(k_1{k}_2\right)=0$, $I_{O_1^{\psi }}\left(k_1{k}_2\right)=0.1$, $F_{O_1^{\psi }}\left(k_1{k}_2\right)=0.7$, $T_{O_2^{\psi }}\left(k_1{k}_2\right)=0.3$, $I_{O_2^{\psi }}\left(k_1{k}_2\right)=0.4$, $F_{O_2^{\psi }}\left(k_1{k}_2\right)=0.7$, $T_{O_3^{\psi }}\left(k_1{k}_2\right)=0$, $I_{O_3^{\psi }}\left(k_1{k}_2\right)=0.1$, $F_{O_3^{\psi }}\left(k_1{k}_2\right)=0.7$. This shows $k_1{k}_2\in O_2^{\psi }$.

Hence, ${\check{G}}_i^{\psi c}$ =$(O,O_1^{\psi },O_2^{\psi },O_3^{\psi })$ is a ψ-complement of an INGS ${\check{G}}_i$ as presented in Figure 12.

Proposition 1.

A ψ-complement of an INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is a strong INGS. Moreover, if $\psi \left(h\right)=t$, where $h,t\in \{1,2,\dots ,r\}$; then, all $O_t$-edges in an INGS $(O,O_1,O_2,\dots ,O_r)$ become $O_h^{\psi }$-edges in $(O,O_1^{\psi },O_2^{\psi },\dots ,O_r^{\psi })$.

Proof. 

By definition of $\psi$-complement,

$$\begin{array}{ccc}\hfill T_{O_h^{\psi }}\left(kl\right)& =& T_O\left(k\right)\wedge T_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigvee }}{T}_{\psi \left(O_q\right)}\left(kl\right),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill I_{O_h^{\psi }}\left(kl\right)& =& I_O\left(k\right)\wedge I_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigvee }}{I}_{\psi \left(O_q\right)}\left(kl\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill F_{O_h^{\psi }}\left(kl\right)& =& F_O\left(k\right)\vee F_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigwedge }}{F}_{\psi \left(O_q\right)}\left(kl\right),\hfill \end{array}$$

(3)

for $h\in \{1,2,\dots ,r\}$. For Expression 1.

As $T_O\left(k\right)\wedge T_O\left(l\right)\ge 0$, ${\displaystyle \underset{q\ne h}{\bigvee }}{T}_{\psi \left(O_q\right)}\left(kl\right)\ge 0$ and $T_{O_h}\left(kl\right)\le T_O\left(k\right)\wedge T_O\left(l\right)$ $\forall O_h$.

$\Rightarrow {\displaystyle \underset{q\ne h}{\bigvee }}{T}_{\psi \left(O_q\right)}\left(kl\right)\le T_O\left(k\right)\wedge T_O\left(l\right)\Rightarrow T_O\left(k\right)\wedge T_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigvee }}{T}_{\psi \left(O_q\right)}\left(kl\right)\ge 0$.

Hence, $T_{O_h^{\psi }}\left(kl\right)\ge 0$ $\forall h$.

Furthermore, $T_{O_h^{\psi }}\left(kl\right)$ gets a maximum value, when ${\displaystyle \underset{q\ne h}{\bigvee }}{T}_{\psi \left(O_q\right)}\left(kl\right)$ is zero. Clearly, when $\psi \left(O_h\right)=O_t$ and $kl$ is an $O_t$-edge, then ${\displaystyle \underset{q\ne h}{\bigvee }}{T}_{\psi \left(O_q\right)}\left(kl\right)$ attains zero value. Hence,

$$\begin{array}{ccc}\hfill T_{O_h^{\psi }}\left(kl\right)& =& T_O\left(k\right)\wedge T_O\left(l\right),for\left(kl\right)\in O_t,\psi \left(O_h\right)=O_t.\hfill \end{array}$$

(4)

Similarly, for I, the results are:

Since $I_O\left(k\right)\wedge I_O\left(l\right)\ge 0$, ${\displaystyle \underset{q\ne h}{\bigvee }}{I}_{\psi \left(O_q\right)}\left(kl\right)\ge 0$ and $I_{O_h}\left(kl\right)\le I_O\left(k\right)\wedge I_O\left(l\right)$ $\forall O_h$.

$\Rightarrow {\displaystyle \underset{q\ne h}{\bigvee }}{I}_{\psi \left(O_q\right)}\left(kl\right)\le I_O\left(k\right)\wedge I_O\left(l\right)\Rightarrow I_O\left(k\right)\wedge I_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigvee }}{I}_{\psi \left(O_q\right)}\left(kl\right)\ge 0$.

Therefore, $I_{O_h^{\psi }}\left(kl\right)$ $\ge 0$∀ i.

Value of the $I_{O_h^{\psi }}\left(kl\right)$ is maximum when ${\displaystyle \underset{q\ne h}{\bigvee }}{I}_{\psi \left(O_q\right)}\left(kl\right)$ gets zero value. Clearly, when $\psi \left(O_h\right)=O_t$ and $kl$ is an $O_t$-edge, then ${\displaystyle \underset{q\ne h}{\bigvee }}{I}_{\psi \left(O_q\right)}\left(kl\right)$ is zero. Thus,

$$\begin{array}{ccc}\hfill I_{O_h^{\psi }}\left(kl\right)& =& I_O\left(k\right)\wedge I_O\left(l\right),for\left(kl\right)\in O_t,\psi \left(O_h\right)=O_t.\hfill \end{array}$$

(5)

On a similar basis for F in $\psi$-complement, the results are:

Since $F_O\left(k\right)\vee F_O\left(l\right)\ge 0$, ${\displaystyle \underset{q\ne h}{\bigwedge }}{F}_{\psi \left(O_q\right)}\left(kl\right)\ge 0$ and $F_{O_h}\left(kl\right)\le F_O\left(k\right)\vee F_O\left(l\right)$ $\forall O_h$.

$\Rightarrow {\displaystyle \underset{q\ne h}{\bigwedge }}{F}_{\psi \left(O_q\right)}\left(kl\right)\le F_O\left(k\right)\vee F_O\left(l\right)\Rightarrow F_O\left(k\right)\vee F_O\left(l\right)-{\displaystyle \underset{q\ne h}{\bigwedge }}{F}_{\psi \left(O_q\right)}\left(kl\right)\ge 0$.

Hence, $F_{O_h^{\psi }}\left(kl\right)$$\ge 0$$\forall h$.

Furthermore, $F_{O_h^{\psi }}\left(kl\right)$ is maximum, when ${\displaystyle \underset{q\ne h}{\bigwedge }}{F}_{\psi \left(O_q\right)}\left(kl\right)$ is zero. Definitely, when $\psi \left(O_h\right)=O_t$ and $kl$ is an $O_t$-edge, then ${\displaystyle \underset{q\ne h}{\bigwedge }}{F}_{\psi \left(O_q\right)}\left(kl\right)$ is zero. Hence,

$$\begin{array}{ccc}\hfill F_{O_h^{\psi }}\left(kl\right)& =& F_O\left(k\right)\vee F_O\left(l\right),for\left(kl\right)\in O_t,\psi \left(O_h\right)=O_t.\hfill \end{array}$$

(6)

Expressions (4)–(6) give the required proof. ◻

Definition 25.

Let ${\check{G}}_i=(O,O_1,O_2,\dots ,O_r)$ be an INGS and ψ be any permutation on $\{1,2,\dots ,r\}$. Then,

(i) 

${\check{G}}_i$ is a self-complementary INGS if ${\check{G}}_i$ is isomorphic to ${\check{G}}_i^{\psi c}$;

(ii) 

${\check{G}}_i$ is a strong self-complementary INGS if ${\check{G}}_i$ is identical to ${\check{G}}_i^{\psi c}$.

Definition 26.

Let ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ be an INGS. Then,

(i) 

${\check{G}}_i$ is a totally self-complementary INGS if ${\check{G}}_i$ is isomorphic to ${\check{G}}_i^{\psi c}$, ∀ permutations ψ on $\{1,2,\dots ,r\}$;

(ii) 

${\check{G}}_i$ is a totally-strong self-complementary INGS if ${\check{G}}_i$ is identical to ${\check{G}}_i^{\psi c}$, ∀ permutations ψ on $\{1,2,\dots ,r\}$.

Example 15.

INGS ${\check{G}}_i$ = $(O,O_1,O_2,O_3)$ in Figure 13 is totally-strong self-complementary INGS.

Theorem 1.

A strong INGS is a totally self-complementary INGS and vice versa.

Proof. 

Consider any strong INGS ${\check{G}}_i$ and Permutation $\psi$ on {1,2, …, r}. By proposition 1, $\psi$-complement of an INGS ${\check{G}}_i$ = $(O,O_1,O_2,\dots ,O_r)$ is a strong INGS. Moreover, if ${\psi }^{-1}\left(t\right)=h$, where $h,t\in \{1,2,\dots ,r\}$, then all $O_t$-edges in an INGS $(O,O_1,O_2,\dots ,O_r)$ become $O_h^{\psi }$-edges in $(O,O_1^{\psi },O_2^{\psi },\dots ,O_r^{\psi })$, this leads

$$\begin{gathered} T_{O_t}\left(kl\right)=T_O\left(k\right)\wedge T_O\left(l\right)=T_{O_h^{\psi }}\left(kl\right),I_{O_t}\left(kl\right)=I_O\left(k\right)\wedge I_O\left(l\right)=I_{O_h^{\psi }}\left(kl\right), \\ {F}_{O_t}\left(kl\right)=F_O\left(k\right)\vee F_O\left(l\right)=F_{O_h^{\psi }}\left(kl\right). \end{gathered}$$

Therefore, under $g:P\to P$ (identity mapping), ${\check{G}}_i$ and ${\check{G}}_i^{\psi }$ are isomorphic, such that

$$T_O\left(k\right)=T_O\left(g\left(k\right)\right),I_O\left(k\right)=I_O\left(g\left(k\right)\right),F_O\left(k\right)=F_O\left(g\left(k\right)\right)$$

and

$$\begin{gathered} T_{O_t}\left(kl\right)=T_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right)=T_{O_h^{\psi }}\left(kl\right), \\ {I}_{O_t}\left(kl\right)=I_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right)=I_{O_h^{\psi }}\left(kl\right), \\ {F}_{O_t}\left(kl\right)=F_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right)=F_{O_h^{\psi }}\left(kl\right), \end{gathered}$$

$\forall kl\in P_t$, for ${\psi }^{-1}\left(t\right)=h$; h,t = $1,2,\dots ,r$.

For each permutation $\psi$ on $\{1,2,\dots ,r\}$, this holds. Hence, ${\check{G}}_i$ is a totally self-complementary INGS.

Conversely, let ${\check{G}}_i$ is isomorphic to ${\check{G}}_i^{\psi }$ for each permutation $\psi$ on $\{1,2,\dots ,r\}$. Then, by definitions of $\psi$-complement of INGS and isomorphism of INGS, we have

$$\begin{gathered} T_{O_t}\left(kl\right)=T_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right)=T_O\left(g\left(k\right)\right)\wedge T_O\left(g\left(l\right)\right)=T_O\left(k\right)\wedge T_O\left(l\right), \\ {I}_{O_t}\left(kl\right)=I_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right)=I_O\left(g\left(k\right)\right)\wedge I_O\left(g\left(l\right)\right)=T_O\left(k\right)\wedge I_O\left(l\right), \\ {F}_{O_t}\left(kl\right)=F_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right)=F_O\left(g\left(k\right)\right)\vee F_O\left(g\left(l\right)\right)=F_O\left(k\right)\vee F_O\left(l\right), \end{gathered}$$

$\forall kl\in P_t$, t = 1,2,...,r. Hence, ${\check{G}}_i$ is strong INGS. ◻

Remark 1.

Each self-complementary INGS is a totally self-complementary INGS.

Theorem 2.

If $\check{G}$ = $(P,P_1,P_2,\dots ,P_r)$ is a totally strong self-complementary GS and $O=(T_O,I_O,F_O)$ is an IN subset of P, where $T_O,I_O,F_O$ are the constant functions, then any strong INGS of $\check{G}$ with IN vertex set O is necessarily totally-strong self-complementary INGS.

Proof. 

Let u$\in [0,1]$, v$\in [0,1]$ and w $\in [0,1]$ be three constants, and

$$T_O\left(k\right)=u,I_O\left(k\right)=v,F_O\left(k\right)=w \forall k\in P.$$

Since $\check{G}$ is a totally strong self-complementary GS, so, for each permutation ${\psi }^{-1}$ on $\{1,2,\dots ,r\},$ there exists a bijective mapping $g:P\to P$, such that, for each $P_t$-edge $\left(kl\right)$, (g(k)g(l)) [a $P_h$-edge in $\check{G}$ ] is a $P_t$-edge in ${\check{G}}^{{\psi }^{-1}c}$. Thus, for every $O_t$-edge $\left(kl\right)$, (g(k)g(l)) [an $O_h$-edge in ${\check{G}}_i$ ] is an $O_t^{\psi }$-edge in ${\check{G_i}}^{{\psi }^{-1}c}$.

Moreover, ${\check{G}}_i$ is a strong INGS, so

$$T_O\left(k\right)=u=T_O\left(g\left(k\right)\right),I_O\left(k\right)=v=I_O\left(g\left(k\right)\right),F_O\left(k\right)=w=F_O\left(g\left(k\right)\right) \forall k\in P$$

and

$$\begin{gathered} T_{O_t}\left(kl\right)=T_O\left(k\right)\wedge T_O\left(l\right)=T_O\left(g\left(k\right)\right)\wedge T_O\left(g\left(l\right)\right)=T_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right), \\ {I}_{O_t}\left(kl\right)=I_O\left(k\right)\wedge I_O\left(l\right)=I_O\left(g\left(k\right)\right)\wedge I_O\left(g\left(l\right)\right)=I_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right), \\ {F}_{O_t}\left(kl\right)=F_O\left(k\right)\vee I_O\left(l\right)=F_O\left(g\left(k\right)\right)\vee F_O\left(g\left(l\right)\right)=F_{O_h^{\psi }}\left(g\left(k\right)g\left(l\right)\right), \end{gathered}$$

$\forall kl\in P_h$, $h=1,2,\dots ,r$.

This shows that ${\check{G}}_i$ is a strong self-complementary INGS. This exists for each permutation $\psi$ and ${\psi }^{-1}$ on set $\{1,2,\dots ,r\}$, thus ${\check{G}}_i$ is a totally strong self-complementary INGS. Hence, required proof is obtained. ◻

Remark 2.

Converse of the Theorem 2 may or may not true, as an INGS shown in Figure 2 is totally strong self-complementary INGS, and it is also a strong INGS with a totally strong self-complementary underlying GS but $T_O$, $I_O$, $F_O$ are not the constant-valued functions.

3. Application

First, we explain the general procedure of this application by the following algorithm.

Algorithm: Crucial interdependence relations

Step 1.

Input vertex set P = $\{B_1,B_2,\dots ,B_n\}$ and IN set O defined on P.

Step 2.

Input IN set of interdependence relations of any vertex with all other vertices and calculate T, F, and I of every pair of vertices by using, $T\left(B_i{B}_j\right)\le min(T\left(B_i\right),T\left(B_j\right))$, $F\left(B_i{B}_j\right)\le max(F\left(B_i\right),F\left(B_j\right))$, $I\left(B_i{B}_j\right)\le min(I\left(B_i\right),I\left(B_j\right))$.

Step 3.

Repeat the Step 2 for every vertex in P.

Step 4.

Define relations $P_1,P_2,\dots ,P_n$ on set P such that $(P,P_1,P_2,\dots ,P_n)$ is a GS.

Step 5.

Consider an element of that relation, for which its value of T is comparatively high, and its values of F and I are lower than other relations.

Step 6.

Write down all elements in relations with T, F and I values, corresponding relations $O_1,O_2,\dots ,O_n$ are IN sets on $P_1,P_2,P_3,\dots ,P_n$, respectively, and $(O,O_1,O_2,\dots ,O_n)$ is an INGS.

Human beings, the main creatures in the world, depend on many things for their survival. Interdependence is a very important relationship in the world. It is a natural phenomenon that nobody can be 100% independent, and the whole world is relying on interdependent relationships. Provinces or states of any country, especially of a progressive country, can not be totally independent, more or less they have to depend on each other. They depend on each other for many things, that is, there are many interdependent relationships among provinces or states of a progressive country—for example, education, natural energy resources, agricultural items, industrial products, and water resources, etc. However, all of these interdependent relationships are not of equal importance. Some are very important to run the system of a progressive country. Between any two provinces, all interdependent relationships do not have the same strength. Some interdependent relationships are like the backbone for the country. We can make an INGS of provinces or states of a progressive country, and can highlight those interdependent relationships, due to which the system of the country is running properly. This INGS can guide the government as to which interdependent relationships are very crucial, and they must try to make them strong and overcome the factors destroying or weakening them.

We consider a set P of provinces and states of Pakistan:

P = {Punjab, Sindh, Khyber Pakhtunkhawa(KPK), Balochistan, Gilgit-Baltistan, Azad Jammu and Kashmir(AJK) }. Let O be the IN set on P, as defined in

Table 1. IN set O of provinces of Pakistan.

Provinces or States	T	I	F
Punjab	0.5	0.3	0.3
Sindh	0.5	0.4	0.4
Khyber Pakhtunkhawa(KPK)	0.4	0.4	0.4
Balochistan	0.3	0.4	0.4
Gilgit-Baltistan	0.3	0.4	0.4
Azad Jammu and Kashmir	0.3	0.4	0.3

.

In Table 1, symbol T demonstrates the positive role of that province or state for the strength of the Federal Government, and symbol F indicates its negative role, whereas I denotes the percentage of ambiguity of its role for the strength of the Federal Government. Let us use the following alphabets for the provinces’ names:

PU = Punjab, SI = Sindh, KPK = Khyber Pakhtunkhwa, BA = Balochistan, GB = Gilgit-Baltistan, AJK = Azad Jammu and Kashmir. For every pair of provinces of Pakistan in set P, different interdependent relationships with their T, I and F values are demonstrated in

Table 2. IN set of interdependent relations between Punjab and other provinces.

Type of Interdependent Relationships	(PU, SI)	(PU, KPK)	(PU, BA)
Education	(0.5, 0.1, 0.1)	(0.4, 0.3, 0.2)	(0.3, 0.2, 0.2)
Natural energy resources	(0.3, 0.2, 0.3)	(0.4, 0.2, 0.2)	(0.3, 0.2, 0.1)
Agricultural items	(0.3, 0.2, 0.2)	(0.4, 0.2, 0.1)	(0.3, 0.2, 0.1)
Industrial products	(0.4, 0.2, 0.1)	(0.4, 0.1, 0.1)	(0.3, 0.1, 0.1)
Water resources	(0.3, 0.1, 0.1)	(0.4, 0.3, 0.2)	(0.2, 0.2, 0.2)

,

Table 3. IN set of interdependent relationships between Sindh and other provinces.

Type of Interdependent Relationships	(SI, KPK)	(SI, BA)	(SI, GB)
Education	(0.3, 0.2, 0.1)	(0.3, 0.2, 0.3)	(0.3, 0.2, 0.4)
Natural energy resources	(0.3, 0.2, 0.3)	(0.3, 0.1, 0.0)	(0.2, 0.2, 0.4)
Agricultural items	(0.4, 0.1, 0.1)	(0.3, 0.1, 0.2)	(0.3, 0.1, 0.1)
Industrial products	(0.4, 0.2, 0.1)	(0.3, 0.2, 0.2)	(0.3, 0.2, 0.2)
Water resources	(0.3, 0.2, 0.2)	(0.2, 0.3, 0.2)	(0.2, 0.2, 0.3)

,

Table 4. IN set of interdependent relationships between KPK and other provinces.

Type of Interdependent Relationships	(KPK, BA)	(KPK, GB)	(KPK, AJK)
Education	(0.1, 0.4, 0.3)	(0.1, 0.4, 0.3)	(0.1, 0.4, 0.4)
Natural energy resources	(0.3, 0.2, 0.1)	(0.3, 0.2, 0.2)	(0.3, 0.3, 0.2)
Agricultural items	(0.1, 0.2, 0.4)	(0.1, 0.4, 0.4)	(0.1, 0.3, 0.3)
Industrial products	(0.1, 0.3, 0.4)	(0.1, 0.4, 0.3)	(0.1, 0.2, 0.2)
Water resources	(0.3, 0.2, 0.2)	(0.3, 0.3, 0.2)	(0.3, 0.2, 0.2)

,

Table 5. IN set of interdependent relationships between AJK and other provinces.

Type of Interdependent Relationships	(AJK, PU)	(AJK, SI)	(AJK, BA)
Education	(0.3, 0.1, 0.1)	(0.1, 0.4, 0.3)	(0.1, 0.3, 0.4)
Natural energy resources	(0.1, 0.2, 0.3)	(0.2, 0.4, 0.3)	(0.3, 0.3, 0.3)
Agricultural items	(0.3, 0.2, 0.1)	(0.3, 0.3, 0.2)	(0.3, 0.2, 0.2)
Industrial products	(0.3, 0.2, 0.2)	(0.3, 0.2, 0.2)	(0.3, 0.2, 0.3)
Water resources	(0.3, 0.2, 0.1)	(0.3, 0.3, 0.2)	(0.3, 0.0, 0.1)

and

Table 6. IN set of interdependent relationships of Gilgit-Baltistan with other provinces.

Type of Interdependent Relationships	(GB, PU)	(GB, BA)	(GB, AJK)
Education	(0.3, 0.2, 0.1)	(0.1, 0.4, 0.4)	(0.2, 0.1, 0.4)
Natural energy resources	(0.1, 0.3, 0.4)	(0.3, 0.1, 0.0)	(0.2, 0.2, 0.4)
Agricultural items	(0.3, 0.2, 0.2)	(0.1, 0.3, 0.3)	(0.1, 0.4, 0.4)
Industrial products	(0.3, 0.3, 0.2)	(0.2, 0.4, 0.4)	(0.1, 0.4, 0.2)
Water resources	(0.2, 0.3, 0.3)	(0.2, 0.3, 0.2)	(0.3, 0.1, 0.1)

.

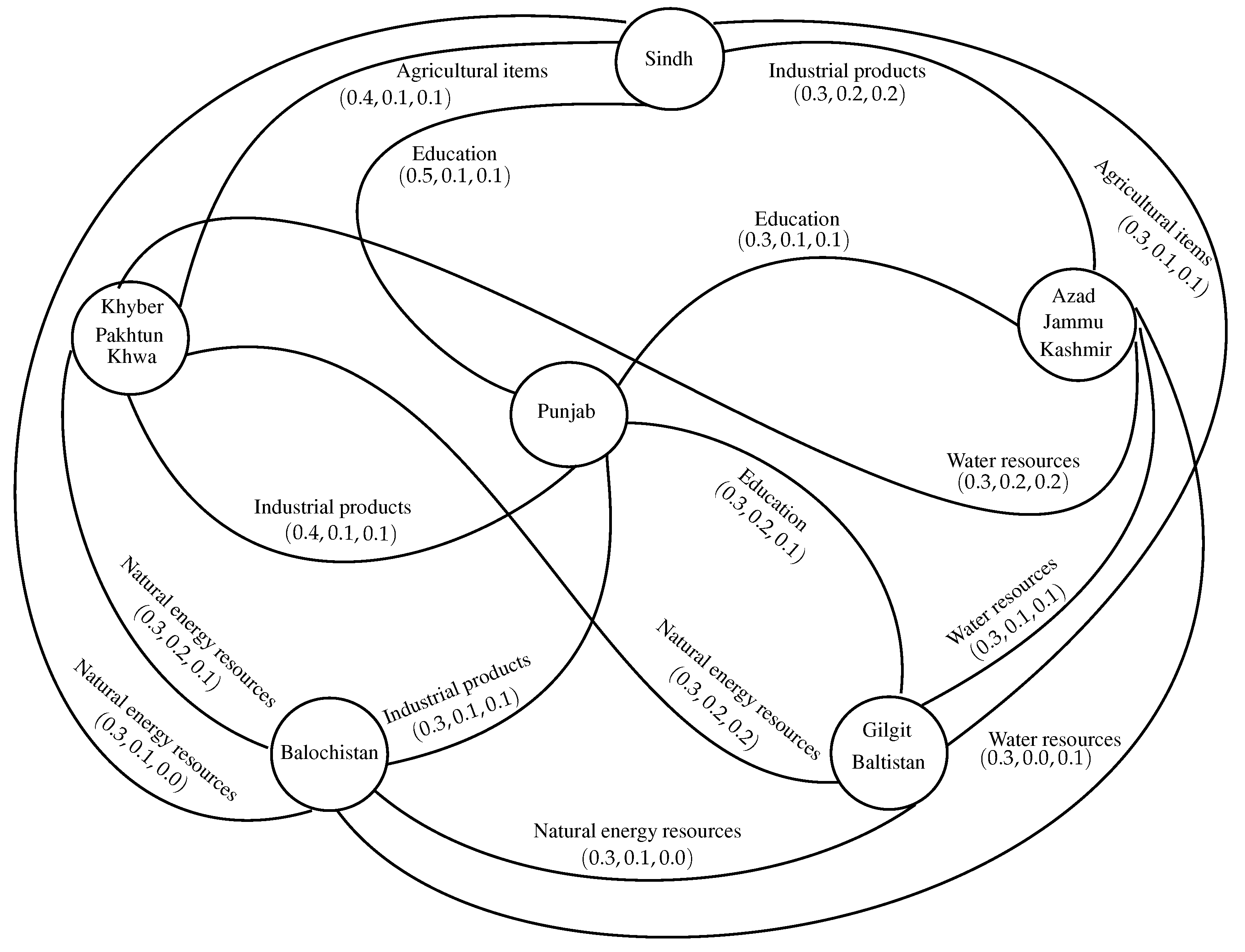
Many relations can be defined on the set P, we define following relations on set P as:

$P_1$ = Education, $P_2$ = Natural energy resources, $P_3$ = Agricultural items, $P_4$ = Industrial products, $P_5$ = Water resources, such that $(P,P_1,P_2,P_3,P_4,P_5)$ is a GS. Any element of a relation demonstrates a particular interdependent relationship between these two provinces. As $(P,P_1,P_2,P_3,P_4,P_5)$ is GS; this is why any element can appear in only one relation. Therefore, any element will be considered in that relationship, whose value of T is high, and values of I, F are comparatively low, using the data of above tables.

Write down T, I and F values of the elements in relations according to the above data, such that $O_1$, $O_2$, $O_3$, $O_4$, $O_5$ are IN sets on relations $P_1$, $P_2$, $P_3$, $P_4$, $P_5$, respectively.

Let $P_1$ = $\left\{\right(\mathrm{Punjab},\mathrm{Sindh}),(\mathrm{Gilgit}-\mathrm{Baltistan},\mathrm{Punjab}),(\mathrm{AzadJammuandKashmir},\mathrm{Punjab}\left)\right\}$;

$P_2$ = {(Sindh, Balochistan), (Khyber Pakhtunkhawa, Balochistan), (Balochistan, Gilgit-Baltistan), (Khyber Pakhtunkhawa, Gilgit-Baltistan)};

$P_3$ = {(Sindh, Khyber Pakhtunkhwa), (Gilgit-Baltistan, Sindh)};

$P_4$ = $\left\{\right(\mathrm{Punjab},\mathrm{KhyberPakhtunkhwa}),(\mathrm{Sindh},\mathrm{AzadJammuandKashmir}),(\mathrm{Balochistan},\mathrm{Punjab}\left)\right\}$;

$P_5$ = $\left\{\right(\mathrm{KheberPakhtunkhwa},\mathrm{AzadJammuandKashmir}),(\mathrm{Balochistan},\mathrm{AzadJammuandKashmir}),(\mathrm{Gilgit}-\mathrm{Baltistan},\mathrm{Azad} \mathrm{Jammu} and \mathrm{Kashmir}\left)\right\}$.

Let $O_1$ = $\left\{\right((PU,SI),0.5,0.1,0.1),((GB,PU),0.3,0.2,0.1),((AJK,PU),0.3,0.1,0.1\left)\right\}$,

$O_2$ = $\left\{\right((SI,BA),0.3,0.1,0.0),((KPK,BA),0.3,0.2,0.1),((BA,GB),0.3,0.1,0.0),((KPK,GB),0.3,0.2,0.2\left)\right\}$,

$O_3$ = $\left\{\right((SI,KPK),0.4,0.1,0.1),((GB,SI),0.3,0.1,0.1),\}$,

$O_4$ = $\left\{\right((PU,KPK),0.4,0.1,0.1),((SI,AJK),0.3,0.2,0.2),((BA,PU),0.3,0.1,0.1\left)\right\}$,

$O_5=\{((KPK,AJK),0.3,0.2,0.2),((BA,AJK),0.3,0.0,0.1),((GB,AJK),0.3,0.1,0.1)\}$.

Obviously, (O, $O_1$, $O_2$, $O_3$, $O_4$, $O_5$) is an INGS as shown in Figure 14.

Every edge of this INGS demonstrates the most dominating interdependent relationship between those two provinces—for example, the most dominating interdependent relationship between Punjab and Gilgit-Baltistan is education, and its T, F and I values are 0.3, 0.2 and 0.1, respectively. It shows that education is the strongest connection bond between Punjab and Gilgit-Baltistan; it is $30\%$ stable, $10\%$ unstable, and $20\%$ unpredictable or uncertain. Using INGS, we can also elaborate the strength of any province, e.g., Punjab has the highest vertex degree for interdependent relationship education, and Balochistan has the highest vertex degree for the interdependent relationship natural energy resources. This shows that the strength of Punjab is education, and the strength of Balochistan is the natural energy resources. This INGS can be very helpful for Provincial Governments, and they can easily estimate which kind of interdependent relationships they have with other provinces, and what is the percentage of its stability and instability. It can also guide the Federal Government in regards to, between any two provinces, which relationships are crucial and what is their status. The Federal Government should be conscious of making decisions such that the most crucial interdependent relationships of its provinces are not disturbed and need to overcome the counter forces that are trying to destroy them.

4. Conclusions

Graph theory is a useful tool for solving combinatorial problems of different fields, including optimization, algebra, computer science, topology and operations research. An intuitionistic neutrosophic set constitutes a generalization of an intuitionistic fuzzy set. In this research paper, we have introduced the notion of intuitionistic neutrosophic graph structure. We have discussed a real-life application of intuitionistic neutrosophic graph structure in decision-making. Our aim is to extend our research work to (1) fuzzy rough graph structures; (2) rough fuzzy graph structures; (3) soft rough graph structures; and (4) roughness in graph structures.