1. Introduction
As there is an explosive increase in the utilization of wireless mobile communication, the demand for high-speed data rates among the users of 3G and 4G wireless mobile communications has increased considerably. The need to achieve a reliable communication at high data rates is challenging and is an important part of the problem in today’s rapidly developing world. The performance of high-speed wireless communication systems is limited by harsh variation in the signal strength by the phenomena commonly known as fading. Using a diversified signal processing technique in which the same signal appears in multiple instances in time, frequency or antennas that fade independently can reduce the harsh effects of fading. In recent years, a relatively new technique has emerged known as cooperative communication in a wireless system. The basic idea of this technique is that two or more than two mobile users share the same information and cooperatively communicate the information signal at a common destination. The authors in [
1,
2] proved, by performing rigorous information theoretic analysis, that the cooperation technique leads to higher data rate as compared to a non-cooperative counterpart. In this context, in order to exploit spatial diversity, some repetitive algorithms such as “decoded and forward (DF)” and “amplify and forward (AF)” were developed for improving the bit error rate (BER) but at the cost of reduced spectral efficiency [
3]. After a year or so the same authors in [
3] published a paper [
4] in which they conceived the idea of user cooperation in space-time domain and developed the distributed space time coding protocol that fully exploits spatial diversity among cooperating users. After that, a slightly different framework has emerged in the literature commonly known as coded cooperation [
5]. In this technique, instead of only repeating information bits, each user transmits an extra redundancy for its cooperating partner. Later this technique was also developed for multiple cooperating users [
6]. The distributed coded cooperation scheme based in turbo code was originally investigated in [
7]. Moreover, there has been a plethora of research on wireless cooperative communication systems using massive relays. The authors in [
8] investigated the performance analysis of coded cooperation communication in cluster of relays. The authors in [
9] implemented the classical Reed Muller code [
10] in coded cooperation scenario over multiple relays.
In broadband wireless communication, OFDM is an effective technique that mitigates the effect of inter-symbol interference (ISI) and offers high spectral efficiency. The combination of OFDM with MIMO antennas has been very famous over the last two decades as it effectively exploits spatial and frequency diversities in frequency selective MIMO channels [
11]. In order to get more benefit in terms of spatial and temporal diversities the authors in [
12] have considered an application of an amplify and forward protocol in OFDM system. In [
13] authors have analyzed the performance of MIMO-OFDM system in relay-assisted user-cooperative wireless communication. A coded OFDM based on time division multiple access scheme in cooperative wireless communication was investigated in [
14]. This scheme is similar to the previously coded cooperative schemes [
5] in which a source node broadcasts all its subcarrier towards both destination and partner user (relay) in first half of the code word in a first time slot. After successfully decoding, the partner user will re-transmit all the subcarriers to the destination in second half of the code word in a second time slot. Recently an author in [
15] has investigated the performance of the OFDM system based on decode and forward cooperative communication using multiple relays over time dispersive fading channels.
Many researchers have focused their attention on developing better cooperative strategies in order to make a practical wireless standard for future wireless communication systems. Nevertheless, there has not been much work reported in the literature that exploits the basic structure of the channel code to enhance diversity through coded-cooperation. More specifically, in case of turbo code, employing good interleavers design always plays a critical role in enhancing the overall bit error rate (BER) performance of the code in a coded cooperation wireless system [
16]. A plethora of research has already been done in designing suitable interleaver in [
17]. Furthermore, it has been found in [
18] that CMI qualifies to be an optimum choice of interleaver. The area of distributed turbo coded cooperation in a fast Rayleigh fading channels using OFDM associated with Alamouti space time block code (STBC) with code matched interleaver at the relay have been unexplored to date. This paper aims to investigate the above scenario. To the best of our knowledge the closest work to our manuscript lies in [
18], where the authors proposed a modified code matched interleaver for distributed turbo coded cooperative non-OFDM systems using single antenna at each node and employed binary phase shift keying (BPSK) as the only modulation technique. However, the literature [
18] did not consider the distributed turbo coded OFDM with multiple antennas at each cooperating node. It has also not considered higher-order modulation in its design. Therefore, addressing these matters are the main motivation and contribution of this manuscript.
The remaining part of the manuscript is organized as follows.
Section 2 presents the basic theory of turbo coded OFDM with MIMO antennas.
Section 3 discusses the brief overview of CMI.
Section 4 primarily deals with proposed turbo coded OFDM with MIMO antennas scheme in cooperative scenario. Joint iterative SISO decoding for turbo coded cooperative OFDM is explained in
Section 5. In
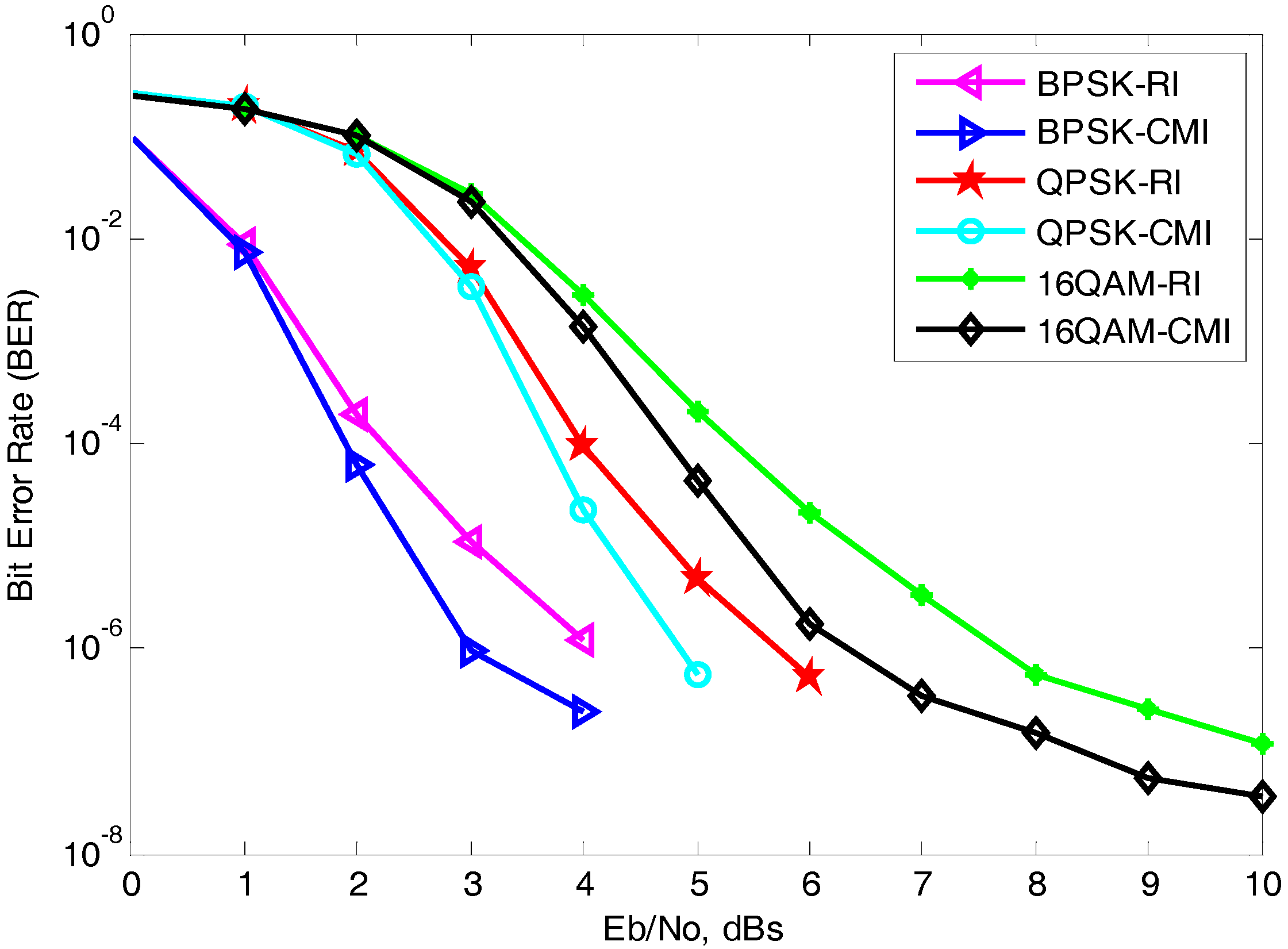
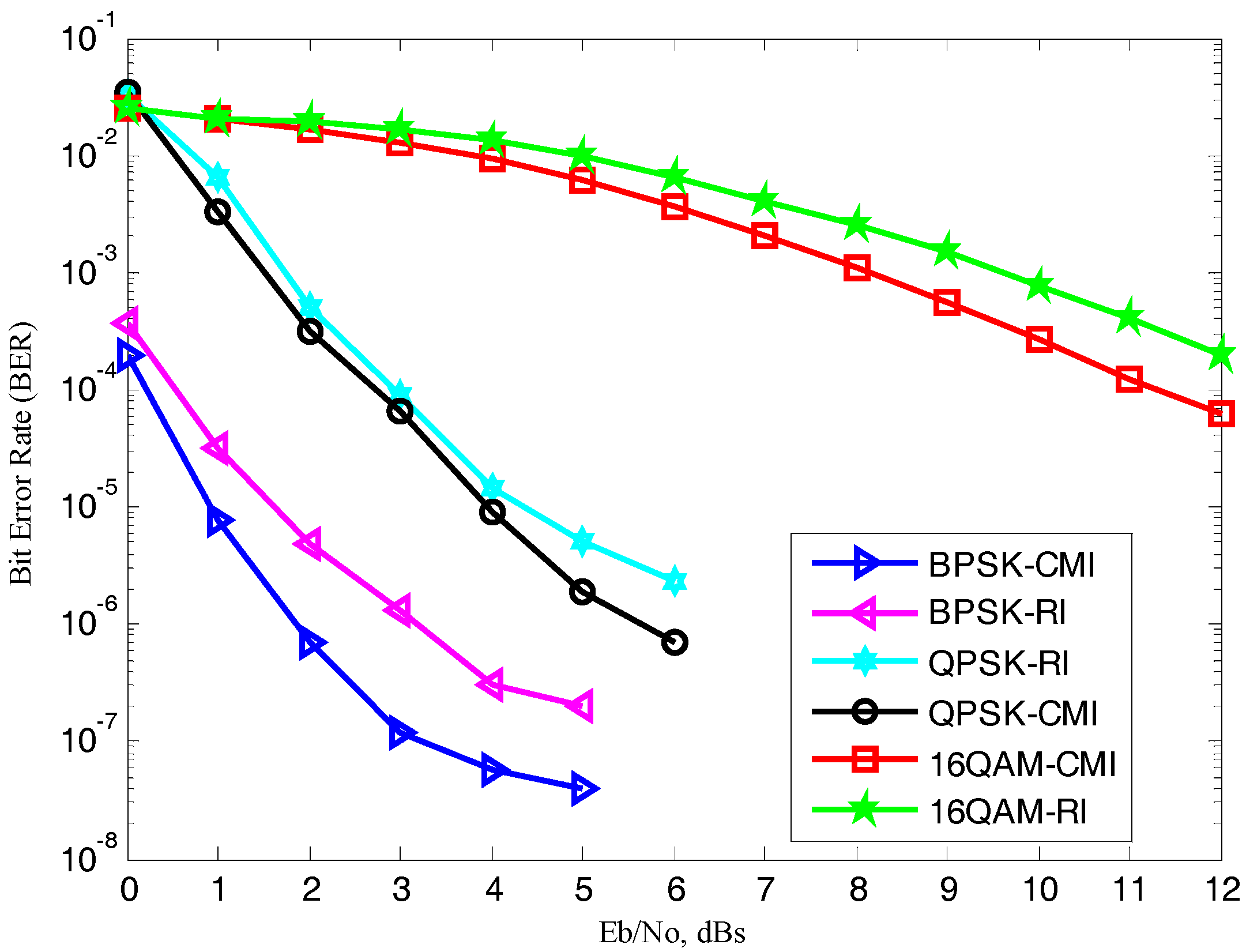
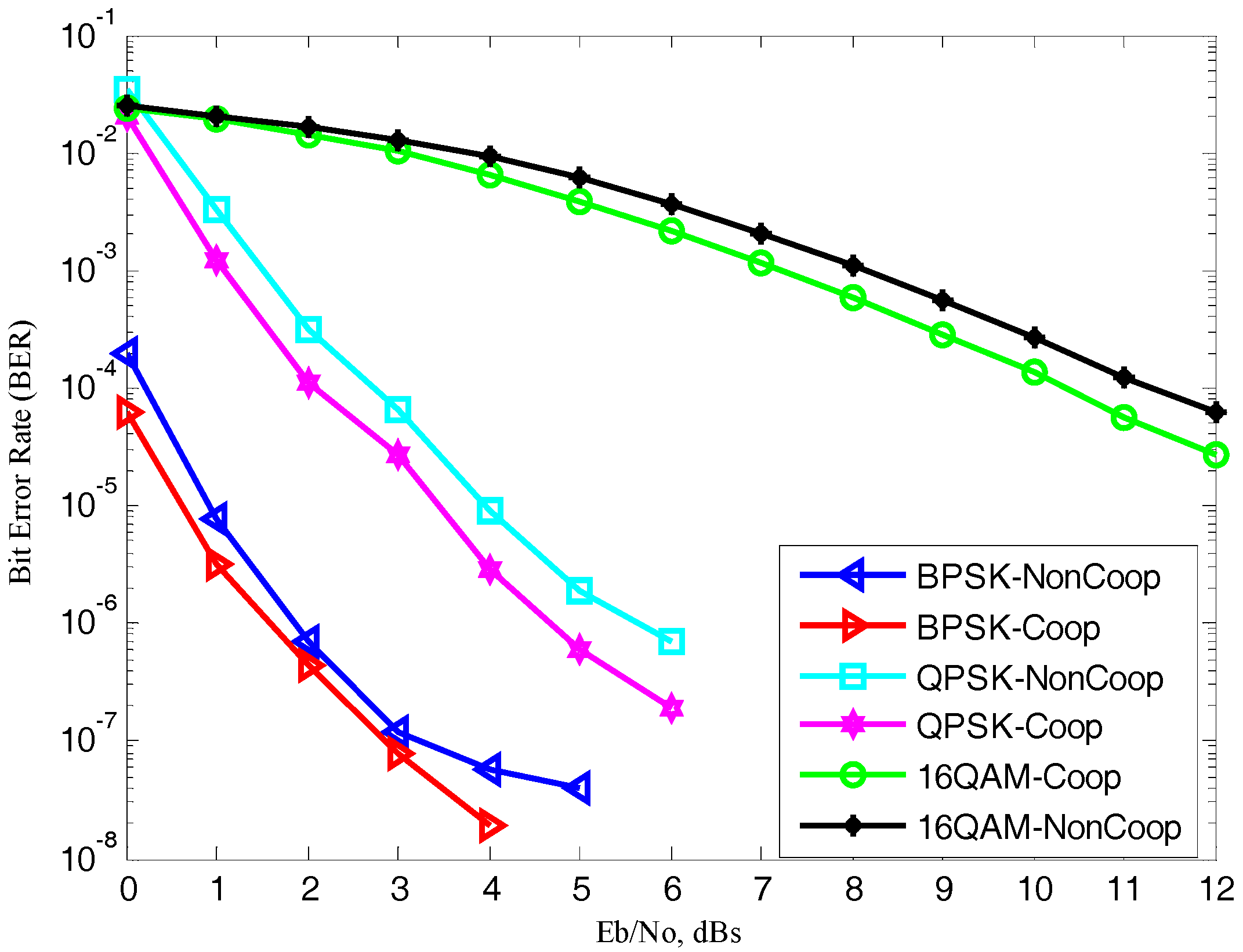
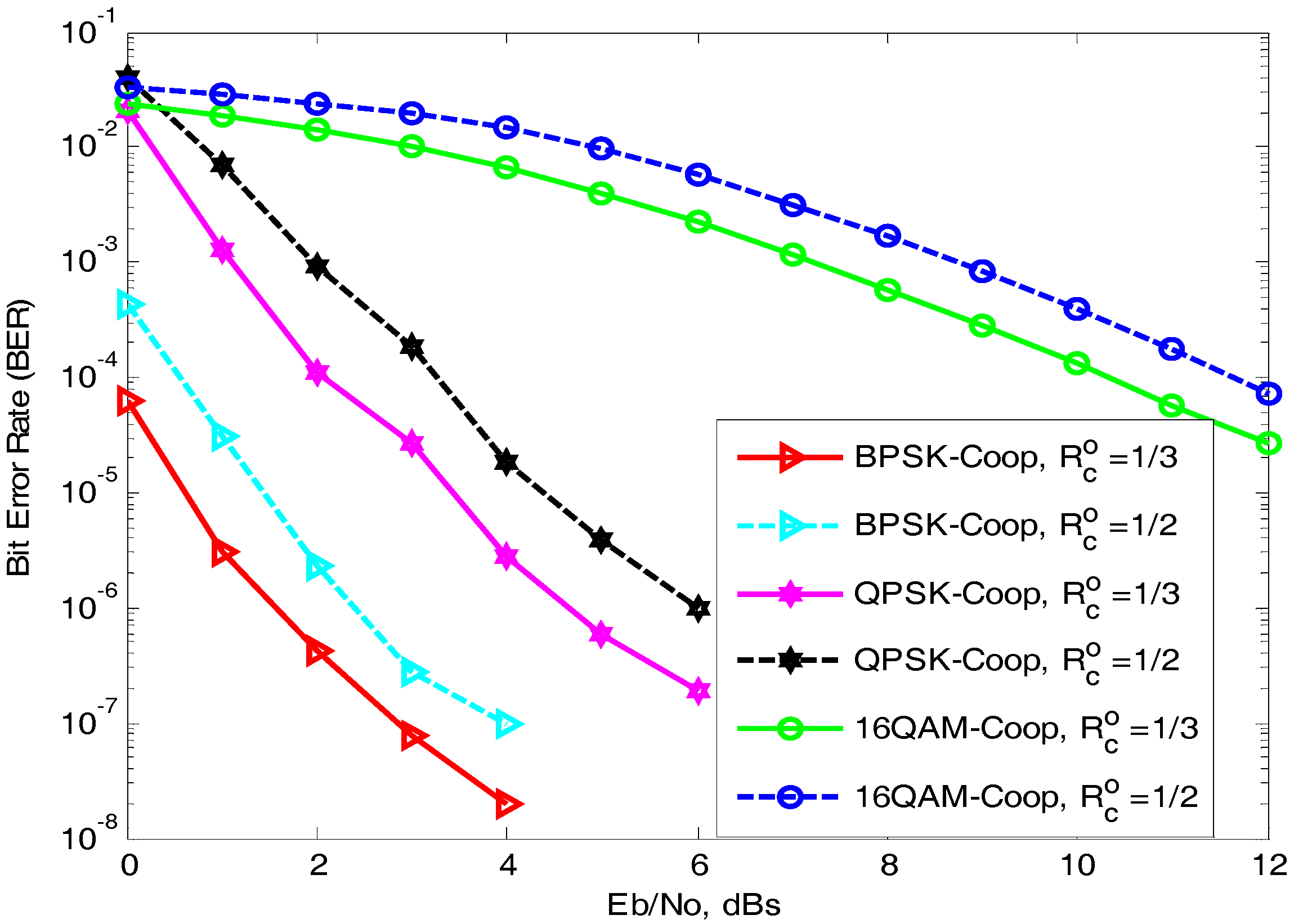
Section 6, the BER performance comparison of CMI with uniform random interleaver (RI) for turbo coded OFDM with different modulation techniques over AWGN channel are discussed. Furthermore, turbo coded OFDM with MIMO (2 × 2) antennas over fast Rayleigh fading channels under different modulation schemes are also discussed. Monte Carlo simulated results of turbo coded-OFDM with MIMO (2 × 2) antennas in cooperation with different modulation schemes under CMI are presented and discussed in this section. Finally, the paper comes to an end with the conclusion drawn in
Section 7.
2. Turbo Coded OFDM with MIMO (2 × 2)
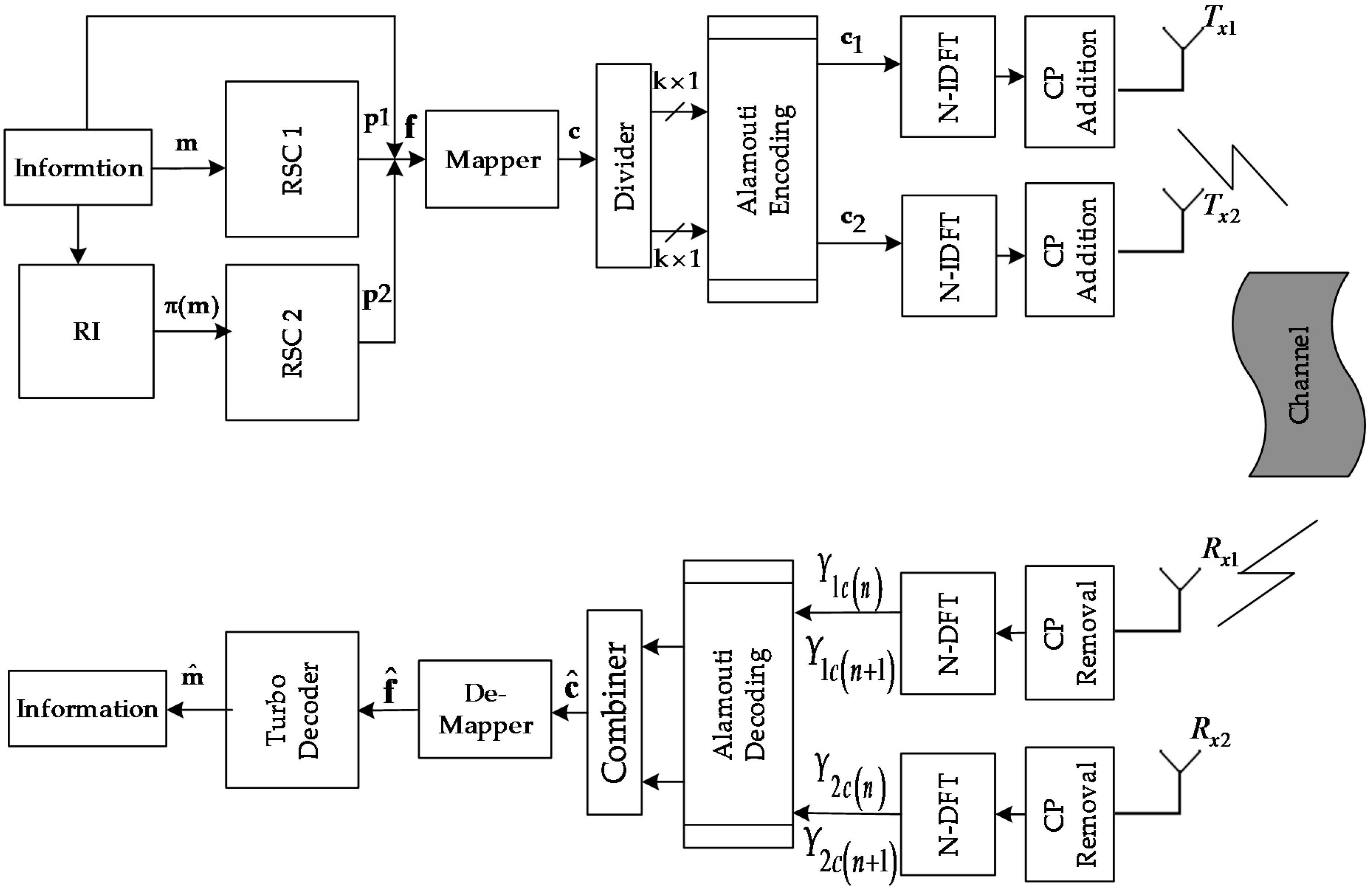
The turbo coded OFDM based on MIMO antennas is depicted in
Figure 1. The information sequence of bits
m is passed through recursive convolutional encoder-1 (RSC-1) that forms the parity sequences of bits
p1. At the same time, information sequences of bits m are also fed into recursive systematic convolutional encoder-2 (RSC-2) via random interleaver (RI) that gives parity sequence of bits
p2. The interleaver rearranges the information bits according certain design criteria. The purpose of the interleaver is to de-correlate the information bit sequence so that an iterative decoding, i.e., based on exchange of extrinsic information between the constituent decoders, can be applied [
19]. The two corresponding parities sequences of bits along with information bits form the encoded turbo frame
f. The encoded sequences of bits in turbo encoded frame
f are mapped into a mapper that generates digitally modulated complex symbols c, i.e., QPSK, 16 QAM etc. Then, Alamouti encoding [
20] is applied to obtain the two parallel encoded signals
and
. At time slot 1 and 2 (i.e.,
and
where
T is OFDM symbol time)
and
are sent in two parallel paths, respectively. Then N-point inverse discrete Fourier transform (IDFT) operation is applied to these sequences of symbols, which transforms the corresponding signal in time-domain. Finally, a cyclic prefix is appended to get corresponding OFDM symbols, which are transmitted with the antenna
and antenna
respectively via fast frequency selective Rayleigh fading channel H. The insertion of a cyclic prefix transforms the linear convolution operation into circular convolution operation. A well-known property of the DFT is that circular-convolution in time-domain results in multiplication in frequency-domain. Moreover, it is assumed that channel entries do not change for two consecutive Alamouti space-time block codes. Therefore, the channel qualifies to be called a fast Rayleigh fading channel. Also, the transmitter does not know the about channel entries and receiver has a full knowledge about channel H.
The received signal after removal of cyclic prefix and N-DFT operation at time slot 1 and time slot 2 are modeled as follows:
where the operator “
” denotes the circular convolution.
and
are the corresponding frequency domain representation of
and
respectively. The subscript c of
,
,
and
represents the combined received signal at receive antenna1
, receive antenna2
in time slot-1 and time slot-2 respectively. The terms such as
,
,
and
are the noise terms of antenna of receive antenna1
, receive antenna2
in time slot 1 and time slot 2 respectively. Thus, the received signal vectors are obtained in Equations (1)–(8). Moreover,
represents channel impulse response from transmit antenna1
to the received antenna1
,
represents channel impulse response from transmit antenna1
to the received antenna2
,
represents channel impulse response from transmit antenna2
to the received antenna1
and
represents channel impulse response from transmit antenna2
to the received antenna2
. Subsequently
,
,
and
are diagonal matrix whose diagonal entries are DFTs of the corresponding channel impulse response. Now the Alamouti STBC decoding in frequency domain is given as follows:
The estimated signals i.e., and are combined to get the signal . The signal is given as input to the de-mapper that performs the corresponding demodulation process to obtain the estimated sequence of soft bits . Finally, joint turbo decoding is performed to get final estimation of information sequences . The details of joint turbo decoding will be discussed in the subsequent section of this manuscript.
3. Code Matched Interleaver (CMI)
The performance of any coded-cooperative system depends on the construction of a better code at the destination node. A code is better or not it depends on its distance spectrum properties, which will directly affect its error capability. Turbo code is considered to be a better code mainly because of good distance properties and its convenient structure that can be effectively deployed in cooperative scenarios due to its particular distributive nature in its encoding scheme. Once the turbo code is distributed for coded cooperation, the interleaver is usually placed in the relay node, which is situated near to the destination. Furthermore, if the relay has to contribute in obtaining a better code at the destination then it must generate high weight code words. The high weight code words can only be generated if the interleaver is well capable of breaking the low weight code words into high weight code words. The only interleaver that fully accomplishes this task is the code-matched interleaver (CMI) [
17]. The CMI interleaver matches the distance spectrum of the constituent code. At low to medium SNR regime (0–3 dB) the interleaver size plays an effective role in improving the performance of the turbo code. However, at medium to high SNR regime (3–8 dB), the spectral lines of constituent encoders determine the performance the turbo code. CMI eliminates the first few spectral lines of distance spectrum thereby causing an increase in its code free distance
. As a result, the code performance at high SNR regime is improved considerably.
In distributed turbo code, the performance of iterative decoders is also a crucial factor that affects the BER performance of the cooperative communication. The effective exchange of extrinsic information in the iterating decoding is heavily dependent on free distance
of the turbo code. The lower free distance
will degrade the performance of iterative decoding in cooperative communication at the destination. At high SNR, the BER curve saturates and becomes flat. This action is called an “error floor” [
21]. CMI breaks the low weigh information code word that would have formed if any other interleaver might have used. Thus, CMI causes a lower error floor region (due to the minimum free distance). The details of the construction of CMI are presented in [
17]. However, we briefly discuss the construction of CMI in this section.
Let us consider two identical 4-state recursive systematic convolutional encoders each having a generator matrix where is feed forward polynomial and is feedback polynomial. The information sequence is encoded by RSC-1 that results in pair, where is the parity sequence. After the interleaving the information sequences , the interleaved information sequence is passed to RSC-2 that generates pair, where is another parity sequence. Let be the weight of the information sequence and likewise and be the weights of the corresponding parity sequences produced by RSC-1 and RSC-2 respectively. Then, the net weight of the turbo code can be written as follows
The low weight-2 input sequence, which is responsible for low weight code word can be represented by the following polynomial equation:
where
k1 = 1, 2, 3, … is a positive integer, α is the minimum distance between “1”s in weight-2 information sequence
,
is the time delay,
= 1, 2, 3 …. The interleaved information
can also be represented in polynomial form.
where
k2 = 1, 2, 3, … is a positive integer,
is the time delay, such that
= 1, 2, 3 …. Let
be the minimum parity check sequence generated by a weight-2 input sequence. Then the weight of
j-th parity bit sequence is given as follows:
where
= 1, 2, 3, 4 …,
j = 1, 2. The net weight of the turbo code generated by weight-2 input sequences is given as:
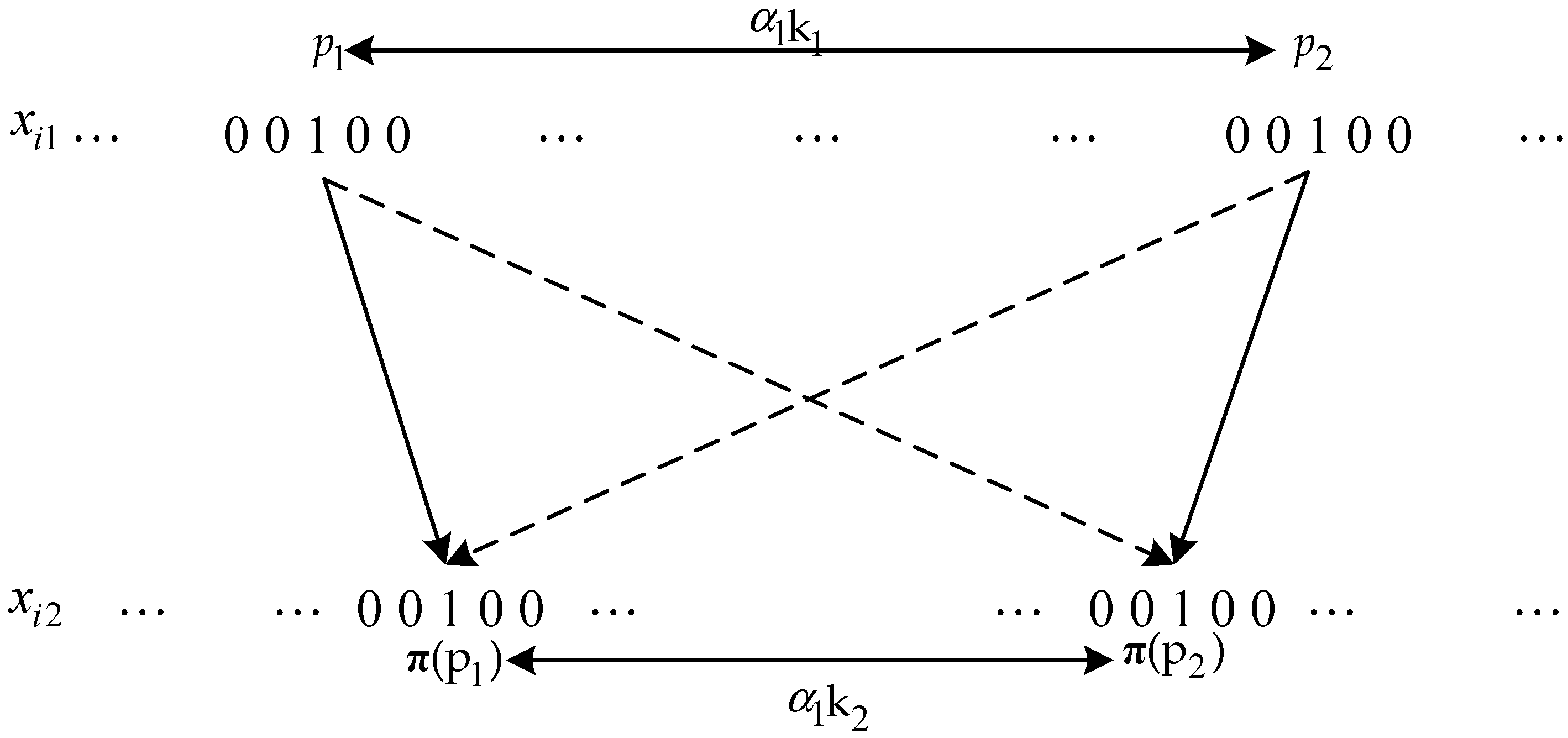
Suppose that the positions of “1”s in weight-2 information sequence
are denoted by
,
. The information sequence
after passing through interleaver scrambles the bits. The new position of “1”s becomes
as shown in
Figure 2.
Let’s take the most damaging case for weight-2 information sequence as
This case is the worst case because spacing between the consecutive two “1”s between the original and the interleaved sequences are both multiple of
. This will cause the interleaved information sequence still divisible by RSC-2 that will eventually result in low parity weight sequences. Thus, the net weight of turbo code word will be lowered and will decrease the overall performance of turbo code. Therefore, to prevent this worst-case scenario to happen, the interleaver must meet the following design mapping criteria:
However, not all the weight-2 input sequences are bad only those weight-2 input pattern that produce low weight code words that severely affects the BER performance should be removed in the interleaver design. Therefore a parameter,
commonly known as threshold is usually defined where
represents weight-2 or weight-4 sequences. If the weight of the code word lies outside the threshold value
, then that particular weight-2 sequence is not considered as bad pattern and interleaver must not remove that input pattern. The details of threshold
are presented in [
16]. The value of threshold
varies for each turbo code. Applying threshold
to Equation (13) we obtain the following inequality
Thus, the weight-2 information sequence is considered to be a bad sequence if it satisfies (17) and (20) simultaneously. The weight-3 information sequences, which result in low weight turbo code word is effectively removed by using S random constraint condition. The design steps of S-random interleaver are well formulated in [
21]. We also consider a weight-4 sequence, which usually produces low weight parity sequence that degrades the performance of overall turbo code. A weight-4 sequence becomes weight-2 error pattern after interleaving which also produces bad weight code word. By same procedure, as weight-2 sequence, the new weight generated by weight-4 input sequence
can be expressed as follows:
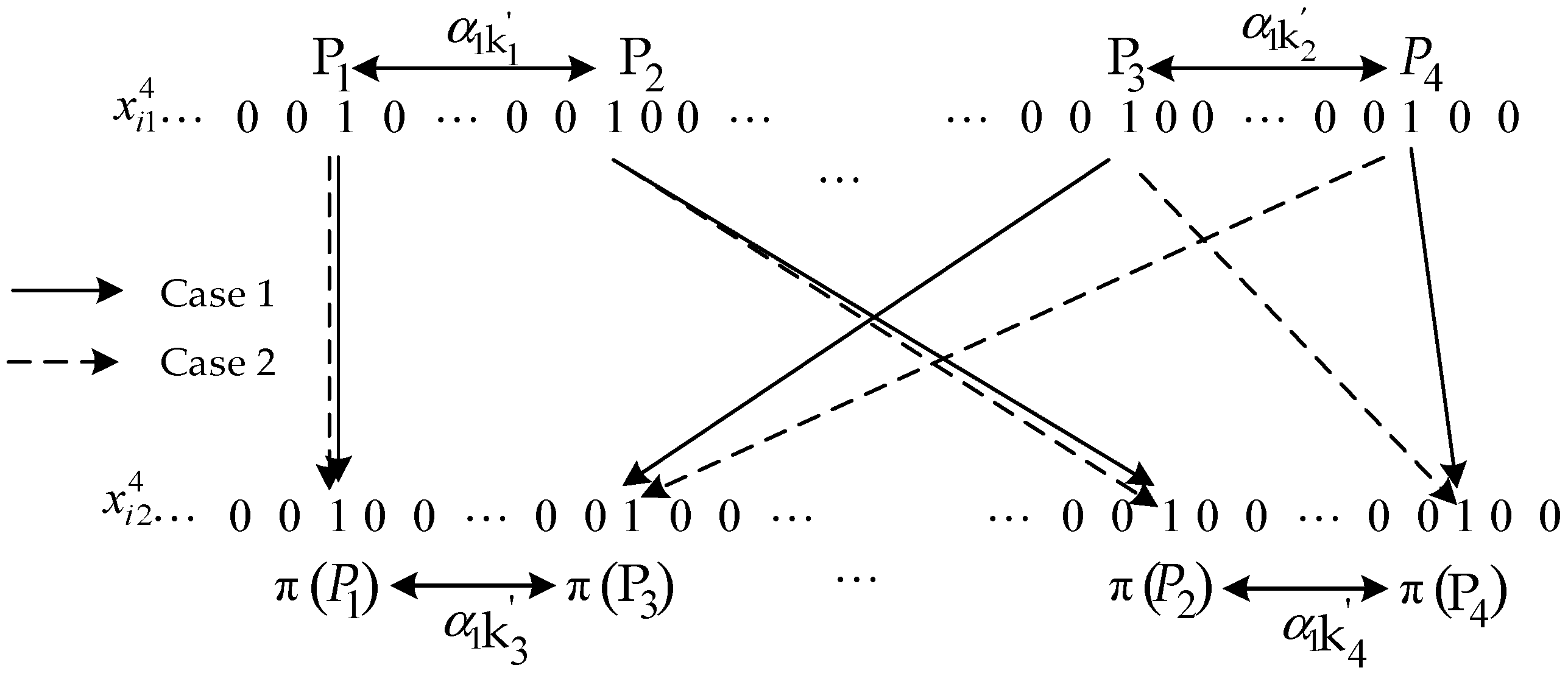
Suppose that the positions of “1”s are represented by
,
,
and
for weight-4 information sequence
where, as
. The information sequence
is passed through an interleaver then positions of “1”s in the interleaved sequence is denoted by
and
. The scenario is depicted in
Figure 3. The worst case for weight-4 information sequence
is given as follow:
OR
However such a bad scenario can be avoided if the interleaver incorporates the following mapping criterion
OR
As mentioned earlier that not all the weight-2 sequences are bad, the same is the case with weight-4 sequences. There are such a weight-4 sequences which does not satisfy (23) but still they are not considered as bad sequences. Similarly, there is a threshold parameter
in given [
16]. Applying this parameter
to the weight-4 input sequences results in the following inequality
The weight-4 sequence will only be classified as bad weight-4 sequence if and only if it satisfies both the inequality (23) and (25) simultaneously. Otherwise weight-4 sequence will not degrade the performance of turbo code. The effect of input sequence with input weight w > 4 on over all turbo code performance is very negligible. Therefore, we will not consider them in the interleaver design.
A four–state turbo code having two identical recursive systematic convolutional encoders each with generator polynomial
is considered in this manuscript. The values of threshold parameters such as
,
and
are found in [
21]. The parameters values are
and
. The weight-2 information sequence that causes minimum parity sequence is given as (…010010…). The parity sequence that is produced by considered weight-2 information sequences by RSC-1 is given as (…011110…). The value of
and
is considered for this specific code. To design CMI all the design mapping criteria that were aforementioned in this section must be taken into an account.
4. Turbo Coded OFDM with MIMO Antennas in Cooperation
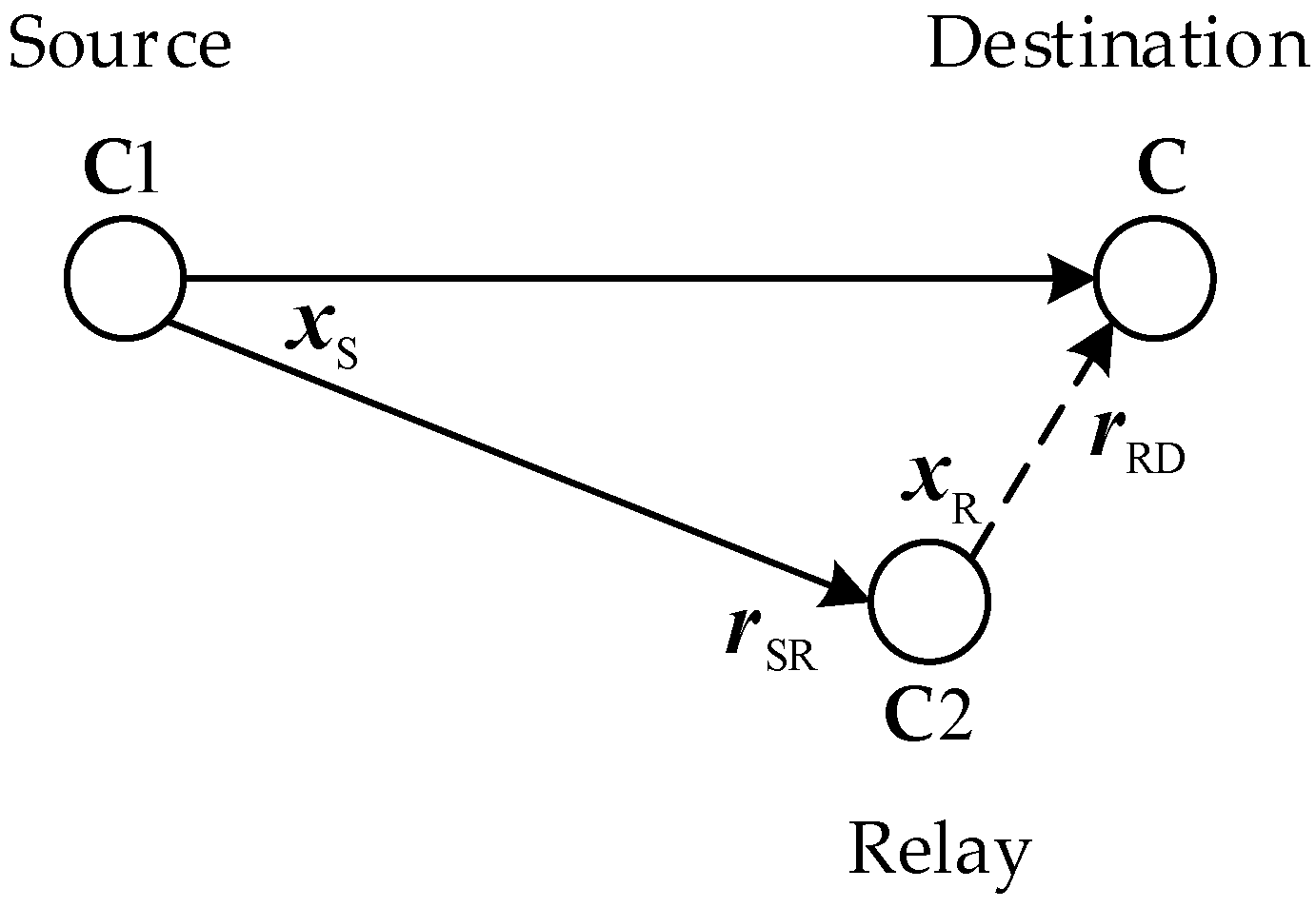
The concept of wireless communication based on three terminal networks using OFDM over frequency selective fading channels can be found in the excellent tutorial survey article detailed in [
22]. The three terminals are source-S, relay-R, and destination-D, as shown in
Figure 4.
The whole code is divided in two codes C1 and C2. C1 is placed at source-S and C2 is placed in relay-R. The relay-R is mostly located near to destination-D. The whole transmission from source-S to destination-D is accomplished in two time slots. In first time slot the source-S encodes the information sequence of bits through code C1 and broadcast it towards both relay-R and destination-D. After, the corresponding de-modulation, the relay-R receives the signal in first time slot. The relay-R decodes the information sequence. Usually this decoding is assumed to be an ideal decoding due to the assumption that source-S to relay-R channel is completely noiseless. Moreover, the Relay-R encodes the information sequences with other code C2 and re-transmits them to the destination-D through a Rayleigh fading channel in second time slot after modulation. Finally, the received signals from the source-S and relay-R are demodulated by soft input soft output SISO demodulator and is estimated using joint iterating decoding employed at the destination-D.
The way the turbo code is structured makes it suitable for its deployment in coded cooperative scenario. Turbo code is disturbed to source-S and relay-R in such way that the cooperation between theses nodes takes place. It forms an important class of cooperative communication commonly known as distributed turbo codes (DTC) [
5].
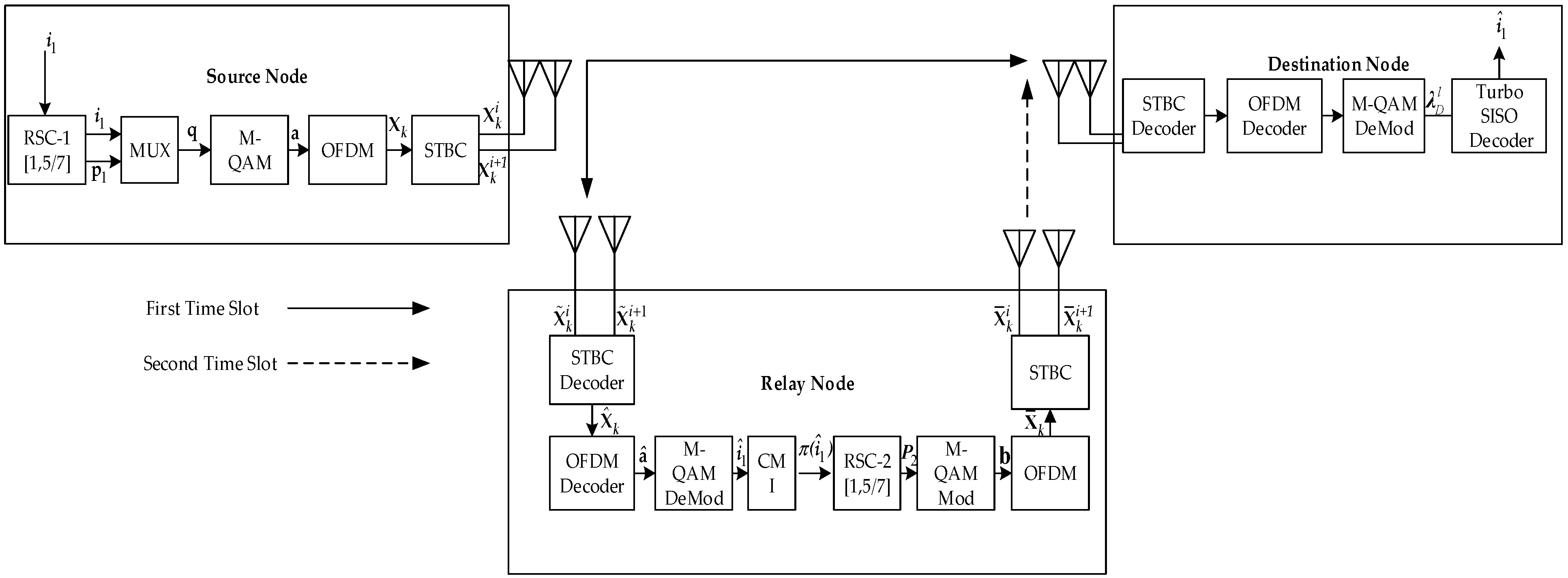
The turbo coded OFDM with MIMO antennas are deployed in a cooperation communication scenario as shown in the
Figure 5. The scheme completes the transmission of one turbo coded OFDM frame in two time slots. The source-S node consists of 1/2 rate RSC-1 encoder, mapper, OFDM block and Alamouti STBC. The information sequence of bits
is applied to RCS-1 encoder that transforms the information sequences of bits
into coded sequences of bits
q. The coded sequence of bits
q consists of information sequence of bits
and parity sequence of bits
. The coded sequences of bits
q are mapped into complex symbols
a using different constellations such as BPSK, QPSK and 16QAM. The coded symbols
a takes the form of RSC-1 encoded OFDM symbols
as they are passed through OFDM block by incorporating N-point IDFT and appending cyclic prefix. The RSC-1 encoded OFDM symbols
are given as input to Alamouti Space time block code. Alamouti encoding [
20] is applied to RSC-1 encoded OFDM symbols
that will result in two parallel sequences
and
. These two Alamouti code words are broadcasted over the radio frequency (RF) channel towards both relay-R and destination-D. The signal received at the destination D during the first time slot is modelled as
where
is the Alamouti space time code word,
is the channel matrix between source-S and destination node. The channel matrix is assumed to be a Rayleigh fading channel whose entries are independent and identically distributed (I.I.D) complex Gaussian random variables with zero mean and variance ½ per dimension.
is the complex Gaussian noise matrix whose entries are modelled as I.I.D complex Gaussian random variables with zero mean and variance
N0/2 per dimension. The channel entries remain static during the transmission of one complete Alamouti STBC. Therefore, the channel qualifies to be called as fast Rayleigh fading channel. At the same time, in first time slot the signal received at the relay-R is modeled as
where
is the Alamouti space time code word
and
channel matrix and Gaussian noise matrix defined similarly as
and
respectively. The received signal
is decoded using Alamouti decoding [
19].
The signal is passed through OFDM decoder and corresponding soft demodulator to estimate the original information sequence
. The estimated information sequence
may or may not be same as original information sequence
. It depends upon the source-S to relay-R channel. The estimated information sequence
is interleaved by CMI that permutes the estimated information sequence
in an optimum way. The relay-R encodes the interleaved estimated information sequence
using RSC-2 encoder. The RSC-2 encoded sequences of parity bits
are mapped into digital modulator to obtain the complex digital modulated symbols
b. The RSC-2 encoded symbols
b is delivered to OFDM block which takes N point IDFT and appends a cyclic prefix to form RSC-2 encoded OFDM symbol
. The resulted RSC-2 encoded OFDM symbol
is again given as input to Alamouti STBC which results in two parallel sequences
and
. These two Alamouti code words are propagated towards destination-D according to Alamouti encoding scheme [
20]. The signal received at the destination-D during the second time slot is modelled as follows as:
where
and
are channel matrix and Gaussian noise matrix respectively and are defined similarly as
and
.
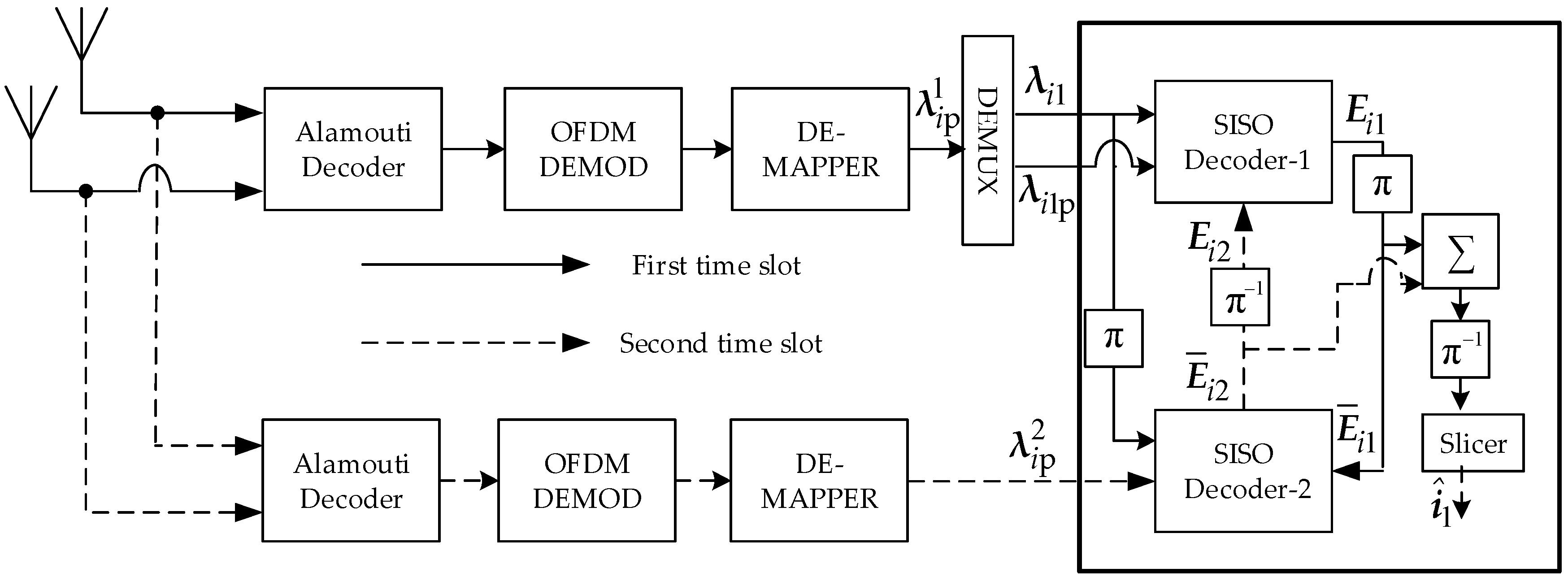
The received signals and are delivered to Alamouti STBC decoder and OFDM demodulator in their respected time slots. OFDM demodulator takes N-point DFT and removes the cyclic prefix to form the complex symbols. These complex symbols are digitally demodulated by SISO demodulator. SISO demodulator produces log likelihood ratios (LLRs) for each of the received coded bits. These soft bit LLRs for first and second time slot are given an input to joint iterative turbo decoder, which iterates for a desired number of iterations and pass the updated LLRs to the slicer. The term joint here refers to the fact the decoding of the signals and are performed together rather than decoding each of the received signal separately. The joint iterative turbo decoding for the proposed scheme is comprehensively discussed in the subsequent section of the manuscript. In the end the slicer performs the hard decoding operation on each received soft bit to recover the original transmitted sequence of information bits .
The source-S node transmits
M1 code word bits (RSC-1 encoded OFDM code word) during first time slot to decoder 1 (as it corresponds to the RSC-1 encoder at the source-S) and relay-R node transmits
M2 code word bits (RSC-2 encoded OFDM code word) during the second time slot to decoder 2 (as it corresponds to the RSC-2 encoder at the relay-R). The total code word bits reach at the destination during one complete transmission is
M =
M1 +
M2. Thus, the code rate for the proposed scheme is given as follows:
where
is 1/3 for the proposed coded cooperative scheme.