Abstract
The interplay between retrocausality and the time-reversal symmetry of the dynamical law of quantum mechanics underscores the significance of the measurement dynamics with the use of indivisible and discrete quantum particles to be mediated. One example of empirical evidence demonstrating the significance of retrocausality going along with time-reversal symmetry is seen in the operation of a reaction cycle to be expected in chemical evolution. A reaction cycle can hold itself when the causative operation of the cycle remains robust, even when facing frequent retrocausal interventions of a quantum-mechanical origin. Quantum mechanics in and of itself has potential in raising a reaction cycle in the prebiotic phase of chemical evolution, even without any help of artefactual scaffoldings of an external origin.
1. Introduction
As far as the issue of symmetry is concerned, it has been taken for granted that classical mechanics is both symmetric in time-reversal and causal. The Wheeler-Feynman time-symmetric theory applied to classical electrodynamics [1] does not violate causality if the radiation emitted by each particle in the universe is completely absorbed by all of the other particles also present in the universe. The absorber theory certainly satisfies the weak causality, admitting no possibility of sending a controllable message from one observer to another faster than light. In a much stronger context, on the other hand, the bilking argument of Black [2], developed within the classical regime, legitimately dismisses retrocausality as noting that the observer of an effect cannot do away with its cause, already done and identified as such by the same observer. Both a cause and its effect are measurable in an irrevocable manner in the classical scheme claiming that measurable objects should be out there as they are even without being accompanied by their actual measurements.
In contrast, quantum mechanics can become both symmetric in time-reversal and retrocausal, especially when the indivisible discreteness of each quantum particle involved in the act of measurement is strictly and legitimately observed [3]. A typical demonstration of retrocausality in quantum mechanics, though not controllable externally as being contrary to the case of causality, is seen in the sudden disappearance of the interference of a single quantum particle with itself immediately after the intervention of a measurement. When a quantum particle passing through a two-slit in the standard two-slit experiment is subject to a weak measurement intended to identify which slit of the two the particle has actually been passing through, in the immediate outside of the exits of both slits, the burgeoning interference would suddenly disappear in a retrocausative manner [4]. Quantum mechanics is peculiar in its competence for addressing something which would eventually disappear in the end. There is no likelihood of identifying an indivisible discrete quantum particle mediating the act of measurement in a divisible manner, whether it may be a photon or an electron, or whatever else for this matter.
One likely scheme of interpreting the sudden disappearance of the interference of a single quantum particle with itself could be the undoing of the interference going to be formed. Such an undoing of the burgeoning interference may be figured out as appealing to the abrupt intervention of turning the direction of the flow of time backwards so as to point to the initial stage prior to the onset of interference. The dynamical law of quantum mechanics is certainly symmetric in time-reversal when measurement is left out.
In short, while they can interfere with themselves in propagation, quantum particles come in lumps in measurement. The apparent retrocausality having the capacity of looking backwards in time applies to the agency internal to a quantum. Retrocausality in quantum phenomena does not offend the classical stipulation of Black’s bilking argument [2] asking that what has been measured cannot be undone, since the quantum interference to disappear remains non-measurable on the spot.
“The results of experiments in quantum mechanics can be predicted correctly either by assigning a forward-evolving state to the system based on the preparation outcome or by assigning a state that evolves backwards in time based on the measurement outcome” (Pegg, quoted from [5]). Accordingly, the retrocausal aspect of the backward causation of a quantum nature imputed to the posterior measurement has to be consequential to the forward causation upon the prior preparation. In particular, the experimental likelihood of closed causal loops or reaction cycles is upon the physical affinity acting between the causal outcome of the prior preparation and the retrocausal outcome of the posterior measurement in the attempted experiment. Put simply, the repeated conversion of the preceding non-measurable retrocausal outcome into the succeeding measurable normal cause comes to provide the emerging consistent loops with their robust scaffoldings in advance. Quantum phenomena are selectively synthetic in trimming off inconsistent quantum interferences in retrospect so as to form a consistent causal loop in the effect.
More specifically, quantum mechanics, even in theory alone, is versatile enough both in creation and annihilation of quantum particles by turning the direction of time back and forth interchangeably.
In fact, the onset of the retrocausal operation following the law of quantum mechanics without being accompanied by any measurement is imputed to the completed causal operation of preserving the indivisible discreteness of the quantum particle mediating the actual measurement. The measurable causal operation conditioned on the non-measurable retrocausal one, which is no more than a hidden indeterminate implication masked by and buried under the uncertainty principle, is unique to quantum phenomena, while such a retrocausality is inconceivable in the classical regime. The effect of a non-measurable retrocausal outcome could become perceivable, at most, indirectly only through the succeeding measurable cause. Retrocausality in quantum theory has already been well worked out in the sound conceptual or philosophical contexts [6,7,8,9,10,11]. We shall follow this tradition in the present article. At the same time, a new addition we are going to make is to work out an opportunity for retrocausality to become operative even in more concrete cases, including chemical reactions, without offending the established dictum that what has been measured cannot be undone any more.
The dynamical law being symmetric in time-reversal can dismiss the cause of the burgeoning quantum interferences in a retrocausal manner simply by reversing the direction of time alone. Measurement in the quantum regime is already selective of itself in pruning off incompatible quantum interferences from within in retrospect.
The retrocausal aspect associated with the actual measurement of a quantum origin will more explicitly be elucidated when chemical reactions are focused upon.
2. Retrocausality in Chemical Reactions
Just for the sake of simplifying the argument, let us imagine that there is a reaction environment with the potential of incorporating three different kinds of chemical reactants, A, B and C, in which these three are further supposed to participate in the two competing transformation reactions: A←B and B→C. Each of the transformation reactions, A←B and B→C, is an instance of measurement proceeding internally [12].
In the transformation reaction B→C, for instance, some of the constituent atoms as the quantum particles residing within the reactant B can be transferred to the reaction product C. What is unique to this transformation reaction is that the product C can serve as an apparatus of a natural origin for measuring the reactant B by receiving some of the quantum particles constituting the reactant B. Here, the process of measurement is equated with the act of receiving quantum particles of whatever sort from what is going to be measured. Retrocausality would provide a unique interpretation of the collapse of the wave function that has been frequently quoted as referring to the results of measurement. The sudden collapse may be equated with the sudden elimination of the inconsistent quantum interferences that is consequential to the act of measurement of an internal origin.
A similar measurement of internal origin may also apply to the transformation reaction A←B. The material process of measurement proceeding between any pair of two parties is unique in processing the intervening quantum particles of whatever kind in an indivisible and discrete manner.
What is specific to the measurement dynamics mediated by quantum particles is the mutual exclusivity of an internal origin. If the measurement B→C is in place, there would be no actual likelihood of another measurement A←B to take place at the same moment when both A and C would be supposed to share the same quantum particles found in B. Even if the quantum-mechanical linear superposition of both reactions of A←B and B→C is conceivable in quantum theory alone, these two may remain mutually exclusive in the actual measurement. The indivisible quantum particles latent in B cannot be shared by both the products A and C at the same time.
Then, a subtle conflict may arise between the mutual inclusivity latent in the linear superposition of different reactions of a quantum theoretical origin and the mutual exclusivity stemming from the indivisible discreteness of the quantum particles to be mediated in the actual measurement on the empirical ground. One possible measure for mitigating the present conflict between the quantum theory and the actual measurement on the empirical ground may be to make an appeal to the occurrence of retrocausality available to quantum phenomena.
For instance, suppose that a linear superposition of both reactions A←B and B→C can initially be allowed to get started even only ephemerally. Then, the reaction that is immediately going to be nullified as facing the actual measurement could be the one that may fail in the acquisition of the quantum particles mediating the process of measurement. The failing reaction branch may effectively be going to proceed backwards to the original birthplace of the superposition in a retrocausal manner and then be nullified in the end. To be sure, quantum mechanics in theory guarantees the dynamical law satisfying the time-reversal symmetry.
Retrocausality in quantum phenomena is thus resource-sensitive. That is to say that the surviving reaction branch is the one that must be fastest in the resource intake among the possible contenders, while these contenders are mutually exclusive in their likelihood of actual occurrence. The mutual exclusivity stems from the fact that the resource takes the form of the indivisible quantum particles which mediate the process of measurement of material origin. There is no leftover of the quantum resources for measurement toward the latecomers because of the indivisible discreteness of the intervening quantum particles constituting the resources required for the act of measurement. There is no likelihood for sharing the indivisible resources among the competing contenders. The rule applied here is the principle of first come, first served. The winner eventually takes all. The measurement dynamics taking the retrocausal operation into account in an implicit manner is already selectively synthetic.
Needless to say, retrocausality of a quantum-mechanical origin may methodologically be dismissed quite easily in the standard practice of thermodynamics in thermal equilibrium. The measurement dynamics grounded in retrocausality can easily be dismissed once the idea of a statistical ensemble of systems upholding an equilibrium thermodynamics is taken for granted. The ensemble cannot hold the quantum coherence that is prerequisite to the operation of retrocausality with which each quantum system is at home. Claiming for a statistical ensemble of systems on a theoretical ground alone does not serve as a substitute for the actual measurement for identifying the nature of each system belonging to the ensemble. The quantum states referred to in the ensemble dynamics are the mixed ones that can coexist simply by declaration as carrying no coherence among themselves. Those mixed states that may not be coexistent are inconceivable as a matter of principle exclusively on methodological grounds. In contrast, the pure states that cannot coexist in measurement are required to substantiate their non-coexistence by nullifying the intervening quantum coherence to be formed between them in the light of retrocausality.
The ensemble dynamics does not equip itself with the selectively synthetic capacity which the measurement dynamics, with use of the retrocausality applied to a single quantum system, intrinsically takes for granted.
Further implications of retrocausality of a quantum origin would be more sharply pronounced if the issue of the emergence of a reaction cycle in chemical evolution is addressed.
3. Reaction Cycle
The onset of a reaction cycle must have been a major stepping stone in chemical evolution, while there must still have been a long way to go to reach the actual origins of life, even if we start from there. Imagine, for instance, a cycle of transformation reactions in terms of reactants A, B,…,Y, Z in the form of A→B→C···→Y→Z→A as constantly taking in the necessary resources from the neighborhood environment and letting the resulting disposals leave there. What is unique to the operation of the reaction cycle is that the production of any reactant in the cycle is causative in the forward direction of time. At the same time, the causative operation of the reaction cycle would remain robust enough as being subject to frequent retrocausative interventions of a quantum origin for actualizing each reaction step constituting the cycle.
The reaction cycle in the form of a closed chain of sequential transformation reactions holds itself with the use of chemical affinities. The contrast between the potential and the actual is already implicit in the measurement dynamics of a quantum origin. The quantum state before its actual measurement is not decisive yet on the actual determination of its basis set, and the basis set of the states to be determined remains in the potential. The potential has turned out to be the actual only after the act of measurement. Again, the actual constantly serves as the source of the updated potential to follow, since it will remain open to how it is going to be measured subsequently.
When the transformation reaction A→B is focused upon in the absence of the reactant B initially, the agency of pulling in the reactant B on the scene must be the reaction environment itself housing the initial reactant A. The emergence of reactant B in the reaction downstream is the environmental way of measuring the reactant A to be located in the immediate upstream. Accordingly, a similar line of argument would also apply to the emergence of C as the environmental way of measuring B internally, and so on.
One example of experimental evidence supporting the occurrence of a closed chain of transformation reactions that defies to be anchored at thermodynamics in thermal equilibrium is the possibility of a reaction cycle running in a simulated hydrothermal environment. In particular, the hydrothermal environment is unique in constantly mixing hot water with cold water in a geologically coordinated manner. A case in point is to see the experimental likelihood of the abiotic operation of the oxidative citric acid cycle in the absence of both biological enzymes and co-enzymes in a simulated hydrothermal environment [13]. As a matter of fact, the citric acid cycle is ubiquitous in full-blown biology [14].
The oxidative citric acid cycle consists of a closed chain of sequential transformation reactions of carboxylic acid molecules running circularly in the order of oxaloacetate→citrate→isocitrate→α-ketoglutarate→succinate→fumarate→malate→oxaloacetate. In order to examine whether the reaction environment could actually exhibit a chemical affinity for inducing the downstream reactant from the immediate upstream reactant via its own internal measurement, we prepared the flow reactor, simulating the hydrothermal circulation of seawater [15]. The reaction fluid running through the reactor in a closed manner included only the three different kinds of carboxylic acid molecules of α-ketoglutarate, succinate and fumarate with its concentration of 20 mM for each initially.
The intent of this experiment was to see whether malate or oxaloacetate, to be located in the downstream below the three different kinds of reactants including α-ketoglutarate, succinate and fumarate, could be synthesized in the presence of only the original three different kinds of reactants located in the upstream initially. The major protocol of the flow reactor operation was such that the time required for the reaction fluid to complete one cycle of the closed run was roughly 1 min; the residence time of the fluid in the high-temperature chamber maintained at 180 °C was limited only to 1.8 s within each cycle; and the temperature of the fluid staying outside the high-temperature chamber was maintained at 0 °C. The reaction fluid thus experienced the impulse of abrupt heating up to 180 °C only over a very short duration in each cycle, and sudden prolonged quenching down to 0 °C during the rest of each cycle, and this cycle was repeated indefinitely. Our results are summarized in Figure 1.
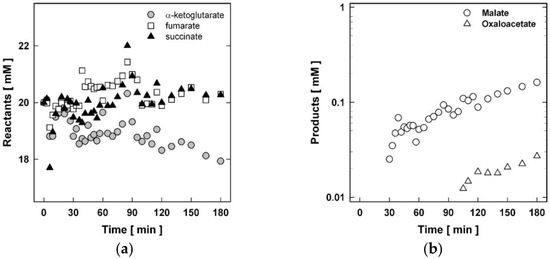
Figure 1.
Time courses of reactants including α-ketoglutarate, succinate and fumarate set at 20 mM for each initially (a) and products including malate and oxaloacetate synthesized from the reactants (b). The temperature of the high-temperature chamber, which could be a hot place for initiating various synthetic reactions, was raised from room temperature up to 180 °C over the first 30 min linearly and was maintained at that temperature since then. The pH of the reaction fluid measured at 0 °C was maintained at 1.85 ± 0.01 throughout the experiment. The observed data included ±1% experimental errors for repetitions in a single run of the experiment.
The buildup of the synthesis of malate was identified at about 30 min after the start of the flow reactor operation. The present buildup of malate was due to the environment-induced chemical affinity latent in the reaction fluid containing only the three different kinds of initial reactants including α-ketoglutarate, succinate and fumarate. No synthesis of isocitrate located in the immediate upstream ahead of α-ketoglutarate was identified in the present set up. The synthesis of malate thus happens to be the environmental way of measuring the reactant fumarate internally by the emerging malate molecule as inheriting most of the atomic scaffolding of a quantum origin from the fumarate molecule designated to be located in the immediate upstream.
Once malate was synthesized in the reaction fluid, the immediate environments for the succeeding synthetic reaction came to include malate also, in addition to the three different kinds of reactants prepared initially. The environment-induced chemical affinities could thus be updated accordingly. Its consequence was identified with the new synthesis of oxaloacetate at about 110 min after the start of the reactor operation, in which oxaloacetate was located in the immediate downstream when viewed from the malate. On the other hand, however, the buildup of the synthesis of malate and, accordingly, oxaloacetate also was not identified when the initial reactants included only succinate and fumarate, although both are located in the reaction upstream when viewed from malate. The experiments revealed that the synthesis of malate may require the reaction fluid of the three different kinds of upstream reactants including α-ketoglutarate, succinate and fumarate at least initially.
Needless to say, the observed synthesis of both malate and oxaloacetate from the initial reactants including α-ketoglutarate, succinate and fumarate may be required to face and overcome a severe criticism raised against it. That is about seeking a countermeasure against arguing for the seemingly thermodynamic unlikelihood of such a synthesis in the first place. The synthesis of oxaloacetate from malate is endergonic with the difference of the Gibbs free energy by the amount of roughly ∆G ≈ 30 kJ/mol. This may imply that the population ratio of oxaloacetate to malate to be estimated thermodynamically at 0 °C, which is simply equated with the dimensionless equilibrium constant in chemical kinetics, could significantly decrease roughly to the order of the Boltzmann factor exp(−∆G/κBT) ≈ 1.82 × 10−6 with T = 273 K, in which κB is the Boltzmann constant. Furthermore, even at an elevated temperature as high as 180 °C near the hot spot inside the flow reactor, the Boltzmann factor exp(−∆G/κBT) ≈ 3.47 × 10−4 with T = 453 K would still remain far less than the actual population ratio of oxaloacetate to malate that was measured to be roughly of the order of 0.1 at about 110 min after the start of the flow reactor operation (see Figure 1b).
What has been going on in the flow reactor is not something comprehensible within the framework of the succession of standard thermodynamics in thermal equilibrium conditioned by each variable temperature. The population ratio of oxaloacetate to malate may not exceed 3.47 × 10−4 if our experiment is going to be grasped within the framework of the moving equilibrium thermodynamics to be specified at variable temperatures between 0 °C and 180 °C.
Nonetheless, the observed enhancement of the population ratio of oxaloacetate to malate is factual and must certainly be comprehensible physically. The synthesis of malate and oxaloacetate in sequence is selective in availing itself of the necessary quantum resources exclusively as avoiding making a mixture with others concurrently. One measure for vindicating the present physical observation is to pay attention to the shortness of the residence time over which the portion of the reaction fluid visits the hot spot in each run of the cycle. The shortness of the residence time at the hot spot would guarantee the preservation of the products synthesized at that spot when they are rapidly transferred to the cold surrounding environment. Both the short visit to the hot spot and the rapid quenching of the synthesized products for a relatively prolonged period in the cold surrounding locale could prevent the decomposition of the products, which may also be expected at the higher temperature site if they are allowed to stay there for long. In fact, the observed population ratio of oxaloacetate to malate lowered down toward 3.47 × 10−4 as theoretically expected in thermodynamics at 180 °C when the residence time at the hot spot was made longer than 5 s within each cycle lasting over roughly 1 min (data not presented).
Repeating the cycle of the short visit to the hot spot and the longer stay in the cold environment can thus enhance the synthetic capacity latent in the reaction fluid as revealed in the experiments simulating the hydrothermal circulation of seawater in the vicinity of a hot vent on the ocean floor.
4. Discussion
When a chain of sequential transformation reactions happens to be closed and to eventually be made circular, the resulting reaction cycle comes to incorporate into itself a specific atomic scaffolding of a selective nature that could guarantee the causal operation of the underlying chemical reactions even in the face of frequent retrocausal interventions of a quantum origin. What is responsible for implementing the physical outfit upon the robust atomic scaffolding for running a reaction cycle in a concrete manner is the act of measurement imputable to the environment itself. In any case, the environment is already implicit in the act of measurement with regard to relating any one of its components to any other through the transference of the quantum particles while acting upon the mutable boundary conditions applied to the immutable physical laws of motion.
In addition, once a reaction cycle is formed in a durable manner, the cycle can internalize some of the measurement capacity of the environmental origin into itself while keeping the atomic scaffolding of the cycle intact. The residual measurement capacity imparted to the reaction cycle is the one required for identifying the necessary resources for keeping the cycle itself durable physically. The material substrate for upholding the robust atomic scaffolding now turns out to be the internal observer feeding upon the necessary resources.
The durability of a reaction cycle is thus seen in the integrated activity of both the constant intake of the necessary resources from the outside and the constant release of the disposals to the outside. The current release of the disposals sets the condition for the subsequent intake of the resources. Equivalently, the current intake of the resources sets the condition for the subsequent release of the disposals. This observation then comes to imply that the concurrent measurement of the two distinguishable conditions by the one and same internal observer would yield the equivalence of the two conditions in their implication, in which the equivalence is to be guaranteed by the empirical durability of the reaction cycle of interest.
The internal observer taking the act of identifying the condition for making its own occurrence actual as being synonymous with the very deed of its actual implementation can make itself durable thanks to Bayes’ theorem. The durability of a reaction cycle resides in the interplay between the datum d for the actual occurrence of the cycle and the hypothesis h for the condition for the occurrence of such a cycle. When the external observer refers to the likelihood or the prior probability p(d|h) of the event of expecting d upon h envisioned by the reaction cycle as the internal observer, the posterior probability of the hypothesis h, given the observed datum d, is embodied in Bayes’ theorem p(h/d) = p(d|h)p(h)/p(d). What is specific to Bayes’ theorem is its capacity of relating the prior expectation by the internalist to the posterior observation by the externalist. The internalist here is regarded as being an internal Bayesian subject by the externalist.
The joint probability p(d∩h), referring to the conjunction of d and h enacted by the internal observer, would then come to reduce to p(d) (=p(d∩h)) in the eyes of the internal observer to whom h remains inseparable from d, for the chemical affinities exhibited by the focused reaction cycle would be nothing other than the hypotheses entertained by the cycle as the internal observer. The conjunction of the datum and the hypothesis implies that the datum is realized as carrying the hypothesis that is prerequisite to the succeeding datum production to come. The data remain inseparable from the hypotheses toward the Bayesian internalist grounded legitimately in the material basis, while both may seem separable toward the externalist grounded strictly in the methodological basis, enforcing such a separation simply as a matter of imposed stipulation.
As referring to the conditional probabilities such as p(h/d)(=p(d∩h)/p(d)) and p(d/h)(=p(d∩h)/p(h)), can one readily obtain p(h/d) = 1 and p(d/h) = 1, the latter of which is derived from p(d/h) = p(d)/p(h) ≤ 1 with the use of p(h) ≤ p(d) thanks to p(h/d) = 1. The equalities p(h/d) = 1 and p(d/h) = 1 now guarantee the duration of the repeated cycle of the products (data) preparing the condition for the production to come with probability unity and the production (hypotheses) preparing the products also with probability unity. No matter how small the prior probability p(h)(=p(d)) may be, the product having the capacity of identifying the condition for the similar production to come, once it happens to appear, could repeatedly be updated in a durable manner with probability unity since then. On the other hand, however, if the two conditions for resource intake and for disposal release are taken to be completely independent of each other, it would be required to go back to the stage before the emergence of a robust atomic scaffolding supporting a durable reaction cycle.
Retrocausality in quantum phenomena is pivotal in forming a closed loop of causations ab initio thanks to the built-in scheme of constantly letting the succeeding effect update the preceding cause. Such an update scheme of a selective nature calling for the task of pruning off the incompatible quantum interferences internally in retrospect, in the light of a measurement in the quantum regime, is not available to the classical regime. The likelihood of a causal loop is found within the capacity of adjusting the past to the present, instead of adjusting the present to the irrevocable past. Otherwise, the loop would lose its robustness once it happens to suffer disturbing influences from the outside. In fact, there has been an experimental confirmation on the establishment of a consistency between causality and retrocausality with the use of an artefactual quantum circuit of circulating photons [16]. The focused consistency was revealed in the precipitation of pure quantum states, rather than mixed states, when the photons in the output from the circuit were measured.
Adjusting the past to the present is simply no more than just regulating the past so as to meet the present.
The inconsistent causal loop such as the one that we encounter as facing the grandfather paradox in the theory of general relativity is foreign to the quantum scheme. In the latter, any incongruence between causality and retrocausality is going to be ameliorated in the succeeding causal operation to come while such an incongruence constantly happens to pop up because of the persistent genesis of the quantum interferences following the act of measurement. At the same time, the inconsistent quantum interferences are constantly eliminated through the retrocausal operation that is not measurable. Quantum mechanics differs from classical mechanics in admitting the non-measurable retrocausal operation in time when the direction of time is reversed. In contrast, the classical counterpart may easily become defunct once the measurable inconsistencies happen to intervene, as revealed in the grandfather paradox. The non-measurable retrocausal operation being capable of ameliorating such inconsistencies is simply inconceivable in the classical regime.
One might be annoyed by the criticism as saying, “There is complete time-symmetry in classical physics, and yet no apparent retrocausality. Why should QM be any different?” Price quoted this criticism in [3]. In fact, the difference is substantial. While there is no distinction between the state function in theory and its measurement in classical mechanics, quantum mechanics does distinguish the state function or the wave function from its measurable substitute. Retrocausality is apparently a must for quantum mechanics in order to establish the consistency between the two realms, at least in retrospect. In classical mechanics, on the other hand, there is no inconsistency to start with between the state function and its measurement, and thus no need for asking for help from retrocausality. Classical physics can remain indifferent to retrocausality.
Biological phenomena full of causal loops have the built-in scheme of maneuvering the retrocausality internally so as to precipitate the consistent loops being accessible externally only in the effect in retrospect. Retrocausality carrying a regulative capacity of looking backwards in time could have been instrumental for starting up biology on empirical grounds, while it is not controllable externally because of its sole reliance on the agency internal to a quantum. The likelihood of causal loops could be saved only when the regulation of the past in the present is allowed without being accompanied by any measurement mediated by quantum particles during the retrocausal operation. What is significant to retrocausality is found in its role of persistently preventing the inconsistent quantum interferences from being measured and identified as such externally while the occurrence of such interference to be eliminated is inevitable in any case in the quantum world.
Conversely, no retrocausality would be likely in the classical world since every cause allowed there is taken to be controllable and measurable externally, and to remain irrevocable once identified. The popping up of inconsistent interferences from within is inconceivable in the classical world. There is no need for looking backwards in time in the classical world. The likelihood of a robust causal loop could be guaranteed only when both the forward and the backward propagation of influences can meet together and have a chance of negotiating between the two so as to prevent any frozen inconsistencies from being left behind in the record.
The quantum world is unique in precipitating consistent causal loops that could remain robust against those ephemeral inconsistencies allowed to intervene only in the retrocausal operation. No causal loop is in the classical world. Accordingly, no life is in the classical world. In essence, retrocausality of a quantum origin owes its occurrence to the preservation of the indivisible discreteness of each quantum involved in measurement on its own.
5. Concluding Remarks
Even long before Darwinian selection got started, chemical evolution could already have been selectively synthetic enough in and of itself with the use of retrocausality going along with the time-reversal symmetry of a quantum-mechanical origin. Non-measurable retrocausality available to quantum mechanics could be a prerequisite to the likelihood of measurable causal loops that are ubiquitous in biology. Quantum phenomena are of themselves selective, once measurement of an internal origin intervenes, in trimming off the incompatible quantum interferences from within, even in the absence of replicating molecules. Furthermore, chemical reactions as an instance of the transference of the intervening quantum particles are a representative example of the measurement of an internal origin par excellence.
One empirical requirement for making the selectively synthetic chemical reactions of a quantum origin likely in the prebiotic phase must have been the geological conditions of letting the reaction solutions constantly experience a sharp temperature gradient repeatedly. One promising candidate for facilitating the short visit to the hot and the longer stay in the cold in a repeated manner may be found in the natural scheme of the hydrothermal circulation of seawater near hot vents on the ocean floor. Thus, quantum mechanics in and of itself has potential in raising a reaction cycle in the prebiotic phase of chemical evolution, even without any help of artefactual scaffoldings of an external origin.
Acknowledgments
Thanks are due to Atsushi Nemoto for the help for conducting the experiments reported in this article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Wheeler, J.A.; Feynman, R.P. Interaction with the absorber as the mechanism of radiation. Rev. Mod. Phys. 1945, 17, 157–161. [Google Scholar] [CrossRef]
- Black, M. Why cannot an effect precede its cause. Analysis 1956, 16, 49–58. [Google Scholar] [CrossRef]
- Price, H. Does time-symmetry imply retrocausality? How the quantum world says “Maybe”? Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2012, 43, 75–83. [Google Scholar] [CrossRef]
- Mahler, D.H.; Rozema, L.; Fisher, K.; Vermeyden, L.; Resch, K.J.; Wiseman, H.M.; Steinberg, A. Experimental nonlocal and surreal Bohmian trajectories. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef] [PubMed]
- Pegg, D.T. Retrocausality and quantum mechanics. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2008, 39, 830–840. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bergmann, P.G.; Lebowitz, J.L. Time symmetry in the quantum process of measurement. Phys. Rev. 1964, 134. [Google Scholar] [CrossRef]
- Cramer, J.G. The transactional interpretation of quantum mechanics. Rev. Mod. Phys. 1986, 58, 647–687. [Google Scholar] [CrossRef]
- Smith, N.J.J. Bananas enough for time travel? Brit. J. Philos. Sci. 1997, 48, 363–389. [Google Scholar] [CrossRef]
- Kastner, R.E. Cramer’s transactional interpretation and causal loop problems. Synthese 2006, 150, 1–14. [Google Scholar] [CrossRef]
- Aharonov, Y.; Cohen, E.; Gruss, E.; Landsberger, T. Measurement and collapse within the two-state-vector formalism. Quantum Stud. Math. Found. 2014, 1, 133–146. [Google Scholar] [CrossRef]
- Price, H.; Wharton, K. Disentangling the quantum world. Entropy 2015, 17, 7752–7767. [Google Scholar] [CrossRef]
- Matsuno, K. Protobiology: Physical Basis of Biology; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Matsuno, K. Chemical evolution as a concrete scheme for naturalizing the relative-state of quantum mechanics. BioSystems 2012, 109, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, B.B.; Gruissem, W.; Jones, R.L. Biochemistry & Molecular Biology of Plants, 1st ed.; American Society of Plant Physiologists: Rockville, MD, USA, 2000. [Google Scholar]
- Imai, E.; Honda, H.; Hatori, K.; Brack, A.; Matsuno, K. Elongation of oligopeptides in a simulated submarine hydrothermal system. Science 1999, 283, 831–833. [Google Scholar] [CrossRef] [PubMed]
- Ringbauer, M.; Broome, M.A.; Myers, C.R.; White, A.G.; Ralph, T.C. Experimental simulation of closed timelike curves. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).