Symmetries, Information and Monster Groups before and after the Big Bang

Abstract

The Monster group, the biggest of the sporadic groups, is equipped with the highest known number of dimensions and symmetries. Taking into account variants of the Borsuk–Ulam theorem and a novel topological approach cast in a physical fashion that has the potential to be operationalized, the universe can be conceived as a lower-dimensional manifold encompassed in the Monster group. Our universe might arise from spontaneous dimension decrease and symmetry breaking that occur inside the very structure of the Monster Module. We elucidate how the energetic loss caused by projection from higher to lower dimensions and by the Monster group’s non-abelian features is correlated with the present-day asymmetry in the thermodynamic arrow. By linking the Monster Module to its theoretical physical counterparts, it is then possible to calculate its enthalpy and Lie group trajectories. Our approach also reveals how a symmetry break might lead to a universe based on multi-dimensional string theories and CFT/AdS (anti-de Sitter/conformal field theory) correspondence.

The Mode is an enclosed, detectable manifestation of the Substance… The Substance is equipped with infinite attributes

(Spinoza, Ethica, pars I)

1. Introduction

The Fischer–Griess Monster group, the largest among the twenty-six sporadic groups, is equipped with 196,883 dimensions and an order of about 10⁵⁴ elements [1]. It is noteworthy that the Monster Module displays the highest known number of symmetries [2]. It has been recently proposed that the symmetries, widespread invariances occurring at every level of organization in our universe, may be regarded as the most general feature of physical systems, perhaps also more general than thermodynamic constraints [3,4]. Therefore, giving insights into the Monster symmetries would provide a very general approach to systems function, universe evolution and energetic dynamics. Here we show how a novel symmetry-based, topological approach sheds new light on the Monster’s features. We provide a foundation for the Monster’s physical counterparts, cast in a fashion that has the potential to be operationalized, which can be used for the assessment of our universe’s evolution and, in particular, pre-Big Bang scenarios.

This paper comprises six sections, including the introduction. In the second section, we describe a generalized version of the Borsuk–Ulam theorem, in order to provide the topological machinery for further evaluations of the Monster in the context of theoretical physics. The third section assesses the relationships between the Monster and the modular j-function. Section four explains how the universe might originate from the Monster Module, due to a dimension loss, linking the Monster group to theoretical physics counterparts. Furthermore, taking into account energetic arguments dictated by topological dimensions decrease, the section explains why and how our universe is equipped with the symmetry breaks, which give rise to the thermodynamic arrow. Section five elucidates various physical features of the Monster. In the final sixth section, we raise a number of still open questions.

2. Topological Tools

2.1. The Standard Version of the Borsuk–Ulam Theorem (BUT)

The Borsuk–Ulam Theorem [5] is given in the following form by [6].

Borsuk–Ulam Theorem.

Let $f:S^n\to R^n$ be a continuous map. Then there exists $x\in S^n\subseteq R^{n+1}$ such that $f(x)=f(-x).$

Proof. 

A beautiful and concise proof of this theorem is given by [7], and not repeated here. □

This means that antipodal points on n-sphere $S^n$ map to $R^n$, which is the n-dimensional Euclidean space [8,9]. Points on an n-sphere $S^n$ are antipodal, provided the points are diametrically opposite [10]. The original formulation of BUT displays versatile ingredients that can be modified, resulting in BUT with different guises: proximally continuous mappings and antipodal (or non-antipodal) points with matching description and bijection mappings from a higher to a lower dimension.

In the sequel, the notion antipodal point is extended antipodal regions. A region on the surface of an n-sphere $S^n$ is a part (subset) of $S^n$. A surface region $\neg x$ is the antipode of x, provided $x\ne \neg x$ and x has the same feature values (characteristics) as $\neg x$. For more about this, see [11]. From a physics perspective, a region is a relativistic mass in a slice of space swept out a moving particle. The particles on a physical n-sphere are moving at the same velocity. For every physical region with mass $x\in S^n$, we can always find $\neg x$ (the analog of the antipode –x of a point on the surface of $S^n$) with the same characteristics (velocity and mass). In effect, for the relativistic energy $e_x=m_x{c}^2$, we can find its antipodal energy $e_{\neg x}$ for $\neg x\in S^n$. To be an antipodal energy $e_{\neg x}$, we weaken the original notion to antipodes, with $\neg x$ being a particle on $S^n$ that has characteristics that match those of $x\in S^n$. This leads to an energetic form of BUT (energy-BUT) for antipodal particles$x,\neg x\in S^n$:

Energy-Borsuk–Ulam Theorem.

Let $f:S^n\to R^n$ be a continuous map. Then there exists $x\in S^n\subseteq R^{n+1}$ such that $f(x)=f(\neg x)$ and $e_x=e_{\neg x}$.

Proof. 

$f(x)=f(\neg x)$ a feature vector in $R^{n+1}$. Since, for each $x\in S^n$ there is $\neg x\in S^n$ with the same velocity and mass, the result follows, i.e., $f(x)=f(\neg x)$ and $e_x=e_{\neg x}.$ □

2.2. BUT Variants

We resume with some BUT variants described by Peters [12] and Tozzi and Peters [3]. The concept of antipodal points can be generalized to countless types of signals. Two opposite points encompass not just the description of simple topological points, but also of spatial and temporal patterns, vectors and tensors, functions, signals, thermodynamic parameters, trajectories, symmetries [3]. The two antipodal points standing for different systems features are assessed at one level of observation, while the single point is assessed at a lower level. The antipodal points restriction from the classical BUT is no longer needed, because the applications on an n-sphere can be generalized not just for the evaluation of diametrically opposite points, but also of non-antipodal ones. We are allowed to take into account homotopic regions on an n-sphere that are either adjacent or far apart. This means that the points (or regions) [13] with the same feature value do not need necessarily to be antipodal, in order to be described together [12]. The original formulation of BUT describes the presence of antipodal points on spatial manifolds in every dimension, provided the n-sphere is a convex, positive-curvature structure. However, many physical functions occur on manifolds endowed with other types of geometry: for example, the hyperbolic one [14,15]. Whether the manifold displays a concave, convex or flat activity, this does not have an impact: we may always find the points with matching description predicted by BUT. Although BUT has been originally described just in case of n being a natural number that expresses a spatial dimension, its value in Sⁿ can also stand for other types of numbers. The n value can be also cast as an integer, a rational or an irrational number. This allows us to use the n parameter as a versatile tool for the description of systems symmetries [3]. A BUT variant tells us that we can find a pair of opposite points an n-dimensional sphere, that display the same encoding not just on a Rⁿ manifold, but also on an n−1 sphere. A symmetry break occurs when the symmetry is present at one level of observation, but hidden at another level [4]. This means that symmetries can be found when evaluating the system in a proper dimension, while they disappear (are hidden or broken) when the same system is embedded in just one dimension lower.

Here we introduce recently developed, unpublished BUT variants. The first is a BUT corollary, which states that a Sⁿ manifold does not map just to a Rⁿ⁻¹ Euclidean space, but straight to a Sⁿ⁻¹ manifold. In other words, the Euclidean space is not mentioned in this formulation. Indeed, in many applications, e.g., in fractal systems, we do not need a Euclidean manifold at all. A manifold, in this case Sⁿ, may exist in and on itself, by an internal point of view, and does not need to be embedded in any dimensional space [13]. Therefore, we do not need an Sⁿ manifold curving into a dimensional space Rⁿ: we may think that the manifold just does exist by itself. An important consequence of this BUT version is that a n-sphere may map on itself. The mapping of two antipodal points to a single point in a dimension lower can be a projection internal to the same n-sphere.

The second and foremost variant is the above mentioned termed energy-BUT.There exists a physical link between the abstract concept of BUT and the real energetic features of systems formed by two spheres Sⁿ and Sⁿ⁻¹. An n-sphere Sⁿ is equipped with two antipodal points, standing for symmetries according to BUT.BUT is enriched by considering an n-sphere $S^n$ as a manifold, which is a Hausdorff space with a countable basis where each point has a neighbourhood that is homeomophic to some Euclidean space. Briefly, a space is Hausdorff, provided distinct points belong to disjoint neighbourhoods (distinct points live in separate houses [16]). A mapping $f:X\to Y$ is homeomorphic, provided f on X is 1-1, onto Y and has a continuous inverse. For the sake of intuition, we illustrate the notion of homeomorphic neighbourhoods in terms of planar homeomorphic energistic neighbourhoods. Let $p,x\in S^n$, radius $r>0$ and $\Vert e_x-e_p\Vert =\sqrt{{e_x}^2+{e_p}^2}$ (norm of energies associated with the points x, p) for an open neighbourhood $N\left(p,r\right)$ defined by

$$N\left(p,r\right)=\left\{x\in R^2:\Vert e_x-e_p\Vert <r\right\}.$$

Then a homeomorphic mapping $f:N\left(p,r\right)\to R^2$ is defined by

$$f(x)=\frac{e_x}{{\displaystyle {\sum }_{i=1}^{\left|N\left(p,r\right)\right|}{e}_y}}, x,y\notin N\left(p,r\right).$$

For more about manifolds, see [12]. When these opposite points map to an n-dimensional Euclidean manifold where Sⁿ⁻¹ lies, a symmetry break/dimensionality reduction occurs, and a single point is achieved [11]. It is widely recognized that a decrease in symmetry goes together with a reduction in entropy and free-energy (in a closed system). This means that the single mapping function on Sⁿ⁻¹ displays energy parameters lower than the sum of the two corresponding antipodal functions on Sⁿ. Therefore, a decrease in dimensions gives rise to a decrease of energy and energy requirements. BUT no longer depends on thermodynamic parameters, but rather on topological features such as affine connections and homotopies. The energy-BUT concerns not just energy, but also information. Indeed, two antipodal points contain more information than their single projection in a lower dimension. Dropping down a dimension means each point in the lower dimensional space is simpler, because each point has one less coordinate. In sum, energy-BUT provides a way to evaluate the decrease of energy in topological, other than thermodynamic, terms.

Another novel variant of BUT is the region-based BUT. This is a straightforward extension of what is known as region-BUT (briefly, reBUT).

Region-Based Borsuk–Ulam Theorem (ReBUT).

Let $2^{S^n}$ be a collection of nonempty surface regions of $S^n$ and let there be a continuous map. Then there exists $x\in 2^{S^n}\subseteq R^{n+1}$ such that $f(x)=f(\neg x)$.

Proof. 

$f(x),f(\neg x)$ a feature vector in $R^{n+1}$. We can always find region $\neg x\in 2^{S^n}$ that is antipodal to $x\in 2^{S^n}$, i.e., $\neg x\cap x=\varnothing$ and $\neg x,x$, have matching descriptions in $R^{n+1}$, minimally, equal velocity and mass while moving along the path through space swept out by $S^n$ (called a world canal during the course of its history [17]). Hence,

$$f(x)=f(\neg x).\square$$

The usual continuous function required by reBUT (region-based BUT in [3]) is replaced by a proximally continuous function, which guarantees that, whenever a pair of strings (regions that are world lines) are close (near enough to have common elements), then we always know that their mappings will be also be close. A string is a region of space with non-zero width and either bounded or unbounded length. As a particle moves through space following a world line [18], interactions occur at the junctions of world lines. Let $\tau$ the proper time of a particle, measured by clock travelling with a particle and integration along the world line of the particle. The $actio{n}_{particle}$ of a freely moving particle is defined by

$$actio{n}_{particle}=-m{c}^2{\displaystyle \int d\tau }.$$

As time evolves, a particle leaves a trace of its movements along a surface, which are “remembered”. A string is then a remembered part of a hypersphere surface over which a particle travels. In terms of quantum theory, a string is a path defined by a moving particle. Put another way, a string is path-connected and its path is defined by a sequence of adjacent fat surface points. The points are fat because they are physical as opposed to abstract geometric points. In other words, a string A(briefly, strA) is a thin region of space that has describable features such as connectedness, length, open-ended or closed-ended, and shape. Strings $\text{str}A,\neg \text{str}A$ are antipodal, provided $\text{str}A$ and $\neg \text{str}A$ are disjoint and yet have the same description. Strings $\text{str}A,\neg \text{str}A$ are examples of antipodal sets [19]. The description of $\text{str}A$ (briefly, $\Phi \left(\text{str}A\right)$) is a feature vector in Rⁿ, where each component of $\Phi \left(\text{str}A\right)$ is a feature value of $\text{str}A$.

2.3. Quantum String Axioms

• Every string has an action.
• If $\text{str}A,\neg \text{str}A$ are antipodal, then $actio{n}_{strA}=actio{n}_{\neg strA}$.
• Separate strings with k features with the same description are antipodal.
• There is a set $\left\{\neg \text{str}A\right\}$ of antipodal strings for every string $\text{str}A$.

Let X be a topological space equipped with descriptive proximity${\delta }_{\Phi }$. $\text{str}A {\delta }_{\Phi } \neg \text{str}A$ reads $\text{str}A$, and $\neg \text{str}A$ have the same description. Let $2^{S^n}$ denote the family of sets on the surface of a hypersphere $S^n$ and $\text{str}A,\neg \text{str}A\in 2^{S^n}$ are antipodal strings on $S^n$. A function $f:2^{S^n}\to R^n$ is proximally continuous, provided $\text{str}A {\delta }_{\Phi } \neg \text{str}A$ implies $f\left(\text{str}A\right) {\delta }_{\Phi } f\left(\neg \text{str}A\right)$. With these observations about strings, we obtain the following results.

Lemma. [strBUT].

If $f:2^{S^n}\to R^n$ is proximally continuous, $f\left(\text{str}A\right)=f\left(\neg \text{str}A\right)$ for some $\text{str}A$ in $2^{S^n}$.

Proof. 

Case n = 1. Let each $\text{str}A$ have one feature, namely, action. Assume antipodal strings $\text{str}A,\neg \text{str}A$ with n features are descriptively close, i.e., $\text{str}A {\delta }_{\Phi } \neg \text{str}A$. Since f is proximally continuous, we have $f\left(\text{str}A\right) {\delta }_{\Phi } f\left(\neg \text{str}A\right)$. From Axiom 2, $actio{n}_{strA}=actio{n}_{\neg strA}$. Hence, from the definition of the descriptive proximity ${\delta }_{\Phi }$, $f\left(\text{str}A\right)=f\left(\neg \text{str}A\right)$.

Case n> 1. The proof is symmetric with case n = 1 and Axiom 3. □

Theorem 1.

If $f:2^{S^n}\to R^k, k>0$ is proximally continuous, $actio{n}_{strA}=actio{n}_{\neg strA}$ for some $\text{str}A$ in $2^{S^n}$.

Proof. 

We consider only the case for k = 1, for strings whose only feature is action. The desired result is immediate from the strBUT Lemma and Axiom 2. This result is easily extended to the case where k > 1 for strings with k features. □

Theorem 2.

If $f:2^{S^n}\to 2^{R^k}, k>0$ is proximally continuous, $f(A)=f(\neg A)$ for each $\neg \text{str}A$ in the set of antipodes $\left\{\neg \text{str}A\right\}\in 2^{S^n}$.

Proof. 

Immediate from the Theorem 1. □

In order to map Sⁿ to Sⁿ⁻¹, we need to work with lower dimensional spaces containing regions where each point in Sⁿ⁻¹ has one less coordinate than a point in Sⁿ.

Let X be a topological space equipped with Lodato proximity [12]. $\text{str}A \delta \neg \text{str}A$ reads $\text{str}A$ and $\neg \text{str}A$ are close. Dochviri and Peters [20] introduce a natural approach in the evaluation of the nearness of sets in topological spaces. The objective is to classify levels of nearness of sets relative to each given set. The main result is a proximity measure of nearness for disjoint sets in an extremely disconnected topological space. Let $\text{int}(\text{str}A)$ be the set of points in the interior of $\text{str}A$. Another result is that if strings $\text{str}A,\neg \text{str}A$ are nonempty semi-open sets such that $\text{str}A \delta \neg \text{str}A$, then $\text{int}(\text{str}A) \delta \text{int}(\neg \text{str}A)$.

An important feature is that the manifolds M^d and M^d−1 are topological spaces equipped with a strong descriptive proximity relation. Recall that in a topological space M, every subset in M and M itself are open sets. A set E in M is open, provided all points sufficiently near E belong to E [21]. The description-based functions in BUT are strongly proximally continuous and their domain can be mathematical, physical or biological features of world line shapes. Let A, B be subsets in the family of sets in M (denoted by $2^M$) and let $f:2^M\to R^n,A\in 2^M,f(A)=$ a feature vector that describes A. That is, $f(A),f(B)$ are descriptions of A and B. Nonempty sets are strongly near, provided the sets of have elements in common. The function f is strongly proximally continuous, provided A strongly near B implies $f(A)$ is strongly near $f(B)$. This means that strongly near sets have nonempty intersection. From a BUT perspective, multiple sets of objects in M^d are mapped to $f\left(A\cap B\right)$, which is a description of those objects common to A and B. In other words, the functions in BUT are set-based embedded in a strong proximity space. In particular, each set is a set of contiguous points in a path traced by a moving particle. The path is called a world line. Pairs of world lines have squiggly, twisted shapes opposite each other on the surface of a manifold. Unlike the antipodes in a conventional hypersphere assumed by the BUT, the antipodes are now sets of world lines that are discrete and extremely disconnected. Sets are extremely disconnected, provided the closure of every set is an open set [20], is in the discrete space and the intersection of the closure of the intersection of every pair of antipodes is empty. The shapes of the antipodes are separated and belong to a computational geometry. That is, the shapes of the antipodal world lines approximate the shapes in conventional homotopy theory [22]. The focus here is on the descriptions (sets of features) of world line shapes. Mappings onsets with matching description, or, in other words, mappings on descriptively strongly proximal sets, here means that such mappings preserve the nearness of pairs of sets. The assumption made here is that antipodal sets live in a descriptive Lodato proximity (DLP) space. Therefore, antipodal sets satisfy the requirements for a DLP [12]. Let $\delta$ be a DLP and write $A \delta B$ to denote the descriptive nearness of antipodes A and B, and let f be a DLP continuous function. This means $A \delta B \text{implies} f(A) \delta f(B)=f(A)\cap f(B)\ne \varnothing$.

Example. 

Assume that antipodes A and B have symmetries (shape, bipolar, color, overlap, path-connectedness), and f is DLP strongly continuous function, then $A \delta B \Rightarrow f(A) \delta f(B)$.

This means that whenever A and B are descriptively close, then A is mapped to $f(A)$ and B is mapped to $f(B)$ and $f(A) \delta f(B)$. If we include in the description of A and B the location of the discrete points in A and B, then the DLP mapping is invertible. That is,$f(A)$ maps to A, $f(B)$ maps to B and $f(A) \delta f(B) \text{implies} A \delta B$.

Figure 1 provides an example of antipodal sets in case of a pair of closed regions, e.g., strings.

2.4. Generalized BUT (genBUT)

We conclude this section by introducing a generalized version of BUT, which encompasses all the previously described variants. This version allows the study of the Monster in the context of theoretical physics. Gen-BUT states that: Multiple sets of objects with matching descriptions in a d-dimensional manifold M^d are mapped to a single set of objects in M^d−1 and vice versa. The sets of objects, which can be mathematical, physical or biological features, do not need to be antipodal and their mappings need not to be continuous. The term matching description means the sets of objects display common feature values or symmetries. M stands for a manifold with any kind of curvature, either concave, convex or flat. M^d−1 may also be a part of M^d. The projection from S to R in not anymore required, just M is required. The notation d stands for a natural, or rational, or irrational number. This means that the need for spatial dimensions of the classical BUT is no longer required. The process is reversible, depending on energetic constraints. Note that a force, or a group, an operator, an energetic source, is required, in order to project from one dimension to another.

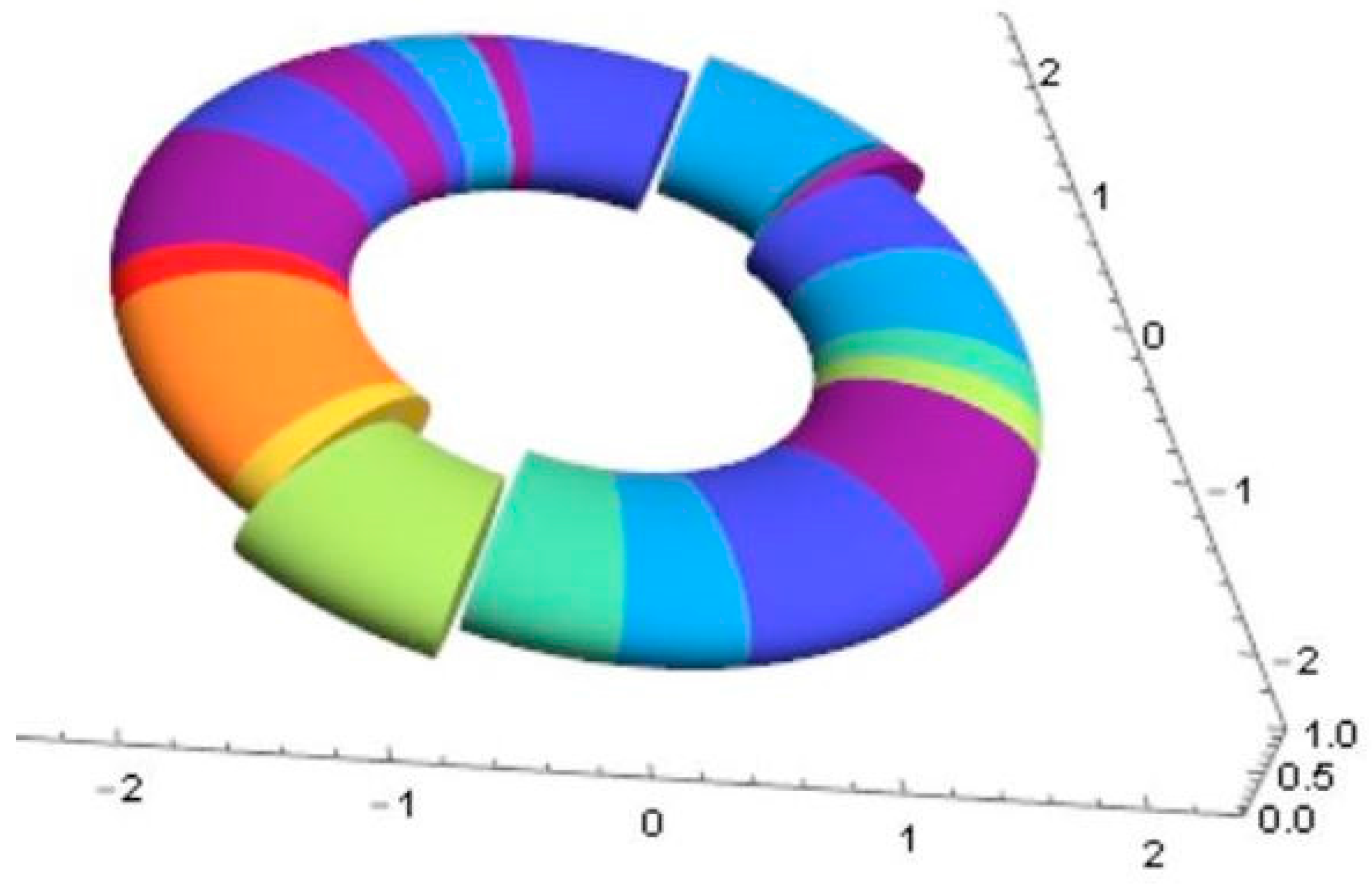
3. Embedding the Monster Group in M^d−1

The Monstrous Moonshine conjecture suggests a puzzling relationship between the Fourier coefficients of the normalized elliptic modular invariant, e.g., the hauptmodul J, the value of which value is 19,884, and the simple sums of dimensions of irreducible representation of the Monster Group M, which is 196,883 [23]. It would seem that a relationship between the symmetries in the plot (range) of the j-function and symmetries in the Monster group products occurs. These symmetries can be visualized as shown in Figure 2.

We might speculate that, in physical terms, the j-function could stand for an activity occurring in the Monster Module during the movements of the Lie Monster Group. In an infinite-dimensional space, the action of the j-function is correlated with the Monster vertex operator Virasoro algebra, e.g., the Monster Module [24].

A topological approach helps to elucidate such an unusual relationship. In the BUT framework, the j-function and the Monster Module are sets of objects with matching descriptions embedded in a M^d manifold, where d stands for their abstract dimension 196,884. Encompassing the two parameters in a M^d manifold allows us to provide a topological commensurability between the Monster Module and the j-function. When we reduce the dimensions to S^196,883, we achieve a single function, e.g., the Monster Lie group. It easy to see that if we map the two functions to a dimension lower, in this case M^196,883, we achieve a single function that retains the features of both. This single function stands for the Monster Group, which is the automorphic Lie group acting on the Monster Module (Figure 3, upper part). In topological terms, as always, two functions on a Sⁿ sphere lead to a single function on a Sⁿ⁻¹ sphere.

4. Of Monsters and Universes

4.1. Dimensions Reduction

We propose a BUT model that describes our universe as located inside the Monster Module. We argue, based on topological and energetic claims, that our universe might arise from a spontaneous loss of dimensions, e.g., an automorphism, occurring in the very structure of the supersymmetric, multidimensional Monster Module. If the Monster stood before the Big-Bang, we are in front of a manifold with the highest possible energy, because it displays the highest number of symmetries: indeed, according to energy-BUT, the more the symmetries, the more the energy. Therefore, every decrease in the symmetries of the original structure (the Monster) halves the energy of the subsequent, less symmetric level (occurring after the Big Bang). It is worthy of mention that the symmetries of the hypothetical M^d structure encompassing our universe do not need to be necessarily of the huge order of 10⁵⁴. Indeed, the Monster group includes several subgroups, classified into the sporadic groups (e.g., Mathieu groups, Leech lattice groups, and so on) [25]: this means that the universe might arise either from the Monster group, or one of its subgroups. In such a vein, one might think different possible physical scenarios:

(a)

The Monster group is progressively formed starting from its subgroups, with a gradual building from blocks.

(b)

The Monster group is the original structure giving rise to our universe.

(c)

The Monster group, the original structure, splits in its subgroups, then one of the subgroups gives rise to our universe.

Because the entropy is increasing in the universe, the first hypothesis is less reasonable: since our universe is moving towards lower free-energy levels, it would be better to start with a higher energetic manifold before the Big Bang, and not vice versa. At the Big Bang, a loss of dimensions and thermodynamic free-energy took place. Going from a higher dimension to a lower one, a sort of quantum jump occurred, in guise of an electron orbit where electrons jump towards more internal levels. Note that the BUT dictates provide a testable hypothesis: every jump towards a lower symmetrical state must halve the previous energetic level. Because a loss of dimensions comes together with a loss of symmetries, just the symmetries embedded in our low-dimensional universe’s dimensions are kept, while the others are apparently lost. The lost symmetries could in theory be restored by inverting the process from our universe’s lower dimensions to the Monster Module’s higher ones, but it would require a source of energy able to perform the inverse projection, and this is not the case of our cosmos.

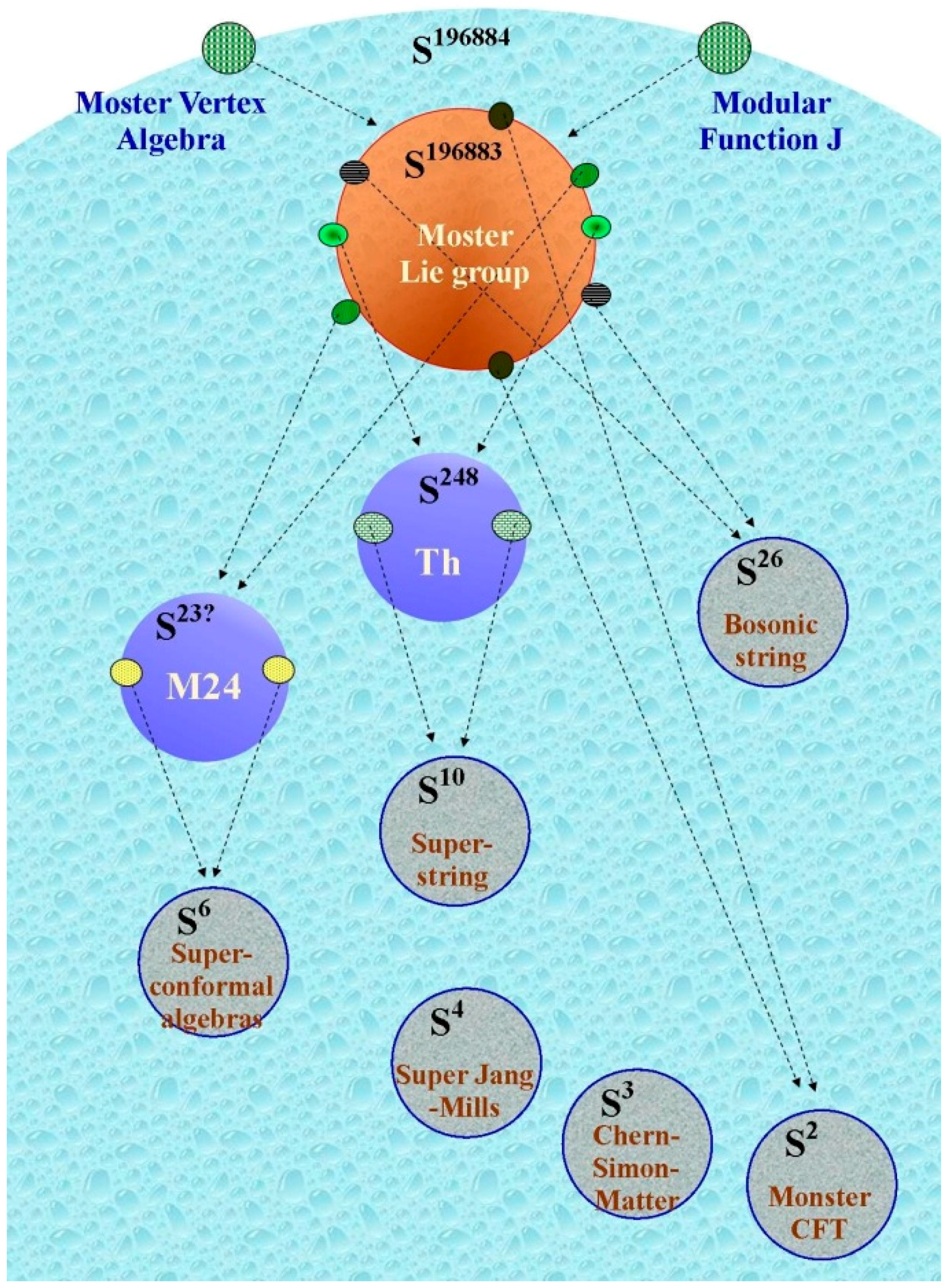
4.2. Topological Relationships between the Monster and String Theories

The Monster group has been already correlated with well-known scenarios in theoretical physics. Moonshine can be regarded as a collection of related examples where algebraic structures have been associated with automorphic functions or forms, because it is also displays relationships with the Lie group E⁸(C) and a lattice vertex operator algebra equipped with a rank 24 Leech lattice [23,26]. Several features of the Monster, either its Module, or its group and subgroups, have been associated with different physical theories. Some examples are depicted in Figure 3 (lower part). For example, links between Monstrous Moonshine and string theories have been proposed: the Monster might stand for the symmetry of a string theory for a Z²-orbifold of free bosons on a Leech lattice torus, in the context of a conformal field theory equipped with partition function j. Recent papers link other sporadic groups (e.g., Monster subgroups) with modular forms, suggesting a more central role for the Umbral Moonshine conjecture [27]. On the other hand, Witten proposed that pure gravity in AdS₃ (anti deSitter) space with maximally negative cosmological constant is AdS/CFT dual to a holomorphic CFT (conformal field theory), with the numbers of the Moonshine coming into play [28]. CFT/AdS is dual to string theories and is involved in many theoretical models: CFT, Chern-Simon-Matter, Super Jang–Mills, Superconformal algebras. The AdS/CFT correspondence means that conformal field theory is like a lower-dimensional hologram, which captures information about the higher-dimensional quantum gravity theory: this is one of the typical frameworks easily describable by a BUT topological apparatus.

4.3. The Problem of Singularity

A problem now arises: how to explain the event, commonly called singularity [29], which, according to our scenario, caused an apparent loss of dimensions in the Monster and gave rise to our universe? In order to answer to this crucial question, it must be taken into account that a particle trajectory on a hypersphere (or in general on every manifold), does not need to be closed: a particle not necessarily goes right through the whole surface, but could also travel just for a short path [30]. In such a vein, a hypothetical particle embedded into the Monster Module, which follows the movements dictated by the Monster Lie group, cannot travel everywhere on the Monster surface, due to the huge number of dimensions. In other words, ergodic pathways cannot be guaranteed when a particle travels on the Monster Module, due to the countless possible trajectories. When a particle travels into the huge Monster manifold’s phase space, it might simply take a random path towards just a few of the countless dimensions. We provide an example from the 26D bosonic string theory. This well-studied model, although partially dismissed, provides a good illustration in order to elucidate such issue. Furthermore, the 26D bosonic string theory takes place on the Leech lattice, e.g., a manifold that is almost ubiquitous in the description of sporadic groups. Bosons’ trajectories in a 24D Leech lattice may follow paths encompassing 196,884 dimensions. The random trajectories followed by moving particles encompass just some of the total Monster’s dimensions. When bosons’ paths fall into lower dimensions, bosons lose energy, according to the energy-BUT dictates. The sudden loss of energy might explain the Big Bang, that arises when the particle moves towards preferential paths in lower dimensions, e.g., when they move towards our universe. Therefore, the singularity might be simply explained by random particles’ movements occurring on small sub-parts of the Monster Module. The Big Bang might just have been occurred naturally, when a particle fell into a Monster’s dimension instead of another. This also means that the chosen paths in low dimensions (our universe) are equipped with just a few of the Monster symmetries. In our universe, the residual Monster symmetries are lost, or, better, hidden, because they become visible when evaluated from a higher dimension. The loss of the other primeval Monster dimensions gives rise to symmetry breaking and the thermodynamic arrow. In order to elucidate why a decrease in symmetries and dimensions leads to our universe equipped with symmetry breakings, it must be also taken into account that almost all the finite groups are non-abelian. This explains why the cosmic rules in our universe are dictated by asymmetric laws: indeed, the intrinsic non-abelian structure of the Monster itself ensures the non-reversibility of the particle patterns. In sum, once taken a path, due to both non-abelian and energetic arguments, it is not possible to reverse the process in our universe, unless other energy is supplied. Note that, because random paths might occur everywhere on the Monster Module, this means that countless universe are allowed, every one equipped with just some of the primeval Monster symmetries. The presence of an ergodic, homogeneous Monster Module before the Big Bang solves the so-called horizon problem too. A few Planck times after the Big Bang, the universe consisted of 10⁹⁰ Planckian size, disconnected regions [31]. Currently, those regions make up our observable universe and resemble one another. The presence of the homogeneous Monster Module before the Big Bang explains, together with the inflationary period, why all the initial disconnected regions displayed the same features.

4.4. The Monster and the Spacetime

The Monster is a manifold that, for the BUT variants, can be also described as a hypersphere. Therefore, our universe is internal to the Monster. The loss of dimensions occurs in the Monster, giving rise to the Big Bang. That is why the fossil background cosmic radiation comes from everywhere, when we look at it [32]. Another problem arises: how can a string-like manifold give rise and encompass the whole universe? A possible solution is that the Monster is not in the space, and the space is bent together with the universe. Concerning the time, the things are more complicated. Indeed, in touch with Veneziano’s pre Big Bang scenarios [31], the time could exist before the singularity, and not arise together with the universe’s spatial dimensions. Indeed, the Monster group needs to be embedded in the time, because it, acting as a Lie group, needs to perform symmetric movements, which may just occur in a given time. It might however be speculated that the time is not required at the Monster Module level, and the Wheeler–DeWitt equation might be valid at such level. This means that, while the Monster Module, embedded in a S^196,884 manifold, lies in infinite dimensions and is atemporal, the lower level, embedded in an S^196,883 manifold, requires the introduction of the parameter time.

5. Quantifying Physical Monster’s Parameters

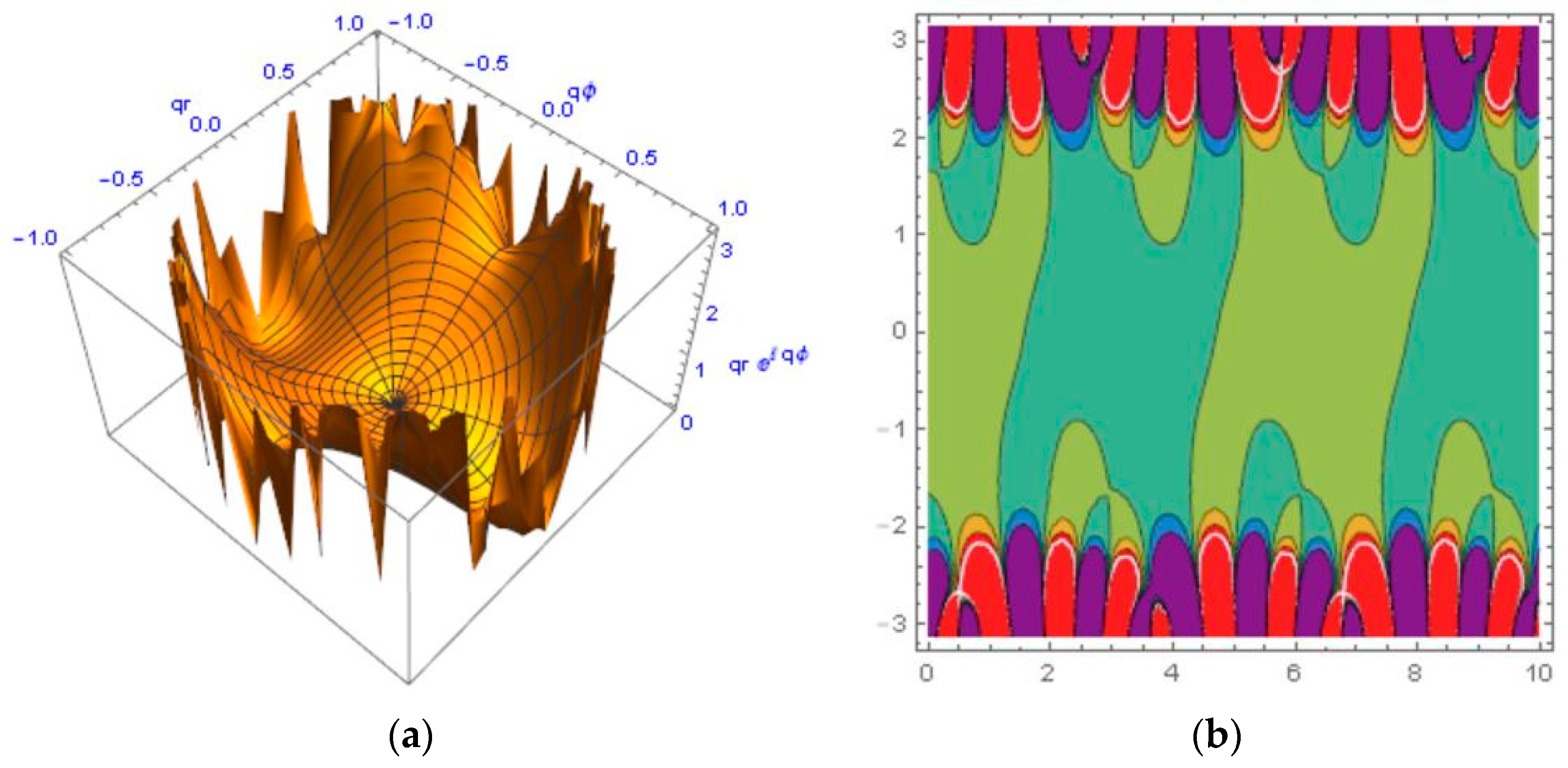
5.1. Towards the Monster’s Enthalpy

The energy-BUT can be used in order to calculate the energetic requirements of Monster Modules in a physical context. Thermodynamics says that:

H = F + T × E

where H is the Enthalpy, F the free-energy, T the temperature (trascurable) and E the entropy. We assume that our universe is closed. We will evaluate the possible values at the Big Bang (H₀, F₀, T₀, E₀) and at the present time (H₁, F₁, T₁, E₁). The current level E₁ of entropy in the universe is estimated in 2.6 ± 0.3 × 10¹²² K [33,34], while T₁ is neglectable. If the universe displays four dimension as currently believed, every dimension contains approximately an average entropy of: E₁/4.

As shown in [33], the current universe displays almost the highest possible values of entropy. Also in the future, the entropy will be just slightly larger than the current value E₁, because a monotonical increase already occurred. This means that E₁ is, more or less, the maximum value of entropy achievable in the whole life of the universe, and also means that the free-energy F₁ is currently very low. Therefore:

E₁ = H₁.

The current E₁ almost equals the total enthalpy H₁ of the universe. Vice versa, at the Big Bang, F₀ and T₀ were very high and E₀ close to zero. This means that, at the Big Bang:

F₀ = H₀ − T₀.

If the Monster occurred before the Big-Bang, we are in front of a manifold with the highest possible energy, because it displays the higher number of symmetries. If the Monster gave rise to our universe, and the Monster displays 196,883 dimensions, the Entropy of the Monster E_M is:

E_M = E₁/4 × 196,883.

Thus, the enthalpy of the Monster H_M stands roughly for the same value:

H_M = E₁/4 × 196,883

The loss of dimensions in the Monster Module, due to the non-abelian movements of the Monster Lie group and the energy-BUT, give rise to different universes with dimensions lower than the Monster, and equipped with less energy and information.

Through the Conway atlas of finite groups, we know the dimensions and the order of every group, including the sporadic ones. It is not difficult to calculate how many dimensions have been lost. We know this number, e.g., 196,883 less 4 (here 4 stands for the four space-time dimensions of our universe, we know how many symmetries are preserved, and we know, for energy-BUT, that every decrease of a single symmetric level denotes the loss of half of the energy. If the pre-Big Bang manifold, e.g., the Monster Module, is equipped with 196,884 dimensions and 10⁵⁴ elements, and if our universe has four dimensions, we have 10⁵⁰ elements in our universe.

Summarizing, once hypothesized a high-energy Monster Module before the rise of our universe, the next step is to reduce the symmetries from the Monster vertex operator to the Monster group, which is the Lie group acting on it. A further step gives rise to a dimensions and symmetries reduction until the emergence of our universe.

5.2. Information

The energy-BUT states that it is not possible to achieve higher information starting from a lower dimensional level. This means that we need to start from the Monster Module, and not vice versa. The process must be top-down, e.g., from the Monster to the universe, and not bottom-up. According to the energy-BUT, a loss of information occurs together with a decrease in dimensions. Therefore, from the Monster to our universe, it occurs a loss if information. You cannot move a particle in our universe from lower to higher dimensions, unless you, for energy-BUT, do not inject novel free-energy or enthalpy. You can just do it locally in the universe, for example when biological entities arise in limited niches, but not everywhere, because the total entropy increases together with a decrease in free-energy. Summarizing, from the highest to the lower levels there is a reduction, and not an emergence of information.

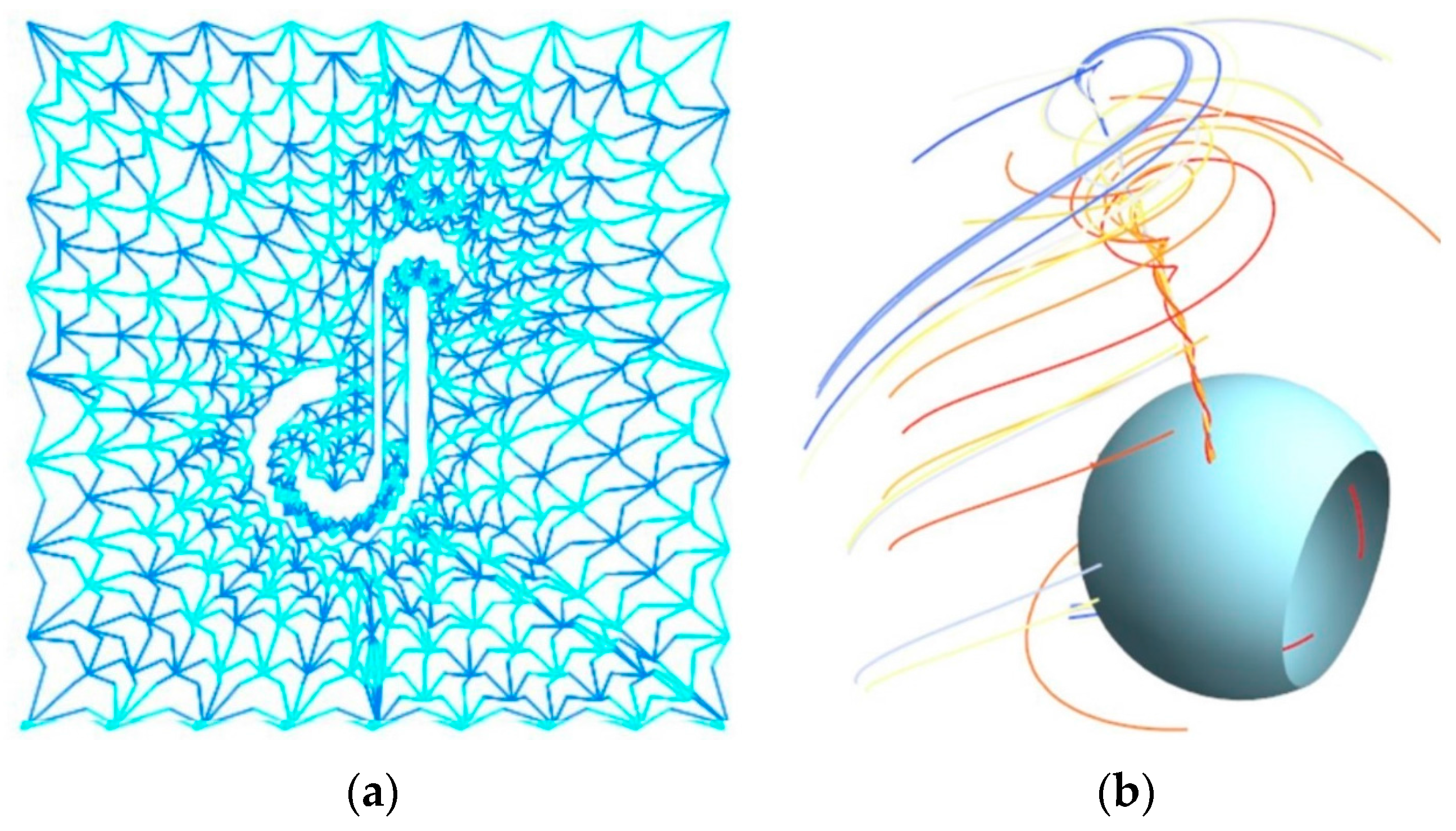
5.3. Watching the Monster: Vertex Algebra

In order to incorporate the j-function into a general context and to visualize the movements of the Monster Group on the Monster Module, we built a simplified 3D model equipped with a hypersphere and a vertex algebra operator. We achieved a low-dimensional model of j-function and its group, embedded into a vertex algebra’s manifold. Briefly, a vertex algebra provides a mathematical formulation of the chiral part of 2-dimensional conformal field theory. The axioms of a vertex algebra are obtained from the properties of quantum field theories and operator product expansions (OPEs). The main tactic flowing from OPEs is that a product of local operators defined at nearby locations can be expanded in a series of local operations [35]. A graphical representation of an OPE is represented in Figure 4A. Let ${\omega }_1,{\omega }_2$ be periods of a doubly periodic function with $\tau \equiv \frac{{\omega }_1}{{\omega }_2}$. Then Klein’s absolute invariant is defined by

$$J\left({\omega }_1,{\omega }_2\right)=\frac{g_2^3\left({\omega }_1,{\omega }_2\right)}{△\left({\omega }_1,{\omega }_2\right)},$$

where $g_2$ is the invariant of the Weierstrass elliptic function. If $H$ is the upper half plane and$\tau \in H, \text{then}$

$$J\left(\tau \right)\equiv J\left(1,\tau \right)=J\left({\omega }_1,{\omega }_2\right).$$

The function $J\left(\tau \right)$ is the j-function modulo a constant multiplicative factor [36,37]. A dynamical system with a strange attractor and invariant tori [38] initialized with the j-function is illustrated in Figure 4b.

6. Questions and Conclusions

Starting from a Spinozian global system, shaped in the guise of a multidimensional and multi-symmetric manifold equipped with a structural order of relationships, we were able to analyse, through a loss of dimensions dictated by the algebraic features of the Monster Module and its Lie group, the individual history of the universe. The universe can be thus conceived of as a manifold at lower dimensions encompassed in higher ones. The Monster Module is a manifold equipped with absolutely the highest dimensions—that is, a manifold consisting in the highest number of symmetries. The Monster Moonshine manifold is prior to its modifications. This may mean that the nature and the flow of events in the universe is a Monster’s self-projection towards less dimensions. The universe stands for a local symmetry, e.g., modifications of the Monster manifold. The Monster Module cannot exist in, and cannot be conceived through, a higher manifold other than itself. Every manifold in the universe exists either in itself or in some higher manifold else, e.g., the Monster Module. The knowledge of a lower dimension manifold in the universe depends on and involves the knowledge of higher dimensions mapping the lower manifold. In the meantime, the Monster Module, which n-dimensions are untouched, is still there. If different trajectories on the Monster Module give rise to different local losses of dimensions, this means that countless universes are possible, each one equipped with different or overlapping symmetries.

We would like to bring to an end with a few unsolved problems.

(a)

Where does the Monster take such a huge amount of enthalpy? It takes us in pre-, pre-Big Bang scenarios. This is the same problem with inflationist models, that do not explain where the energy of the required false vacuum comes from. A link between the Monster group and the false vacuum might be speculated.

(b)

What is the role of the j-function in the pre Big Bang period? Does it provide energy?

(c)

How does the Monstrous Moonshine look like? We could either imagine a timeless, immutable manifold where just the Monster Group movements take place, or as we did, a dynamical, time-dependent structure.

(d)

Does the curvature of the Monster Module change with the passage of time? This could be a very useful information, in order to elucidate the hypothesized step from an ancient anti DeSitter hyperbolic universe to the current, flat one.

(e)

Our universe might not arise directly from the Monster, but by one of its subgroups, e.g., the Th group (Figure 3), which is correlated with the successful superstring 10D theory. Is it possible to split the Leech lattice in which the Monster group is embedded, in order to achieve the lower dimensional E8 lattice where the Th group’s movements take place? It is central to remind that the step from an E8 lattice to the Leech lattice requires ×3 multiplication and peculiar rotations.

(f)

The topological step from the vertex operator algebra to the Lie Monster Group requires a continuous function. Are we in front of a “super” gauge field? In other words, is there a gauge field that causes the first projection depicted at the top of Figure 3? In a topological framework, the feature that links the symmetries at a higher level with the single point at a lower level is the continuous function. If we assess two antipodal points as symmetries, and the single point as symmetry breaks and local transformations, a gauge field could be required, in order to restore the (apparently hidden) symmetry.