A Metric for Secrecy-Energy Efficiency Tradeoff Evaluation in 3GPP Cellular Networks
Abstract
:1. Introduction
2. System Model
2.1. Cellular Network Model
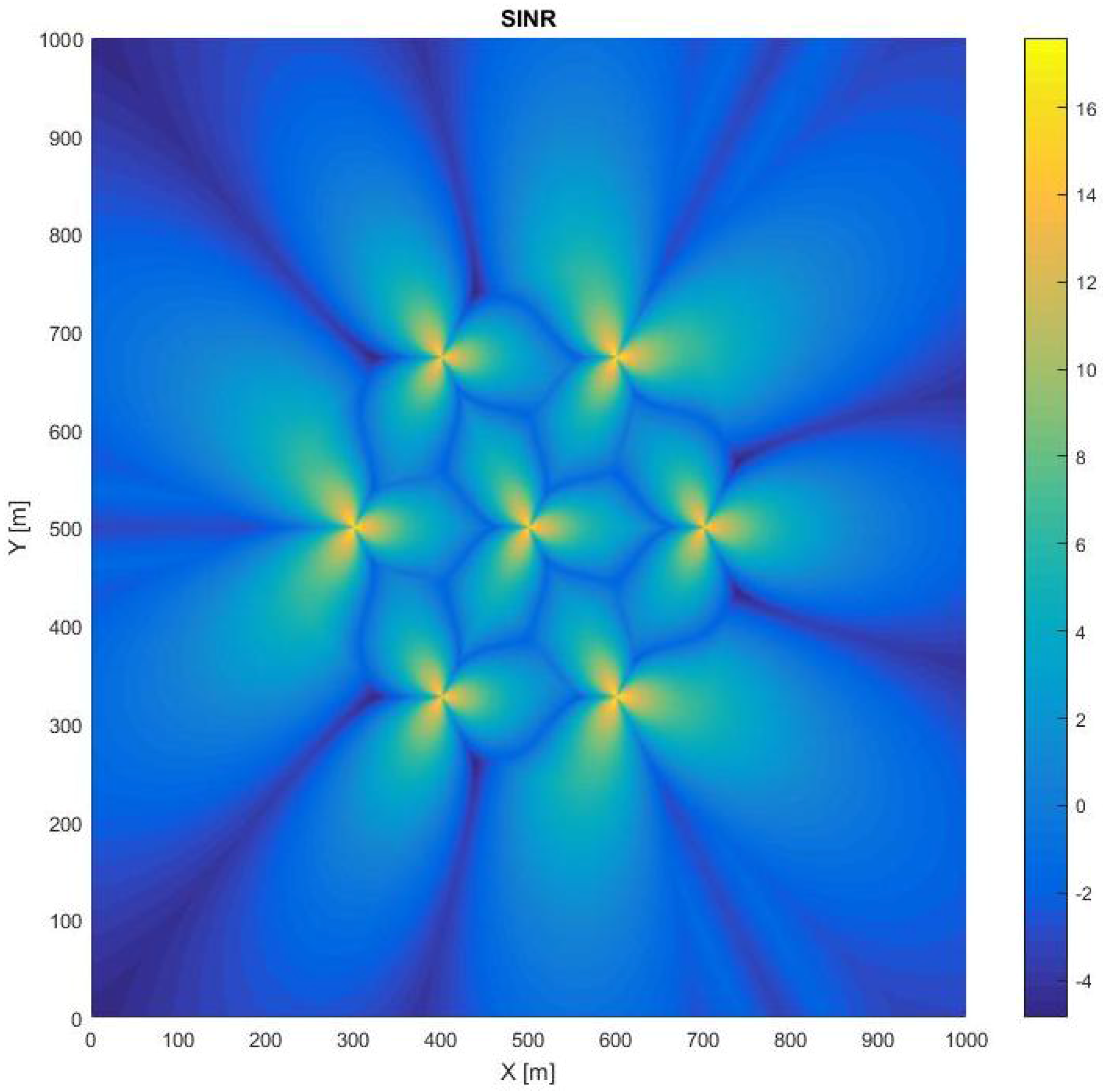
2.2. SINR and Capacity Determination
2.3. Physical-Layer Secrecy
- hB
- is a coefficient inclusive of both the transmit and the receive antenna gains and of path-loss of the Alice-to-Bob channel, being Bob served by Alice;
- P
- is the power level of the sector that is serving Alice;
- NB
- is the power of the equivalent Gaussian noise component perceived by Bob; it includes both thermal noise and interference from the surrounding sectors.
3. Metrics for the Evaluation of the Effective Secrecy–Energy Efficiency Tradeoff
3.1. Effective Secret Area
3.2. New Metrics
- Decide a target secrecy rate that Alice wants to keep with Bob;
- Given the position of Bob and the transmit power of Alice, the extension of the cell is known;
- Compute the secrecy capacity () of each point of the cell area, as Eve was located at that point; in other words, the surface managed by the BS is divided into infinitesimal squares whose surface is equal to and the eavesdropper is supposed to be there for the computing of the secrecy capacity;
- Count each point of the cell area that gives a secrecy capacity equal to or greater than the target rate;
- Compute the effective secrecy area as the ratio between the set of points that give a secrecy capacity equal to or greater than the target rate and the transmit power.
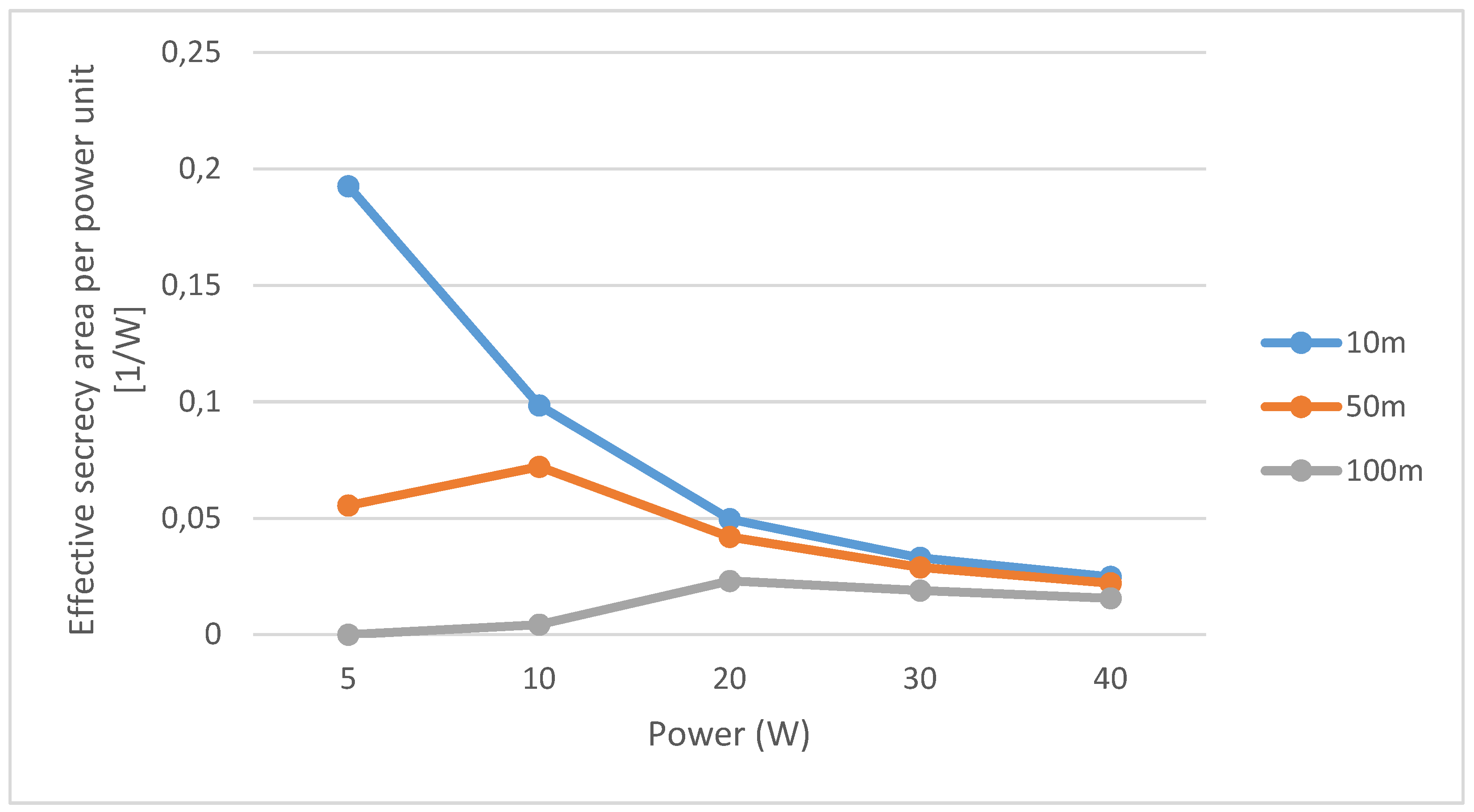
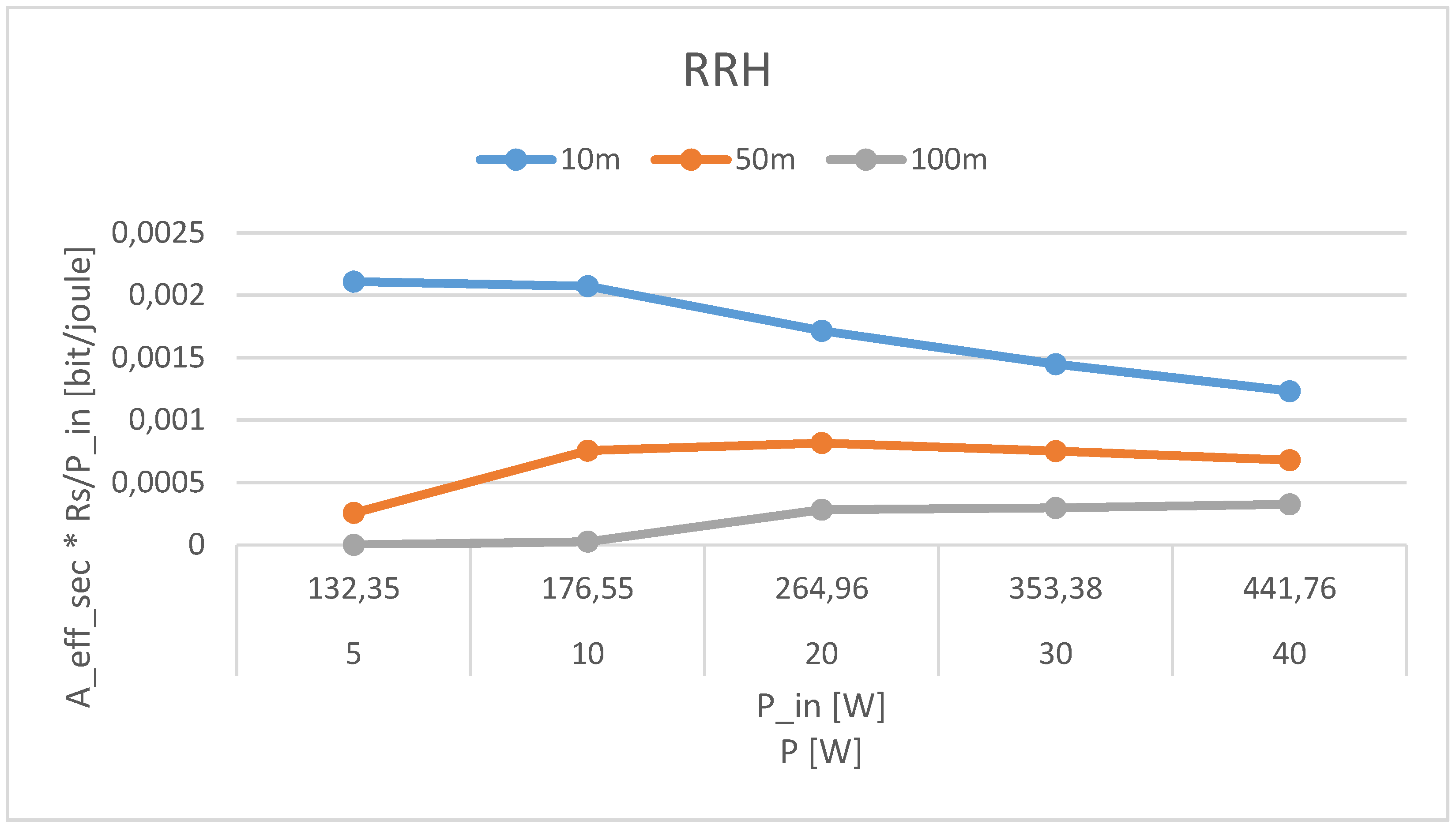
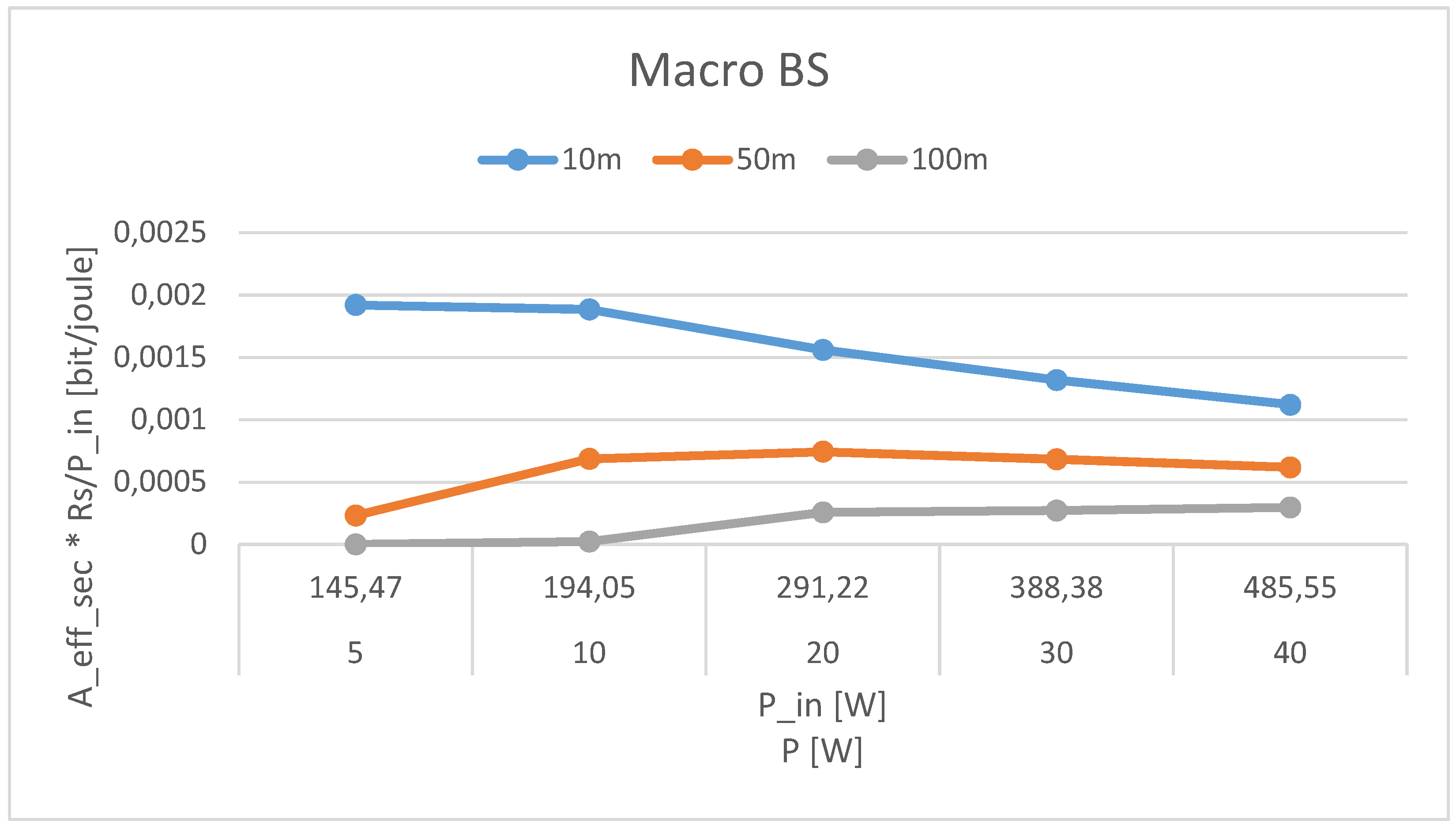
4. Results
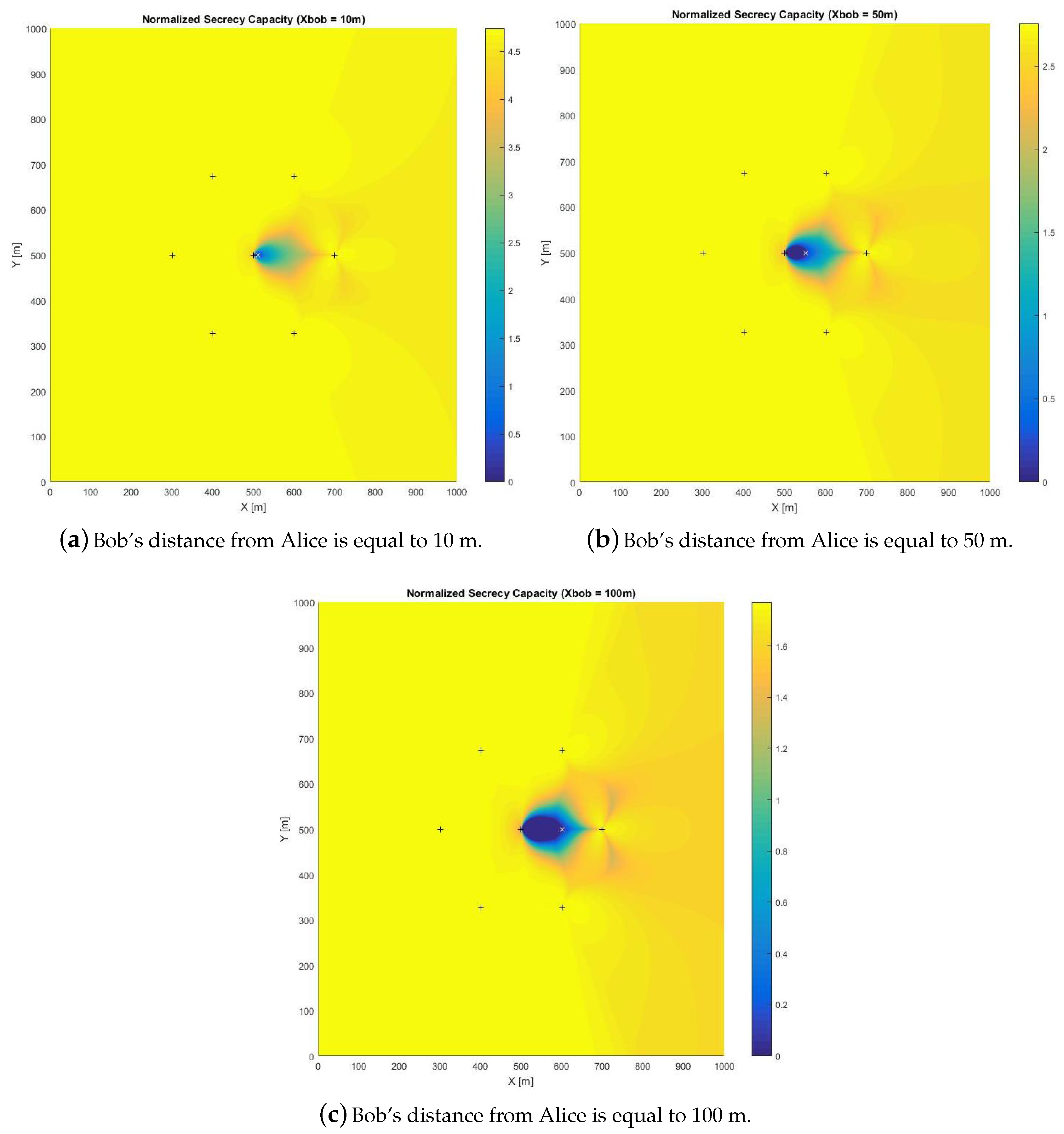
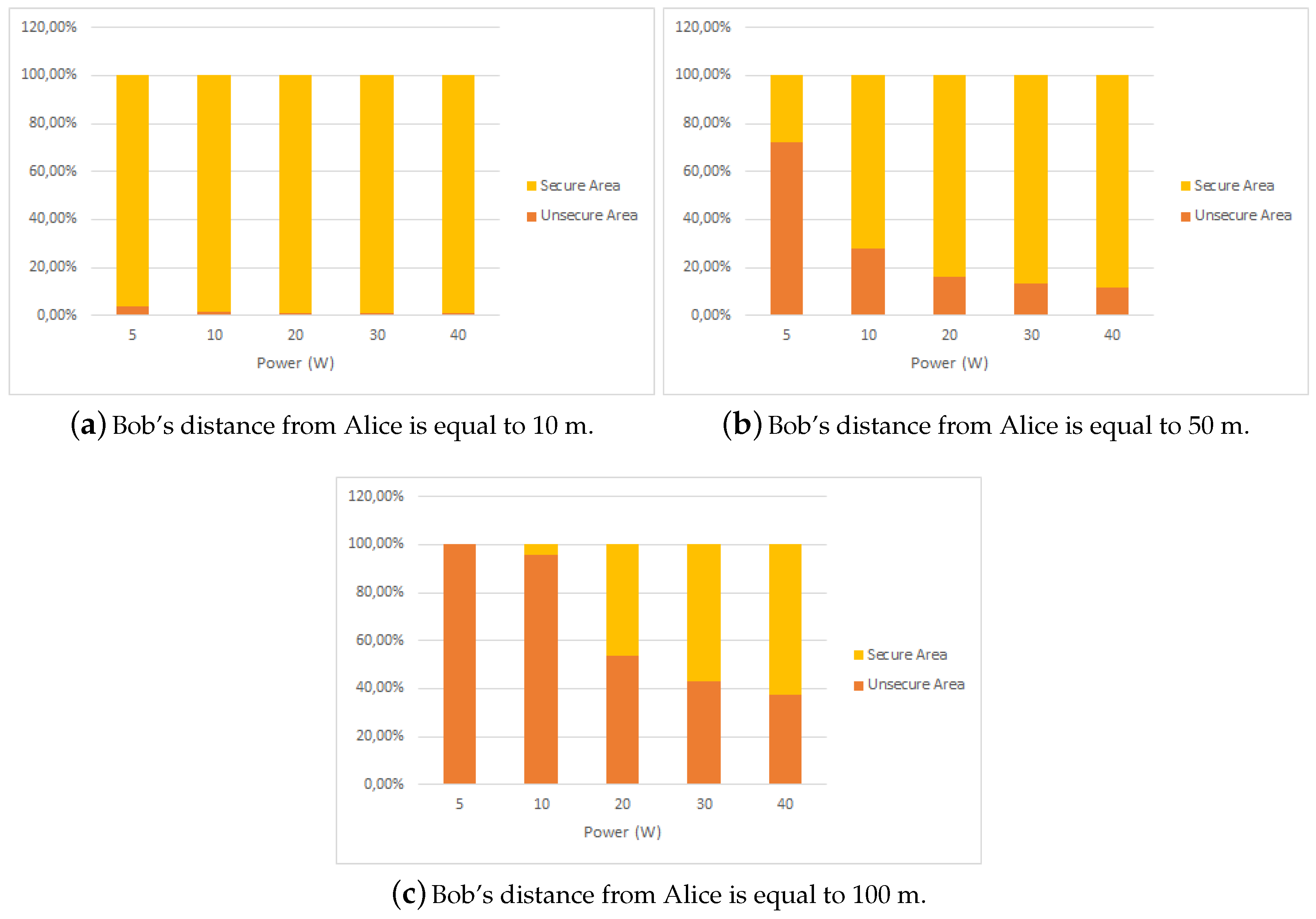
- If Bob is close to Alice (10 m), a power increase does not imply a proportional enlargement in the secure area;
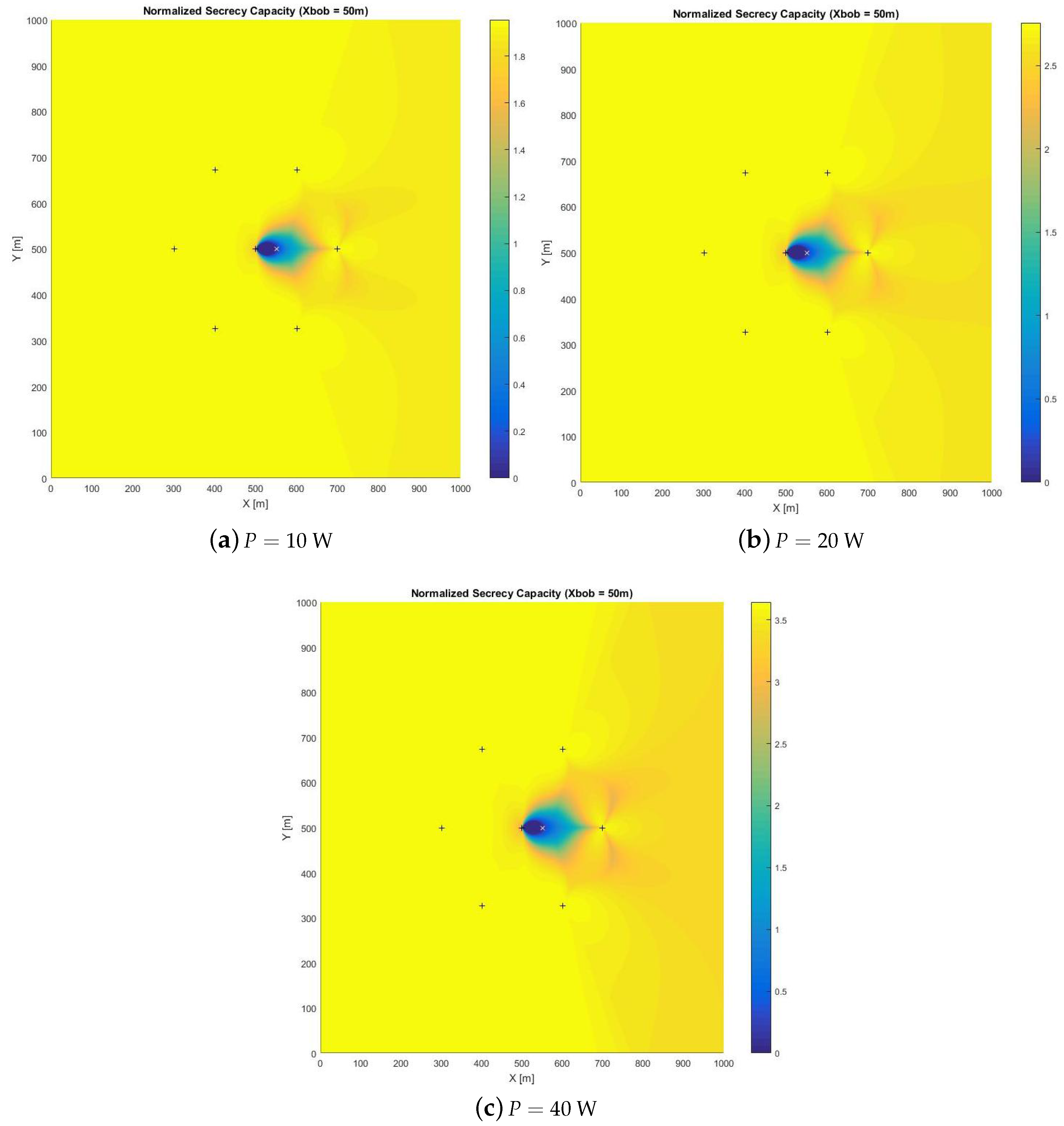
- When Bob is in the middle of the cell (50 m), a power increase is beneficial from the security point of view: the unsecure area becomes smaller; anyway, continuing to increase the power over and over does not imply a remarkably larger secure area; a sort of saturation in the extension of the secure area can be observed when the power increases over 10 W;
- When Bob is in the boundary of the cell (100 m), a higher power is needed to obtain a secure area of about of the cell sector extension; moreover, a higher than 20 W transmit power gives tiny enlargements of the secure area.
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Cheong, L.Y.; Hellman, M. The Gaussian wire-tap channel. IEEE Trans. Inf. Theory 1978, IT-24, 451–456. [Google Scholar] [CrossRef]
- Gopala, P.K.; Lai, L.; El-Gamal, H. On the secrecy capacity of fading channels. IEEE Trans. Inf. Theory 2008, 54, 4687–4698. [Google Scholar] [CrossRef]
- Mucchi, L.; Ronga, L.S.; del Re, E. A novel approach for physical layer cryptography in wireless networks. Wirel. Pers. Commun. 2010, 53, 329–347. [Google Scholar] [CrossRef]
- Mucchi, L.; Ronga, L.S.; del Re, E. Physical layer cryptography and cognitive networks. Wirel. Pers. Commun. 2011, 58, 95–109. [Google Scholar] [CrossRef]
- Mucchi, L.; Ronga, L.; Chisci, G. Noise-loop multiple access. IEEE Trans. Veh. Technol. 2015, 65, 8255–8266. [Google Scholar] [CrossRef]
- The Climate Group, GeSI. SMART 2020: Enabling the Low Carbon Economy in the Information Age. Available online: http://www.gesi.org/files/Reports/Smart%202020%20report%20in%20English.pdf (accessed on 26 October 2016).
- Gartner Study. 2007. Available online: http://www.gartner.com/newsroom/id/503867 (accessed on 26 October 2016).
- Bianco, C.; Cucchietti, F.; Griffa, G. Energy consumption trends in the next generation access network, a telco perspective. In Proceedings of the 2007 29th International Telecommunications Energy Conference (INTELEC), Rome, Italy, 30 September–4 October 2007; pp. 737–742.
- Prakash, S.; Baron, Y.; Liua, R.; Proske, M.; Schlsser, A. Study on the Practical Application of the New Framework Methodology for Measuring the Environmental Impact of ICT Cost/Benefit Analysis; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- Morosi, S.; Piunti, P.; del Re, E. Improving cellular network energy efficiency by joint management of sleep mode and transmission power. In Proceedings of the 2013 24th Tyrrhenian International Workshop on Digital Communications—Green ICT (TIWDC), Genoa, Italy, 23–25 September 2013; pp. 1–6.
- Chen, T.; Yang, Y.; Zhang, H.; Kim, H.; Horneman, K. Network energy saving technologies for green wireless access networks. IEEE Wirel. Commun. 2011, 18, 30–38. [Google Scholar] [CrossRef]
- Feng, D.; Jiang, C.; Lim, G.; Cimini, L.J.; Feng, G.; Li, G.Y. A survey of energy-efficient wireless communications. IEEE Commun. Surv. Tutor. 2013, 15, 167–178. [Google Scholar] [CrossRef]
- Piunti, P.; Cavdar, C.; Morosi, S.; Teka, K.E.; del Re, E.; Zender, J. Energy efficient adaptive cellular network configuration with qos guarantee. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 68–73.
- Auer, G.; Blume, O.; Giannini, V.; Godor, I.; Imran, M.; Jading, Y.; Katranaras, E.; Olsson, M.; Sabella, D.; Skillermark, P.; et al. Deliverable D2.3: Energy efficiency analysis of the reference systems, areas of improvements and target breakdown. Energy Aware Radio Netw. Technol. (EARTH) European Project 2012. Available online: http://cordis.europa.eu/docs/projects/cnect/3/247733/080/deliverables/001-EARTHWP2D23v2.pdf (accessed on 26 October 2016). [Google Scholar]
- De Meulenaer, G.; Gosset, F.; Standaert, F.X.; Pereira, O. On the energy cost of communication and cryptography in wireless sensor networks. In Proceedings of the 2008 IEEE International Conference on Wireless and Mobile Computing, Networking and Communications, Avignon, France, 12–14 October 2008; pp. 580–585.
- Wang, L.; Zhang, X.; Ma, X.; Song, M. Joint optimization for energy consumption and secrecy capacity in wireless cooperative networks. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 941–946.
- LTE Evolved Universal Terrestrial Radio Access—Radio Frequency (RF) System Scenarios (3GPP TR 36.942 version 13.0.0 Release 13). ETSI TR 136 942 V13.0.0. Available online: http://www.etsi.org/deliver/etsi_tr/136900_136999/136942/09.00.01_60/tr_136942v090001p.pdf (accessed on 26 October 2016).
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 29, 656–715. [Google Scholar] [CrossRef]
- Barros, J.; Rodrigues, M.R.D. Secrecy capacity of wireless channels. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 356–360.

| Bob’s Distance | 10 m | 50 m | 100 m |
|---|---|---|---|
| Unsecure Area | % | % | % |
| Secure Area | % | % | % |
| Alice’s Power | 10 W | 20 W | 40 W |
|---|---|---|---|
| Unsecure Area | % | % | % |
| Secure Area | % | % | % |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciabini, F.; Morosi, S.; Mucchi, L.; Ronga, L.S. A Metric for Secrecy-Energy Efficiency Tradeoff Evaluation in 3GPP Cellular Networks. Information 2016, 7, 60. https://doi.org/10.3390/info7040060
Ciabini F, Morosi S, Mucchi L, Ronga LS. A Metric for Secrecy-Energy Efficiency Tradeoff Evaluation in 3GPP Cellular Networks. Information. 2016; 7(4):60. https://doi.org/10.3390/info7040060
Chicago/Turabian StyleCiabini, Fabio, Simone Morosi, Lorenzo Mucchi, and Luca Simone Ronga. 2016. "A Metric for Secrecy-Energy Efficiency Tradeoff Evaluation in 3GPP Cellular Networks" Information 7, no. 4: 60. https://doi.org/10.3390/info7040060
APA StyleCiabini, F., Morosi, S., Mucchi, L., & Ronga, L. S. (2016). A Metric for Secrecy-Energy Efficiency Tradeoff Evaluation in 3GPP Cellular Networks. Information, 7(4), 60. https://doi.org/10.3390/info7040060







