Abstract
The modern encryption methods are reliable if strong keys (passwords) are used, but the human factor issue cannot be solved by cryptographic methods. The best variant is binding all authenticators (passwords, encryption keys, and others) to the identities. When a user is authenticated by biometrical characteristics, the problem of protecting a biometrical template stored on a remote server becomes a concern. The paper proposes several methods of generating keys (passwords) by means of the fuzzy extractors method based on signature parameters without storing templates in an open way.
1. Introduction
Information and knowledge are of great value and possess business potential. When the level of IT development in society is increasing, the necessity of protecting information rises. The number of cyber-crime incidents is increasing, and the damage caused by these incidents is running high. In 2014, the number of incidents cost $2.8 million [1]. This means 117,339 cyber attacks a day on average. The average damage for a large company in 2014 and 2015 was $2.7 million and $2.5 million, respectively [2]. The total amount of damage caused by cybercrimes in the world cannot be calculated, as information about many attacks is hidden and the information value is difficult to define. Some authors [3] have concluded that the annual damage for the world economy caused by cybercrimes costs somewhere from $375 to $575 billion.
The protection of stored data from unauthorized access is done via encryption. Modern encryption methods are reliable if strong keys (passwords) are used, but the human factor makes complicated passwords and long encryption keys meaningless. Even if reliable passwords and key generation meet the necessary requirements in practice (it is not true in the overwhelming majority of cases), the problem of safe password (key) storage and revealing passwords by deceptive means still arises. Therefore, a method of authenticity control via password (an encryption key) request is not reliable enough.
The best solution is to bind all authenticators (passwords and encryption keys) to the owner’s identity. Such binding is integral to a person so it reliably precludes the possibility of forgery in practice. Biometrical characteristics (including dynamic) are inherent and allow for a solution to the above-mentioned human factor prospectively [4,5].
If users are authenticated by biometric characteristics, the issue of protecting biometric data kept at a remote server then becomes important [6].
Thus, the solution to these issues lies in obtaining cryptographic keys and strong passwords on the basis of these secret biometric images, which would allow for the combination of the advantages of both biometric technologies and cryptographic methods to protect users’ biometric data during service procedures. A signature or a handwritten password is proposed in this paper. Several methods of generating key sequences based on fuzzy extractors are described that allow for the retrieval of random uniformly distributed bit sequences from biometric data [7]. This approach gives the owner the possibility of modifying secret biometric images at any time as well as a personal identifier (an authenticator, a key, etc.) binding with this image.
2. Building a Template Database for Open and Hidden Biometric Images for Investigation
A personal reaction rate significantly depends on a user’s temperament [8]; for this reason, a test group consisted of an approximately equal number of sanguine, choleric, melancholic, and phlegmatic persons (according to the results of Eysenck Personality Questionnaire) and an equal number of men and women.
In this study, the data of handwritten passwords were collected using WACOM tablets able to register coordinates of the pen tip and the pen pressure on the tablet surface (1024 pressure levels) with a frequency of 200 Hz. Thus, the tablet registered specified parameters every 5 ms. A special software module helped to collect the handwritten passwords of 200 users. A fixed word or a personal signature (in most cases) was used as the handwritten password. A personal signature is a special kind of password and is the most stable. Every user represented 40 signatures minimum (more than 8000 samples in total). Every test subject was assigned another person who monitored the process of inputting their biometric data. Further, every person monitoring the handwriting of the password (the signature) made 30 attempts to forge this handwritten password, and the software module collected 30 fake samples for every registered user (6000 samples in total).
3. Analysis of Test Persons’ Handwritten Passwords and Signatures and Features Space
Nowadays, different orthogonal basis functions [9] are used to describe the dynamics of a signature; however, there is no comparative evaluation of the information content for all attributes derived from these functions.
For the purpose of computer processing, the functions of the pen position are presented in the form of readings (sampling) and contain information about the dynamics of the pen movement and a signature’s image. Further, we will consider the signature in a system of coordinates O(x,y,p), where x and y are coordinates of the signature on a x- and y-planes, and p is a value of the pen pressure on the tablet. It is necessary to define robust attributes that characterize both a graphic picture and the dynamics of the handwritten password and to select such attributes that provide a minimum intersection of users’ personal samples in a multidimensional space.
Handwritten password instances recorded at various times differ in range (by amplitude and duration). In order to calculate attribute statistical characteristics, all instances must be the same duration and normalized by power. To scale signals by duration, the functions passed through direct transform into Fourier series and inverse transform with the same duration, thus providing a resampling (equal to an average duration of the scaling signals). Here, the process of changing signatures to equal duration is described:
- Discard the first and last values for all dots with zero pressure.
- Perform one-dimensional Fourier transform for x(t), y(t), and p(t).
- Perform the inverse transform of these functions, taking into account that the output dimension should correspond to the nearest minimum integer multiple of the 2nd power.
The next step is the calculation of biometric features for all signatures. All mentioned features can be divided into groups as is shown in Table 1. The following is a detailed description of all groups of features. This is reflected in the scientific literature; similar approaches to feature obtaining have been used by various researchers in the design of subject identification and authentication systems via signatures.

Table 1.
Groups of features are used for key generation at present investigation.
3.1. The Distances between the Dots (Readings) of the Signature
The first approach to building an attribute space is based on a matrix of distances between the dots (readings) of the signature. The whole process of calculating an invariant based on the distance matrix may be divided into a set of steps:
- 4.
- Calculate the step: , where N is the number of dots resulting from the inverse Fourier transform, and Rd is the desirable matrix dimension that is a multiple of the second power.
5. Calculate the distance matrix in the three-dimensional space (pressure is the third dimension) for the whole set of coordinates:
where n is a number of dots between which distances are calculated, i.e., the matrix of distances dimensionality, rij is the distance between the ith and the jth coordinates obtained using the formula:
where xi, yi, pi are the values of the x(t), y(t), p(t) functions at appropriate timing ti.
The distance matrix in the two-dimensional space is calculated in the same way (excluding p). As large numbers of elements require high calculating resources, the calculation should be performed using the h step.
6. Normalize the given matrix using the length of the signature:
where r`ij is a normalized distance between the ith and the jth coordinates:
Elements of the obtained matrix are biometrical characteristics. In this study, the step (h) is selected so that the number of dots is equal to 16 and the number of features is 120. Using a high number of features is meaningless because, with a smaller step, the number of features and the time of processing grow exponentially; herewith, the correlation dependence between features greatly increases.
3.2. Signature Appearance Characteristics
It is worth considering the best practice in forensic graphology and which attributes that characterize the graphical image of the signature (the handwritten password) should be selected:
- The proportion of the length and the width of the signature.
- The center of the signature described by Cx, Cy, and Cp coordinates.
- An angle of slope for the signature. The angle of slope is a cosine of a mean angle of slope for a polygonal path of the signature to the X axis.
- An angle of slope between the centers of halves of the signature. After the center of the signature Cx has been found, the set (X,Y,Z) = {(xi,yi,pi)} should be divided into two subsets L = {(xi,yi,pi)|𝑥𝑖 > Cx} and R = {(xi,yi,pi)|𝑥𝑖 > Cx}. Further, the centers of the obtained sets L and R should be found:
3.3. Daubechies Wavelet Transform Coefficients
It is obvious that the analysis of the frequency domain provides advantages in evaluating noisy signals [10]. A modern mathematical tool for the analysis of spectral characteristics of nonstationary signals is wavelet analysis. Some well-known studies where wavelet transform was applied to calculate attributes using signatures have been noted [11,12,13,14,15]. The present paper proposes a transition from the time-domain representation of the functions of the pen position change to the frequency-domain representation, their research, and a search of dynamical characteristics using a method of multiresolution analysis. This approach is based on a discrete wavelet transform and uses Mallat pyramidal algorithm to decompose initial signals into sequences of wavelet coefficients djk that characterize a structure of the process to be analyzed in different scales (j). These studies considered different bases of Daubechies wavelets (from D4 to D10 [16]). To transit to a new analysis scale, the signal length must be multiple of 2n, where n is a number of factorization levels. If this requirement is not met, the numerical series may be added with deficient values using one of the following ways:
- Periodic addition, which means the beginning of the sequence is put at the end of the numerical series.
- Mirroring data at the ends of the sequence.
- The calculation of special scaling and wavelet functions that are applied to the beginning and the end of the sequence, presupposed by Gram–Schmidt orthogonalization.
A numerical series may be added with zeros as well, but this approach leads to significant mistakes as a rule. In this paper, the time sequence is periodically added with deficient values.
The analyzing signals were discretized at a frequency of 200 Hz; according to the sampling theorem, the high signal frequency is 100 Hz. Thus, for a signal consisting of 256 readings for example, the wavelet coefficients of the first level of decomposition occupy the frequency bandwidth of 50–100 Hz. Wavelet coefficients of the second level describe the harmonics of the spectrum for the bandwidth of 25–50 Hz. The procedure is repeated until there is one wavelet coefficient and one approximation reading at the 9th level. In total, there are 256 coefficients (1 + 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128). This means that the number of coefficients is equal to the number of readings in the initial signal. If the major power of the signal is concentrated around a frequency of 2 Hz, the wavelet coefficients of the 6th level are significant, and the wavelet coefficients of the lower level may be discarded.
The number of wavelet coefficients at any decomposition level depends on the signal duration. The number of wavelet transform coefficients becomes equal and the spread of values decreases when the procedure of scaling functions to the mean duration is performed (Figure 1 and Figure 2). This operation allows transform implementations of the signature of one subject to the same number of features and improves the stability of feature values of this group. Herewith, the distinction of feature values is saved for different subjects (Figure 3).
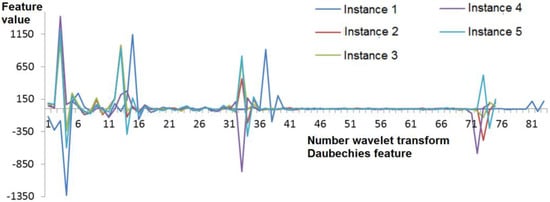
Figure 1.
Wavelet transform coefficients before scaled by the pen pressure function (onto a tablet) to the mean length of a signature instance for a signer.
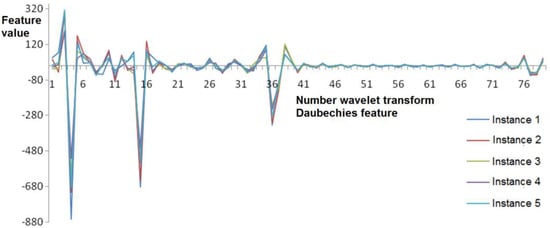
Figure 2.
Wavelet transform coefficients scaled by the pen pressure function (onto a tablet) to the mean length of a signature instance for a signer.
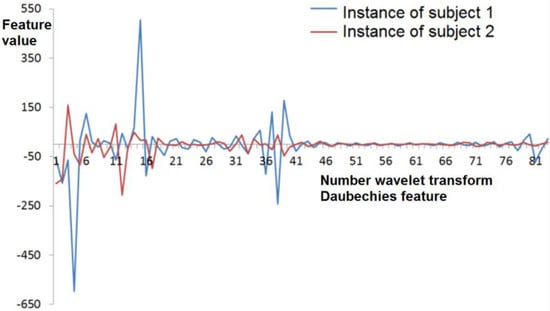
Figure 3.
Wavelet transform coefficients scaled by the pen pressure function (onto a tablet) to the mean length of a signature instance for different signers.
The moment of the “occurring” of a harmonic in a signal is defined as a multiplication of the wavelet coefficient number and the timing resolution for the corresponding level within the accuracy of the timing resolution value. Thus, the physical significance of the wavelet transform coefficients resulting from multidimensional analysis may be treated as characteristics of signal harmonics that belong to a certain frequency bandwidth and occur in the signal at a certain moment in time. These characteristics may be considered as values of signature characteristics.
The quality of the algorithm work depends on the selected wavelet a lot. This research covers the evaluation of stability for signals obtained using Daubechies wavelets D4, D6, D8, and D10. The analysis of resolution levels start from 3 to 6, which corresponds to the spectral range of 1.5625–25 Hz. This spectral range characterizes the dynamics of reproducing handwritten passwords. The statistical data processing was done using the Mann–Whitney U-test, and the differences were considered reliable when p < 0.05. The minimum time of analysis and consequently the worst-quality result is obtained for D2. The high stability (robustness) was proven in practice for the wavelet spectrum when handwritten signatures were input in different time. This will allow for the evaluation of complicated dynamically changing signals that are formed when handwritten passwords are being represented.
The possibilities of use features for each subject from this group can be different and depend on the mean of signature length.
3.4. Fourier Wavelet Transform Coefficients
An easier way to measure dynamic attributes of a signature is based on Fourier transform. Compared with wavelet transform, Fourier does not consider the frequency location in time. At the first stage of calculating, attribute functions are prepared to be decomposed. As a rule, the pressure function of a pen into a tablet and the derived functions of pen movement coordinates or a pen velocity function is calculated using the formula:
where x and y are dot coordinates, t is the time of the recording of the pen position coordinates on the tablet, Δt is a time interval between cases of recordings taken of the pen position coordinates as data functions.
The dependence on the angle between the tablet and a signee’s hand is discarded if the pen velocity function is used.
The function processing is performed in 3 steps:
- Time normalization (resampling, described above).
- Fourier series function decomposition.
- Harmonics amplitude normalization based on power.
The decomposition of a pressure function into harmonics may be performed using fast Fourier transform or discrete Fourier transform. Some authors [4,6] have proposed the use of 16 normalized amplitudes of the first lowest-frequency harmonics as attributes at users’ identification.
3.5. Correlation Coefficients between Functions of the Signature
The authors of the present study have proposed the signature attributes based on the correlative analysis for signees’ identification [4,6]. Values of the correlation coefficients between x(t), y(t), and p(t) functions of the signature and their first-order derivatives are used as attributes.
4. A Fuzzy Extractor Method
Initially, a bit sequence is generated in a random manner, and the bit sequence is encrypted with an error-correcting code [17]. Hemming, Hadamard, Bose-Chaudhuri-Hocquenghem (BCH-codes), and Reed-Solomon coding may be used as error-correcting codes [18]. In this paper, BCH-codes and Hadamard codes are used. Hamming coding is not applied here due to its low correcting ability. Reed-Solomon coding is a particular case of BCH coding. The encrypted sequence is combined with a bit representation of template features of biometric features of a subject (a biometrical template). A vector of mean values for selected attributes is proposed to be used as sample characteristics in this paper. A preliminary template is converted from a decimal vector to a bit sequence. A bit representation of a vector of biometric parameters is obtained by a quantization of feature values. The quantization is a conversion of each value in an 8 bit sequence whereupon the private bit representations are combined in final sequence (the proposed method is described in the following two sections). A combination method is usually an XOR operation. The combination results in an open string that may be stored on a public server. To obtain an earlier generated sequence, a user inputs a new signature (handwritten password) instance that is processed in a proper way, converted in bit sequence, and subtracted from the open string. When biometrical data has been subtracted, the calculated bit sequence differs from the initial one (a sequence that has been encrypted). This is caused by the differences between presented biometrical data and template data (it is not possible to duplicate a signature). Further, the error-correcting code is applied to the string; if a number of mismatched bits in a template and presented attribute values are not higher than the correcting ability of the code, the initial bit sequence (the key sequence) will be found [19].
4.1. On the Presenting of Attribute Values in the Form of a Bit Sequence
It is obvious that “raw” biometrical data on a large scale consist of parts that carry low information content. Here, any initial attribute value with one byte generating a bit sequence out of biometrical attributes was coded.
The coding process is a mapping of the domain of values (all possible attribute values for all users but not for everybody separately) onto a set of values {0, 1, 3, 7, 15, 31, 63, 127, 255, 254, 252, 248, 240, 224, 192, 128} (Figure 4). Each feature value is transformed into one of the numbers of said plurality and is presented in binary format before a template is combined with a public string; otherwise, a newly introduced instance is subtracted from a public string. This method presupposes that the domain of values may become open access information. Further, the bit sequences are combined into one resulting bit sequence that is added with a random string. The “gluing together” process is discussed in the next paragraph.
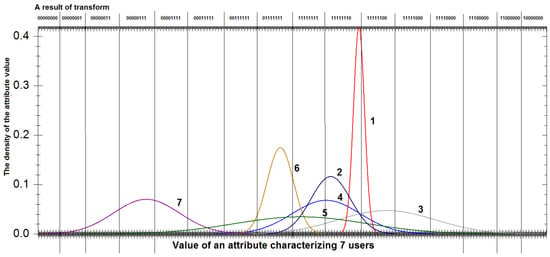
Figure 4.
Encryption of values of resulting bit sequences.
4.2. Evaluation of Feature Informativeness Individually for each Subject
Research [20] shows the relation between the efficiency of error correction and the methods of grouping bits with different probabilities of a single error. Despite efforts in this direction, a single approach for this issue has not yet been developed. Therefore, the present paper proposes a grouping method based on the estimation of the information content of attributes. In this context, the information content is an integral indicator of bit stability in a converted attribute value.
The process of feature informativeness evaluation is produced at the open string forming stage (immediately before the bit sequences combining). This information is saved and used at the key generation stage (when receiving and “detaching” bit representation of open string realization). The procedure consists in the following. The relative frequency of on-bits and zero bits is calculated using all signature instances selected to generate a template for any attribute. Then, the degree of stability is determined for each feature bit as a multiplication of the relative frequency of one-bits by the relative frequency of zero-bits. The multiplication of the stability degree of all bits in a bit representation of features is calculated. An obtained estimate generally characterizes the stability (informative value) of features. The more bits that the frequencies close to 0 or 1 have, the lower the final product is, and the higher the integral estimation of the stability (the information content or value) for the user is.
For example, let 10 instances be input. It is necessary to define an index of the information content for a certain attribute using its converted values: 00011111, 00111111, 00011111, 00001111, 00011111, 01111111, 00111111, 00011111, 11111110, 01111111. The relative frequency of a one byte in bits of the converted value is 0.1; 0.3; 0.5; 0.9; 1; 1; 1; 0.9. Further, the frequencies that are equal 0 or 1 are converted to a number close but not equal to 0 or 1 (for this case, take 0.01 and 0.99); thus, multiplication of this type is calculated: 0.1 × (1 − 0.1) × 0.3 × (1 − 0.3) × 0.5 × (1 − 0.5) × 0.9 × (1 − 0.9) × 0.99 × (1 − 0.99) × 0.99 × (1 − 0.99) × 0.99 × (1 − 0.99) × 0.9 × (1 − 0.9) = 0.1 × (0.9) × 0.3 × (0.7) × 0.5 × (0.5) × 0.9 × (0.1) × 0.99 × (0.01) × 0.99 × (0.01) × 0.99 × (0.01) × 0.9 × (0.1) = 0.0000000000371357684775.
Further, all attributes are ranked by the information content (their order is changed starting from the most informative valued to the less informative valued), and certain numbers of attributes are selected, other attributes are discarded. Bit representation of chosen features is concatenated in a final resulting bit sequence that is combined with a secret key of subject to generate the open string. The best number of attributes when the probabilities of false positives and false negatives are the least is an extractor parameter that we have defined by a series of computing experiments for every initial set of attributes in our research. The number of informative significant attributes and their sequences must be stored on a special data storage device or a dedicated server. At the key generation stage, this information is used to select the most informative significant features from a signature instance of subject that are transformed in private bit sequences (as is described in the previous section). Further, sequences are similarly combined in the resulting sequence that is subtracted from the open text string. A code correcting errors is applied to the result of the aforementioned operation.
5. A Simulation Model of the Cryptographic Key Generation System
The available biometrical data are used to imitate the process of generating secret keys linked to a user. At the first stage, the key sequences are generated using the uniform law. These key sequences in combination with biometrical data will generate open strings and be recovered from the open strings. The available biometrical data will input the extractor with the given parameters in combination with a personal secret key. The open string will output the extractor. The following values are used as parameters:
- a number of recording attributes (when the procedure of estimating the information content for the attribute is used);
- a number of signature (handwritten password) instances;
- an encryption algorithm;
- a block size (for Hadamard codes);
- the error-correcting ability (for BCH codes).
Thus, an open string will be generated for every user.
At the second stage, the initial generated secret keys will be recovered and compared with the initial keys. The situation when the system generated unusual value of the cryptographic key (that does not match the original) is considered a Type I error (false negative). This means that the lower the probability of false negatives is, the higher the stability of key output will be. In practice, the user will not be able to decode data and sign the information resource using a digital signature correctly. The situation when cryptographic keys obtained from biometrical data of two different person coincide is considered a Type II error (false positive) for secret biometrical images. When the false accept rate (FAR) for known biometrical images is estimated, the errors described above are combined with the errors caused by the match of the ith user’s key and the key generated when the ith user’s false signature inputs the extractor. In practice, this mistake leads to unauthorized access to a user’s encrypted data or a forgery of a digital signature. The equal error rate EER is a total percentage of error decisions when EER = FRR = FAR. The process of generating keys repeats with different parameters of the extractor for all instances for all users contained in the database, excluding those instances that were used for building the open string.
6. Results and Their Comparison with Early Achieved Results
Attributes based on the Fourier transform and the correlative analysis of handwritten passwords (signatures) did not demonstrate positive results when applied independently. The probability of error key generation is significant in all cases of extractors .
Attributes of the signature static image are stable, but their quantity is not large (five attributes means five bits); therefore, it is not worth using them independently, as the generated key is not reliable in that case.
Attributes based on calculating the distances between signature dots in a two-dimensional space produce a high percentage of errors. in all cases.
The procedure of estimation and recording only informative valued attributes (a number of attributes is defined on the basis of the desirable key length) decreases the probabilities of error decisions in all cases if the Hadamard or BCH methods are used. On average, the number of Type II errors decreases by 20%–40%.
Table 2 provides the best results of the performed experiments in generating key sequences using the peculiarities of reproducing handwritten passwords and signatures. In all cases, the probability is less than 0.99 in different confidence intervals.

Table 2.
The main results of generating key sequences using handwritten passwords and signatures. IV—the procedure of estimation of informative value (stability) of features; NoI—number of signature instances when forming the open string; KL—the length of generated key in bits; Code—error correction code name; FAR1—the probability of FAR for biometric unknown (secret) image; FAR2—the probability of FAR for biometric known image; CI—confidence interval of FRR, FAR1, and FAR2 probabilities.
The following method provided the best result: A method of generating a key with a length of 264 bits using a user’s handwritten password (signature) on the basis of BCH codes, and ranking the most stable attributes based on the information content for any person independently using the Daubechies wavelet D6 transform establishes distance between coordinates of a signature contour image and other static characteristics of a signature image with a probability of generation Type I and II errors equal to 0.045 and 0.015, respectively (accounting an amateur imitation). The accuracy of the results is 0.99 if the confidence intervals are 0.01 and 0.002. This result exceeds the earlier achieved results in generating keys using signatures. For reference, consider [21,22,23]. In [21], a method of generating keys using signatures of 126 test persons from the database of handwritten signatures MCYTX is employed. This study was supported by the Spain Ministry of Science and Innovation (MCYT TIC2003-08382-C05-01) and the European Commission within the 6th Framework Programme (IST-2002-507634 Biosecure NoE projects). This method demonstrated the following error rates: FRR = 5.30% when FAR = 1.18% for professional imitation and FAR = 0.32% for imitations made without monitoring the authentic signature and handwriting style. In [22], the results are as follows: EER ≈ 6.7% for 40 test persons. In [23], a method of generating a key using a handwritten password with a Type I error rate equal to 28% and a Type II error rate equal to 1.2% is presented. It should be noted that this result was obtained without applying error-correcting codes.
Acknowledgments
This work is partially supported by RFBR grant 15-07-09053.
Author Contributions
Pavel Lozhnikov conceived and designed the experiments; Alexey Sulavko and Danil Volkov performed the experiments; Alexander Eremenko analyzed the data; Alexey Sulavko and Danil Volkov wrote the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IV | the procedure of estimation of informative value (stability) of features |
| NoI | number of signature instances when forming the open string |
| KL | the length of generated key in bits |
| Code | error correction code name |
| FAR1 | the probability of FAR for biometric unknown (secret) image |
| FAR2 | the probability of FAR for biometric known image |
| CI | confidence interval of FRR, FAR1, and FAR2 probabilities |
References
- Managing Cyber Risks in an Interconnected World. Key Findings from The Global State of Information Security Survey 2015. PricewaterhouseCoopers. Available online: http://www.pwc.ru/ru_RU/ru/riskassurance/publications/assets/managing-cyberrisks.pdf (accessed on 20 October 2016). (In Russian)
- Turnaround and Transformation in Cybersecurity. Key Findings from the Global State of Information Security Survey 2016. PricewaterhouseCoopers. Available online: http://www.pwc.ru/ru/riskassurance/publications/assets/gsiss2016-report.pdf (accessed on 20 October 2016).
- Center for Strategic and international Studies, Net Losses: Estimating the Global Cost of Cybercrime, June 2014. Available online: http://csis.org/files/attachments/140609_rp_economic_impact_cybercrime_report.pdf (accessed on 20 October 2016).
- Lozhnikov, P.S.; Sulavko, A.E.; Samotuga, A.E. Personal Identification and the Assessment of the Psychophysiological State While Writing a Signature. Information 2015, 6, 454–466. [Google Scholar] [CrossRef]
- Epifantsev, B.N.; Lozhnikov, P.S.; Kovalchuk, A.S. Hidden identification for operators of information-processing systems by heart rate variability in the course of professional activity. In Proceedings of the Dynamics of Systems, Mechanisms and Machines (Dynamics), Omsk, Russia, 11–13 November 2014; pp. 1–4.
- Lozhnikov, P.S.; Sulavko, A.E.; Volkov, D.A. Application of noise tolerant code to biometric data to verify the authenticity of transmitting information. In Proceedings of the Control and Communications (SIBCON), Omsk, Russia, 21–23 May 2015; pp. 1–3.
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data. In Advances in Cryptology—EUROCRYPT; Springer: Berlin/Heidelberg, Germany, 2004; pp. 79–100. [Google Scholar]
- Epifantsev, B.N. Hidden Identification of Psycho-Physiological State of the Human Operator in the Course of Professional Activity; SibADI Publisher: Omsk, Russia, 2013; p. 198. (In Russian) [Google Scholar]
- Lam, C.F.; Kamins, D. Signature verification through spectral analysis. Patter Recognit. 1989, 22, 39–44. [Google Scholar] [CrossRef]
- Graps, A. An Introduction to Wavelets. IEEE Comput. Sci. Eng. 1995, 2, 50–61. [Google Scholar] [CrossRef]
- Patil, P.; Hegadi, R. Offline Handwritten Signatures Classification Using Wavelet Packets and Level Similarity Based Scoring. Int. J. Eng. Technol. 2013, 5, 421–426. [Google Scholar]
- Ismail, A.; Ramadan, M.; El danaf, T.; Samak, A. Signature Recognition using Multi Scale Fourier Descriptor and Wavelet Transform. Int. J. Comput. Sci. Inf. Secur. 2010, 7, 14–19. [Google Scholar]
- McCabe, A. Neural network-based handwritten signature verification. J. Comput. 2008, 3, 9–22. [Google Scholar] [CrossRef]
- Deng, P.S.; Liao, H.-Y.M.; Ho, C.W.; Tyan, H.-R. Wavelet-based offline handwritten signature verification. Comput. Vis. Image Underst. 1999, 76, 173–190. [Google Scholar] [CrossRef]
- Fahmy, M. Online handwritten signature verification system based on DWT features extraction and neural network classification. Ain Shams Eng. J. 2010, 1, 59–70. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Morelos-Zaragoza, R. The Art of Error Correcting Coding; John Wiley & Sons: Hoboken, NJ, USA, 2006; p. 320. [Google Scholar]
- Solovjeva, F.I. Introduction to Coding Theory; Novosibirsk State University Publisher: Novosibirsk, Russia, 2006; p. 127. (In Russian) [Google Scholar]
- Eremenko, A.V.; Sulavko, A.E. Research of Algorithm for Generating Cryptographic Keys from Biometric Information of Users of Computer Systems; Information Technology; New Technologies Publisher: Moscow, Russia, 2013; pp. 47–51. (In Russian) [Google Scholar]
- Scotti, F.; Cimato, S.; Gamassi, M.; Piuri, V.; Sassi, R. Privacy-Aware Biometrics: Design and Implementation of a Multimodal Verification System. In Proceedings of the Annual Computer Security Applications Conference, Anaheim, CA, USA, 8–12 December 2008; pp. 130–139.
- Santos, M.F.; Aguilar, J.F.; Garcia, J.O. Cryptographic key generation using handwritten signature. In Proceedings of SPIE 6202, Biometric Technology for Human Identification III, Orlando, FL, USA, 17 April 2006; pp. 225–231.
- Yip, K.W.; Goh, A.; Ling, D.N.C.; Jin, A.T.B. Generation of replaceable cryptographic keys from dynamic handwritten signatures. In Proceedings of the ICB 2006 International Conference, Hong Kong, China, 5–7 January 2006; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3832, pp. 509–515. [Google Scholar]
- Hao, F.; Chan, C.W. Private key generation from on-line handwritten signatures. Inf. Manag. Comput. Secur. 2002, 10, 159–164. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).