Abstract
Information in phylogenetic systematic analysis has been conceptualized, defined, quantified, and used differently by different authors. In this paper, we start with the Shannon Uncertainty Measure information measure I, applying it to cladograms containing only consistent character states. We formulate a general expression for I, utilizing a standard format for taxon-character matrices, and investigate the effect that adding data to an existing taxon-character matrix has on I. We show that I may increase when character vectors that encode autapomorphic or synapomorphic character states are added. However, as added character vectors accumulate, I tends to a limit, which generally is less than the maximum I. We show computationally and analytically that limc→∞ I = log2 t, in which t enumerates taxa and c enumerates characters. For any particular t, upper and lower bounds in I exist. We use our observations to suggest several interpretations about the relationship between information and phylogenetic systematic analysis that have eluded previous, precise recognition.
1. Introduction
1.1. Statement of Purpose
Phylogenetic systematic analysis involves using data (i.e., characters) to classify groups (i.e., taxa). Over the past half-century, the evolutionary systematic community has concentrated effort on practice, and several methods and many algorithms for producing branching diagrams from which hierarchical classifications may be obtained have been developed. One theoretical aspect to such practical activities that hitherto has received limited attention and therefore warrants thorough investigation involves the information content in such classifications, especially as this relates to their predictive qualities.
Our general purpose herein is to initiate such thorough investigation. Copious (e.g., genomic) data are becoming available from next-generation-sequencing methods, and classifications are proving to be useful in identifying human pathogens that were unknown heretofore (e.g., SARS, avian flu, novel Ebola strains); the ability to quantify information content could provide a complementary metric in systematic analyses. The challenge is shifting from acquiring to handling data—deciding how to utilise them most efficiently to answer questions about evolution and classification. Information content will constitute a paramount factor in making such decisions. Quantifying information content is the impetus for the current study.
Our specific purpose herein is to provide a first-approach for quantifying information obtained in conducting phylogenetic systematic analyses. The bifurcating branching diagrams (i.e., cladograms)—constructed on the basis of nonintersecting, nested character vectors—are referred to in this paper as “consistent cladograms”. Analyzing consistent cladograms facilitates quantifying the information that is obtained by systematists in constructing classifications (in the strict, technical sense according to Shannon [1] and Shannon and Weaver [2]). We introduce “apomorphic density format” as a normal form for taxon-character matrices from which consistent cladograms are constructed. Using equations from information theory, we derive information measure I. Quantifying information in this manner is important because any classification system method involves dividing an ensemble into groups and obtaining an objective means to evaluate or compare different divisions for a particular ensemble as information accumulates. This provides a means for researchers to measure economy in data collection. We present numerical examples by defining “basal matrices” and using them as taxon-character matrix templates into which we add character vectors. This procedure simulates what occurs to I as systematists acquire additional information, encode that information as data in taxon-character matrices, and conduct cladistic analyses. These analyses thus allow us to study changes in I as a function of changes in character-number. We observe that I has a limit as character number increases but this limiting value counterintuitively is less than the maximum value. On the basis of these demonstrations, we devise more-precise interpretations for previous conceptions about information associated with conducting phylogenetic systematic analyses.
We ground our purposes in the observation that conceptualizing information in biology generally has attracted attention from scientists and philosophers, specifically those interested in genetics, genomics, development, and evolution [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. Information in phylogenetic systematic analysis particularly has been quantified and used as a measure for analyzing characters [18], gauging cladogram resolution [19,20], assessing cladogram topologies [21,22,23,24], proposing that evolution is a nonequilibrium thermodynamic process [25,26,27,28], evaluating classifications [29,30], preferring one among multiple equally parsimonious cladograms [31], combining multiple independent cladograms into a single cladogram, or “supertree”, through matrix representation [32,33,34,35], quantifying diversity among supraspecific taxa [36], and comparing molecular and morphological data [37]. No means for relating these applications has been derived; consequently, information in taxonomic classification has been understood and interpreted inadequately and underutilized, despite its great potential.
Achieving our general and specific purposes will remind researchers about the important role that information content can and should play in contemporary research. The resources available to conduct large-scale phylogenetic systematic analyses usually entail that information obtained is presented only in summary form (e.g., as cladograms), data and analytical details often relegated as supplementary, available as appended small-scale format text and in electronic repositories. The approach described subsequently herein enables researchers to quantify the information content in taxon-character matrices as they relate to the consistent cladograms derived from those matrices. Researchers specifically can evaluate characters—independently or in-combination—on the basis of the information that they provide, relating that information to their state distributions on and, therefore, support for classifications. Such relations bear on evolutionary scenarios when the bifurcating branching diagrams and character states are interpreted respectively as phylogenetic trees (i.e., inferred evolutionary relationships) and trait origins (or transformations). Synthesizing additional theoretical considerations like this in phylogenetic systematic analyses ultimately will strengthen justification for the term “bioinformatics”.
1.2. Consistent Cladograms
In cladistic analyses, cladograms are constructed from taxon-character matrices. Cladograms for which character states that are contained in character vectors nest hierarchically in a nonintersecting manner constitute “consistent cladograms” (i.e., consistent cladograms contain no homoplasous, or inconsistent, character states; in this paper, only characters that are encoded as binary character states are considered). We herein consider exclusively such cladograms because, for each, information measure I can be calculated solely from the taxon-character matrix; whereas calculating I for inconsistent cladograms requires, for each, accessing the taxon-character matrix as well as the corresponding cladogram, itself.
1.3. Information Theory and Cladistic Analysis
The information that is obtained by constructing a consistent cladogram from a taxon-character matrix containing only 0 (plesiomorphic) or 1 (apomorphic) character states is quantified by information measure I and calculated as a difference between information measures,
Both terms on the right side in Equation (1) derive from the Shannon Uncertainty Measure (Shannon, 1948; Shannon and Weaver, 1949). The total information capacity for a taxon-character matrix may be calculated in a surprisal analysis framework (e.g., [38]) as
Referring to [36], the observed information state for a cladogram is calculated as
in which , enumerates the 1s that are contained in the ith column vector and d enumerates the 1s that are contained in the taxon-character matrix [25,26,31,36]. Astute readers will notice that information I is presented hereby in a potential-based, negative manner, as a difference between initial state Iminimum (i.e., complete ignorance) and final state Iobserved (i.e., current knowledge), to accommodate convention.
1.4. Apomorphic Density Format
Because neither Equation (2) nor (3) takes into account positions for 1s within character vectors, or order for character vectors within taxon-character matrices, neither factor affects the information measure I for consistent cladograms. Therefore, to facilitate calculating I by visual inspection, taxon-character matrices from which consistent cladograms would be obtained can be modified in two ways. First, the 1s that are contained in each character vector can be considered as “sinking” toward the bottom and “piling” atop one another. Second, character vectors can be rearranged so that those containing the most 1s are shifted left and those containing the fewest 1s are shifted right. We define taxon-character matrices in this configuration to be in “apomorphic density format.” Reformating the matrices in this manner disconnects the relationship between taxa and character states, but, from the foregoing observations, imparts no effect on I (i.e., the same I would be obtained for consistent cladograms using taxon-character matrices in either original or apomorphic density formats). For instances, the following three matrices yield equal I for the consistent cladogram that is depicted in Figure 1, although calculating I by visual inspection is facilitated greatly using the rightmost one:
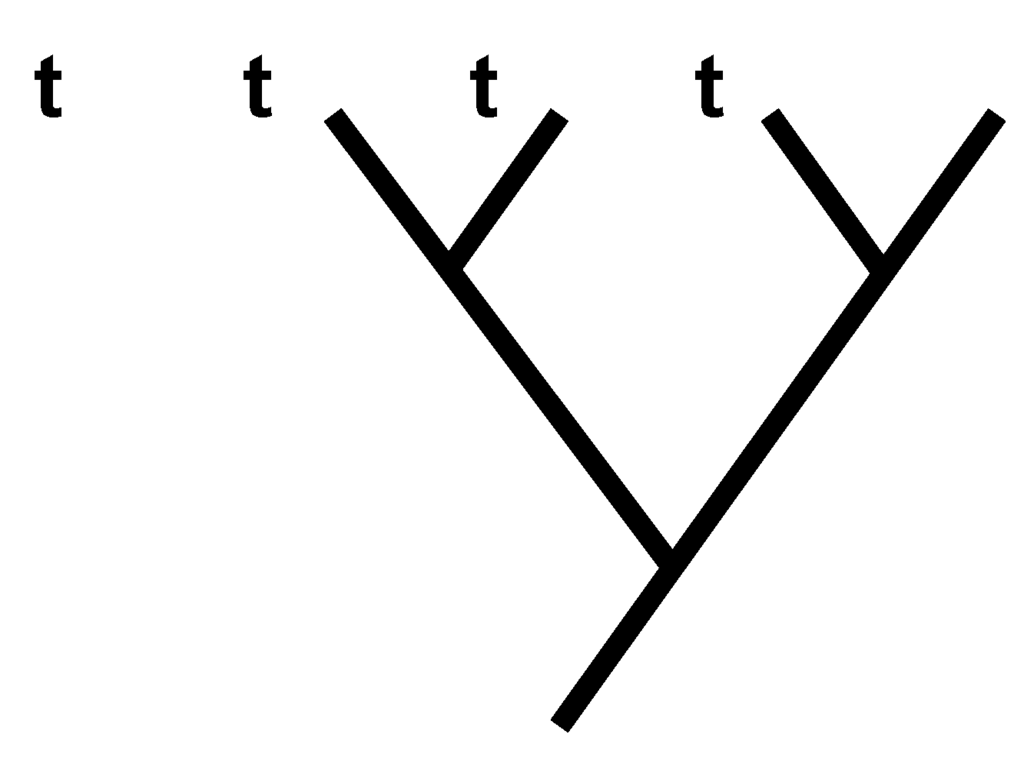
Figure 1.
Consistent cladogram that would be obtained from cladistic analysis involving leftmost matrix (4); in that matrix, row i contains character states for taxon i and columns contain character vectors.
1.5. A General Expression Quantifying I
A general expression quantifying information measure I in association with constructing consistent cladograms can be derived from studying their associated taxon-character matrices in apomorphic density format. Let be positive integers that enumerate character vectors containing i 1s (character vectors containing a single 1 encode autapomorphic character states; character vectors containing t 1s encode synapomorphic character states for and, so, define the “ingroup”; therefore, we adopt notation in which the index variable i runs from 1 through t; no information is available from character vectors containing only 0s; we assume throughout this analysis that proper outgroup analysis has been conducted and outgroup character states comprise only 0s). For instance, the matrices in Equation (4) yield , , and . Taxon-character matrices generally will yield the integers . This convenient prescription can be visualized using the general taxon-character matrix, which is presented in apomorphic density format,
Let d enumerate 1s over all c character vectors. Then
From Equation (2) and matrix (5),
From Equations (3) and (6) and matrix (5),
(a derivation for Equation (8) is provided in Appendix). Using Equations (1), (7), and (8), the information that is obtained by constructing any consistent cladogram from its corresponding taxon-character matrix is
The units with which I is reported are bits, which quantify the information acquired in making binary decisions (i.e., choosing between two equiprobable events).
1.6. Consistent Basal Matrices and Conventions
We define a “consistent basal matrix” to be a taxon-character matrix containing the fewest column vectors that are required to construct a consistent cladogram. For instance, two consistent basal matrices for four taxa are possible:
Matrix (10.1) yields a pectinate cladogram (i.e., a cladogram with a pectinate topology), whereas matrix (10.2) yields a symmetric cladogram (i.e., a cladogram with a symmetric topology; Figure 2a,b).
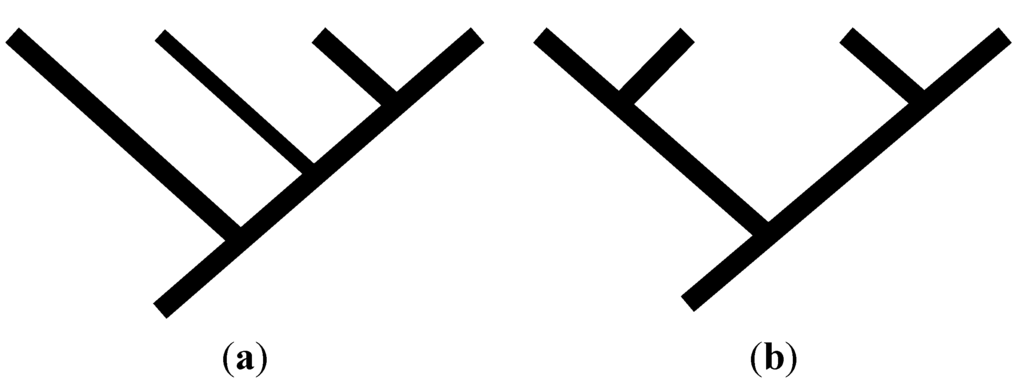
Figure 2.
Cladogram topologies for the two possible consistent basal matrices for four taxa: the pectinate cladogram at the left would be obtained from a cladistic analysis involving consistent basal matrix (10.1); the symmetric cladogram would be obtained from a cladistic analysis involving consistent basal matrix (10.2).
Consider the three consistent basal matrices for five taxa:
To calculate information measure I by visual inspection, matrices (11.1)–(11.3) may be rewritten by representing each character vector by a single number enumerating the 1s that are contained in that column vector:
each consistent basal matrix can be assigned numbers for taxa; total 1s; second-greatest 1s within a character vector; and third-greatest 1s within a character vector. Then, representation Equation (11.4) becomes (5 taxa; 14, 4, 3); Equation (11.5) becomes (5 taxa; 13, 4, 2); and Equation (11.6) becomes (5 taxa; 12, 3, 2). This representation system will prove to be convenient because it corresponds to the order in which plots for I “descend” relative to each other after the maximum has been reached (an observation that is discussed in subsequent sections).
1.7. Adding Character Vectors to Consistent Basal Matrices
Adding autapomorphic or synapomorphic character states to a consistent cladogram corresponds to adding appropriate character vectors to the associated consistent basal matrix. Additional character vectors may encode autapomorphic character states, containing a single 1 (“autapomorphic character vectors”), or synapomorphic character states, containing multiple 1s (“synapomorphic character vectors”).
For four taxa, the following four autapomorphic character vectors are equivalent in their contribution to information measure I:
However, if any among these autapomorphic character vectors were added to a taxon-character matrix and that matrix subsequently were transformed into apomorphic density format, then the character vector(s) would be arranged in the form that is assumed by character vector Equation (12.4); all additional autapomorphic character vectors would assume this form, to facilitate calculating I by visual inspection. Similarly, the following synapomorphic character vectors are equivalent in their contribution to I:
but, as with the autapomorphic character vectors, to facilitate calculating I by visual inspection, all synapomorphic character vectors containing two 1s would be arranged in the same form, the one that is assumed by character vector Equation (13.6).
2. Results and Discussion
2.1. Achieving Maximum I as Autapomorphic Character Vectors are Added to Consistent Basal Matrices
Information as quantified by information measure I has an upper bound; it can be increased by adding to taxon-character matrices autapomorphic character vectors, but it decreases as added character vectors accumulate.
The maximum I that can be obtained by constructing a pectinate 4-taxon cladogram is approximately 2.2467 bits; this is achieved when six autapomorphic character vectors are added to consistent basal matrix (10.1). Thus, the following taxon-character matrix, which is presented in apomorphic density format, will yield the maximum I when a cladogram is constructed from it.
For a symmetric 4-taxon cladogram, the maximum I that can be obtained is approximately 2.2226 bits; this is achieved when five autapomorphic characters are added to consistent basal matrix (10.2), a situation which also is presented in apomorphic density format:
As character vectors are added, I generally is greater for the pectinate than for the symmetric consistent basal matrix case (Figure 3). As with the case involving four taxa, the I that can be obtained by adding to 5-taxon consistent basal matrices character vectors encoding autapomorphic character states is bounded (Figure 4).
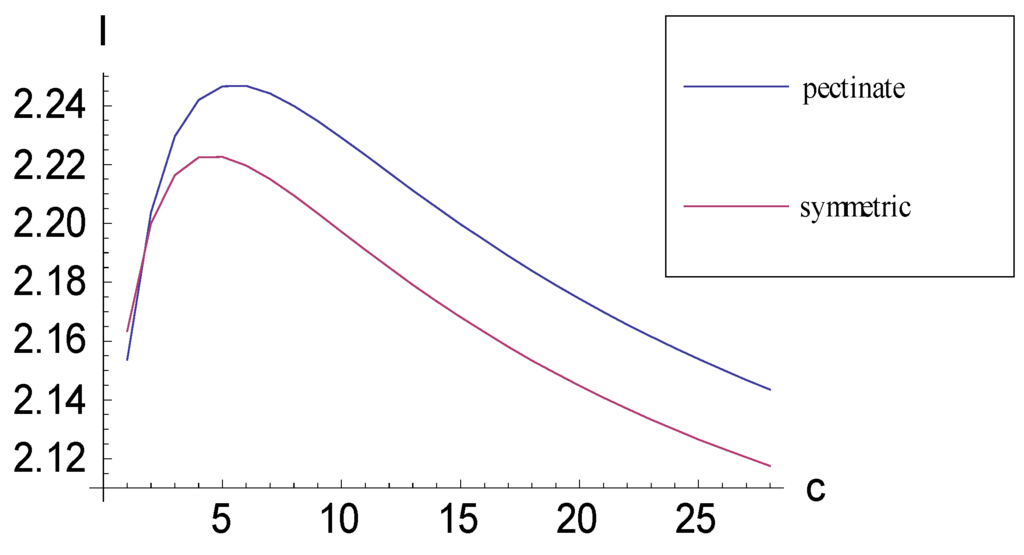
Figure 3.
Plots relating information measure I and added autapomorphic characters c for consistent basal matrices (10.1) (pectinate) and (10.2) (symmetric). An upper bound to I exists in both cases.
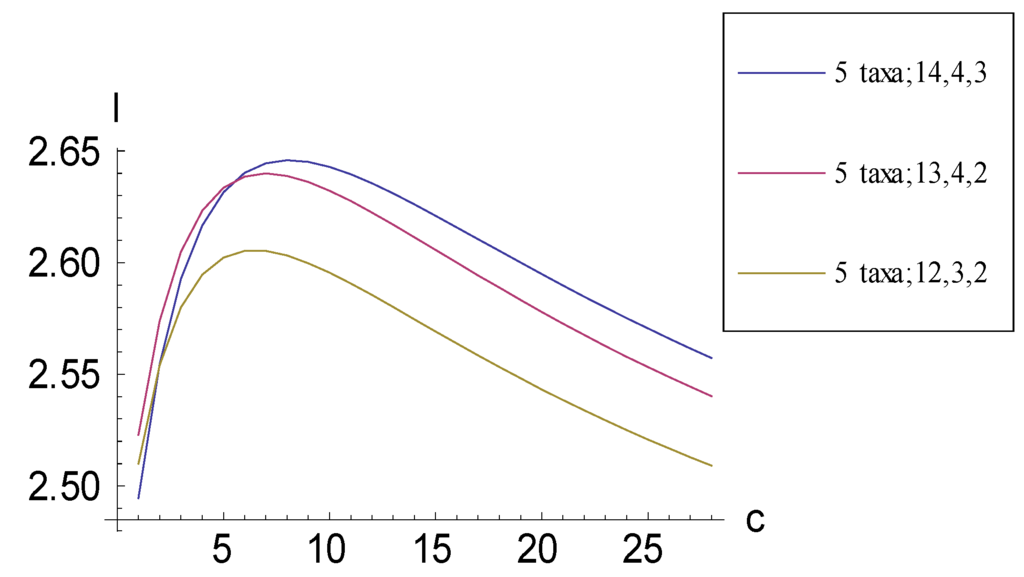
Figure 4.
Plots relating information measure I and added autapomorphic characters c for consistent basal matrices (11.1)–(11.3). An upper bound to I exists in all three cases.
The order in which plots containing t taxa that are presented herein descend after their maxima I have been reached is determined by, first, the total 1s that are contained in the consistent basal matrix; second, for matrices containing equivalent total 1s, the second-greatest 1s within a character vector; and third, the third-greatest 1s within a character vector. Therefore, if two matrices representing the same taxa also contain the same total 1s, then the second-greatest 1s that are contained in a single character vector should be compared to rank-order their representative plots. For instance, between the two representations (a taxa; b, c, d) and (a taxa; b’, c’, d’), if b > b’, then (a taxa; b, c, d) will descend with a greater I after the maximum has been achieved. If b = b’, then c and c’ can be compared in a similar manner.
For t = 4 and 5 taxa, the plot for the pectinate basal consistent matrix case always descends with the greatest I and always achieves the absolute maximum I. For greater t, although the plot for the pectinate basal consistent matrix case eventually descends with the greatest I, the basal consistent matrix corresponding to the plot that reaches the absolute maximum varies (Figure 5, Figure 6 and Figure 7). For six or seven taxa, only one other basal consistent matrix can yield a maximum I that exceeds that for the pectinate cladogram (Figure 5 and Figure 6). For eight taxa, two matrices yield greater maxima (Figure 7).
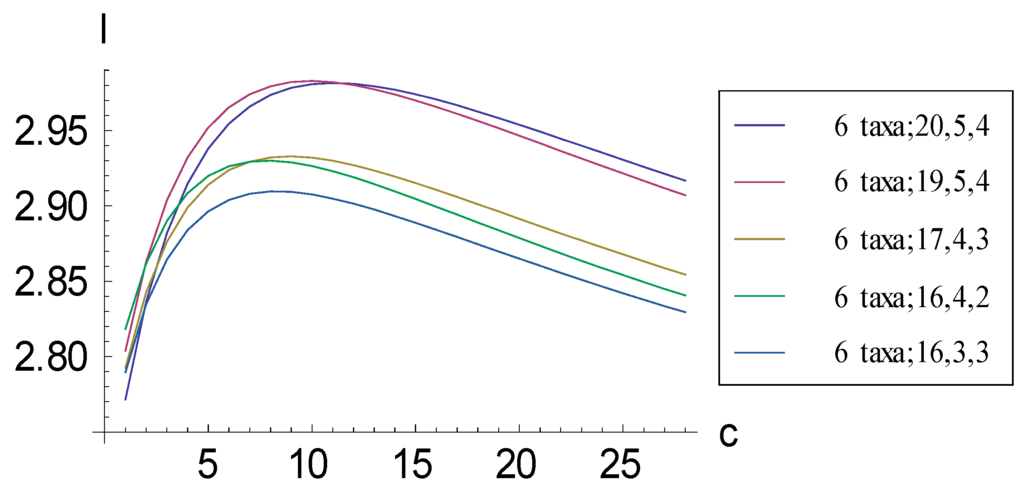
Figure 5.
Plots relating information measure I and added autapomorphic characters c for some consistent basal matrices for six taxa. The absolute maximum I is achieved by representation (6 taxa; 19, 5, 4) rather than by the representation corresponding to the pectinate consistent basal matrix (6 taxa; 20, 5, 4), which contains more 1s. After the absolute maximum has been achieved, plots descend in the order (6 taxa; 20, 5, 4), (6 taxa; 19, 5, 4), (6 taxa; 17, 4, 3), (6 taxa; 16, 4, 2), and (6 taxa; 16, 3, 3).
Generally, as t is increased, more autopomorphic character vectors must be added for I to descend in “order” (i.e., according to the foregoing prescriptions). For instances, almost 50 autapomorphic character vectors must be added to distinguish graphically the top three plots for eight taxa (Figure 7), whereas fewer than 30 character vectors are required for seven taxa (Figure 6).
On the basis of these observations, two predictions concerning increases to I as autapomorphic character vectors are added to consistent basal matrices containing t > 5 taxa can be proffered: (1) the absolute maximum I will be obtained with a taxon-character matrix that would yield most-parsimoniously a nonpectinate cladogram; (2) as t were increased, more and more taxon-character matrices that would yield most-parsimoniously nonpectinate cladograms will be associated with maxima that were greater than the maximum obtained with the matrix that would yield most-parsimoniously a pectinate cladogram.
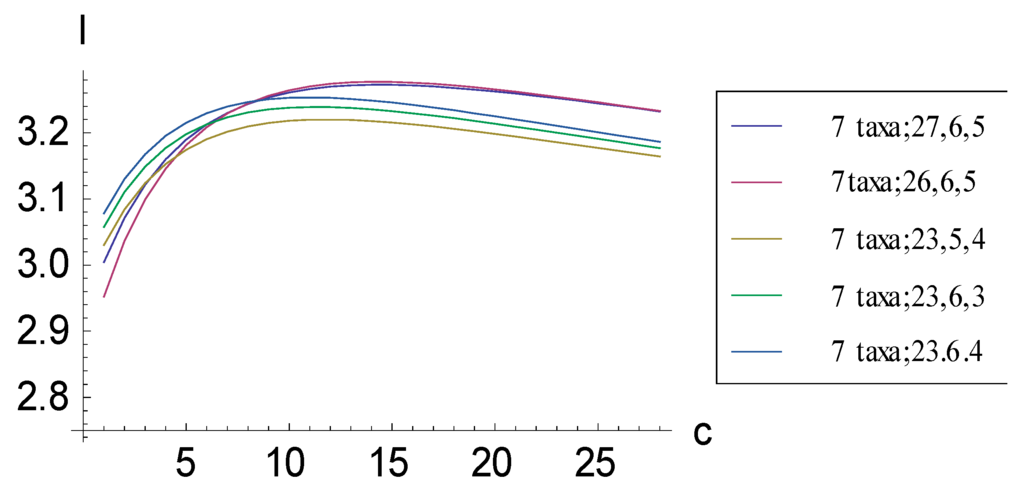
Figure 6.
Plots relating information measure I and added autapomorphic characters c for some consistent basal matrices for seven taxa. The absolute maximum I is achieved by representation (7 taxa; 26, 6, 5) rather than by the representation corresponding to the pectinate consistent basal matrix (7 taxa; 27, 6, 5), which contains more 1s. After the absolute maximum has been achieved, plots descend in the order (7 taxa; 27, 6, 5), (7 taxa; 26, 6, 5), (7 taxa; 23, 6, 4), (7 taxa; 23, 6, 3), and (7 taxa; 23, 5, 4).
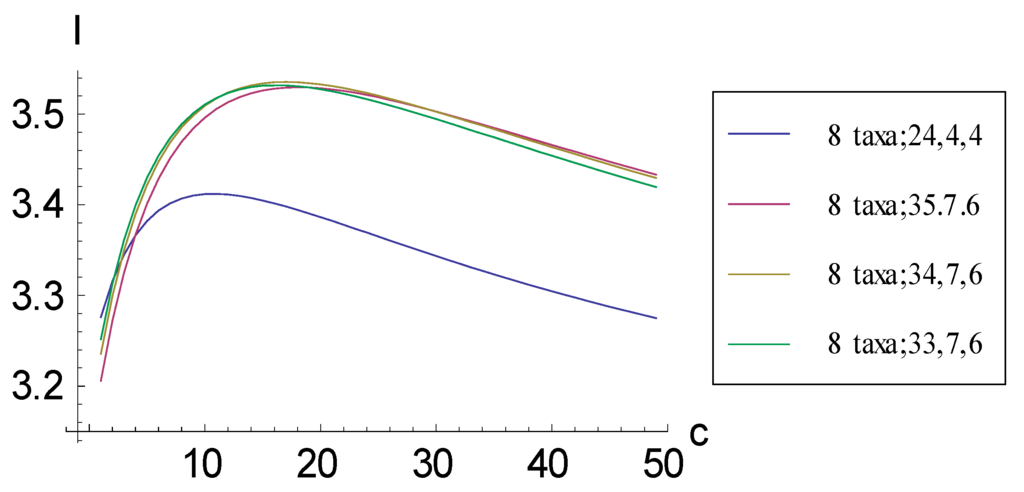
Figure 7.
Plots relating information measure I and added autapomorphic characters c for some consistent basal matrices for eight taxa. The representation corresponding to the pectinate cladogram is (8 taxa; 35, 7, 6), whereas the representation corresponding to the symmetric cladogram is (8 taxa; 24, 4, 4).
2.2. Achieving Maximum I as Synapomorphic Character Vectors are Added to Consistent Basal Matrices
The information measure I also can be increased by adding to taxon-character matrices synapomorphic character vectors; but, ultimately, adding to taxon-character matrices containing t taxa character vectors containing x 1s, where , will decrease the I that is obtained by constructing a cladogram, just as adding autapomorphic character vectors will. Greater xs effect greater decreases (e.g., representation (8 taxa; 24, 4, 4) in Figure 8 and Figure 9).
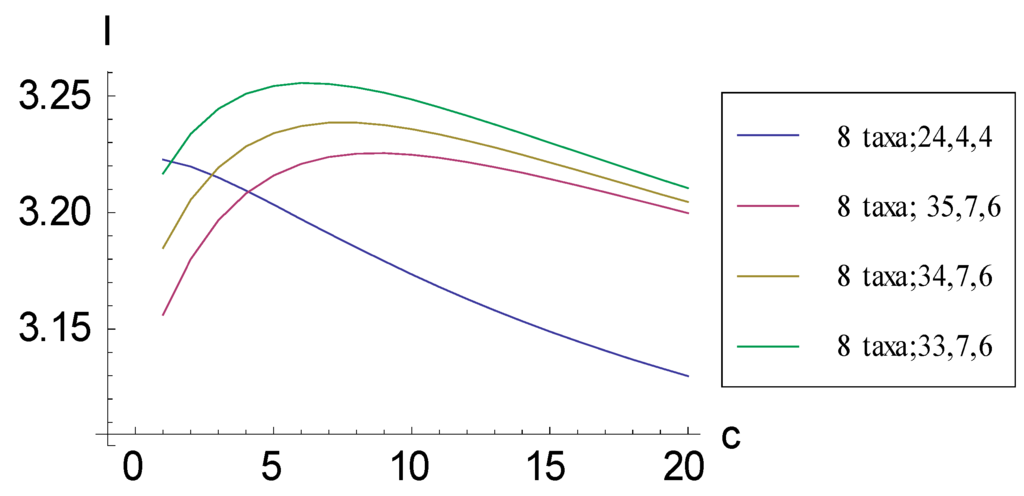
Figure 8.
Plots relating information measure I and added character vectors c containing two 1s (i.e., synapomorphic character states grouping two taxa) for four consistent basal matrices for eight taxa. Three plots descend qualitatively in a similar pattern to those followed when character vectors encoding autapomorphic character states are added (Figure 5, Figure 6 and Figure 7). For the symmetric representation (8 taxa; 24, 4, 4), I changes markedly.
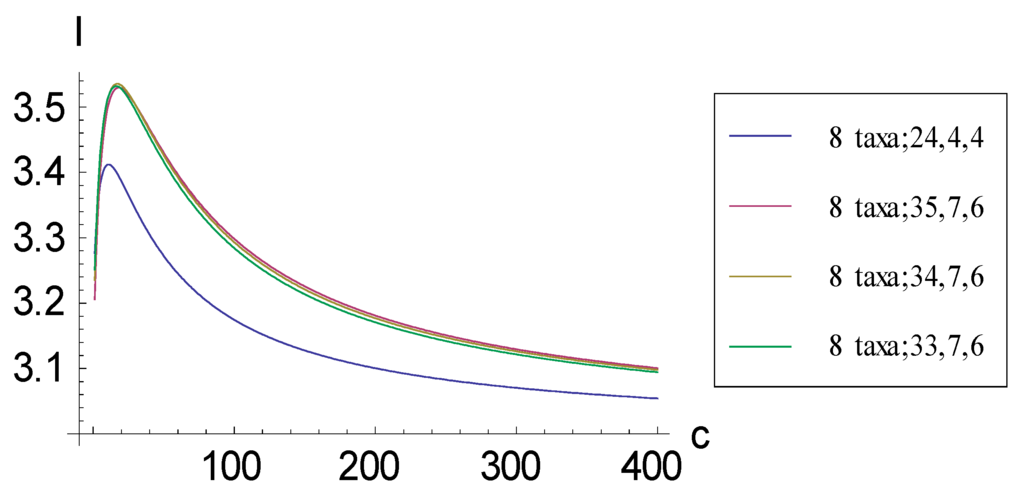
Figure 9.
Plots relating information measure I and added autapomorphic characters c for 4 consistent basal matrices for eight taxa. The axes have been extended with respect to the plot in Figure 8 to reveal how I plots become asymptotic as c becomes very large. In this case, because the representations involve eight taxa, the plots asymptote to three bits. At c = 400, the I for (8 taxa; 24, 4, 4), (8 taxa; 35, 7, 6), (8 taxa; 34, 7, 6), and (8 taxa; 33, 7, 6) are 3.0542, 3.1006, 3.0981, and 3.0943; at c added = 5000, they would be 3.0047, 3.0089, 3.0087, and 3.0083.
2.3. Minima for I
Numerical modeling and computer simulation reveal that augmenting a consistent basal matrix containing t taxa by adding n character vectors containing x ones () diminishes I and the attenuation approaches bits as n approaches infinity. More formally, we present the theorem: if enumerates character vectors containing x ones that are added to a consistent basal matrix, then,
The asymptotic nature for these limits can be understood intuitively. If a column vector containing x 1s were added repeatedly to a consistent basal matrix containing t taxa, then, as the repetition number were to approach infinity, the initial consistent basal matrix would become insignificant. The resulting matrix essentially would become
in which each column vector would contain x ones (i.e., as , the matrix essentially would comprise n character vectors, each containing x ones). The total 1s would equal approximately xn, and I could be estimated using Equations (1)–(3):
We have observed that I approaches this limit in numerical modeling and computer simulation investigations in which autapomorphic or synapomorphic character vectors were added (the interested reader may imagine accumulating autapomorphic character states for one taxon or synapomorphic character states for a group; a formal demonstration for limit Equation (16) is provided in Appendix). We remark that I increases in a complicated manner if a variety of character vector types are added to a consistent basal matrix.
2.4. Information and Phylogenetic Systematic Analyses
Information in phylogenetic systematic analyses has been used as a quantitative metric, means for considering evolution in thermodynamic terms, criterion for choosing among competing systematic classifications, guiding variable in constructing supertrees, parameter for measuring diversity, and basis for comparing data types. We briefly review these applications (in this section) and, on the basis of the foregoing results, render these applications amenable to more-precise interpretation (in the subsequent section).
2.5. Information as a Quantitative Metric
Schuh and Farris [21] defined the “levels sum” measure to quantify information; this metric may be calculated by constructing a matrix with terminal taxa along both edges, entering as matrix elements counts for pairwise informative components, and summing all elements (Figure 10). Rohlf and Sokal [19] and Rohlf et al. [20] considered resolution as a proxy for information and provided a means for quantification on the basis of clades (Figure 10). Nelson [22] decomposed cladogram information into “component” and “term” partitions: component information may be quantified by enumerating clades above the most-basal node; term information may be quantified by summing cumulatively nested clades (Figure 10). Mickevich and Platnick [23] considered 14 measures: component information, term information, total (component + term) information, “proportion of the maximal possible total information”, “number of three-taxon statements”, “number of character state distributions prohibited by cladograms with non-terminal polychotomies”, levels sum, “number of fully resolved cladograms allowed by a Nelson consensus”, “number of resolutions prohibited by a Nelson consensus”, “proportion of total number of resolutions that are prohibited by a Nelson consensus”, “number of resolutions allowed by an Adams consensus”, “number of resolutions prohibited by an Adams consensus” and the “general information index” (Figure 10); they stipulated that cladograms containing polychotomies should constitute minimally informative classifications and found that pectinate cladograms comprising constitute maximally informative classifications. Page [24] evaluated critically the points that had been made by Mickevich and Platnick, arguing that they failed to provide compelling reasons for “not equating the information of a tree topology with its degree of resolution”; Page also provided a formula for calculating WISS (Weighted Invariant Step Strategy) total steps (“total information” in [23]); observed that WISS ignores prohibited taxonomic statements; and showed that the conclusions that were drawn by Mickevich and Platnick [23] (i.e., that pectinate cladograms are most-informative) failed to account for prohibited taxonomic statements and derived from a particular perspective about taxonomic structure (i.e., structure = “clusters”, or monophyletic taxa).
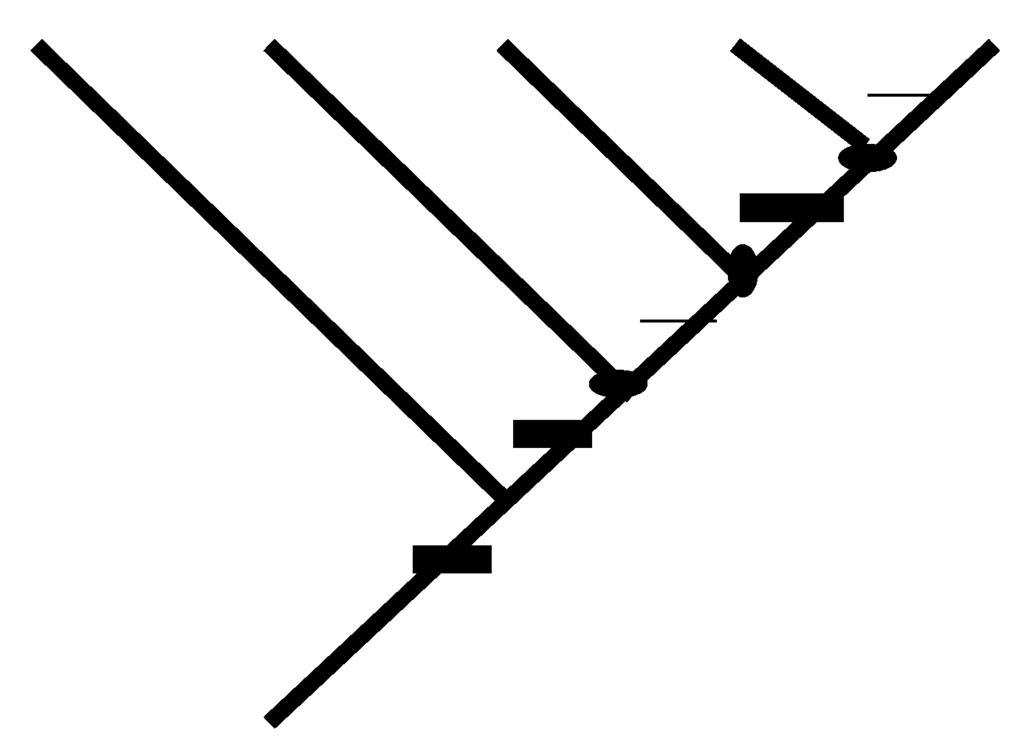
Figure 10.
Information measures for a pectinate cladogram containing five taxa. The levels sum measure [21] is calculated by enumerating pairwise informative components, here 10 (four with the most-basal taxon, three with the next most-basal taxon, two with the second-least basal taxon, and one between the two least-basal taxa). Resolution [19,20] may be calculated by enumerating nodes (shown as dots) above the ingroup node and dividing by n-2, here 3/3 = 1. Component information [22] may be quantified by enumerating clades (shown as dots) above the most-basal node, here 3. Term information [22] may be quantified by summing cumulatively nested clades (above the most-basal node), here 6. Total information = term information + component information [22], here 9. Other measures include the proportion of the maximal possible total information [23], here 9/9 = 1; number of three-taxon statements (Mickevich and Platnick, 1989), here 10; number of character state distributions prohibited by cladograms with non-terminal polychotomies [23], here 22; number of fully resolved cladograms allowed by a Nelson consensus [23], here 1; number of resolutions prohibited by a Nelson consensus [23], here 104; proportion of total number of resolutions that are prohibited by an Adams consensus [23], here 1; number of resolutions allowed by an Adams consensus [23], here 1; and the general information index—proportion of the maximal possible total information x proportion of total number of resolutions that are prohibited by an Adams consensus, here 1.
2.6. Information as a Means for Considering Evolution in Thermodynamic Terms
Wiley and Brooks [25,26] quantified information, on the basis of the second law of thermodynamics—particularly the Shannon Uncertainty Measure [1,2], to propose that evolution is a natural process in which the entropy that is produced is minimized. According to their formulation, energy is used to organize information as traits in ancestors and, through those traits, organized information is inherited by descendants. Thus, traits serve as “entropy capacitors”, providing mechanisms for preserving organization and storing the concomitant entropy that was produced by ancestors, thereby minimizing total entropy production within a lineage over time. These historical constraints on species evolution are interpreted as shared derived traits originating on phylogenetic trees (i.e., inferred from synapomorphic character states on cladograms), which provide a record from which information (i.e., “negentropy”) can be quantified.
2.7. Information as a Criterion for Choosing among Competing Systematic Classifications
Brooks et al. [31] quantified information to promote the measure D, which was formulated on the basis of the Shannon Uncertainty Measure [1,2], as an optimality criterion in cladistic analysis. Given cladograms that are equally parsimonious, D provides a measure that is more sensitive to but less biased by character state types (i.e., symplesiomorphic, autapomorphic, and synapomorphic character states) than are other measures (e.g., the consistency index).
2.8. Information as a Guiding Variable in Constructing Supertrees
Purvis [32] proposed a coding scheme that eliminated redundant information (and, thereby, eliminated disproportionate weightings for large cladograms) in creating matrices from which supertrees may be determined [38,39,40]. Ronquist [33] and Wilkinson et al. [35] criticized that coding scheme; in particular, Wilkinson et al. showed that it failed to remove all redundant information and proposed an alternative, weighting scheme that may be used in a complementary manner and involved the “cladistic information content”,
where N enumerates bifurcating cladograms.
CIC = −Log[Npermitted/Ntotal]
2.9. Information as a Parameter for Measuring Diversity
Stone [36] quantified information on the basis of the Shannon Uncertainty Measure [1,2] to provide a means for comparing diversity among higher taxa. The information for groups within a clade for which identical characters have been diagnosed will differ substantially if certain groups contain substantially more species than do others. Therefore, by comparing information, researchers can gauge species richness or “retrodictively” assess radiations in a quantitative manner.
2.10. Information as a Basis for Comparing Data Types
Cotton and Wilkinson [37] utilized the CIC [35] to assess the information conveyed by phylogenetic data. They converted a formula that had been derived by Carter et al. [41] to quantify the proportion among binary trees that fit an unordered character without cost and used it to show that molecular data are more informative than are morphological data but less so than other information measures might indicate.
3. Conclusions
3.1. Interpretation
Common to the aforementioned uses for information in phylogenetic systematic analysis is a quantification for the “knowledge state” characterizing the taxonomist. Equation (9) is suited ideally for generalizing this quantification, as it is formulated on the basis of information theory and involves subtracting from the total information potentially available (Imaximum) the information that currently is available (Iobserved). This generalization property will assist systematists in comprehending information, however measured (i.e., whether on the basis of cladogram properties, as described in the subsection “Information as a Quantitative Metric”, or according to information theory proper, as described in the other three subsections in the preceding section).
3.2. Information as a Quantitative Metric
For instance, using the analyses that are presented herein, we now can reconcile the discrepancy between conclusions drawn by Mickevich and Platnick [23]—that pectinate cladograms constitute maximally informative classifications—and conclusions reached by Page [24]—that, in drawing their conclusion, Mickevich and Platnick had ignored prohibited taxonomic statements and considered taxonomic structure exclusively as clusters. Mickevich and Platnick had restricted their analysis predominantly to t = 5 taxa, as they felt that this constituted “the smallest number of taxa for which there is a diversity of cladogram topologies to be interesting.” As shown herein, for t = 5 taxa (and c > 5 characters), the pectinate cladogram is the maximally informative consistent cladogram; whereas, for t > 5, nonpectinate cladograms may yield more information. Because Mickevich and Platnick had confined their attention to the specific case t = 5 taxa, the generalities that could be posited from their analyses were limited, a constraint that Page observed intuitively and demonstrated.
3.3. Information as a Means for Considering Evolution in Thermodynamic Terms
Concerning Wiley and Brooks’ [25,26] proposal that evolution is a natural process in which the entropy that is produced is minimized, we observe that their formulation concerns organizational changes over time that involve changes to t, rather than organization within a particular phylogenetic tree (for which t would be fixed). Testing hypotheses that derive from their theory would be conducted most-effectively using paleontological data (i.e., extinct taxa for which dated fossil material over epochs were available), as changes in information over time could be analyzed (i.e., with increasing t and fixed c).
3.4. Information as a Criterion for Choosing among Competing Systematic Classifications
Concerning the D criterion that was proposed by Brooks et al. [31], the results that are presented herein indicate that D yields a maximum but would approach the asymptote (which is less than the maximum) as more data were accumulated for any group under analysis. This behavior ought to be considered in invoking the “greatest-D criterion” in any particular phylogenetic systematic analysis (i.e., for any particular t). Brooks et al. recognized that greater D sometimes could be obtained from less-than-most-parsimonious cladograms. In this respect, the results that are presented herein explain the authors’ caution: “the D measure is to be used to choose among trees after the set of trees has been reduced to those of equally-shortest length”.
3.5. Information as a Guiding Variable in Constructing Supertrees
Concerning the methods proposed by Purvis [32], Ronquist [33], and Wilkinson et al. [35] for constructing supertrees, different coding schemes (i.e., matrices containing different character vectors) indeed will yield different information, and Equation (9) provides an independent means for assessing whether information will increase upon recoding.
3.6. Information as a Parameter for Measuring Diversity
Concerning Stone’s [36] using information as a means for comparing diversity among higher taxa, the results that are contained herein show that information may be implemented heuristically in this manner; in fact, if sister groups were to be compared, then accumulating autapomorphic character states for one taxon in each sister group or synapomorphic character states for each sister group would enable researchers to correlate information content with diversity directly (trivially, via limit Equation (16)). For situations in which different character state types were amassed for different taxa, information content and diversity would be related but in a more-complicated manner.
3.7. Information as a Basis for Comparing Data Types
Finally, concerning the proposal by Cotton and Wilkinson [37] to use information as a basis for comparing data types, the results that are contained herein entail that the information that may be obtained from any data type is bounded if those data would yield most-parsimoniously a consistent cladogram; if t > 5, then only data that would yield most-parsimoniously a nonpectinate consistent cladogram would yield maximum information, especially for large t.
3.8. Prospectus
Information is being applied increasingly in phylogenetic-systematic-related analyses, as data from genome projects amass and analyses involving entire genomes become more common. For instances, information has been used in cladogram construction [42,43,44], for drug discovery [45], as a guide in pharmacological data mining [46], with assessing Markov processes [47], and to calculate probabilities for chemical words in DNA sequences [48]. Possessing a more-precise interpretation for how information in phylogenetic systematic analysis has been used could assist in formalizing links between biology and information (ultimately justifying the term “bioinformatics”) and ultimately a synthesis between bioinformatics and evolution.
Acknowledgments
The information contained in this paper was produced as a consequence from a casual placement in 2003 summer by Jonathan Long and with support from the Natural Sciences and Engineering Research Council of Canada, Canada Research Chairs Program, and Individual Discovery Grants 238452 (to Walter Craig) and 261590 (to Jonathon Stone); Shared Hierarchical Academic Research Computing Network; and McMaster University. Comments, suggestions, and additional information were provided by Dick Morton, Roderic Page, and two anonymous reviewers.
Author Contributions
Both authors contributed to all components to the research described herein; Jonathon Stone contributed to analysis, Walter Craig contributed predominantly to mathematics, and Jonathon Stone contributed predominantly to composition. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Deriving Equation (8)
Demonstrating the Limit for Equation (16)
Consider a taxon-character matrix A comprising ai columns containing i ones. Let
as in Equation (1). The quantity I may be expressed as
Normalize this expression by setting
so that
is a probably measure, which, for functions , the sums
represent the expectation value. In this notation, the difference
Take the function
which is convex in the variable . Then
the inequality being implied by Jensen’s inequality for convex functions.
Theorem
Let t be fixed and , in a way such that, for some x, while, for all other , are bounded. Then
Proof
One may let , letting some or all of the diverge to infinity, as well, but in a manner such that . In the limit, the proportion among columns containing x ones converges to 1, and the probability measures given by
converge to a δ-measure concentrated at the point i = x. In this case,
and the quantity has a limit:
In particular, the quantity
converges to zero, which is the result in question.
We remark that, if two (or more) s diverge to infinity in a manner such that the ratio tends to a non-zero constant, then the measure
converges as to a measure that is supported at more than one point; the strict Jensen’s inequality will imply that
This makes sense intuitively, as one is acquiring different information about a positive proportion among the taxa (those described through the s, rather than those described by the s).
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 279–423, 623–656. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Brillouin, L. Science and Information Theory; Academic Press: New York, NY, USA, 1962. [Google Scholar]
- Johnson, J.A. Information theory in biology after 18 years. Science 1970, 168, 1545–1550. [Google Scholar] [CrossRef] [PubMed]
- Atlan, H. L’Organisation Biologique et la Theorie de L’Information; Hermann Press: Paris, France, 1972. (In French) [Google Scholar]
- Gatlin, L.L. Information Theory and the Living System; Columbia University Press: New York, NY, USA, 1972. [Google Scholar]
- Prigogine, I.; Nicolis, G.; Babloyantz, A. Thermodynamics of evolution. Phys. Today 1972, 25, 23–28, 38–44. [Google Scholar] [CrossRef]
- Saunders, P.T.; Ho, M.W. On the increase in complexity in evolution. J. Theor. Biol. 1976, 63, 375–384. [Google Scholar] [CrossRef]
- Saunders, P.T.; Ho, M.W. On the increase in complexity in evolution II. The relativity of complexity and the principle of minimum increase. J. Theor. Biol. 1981, 90, 515–530. [Google Scholar] [CrossRef]
- Wicken, J.S. The generation of complexity in evolution: A thermodynamic and information-theoretical discussion. J. Theor. Biol. 1979, 77, 349–365. [Google Scholar] [CrossRef]
- Wicken, J.S. A thermodynamic theory of evolution. J. Theor. Biol. 1979, 87, 9–23. [Google Scholar] [CrossRef]
- Maynard Smith, J. The concept of information in biology. Philos. Sci. 2000, 67, 177–194. [Google Scholar] [CrossRef]
- Sterelny, K. The “genetic program” program: A commentary on Maynard Smith on information in biology. Philos. Sci. 2000, 67, 195–201. [Google Scholar] [CrossRef]
- Godfrey-Smith, P. Information, arbitrariness, and selection: Comments on Maynard Smith. Philos. Sci. 2000, 67, 202–207. [Google Scholar] [CrossRef]
- Sarkar, S. Information in genetics and developmental biology: Comments on Maynard Smith. Philos. Sci. 2000, 67, 208–213. [Google Scholar] [CrossRef]
- Kauffman, S.; Logan, R.K.; Este, R.; Goebel, R.; Hobill, D.; Shmulevich, I. Propagating organization: An enquiry. Biol. Philos. 2007, 23, 27–45. [Google Scholar] [CrossRef]
- Logan, R.K. What is information? Why is it relativistic and what is its relationship to materiality, meaning and organization? Information 2012, 3, 68–91. [Google Scholar] [CrossRef]
- Hawksworth, F.G.; Estabrook, G.F.; Rogers, D.F. Application of an information theory model for character analysis in the genus Arceuthobium (Viscaceae). Taxon 1968, 17, 605–619. [Google Scholar] [CrossRef]
- Rohlf, F.J.; Sokal, R.R. Comparing numerical taxonomic studies. Syst. Zool. 1982, 30, 459–490. [Google Scholar] [CrossRef]
- Rohlf, F.J.; Coless, D.H.; Hart, G. Taxonomic congruence reexamined. Syst. Zool. 1983, 32, 144–158. [Google Scholar] [CrossRef]
- Schuh, R.T.; Farris, J.S. Methods for investigating taxonomic congruence and their application to the Leptopodomorpha. Syst. Zool. 1981, 30, 331–351. [Google Scholar] [CrossRef]
- Nelson, G. Cladistic analysis and synthesis: Principles and definitions, with a historical note on Adanson’s Families des Plantes (1763–1764). Syst. Zool. 1979, 28, 1–21. [Google Scholar] [CrossRef]
- Mickevich, M.F.; Platnick, N.I. On the information content of classifications. Cladistics 1989, 5, 33–47. [Google Scholar] [CrossRef]
- Page, R.D.M. Comments on the information content of classifications. Cladistics 1992, 8, 87–95. [Google Scholar] [CrossRef]
- Wiley, E.O.; Brooks, D.R. Victims of history—A nonequilibrium approach to evolution. Syst. Zool. 1982, 31, 1–24. [Google Scholar] [CrossRef]
- Wiley, E.O.; Brooks, D.R. Nonequilibrium thermodynamics and evolution: A response to Løvtrup. Syst. Zool. 1983, 32, 209–219. [Google Scholar] [CrossRef]
- Løvtrup, S. Victims of ambition: Comments on the Wiley and Brooks approach to evolution. Syst. Zool. 1983, 32, 90–96. [Google Scholar] [CrossRef]
- Duncan, T.; Estabrook, G.F. An operational method for evaluating classifications. Syst. Bot. 1976, 1, 373–382. [Google Scholar] [CrossRef]
- Carpenter, K.E. Optimal cladistic and quantitative evolutionary classifications as illustrated by fusilier fishes (Teleostei: Caesionidae). Syst. Biol. 1993, 42, 142–154. [Google Scholar] [CrossRef]
- Brooks, D.R.; Wiley, E.O. Evolution as Entropy; University of Chicago Press: Chicago, IL, USA, 1988. [Google Scholar]
- Brooks, D.R.; O’Grady, R.T.; Wiley, E.O. A measure of the information content of phylogenetic trees, and its use as an optimality criterion. Syst. Zool. 1986, 35, 571–581. [Google Scholar] [CrossRef]
- Purvis, A. A modification to Baum and Ragan’s method for combining phylogenetic trees. Mol. Phylogenet. Evol. 1995, 1, 53–58. [Google Scholar]
- Ronquist, F. Matrix representation of trees, redundancy, and weighting. Syst. Biol. 1996, 45, 247–253. [Google Scholar] [CrossRef]
- Thorley, J.L.; Wilkinson, M.; Charleston, M. The Information Content of Consensus Trees. In Advances in Data Science and Classification: Studies in Classification, Data Analysis and Knowledge Organisation; Rizzi, A., Vichi, M., Bock, H.-H., Eds.; Springer: Berlin, Germany, 1998; pp. 91–98. [Google Scholar]
- Wilkinson, M.; Cotton, J.A.; Thorley, J.L. The information content of trees and their matrix representation. Syst. Biol. 2004, 53, 989–1001. [Google Scholar] [CrossRef] [PubMed]
- Stone, J.R. Information obtained in cladistic analysis. Biosystems 2001, 61, 33–39. [Google Scholar] [CrossRef]
- Cotton, J.A.; Wilkinson, M. Quantifying the potential utility of phylogenetic characters. Taxon 2008, 57, 131–136. [Google Scholar]
- Levine, R.D.; Bernstein, R.B. Molecular Reaction Dynamics; Clarendon Press: Oxford, UK, 1974. [Google Scholar]
- Baum, B.R. Combining trees as a way of combining data sets for phylogenetic inference, and the desirability for combining gene trees. Taxon 1992, 41, 1–10. [Google Scholar] [CrossRef]
- Ragan, M.A. Phylogenetic inference based on matrix representations of trees. Mol. Phylogenet. Evol. 1992, 1, 538–558. [Google Scholar] [CrossRef]
- Carter, M.; Hendy, M.D.; Penny, D.; Székely, L.A.; Wormald, N.C. On the distribution of lengths of evolutionary trees. SIAM J. Discret. Math. 1990, 3, 38–47. [Google Scholar] [CrossRef]
- Goldman, N. Phylogenetic information and experimental design in molecular systematics. Proc. R. Soc. Lond. B 1998, 265, 1779–1786. [Google Scholar] [CrossRef] [PubMed]
- Massingham, T.; Goldman, N. EDIBLE: Experimental design and information calculations in phylogenetics. Bioinformatics 2000, 16, 294–295. [Google Scholar] [CrossRef] [PubMed]
- Posada, D.; Buckley, T.R. Model selection and model averaging in phylogenetics: Advantages of Akaike information criterion and Bayesian approaches over likelihood ratio tests. Syst. Biol. 2004, 53, 793–808. [Google Scholar] [CrossRef] [PubMed]
- Fuhrman, S.; Cunningham, M.J.; Wen, X.; Zweiger, G.; Seilhamer, J.J.; Somogyi, R. The application of Shannon entropy in the identification of putative drug targets. Biosystems 2000, 55, 5–14. [Google Scholar] [CrossRef]
- Robson, B. Clinical and pharmacogenomic data mining: 3. zeta theory as a general tactic for clinical bioinformatics. J. Proteom. Res. 2004, 4, 445–455. [Google Scholar] [CrossRef] [PubMed]
- Mossel, E.; Steel, M. How Much Can Evolved Characters Tell Us about the Tree That Generated Them? In Mathematics of Evolution and Phylogeny; Gascuel, O., Ed.; Oxford University Press: New York, NY, USA, 2005; pp. 384–412. [Google Scholar]
- Chen, H.-D.; Chang, C.-H.; Hsieh, L.-C.; Lee, H.-C. Divergence and Shannon information in genomes. Phys. Rev. Lett. 2005, 94, 178103. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).