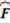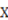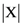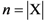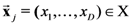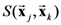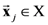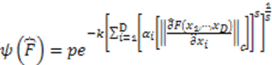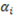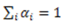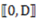Complexity over Uncertainty in Generalized Representational Information Theory (GRIT): A Structure-Sensitive General Theory of Information
Abstract
:1. Introduction
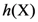 associated with the finite set
associated with the finite set  is the logarithm to some base b of the size of X as shown in Equation (1).
is the logarithm to some base b of the size of X as shown in Equation (1).
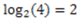 . This is the length of the four distinct strings of 2 symbols required to assign distinguishing labels to the 4 objects in S. As a second example, if we wish to compute the information content of the set of all the English words (about 998,000) we can set the base of the logarithm to two (for the two symbols 1 and 0) and discover that the amount of information associated with the set is approximately 20 bits. This means that it only takes a string or sequence of approximately twenty 0 and 1 symbols to discriminate any one word from all the rest of the words in the English dictionary. Note that this measure and definition of information does not concern the meaning of the words. The information content of the meaning of all the words of the English dictionary would be far greater than 20 bits, as would be the information content of any set that contains components of the original elements that are under consideration. Indeed, information as a quantity depends to a large extent on such multilevel granularity and object decomposition.
. This is the length of the four distinct strings of 2 symbols required to assign distinguishing labels to the 4 objects in S. As a second example, if we wish to compute the information content of the set of all the English words (about 998,000) we can set the base of the logarithm to two (for the two symbols 1 and 0) and discover that the amount of information associated with the set is approximately 20 bits. This means that it only takes a string or sequence of approximately twenty 0 and 1 symbols to discriminate any one word from all the rest of the words in the English dictionary. Note that this measure and definition of information does not concern the meaning of the words. The information content of the meaning of all the words of the English dictionary would be far greater than 20 bits, as would be the information content of any set that contains components of the original elements that are under consideration. Indeed, information as a quantity depends to a large extent on such multilevel granularity and object decomposition.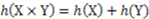 . We shall revisit these three axioms in our discussion of the probabilistic approach to information in Section 2.
. We shall revisit these three axioms in our discussion of the probabilistic approach to information in Section 2.2. From Sets of Entities to Probability of Events
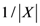 which yields a negative quantity after its logarithm is taken. But negative information is not allowed in Hartley information theory. Again, this probabilistic interpretation is only valid when uniform random sampling is assumed. Nonetheless, it was this kind of simple insight that contributed to the generalization of information proposed by Shannon and later by Shannon and Weaver in their famous mathematical treatise on information [6,7]. Henceforth, we shall refer to their framework as SWIT (Shannon–Weaver Information Theory) and to their basic measure of information as SIM. In these two seminal papers it was suggested that by construing the carriers of information as the degrees of uncertainty of events (and not sets of objects), Hartley’s measure could be generalized to non-uniform distributions. That is, by taking the logarithm of a random variable, one could quantify information as a function of a measure of uncertainty as follows.
which yields a negative quantity after its logarithm is taken. But negative information is not allowed in Hartley information theory. Again, this probabilistic interpretation is only valid when uniform random sampling is assumed. Nonetheless, it was this kind of simple insight that contributed to the generalization of information proposed by Shannon and later by Shannon and Weaver in their famous mathematical treatise on information [6,7]. Henceforth, we shall refer to their framework as SWIT (Shannon–Weaver Information Theory) and to their basic measure of information as SIM. In these two seminal papers it was suggested that by construing the carriers of information as the degrees of uncertainty of events (and not sets of objects), Hartley’s measure could be generalized to non-uniform distributions. That is, by taking the logarithm of a random variable, one could quantify information as a function of a measure of uncertainty as follows.
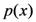 . SIM is then defined as a monotonic function (i.e., the log function to some base b, usually base 2) of the probability of x as shown in Equation (2). For example, if the event is the outcome of a single coin toss, the amount of information conveyed is the negative logarithm of the probability of the random variable x when it assumes a particular value representative of an outcome (1 for tails or 0 for heads). If the coin is equally likely to land on either side, then it has a uniform probability mass function and the amount of information transmitted by x = 1 is ½. Taking its logarithm base 2 tells us that 1 bit of information has been transmitted by knowledge that the random variable equals 1 because it requires 1 bit of information to distinguish this state of the random variable from the only other state when x is 0.
. SIM is then defined as a monotonic function (i.e., the log function to some base b, usually base 2) of the probability of x as shown in Equation (2). For example, if the event is the outcome of a single coin toss, the amount of information conveyed is the negative logarithm of the probability of the random variable x when it assumes a particular value representative of an outcome (1 for tails or 0 for heads). If the coin is equally likely to land on either side, then it has a uniform probability mass function and the amount of information transmitted by x = 1 is ½. Taking its logarithm base 2 tells us that 1 bit of information has been transmitted by knowledge that the random variable equals 1 because it requires 1 bit of information to distinguish this state of the random variable from the only other state when x is 0. real number interval: Thus, the smaller a fraction, the bigger the absolute value of its logarithm. Finally, with respect to the third axiom, information as a quantity is additive under SWIT in the sense that for any two independent events, the information gain from observing both of them is the sum of the information gain from each of them separately—more formally,
real number interval: Thus, the smaller a fraction, the bigger the absolute value of its logarithm. Finally, with respect to the third axiom, information as a quantity is additive under SWIT in the sense that for any two independent events, the information gain from observing both of them is the sum of the information gain from each of them separately—more formally, 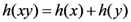 —when h is the logarithmic function of the probabilities of the two events.
—when h is the logarithmic function of the probabilities of the two events.2.1. Criticisms of SWIT
3. Concepts and Complexity as the Building Blocks of Information
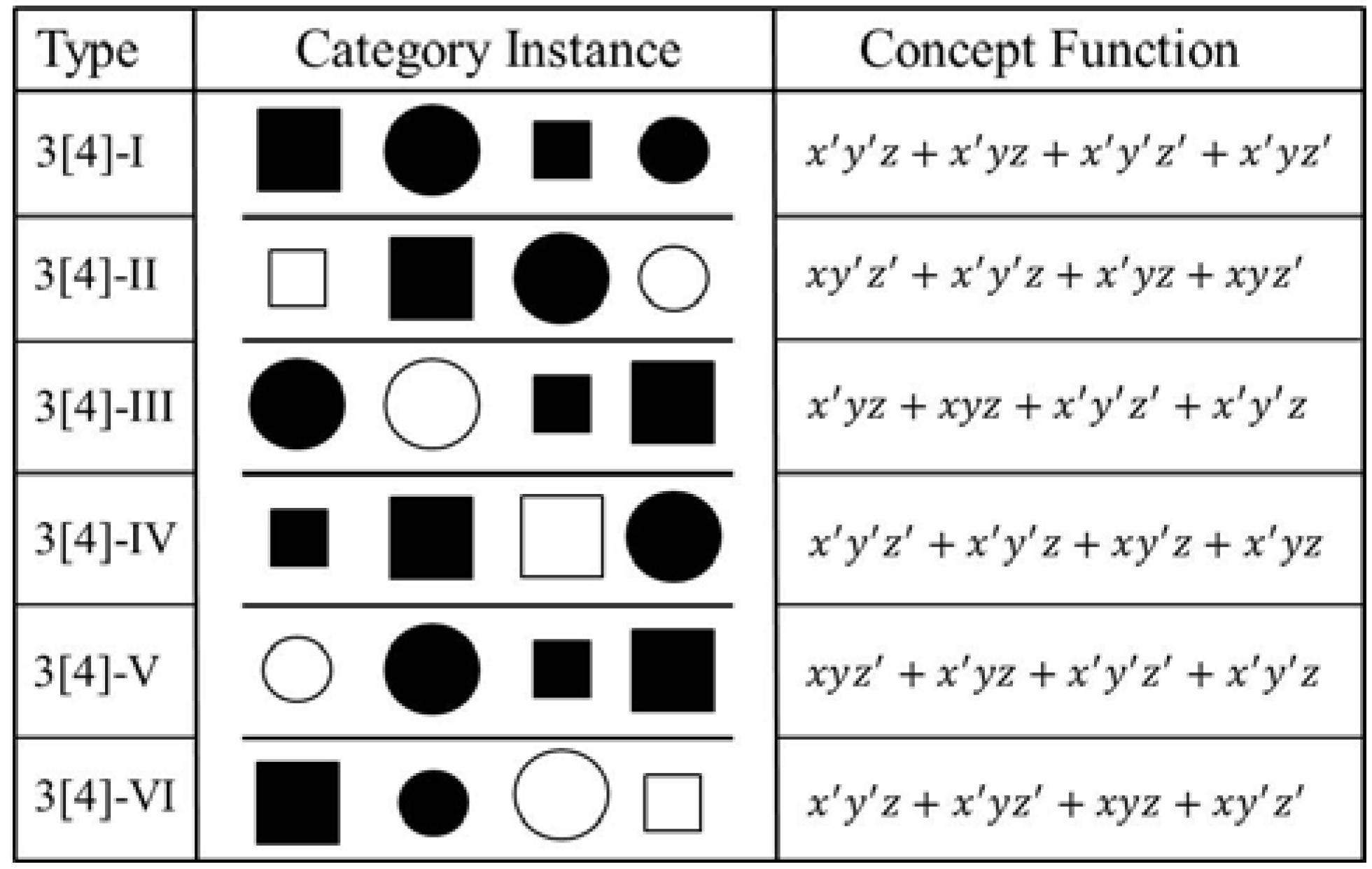
| Category | Objects | Information |
|---|---|---|
| 3[4]-1 | {001, 011, 000, 010} | [0.20, 0.20, 0.20, 0.20] |
| 3[4]-2 | {100, 001, 011, 110} | [0.05, 0.05, 0.05, 0.05] |
| 3[4]-3 | {011, 111, 000, 001} | [−0.08, −0.31, −0.31, −0.08] |
| 3[4]-4 | {000, 001, 101, 011} | [−0.31, 0.78, −0.31, −0.31] |
| 3[4]-5 | {110, 011, 000, 001} | [−0.41, −0.22, −0.22, 0.52] |
| 3[4]-6 | {001, 010, 111, 100} | [−0.25, −0.25, −0.25, −0.25] |
4. Conclusions
Technical Appendix
An Introduction to Generalized Representational Information Theory (GRIT)
 interval) for the particular dimensions. For example, the brightness dimension may have five fixed values representing five levels of brightness in a continuum standardized from 0 to 1 (from least bright to most bright).
interval) for the particular dimensions. For example, the brightness dimension may have five fixed values representing five levels of brightness in a continuum standardized from 0 to 1 (from least bright to most bright). stands for blue,
stands for blue, 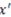 stands for red,
stands for red, 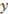 stands for round, and
stands for round, and 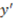 stands for square, then the two-variable concept function
stands for square, then the two-variable concept function 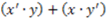 (where “
(where “  ” denotes “or”, “
” denotes “or”, “  ” denotes “and”, and “
” denotes “and”, and “  ” denotes “not-
” denotes “not-  ”) defines the category which contains two objects: a red and round object and a blue and square object. Clearly, the choice of labels in the expression is arbitrary. Hence, there are many Boolean expressions that define the same category structure [33,34]. In this paper, concept functions will be represented by capital letters of the English alphabet (e.g., F, G, H), while the sets that such functions define in extension will be denoted by a set bracket symbol of their corresponding function symbols. For example, if F is a Boolean function in disjunctive normal form (DNF),
”) defines the category which contains two objects: a red and round object and a blue and square object. Clearly, the choice of labels in the expression is arbitrary. Hence, there are many Boolean expressions that define the same category structure [33,34]. In this paper, concept functions will be represented by capital letters of the English alphabet (e.g., F, G, H), while the sets that such functions define in extension will be denoted by a set bracket symbol of their corresponding function symbols. For example, if F is a Boolean function in disjunctive normal form (DNF),  is the category that it defines it. A DNF is a Boolean formula consisting of sums of products that are a verbatim object per object description of the category of objects (just as the example given above).
is the category that it defines it. A DNF is a Boolean formula consisting of sums of products that are a verbatim object per object description of the category of objects (just as the example given above).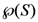 is the set of all such representations. Since there are
is the set of all such representations. Since there are 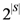 elements in
elements in 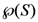 , then there are
, then there are 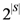 possible representations of S (
possible representations of S ( 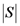 stands for cardinality or size of the set S). Some representations capture the structural (i.e., relational) “essence” or nature of S better than others. In other words, some representations carry more representational information (i.e., more conceptual significance) about S than others. For example, consider a well-defined category with three objects defined over three dimensions (color, shape, and size) consisting of a small black circle, a small black square, and a large white circle. The small black circle better captures the character of the category as a whole than does the large white circle. In addition, it would seem that, (1) for any well-defined category S, all the information in S is conveyed by S itself; and that (2) the empty set
stands for cardinality or size of the set S). Some representations capture the structural (i.e., relational) “essence” or nature of S better than others. In other words, some representations carry more representational information (i.e., more conceptual significance) about S than others. For example, consider a well-defined category with three objects defined over three dimensions (color, shape, and size) consisting of a small black circle, a small black square, and a large white circle. The small black circle better captures the character of the category as a whole than does the large white circle. In addition, it would seem that, (1) for any well-defined category S, all the information in S is conveyed by S itself; and that (2) the empty set 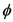 carries no information about S. The aim of our measure is to measure the amount and quality of conceptual information carried by representations or representatives of the category S about S while obeying these two basic requirements and capturing the conceptual significance of S.
carries no information about S. The aim of our measure is to measure the amount and quality of conceptual information carried by representations or representatives of the category S about S while obeying these two basic requirements and capturing the conceptual significance of S.Categorical Invariance Theory
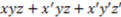 . Let's encode the features of the objects in this category using the digits “1” and “0” so that each object may be representable by a binary string. For example, “111” stands for the first object when x = 1 = square, y = 1 = small, and z = 1 = black. Thus, the entire set can be encoded by {111, 011, 000}. If we transform this set in terms of the shape dimension by assigning the opposite shape value to each of the objects in the set, we get the perturbed set {011, 111, 100}. Now, if we compare the original set to the perturbed set, they have two objects in common with respect to the dimension of shape. Thus, two out of three objects remain the same. This proportion, referred to as the “dimensional kernel”, is a measure of the partial invariance of the category with respect to the dimension of shape. The first pane of Figure 2 illustrates this transformation. Doing this for each of the dimensions, we can form an ordered set, or vector, consisting of all the dimensional kernels (one per dimension) of the concept function or category type (see Figure 2 and the example after Equation (7)).
. Let's encode the features of the objects in this category using the digits “1” and “0” so that each object may be representable by a binary string. For example, “111” stands for the first object when x = 1 = square, y = 1 = small, and z = 1 = black. Thus, the entire set can be encoded by {111, 011, 000}. If we transform this set in terms of the shape dimension by assigning the opposite shape value to each of the objects in the set, we get the perturbed set {011, 111, 100}. Now, if we compare the original set to the perturbed set, they have two objects in common with respect to the dimension of shape. Thus, two out of three objects remain the same. This proportion, referred to as the “dimensional kernel”, is a measure of the partial invariance of the category with respect to the dimension of shape. The first pane of Figure 2 illustrates this transformation. Doing this for each of the dimensions, we can form an ordered set, or vector, consisting of all the dimensional kernels (one per dimension) of the concept function or category type (see Figure 2 and the example after Equation (7)).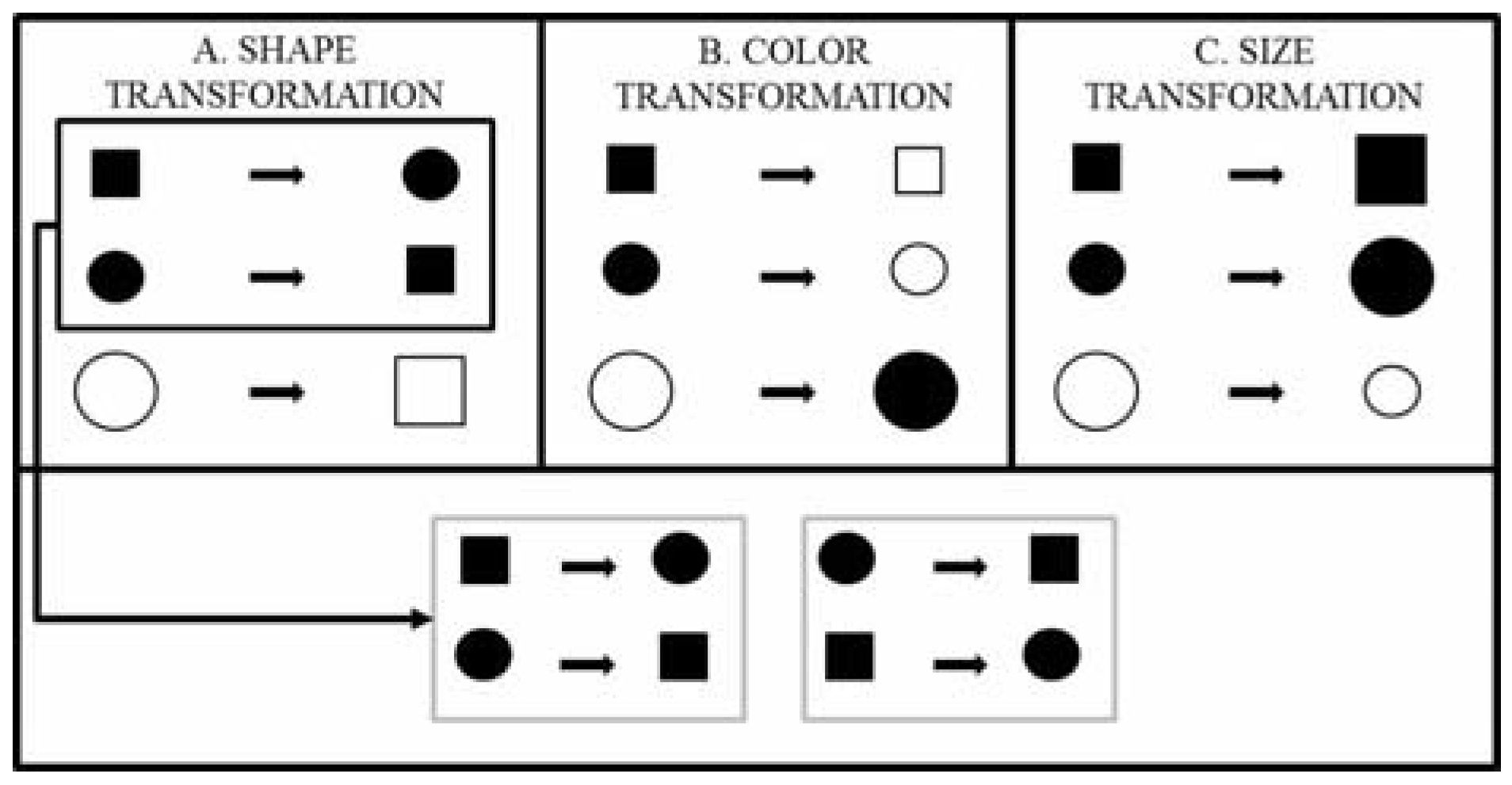
 stands for the logical manifold of the concept function F and where a “hat” symbol over the partial differentiation symbol indicates discrete differentiation (for a detailed and rigorous explanation, see [20,21]). Discrete partial derivatives are somewhat analogous to continuous partial derivatives in Calculus. Loosely speaking, in Calculus, the partial derivative of an n variable function
stands for the logical manifold of the concept function F and where a “hat” symbol over the partial differentiation symbol indicates discrete differentiation (for a detailed and rigorous explanation, see [20,21]). Discrete partial derivatives are somewhat analogous to continuous partial derivatives in Calculus. Loosely speaking, in Calculus, the partial derivative of an n variable function  is defined as how much the function value changes relative to how much the input value(s) change as seen below:
is defined as how much the function value changes relative to how much the input value(s) change as seen below:
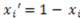 with
with 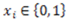 ) is analogous to the continuous partial derivative except that there is no limit taken because the values of
) is analogous to the continuous partial derivative except that there is no limit taken because the values of 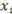 can be only 0 or 1.
can be only 0 or 1.
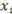 changes, and the value of the derivative is 0 if the function assignment does not change when
changes, and the value of the derivative is 0 if the function assignment does not change when 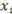 changes. Note that the value of the derivative depends on the entire vector
changes. Note that the value of the derivative depends on the entire vector 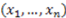 (abbreviated as
(abbreviated as 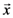 in this note) and not just on
in this note) and not just on 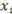 . As an example, consider the concept function AND, denoted as
. As an example, consider the concept function AND, denoted as 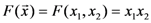 (Equivalently, we could also write this function as
(Equivalently, we could also write this function as 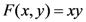 . Because this is more readable than the vector notation, we shall continue using it in other examples.). Also, consider the particular point
. Because this is more readable than the vector notation, we shall continue using it in other examples.). Also, consider the particular point 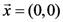 . At that point, the derivative of the concept function AND with respect to
. At that point, the derivative of the concept function AND with respect to 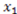 is 0 because the value of the concept function does not change when the stimulus changes from
is 0 because the value of the concept function does not change when the stimulus changes from 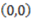 to
to 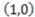 . If instead we consider the point
. If instead we consider the point 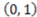 , the derivative of AND with respect to
, the derivative of AND with respect to 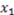 is 1 because the value of the concept function does change when the stimulus changes from
is 1 because the value of the concept function does change when the stimulus changes from 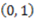 to
to 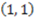 .
. is the number of objects in the category defined by the concept function F).
is the number of objects in the category defined by the concept function F).

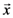 stands for an object defined by D dimensional values
stands for an object defined by D dimensional values 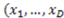 ). The general summation symbol represents the sum of the partial derivatives evaluated at each object
). The general summation symbol represents the sum of the partial derivatives evaluated at each object 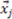 from the Boolean category
from the Boolean category  (this is the category defined by the concept function F). The partial derivative transforms each object
(this is the category defined by the concept function F). The partial derivative transforms each object 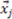 in respect to its i-th dimension and evaluates to 0 if, after the transformation, the object is still in
in respect to its i-th dimension and evaluates to 0 if, after the transformation, the object is still in  (it evaluates to 1 otherwise). Thus, to compute the proportion of objects that remain in
(it evaluates to 1 otherwise). Thus, to compute the proportion of objects that remain in  after changing the value of their
after changing the value of their  -th dimension, we need to divide the sum of the partial derivatives evaluated at each object
-th dimension, we need to divide the sum of the partial derivatives evaluated at each object 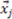 by
by  (the number of objects in
(the number of objects in 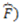 and subtract the result from 1. The absolute value symbol is placed around the partial derivative to avoid a value of negative 1 (for a detailed explanation, see [9,20,21]).
and subtract the result from 1. The absolute value symbol is placed around the partial derivative to avoid a value of negative 1 (for a detailed explanation, see [9,20,21]). of the concept function F (and of any category it defines) is given by the Equation below:
of the concept function F (and of any category it defines) is given by the Equation below:
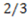 . Conducting a similar analysis in respect to the dimensions of color and size, its logical manifold computes to
. Conducting a similar analysis in respect to the dimensions of color and size, its logical manifold computes to 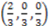 and its degree of categorical invariance is:
and its degree of categorical invariance is:
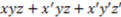 used in our example at the beginning of Section 3 has been rewritten in an entirely equivalently form as
used in our example at the beginning of Section 3 has been rewritten in an entirely equivalently form as  in order to be consistent with the vector notation introduced above. Henceforth, we shall use both ways of specifying concept functions and it will be left to reader to make the appropriate translation. We do this since the non-vector notation is more intuitive and less confusing to comprehend structurally.
in order to be consistent with the vector notation introduced above. Henceforth, we shall use both ways of specifying concept functions and it will be left to reader to make the appropriate translation. We do this since the non-vector notation is more intuitive and less confusing to comprehend structurally.Structural Complexity
 of a well-defined category
of a well-defined category  and its subjective structural complexity
and its subjective structural complexity 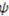 . The structural complexity of a well-defined category is directly proportional to the cardinality or size
. The structural complexity of a well-defined category is directly proportional to the cardinality or size  of the category (in other words,
of the category (in other words,  ), and indirectly proportional to a monotonically increasing function of the degree of invariance of the concept function
), and indirectly proportional to a monotonically increasing function of the degree of invariance of the concept function 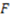 that defines the category. This relationship is expressed formally by the parameter-free Equation (9) below where
that defines the category. This relationship is expressed formally by the parameter-free Equation (9) below where  is a well-defined category. The intuition here is that the raw complexity measured by the number of items in a category is cut down or diminished by the degree of structural homogeneity or patternfullness of the category as measured by its degree of invariance.
is a well-defined category. The intuition here is that the raw complexity measured by the number of items in a category is cut down or diminished by the degree of structural homogeneity or patternfullness of the category as measured by its degree of invariance.
 of the concept function F can potentially be equal to zero, we have added a 1 to
of the concept function F can potentially be equal to zero, we have added a 1 to  to avoid division by zero in Equation (9) above. Then, the structural complexity
to avoid division by zero in Equation (9) above. Then, the structural complexity  of a category
of a category  is directly proportional to its cardinality and indirectly proportional to its degree of invariance (plus one):
is directly proportional to its cardinality and indirectly proportional to its degree of invariance (plus one):
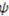 of a category
of a category  as being directly proportional to its cardinality and indirectly proportional to the exponent of its degree of invariance.
as being directly proportional to its cardinality and indirectly proportional to the exponent of its degree of invariance.
Representational Information
 is the rate of change of the structural complexity of
is the rate of change of the structural complexity of  . Simply stated, the representational information carried by an object or objects from a well-defined category
. Simply stated, the representational information carried by an object or objects from a well-defined category  is the percentage increase or decrease (i.e., rate of change or growth rate) in structural complexity that the category experiences whenever the object or objects are removed [36].
is the percentage increase or decrease (i.e., rate of change or growth rate) in structural complexity that the category experiences whenever the object or objects are removed [36]. be a well-defined category defined by the concept function
be a well-defined category defined by the concept function 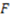 and let the well-defined category R be a representation of
and let the well-defined category R be a representation of  (i.e.,
(i.e., 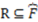 or
or 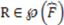 ). Then, if
). Then, if 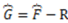 , the amount of representational information
, the amount of representational information  of R in respect to
of R in respect to  is determined by Equation (12) below where
is determined by Equation (12) below where  and
and 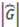 stand for the number of elements in
stand for the number of elements in  and in
and in 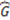 respectively.
respectively.
 but it characterizes the objects in the subset as highly unique or unrepresentative of those in
but it characterizes the objects in the subset as highly unique or unrepresentative of those in  ; while a relatively large positive value indicates that high RI is conveyed the subset of
; while a relatively large positive value indicates that high RI is conveyed the subset of  but it characterizes the objects in the subset as highly representative of those in
but it characterizes the objects in the subset as highly representative of those in  . In the following examples, it will be shown that, intuitively, the RI values make perfect sense for representations of the same size (i.e., with the same number of objects).
. In the following examples, it will be shown that, intuitively, the RI values make perfect sense for representations of the same size (i.e., with the same number of objects).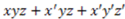 where
where  = square,
= square, 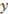 = black, and
= black, and 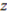 = small used above as an example (Table 2 displays the category). To be consistent with the vector notation introduced, this concept function can also be written as:
= small used above as an example (Table 2 displays the category). To be consistent with the vector notation introduced, this concept function can also be written as: 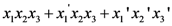 , and as before, we leave it up to the reader to make the necessary translation. As before, the objects of this category may be encoded in terms of zeros and ones, and the category may be encoded by the set {111, 011, 000} to facilitate reference to the actual objects. The amount of subjective representational information conveyed by the singleton (single element) set containing the object encoded by 111 (and defined by the rule
, and as before, we leave it up to the reader to make the necessary translation. As before, the objects of this category may be encoded in terms of zeros and ones, and the category may be encoded by the set {111, 011, 000} to facilitate reference to the actual objects. The amount of subjective representational information conveyed by the singleton (single element) set containing the object encoded by 111 (and defined by the rule  ) in respect to the category encoded by
) in respect to the category encoded by 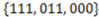 (and defined by the concept function
(and defined by the concept function 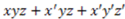 ) is computed as shown in 13 and 14 below:
) is computed as shown in 13 and 14 below:

 and
and 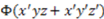 and get:
and get:

 (i.e., −0.52). Likewise, the other two singleton representations ({111} and {011}, respectively) are more informative because the absence of 111 and 000 respectively from
(i.e., −0.52). Likewise, the other two singleton representations ({111} and {011}, respectively) are more informative because the absence of 111 and 000 respectively from  results in a 30% increase in the structural complexity of
results in a 30% increase in the structural complexity of  . The reader is directed to Figure 3 below, showing a visuo-perceptual instance of the category structure, in order to confirm these results intuitively.
. The reader is directed to Figure 3 below, showing a visuo-perceptual instance of the category structure, in order to confirm these results intuitively.  |  |  |  |
|---|---|---|---|
| {111} | {111, 011, 000} | {011, 000} | 0.30 |
| {011} | {111, 011, 000} | {111, 000} | 0.30 |
| {000} | {111, 011, 000} | {111, 011} | −0.52 |
 concept function.
concept function.
| Category | Objects | Information |
|---|---|---|
| 3[4]-1 | {000, 001, 100, 101} | [0.20, 0.20, 0.20, 0.20] |
| 3[4]-2 | {000, 010, 101, 111} | [0.05, 0.05, 0.05, 0.05] |
| 3[4]-3 | {101, 010, 011, 001} | [−0.31, −0.31, −0.08, −0.08] |
| 3[4]-4 | {000, 110, 011, 010} | [−0.31, −0.31, −0.31, 0.78] |
| 3[4]-5 | {011, 000, 101, 100} | [−0.41, −0.22, −0.22, 0.52] |
| 3[4]-6 | {001, 010, 100, 111} | [−0.25, −0.25, −0.25, −0.25] |
From Binary to Continuous Domains: The Similarity-Invariance Principle
 real number interval, all that is needed is a generalization of the structural or logical manifold (capital lambda) of a binary category so that it also applies to any continuous category. Every other aspect of the theory described above remains the same. To generalize the logical manifold operator we introduce the following equivalence between the pairwise symmetries in sets of objects (which identify pairs of invariants) and the partial similarity between the same two objects with respect to a particular dimension. Figure 4 illustrates this intuitive equivalence with respect to the shape dimension. It simply means that the relational symmetries on which categorical invariance theory is based are equivalent to pairs of objects being identical when disregarding one of their dimensions. We shall call the disregarded dimension the anchored dimension.
real number interval, all that is needed is a generalization of the structural or logical manifold (capital lambda) of a binary category so that it also applies to any continuous category. Every other aspect of the theory described above remains the same. To generalize the logical manifold operator we introduce the following equivalence between the pairwise symmetries in sets of objects (which identify pairs of invariants) and the partial similarity between the same two objects with respect to a particular dimension. Figure 4 illustrates this intuitive equivalence with respect to the shape dimension. It simply means that the relational symmetries on which categorical invariance theory is based are equivalent to pairs of objects being identical when disregarding one of their dimensions. We shall call the disregarded dimension the anchored dimension.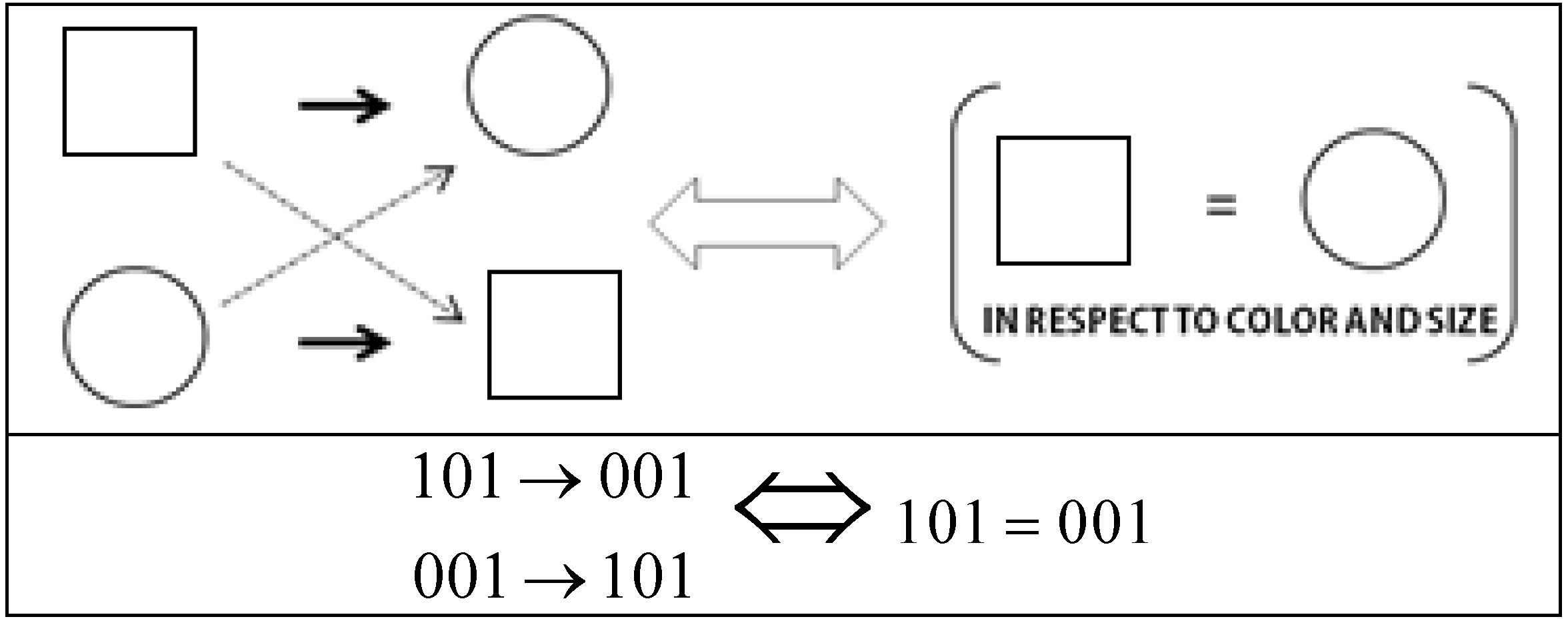
- (1) Let
be a stimulus set and
stand for the cardinality (i.e., the number of elements) of X.
- (2) Let the object-stimuli in
be represented by the vectors
(where
).
- (3) Let the vector
be the j-th D-dimensional object-stimulus in
(where D is the number of dimensions of the stimulus set).
- (4) Let
be the value of the i-th dimension of the j-th object-stimulus in X. We shall assume throughout our discussion that all dimensional values are real numbers greater than or equal to zero.
- (5) Let
stand for the similarity of object-stimulus
to object-stimulus
as determined by the assumption made in multidimensional scaling theory that stimulus similarity is some monotonically decreasing function of the psychological distance between the stimuli.
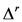 (aka Minkowski distance) between two object-stimuli
(aka Minkowski distance) between two object-stimuli 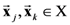 with attention weights
with attention weights 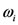 as:
as:
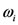 represents the selective attention allocated to dimension
represents the selective attention allocated to dimension 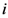 such that
such that 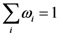 . We use this parameter family to represent individual differences in the process of assessing similarities between object-stimuli at this level of analysis. For the sake of simplifying our explanation and examples below, we shall disregard this parameter. Next we introduce a new kind of distance operator termed the partial psychological distance operator
. We use this parameter family to represent individual differences in the process of assessing similarities between object-stimuli at this level of analysis. For the sake of simplifying our explanation and examples below, we shall disregard this parameter. Next we introduce a new kind of distance operator termed the partial psychological distance operator  to model dimensional anchoring and partial similarity assessment.
to model dimensional anchoring and partial similarity assessment.
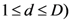 . In other words, it computes the partial psychological distance between the exemplars corresponding to the object-stimuli
. In other words, it computes the partial psychological distance between the exemplars corresponding to the object-stimuli 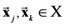 , by excluding dimension d in the computation of the Minkowski generalized metric. For example, if the stimulus set X consists of four object-stimuli, we represent the partial pairwise distances between the four corresponding exemplars with respect to dimension d with the following partial distances matrix:
, by excluding dimension d in the computation of the Minkowski generalized metric. For example, if the stimulus set X consists of four object-stimuli, we represent the partial pairwise distances between the four corresponding exemplars with respect to dimension d with the following partial distances matrix:


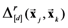 in the
in the  interval using the following linear transformation
interval using the following linear transformation 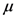 where the
where the  and
and  of a matrix are respectively its largest and smallest element, and the
of a matrix are respectively its largest and smallest element, and the 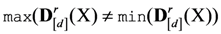 for any d and r.
for any d and r.
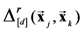 and set r = 1 (i.e., we use the city block metric in our example) as shown in Equation (21) below.
and set r = 1 (i.e., we use the city block metric in our example) as shown in Equation (21) below.

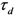 for each dimension
for each dimension 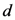 we can get the following expression which is functionally analogous to the local homogeneity operator given in Equation (6) (for any pair of objects
we can get the following expression which is functionally analogous to the local homogeneity operator given in Equation (6) (for any pair of objects 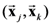 where
where 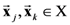 ,
, 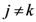 , and
, and  ):
):
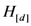 of a D-dimensional stimulus set X with respect to dimension d.
of a D-dimensional stimulus set X with respect to dimension d. 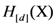 is the ratio between the sum of the similarities corresponding to distances that are zero or close to zero (depending on the value of the discrimination resolution threshold) in the matrix
is the ratio between the sum of the similarities corresponding to distances that are zero or close to zero (depending on the value of the discrimination resolution threshold) in the matrix 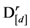 (for a particular anchored dimension d) and the number of items in the stimulus set X. In other words,
(for a particular anchored dimension d) and the number of items in the stimulus set X. In other words, 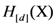 is the ratio between: (1) The sum of the similarities in the matrix
is the ratio between: (1) The sum of the similarities in the matrix 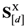 (for a particular anchored dimension d) that correspond to distances in the
(for a particular anchored dimension d) that correspond to distances in the 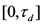 discrimination resolution interval; and (2) the number of items in the dataset X. When the partial distances are close to zero, the points are for all intent and purpose treated as perfectly similar or identical.
discrimination resolution interval; and (2) the number of items in the dataset X. When the partial distances are close to zero, the points are for all intent and purpose treated as perfectly similar or identical. . Equation (24) below shows the matrix used to calculate the degree of partial homogeneity (with respect to dimension 1) of A when we let
. Equation (24) below shows the matrix used to calculate the degree of partial homogeneity (with respect to dimension 1) of A when we let 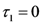 and r = 1.
and r = 1.| D1 | D2 | D3 | D4 | |
|---|---|---|---|---|
| O1 | 1 | 1 | 1 | 0 |
| O2 | 1 | 1 | 0 | 1 |
| O3 | 1 | 1 | 0 | 0 |
| O4 | 1 | 1 | 1 | 1 |




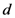 the discrimination resolution threshold
the discrimination resolution threshold 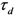 will be a relatively small number dependent on the discriminatory capacities of the observer. Also, the above Equation assumes that, for any d and any r,
will be a relatively small number dependent on the discriminatory capacities of the observer. Also, the above Equation assumes that, for any d and any r, 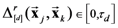 are the only partial deltas that partake in determining the partial similarity matrices. Finally, since we standardized the partial distance metric in Equation (21), then we can also say that
are the only partial deltas that partake in determining the partial similarity matrices. Finally, since we standardized the partial distance metric in Equation (21), then we can also say that  . To simplify our discussion, in the remaining computations in this paper we shall let
. To simplify our discussion, in the remaining computations in this paper we shall let 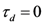 for all subjects and any dimension
for all subjects and any dimension 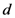 ; however, this value may also be treated as a free parameter that accounts for individual differences in classification performance. The assumption is that humans vary in their capacity to discriminate between stimuli and in their criterion for discriminating (in this paper we shall not investigate this latter option: That is, we shall not try to derive estimates for
; however, this value may also be treated as a free parameter that accounts for individual differences in classification performance. The assumption is that humans vary in their capacity to discriminate between stimuli and in their criterion for discriminating (in this paper we shall not investigate this latter option: That is, we shall not try to derive estimates for 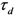 ). In either case, we assume that the primary goal of the human conceptual system is to optimize classification performance via the detection of invariants.
). In either case, we assume that the primary goal of the human conceptual system is to optimize classification performance via the detection of invariants.| Dimension | Standardized | Standardized Similarity | Perceived | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance Matrix | Matrix | Local Homogeneity | ||||||||||
| 1 | 1110 | 1101 | 1100 | 1111 | 1110 | 1101 | 1100 | 1111 | 0/4=0 | |||
| 1110 | 0 | 1 | 0.5 | 0.5 | 1110 | 1 | 0.37 | 0.61 | 0.61 | |||
| 1101 | 1 | 0 | 0.5 | 0.5 | 1101 | 0.37 | 1 | 0.61 | 0.61 | |||
| 1100 | 0.5 | 0.5 | 0 | 1 | 1100 | 0.61 | 0.61 | 1 | 0.37 | |||
| 1111 | 0.5 | 0.5 | 1 | 0 | 1111 | 0.61 | 0.61 | 0.37 | 1 | |||
| 2 | 1110 | 1101 | 1100 | 1111 | 1110 | 1101 | 1100 | 1111 | 0/4=0 | |||
| 1110 | 0 | 1 | 0.5 | 0.5 | 1110 | 1 | 0.37 | 0.61 | 0.61 | |||
| 1101 | 1 | 0 | 0.5 | 0.5 | 1101 | 0.37 | 1 | 0.61 | 0.61 | |||
| 1100 | 0.5 | 0.5 | 0 | 1 | 1100 | 0.61 | 0.61 | 1 | 0.37 | |||
| 1111 | 0.5 | 0.5 | 1 | 0 | 1111 | 0.61 | 0.61 | 0.37 | 1 | |||
| 3 | 1110 | 1101 | 1100 | 1111 | 1110 | 1101 | 1100 | 1111 | 4/4=1 | |||
| 1110 | 0 | 1 | 0 | 1 | 1110 | 1 | 0.37 | 1 | 0.37 | |||
| 1101 | 1 | 0 | 1 | 0 | 1101 | 0.37 | 1 | 0.37 | 1 | |||
| 1100 | 0 | 1 | 0 | 1 | 1100 | 1 | 0.37 | 1 | 0.37 | |||
| 1111 | 1 | 0 | 1 | 0 | 1111 | 0.37 | 1 | 0.37 | 1 | |||
| 4 | 1110 | 1101 | 1100 | 1111 | 1110 | 1101 | 1100 | 1111 | 4/4=1 | |||
| 1110 | 0 | 1 | 1 | 0 | 1110 | 1 | 0.37 | 1 | 0.37 | |||
| 1101 | 1 | 0 | 0 | 1 | 1101 | 0.37 | 1 | 0.37 | 1 | |||
| 1100 | 1 | 0 | 0 | 1 | 1100 | 1 | 0.37 | 1 | 0.37 | |||
| 1111 | 0 | 1 | 1 | 0 | 1111 | 0.37 | 1 | 0.37 | 1 | |||
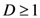 dimensions and for any pair of objects
dimensions and for any pair of objects 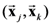 (such that
(such that 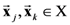 ,
, 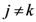 , and
, and 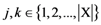 ) is given by the Euclidean metric as follows:
) is given by the Euclidean metric as follows:
 be a well-defined category and let the well-defined category R be a representation of
be a well-defined category and let the well-defined category R be a representation of  (i.e.,
(i.e., 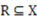 or
or 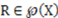 ). Then, if
). Then, if  , the amount of representational information
, the amount of representational information  of R in respect to
of R in respect to  is determined by Equation (29) below where
is determined by Equation (29) below where 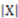 and
and 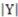 stand for the number of elements in
stand for the number of elements in  and in
and in 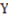 respectively and
respectively and 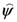 is the generalized perceived degree of structural complexity of a well-defined category (with
is the generalized perceived degree of structural complexity of a well-defined category (with  normally set to 0).
normally set to 0).
Acknowledgments
References and Notes
- Devlin, K. Logic and Information; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Luce, R.D. Whatever happened to information theory in psychology? Rev. Gen. Psychol. 2003, 7, 183–188. [Google Scholar] [CrossRef]
- Floridi, L. The Philosophy of Information; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Devlin, K. Claude Shannon, 1916–2001. Focus News. Math. Assoc. Am. 2001, 21, 20–21. [Google Scholar]
- Hartley, R.V.L. Transmission of information. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Vigo, R. Representational information: A new general notion and measure of information. Inf. Sci. 2011, 181, 4847–4859. [Google Scholar] [CrossRef]
- Klir, G.J. Uncertainty and Information: Foundations of Generalized Information Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef]
- Laming, D.R.J. Information Theory of Choice-Reaction Times; Academic Press: New York, NY, USA, 1968. [Google Scholar]
- Deweese, M.R.; Meister, M. How to measure the information gained from one symbol. Network 1999, 10, 325–340. [Google Scholar] [CrossRef]
- Butts, D.A. How much information is associated with a particular stimulus? Network 2003, 14, 177–187. [Google Scholar] [CrossRef]
- Laming, D. Statistical information, uncertainty, and Bayes’ theorem: Some applications in experimental psychology. In Symbolic and Quantitative Approaches to Reasoning with Uncertainty; Benferhat, S., Besnard, P., Eds.; Springer-Verlag: Berlin, Germany, 2001; pp. 635–646. [Google Scholar]
- Dretske, F. Knowledge and the Flow of Information; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Tversky, A.; Kahneman, D. Availability: A heuristic for judging frequency and probability. Cogn. Psychol. 1973, 5, 207–233. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Extension versus intuitive reasoning: The conjunction fallacy in probability judgment. Psychol. Rev. 1983, 90, 293–315. [Google Scholar] [CrossRef]
- Vigo, R. A dialogue on concepts. Think 2010, 9, 109–120. [Google Scholar] [CrossRef]
- Vigo, R. Categorical invariance and structural complexity in human concept learning. J. Math. Psychol. 2009, 53, 203–221. [Google Scholar] [CrossRef]
- Vigo, R. Towards a law of invariance in human conceptual behavior. In Proceedings of the 33rd Annual Conference of the Cognitive Science Society, Austin, TX, USA, 21 July 2011; Carlson, L., HÖlscher, C., Shipley, T., Eds.; Cognitive Science Society: Austin, TX, USA, 2011. [Google Scholar]
- Vigo, R. The gist of concepts. Cognition 2012. Submitted for publication. [Google Scholar]
- Feldman, D.; Crutchfield, J. A survey of “Complexity Measures”, Santa Fe Institute: Santa Fe, NM, USA, 11 June 1998; 1–15.
- Vigo, R. A note on the complexity of Boolean concepts. J. Math. Psychol. 2006, 50, 501–510. [Google Scholar] [CrossRef]
- Vigo, R. Modal similarity. J. Exp. Artif. Intell. 2009, 21, 181–196. [Google Scholar] [CrossRef]
- Vigo, R.; Basawaraj, B. Will the most informative object stand? Determining the impact of structural context on informativeness judgments. J. Cogn. Psychol. 2012, in press. [Google Scholar]
- Vigo, R.; Zeigler, D.; Halsey, A. Gaze and information processing during category learning: Evidence for an inverse law. Vis. Cogn. 2012. Submitted for publication. [Google Scholar]
- Bourne, L.E. Human Conceptual Behavior; Allyn and Bacon: Boston, MA, USA, 1966. [Google Scholar]
- Estes, W.K. Classification and Cognition; Oxford Psychology Series 22; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Garner, W.R. The Processing of Information and Structure; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Garner, W.R. Uncertainty and Structure as Psychological Concepts; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Kruschke, J.K. ALCOVE: An exemplar-based connectionist model of category learning. Psychol. Rev. 1992, 99, 22–44. [Google Scholar] [CrossRef]
- Aiken, H.H. The staff of the Computation Laboratory at Harvard University. In Synthesis of Electronic Computing and Control Circuits; Harvard University Press: Cambridge, UK, 1951. [Google Scholar]
- Higonnet, R.A.; Grea, R.A. Logical Design of Electrical Circuits; McGraw-Hill: New York, NY, USA, 1958. [Google Scholar]
- For the readers’ convenience, the parameterized variants of Equations (10) and (11) (see main text) respectively as introduced by Vigo (2009, 2011) are as follows:
and
. The parameter
in both expressions stands for a human observer’s degree of sensitivity to (i.e., extent of detection of) the invariance pattern associated with the i-th dimension (this is usually a number in the closed real interval
such that
). k is a scaling parameter in the closed real interval
(D is the number of dimensions associated with the category) that indicates the overall ability of the subject to discriminate between dimensions (a larger number indicates higher discrimination) and c is a constant parameter in the closed interval
which captures possible biases displayed by observers toward invariant information (c is added to the numerator and the denominator of the ratios that make up the logical or structural manifold of the well-defined category). Finally, s is a parameter that indicates the most appropriate measure of distance as defined by the generalized Euclidean metric (i.e., the Minkowski distance measure). In our investigation, the best predictions are achieved when s = 2 (i.e., when using the Euclidean metric). Optimal estimates of these free parameters on the aggregate data provide a baseline to assess any individual differences encountered in the pattern perception stage of the concept learning process and may provide a basis for more accurate measurements of subjective representational information
- We could simply define the representational information of a well-defined category as the derivative of its structural complexity. We do not because our characterization of the degree of invariance of a concept function is based on a discrete counterpart to the notion of a derivative in the first place.
- Nosofsky, R.M. Choice, similarity, and the context theory of classification. J. Exp. Psychol. Learn. Mem. Cogn. 1984, 10, 104–114. [Google Scholar] [CrossRef]
- Shepard, R.N.; Romney, A.K. Multidimensional Scaling: Theory and Applications in the Behavioral Sciences; Seminar Press: New York, NY, USA, 1972; Volume I. [Google Scholar]
- Kruskal, J.B.; Wish, M. Multidimensional Scaling; Sage University Paper series on Quantitative Application in the Social Sciences 07-011; Beverly Hills and London: Beverly Hills, CA, USA, 1978. [Google Scholar]
- Shepard, R.N. Towards a universal law of generalization for psychological science. Science 1987, 237, 1317–1323. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vigo, R. Complexity over Uncertainty in Generalized Representational Information Theory (GRIT): A Structure-Sensitive General Theory of Information. Information 2013, 4, 1-30. https://doi.org/10.3390/info4010001
Vigo R. Complexity over Uncertainty in Generalized Representational Information Theory (GRIT): A Structure-Sensitive General Theory of Information. Information. 2013; 4(1):1-30. https://doi.org/10.3390/info4010001
Chicago/Turabian StyleVigo, Ronaldo. 2013. "Complexity over Uncertainty in Generalized Representational Information Theory (GRIT): A Structure-Sensitive General Theory of Information" Information 4, no. 1: 1-30. https://doi.org/10.3390/info4010001
APA StyleVigo, R. (2013). Complexity over Uncertainty in Generalized Representational Information Theory (GRIT): A Structure-Sensitive General Theory of Information. Information, 4(1), 1-30. https://doi.org/10.3390/info4010001