Semantic Information and the Trivialization of Logic: Floridi on the Scandal of Deduction
Abstract
:1. Introduction
Half a century later, Floridi’s main contribution has probably been that of taking up Shannon’s challenge from a philosophical perspective, by engaging in the bold project of cleaning up the area and taming the “notoriously polymorphic and polysemantic” [2], although increasingly pervasive, notion of information. This ambitious program has been carried out to a considerable extent in a series of papers and, above all, in his main work on this subject, The Philosophy of Information [4].The word “information” has been given many different meanings by various writers in the field of information theory. It is likely that at least a number of these will prove sufficiently useful in certain applications to deserve further study and permanent recognition. It is hardly to be expected that a single concept of information would satisfactorily account for the numerous possible applications of this general field [3].
2. The Received View
2.1. Logical Empiricism and the Trivialization of Logic
According to the logical empiricists, the truths of logic and mathematics are necessary and do not depend on experience. Given their rejection of any synthetic a priori knowledge, this position could be justified only by claiming that logical and mathematical statements are “analytic”, i.e., true “by virtue of language”. More explicitly, they thought their truth can be recognized, at least in principle, by means only of the meaning of the words that occur in them. Since information cannot be increased independent of experience, such analytic statements must also be “tautological”, i.e., carry no information content. Hence:In such a way logical analysis overcomes not only metaphysics in the proper, classical sense of the word, especially scholastic metaphysics and that of the systems of German idealism, but also the hidden metaphysics of Kantian and modern apriorism. The scientific world-conception knows no unconditionally valid knowledge derived from pure reason, no “synthetic judgments a priori” of the kind that lie at the basis of Kantian epistemology and even more of all pre- and post-Kantian ontology and metaphysics. [...] It is precisely in the rejection of the possibility of synthetic knowledge a priori that the basic thesis of modern empiricism lies. The scientific world-conception knows only empirical statements about things of all kinds, and analytic statements of logic and mathematics [10] (p. 308).
This view of deductive reasoning as informationally void is usually supported by resorting to elementary examples, as in this well-known passage by Hempel:The conception of mathematics as tautological in character, which is based on the investigations of Russell and Wittgenstein, is also held by the Vienna Circle. It is to be noted that this conception is opposed not only to apriorism and intuitionism, but also to the older empiricism (for instance of J.S. Mill), which tried to derive mathematics and logic in an experimental-inductive manner as it were [10] (p. 311).
Despite its highly counterintuitive implications—at least in the ordinary sense of the word “information”, it is hard to accept that all the mathematician’s efforts never go “one iota” beyond the information that was already contained in the axioms of a mathematical theory—this view of deductive reasoning caught on and became part of the logical folklore. Most of its philosophical appeal probably lies in the fact that it appears to offer the strongest possible justification of deductive practice: logical deduction provides an infallible means of transmitting truth from the premises to the conclusion for the simple reason that the conclusion adds nothing to the information that was already contained in the premises. However, as Michael Dummett put it:It is typical of any purely logical deduction that the conclusion to which it leads simply re-asserts (a proper or improper) part of what has already been stated in the premises. Thus, to illustrate this point by a very elementary example, from the premise “This figure is a right triangle”, we can deduce the conclusion, “This figure is a triangle”; but this conclusion clearly reiterates part of the information already contained in the premise. [...] The same situation prevails in all other cases of logical deduction; and we may, therefore, say that logical deduction—which is the one and only method of mathematical proof—is a technique of conceptual analysis: it discloses what assertions are concealed in a given set of premises, and it makes us realize to what we committed ourselves in accepting those premises; but none of the results obtained by this technique ever goes by one iota beyond the information already contained in the initial assumptions [11] (p. 9).
Indeed—as we shall argue in Section 3—this trivialization of logic is a philosophical overkill: a definitive foundation for deductive practice is obtained at the price of its informativeness. Logic lies on a bedrock of platitude.Once the justification of deductive inference is perceived as philosophically problematic at all, the temptation to which most philosophers succumb is to offer too strong a justification: to say, for instance, that when we recognize the premises of a valid inference as true, we have thereby already recognized the truth of the conclusion [12] (p. 195).
2.2. Quine on Logical Truth
Yes so, on this score I think of the truths of logic as analytic in the traditional sense of the word, that is to say true by virtue of the meaning of the words. Or as I would prefer to put it: they are learned or can be learned in the process of learning to use the words themselves, and involve nothing more [17] (p. 199). (Quoted in [18].)
2.3. Semantic Information
By way of contrast, they put forward a Theory of Semantic Information, in which “the contents of symbols” were “decisively involved in the definition of the basic concepts” and “an application of these concepts and of the theorems concerning them to fields involving semantics thereby warranted” [20] (p. 148). The basic idea is simple and can be briefly explained as follows.The Mathematical Theory of Communication, often referred to also as “Theory of (Transmission of) Information”, as practised nowadays, is not interested in the content of the symbols whose information it measures. The measures, as defined, for instance, by Shannon, have nothing to do with what these symbols symbolise, but only with the frequency of their occurrence. [...] This deliberate restriction of the scope of the Statistical Communication Theory was of great heuristic value and enabled this theory to reach important results in a short time. Unfortunately, however, it often turned out that impatient scientists in various fields applied the terminology and the theorems of Communication Theory to fields in which the term “information” was used, presystematically, in a semantic sense, that is, one involving contents or designata of symbols, or even in a pragmatic sense, that is, one involving the users of these symbols [20].
The amount of positive information about the world which is conveyed by a scientific statement is the greater the more likely it is to clash, because of its logical character, with possible singular statements. (Not for nothing do we call the laws of nature “laws”: the more they prohibit the more they say.) [21] (p. 19).[...]It might then be said, further, that if the class of potential falsifiers of one theory is “larger” than that of another, there will be more opportunities for the first theory to be refuted by experience; thus compared with the second theory, the first theory may be said to be “falsifiable in a higher degree”. This also means that the first theory says more about the world of experience than the second theory, for it rules out a larger class of basic statements. [...] Thus it can be said that the amount of empirical information conveyed by a theory, or its empirical content, increases with its degree of falsifiability [21] (p. 96).
3. The Anomalies of the Received View
3.1. The Bar-Hillel-Carnap Paradox
Popper had also realized that his closely related notion of empirical content worked reasonably well only for consistent theories, since all basic statements are potential falsifiers of all inconsistent theories, which would therefore, without this requirement, turn out to be the most scientific of all. So, for him, “the requirement of consistency plays a special role among the various requirements which a theoretical system, or an axiomatic system, must satisfy” and “can be regarded as the first of the requirements to be satisfied by every theoretical system, be it empirical or non-empirical” [21] (p. 72). So, “whilst tautologies, purely existential statements and other nonfalsifiable statements assert, as it were, too little about the class of possible basic statements, self-contradictory statements assert too much. From a self-contradictory statement, any statement whatsoever can be validly deduced” [21] (p. 71). In fact, what Popper claimed was that the information content of inconsistent theories is null, and so his definition of empirical information content as monotonically related to the set of potential falsifiers was intended only for consistent ones:It might perhaps, at first, seem strange that a self-contradictory sentence, hence one which no ideal receiver would accept, is regarded as carrying with it the most inclusive information. It should, however, be emphasized that semantic information is here not meant as implying truth. A false sentence which happens to say much is thereby highly informative in our sense. Whether the information it carries is true or false, scientifically valuable or not, and so forth, does not concern us. A self-contradictory sentence asserts too much; it is too informative to be true [22] (p. 229).
But the importance of the requirement of consistency will be appreciated if one realizes that a self-contradictory system is uninformative. It is so because any conclusion we please can be derived from it. Thus no statement is singled out, either as incompatible or as derivable, since all are derivable. A consistent system, on the other hand, divides the set of all possible statements into two: those which it contradicts and those with which it is compatible. (Among the latter are the conclusions which can be derived from it.) This is why consistency is the most general requirement for a system, whether empirical or non-empirical, if it is to be of any use at all [21] (p. 72).
3.2. The Scandal of Deduction
If in an inference the conclusion is not contained in the premises, it cannot be valid; and if the conclusion is not different from the premises, it is useless; but the conclusion cannot be contained in the premises and also possess novelty; hence inferences cannot be both valid and useful [23] (p. 173).
The standard answer to this question has a strong psychologistic flavour. According to Hempel: “a mathematical theorem, such as the Pythagorean theorem in geometry, asserts nothing that is objectively or theoretically new as compared with the postulates from which it is derived, although its content may well be psychologically new in the sense that we were not aware of its being implicitly contained in the postulates” ([11] (p. 9), Hempel’s emphasis.) This implies that there is no objective (non-psychological) sense in which deductive inference yield new information. Hintikka’s reaction to this typical neopositivistic way out of the paradox is worth quoting in full:C.D. Broad has called the unsolved problems concerning induction a scandal of philosophy. It seems to me that in addition to this scandal of induction there is an equally disquieting scandal of deduction. Its urgency can be brought home to each of us by any clever freshman who asks, upon being told that deductive reasoning is “tautological” or “analytical” and that logical truths have no “empirical content” and cannot be used to make “factual assertions”: in what other sense, then, does deductive reasoning give us new information? Is it not perfectly obvious there is some such sense, for what point would there otherwise be to logic and mathematics? [5] (p. 222).
If no objective, non-psychological increase of information takes place in deduction, all that is involved is merely psychological conditioning, some sort of intellectual psychoanalysis, calculated to bring us to see better and without inhibitions what objectively speaking is already before your eyes. Now most philosophers have not taken to the idea that philosophical activity is a species of brainwashing. They are scarcely any more favourably disposed towards the much more far-fetched idea that all the multifarious activities of a contemporary logician or mathematician that hinge on deductive inference are as many therapeutic exercises calculated to ease the psychological blocks and mental cramps that initially prevented us from being, in the words of one of these candid positivists, “aware of all that we implicitly asserted” already in the premises of the deductive inference in question [5] (pp. 222-223).
3.3. Wittgenstein and the “Perfect Notation”
In accordance with Wittgenstein’s idea, one could specify a procedure that translates sentences into a “perfect notation” that fully brings out the information they convey, for instance by computing the whole truth-table for the conditional that represents the inference. Such a table displays all the relevant possible worlds and allows one to distinguish immediately those that make a sentence true from those that make it false, the latter representing (collectively) the “semantic information” carried by the sentence. Once the translation has been performed, logical consequence can be recognized by “mere inspection”.When the truth of one proposition follows from the truth of others, we can see this from the structure of the propositions. (Tractatus, 5.13)In a suitable notation we can in fact recognize the formal properties of propositions by mere inspection of the propositions themselves. (6.122).Every tautology itself shows that it is a tautology. (6.127(b))
3.4. Hintikka on the Scandal of Deduction
Hintikka’s positive proposal consists in distinguishing between two objective and non-psychological notions of information content: “surface information”, which may be increased by deductive reasoning, and “depth information” (equivalent to Bar-Hillel and Carnap’s “semantic information”), which may not. While the latter justifies the traditional claim that logical reasoning is tautological, the former vindicates the intuition underlying the opposite claim. In his view, first-order deductive reasoning may increase surface information, although it never increases depth information (the increase being related to deductive steps that introduce new individuals). Without going into details (for a criticism of Hintikka’s approach see [25]), we observe here that Hintikka’s proposal classifies as non-analytic only some inferences of the non-monadic predicate calculus and leaves the “scandal of deduction” unsettled in the domain of propositional logic:[. . . ] measures of information which are not effectively calculable are well-nigh absurd. What realistic use can there be for measures of information which are such that we in principle cannot always know (and cannot have a method of finding out) how much information we possess? One of the purposes the concept of information is calculated to serve is surely to enable us to review what we know (have information about) and what we do not know. Such a review is in principle impossible, however, if our measures of information are non-recursive [5] (p. 228).
Hence, in Hintikka’s view, for every finite set of Boolean sentences Γ and every Boolean sentence φ,The truths of propositional logic are [...] tautologies, they do not carry any new information. Similarly, it is easily seen that in the logically valid inferences of propositional logic the information carried by the conclusion is smaller or at most equal to the information carried by the premises. The term “tautology” thus characterizes very aptly the truths and inferences of propositional logic. One reason for its one-time appeal to philosophers was undoubtedly its success in this limited area” ([5] (p. 154)).

3.5. The Problem of Logical Omniscience
4. Floridi on the Received View
4.1. Floridi on the BCP
4.2. Floridi on the Scandal of Deduction
Accordingly, in his The logic of being informed [34] Floridi chooses to downplay the related “problem of logical omniscience”, there renamed as the problem of “information overload”. He argues that the notion of “being informed” can be adequately captured by a normal modal logic, that he calls Information Logic (IL)—where Da is renamed Ia and the sentence Iaφ is interpreted as “the agent a is informed (holds the information) that φ”—and that K can be safely taken as an axiom of this logic. However, as already observed in Section 3.5, if combined with the “inevitable inclusion of the rule of necessitation” [34] (p. 18), that is N, the axiom K implies (2), namely, that “being informed” is preserved under logical entailment. So, endorsing K and N, under this interpretation of Ia, implies that logical truths and logical deductions are utterly uninformative: whenever ψ ├ φ, any agent who is informed (holds the information) that ψ must also be informed (hold the information) that φ. This is tantamount to saying that logic is informationally trivial and that the information an agent obtains from the conclusion of a deductive argument, no matter how complex, is already included in the information she obtains from the premises. So the problem of information overload (aka. “logical omniscience”) and the scandal of deduction are two sides of the same coin.[...] indeed, according to MTI [Mathematical Theory of Information], TWSI [Theory of Weakly Semantic Information] and TSSI [Theory of Strongly Semantic Information], tautologies are not informative. This seems both reasonable and unquestionable. If you wish to know what the time is, and you are told that “it is either 5pm or it is not” then the message you have received provides you with no information [8] (p. 169).
In the context of the problems discussed in this paper, the first condition is the crucial one: if the metaphor of the “ideal agent” is to be useful at all, we need to associate it with a theory of how the actual logical behaviour of real agents approximates the theoretical behaviour of idealized agents. It does not seem, however, that this condition can be met by IL, at least in its current formulation.A logic is an idealization of certain sorts of real-life phenomena. By their very nature, idealizations misdescribe the behaviour of actual agents. This is to be tolerated when two conditions are met. One is that the actual behaviour of actual agents can defensibly be made out to approximate to the behaviour of the ideal agents of the logician’s idealization. The other is the idealization’s facilitation of the logician’s discovery and demonstration of deep laws [36] (p. 158).
- By the Inverse Relationship Principle, “information goes hand in hand with unpredictability” [34] (p. 19); since every tautology has probability 1, if φ is a tautology, then φ is completely uninformative.
- Hence, an agent’s information cannot be increased by receiving the (empty) information that φ.
- This situation is indistinguishable from the one in which the agent actually holds the (empty) information that φ. In other words:
So, we can consider “a holds the information that φ” as synonymous with “a’s information is not increased by receiving the information that φ”.If you ask me when the train leaves and I tell you that either it does or it does not leave at 10:30 am, you have not been informed, although one may indifferently express this by saying that what I said was uninformative in itself or that (it was so because) you already were informed that the train did or did not leave at 10:30 am anyway [34] (p. 19). - Hence, we can assume that, for every tautology φ, a holds the information that φ.
It may be objected that, if P ≠ NP , there will always be infinitely many tautologies that the agent a is = not able to recognize within feasible time. More precisely, there will be infinite classes of tautologies that all the procedures available to a are not able to recognize in time bounded above by a polynomial in the size of the input. In practice, this means that, no matter how large a’s computational resources are, there will always be tautologies in one of these classes that go far beyond them. Floridi’s argument seems to assume that even if φ is one of such tautologies that are “hard” for a, φ should be regarded as uninformative for a, although a has no feasible means of recognizing φ as a tautology. However, under these circumstances, a has no feasible means to distinguish this situation from an analogous situation in which φ is not a tautology and so a’s information has actually been increased from learning that φ. Following Floridi’s line of argument, we should therefore say that, whenever φ is a tautology, a always holds, in some “objective” sense, the information that φ, although this situation is not practically distinguishable from a situation in which φ is not a tautology and a does not hold the information that φ. A similar problem arises, perhaps even more strikingly, when a valid inference of φ from Γ is “hard” for the agent a. Again, the conditional probability P (φ | Γ) is equal to 1 and so φ adds nothing to the information carried by Γ. However, it may make a lot of practical difference for a to actually hold the information that φ indeed follows from Γ, and this may significantly affect his decisions and his overall behaviour.It turns out that the apparent difficulty of information overload can be defused by interpreting ├ φ ⟹ ├ Iφ as an abbreviation forwhich does not mean that a is actually informed about all theorems provable in PC [Propositional Calculus] as well as in KTB-IL [Information Logic]—as if a contained a gigantic database with a lookup table of all such theorems—but that, much more intuitively, any theorem φ provable in PC or in KTB-IL (indeed, any φ that is true in all possible worlds) is uninformative for a [34] (p. 19).├ φ ⟹ P (φ)=1 ⟹ Inf (φ)= 0 ⟹ ├ Iφ
Given the obvious interplay between meaning-theories—in our context theories on the meaning of the logical operators—and theories of semantic information, the above requirement is, at the same time, a requirement on the relevant notion of semantic information and on the meaning-theories that may be sensibly associated with this notion. One may well maintain, as we do, that it makes perfectly good sense to regard a sentence as uninformative for an agent a if it follows “analytically”, i.e., by virtue only of the meaning of the logical operators, from the information that a actually holds. But, in the light of the Strong Manifestability Requirement (SMR), this meaning cannot be their classical meaning and the residual notion of semantic information cannot be any of the current ones, because both the standard way of fixing the meaning of the classical logical operators and the corresponding notion(s) of semantic information do not satisfy SMR. So, SMR constrains both the way in which the meaning of the logical operators is fixed and the way in which the notion of semantic information is characterized.Strong Manifestability. If an agent a grasps the meaning of a sentence φ, then a should be able to tell, in practice and not only in principle, whether or not (s)he holds the information that φ is true, or the information that φ is false or neither of them.
5. A Kantian View?
5.1. Informational Semantics
Here by saying that a actually holds the information that φ is true (respectively false) we mean that a possesses a feasible procedure to obtain this information.Informational semantics. The meaning of an n-ary logical operator * is determined by specifying the necessary and sufficient conditions for an agent a to actually hold the information that a sentence of the form *(φ1,...,φn) is true, respectively false, in terms of the information that a actually holds about the truth or falsity of φ1,...,φn.
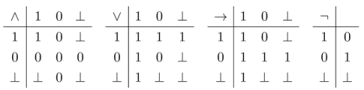 |
- we actually hold the information that ψ∨φ is true if and only if we actually hold the information that ψ is true or we actually hold the information that φ is true;
- we actually hold the information that ψ∧φ is false if and only if we actually hold the information that ψ is false or we actually hold the information that φ is false.
5.2. Informational Meaning and Surface Semantic Information
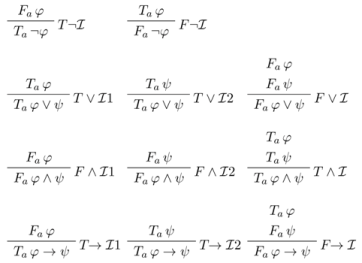 |
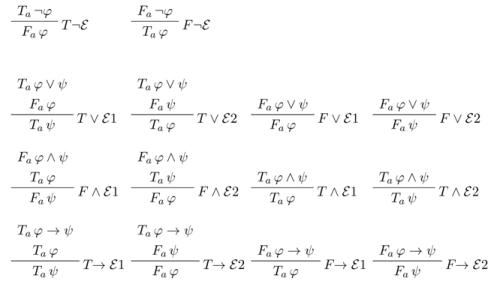 |
- for no sentence φ, Tφ and Fφ are both in X;
- if Sψ (where S is either T or F ) follows from the signed sentences in X by a chain of applications of the basic intelim rules, then Sψ also belongs to X.
Let us say that a set Γ of sentences is analytically inconsistent if there is a sequence of applications of the intelim rules that leads from {Tψ | ψ∈ Γ} to both Tφ and Fφ for some sentence φ. It follows from the definition of information state that if Γ is analytically inconsistent, {Tψ | ψ∈ Γ} a cannot be included in any information state.[This principle] is a universal but purely negative criterion of all truth. But it belongs to logic alone, because it is valid of all cognitions, merely as cognitions and without respect to their content, and declares that the contradiction entirely nullifies them [37].
 P is equal either to the top element ⊤, if Pu is empty, or to ∩Pu otherwise. However, the top element of this complete lattice, namely the set ⊤ of all signed sentences, is not an information state.
P is equal either to the top element ⊤, if Pu is empty, or to ∩Pu otherwise. However, the top element of this complete lattice, namely the set ⊤ of all signed sentences, is not an information state.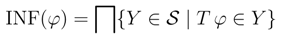
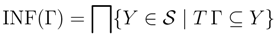
Unlike hidden classical inconsistencies, which may be hard to discover even for agents equipped with powerful (but still bounded) computational resources, analytic inconsistency rests, as it were, on the surface and can be feasibly detected. So, we always have a feasible means to establish that our premises are analytically consistent and for consistent premises the consequence relation ├ is not explosive, even if these premises are classically inconsistent.Obviously, once a contradiction has been discovered, no one is going to go through it: to exploit it to show that the train leaves at 11:52 or that the next Pope will be a woman [12] (p. 209).
5.3. Actual vs. Virtual Information
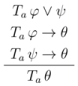

One could say, by analogy, that analytical inferences are those that are recognized as sound via steps that are all “explicative”, that is, descending immediately from the meaning of the logical operators, as given by the necessary and sufficient conditions expressed by the elimination and introduction rules, while synthetic ones are those that are “augmentative”, involving some intuition that goes beyond this meaning, i.e., involving the consideration of virtual information. So, we could paraphrase Kant and say that an inference is analytic only if it adds in the conclusion nothing to the information contained in the premises, but only analyses it in its constituent pieces of information, which were “thought already in the premises, although in a confused manner”. The confusion vanishes once the meaning of the logical operators is properly explicated.Analytical judgements (affirmative) are therefore those in which the connection of the predicate with the subject is cogitated through identity; those in which this connection is cogitated without identity, are called synthetical judgements. The former may be called explicative, the latter augmentative judgements; because the former add in the predicate nothing to the conception of the subject, but only analyse it into its constituent conceptions, which were thought already in the subject, although in a confused manner; the latter add to our conceptions of the subject a predicate which was not contained in it, and which no analysis could ever have discovered therein.[...]In an analytical judgement I do not go beyond the given conception, in order to arrive at some decision respecting it. [...] But in synthetical judgements, I must go beyond the given conception, in order to cogitate, in relation with it, something quite different from what was cogitated in it [...] [37].

6. Conclusions
Acknowledgements
References
- D’Agostino, M.; Floridi, L. The enduring scandal of deduction. Is propositionally logic really uninformative? Synthese 2009, 167, 271–315. [Google Scholar] [CrossRef]
- Floridi, L. Semantic Conceptions of Information. Stanford Enciclopedya of Philosophy, 2011. Available online: http://plato.stanford.edu/entries/information-semantic/ (accessed on 26 December 2012).
- Shannon, C. Abstract to “The Lattice Theory of Information". In Claude Elwood Shannon: Collected Papers; Sloane, N., Wyner, A., Society, I.I.T., Eds.; IEEE Press: New York, NY, USA, 1993; p. 180. [Google Scholar]
- Floridi, L. The Philosophy of Information; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Hintikka, J. Logic, Language Games and Information. Kantian Themes in the Philosophy of Logic; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Floridi, L. Outline of a Theory of Strongly Semantic Information. Mind. Mach. 2004, 14, 197–222. [Google Scholar] [CrossRef]
- Floridi, L. Is Information Meaningful Data? Philos. Phenomen. Res. 2005, 70, 351–370. [Google Scholar] [CrossRef]
- Floridi, L. The Philosophy of Information; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Tennant, N. Natural Logic; Edinburgh University Press: Edimburgh, UK, 1990. [Google Scholar]
- Hahn, H.; Neurath, O.; Carnap, R. The scientific conception of the world [1929]. In Empiricism and Sociology; Neurath, M., Cohen, R., Eds.; Reidel: Dordrecht, The Netherlands, 1973. [Google Scholar]
- Hempel, C. Geometry and Empirical Science. Am. Math. Mon. 1945, 52, 7–17. [Google Scholar] [CrossRef]
- Dummett, M. The Logical Basis of Metaphysics; Duckworth: London, UK, 1991. [Google Scholar]
- Quine, W. Two dogmas of empiricism. In From a Logical Point of View; Harvard University Press: Cambridge, MA, USA, 1961; pp. 20–46. [Google Scholar]
- Davidson, D. On the very idea of a conceptual scheme. Proc. Address. Am. Philos. Assoc. 1974, 47, 5–20. [Google Scholar] [CrossRef]
- Quine, W. Two dogmas in retrospect. Can. J. Philos. 1991, 21, 265–274. [Google Scholar]
- Quine, W. The Roots of Reference; Open Court: LaSalle, IL, USA, 1973. [Google Scholar]
- Bergstr¨om, L.; Føllesdag, D. Interview with Willard van OrmanQuine, November 1993. Theoria 1994, 60, 193–206. [Google Scholar]
- Decock, L. True by virtue of meaning. Carnap and Quine on the analytic-synthetic distinction. 2006. Available online: http://vu-nl.academia.edu/LievenDecock/Papers/866728/Carnap_and_Quine_on_some_analytic-synthetic_distinctions (accessed on 27 December 2012).
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Bar-Hillel, Y.; Carnap, R. Semantic Information. Br. J. Philos. Sci. 1953, 4, 147–157. [Google Scholar]
- Popper, K. The Logic of Scientific Discovery; Hutchinson: London, UK, 1959. [Google Scholar]
- Carnap, R.; Bar-Hillel, Y. An Outline of a Theory of Semantic Information. In Language and Information; Bar-Hillel, Y., Ed.; Addison-Wesley: London, UK, 1953; pp. 221–274. [Google Scholar]
- Cohen, M.; Nagel, E. An Introduction to Logic and Scientific Method; Routledge and Kegan Paul: London, UK, 1934. [Google Scholar]
- Carapezza, M.; D’Agostino, M. Logic and the myth of the perfect language. Log. Philos. Sci. 2010, 8, 1–29. [Google Scholar]
- Sequoiah-Grayson, S. The Scandal of Deduction. Hintikka on the Information Yield of Deductive Inferences. J. Philos. Log. 2008, 37, 67–94. [Google Scholar] [CrossRef]
- Cook, S.A. The complexity of theorem-proving procedures. In STOC ’71: Proceedings of the Third Annual ACM Symposium on Theory of Computing; ACM Press: New York, NY, USA, 1971; pp. 151–158. [Google Scholar]
- Finger, M.; Reis, P. On the predictability of classical propositional logic. Information 2013, 4, 60–74. [Google Scholar]
- Primiero, G. Information and Knowledge. A Constructive Type-Theoretical Approach; Springer: Berlin, Germany, 2008. [Google Scholar]
- Sillari, G. Quantified Logic of Awareness and Impossible Possible Worlds. Rev. Symb. Log. 2008, 1, 1–16. [Google Scholar]
- Duží, M. The Paradox of Inference and the Non-Triviality of Analytic Information. J. Philos. Log. 2010, 39, 473–510. [Google Scholar] [CrossRef]
- Jago, M. The content of deduction. J. Philos. Log. 2013, in press.. [Google Scholar]
- Halpern, J.Y. Reasoning About Knowledge: A Survey. In Handbook of Logic in Artificial Intelligence and Logic Programming; Gabbay, D.M., Hogger, C.J., Robinson, J., Eds.; Clarendon Press: Oxford, UK, 1995; Volume 4, pp. 1–34. [Google Scholar]
- Meyer, J.J.C. Modal Epistemic and Doxastic Logic. In Handbook of Philosophical Logic, 2nd; Gabbay, D.M., Guenthner, F., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; Volume 10, pp. 1–38. [Google Scholar]
- Floridi, L. The Logic of Being Informed. Logiqueet Analyse 2006, 49, 433–460. [Google Scholar]
- Primiero, G. An epistemic logic for being informed. Synthese 2009, 167, 363–389. [Google Scholar] [CrossRef]
- Gabbay, D.M.; Woods, J. The New Logic. Log. J. IGPL 2001, 9, 141–174. [Google Scholar] [CrossRef]
- Kant, I. Critique of Pure Reason [1781], Book II, Chapter II, Section I. Available online: http://ebooks.adelaide.edu.au/k/kant/immanuel/k16p/index.html (accessed on 27 December 2012).
- D’Agostino, M. Analytic inference and the informational meaning of the logical operators. Logiqueet Analyse 2013, in press.. [Google Scholar]
- D’Agostino, M. Classical Natural Deduction. In We Will Show Them! Artëmov, S.N., Barringer, H., d’Avila Garcez, A.S., Lamb, L.C., Woods, J., Eds.; College Publications: London, UK, 2005; pp. 429–468. [Google Scholar]
- D’Agostino, M.; Finger, M.; Gabbay, D.M. Semantics and proof theory of depth-bounded Boolean logics. Theor. Comput. Sci. 2013, in press.. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
D'Agostino, M. Semantic Information and the Trivialization of Logic: Floridi on the Scandal of Deduction. Information 2013, 4, 33-59. https://doi.org/10.3390/info4010033
D'Agostino M. Semantic Information and the Trivialization of Logic: Floridi on the Scandal of Deduction. Information. 2013; 4(1):33-59. https://doi.org/10.3390/info4010033
Chicago/Turabian StyleD'Agostino, Marcello. 2013. "Semantic Information and the Trivialization of Logic: Floridi on the Scandal of Deduction" Information 4, no. 1: 33-59. https://doi.org/10.3390/info4010033
APA StyleD'Agostino, M. (2013). Semantic Information and the Trivialization of Logic: Floridi on the Scandal of Deduction. Information, 4(1), 33-59. https://doi.org/10.3390/info4010033




