FedRazor: Two-Stage Federated Unlearning via Representation Divergence and Gradient Conflict Trimming

Abstract

Federated unlearning removes a client’s influence from a trained federated model without full retraining, which is required by data deletion regulations but remains difficult due to gradient coupling and recovery instability. Existing methods often rely on historical training records or suffer from severe utility degradation and model reverting after recovery. We propose FedRazor, a two-stage federated unlearning framework that achieves stable client-level unlearning through representation divergence and gradient direction control. In Stage I, FedRazor weakens dependence on forgotten data using two complementary objectives. A Divergence-Smoothing Loss reduces prediction confidence on forgotten labels, while a Feature Mean Divergence loss pushes forgotten representations away from the retained feature center. To protect retained performance, we introduce PCGrad Razor, which trims gradient components that conflict with retained gradients during aggregation. This stage produces an intermediate unlearned model without storing historical updates. In Stage II, FedRazor restores retained utility using directional gradient trimming. Gradients aligned with the unlearning displacement direction are removed, preventing forgotten information from re-entering the model during recovery. Experiments on MNIST, CIFAR-10, and CIFAR-100 under IID and non-IID settings show that FedRazor consistently reduces attack success rate to near zero while preserving retained accuracy. On CIFAR-10 Pat-50, FedRazor achieves ASR = 0.026 with retained accuracy 0.659 after post-training, outperforming strong baselines in stability and unlearning robustness.

1. Introduction

Federated learning (FL) enables distributed training without sharing raw data [1]. It is used in mobile systems, healthcare, and finance [2,3]. In FL, each client trains locally and uploads updates to a server. The server aggregates updates to form a global model [4]. This design reduces data exposure, but it does not remove what the model has learned.

Privacy laws create a concrete requirement for data removal. GDPR and CCPA grant the right to be forgotten (RTBF) [5,6]. In centralized learning, a common solution is data deletion and retraining [7]. FL makes this solution costly and unclear. Client contributions are coupled in the global model [1,8]. So, simple deletion cannot guarantee forgetting. Federated unlearning (FU) targets RTBF in FL. FU removes a client’s influence without full retraining [9]. The main question is direct. How can we forget one client and keep the model useful?

Prior FU methods face limits in scale and stability. FedEraser stores and validates historical updates to remove a client [10]. This design needs heavy storage and verification cost [9,11]. Other methods reduce this reliance in different ways. FedAU approximates forgetting using auxiliary models [12]. SCMA requires each client to compute a new local vector for unlearning [13]. FedKDU uses knowledge distillation to rebuild a model without raw data [14]. FedRecovery stores gradients and rolls them back during unlearning [15].

Two challenges block practical FU. First, many methods still need large historical records. This increases storage and compute cost. It hurts deployment at scale [9,11]. Second, unlearning can harm retained clients. Gradients from the target client may conflict with retained gradients [16]. The update then damages key parameters for retained tasks. This causes utility drop or even catastrophic forgetting [17].

We propose FedRazor, a two-stage FU framework. FedRazor aims to forget efficiently without storing long histories. Stage I drives representation divergence for the target client. We add a Divergent Smoothing Loss (DSL) at the output layer. DSL reduces confidence on target labels. We also add a Feature Mean Divergence (FMD) loss at the feature layer. FMD pushes target features away from the retained global feature center. This weakens target prediction while keeping retained representations stable. We then apply PCGrad Razor. It removes gradient components that conflict with retained clients. This yields smooth unlearning without historical logs. Stage II prevents forgotten knowledge from coming back. We map the retained-client gradients with directional trimming. We remove the component aligned with the unlearning direction. The final update becomes orthogonal to the unlearning trajectory. This recovers utility while blocking revert toward the original model. FedRazor therefore balances forgetting strength and training stability. It also reduces storage and compute overhead.

Our contributions are as follows.

• We introduce DSL and FMD for the target client. They suppress target predictions while keeping representations consistent. We also propose PCGrad Razor to remove gradient conflicts. This enables efficient and smooth federated unlearning.
• We propose a gradient direction mapping mechanism. It trims retained-client gradients to be orthogonal to the unlearning direction. This prevents forgotten knowledge from reappearing during later training.
• We evaluate FedRazor across datasets and unlearning settings. Results show that FedRazor improves unlearning efficiency and stability. It also reduces storage and compute cost versus strong FU baselines.

2. Related Work

2.1. Centralized Machine Unlearning

Centralized machine unlearning is a specific implementation of machine unlearning. It removes identified samples and their contributions from a trained model [18]. These methods are designed for centralized training with a single global model [19]. They aim to approximate the performance of full retraining with lower computational cost [20]. Recent studies focus on efficient approximate unlearning in complex scenarios [21]. They propose influence estimation strategies to identify the contribution of target data [22,23,24,25,26]. Other approaches apply local intervention strategies or higher-order information for multi-class unlearning [27,28]. These methods significantly improve unlearning efficiency.

Despite these advances, most centralized unlearning methods require full access to all training data. They do not consider data heterogeneity or access constraints in federated environments [29]. This limitation breaks unlearning methods that rely on a single training trajectory [30]. As a result, unlearning may fail or degrade global model performance. Therefore, centralized unlearning methods are insufficient for federated settings. Federated unlearning methods are required to meet unlearning demands under distributed constraints.

2.2. Federated Unlearning

Federated unlearning differs from centralized machine unlearning. It supports class-level, sample-level, and client-level unlearning [31]. The goal is to remove the contribution of specific clients from the global model under access constraints [32]. Existing methods can be divided into parameter intervention and local model reconstruction. Parameter intervention methods directly modify model parameters. Sparse adapter-based strategies regulate client contributions through adapter design [33,34]. Incremental update strategies remove target influence through reverse or compensatory updates without full retraining [10,15,35,36]. Active unlearning strategies weaken model dependence on target data or clients through objective optimization [37,38,39].

Local model reconstruction methods construct temporary local models or perform partial retraining [40,41].They aim to forget target data or clients through localized model updates. Although these methods improve unlearning efficiency, they have limitations. They cannot guarantee complete unlearning or global model stability. They also suffer from the risk of knowledge reintroduction.

Moreover, recent studies have focused on verifiable and auditable federated unlearning, including unlearning certification, formal evaluation metrics, and robustness against post-unlearning attacks [9,42,43]. These works provide the foundations for trustworthy unlearning. They develop verifiable unlearning mechanisms, measure unlearning effectiveness, and improve models’ resilience to attacks after unlearning [44,45,46]. This highlights the significance of the FedRazor framework, which removes the influence of target clients through a two-stage process at the representation level. It preserves model stability and can be integrated with verifiable unlearning and formal evaluation frameworks.

3. Methods

This section presents the proposed federated unlearning method FedRazor. The method consists of two stages. The first stage performs representation-level unlearning on all clients. The second stage restores performance using only retained clients while constraining gradient directions. We first define the problem and notation. We then describe the FedRazor architecture and its components. Finally, we present full pseudo-code so that the method is reproducible from the main text.

3.1. Problem Formulation

Let $\mathcal{C}=\{1,2,\dots ,N\}$ denote the set of all clients. Each client $i\in \mathcal{C}$ holds a local dataset ${\mathcal{D}}_i$. Let $\mathcal{U}\subset \mathcal{C}$ be the set of forgotten clients that request unlearning, and let $\mathcal{R}=\mathcal{C}\setminus \mathcal{U}$ be the set of retained clients. The retained data is ${\mathcal{D}}_R={\bigcup }_{i\in \mathcal{R}}{\mathcal{D}}_i.$ This notation separates forgotten and retained data at the client level.

The global model has parameters $\theta \in {\mathbb{R}}^d$. The initial parameters before training are ${\theta }_0\in {\mathbb{R}}^d$. Given an input–label pair $(x,y)$, the model outputs class probabilities $p_{\theta }(y\mid x)$ over K classes. The model also produces an intermediate feature representation $f_{\theta }\left(x\right)\in {\mathbb{R}}^m$. We use the L2-normalized feature

$${\widehat{f}}_{\theta }\left(x\right)={\displaystyle \frac{f_{\theta }\left(x\right)}{\parallel f_{\theta }{\left(x\right)\parallel }_2}}.$$

(1)

Equation (1) defines the normalized feature used later in the representation-level unlearning loss.

Let $\mathcal{l}(·,·)$ denote a standard supervised loss, for example cross-entropy. Let ${\theta }^{-U}$ denote the ideal parameters obtained by retraining from scratch on ${\mathcal{D}}_R$ without any data from $\mathcal{U}$. Let $D(\theta ,{\theta }^{-U})$ be a divergence measure between models, and let $ϵ>0$ be an allowed unlearning tolerance. FedRazor aims to maintain performance on retained data while making the final model close to ${\theta }^{-U}$

$$\underset{\theta }{min}{\mathbb{E}}_{(x,y)\in {\mathcal{D}}_R}\mathcal{l}(p_{\theta }\left(x\right),y)\mathrm{s}.\mathrm{t}.D(\theta ,{\theta }^{-U})\le ϵ.$$

(2)

Equation (2) states the federated unlearning objective: the model should behave as if it had never seen data from the forgotten clients, while keeping accuracy on retained data.

Directly computing ${\theta }^{-U}$ is expensive in federated settings. FedRazor therefore uses a two-stage procedure that approximates the constraint in Equation (2) through representation divergence and gradient direction control.

3.2. FedRazor Architecture

Figure 1 summarizes FedRazor as a two-stage pipeline triggered by an unlearning request. In Stage I, the global model is updated using both forgotten and retained clients. Forgotten clients optimize a representation objective and upload gradients containing the information to be removed. The server then applies PCGrad Razor to eliminate gradient components that conflict with updates from retained clients, while the retained clients provide feature statistics to maintain a stable center feature $\mu$, resulting in an intermediate unlearned model ${\theta }_U$.

Stage II refines the model using retained clients only. The server computes the displacement direction $h={\theta }_U-{\theta }_0$ from the pre-unlearning model. Each retained client trims its gradient component aligned with h before aggregation. The server aggregates the trimmed gradients to obtain the final model ${\theta }^{★}$. This stage improves retained accuracy while preventing forgotten knowledge from re-entering the model.

3.2.1. Stage I: Representation-Level Unlearning

Stage I takes the current global parameters $\theta$ as input and returns an intermediate model ${\theta }_U$ after unlearning. This stage has three components. The Divergence-Smoothing Loss (DSL) reduces the model’s confidence on forgotten labels at the output layer. The Feature Mean Divergence (FMD) forces forgotten features to move away from a global retained feature center. The PCGrad Razor trims gradient conflicts between forgotten and retained clients on the server. Together, these components weaken dependence on forgotten data in both output and representation spaces while limiting damage to retained performance.

The total loss for forgotten data in Stage I is

$${\mathcal{L}}_U={\mathcal{L}}_{\mathrm{dsl}}+\lambda {\mathcal{L}}_{\mathrm{fmd}},$$

(3)

where $\lambda >0$ is a trade-off hyperparameter. Equation (3) defines the Stage I objective as a combination of output-level and feature-level unlearning losses.

Divergence-Smoothing Loss (DSL).

For any forgotten example $(x,y)\in {\mathcal{D}}_U$, we define the output-level loss

$${\mathcal{L}}_{\mathrm{dsl}}=-log\left(1-{\displaystyle \frac{p_{\theta }(y\mid x)}{2}}\right).$$

(4)

Equation (4) defines DSL, which penalizes high confidence on the original label. When the model still memorizes the example, $p_{\theta }(y\mid x)\approx 1$, the term $1-p_{\theta }(y\mid x)/2$ approaches $0.5$, and the loss is large. When the model has forgotten the example, $p_{\theta }(y\mid x)\approx 1/K$, and the loss becomes small.

The role of DSL is to act in the output probability space. Unlike entropy maximization that increases uncertainty or adversarial label flipping that changes labels. FedRazor uses client gradients to reduce confidence on forgotten labels, maintaining training stability and preventing forgotten information from being recovered.

Feature Mean Divergence (FMD).

Stage I also introduces a representation-level loss based on a global feature mean. Only retained clients contribute to the feature statistics. On a given communication round, the server collects normalized features ${\widehat{f}}_i$ from retained clients and computes the round-wise mean:

$${\mu }_t={\displaystyle \frac{1}{N_t}}\sum _i{\widehat{f}}_i,$$

(5)

where $N_t$ is the number of features aggregated in that round. Equation (5) defines the instantaneous feature mean over retained clients for one round.

To smooth fluctuations across rounds, the server maintains an exponential moving average (EMA) of the global feature mean:

$$\mu \leftarrow (1-\alpha )\mu +\alpha {\mu }_t,$$

(6)

where $\alpha \in (0,1]$ is the EMA coefficient. Equation (6) updates the global feature center by interpolating between the previous center and the current round statistics.

For a forgotten sample x, with normalized feature ${\widehat{f}}_{\theta }\left(x\right)$ and normalized mean $\widehat{\mu }=\mu /{\parallel \mu \parallel }_2$, the feature divergence loss is

$${\mathcal{L}}_{\mathrm{fmd}}={\displaystyle \frac{1}{m}}{∥{\widehat{f}}_{\theta }\left(x\right)-\widehat{\mu }∥}_2^2.$$

(7)

Equation (7) defines FMD as the squared Euclidean distance between the forgotten feature and the retained feature center, normalized by the feature dimension m.

The role of FMD is to operate in the representation space. It separates forgotten samples from retained data to reduce the chance that subsequent training reconstructs similar representations. This applies only to forgotten clients and leverages the retained clients’ feature center with PCGrad Razor to effectively limit unintended drift on retained data.

PCGrad Razor for Gradient Conflict Trimming.

In each communication round, the server aggregates gradients from all clients. Let $g_u\in {\mathbb{R}}^d$ denote the average gradient over forgotten clients, and let $g_r\in {\mathbb{R}}^d$ denote a gradient from a retained client. The average forgotten gradient is

$$g={\displaystyle \frac{1}{\left|\mathcal{U}\right|}}\sum _{u\in \mathcal{U}}{g}_u.$$

(8)

Equation (8) defines the mean forgotten gradient across unlearning clients.

If $\langle g,g_r\rangle <0$, the forgotten and retained gradients point in conflicting directions. In this case, the PCGrad Razor modifies the forgotten gradient as

$$g\leftarrow g-{\lambda }_u{\displaystyle \frac{\langle g,g_r\rangle }{\parallel g_r{\parallel }_2^2}}{g}_r,$$

(9)

where ${\lambda }_u>0$ is a trimming coefficient. Equation (9) removes the component of g that conflicts with $g_r$.

The role of the PCGrad Razor is to operate in gradient space. It separates the unlearning update and the retained update by trimming conflicting components. This reduces the degradation of retained performance caused by aggressive unlearning updates.

After several rounds of Stage I with DSL, FMD, and PCGrad Razor, the server obtains the intermediate parameters ${\theta }_U$. At this point, the model exhibits lower confidence on forgotten examples, forgotten representations have moved away from the retained feature center, and performance on retained data remains acceptable.

3.2.2. Stage II: Directional Gradient Trimming

Stage II runs only on retained clients. It takes ${\theta }_U$ as input and produces the final model ${\theta }^{★}$ as output. The goal is to restore accuracy on retained data while preventing the optimization from moving back along the direction that encoded forgotten information during Stage I.

To capture the overall direction of the unlearning trajectory, we define the model displacement relative to the initialization:

$$h=\theta -{\theta }_0.$$

(10)

Equation (10) defines the displacement vector $h\in {\mathbb{R}}^d$, which represents how far and in which direction the current model has moved from the initial parameters. Stage I tends to move the model along directions that remove forgotten information, so h summarizes these directions.

In each round of Stage II, each retained client computes a local gradient g using a standard supervised loss on its retained data. Before aggregation, the server applies directional trimming to each gradient:

$$g\leftarrow g-{\lambda }_p{\displaystyle \frac{\langle g,h\rangle }{{\parallel h\parallel }_2^2}}h\mathrm{if}{\displaystyle \frac{\langle g,h\rangle }{\parallel g\parallel \parallel h\parallel }}>{\tau }_p,$$

(11)

where ${\lambda }_p>0$ is a trimming strength and ${\tau }_p\in [-1,1]$ is a cosine similarity threshold. Equation (11) removes the component of g that is too aligned with the displacement direction h when the cosine similarity exceeds ${\tau }_p$.

The role of directional gradient trimming is to restrict Stage II updates to be mostly orthogonal to the Stage I unlearning direction. This prevents the recovery process from walking back along the path that would reintroduce forgotten information. Instead, the model is encouraged to improve performance using new directions supported only by retained data.

After trimming, the server averages the gradients and performs a standard update:

$$\theta \leftarrow \theta -\eta g,$$

(12)

where $\eta >0$ is the learning rate and g is the mean trimmed gradient over retained clients. Equation (12) defines the Stage II parameter update under directional constraints. After several rounds, this process yields the final model ${\theta }^{★}$, which maintains unlearning while improving accuracy on retained data.

3.3. Full FedRazor Algorithm and Pseudo-Code

This subsection presents the complete FedRazor algorithm. It describes all server–client interactions and how each module is instantiated in practice. The inputs are the client set $\mathcal{C}$, the forgotten client set $\mathcal{U}$, the retained set $\mathcal{R}=\mathcal{C}\setminus \mathcal{U}$, the initial parameters ${\theta }_0$, the number of communication rounds $T_U$ in Stage I and $T_R$ in Stage II, the learning rates ${\eta }_U$ and ${\eta }_R$, the loss weights $\lambda$, ${\lambda }_u$, ${\lambda }_p$, and the EMA coefficient $\alpha$. The output is the final model ${\theta }^{★}$. The helper routine TrainOnClient runs local training on a client and returns its average gradient and, when needed, feature statistics.

Algorithm 1 summarizes the two-stage procedure. The first part of the algorithm corresponds to Stage I and uses DSL, FMD, and the PCGrad Razor, as defined in Equations (4), (7) and (9). The second part corresponds to Stage II and uses the displacement direction and directional gradient trimming defined in Equations (10) and (11).

Algorithm 1: FedRazor two-stage federated unlearning

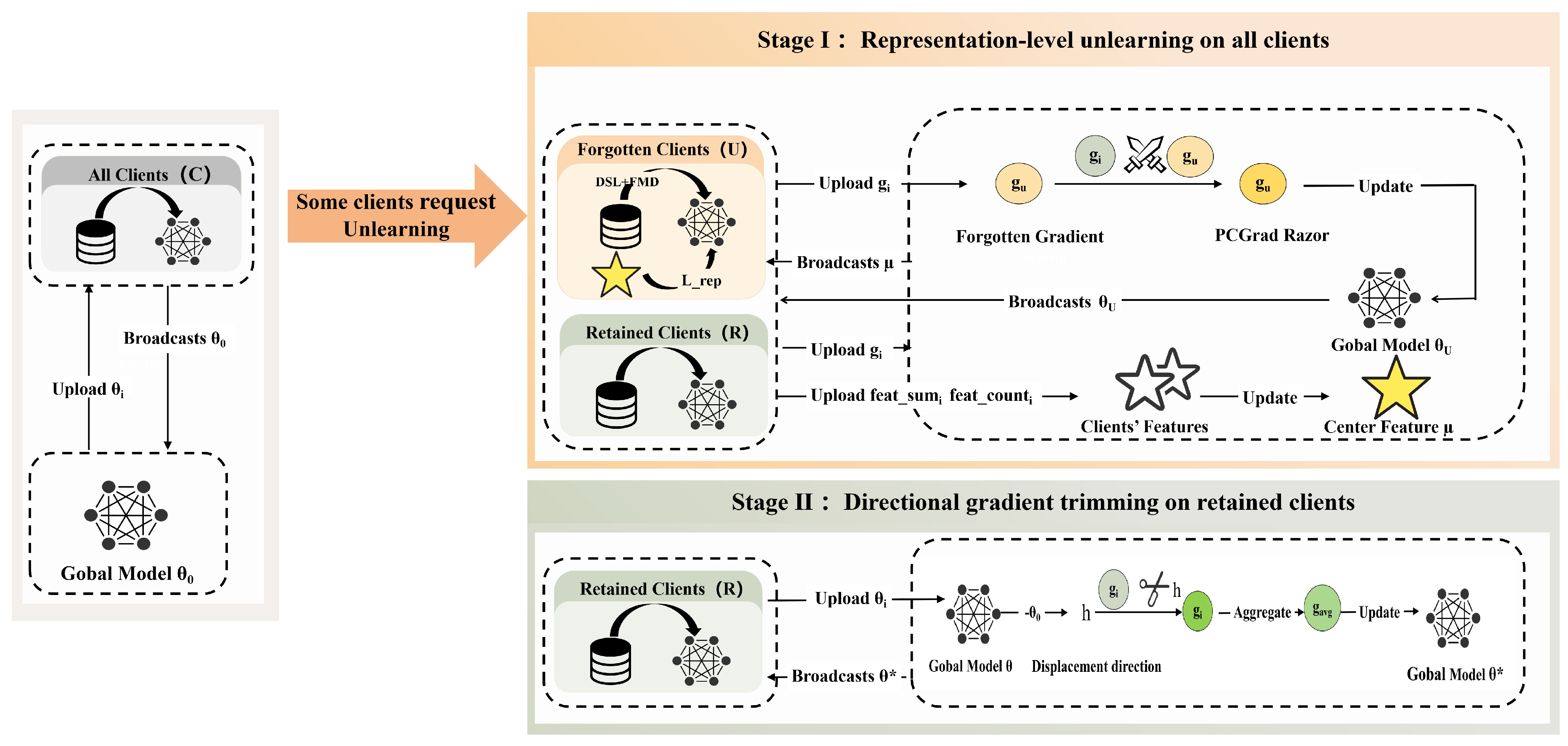
4. Experimental Setup

This section evaluates FedRazor on standard image classification benchmarks under federated unlearning scenarios. We first describe the experimental setup, including datasets, models, federated learning configuration, metrics, baselines, ablation design, and implementation details. Subsequent subsections present quantitative and qualitative results based on this setup.

4.1. Datasets

We use three widely adopted image classification datasets. This choice covers simple and complex label spaces and both grayscale and color images.

First, we use MNIST [47], which is a ten-class handwritten digits dataset. Each image has resolution $28\times 28$ and a single grayscale channel. The dataset contains $60,000$ training images and $10,000$ test images. MNIST provides a simple benchmark to study basic unlearning behavior.

Second, we use CIFAR-10 [48], which is a ten-class natural image dataset. Each image has resolution $32\times 32$ and three color channels. The dataset has $50,000$ training images and $10,000$ test images. CIFAR-10 introduces more diverse content and background, which is useful to test robustness of unlearning under realistic conditions.

Third, we use CIFAR-100 [48], which is a hundred-class natural image dataset. Each image also has resolution $32\times 32$ with three channels. The dataset has $50,000$ training images and $10,000$ test images. CIFAR-100 has a much larger label space, which makes both backdoor injection and unlearning more challenging.

We simulate different client data heterogeneity levels by partitioning each dataset into client shards. We denote by N the total number of clients and by $N_C$ the number of distinct classes assigned to each client. We use four partition patterns.

In the Pat-10 setting, each client holds only $10\%$ of the total classes. For MNIST and CIFAR-10, this corresponds to $N_C=1$. For CIFAR-100, this corresponds to $N_C=10$. This pattern creates highly non-IID data.

In the Pat-20 setting, each client holds $20\%$ of the total classes. For MNIST and CIFAR-10, this corresponds to $N_C=2$. For CIFAR-100, this corresponds to $N_C=20$. This pattern remains non-IID but less extreme.

In the Pat-50 setting, each client holds $50\%$ of the total classes. For MNIST and CIFAR-10, this corresponds to $N_C=5$. For CIFAR-100, this corresponds to $N_C=50$. This pattern approximates a moderate heterogeneity level.

In the IID setting, each client can observe all classes. For MNIST and CIFAR-10, this corresponds to $N_C=10$. For CIFAR-100, this corresponds to $N_C=100$. For all patterns, we use balanced partitioning, that is, each client receives approximately the same number of samples. This balanced design avoids degenerate cases where one client dominates the training signal.

4.2. Model Architectures

We choose one model per dataset that is standard and well understood. This allows us to focus on the unlearning behavior rather than on architectural novelty.

For MNIST, we use LeNet-5 [47]. This is a classical convolutional network with two convolutional layers followed by two fully connected layers. LeNet-5 is sufficient to reach near-saturated accuracy on MNIST and has a simple structure that facilitates interpretation.

For CIFAR-10, we use a CNN_CIFAR10 model. This is a small convolutional neural network tailored to $32\times 32$ color images. It uses several convolutional and pooling layers followed by fully connected layers. The model has enough capacity to capture the diversity in CIFAR-10 while remaining efficient in the federated setting.

For CIFAR-100, we use NFResNet-18 [49], a Normalizer-Free ResNet-18 variant introduced by Brock. NFResNet-18 removes normalizers and uses carefully scaled residual connections. It achieves strong accuracy on CIFAR-100 and represents a modern architecture for more complex benchmarks.

In all models, we treat the penultimate layer as the feature extractor. The output of this layer corresponds to $f_{\theta }\left(x\right)$ in Equation (1) and is used in the Feature Mean Divergence loss.

4.3. Federated Learning and Backdoor Setup

We adopt a unified federated learning configuration across all datasets to isolate the effect of unlearning. We denote by N the total number of clients, by B the local batch size, by C the client participation ratio, and by E the number of local epochs per round.

We set the total number of clients to $N=10$. We randomly select one client as the forgotten client. Thus the number of forgotten clients is $\text{unlearn\_cn} = 1$, and this client belongs to $\mathcal{U}$. The other nine clients belong to $\mathcal{R}$. We use a local batch size of $B=200$ on all clients. We set the client participation ratio to $C=1.0$, which means all clients participate in every communication round. We set the number of local epochs per round to $E=1$. All local training uses batch gradient descent, that is, each batch is processed exactly once per local epoch. We fix the random seed to 1 for all experiments to ensure reproducibility.

We separate training into a pre-training phase and an unlearning phase.

In the pre-training phase, we use FedAvg as the federated optimization algorithm. We denote by R the number of communication rounds in this phase and set $R=2000$. The server learning rate in pre-training is $\mathrm{lr}=0.05$. We apply an exponential learning rate decay with decay factor $0.999$ per round. The goal of this phase is to train an initial global model that has converged on the federated data distribution.

We inject a backdoor only on the forgotten client during pre-training. Specifically, we apply a trigger pattern to a fraction of the forgotten client’s training data and relabel these samples to a fixed target class. The attack ratio on the forgotten client is $80\%$, meaning $80\%$ of its local training samples contain the backdoor trigger. This simulates a strong client-side poisoning attack. Other clients in $\mathcal{R}$ do not contain any backdoor triggers.

In the unlearning phase, we start from the converged model of the pre-training phase and apply FedRazor or baselines. We denote by $U_R$ the total number of rounds in the unlearning phase. We set $U_R=200$ and split these rounds into two equal parts. The first 100 rounds correspond to the unlearning stage (Stage I in Section 3.2.1). The last 100 rounds correspond to the post-training stage (Stage II in Section 3.2.2).

In Stage I of FedRazor, we use an unlearning learning rate $\mathrm{lr}=4\times {10}^{-4}$ at the server. This learning rate controls the strength of the DSL and FMD updates. In Stage II, we use a smaller learning rate $\text{r\_lr} = {10}^{-6}$, which allows fine-grained performance recovery under directional trimming. We keep the same learning rate decay factor $0.999$ across the unlearning phase. The goal of this phase is to remove the influence of the forgotten client’s data while preserving or restoring performance for retained clients.

All baselines use the same pre-training and client-side settings. We only change the unlearning strategy.

4.4. Evaluation Metrics

We evaluate each method from three perspectives: unlearning effectiveness, retained performance, and efficiency. We denote by ASR the attack success rate and by ${\mathrm{Acc}}_R$ the retained accuracy.

Following common practice in federated unlearning and backdoor removal studies [14,16], we evaluate unlearning effectiveness using Attack Success Rate (ASR). ASR measures how often the model predicts the target backdoor label when presented with backdoor-triggered inputs. Concretely, we construct a backdoor test set by applying the trigger pattern to the test images and setting the label to the target class. We then compute the classification accuracy of the forgotten client’s backdoor classifier on this triggered test set. This accuracy is reported as ASR. A lower ASR indicates better unlearning performance. Ideally, ASR should approach zero.

For retained performance, we use Retained Client Local Test Accuracy. For each retained client $i\in \mathcal{R}$, we evaluate the final global model on the client’s clean local test set and obtain an accuracy ${\mathrm{Acc}}_i$. We then compute the mean retained accuracy

$${\mathrm{Acc}}_R={\displaystyle \frac{1}{\left|\mathcal{R}\right|}}\sum _{i\in \mathcal{R}}{\mathrm{Acc}}_i.$$

This expression defines the average test accuracy over retained clients. A higher ${\mathrm{Acc}}_R$ indicates that the unlearning process has preserved task performance on clean data.

For efficiency, we measure communication time and computation time. Communication time is the wall-clock time spent on sending and receiving model parameters and gradients between the server and clients during the unlearning phase. Computation time is the wall-clock time spent on local training and server-side processing during the same phase. These metrics allow us to compare the practical overhead of FedRazor against baselines.

For all metrics, we run each configuration with 5 independent random seeds. We report the mean and standard deviation across these runs. When space allows, we also report approximate $95\%$ confidence intervals assuming normality. This practice reflects the variability of federated training dynamics.

4.5. Baselines

We compare FedRazor with a representative set of existing federated unlearning and backdoor removal methods. The baseline set is denoted by $\mathcal{B}$. All methods share the same pre-training procedure and backdoor injection setup; differences only arise in the unlearning stage.

FedEraser [10] is a retraining-based federated unlearning method that approximates data removal by reusing historical checkpoints and partial retraining. It is a widely adopted baseline for client-level unlearning due to its conceptual simplicity and relatively moderate overhead. We include FedEraser as it serves as a canonical reference for retraining-based unlearning in federated settings.

FedRecovery [15] represents recovery-based unlearning approaches that reconstruct an unlearned model by leveraging historical training information and retained gradients. Compared with full retraining, FedRecovery can significantly reduce computational cost while maintaining reasonable model utility. We select this method as it reflects a recent line of work on replay- and recovery-based federated unlearning.

MoDe [35] is a momentum-degradation-based federated unlearning method that attenuates the influence of forgotten data by modifying the optimization dynamics. MoDe has also been evaluated in backdoor-related unlearning scenarios, making it a relevant baseline for assessing the effectiveness of FedRazor in removing malicious behaviors.

In extended experiments, we additionally consider EWCSGA [14] and FUPGA [8], which are gradient-ascent-based unlearning methods with different regularization or projection mechanisms to control model degradation. Although these methods are not always optimal across all metrics, they represent alternative unlearning paradigms based on gradient manipulation.

Overall, the baseline set $\mathcal{B}$ spans multiple unlearning paradigms, including retraining-based, recovery-based, optimization-dynamics-based, and gradient-based methods. This diversity allows for a comprehensive and fair evaluation of FedRazor under different unlearning philosophies.

All baselines are tuned according to their original papers or public implementations. We ensure that each baseline operates under a comparable computational budget to FedRazor, including the number of unlearning rounds and local training epochs.

4.6. Implementation Details

We implement all methods in Python using PyTorch as the deep learning framework. We set the PyTorch version to 2.0 and the Python version to 3.10. We simulate clients on a single machine using separate processes. All experiments run on a server with an 8-core CPU, 64 GB of RAM, and a single NVIDIA RTX 3090 GPU with 24 GB of memory. We use CUDA for GPU acceleration and fix all library-level random seeds for reproducibility.

For FedRazor, we set the Stage I unlearning learning rate to $\mathrm{lr}=4\times {10}^{-4}$ and the Stage II learning rate to $\text{r\_lr} = {10}^{-6}$ as described in Section 4.3. We set the EMA coefficient in Equation (6) to $\alpha =0.1$. We tune the loss weight $\lambda$ in Equation (3), the trimming coefficient ${\lambda }_u$ in Equation (9), and the directional trimming coefficient ${\lambda }_p$ in Equation (11) on a validation subset.

5. Results

5.1. Main Comparison on CIFAR-10 Under Pat-50

We first report the main comparison on CIFAR-10 under the Pat-50 setting with N = 10 clients and 1 forgotten client, following the standard federated unlearning protocol described in Section 3.1 We evaluate (i) unlearning effectiveness using attack success rate (ASR, lower is better) and (ii) retained utility using mean retained accuracy (R-Acc, higher is better), as defined in Section 4.4.

Table 1. CIFAR-10 (Pat-50, $N=10$): ASR and mean R-Acc (std.) after the unlearning stage (U) and after post-training (P). For methods without an explicit post-training phase, we report their final values in both columns (marked by †) to keep a consistent table layout. “r” indicates ASR increase due to model reverting as reported in the baseline source.

Method	After Unlearning (U)		After Post-Training (P)
	ASR↓	R-Acc↑	ASR↓	R-Acc↑
Retraining †	0.009	0.583 (0.149)	0.009	0.583 (0.149)
FedEraser †	0.026	0.571 (0.128)	0.026	0.571 (0.128)
FedRecovery	0.102	0.476 (0.346)	0.598r	0.643 (0.138)
MoDe	0.066	0.199 (0.119)	0.035	0.582 (0.173)
EWCSGA	0.000	0.381 (0.426)	0.592r	0.652 (0.118)
FUPGA	0.000	0.388 (0.433)	0.602r	0.658 (0.091)
FedRazor (Ours)	0.014	0.652 (0.017)	0.026	0.659 (0.016)

compares the model status after the unlearning stage (round 100) and after the post-training stage (round 200). Several baselines (FedRecovery, EWCSGA, and FUPGA) exhibit a clear model reverting behavior: their ASR values increase sharply after post-training (marked by “r” in the original report), even though R-Acc can be recovered. In contrast, FedRazor maintains a low ASR after post-training while preserving (and slightly improving) R-Acc, indicating that the second-stage directional trimming successfully prevents the recovery process from moving back toward the forgotten direction.

• Quantitative analysis.

On CIFAR-10 Pat-50, FedRazor achieves a strong utility–unlearning trade-off. After unlearning, FedRazor reaches ASR = 0.014 while retaining R-Acc = 0.652, which is substantially higher than utility-degrading baselines such as MoDe (0.199) and comparable to the best utility among the compared methods. More importantly, during post-training, FedRazor avoids the reverting issue: its ASR remains low (0.026), whereas FedRecovery/EWCSGA/FUPGA suffer large ASR rebounds (0.598/0.592/0.602 with “r”). This supports the design motivation of Stage II: recovery should be constrained to prevent re-introducing forgotten information.

• Qualitative interpretation.

The observed “reverting” in several baselines suggests that naive recovery on retained clients can steer the model back toward the pre-unlearning solution manifold. FedRazor mitigates this by restricting recovery updates that are overly aligned with the Stage I unlearning displacement direction, allowing utility recovery without re-learning the forgotten backdoor behavior.

5.2. Cross-Dataset Comparison Under Pat-20 (MNIST and CIFAR-100)

To assess robustness across different label-space complexities,

Table 2. Pat-20 comparison on MNIST and CIFAR-100: ASR and mean R-Acc.

Dataset	Method	ASR ↓	R-Acc ↑
MNIST (Pat-20)	FedRecovery	0.038	0.716
	MoDe	0.039	0.723
	EWCSGA	0.000	0.527
	FUPGA	0.000	0.535
	FedRazor (Ours)	0.001	0.912 (0.046)
CIFAR-100 (Pat-20)	FedRecovery	0.000	0.214
	MoDe	0.027	0.160
	EWCSGA	0.000	0.093
	FUPGA	0.000	0.090
	FedRazor (Ours)	0.002	0.315 (0.040)

shows that the comparison of methods on MNIST and CIFAR-100 under Pat-20.

• Quantitative analysis.

FedRazor consistently improves retained utility under Pat-20 while maintaining near-zero ASR. On MNIST, FedRazor reaches R-Acc = 0.912 with ASR = 0.001, which is a large utility improvement compared with EWCSGA/FUPGA while preserving the unlearning effect. On CIFAR-100, FedRazor obtains R-Acc = 0.315 at ASR = 0.002, outperforming all compared baselines in retained utility, highlighting the benefit of combining representation divergence (Stage I) with constrained recovery (Stage II) on a harder 100-class benchmark.

5.3. FedRazor Stage-Wise Results Under Different Heterogeneity Levels

Finally, we report a complete stage-wise evaluation of FedRazor across IID/Pat-10/Pat-20/Pat-50 on MNIST, CIFAR-10, and CIFAR-100. These results allow us to inspect how the two-stage design behaves under increasing heterogeneity.

Table 3. FedRazor on MNIST: stage-wise ASR and R-Acc (std) under IID/Pat-10/Pat-20/Pat-50.

Stage	Metric	IID	Pat-10	Pat-20	Pat-50
Pre-train (${\omega }_0$)	ASR ↓	0.803	0.987	0.996	0.999
	R-Acc ↑	0.983 (0.003)	0.952 (0.021)	0.967 (0.014)	0.978 (0.007)
Stage I (Unlearning)	ASR ↓	0.007	0.001	0.001	0.003
	R-Acc ↑	0.985 (0.004)	0.899 (0.062)	0.912 (0.046)	0.949 (0.033)
Stage II (Post-train)	ASR ↓	0.007	0.001	0.003	0.016
	R-Acc ↑	0.986 (0.004)	0.941 (0.024)	0.951 (0.012)	0.974 (0.008)

,

Table 4. FedRazor on CIFAR-10: stage-wise ASR and R-Acc (std) under IID/Pat-10/Pat-20/Pat-50.

Stage	Metric	IID	Pat-10	Pat-20	Pat-50
Pre-train (${\omega }_0$)	ASR ↓	0.435	0.676	0.953	0.842
	R-Acc ↑	0.737 (0.022)	0.468 (0.116)	0.598 (0.124)	0.658 (0.011)
Stage I (Unlearning)	ASR ↓	0.044	0.001	0.002	0.014
	R-Acc ↑	0.747 (0.021)	0.452 (0.107)	0.585 (0.128)	0.652 (0.017)
Stage II (Post-train)	ASR ↓	0.044	0.004	0.018	0.026
	R-Acc ↑	0.747 (0.020)	0.463 (0.101)	0.598 (0.112)	0.659 (0.016)

and

Table 5. FedRazor on CIFAR-100: stage-wise ASR and R-Acc (std) under IID/Pat-10/Pat-20/Pat-50.

Stage	Metric	IID	Pat-10	Pat-20	Pat-50
Pre-train (${\omega }_0$)	ASR ↓	0.103	0.266	0.169	0.124
	R-Acc ↑	0.407 (0.015)	0.299 (0.038)	0.336 (0.042)	0.380 (0.016)
Stage I (Unlearning)	ASR ↓	0.006	0.000	0.002	0.006
	R-Acc ↑	0.410 (0.014)	0.284 (0.059)	0.315 (0.040)	0.376 (0.045)
Stage II (Post-train)	ASR ↓	0.006	0.010	0.003	0.010
	R-Acc ↑	0.409 (0.014)	0.298 (0.028)	0.343 (0.029)	0.396 (0.014)

summarize the pre-training model, the intermediate unlearned model after Stage I, and the final model after Stage II.

In addition, we evaluate FedRazor in a multi-client unlearning scenario.

Table 6. FedRazor on MNIST: stage-wise ASR and retained accuracy for single-client and two-client unlearning under IID/Pat-10.

Unlearning Setting	Stage	Metric	IID	Pat-10
Single Client	Pre-train (${\omega }_0$)	ASR ↓	0.803	0.987
		R-Acc ↑	0.983 (0.003)	0.952 (0.021)
	Stage I (Unlearning)	ASR ↓	0.007	0.001
		R-Acc ↑	0.985 (0.004)	0.899 (0.062)
	Stage II (Post-train)	ASR ↓	0.007	0.001
		R-Acc ↑	0.986 (0.004)	0.941 (0.024)
Two Clients	Pre-train (${\omega }_0$)	ASR ↓	0.803	0.987
		R-Acc ↑	0.983 (0.003)	0.952 (0.021)
	Stage I (Unlearning)	ASR ↓	0.007	0.008
		R-Acc ↑	0.985 (0.004)	0.909 (0.039)
	Stage II (Post-train)	ASR ↓	0.009	0.011
		R-Acc ↑	0.986 (0.005)	0.930 (0.029)

shows a stage-wise comparison of single-client and two-client unlearning on the MNIST dataset. The results show that FedRazor maintains stable unlearning performance and model utility in the multi-client unlearning scenario.

• Stage-wise observations.

Across datasets, Stage I sharply suppresses ASR from high pre-training values to near-zero levels, confirming effective backdoor unlearning. Stage II generally improves or preserves R-Acc while keeping ASR low, indicating that constrained recovery can regain utility without re-learning forgotten behavior. The benefit of Stage II is most visible in non-IID settings where naive recovery is prone to reverting; here, FedRazor maintains low ASR with stable R-Acc.

5.4. Ablation Study

FedRazor consists of two key components in our final ablation design: (i) GradRazor, which trims harmful/forgetting-aligned gradients to stabilize forgetting and recovery; (ii) CombProj, a combination projection mechanism that constrains update directions to mitigate conflicts. To quantify their contributions and interactions, we remove one component at a time and also remove both jointly. We report the final model performance after Stage II (post-training), using ASR (lower is better) and retained accuracy R-Acc (higher is better). We also study FedRazor’s sensitivity to key hyperparameters to assess robustness.

• Main ablation results.

Table 7. Ablation on Pat-20: final ASR and R-Acc after Stage II.

Dataset	Variant	ASR ↓	R-Acc ↑
MNIST	Full (Ours)	0.003	0.951
	w/o CombProj	0.003	0.951
	w/o GradRazor	0.017	0.917
	w/o GradRazor + CombProj	0.603	0.950
CIFAR-10	Full (Ours)	0.018	0.598
	w/o CombProj	0.019	0.599
	w/o GradRazor	0.116	0.536
	w/o GradRazor + CombProj	0.649	0.599
CIFAR-100	Full (Ours)	0.003	0.343
	w/o CombProj	0.004	0.345
	w/o GradRazor	0.018	0.337
	w/o GradRazor + CombProj	0.035	0.349

and

Table 8. Ablation on Pat-50: final ASR and R-Acc after Stage II.

Dataset	Variant	ASR ↓	R-Acc ↑
MNIST	Full (Ours)	0.016	0.974
	w/o CombProj	0.017	0.974
	w/o GradRazor	0.154	0.957
	w/o GradRazor + CombProj	0.862	0.972
CIFAR-10	Full (Ours)	0.026	0.659
	w/o CombProj	0.029	0.659
	w/o GradRazor	0.040	0.648
	w/o GradRazor + CombProj	0.315	0.671
CIFAR-100	Full (Ours)	0.010	0.396
	w/o CombProj	0.010	0.397
	w/o GradRazor	0.009	0.379
	w/o GradRazor + CombProj	0.019	0.398

summarize the ablation results under Pat-20 and Pat-50 across MNIST, CIFAR-10, and CIFAR-100. Full denotes FedRazor with both components enabled.

Table 9. Performance comparison across hyperparameter settings.

Hyperparameter	Value	ASR ↓	R-Acc ↑
${\alpha }_{ema}$	0.05	0.001	0.941 (0.024)
	0.1	0.001	0.941 (0.024)
	0.2	0.001	0.941 (0.024)
${\lambda }_{proj}$	0.5	0.001	0.941 (0.024)
	1.0	0.001	0.941 (0.024)
	1.5	0.001	0.941 (0.024)
${\lambda }_{unlearn}$	0.5	0.007	0.927 (0.050)
	1.0	0.001	0.941 (0.024)
	1.5	0.001	0.933 (0.033)

reports the performance of the Full FedRazor under different hyperparameter settings.

• Quantitative findings.

(1) GradRazor is the most critical component. Removing GradRazor consistently increases ASR and often reduces retained utility, especially under non-IID settings. For example, on MNIST Pat-50, ASR rises from 0.016 (Full) to 0.154 (w/o GradRazor); on CIFAR-10 Pat-20, ASR increases from 0.018 to 0.116. In many cases, R-Acc also drops when GradRazor is removed (e.g., MNIST Pat-20: 0.951 → 0.917; CIFAR-10 Pat-20: 0.598 → 0.536), indicating that GradRazor benefits both forgetting and utility preservation.

(2) Strong synergy between GradRazor and CombProj. Jointly removing GradRazor and CombProj causes severe forgetting failure in non-IID scenarios: MNIST Pat-20 ASR reaches 0.603, CIFAR-10 Pat-20 reaches 0.649, and MNIST Pat-50 reaches 0.862. These values are dramatically higher than removing GradRazor alone, demonstrating that CombProj is most effective when paired with GradRazor.

(3) CombProj alone yields minor changes but stabilizes the full pipeline. When only CombProj is removed, ASR/R-Acc changes are typically small (e.g., CIFAR-10 Pat-20: ASR 0.018 → 0.019; CIFAR-100 Pat-20: ASR 0.003 → 0.004), suggesting that CombProj is not the primary driver of forgetting by itself, but serves as a stabilizer that amplifies the effect of GradRazor when both are used.

(4) Performance Across Hyperparameter Settings. FedRazor is robust to ${\alpha }_{ema}$ and ${\lambda }_{proj}$, causing only minor changes (e.g., ASR 0.001; R-Acc 0.941), while ${\lambda }_{unlearn}$ is more sensitive: low values reduce forgetting, moderate values stabilize it (e.g., ASR 0.001 → 0.007; R-Acc 0.941 → 0.933), showing that proper tuning of ${\lambda }_{unlearn}$ can improve forgetting without harming retained performance.

• Qualitative interpretation.

Overall, the ablation results support the following mechanism: GradRazor directly controls forgetting stability and prevents re-introduction of forgotten behavior during recovery, while CombProj constrains update directions to reduce harmful interactions and enables GradRazor to operate effectively. Consequently, the full configuration achieves the best balance between low ASR and high R-Acc, particularly under heterogeneous (Pat-20/Pat-50) partitions. Moderate tuning of key hyperparameters can further enhance forgetting without harming retained performance.

5.5. Time Consumption

To evaluate the time cost of FedRazor, we report the communication, gradient upload, PCGrad Razor, and Combined Razor times over selected consecutive rounds, with statistics summarized in

Table 10. Time statistics for communication and razor operations over consecutive rounds (s).

Communication ↓	Gradient Upload ↓	PCGrad Razor ↓	Combined Razor ↓
581.47	581.26	0.87	0.57
608.72	608.52	0.76	0.59
566.89	566.70	0.77	0.56
559.51	559.31	0.83	0.53
545.49	545.30	0.58	0.57
576.61 (17.73)	576.41 (17.73)	0.80 (0.11)	0.57 (0.02)

.

• Quantitative analysis.

Over consecutive rounds, stage times gradually decrease (e.g., Communication 581.47 → 545.49; Gradient Upload 581.26 → 545.30; PCGrad Razor 0.87 → 0.58). Communication and Gradient Upload take most of the time (e.g., Communication average 576.61; Gradient Upload average 576.41). Razor operate efficiently and stably (e.g., PCGrad Razor average 0.80; Combined Razor average 0.57), indicating that FedRazor achieves high usability while maintaining low time overhead.

• Qualitative interpretation.

Overall, communication and gradient upload are the main time-consuming steps. PCGrad Razor and Combined Razor add minimal overhead and have little effect on total time. The low-cost Razor operations are especially helpful in early high-load stages and improve overall efficiency. Therefore, FedRazor maintains low time consumption while achieving high usability.

6. Limitations

Although FedRazor demonstrates strong performance in experiments, the method still exhibits several limitations.

First, it introduces hyperparameters for loss weighting and gradient clipping that need careful tuning.

Second, FedRazor assumes clients targeted for unlearning can participate during online unlearning. In fully offline scenarios, unlearning relies only on historical models or server information, which may reduce effectiveness.

Third, in long-running or continuously trained federated systems, the initial model ${\theta }_0$ may gradually diverge from the current optimum.

Fourth, FMD assumes retained clients are honest, which may limit reliability in partially trusted or adversarial environments.

Finally, due to experimental constraints, all evaluations were conducted on small visual datasets (MNIST, CIFAR-10, CIFAR-100), and performance on larger models or non-visual tasks remains to be studied.

These limitations point to future work, including offline unlearning, reducing reliance on hyperparameter tuning, and evaluating robustness in heterogeneous or partially trusted environments.

7. Conclusions

This paper presented FedRazor, a two-stage federated unlearning framework designed to remove a client’s influence while maintaining model utility for retained clients. FedRazor addresses two key challenges in federated unlearning: unstable forgetting caused by gradient conflicts and model reverting during post-unlearning recovery.

FedRazor achieves unlearning through a clear separation of roles across stages. The first stage weakens dependence on forgotten data by enforcing divergence in both output space and representation space, while PCGrad Razor mitigates conflicts between forgotten and retained gradients. The second stage focuses on recovery under constraints, trimming gradient components aligned with the unlearning trajectory to prevent reintroduction of forgotten information. Together, these mechanisms approximate retraining-from-scratch behavior without storing historical updates.

Extensive experiments on MNIST, CIFAR-10, and CIFAR-100 show that FedRazor consistently suppresses backdoor attack success rates to near zero while preserving or improving retained accuracy across different data heterogeneity levels. Compared with recovery-based and gradient-based baselines, FedRazor avoids the common reverting phenomenon after post-training and achieves a more stable utility–forgetting trade-off.

Looking forward, FedRazor can be extended to broader scenarios, such as offline clients, sample-level unlearning, larger models, and non-visual tasks, which would further enhance its applicability and impact.